Open Access Article
Open Access ArticleConcentration dependence of As2S3 chalcogenide glass cluster size in amine solution
Nikita S. Dutta and
Craig B. Arnold*
and
Craig B. Arnold*
Department of Mechanical and Aerospace Engineering, Princeton Institute for the Science and Technology of Materials, Princeton University, Princeton, New Jersey 08544, USA. E-mail: cbarnold@princeton.edu
First published on 19th October 2018
Abstract
Solution processing chalcogenide glasses is a common and effective first step in optoelectronic device fabrication. Arsenic(III) sulfide (As2S3) is believed to take on a nanoscale cluster structure in n-propylamine and n-butylamine, which affects the morphology and properties of the deposited material; however, the size of these clusters and the mechanism of size determination are poorly understood. We combine experimental and analytical techniques to investigate As2S3 cluster size in n-propylamine and its dependence on solution concentration. We find that the cluster size increases with concentration and show that this trend is consistent across independent experimental techniques. We then explain these results by proposing a simplified dissolution mechanism and deriving cluster size through a free energy argument. Our findings enable informed control of chalcogenide glass cluster size during solution processing and improved property control in optoelectronic device fabrication.
1 Introduction
Chalcogenide glasses (ChGs) have long been of interest for optoelectronic applications. Their transmission in the mid-infrared (mid-IR) enables waveguides and optical fibers for chemical sensing, thermal imaging, and medicine.1–4 Their high optical nonlinearities and photoinduced phenomenon like photoexpansion, photodarkening, and photocrystallization give rise to applications in optical switching and information storage.5–9 Doping with metallic nanoparticles can be used to enhance these desirable traits.10,11A variety of processing methods are available for ChGs; among these, solution processing is popular for its flexibility.12 The glasses dissolve in organic solvents and can then be doped, spin coated, or even inkjet printed with relative ease.12–15 Previous research has shown numerous successful applications, including molded mid-IR waveguides, drop-cast photonic crystals, and optical fibers with a nonlinearity-enhancing ChG coating.16–19
The pioneering work on ChG solutions was done by Chern et al. using As2S3 in n-propylamine and n-butylamine as test systems.20 Nuclear magnetic resonance showed the presence of an amine salt—evidence of a solvent–solute reaction—while UV absorption remained similar to that of the bulk glass. They hypothesized that As2S3 took on a molecular structure in solution, consisting of nano-sized As2S3 clusters within an amine salt shell. Years later, Kohoutek et al. used results from dynamic light scattering (DLS) to claim that the size of the clusters increased with concentration.21
Cluster size is an important attribute of solutions as ChGs, like many materials, have shown size-dependent optical properties at the nanoscale, and As2S3 solutions are a useful system since they are technologically relevant with a structure mirrored by solutions of other ChGs and even some crystals.22–24 Despite this, the proposed concentration dependence of As2S3 cluster size has not been verified by independent methods and the processes underlying size determination have not been explained. This limits the improvement of ChG solution processing to inefficient reverse engineering.
In this work, we address this gap in knowledge by fully exploring the size of As2S3 clusters in n-propylamine. By combining DLS with viscosity measurements and cryo-transmission electron microscopy (cryo-TEM), we investigate the concentration dependence of cluster size through independent approaches. We then propose a simple dissolution model grounded in basic thermodynamics to explain the observed increasing trend.
2 Experimental
2.1 Materials
As2S3 solutions were prepared by dissolving amorphous As2S3 powder (Alfa Aesar 99.999%) in n-propylamine (Sigma-Aldrich 99.9%) at ten concentrations: 0.01, 0.04, 0.07, 0.1, 0.2, 0.3, 0.4, 0.7, 0.8, and 1.0 moles per liter solvent (mol Lsolv−1). Subsets of these concentrations were used for each kind of measurement, depending on restrictions of the technique. Solutions were prepared in a nitrogen atmosphere glovebox to avoid oxidation and humidity. Each was left for a week to dissolve and passed through a 0.1 μm millipore filter prior to characterization.2.2 Room temperature measurements
Samples for DLS were sealed in an optical glass cuvette with a polytetrafluoroethylene stopper, and measurements were performed using a Malvern Zetasizer Nano with backscatter detector and a 633 nm laser. Approximate measurements of relative kinematic viscosity were performed by timing solutions as they flowed through a segment of a capillary tube and comparing to the time taken by the pure solvent. These values were converted to relative dynamic viscosities using the known density of each solution.2.3 Cryo-electron microscopy
Samples for cryo-TEM were prepared using an FEI Vitrobot. Solution was deposited on a 200 mesh copper grid with a Quantifoil substrate and 1.2 μm holes. The sample was blotted before being plunged into liquid nitrogen. Nitrogen was used in lieu of the normal liquid ethane bath to avoid dissolving the organic solvent, as per Oostergetel et al.25 Micrographs were acquired on a Thermo Scientific Titan Krios G3 with Volta Phase Plate, operated at 300 kV and 165k× magnification.Concentrated solutions blotted poorly in the Vitrobot, while highly dilute solutions showed little to no features during imaging. Thus, the mid-range concentrations 0.2, 0.3, and 0.4 mol Lsolv−1 were used for the cryo-TEM analysis. Distributions of cluster sizes were measured in ImageJ on micrographs taken at similar levels of defocus.26 The z-average size was computed for easier comparison to DLS using the formula:
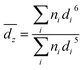 | (1) |
3 Results and discussion
The z-average sizes of As2S3 clusters in n-propylamine determined by DLS are shown in Fig. 1, alongside similar data from Lu et al.13 Data from Kohoutek et al. for As33S67 in n-butylamine is presented as well for qualitative comparison.21 All experiments show a concentration-dependent increase in cluster size with consistent slope, even as we have expanded the range explored in the previous studies.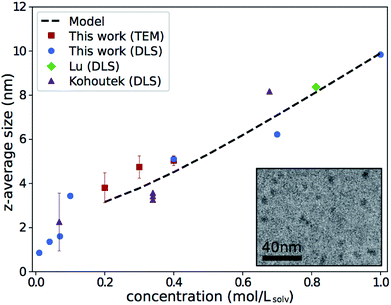 | ||
| Fig. 1 Z-average size of As2S3 clusters in amines. Results from this work, Lu are for As2S3 in n-propylamine; results from Kohoutek are for As33S67 in n-butylamine, and only values acquired with a 632.8 nm laser are shown.13,21 Error bars for this work show the standard deviation of repeat measurements and are often smaller than the marker. Inset shows an example cryo-TEM micrograph of 0.3 mol Lsolv−1 solution. Electron-dense As2S3 clusters appear as dark spots on n-propylamine background. | ||
Interpreting this trend requires that we first consider any experimental artifacts that may affect its validity. In DLS, such artifacts can arise from the fact that the cluster size is not directly measured, but rather is calculated from the measured diffusion coefficient using the Stokes–Einstein equation:
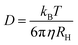 | (2) |
To check if viscosity increases are responsible for the observed trend, the viscosity of the solution relative to that of the pure solvent was measured over a range of concentrations. The data, shown in Fig. 2, is consistent with results from Song.28 While there is a clear viscosity increase with concentration, it is not steep enough to fully explain the trend observed in Fig. 1.
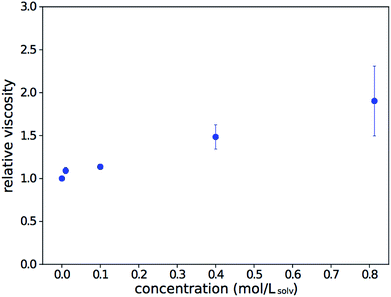 | ||
| Fig. 2 Relative dynamic viscosity of As2S3 solutions in n-propylamine, compared to that of the pure solvent. Error bars show the standard error of repeat measurements. | ||
Size measurements were also taken in cryo-TEM—a direct technique not affected by viscosity changes—as a separate verification in the range of concentrations where it was feasible. An example micrograph is shown in the inset of Fig. 1. Results of the size measurements, shown by the red square markers in Fig. 1, were consistent with DLS. This further establishes that the observed trend is not purely a DLS artifact.
3.1 Dissolution analysis
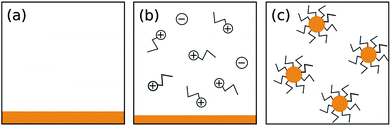
Previous efforts to describe the dissolution of As–S compounds in amines have focused on the mechanism of chemical interaction between the solvent and solute.20,29 While these proposals explain some of the process, they are not sufficient to understand why cluster size should vary for different concentrations of the same composition of glass. Thus, to explain our results, we take a different approach and consider As2S3 cluster formation as a question of thermodynamics.To begin, we propose a simplified dissolution model where the process occurs in two steps: (1) a chemical reaction between n-propylamine solvent and As2S3 solute produces the amine salt detected by Chern et al. and (2) the amine salt and unreacted solute minimize surface energy by forming micelle-like clusters.20 This process is illustrated in Fig. 3 and is highly general, leaving room for the subsequent calculations to be applied to similar systems.
Within this model, the average cluster size at a given concentration must depend on the ratio of amine salt to unreacted As2S3. We can calculate this by considering the governing chemical reaction of the system:12
| As2S3 + 6C3H7NH2 → (C3H7NH3)3AsS3 + (C3H7NH)3As | (3) |
After ξ moles of As2S3 have reacted, the number of moles of a component i is given by:
| ni = ni,0 + νiξ | (4) |
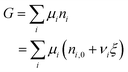 | (5) |
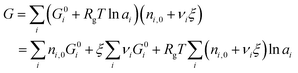 | (6) |
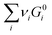 is simply the steady-state free energy of reaction, ΔG0R. This gives the final generalized result:
is simply the steady-state free energy of reaction, ΔG0R. This gives the final generalized result:
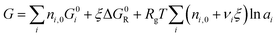 | (7) |
We can now apply eqn (7) to the As2S3 and n-propylamine system. For a solution mixed at concentration c mol Lsolv−1, there are c starting moles of As2S3 (nA,0 = c mol) and approximately 12 starting moles of n-propylamine (nB,0 = 12 mol) that react as described in eqn (3). Inserting this into eqn (7) gives:
G = cG0A + (12 mol)G0B + ξΔG0R + RgT[(c − ξ)ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aA + (12 mol − 6ξ)ln aA + (12 mol − 6ξ)ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aB + ξ(ln aB + ξ(ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aC + ln aC + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aD)] aD)]
| (8) |
G = cG0A + (12 mol)G0B + ξΔG0R + RgTξ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) aC aC
| (9) |
For a sufficiently dilute solution, we can approximate the activity aC of component C as its molarity. This is given by the moles of component C divided by the combined volume of component C and the solvent; components A and D are not dissolved, so their volumes do not contribute. Inspecting eqn (3) shows that approximately half of the reacted solvent volume goes into component C, so we can use the solvent density ρB and molecular weight MWB to approximate the solution volume:
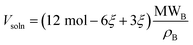 | (10) |
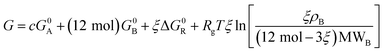 | (11) |
It is clear from eqn (11) that the Gibbs free energy increases with concentration; this makes sense, since we have not written G in per molar form. However, since c and ξ never appear in the same term of the Gibbs function, the derivative 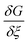 must not have a c dependence. This means the equilibrium extent of reaction—the value ξeq that minimizes G—is independent of solution concentration, depending only on material constants and temperature.
must not have a c dependence. This means the equilibrium extent of reaction—the value ξeq that minimizes G—is independent of solution concentration, depending only on material constants and temperature.
To relate this conclusion to the average As2S3 cluster size at varying concentrations, we make three geometric assumptions:
(1) The clusters are approximately spherical. This is supported by our cryo-TEM micrographs; the clusters pictured in the inset of Fig. 1 are generally round in shape.
(2) The clusters follow the form proposed by Chern et al.—an amine salt on the surface and as-bulk As2S3 within the volume—the justification for which is well explained in their original work.20
(3) Each molecule contributes either a characteristic volume or characteristic surface area to the cluster it is part of. This assumes a uniform solid density, reasonable in the absence of external forces.Following these assumptions, we will use the terms VA (volume contributed by an As2S3 molecule) and SAC (surface area contributed by a (C3H7NH3)3AsS3 molecule) to proceed with the calculation.
If we mix c mol of As2S3 and 1 L of solvent, the number of clusters at equilibrium can be written in two ways. The first is found by dividing the total volume of As2S3 available for cluster formation by the volume of an individual cluster:
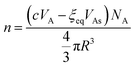 | (12) |
The second expression for n is found by dividing the total surface area available for cluster formation by the surface area of an individual cluster:
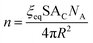 | (13) |
We can now equate eqn (12) and (13):
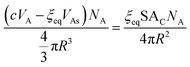 | (14) |
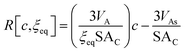 | (15) |
Since ξeq is independent of c, eqn (15) shows a linear relationship between cluster size and solution concentration. The slope, 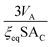 , contains only positive terms and must therefore be increasing.
, contains only positive terms and must therefore be increasing.
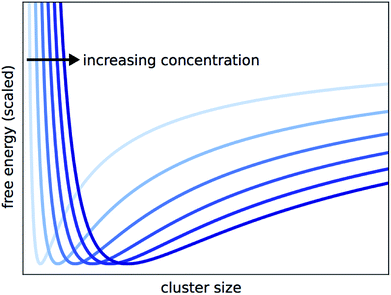
By solving eqn (15) for ξeq and inserting into eqn (11) as ξ, we can obtain the Gibbs free energy of a solution where at some arbitrary ξ, the reaction halts and clusters form. This allows us to plot the free energy against the cluster size that results from each ξ. The predicted cluster size, which corresponds to the true ξeq, will minimize the Gibbs function. This is shown for different concentrations in Fig. 4. Each G curve is scaled to account for the cG0A term in eqn (11), so the curves line up vertically and can be more easily compared. With this view, it is clear that the predicted cluster size increases with concentration.
To attain z-averages from the model for comparison with experiments, the average cluster size was calculated from eqn (15) and used to generate a normal distribution of sizes with the standard deviation observed in cryo-TEM. The z-averages were then calculated using eqn (1). The true ξeq for the system could not be calculated without ΔG0R, so ΔG0R was used as a parameter to fit the results of the model to our experimental data.
The results of these calculations are shown by the dashed line in Fig. 1. The values correspond to ΔG0R = −16.2 kJ mol−1. The fact that ΔG0R is negative implies an exothermic reaction, in line with the fact that the dissolution happens spontaneously. However, the magnitude of ΔG0R is relatively low, suggesting it is only energetically favorable to produce a small amount of product. This is consistent with Chern et al.'s observation that optical properties of concentrated solutions stay similar to those of bulk As2S3.20 Thus, the value is in line with expectations, indicating a reasonable fit.
Note that the dashed line in Fig. 1 is limited to concentrations ≥0.2 mol Lsolv−1. This is because the dissolution model assumes the initial moles of As2S3 ≥ ξeq, and ξeq ≈ 0.2 mol for 1 L solvent for the calculation plotted. A different approach must be taken for concentrations below this limit, which is beyond the scope of the present work. Nevertheless, in the region for which the model is applicable, the calculations show good trend agreement with experiments.
4 Conclusions
The size of As2S3 clusters in amine solution and its dependence on concentration has been explored. We established the increase of cluster size with solution concentration over a larger range than had been considered in previous work. By combining DLS with viscosity measurements and cryo-TEM, we addressed the possibility that this trend was an experimental artifact.To explain these results, we proposed a simplified dissolution model consisting of a chemical reaction step and a structuring step; the observed concentration dependence then followed from solution thermodynamics. This approach was highly general and can be applied to other systems where dissolution is controlled by a reaction similar to eqn (3). Our calculations showed good trend agreement with experiments and together present a method for informed size control of As2S3 clusters that will enable improved property control in solution processing and optoelectronic device fabrication.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Leon Wang and Robert Prud'homme for use of and assistance with their DLS setup. The authors also thank Paul Shao, John Schreiber, and Nan Yao for many hours of support with the cryo-TEM. This research was supported by NSF through Princeton University's Materials Research Science and Engineering Center (DMR-1420541).Notes and references
- B. J. Eggleton, B. Luther-Davies and K. Richardson, Nat. Photonics, 2011, 5, 141–148 CrossRef CAS.
- C. Tsay, E. Mujagic, C. K. Madsen, C. F. Gmachl and C. B. Arnold, Opt. Express, 2010, 18, 15523–15530 CrossRef CAS PubMed.
- T. Kanamori, Y. Terunuma, S. Takahashi and T. Miyashita, J. Lightwave Technol., 1984, 2, 607–613 Search PubMed.
- J. S. Sanghera and I. D. Aggarwal, J. Non-Cryst. Solids, 1999, 256–257, 6–16 CrossRef.
- J. S. Sanghera, C. M. Florea, L. B. Shaw, P. Pureza, V. Q. Nguyen, M. Bashkansky, Z. Dutton and I. D. Aggarwal, J. Non-Cryst. Solids, 2008, 354, 462–467 CrossRef CAS.
- K. Petkov and P. J. S. Ewen, J. Non-Cryst. Solids, 1999, 249, 150–159 CrossRef CAS.
- A. E. Owen, A. P. Firth and P. J. S. Ewen, Philos. Mag. B, 1985, 52, 347–356 CAS.
- J. M. Harbold, F. O. Ilday, F. W. Wise, J. S. Sanghera, V. Q. Nguyen, L. B. Shaw and I. D. Aggarwal, Opt. Lett., 2002, 27, 119–121 CrossRef CAS PubMed.
- J. Teteris and M. Reinfelde, J. Non-Cryst. Solids, 2003, 326–327, 494–499 CrossRef.
- M. Frumar and T. Wagner, Curr. Opin. Solid State Mater. Sci., 2003, 7, 117–126 CrossRef CAS.
- A. Lepicard, F. Adamietz, V. Rodriguez, K. Richardson and M. Dussauze, Opt. Mater. Express, 2018, 8, 1613–1624 CrossRef.
- Y. Zha, M. Waldmann and C. B. Arnold, Opt. Mater. Express, 2013, 3, 1259–1272 CrossRef.
- C. Lu, J. M. P. Almeida, N. Yao and C. Arnold, Appl. Phys. Lett., 2014, 105, 1–4 Search PubMed.
- E. A. Sanchez, M. Waldmann and C. B. Arnold, Appl. Opt., 2011, 50, 1974–1978 CrossRef CAS PubMed.
- S. Novak, P. T. Lin, C. Li, C. Lumdee, J. Hu, A. Agarwal, P. G. Kik, W. Deng and K. Richardson, ACS Appl. Mater. Interfaces, 2017, 9, 26990–26995 CrossRef CAS PubMed.
- Y. Zha, P.-T. Lin, L. Kimerling, A. Agarwal and C. B. Arnold, ACS Photonics, 2014, 1, 153–157 CrossRef CAS.
- Y. Zou, L. Moreel, H. Lin, J. Zhou, L. Li, S. Danto, J. D. Musgraves, E. Koontz, K. Richardson, K. D. Dobson, R. Birkmire and J. Hu, Adv. Opt. Mater., 2014, 2, 759–764 CrossRef CAS.
- T. Kohoutek, J. Orava, T. Sawada and H. Fudouzi, J. Colloid Interface Sci., 2011, 353, 454–458 CrossRef CAS PubMed.
- C. Markos, S. N. Yannopoulos and K. Vlachos, Opt. Express, 2012, 20, 14814–14824 CrossRef CAS PubMed.
- G. C. Chern and I. Lauks, J. Appl. Phys., 1983, 54, 2701–2705 CrossRef CAS.
- T. Kohoutek, T. Wagner, M. Frumar, A. Chrissanthopoulos, O. Kostadinova and S. N. Yannopoulos, J. Appl. Phys., 2008, 103, 1–6 CrossRef.
- R. Tintu, V. P. N. Nampoori, R. Radhakrishnan, N. V. Unnikrishnan and S. Thomas, J. Optoelectron. Adv. Mater., 2012, 14, 918–922 CAS.
- M. Waldmann, J. D. Musgraves, K. Richardson and C. B. Arnold, J. Mater. Chem., 2012, 22, 17848–17852 RSC.
- J. Wang, M. Lin, T. Zhang, Y. Yan, P. C. Ho, Q.-H. Xu and K. P. Loh, J. Am. Chem. Soc., 2008, 130, 11596–11597 CrossRef CAS PubMed.
- G. T. Oostergetel, F. J. Esselink and G. Hadziioannou, Langmuir, 1995, 11, 3721–3724 CrossRef CAS.
- C. A. Schneider, W. S. Rasband and K. W. Eliceiri, Nat. Methods, 2012, 9, 671–675 CrossRef CAS PubMed.
- J. Tuoriniemi, A.-C. J. H. Johnsson, J. P. Holmberg, S. Gustafsson, J. A. Gallego-Urrea, E. Olsson, J. B. C. Pettersson and M. Hassellov, Sci. Technol. Adv. Mater., 2013, 15, 035009 CrossRef PubMed.
- S. Song, Ph.D. thesis, Princeton University, 2011.
- S. Slang, K. Palka, L. Loghina, A. Kovalskiy, H. Jain and M. Vlcek, J. Non-Cryst. Solids, 2015, 426, 125–131 CrossRef CAS.
- Y. Zha, S. Fingerman, S. J. Cantrell and C. B. Arnold, J. Non-Cryst. Solids, 2013, 369, 11–16 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2018 |