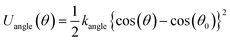Open Access Article
Open Access ArticleThe penetration of a charged peptide across a membrane under an external electric field: a coarse-grained molecular dynamics simulation
Bin Wanga,
Jianhua Zhang *a,
Youyu Zhanga,
Zheng Maoa,
Nan Lua and
Qing Huo Liu*b
*a,
Youyu Zhanga,
Zheng Maoa,
Nan Lua and
Qing Huo Liu*b
aInstitute of Electromagnetics and Acoustics, Department of Electronic Science, Xiamen University, Xiamen, 361005, P. R. China. E-mail: jhzh@xmu.edu.cn
bDepartment of Electrical and Computer Engineering, Duke University, Durham, NC 27708, USA. E-mail: qhliu@duke.edu
First published on 11th December 2018
Abstract
The processes of single polyarginine (R8) peptide penetration through planar and vesicle membranes under an external electric field are simulated via a coarse-grained molecular dynamics (CGMD) simulation. The results show that the external electric field can greatly enhance the penetration possibility of the R8 peptide through membranes. For different membranes (planar membrane and curved vesicle membrane), the amplitudes of electric fields needed for penetration are different. The penetration time of the R8 peptide across membranes decreases with the increasing amplitude of the external electric field applied. Under a constant electric field, the length of penetration time for different membranes is also different. For a better understanding of the mechanism of the penetration, we analyzed the Potential Mean Force (PMF) of the R8-membrane systems and found that the PMFs of the planar membrane and the curved vesicle membrane have a large difference. This may be one of the main factors that induces the different penetration processes of the R8 peptide across membranes when they respond to the same external electric field. All these findings shed light on the role of external electric field on the penetration of R8 peptide through membranes and also give some insights into the effects of membrane curvature on the transportation processes of the peptide carriers.
Introduction
As amino acids with a short sequence, cell-penetrating peptides (CPPs) have been one of the technologies widely studied due to their high transport efficiency, low cytotoxicity, and the ease of molecular design in terms of cellular delivery of bioactive molecules.1 They were used as carriers to transport various cargoes such as small RNA/DNA, plasmids, antibodies, and nanoparticles (NPs) into cells.2–5 Furthermore, numerous CPP-based treatments have already entered clinical trials.6–8 For instance, the surface modification of nanostructured lipid carriers with R11 peptide can be used to improve the transport of drugs across deeper skin layers,6 and another work revealed that five CPPs and one antimicrobial peptide, which are harmless towards mammalian cells, can act as antifungal agents against malassezia sympodialis.8Other than experiments, some simulations of CPPs carrying specific molecules into cells have also been performed in recent years. Li et al. investigated the translocation of poly-arginine and its conjugated particle across asymmetric membranes via CGMD simulations.9 They found that the hydrophobic particle is easier to be transported by peptide through a membrane compared with the hydrophilic one. He et al. also used CGMD simulation to study the penetration of the R8 peptide across planar membranes under tension.10 These two works exhibited the efficient peptide transport process across planar membranes. However, they also reflected a limitation of peptide transport in simulations that a high concentration was required for the transport of the peptides. Therefore, the employment of a technique which can help peptides overcome biomembrane barrier more efficiently is a meaningful issue.
On the other hand, the main techniques of drug delivery, including peptide drug delivery, can be divided into carriers-based delivery and direct delivery.11 Although drug-conjugated carriers are mainly used to enhance the drug delivery efficiency,12–14 direct delivery can further increase the transport efficiency of drug through controllable parameters such as magnetic or electrical force11,15 etc. As one of the improvement strategies, external electric field has been widely applied to study the interaction of nanoparticles with membrane due to its high efficiency and simplicity.16–18
Electroporation is a developing technique which can be used to deliver extracellular materials into cells by the pathway of direct permeation. In this technique, applied electric field can induce numerous nano-scale transient aqueous pores in the membrane to increase the permeability of the membrane, leading to a direct permeation of extracellular materials into cells. In recent decades, electroporation has been widely adapted as a tool to prompt drug delivery.19–23 Among these drug molecules delivery, peptide delivery is a potentially promising and essential issue for therapeutics because of its crucial role in maintaining cellular functions. For instance, Dübel's group successfully delivered antibodies into the cytosol from the outside via electroporation in their evolution experiment of antibody delivery.24 Also, Achillefs Kapanidis et al. delivered fluorescently labeled protein into cells using their electroporation-based protocol and found that the internalization of protein increases with the increased applied electric voltage.25
Although some works26–28 have studied the electroporation-mediated peptide drug delivery, the effect of external electric field on the transport of peptide remains poorly understood. In the present work, we will mimic the penetration of the charged peptide across membrane under external electric fields using CGMD simulation to investigate the effects of various electric field on the transport efficiency of R8 peptide across membranes.
Furthermore, liposome vesicles are employed as a source of curved biomembrane in our simulations to mimic actual cells. Liposome vesicles have also been broadly used as drug carrier12,13 and cell mimicking.29,30 More recently, one work has been conducted to investigate the interaction of R8 peptides with vesicle via both experiments and simulations.31 However, few works have been reported to study the difference of the penetration process of the peptide through the planar and curved membranes especially under an external electric field. Therefore, the introduction of vesicle can also help us to better understand the effects of membrane curvature on the peptide penetration.
Taking the aforementioned into consideration, two simulation systems, R8 peptide-planar membrane and R8 peptide-vesicle systems, are constructed using CGMD models. First, we run each of the systems for a limited time scale to investigate the interaction between the R8 peptide and membranes without any external electric field, and then we add an electric field with various intensity on the systems to observe the effect of the amplitude of electric field on the penetration processes. The simulation results provide an insight into the role of electric field in prompting peptide drug delivery and some new knowledge into the difference of R8 peptide crossing planar and curved membranes.
Model and methods
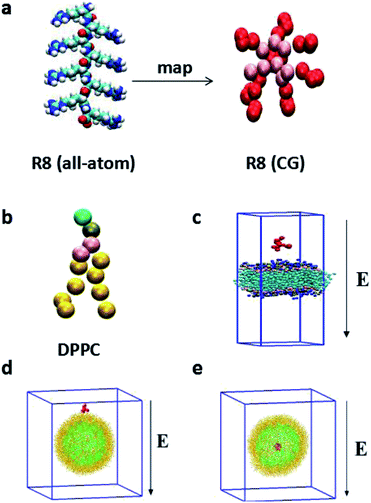
Compared with all-atom molecular dynamics (AAMD) method,32,33 the CGMD method, in which four atoms are represented by a single CG bead, allows itself to be used in the investigation of the systems in larger temporal and spatial scales and greatly reduces the computational cost. In particular, the MARTINI force field has been broadly used in the study of the interaction between NPs and biomembranes in the CGMD simulations.34 Compared with all-atom model, MARTINI model can still truly represent some intrinsic chemical structure and maintain an interaction between different interaction sites9 and can obtain a much larger space scale and longer time scale.18 The MARTINI force field contains four particle types: polar (P), apolar (C), nonpolar (N), and charged (Q), they are defined to accurately describe the chemical properties of represented atoms.35The R8 peptide in our simulations is constructed based on the extended Martini force for proteins (Martini_v2.2)36 and comprised of eight arginine amino acids (see Fig. 1a). Each arginine contains four beads, backbone bead (P5) and three side chains beads (N0, Qd, and D). Particularly, D bead bears one positive charge, thus the whole R8 peptide appears eight positive charges. Besides, the bond, angle, and dihedral potential energy functions are used to simulate bonded interactions, while the Lennard-Jones (L-J) potential and Coulomb energy functions are applied to describe non-bonded interactions. Such a R8 peptide model has been successfully applied in the study of the interaction between the R8 peptide and planar membrane.10
As amphiphilic molecule, a DPPC lipid molecule contains hydrophilic head group, glycerin backbone, and two hydrophobic carbon tails. It can be mapped into 12 beads in Martini force field, where the positively charged choline (NC3) group, the negatively charged phosphate group (PO4), the glycerol group (GL1, GL2), and the carbon tail are represented by type Q0, type Qa, type Na, type C1, respectively.
The water molecules are modeled by the polarizable Martini water model, and these polarized water molecules37 are used as solvent in all systems to model the interaction of water with charged particles in a more realistic way. In this water CG model, the water molecule consists of three CG beads. The central bead W is neutral and interacts with other beads by Lennard-Jones (L-J) potential with ε = 4.0 kJ mol−1 and σ = 0.47 nm. The other two beads WP and WM, which are bound to the central bead with a fixed bond length (0.14 nm), carry a positive (+0.46e) and negative charge (−0.46e) respectively. These two charged beads interact with other beads via a Coulomb interaction only. The dipole momentum of the water depends on the position of the charged beads and can vary from zero to 2ql (q represents the charge, l represents the bond length of W-WP or W-WM). Furthermore, a harmonic angle potential with equilibrium angle θ and force constant kθ is added to control the rotation of WP and WM beads and thus to adjust the distribution of the dipole momentum. The bond angle of WP-W-WM is flexible and constrained by a harmonic potential of
In our simulations, two types of membranes are considered: a planar membrane and a curved vesicle membrane. The planar membrane is formed by self-assemble of 512 DPPC lipids in polarizable water solvent and the whole system is equilibrated for a short time in NPzAT ensemble to allow for a tensionless membrane to prepare further simulations. The total size of the constructed simulation box is 12.68 nm × 12.68 nm × 19.70 nm. Likewise, vesicle membrane is formed by self-assemble of 1182 DPPC lipid molecules in water box with a scale of 25.2 nm × 25.2 nm × 25.2 nm. The detailed information about the formation of the vesicle can be obtained in the literature.29 The vesicle has a small radius of about 8 nm. The vesicle with such a small size has been experimentally produced31 and successfully applied in the simulations.34,38
In the present work, we focus on the transport of the R8 peptide through membranes via an external electric field. The external electric field E is taken into account as a force, Fi = qiE for all CG beads with a charge qi, including the charged R8 peptide beads, polarize water molecules and other charged particles in the models. The range of the amplitude of applied electric fields is from 0.14 V nm−1 to 0.25 V nm−1. For the planar membrane, the R8 peptide is initially positioned 2.0 nm above the membrane surface (Fig. 1c). While for the vesicle membrane, two conditions are considered: one of them is that the R8 peptide is initially placed above the vesicle surface with a center of mass (C.O.M) distance (9.5 nm) between the peptide and the vesicle (Fig. 1d), in the other one, the R8 peptide is placed in the centre of the vesicle (Fig. 1e). The external electric field is applied along the negative Z direction of simulation box (Fig. 1c–e).
For the R8-planar membrane systems, the MD simulations are performed under the conditions of constant temperature, constant membrane area, and constant pressure along the membrane normal (the NPzAT ensemble). For the R8-vesicle systems, the simulations are examined in an NPT ensemble. The temperature and pressure are maintained at 310 K (ref. 18 and 39) and 1 bar using Berendsen algorithm.40 The L-J interactions are cut at 1.2 nm and smoothly shifted to zero from 0.9 nm to 1.2 nm to reduce cut-off noise. Shift method is applied to calculate electrostatic interactions. Periodic boundary conditions and a time step of 25 fs (ref. 35) are used in all simulations. Moreover, eight chloride ions are added in the simulation box to neutralize the positive charges of the R8 peptide.
In order to obtain the energy cost of the R8 peptide in the penetration processes, the free energy profiles of the penetration are extracted in the form of PMF. In the present work, PMF is calculated from the standard combination of the umbrella sampling protocol41 and an implementation of the weighted histogram analysis method (WHAM).42 Firstly, we obtain a 1D PMF profile as a function of the C.O.M distance between the R8 peptide and the planar membrane via umbrella sampling with CGMD simulations. Pull simulations were performed over a distance of 10.0 nm along the direction of the bilayer normal by applying a constant force of 1000 kJ mol−1 nm−2.41 Configurations with a regular spacing of 0.2 nm are extracted from the trajectory files of the pulling process. The selected configurations are used as the input windows of umbrella sampling and each window is simulated for 10 ns. Secondly, we also obtain the PMF profile as a function of the C.O.M distance between the R8 peptide and the vesicle along the vesicle radial direction in the same way. The entire pulling distance is 10.2 nm and sampling windows are used along the vesicle radial direction with the same separation (0.2 nm) to sample from the centre of the vesicle to the outside of the vesicle.
All simulations above are performed by GROMACS 4.5.5 package43 and results are visualized by Visual Molecular Dynamics (VMD) software.44
Results and discussion
1. Interaction of the R8 peptide with membranes in the absence of external electric fields
In order to examine the interaction of the R8 peptide with the membranes without an applied electric field, the peptide is firstly placed adjacent to the planar membrane and the vesicle membrane at small distances as shown in Fig. 1(c) and (d). Our simulations show that the penetrations of the single R8 peptide into the membranes are not observed without an applied external electric field. The R8 peptide is found to stay in the bulk water at the end of the simulations because of its hydrophilic properties. The observation of the present work is similar with the previous work,9 in which the penetration of a single R9 peptide into an asymmetric membrane was also not observed in their simulations. However, different from present work, a more strongly adsorption of the R9 peptide on the outer leaflet of the asymmetric membrane was found in their work. It may be arose from the different compositions (present: DPPC and previous: DMPC) of lipid membrane used in the two cases. The DPPC lipid has two more C1 beads than the DMPC lipid, as a result, the repulsion of the DPPC lipid with the R8 peptide is bigger than the one of the DMPC lipid with the R8 peptide.2. Free energy profiles
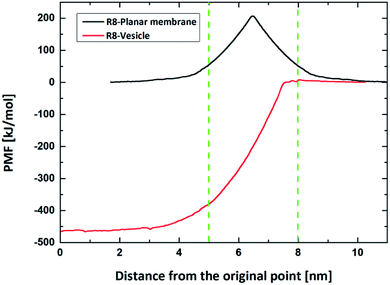
The free energy profiles of the peptide-membrane systems can provide valuable information about the ability of peptide penetration into the membranes. As we know, the possibility of peptide penetration is mainly dependent on the height of the energy barrier across the membrane. To obtain the free energy profiles as a function of the peptide position along the penetration path, we first perform the PMF calculations of peptide across planar membrane along the direction of the bilayer normal from bulk water to the core of membrane. Furthermore, to examine the influence of the curvature of membrane on the free energy, we also do the PMF calculations of the peptide across the vesicle membrane along the radius direction of spherical vesicle. The results are shown in the Fig. 2.For the R8-DPPC planar membrane system, there is an energy barrier with a height about 206.5 kJ mol−1 across the planar membrane on the PMF profile. The energy barrier is nearly symmetric and gets its maximum at the core of the R8 membrane bilayer. The present of energy barrier prevents the peptide penetrating through the DPPC membrane, which is consist with a PMF calculation of a R9 peptide-asymmetric planar membrane bilayer system.9 However, for the R9 peptide-asymmetric membrane bilayer system, there is a local energy minimum on the outer leaflet surface of the membrane, as a result, the peptide can adsorb onto the outer leaflet surface. Differently, in present work local energy minimum is not found near the outer leaflet of DPPC membrane, thus the R8 peptide tends to stay in the bulk water instead of being adhered on the membrane surface.
For the R8-DPPC vesicle system, the PMF contains four regions with features corresponding to: (i) the R8 peptide moves from its original position to the outer leaflet surface of the membrane for about 2.2 nm, we take the initial point as the zero energy reference point. (ii) The R8 peptide passes through the outer leaflet of the membrane. An energy barrier about 7.3 kJ mol−1 is found at about 8 nm in this process, this barrier prevents the R8 peptide from penetrating through the outer leaflet. (iii) The R8 peptide moves from the outer leaflet to the inner leaflet. However, no high barrier exists in the region of the PMF curve compared with the PMF of the R8-planar membrane system. This phenomenon may attribute to the curvature of the vesicle. Kazutami Sakamoto et al. have been demonstrated that the penetration of the R8 peptide into positive (negative) curved membrane can be promoted (suppressed).45 (iv) The R8 peptide penetrates through the inner leaflet and moves to the center of the vesicle. A local energy minimum point appears near the center of the vesicle, this means that the R8 peptide prefers to stay there.
As some previous work showed45,46 the curvature of the membrane has influence on the interaction between the nanoparticles (or molecular) and membranes. These is supported by the difference in the PMF profiles of the R8-planar membrane and the R8-vesicle membrane systems. In the present model, the area per lipid (APL) of outer membrane of the vesicle is about 0.76 nm2 per lipid,38 which is bigger than that in the planar membrane (0.62 nm2 per lipid). According to the work performed by Xiao Cong He et al.,10 the APL can be used to model the tension of the membrane. It means that the curved spherical vesicle membrane has larger surface tension than the planar one. Permeability can be enhanced by increasing membrane tension because sparse lipids in the lipid-poor region provide space through which nanoparticles or large molecules can penetrate.47 This is consistent with the difference of the PMF profiles between vesicle and flat membrane.
3. The penetration of the R8 peptide under an external electric field
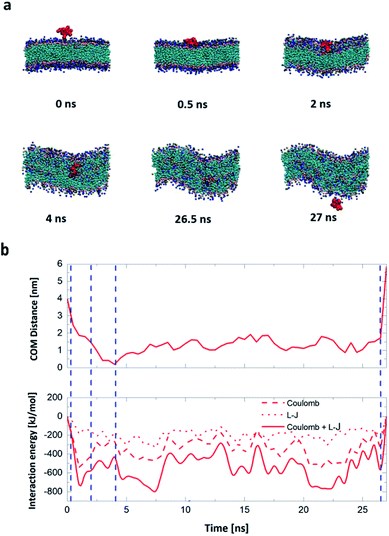
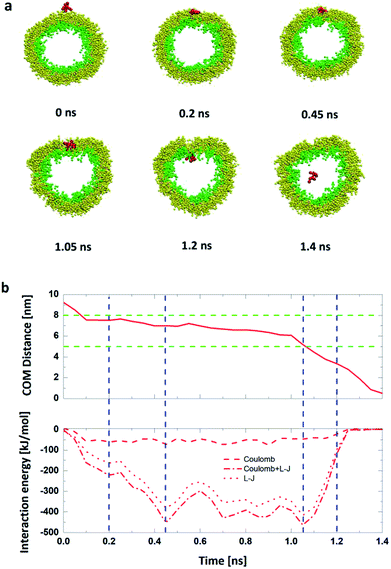
Firstly, we perform the simulations of the translocation of the R8 peptide across a planar DPPC membrane under an external electric field with an amplitude from 0.14 V nm−1 to 0.25 V nm−1. Each simulation runs for 50 ns. And the direct permeation can be observed when the amplitude of electric field is up to 0.17 V nm−1. The key snapshots of the penetration process, the C.O.M distance from the R8 to the planar membrane and the interaction energies between them are shown in Fig. 3. In Fig. 3a, the R8 peptide is initially placed above the membrane surface with a C.O.M distance of 4.0 nm, and then the R8 peptide swiftly reaches the surface of the planar membrane about 0.5 ns and various interaction actions between the R8 peptide and planar membrane. Meanwhile, in the process of the penetration, the membrane is deformed and a hydrophilic pore is formed around the periphery of the R8 peptide, through this pore, the R8 peptide can penetrate across the lipid bilayer and reaches the other side of the membrane. No wrapping behavior of the R8 peptide by membrane is observed. These results are consistent with previous work.18 Furthermore, the movement of beads of membrane and the membrane's deformation in the permeation may also affect the movement trajectory of the R8 peptide, therefore, it can be seen that the C.O.M distance curve combines with the interaction energies curves present partial fluctuation, but overall tendency of their change exhibit that first increase and then decrease to zero.
As shown in Fig. 3b, at the beginning, there is no interaction between the R8 peptide and planar membrane due to that their peripheral distance r = 2.0 nm is larger than the energy cut distance rcut-off = 1.2 nm set in the simulation. The interaction energies increases quickly when the R8 peptide move towards the membrane surface. During the R8 peptide entering the outer leaflet of planar membrane, the interaction energy continues to increase and gets its maximum (727.3 kJ mol−1) at 1 ns. After the R8 peptide penetrating through the outer leaflet of the membrane, the interaction energy increases a bit to 790.6 kJ mol−1. During the R8 peptide permeates across the bilayer membrane, the interaction energy decreases and finally gets zero when the R8 peptide leaves far from the membrane at about 27 ns.
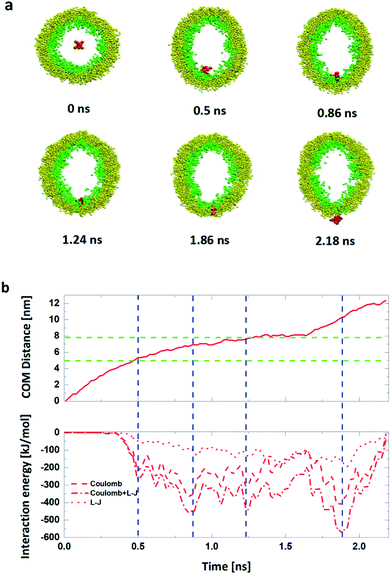
We also analyze the time dependence of the C.O.M distance and the interaction energies between the R8 peptide and the DPPC vesicle to quantitatively describe this penetration process. As shown in Fig. 4b, in the beginning, there has no interaction energies between the R8 peptide and the vesicle due to that their distance is large enough (bigger than the cut-off distance of forces). With simulation time elapsed, the interaction energy increases and reaches its own maximum (463.6 kJ mol−1) at about 1.05 ns, indicating that the R8 peptide has a large interaction with the vesicle membrane when it embeds into the center of the membrane and then causes a large non-bonded energy. At about 1.2 ns, the R8 peptide completely passes across the membrane into the inside of the vesicle, a hydrophilic pore is formed and a deformation of the vesicle emerges.
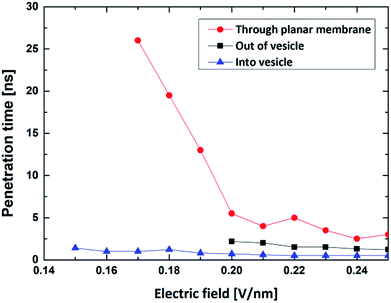
Compared with the former case (in Section 1), this result illustrates that external electric can achieve the translocation of single R8 peptide through the vesicle membrane and that external electric field can dramatically accelerate the translocation process and greatly shorten the transportation time. Furthermore, with the increase of electric field in an appropriate range, the transportation time gradually decrease (see Fig. 6). This may because under the stronger electric field, the R8 peptide is exposed to a larger electric field force, which forces the R8 peptide to overcome the barrier easier.
Also, in this process, detailed phenomenon are observed: the R8 peptide penetrates across the membrane along with the hydrophilic pore formed by the head groups of the inner and outer leaflets of the vesicle membrane.
By comparing the results, we found that the minimum electric field required by the penetration of R8 peptide (a) through the planar membrane, (b) into the vesicle and (c) out of the vesicle are 0.15 V nm−1, 0.17 V nm−1 and 0.20 V nm−1, respectively. This is consistent with the results in the PMF profiles mentioned above: the bigger energy barrier for the R8 peptide across membrane, the larger minimum electric field required. However, the lengths of the penetration time for the three cases under the applied electric fields with same amplitude are in different order. We found that the time for the R8 peptide to penetrates the planar membrane is longer than the one for the R8 to penetrating out of the vesicle under the same electric field, this may attribute to that the electric fields have a larger effect on the two poles of vesicle along the direction of the electric field, leading that the electroporation is more likely to occur in the area near the poles when the intensity of electric field becomes large enough for the poration of membrane.
Also, by comparing the two processes of the R8-vesicle system, it is found that the translocation of the R8 peptide out of the vesicle requires a higher intensity of electric field. This phenomenon can be explained by two aspects: (i) from PMF curve, the energy barrier of the R8 peptide penetrating out of the vesicle (472.6 kJ mol−1) is much bigger than that of the R8 peptide penetrating into the vesicle (7.3 kJ mol−1). Consequently, stronger electric field is needed to overcome the higher energy barrier; (ii) from the lipids topology. The difference of lipids topology can result in different curvatures of membrane, which may bring distinct effects to the penetration of R8 peptide. For example, Sakamoto et al.45 clarified the curvature's effect on the translocation of peptide: they determined the lipid topology by critical packing parameter (CPP) and showed in experiment that penetration of PTD (protein transduction domain) into erythrocyte can be promoted or suppressed by making the membrane surface curvature either positive (CPP < 1) or negative (CPP > 1). These results well support our claim that the curvatures of vesicle also play a vital role in the interaction between R8 peptide and vesicle and have a significant influence for the penetration process of R8 peptide.
Finally, it should be noted that electric field can be regarded as a powerful tool to help peptides to realize penetration activities and that in proper range, the stronger electric field leads to the shorter penetration time (see Fig. 6). The cause of this phenomenon is largely consistent with the aforementioned explanation for the R8's entry into the vesicle.
The strong electric field can induce the electroporation of the membrane system. If the intensity of electric field is strong enough and the treating time is long enough, it is even possible to find the departure of lipid monomers from self-assembled membrane from our testing. Analogously, in a recent study where external electric fields (with an intensity up to the order of magnitude of 0.1 V nm−1) were used to study the motion of charged monomers on self-assembled polymers.16 In the following microseconds of CGMD, they found that the monomer could be detached from the assembly. In our simulations, the range of the intensity of the applied external electric fields is from 0.14 V nm−1 to 0.25 V nm−1. Within a few nanoseconds of CGMD, we observed the penetration of the R8 peptide across membranes but did not found the departure of lipid monomers from membranes. It means that to better realize the transport of the R8 peptide through membranes, besides adjusting the intensity of applied electric field, it also needs to control other parameters (like the length of the applied duration) of the external electric field. For example, in the present case, in order to realize the transport of charged molecules through membranes but not lead to irreversible membrane destruction, nanosecond electric pulses can be employed in the study. In recent years, the development of high intensity nanosecond electric pulse technology makes such investigations to be possible.
Conclusion
The single R8 peptide is hydrophilic so that it prefers to stay in water, as confirmed from the PMF curves of the R8 across the planar and vesicle membranes. For a planar membrane, the PMF continuously increases from the bulk water outside of the membrane to the center of the membrane and reaches its maximum at the center of the membrane. Therefore, it not easy for the peptide to spontaneously penetrate across the planar membrane. For a curved membrane, like the vesicle membrane, as shown in the PMF profile of the R8-vesicle system from the bulk water outside the vesicle toward the center of the vesicle, the PMF slightly increases when the R8 peptide reaches the outer surface of the vesicle; after penetrating through the outer membrane of the vesicle, the PMF shows a sustained decrease and reaches a minimum in the center area of the vesicle. In other words, it is easier for the R8 peptide outside the vesicle to get through vesicle membrane into the center of the vesicle by applying an external driving force on the peptide. Given this, we investigate the translocation of the R8 peptide across both planar and curved vesicle membranes with an external driving force induced by applied electric fields.In the present work, we investigate the penetration of a R8 peptide across planar and vesicle membranes in an external electric field with a direction perpendicular to the membranes via CGMD simulations. We find that the sequence of the critical intensity of the applied electric field for the R8 peptide translocation across different membranes is consistent with the results in the PMF profiles: the higher barrier owned by membrane, the bigger value of critical intensity for translocation required. The results illustrate that the curvature of plasma membrane has a large influence on the translocation of peptide, and the increase of curvature of the membrane may be beneficial to improve the efficiency of the penetration of the peptide across membrane.
Since the peptides carry a certain amount of electric charges, the external electric fields can affect the translocation of the peptides across the membrane. As a result, it is possible to regulate the peptides transport into or out of the cell or vesicle by applying an external electric field. The penetration time is dependent on the intensity of electric field. For both planar and vesicle membranes, the stronger the electric field applied, the shorter the penetration time obtained. When the same intensity of the electric field applied, the R8 peptide translocates through the vesicle membrane more easily than through the planar membrane, whether it translocates into or out of the vesicle. This may be due to the fact that a curved membrane is more easily affected by external electric fields than the planar membrane. In our simulations, when the intensity of electric field is large enough, the vesicle can deform from a spheroid to an ellipsoid. The electric field has a larger effect on the two poles of vesicle along the direction of the electric field, so the electroporation is more likely to occur in the area near the poles.48 As a result, it will greatly increase the possibility for the penetration of the R8 peptide across the vesicle membrane.
This paper studies the process of the penetration of the R8 peptide across the planar and curved vesicle membranes under external electric fields. Our studies deepen the understanding of the mechanism of the translocation of the R8 peptide across membrane. Because of the unique role of the R8 peptide as a carrier in the process of drug transport, our research also provides a feasible and effective means to control the transportation of R8 peptide by applying an external electric field. This technology can improve the accuracy and efficiency of drug transport with peptide based carriers.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by grants from The National Natural Science Foundation of China under contract No. 41390453, Open Research Fund of State Key Laboratory of Cellular Stress Biology, Xiamen University (SKLCSB2018KF012) and the youth nursery fund of the Affiliated Dongnan Hospital of Xiamen University (16Y016).Notes and references
- I. Nakase, G. Tanaka and S. Futaki, Mol. BioSyst., 2013, 9, 855 RSC.
- I. R. de Figueiredo, J. M. Freire, L. Flores, A. S. Veiga and M. Castanho, IUBMB Life, 2014, 66, 182 CrossRef PubMed.
- V. P. Torchilin, Adv. Drug Delivery Rev., 2008, 60, 548 CrossRef CAS PubMed.
- M. Lewin, N. Carlesso, C. H. Tung, X. W. Tang, D. Cory, D. T. Scadden and R. Weissleder, Nat. Biotechnol., 2000, 18, 410 CrossRef CAS PubMed.
- L. Josephson, C.-H. Tung, A. Moore and R. Weissleder, Bioconjugate Chem., 1999, 10, 186 CrossRef CAS PubMed.
- P. Shah, P. Desai, D. Channer and M. Singh, J. Controlled Release, 2012, 161, 735 CrossRef CAS PubMed.
- L. B. Lopes, E. J. Furnish, P. Komalavilas, C. R. Flynn, P. Ashby, A. Hansen, D. P. Ly, G. P. Yang, M. T. Longaker, A. Panitch and C. M. Brophy, J. Invest. Dermatol., 2009, 129, 590 CrossRef CAS PubMed.
- T. Holm, J. Bruchmann, A. Scheynius and U. Langel, Lett. Appl. Microbiol., 2012, 54, 39 CrossRef CAS PubMed.
- Z. Li, H. Ding and Y. Ma, Soft Matter, 2013, 9, 1281 RSC.
- X. He, M. Lin, B. Sha, S. Feng, X. Shi, Z. Qu and F. Xu, Sci. Rep., 2015, 5, 12808 CrossRef CAS PubMed.
- K. Kim and W. G. Lee, J. Mater. Chem. B, 2017, 5, 2726 RSC.
- A. K. Silva, R. D. Corato, T. Pellegrino, S. Chat, G. Pugliese, N. Luciani, F. Gazeau and C. Wilhelm, Nanoscale, 2013, 5, 11374 RSC.
- Q. Zhao, Y. Wang, Y. Yan and J. Huang, ACS Nano, 2014, 8, 11341 CrossRef CAS PubMed.
- N. F. Frazão, E. L. Albuquerque, U. L. Fulco, D. L. Azevedo, G. L. F. Mendonça, P. Lima-Neto, E. W. S. Caetano, J. V. Santana and V. N. Freire, RSC Adv., 2012, 2, 8306 RSC.
- M. Ray, Y.-W. Lee, F. Scaletti, R. Yu and V. M. Rotello, Nanomedicine, 2017, 12, 941 CrossRef CAS PubMed.
- A. Torchi, D. Bochicchio and G. M. Pavan, J. Phys. Chem. B, 2018, 122, 4169 CrossRef CAS PubMed.
- M. L. Yarmush, A. Golberg, G. Sersa, T. Kotnik and D. Miklavcic, Annu. Rev. Biomed. Eng., 2014, 16, 295 CrossRef CAS PubMed.
- K. Shimizu, H. Nakamura and S. Watano, Nanoscale, 2016, 8, 11897 RSC.
- K. Morotomi-Yano, H. Akiyama and K. Yano, Arch. Biochem. Biophys., 2014, 555–556, 47 CrossRef CAS PubMed.
- S. van Drunen Littel-van den Hurk and D. Hannaman, Expert Rev. Vaccines, 2010, 9, 503 CrossRef CAS PubMed.
- J. Ge, E. Neofytou, T. J. Cahill, R. E. Beygui and R. N. Zare, ACS Nano, 2012, 6, 227 CrossRef CAS.
- Y. Zu, S. Huang, W.-C. Liao, Y. Lu and S. Wang, J. Biomed. Nanotechnol., 2014, 10, 982 CrossRef CAS.
- A. G. Pakhomov, E. Gianulis, P. T. Vernier, I. Semenov, S. Xiao and O. N. Pakhomova, Biochim. Biophys. Acta, 2015, 1848, 958 CrossRef CAS PubMed.
- A. L. Marschall, C. Zhang, A. Frenzel, T. Schirrmann, M. Hust, F. Perez and S. Dübel, mAbs, 2014, 6, 943 CrossRef PubMed.
- M. Sustarsic, A. Plochowietz, L. Aigrain, Y. Yuzenkova, N. Zenkin and A. Kapanidis, Histochem. Cell Biol., 2014, 142, 113 CrossRef CAS PubMed.
- C. SchÖnenberger, A. SchÜtz, A. Franco-Obregón and M. Zenobi-Wong, Biotechnol. Lett., 2011, 33, 883 CrossRef PubMed.
- H. A. Benson and S. Namjoshi, J. Pharm. Sci., 2008, 97, 3591 CrossRef CAS.
- I. T. Degim and N. Çelebi, Curr. Pharm. Des., 2007, 13, 99 CrossRef CAS.
- S. Kulin, R. Kishore, K. Helmerson and L. Locascio, Langmuir, 2003, 19, 8206 CrossRef CAS.
- M. S. Long, C. D. Jones, M. R. Helfrich, L. K. Mangeney-Slavin and C. D. Keating, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 5920 CrossRef CAS.
- X. He, M. Lin, J. Guo, Z. Qu and F. Xu, RSC Adv., 2016, 6, 30454 RSC.
- J. L. MacCallum, W. F. Bennett and D. P. Tieleman, Biophys. J., 2008, 94, 3393 CrossRef CAS PubMed.
- S. Dorairaj and T. W. Allen, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 4943 CrossRef CAS.
- J. Zhang, X. Zhao and Q. H. Liu, RSC Adv., 2016, 6, 90388 RSC.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. d. Vries, J. Phys. Chem. B, 2007, 111, 7812 CrossRef CAS PubMed.
- D. H. de Jong, G. Singh, W. F. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schäfer, X. Periole, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2013, 9, 687 CrossRef CAS PubMed.
- S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S. J. Marrink, PLoS Comput. Biol., 2010, 6, e1000810 CrossRef PubMed.
- L. Liu, J. Zhang, X. Zhao, Z. Mao, N. Liu, Y. Zhang and Q. H. Liu, Phys. Chem. Chem. Phys., 2016, 18, 31946 RSC.
- S. Sun, J. T. Y. Wong and T.-Y. Zhang, Soft Matter, 2011, 7, 9307 RSC.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684 CrossRef CAS.
- J. A. Lemkul and D. R. Bevan, J. Phys. Chem. B, 2010, 114, 1652 CrossRef CAS.
- S. Kumar, D. Bouzida, R. H. Swendsen, P. A. Kollman and J. M. Rosenberg, J. Comput. Chem., 1992, 13, 1011 CrossRef CAS.
- M. Awasthi, N. Jaiswal, S. Singh, V. P. Pandey and U. N. Dwivedi, J. Biomol. Struct. Dyn., 2015, 33, 1835 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33 CrossRef CAS.
- K. Sakamoto, K. Aburai, T. Morishita, K. Sakai, H. Sakai, M. Abe, I. Nakase and S. Futaki, Chem. Lett., 2012, 41, 1078 CrossRef CAS.
- H. Lee, Phys. Chem. Chem. Phys., 2013, 15, 16334 RSC.
- L.-T. Yan and X. Yu, ACS Nano, 2009, 3, 2171 CrossRef CAS.
- L. Rems, M. Ušaj, M. Kandušer, M. Reberšek, D. Miklavcic and G. Pucihar, Sci. Rep., 2013, 3, 3382 CrossRef.
| This journal is © The Royal Society of Chemistry 2018 |