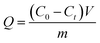Synthesis and characterization of magnetic mesoporous Fe₃O₄@mSiO₂–DODGA nanoparticles for adsorption of 16 rare earth elements

Abstract

In this study, novel magnetic mesoporous Fe₃O₄@mSiO₂–DODGA nanoparticles were prepared for efficiently adsorbing and recycling REEs. Fe₃O₄@mSiO₂–DODGA was characterized by powder X-ray diffraction (XRD), transmission electron microscopy (TEM), vibrating sample magnetometry (VSM), Fourier transform infrared spectroscopy (FT-IR) and thermogravimetric analysis (TGA). The adsorption behavior of Fe₃O₄@mSiO₂–DODGA was investigated by ICP-OES. The results showed that the content of DODGA in the adsorbent was 367 μmol g⁻¹. Fe₃O₄@mSiO₂–DODGA exhibited the highest adsorption rates for 15 REEs, except Tm, in a 2 mol L⁻¹ nitric acid solution. Among these elements, the adsorption rates for Nd, Sm, Eu, Dy, Ho, Yb, Lu, Y and Sc ranged from 85.1% to 100.1%. The desorption rates for all 16 REE ions reached their maximum values when 0.01 mol L⁻¹ EDTA was used as the eluent. The desorption rates for Nd, Ce, Sm, Eu, Ho, Yb, Lu, Y, and Sc were 87.7–99.8%. Fe₃O₄@mSiO₂–DODGA had high stability in 2 mol L⁻¹ HNO₃ and could be used five times without significant loss of adsorption capacity. Moreover, these nanoparticles had high selectivity, and their adsorption rate was not affected even in a high-concentration solution of a coexisting ion. Therefore, 8 REE ions (Nd, Sm, Eu, Ho, Yb, Lu, Y, and Sc) were selected for the study of adsorption kinetics and adsorption isotherm experiments. It was demonstrated that the values of Q_e (equilibrium adsorption capacity) for Nd, Sm, Eu, Ho, Yb, Lu, Y, and Sc were 14.28–60.80 mg g⁻¹. The adsorption of REEs on Fe₃O₄@mSiO₂–DODGA followed the pseudo-second-order kinetic model, Elovich model and Langmuir isotherm model, which indicated that the adsorption process of Fe₃O₄@mSiO₂–DODGA for REEs comprised single-layer adsorption on a non-uniform surface controlled by chemical adsorption. It was concluded that Fe₃O₄@mSiO₂–DODGA represents a new material for the adsorption of REEs in strongly acidic solutions.

---

1. Introduction

Rare earth elements (REEs) have many unique physical and chemical properties, which are widely applied in some modern technologies, including alloys,¹ magnets,² ceramics,³ networks and communication devices. The outstanding properties mentioned above make these devices smaller, lighter and faster in terms of performance and enable devices to exhibit greater efficiency, speed, performance and thermal stability. With the dramatic increase in their global consumption, the requirement for pure REEs has also risen over the past two decades. At present, although the extraction of REEs on a large scale has been industrialized, the separation and purification of REEs are still the main technical difficulties and need further industrial processes.

Therefore, many efforts have been made to develop efficient methods for extracting and purifying REEs, such as liquid–liquid extraction,^4,5 supported liquid extraction⁶ or solid-phase extraction⁷ procedures. These methods all rely on the association constants between ligands and REEs. Liquid–liquid extraction is the most widely used method. The most widely used ligands include di(2-ethylhexyl)phosphoric acid (HDEHP, P204),^8,9 2-ethylhexylphosphonic acid mono(2-ethylhexyl) ester (HEHEHP, P507),¹⁰ and tributyl phosphate (TBP).¹¹ Among the obvious disadvantages inherent in liquid–liquid extraction are the utilization of large volumes of solvents in the extraction procedure and the generation of undesired waste. Supported liquid extraction and solid-phase extraction are relatively environmentally friendly. The combination of a suitable solid phase and effective ligands represents one direction for the development of extraction methods for REEs. Inspired by the above description, nanosized materials are among the candidates for the solid phase. Nanosized materials (e.g., silica nanoparticles,¹² carbon nanotubes,¹³ and magnetic nanoparticles^14,15) with a high surface area ratio have been utilized in various fields.¹⁶ In particular, magnetic nanoparticles are commonly considered for use as internal supporting materials in some fields for the following reasons: their easy preparation via solvothermal reactions and superparamagnetic features for fast separation from complex samples in practical applications.¹⁷ There are several kinds of magnetic solid-phase extraction material that are employed for the adsorption of a single REE such as Eu(III) and Ce(III) in an aqueous solution. These materials mainly include mesoporous SBA-15 modified with the Schiff base N,N′-bis(salicylidene)-1,2-ethylenediamine and decorated on Fe₃O₄ nanoparticles (SBA-15-BSEA-Fe₃O₄-NPs),¹⁸ a Ce(III) ion-imprinted polymer (Ce(III)-IIP) grafted on Fe₃O₄ nanoparticles supported by SBA-15 mesopores (Fe₃O₄@SBA-15-Ce(III)-IIP),¹⁹ a core–shell structured Fe₃O₄@carboxymethylcellulose magnetic composite (Fe₃O₄@CMC),²⁰ an Fe₃O₄/sepiolite composite,²¹ an Fe₃O₄@cyclodextrin magnetic composite (Fe₃O₄@CD-MCs)²² and core–shell structured Fe₃O₄@humic acid magnetic nanoparticles (Fe₃O₄@HA-MNPs).²³

In addition, the ligand is also an important aspect of the design of solid-phase extraction materials. Among the ligands used for adsorbing REEs, N,N,N′,N′-tetraoctyldiglycolamide (TODGA)^24,25 is among the ligands commonly used for separation. In this ligand, the functional group diglycolamide (DGA) plays an important role in coordination with REE ions. Some derivatives based on the DGA chemical structure have been synthesized and used industrially for adsorbing REEs and exhibited excellent enrichment and selectivity.^26,27 Unfortunately, no previous work has been published in which magnetic nanoparticles modified with a diglycolamide ligand were used for the adsorption of REEs. There have been reports on the synthesis of magnetic nanomaterials modified with diglycolamide ligands, including diglycolamic acid-functionalized chitosan-coated Fe₃O₄ (Fe@CS-DGA),²⁸ TODGA-coated magnetite nanoparticles (Fe₃O₄@TODGA),²⁹ and DGA-methacrylate-coated Fe₃O₄ particles (Fe₃O₄@MC-DGA).³⁰ However, these materials were employed for removing Pb(II) and extracting Am(III) and Pu(IV) in a nitric acid solution, but not for the adsorption of REEs.

In this study, mesoporous magnetic Fe₃O₄@mSiO₂–DODGA nanomaterials were prepared by modifying the surface of mesoporous Fe₃O₄ particles with a diglycolamide ligand. In comparison with previously reported materials, 16 REEs other than the radioactive element Pm were used to assess the adsorption properties of the final products. Studies of the influence of coexisting ions and adsorption kinetics demonstrated that Fe₃O₄@mSiO₂–DODGA exhibited better anti-interference performance and a faster adsorption equilibrium process. Moreover, this highly selective Fe₃O₄@mSiO₂–DODGA exhibited high stability and reusability and represents a new solid-phase extraction material for the adsorption of rare earth elements under strongly acidic and high-salinity conditions.

2. Experimental

2.1 Reagents and materials

All reagents were of analytical grade unless otherwise noted. Stock solutions (1.000 g L⁻¹) of 16 REEs (La, Ce, Pr, Nd, Sm, Eu, Gd, Td, Dy, Ho, Er, Tm, Yb, Lu, Y and Sc) were prepared by dissolving appropriate amounts of the corresponding Specpure oxides in dilute HNO₃. Working solutions were prepared daily by appropriately diluting the stock solutions. NaCl, Na₂SO₄, FeCl₃, AlCl₃, CuSO₄, ZnCl₂, NaAc, NaHCO₃, NH₄NO₃, HNO₃, H₂O₂, NH₃·H₂O, CH₂Cl₂, ethanol, carbamide, ethylene glycol, acetic anhydride, oxalyl chloride and tetraethoxysilane (TEOS) were bought from Sinopharm Chemical Reagent Co., Ltd, China. Diglycolic acid, dioctylamine, cetyltrimethylammonium bromide (CTAB), and aminopropyltriethoxysilane (APTES) were purchased from Sigma-Aldrich Chemical Company. High-purity water (18.2 MΩ cm) obtained from a Milli-Q Element system (Millipore, Molsheim, France) was used directly throughout this study. Plastic and glass containers and all other laboratory materials that could come into contact with the samples and standards were stored in 10% (v/v) nitric acid for 24 h and rinsed with high-purity water.

2.2 Material preparation

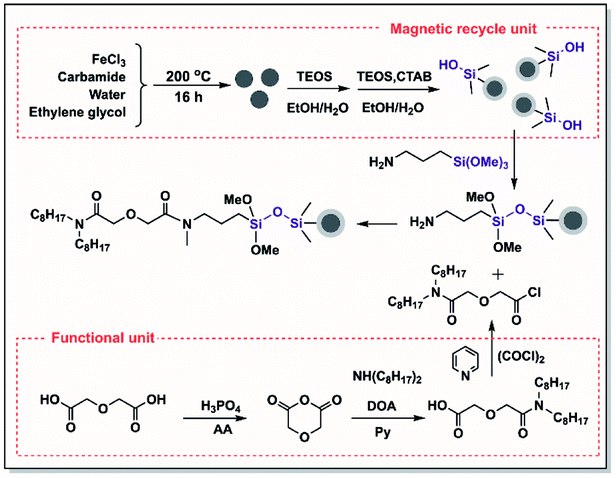
Firstly, a magnetic recycling unit was constructed. Uniform Fe₃O₄ particles prepared via a solvothermal reaction (Scheme 1)³¹ were chosen as the inner supporting materials, which were nanosized and had a much larger specific surface area and superparamagnetic properties. Secondly, amine groups were used to modify the surface of the Fe₃O₄ particles.^32–34 Before this chemical modification, an SiO₂ layer was coated efficiently on the Fe₃O₄ core to protect the Fe₃O₄ core from corrosion by the strong acid in the solution. A further mesoporous SiO₂ layer was created on the surface of Fe₃O₄@SiO₂ to further modify the amino groups to prepare Fe₃O₄@mSiO₂@NH₂. The mesoporous structure increased the specific surface area of the material to enable modification with a greater amount of amino groups.

Scheme 1 Preparation of the functionalized Fe₃O₄ nanoparticles.

In the structure of TODGA, both carbonyl groups are bound to N,N-di(n-octyl)amine groups and have low reactivity. Therefore, N,N-dioctyldiglycolic acid (DODGA-OH) was synthesized.^35,36 This compound has a highly active carboxylic acid group that can be converted into an acyl chloride (DODGA-Cl) and used to modify the magnetic core. In addition, DODGA-OH retains half of the n-octyl substituents in TODGA, which ensures that the functional groups are hydrophobic. Finally, functional magnetic Fe₃O₄@mSiO₂–DODGA nanomaterials were obtained by modifying the diglycolamide functional unit DODGA-Cl with the aminated Fe₃O₄@mSiO₂@NH₂ particles.

2.3 Characterization

Characterization by Fourier transform infrared (FT-IR) spectroscopy was performed with an FT-IR 8400S spectrometer (Shimadzu, Japan). Spectra were recorded over the range of 4000–400 cm⁻¹ in transmission mode, and 32 scans were accumulated at a resolution of 4 cm⁻¹. Magnetic properties were determined with a 7410 vibrating sample magnetometer (VSM, Lake Shore Cryotronics, Inc., Ohio, USA). Morphological observations of the nanoparticles were carried out with a JEM-2010 high-resolution transmission electron microscope (JEOL, Tokyo, Japan). Thermogravimetric analysis (TGA) was conducted using a Mettler Toledo TGA2 analyzer (Switzerland) from 30 to 750 °C at a heating rate of 10 °C min⁻¹. X-ray diffraction (XRD) patterns were recorded in the range of 2θ = 20–80° by step scanning using a Rigaku D/Max-2500 diffractometer (Japan) with Cu Kα radiation. ¹H NMR and ¹³C NMR spectra were recorded with a Bruker AV-400 spectrometer with chemical shifts reported as ppm (in CDCl₃ and DMSO-d₆ with TMS as an internal standard). Mass spectrometric analysis was carried out using an LCQ Fleet mass spectrometer (Thermo Fisher). An ICP-OES system (715-ES, Varian Medical Systems, USA) was used for the determination of REEs.

2.4 Adsorption experiments

2.4.1 Effect of the concentration of HNO₃ on the adsorption of REEs. Batch selection experiments on REEs were carried out in 10.0 mL glass tubes. To determine the optimum concentrations of HNO₃ for the adsorption of REEs, the influence of the concentration of HNO₃ was examined first. A series of REE solutions (containing 16 REEs; the concentration of each REE was 0.2 mg L⁻¹) with different concentrations of HNO₃ (0.01, 0.05, 0.10, 0.50, 1.0, 2.0, and 3.0 mol L⁻¹) were prepared. Then, 10 mg of Fe₃O₄@mSiO₂–DODGA nanoparticles was added to 10 mL of the REE solution under continuous stirring at 25 °C for 24 h. The sorbent was separated with a magnet, and the content of rare earth ions in the supernatant was determined by ICP-OES.

2.4.2 Effect of the concentration of EDTA on the desorption of REEs. Multiple batches of Fe₃O₄@mSiO₂–DODGA nanoparticles loaded with rare earth ions were collected under the same conditions. A series of EDTA solutions (0.002, 0.005, 0.01, 0.02, 0.03, and 0.04 mol L⁻¹) were used to desorb REEs from these Fe₃O₄@mSiO₂–DODGA nanoparticles under continuous stirring at 25 °C for 3 h.

2.4.3 Stability of Fe₃O₄@mSiO₂–DODGA in HNO₃. Fe₃O₄@mSiO₂–DODGA was soaked in HNO₃ (2.0 mol L⁻¹) for different numbers of days. The adsorption rates for 16 rare earth elements in mixed solutions were measured for different immersion times of the adsorbent, and their differences were compared.

2.4.4 Reusability of Fe₃O₄@mSiO₂–DODGA. To assess the recyclability of Fe₃O₄@mSiO₂–DODGA for the adsorption of REEs, 5 cycles of adsorption–desorption tests were conducted. For the desorption process, Fe₃O₄@mSiO₂–DODGA loaded with REEs was washed with deionized water and then immersed in a 0.01 mol L⁻¹ EDTA solution for 3 h after it was separated from the REE solution using a magnet. The adsorbent was washed with deionized water 3 times prior to the next adsorption cycle.

2.4.5 Effect of coexisting ions on the adsorption of REEs. The effect of coexisting ions was determined by adding the corresponding salts of model ions (K⁺, Na⁺, Ca²⁺, Mg²⁺, Fe³⁺, Al³⁺, Zn²⁺, Cu²⁺, SO₄²⁻, Cl⁻, and NO₃⁻) to the solution of REEs.

2.4.6 Adsorption experiments. Fe₃O₄@mSiO₂–DODGA (20 mg) was introduced into 100 mL solutions of single rare earth elements with an initial concentration (C₀) of 20 mg L⁻¹. The experiments were carried out in a water bath, and the solutions were stirred at 25 °C. At certain time intervals (5, 10, 15, 30, 45, 60, 120, 240, 360, and 480 min), the sorbent was separated with a magnet and the supernatant was analyzed to determine the remaining concentration (C_t, mg L⁻¹) using ICP-OES.

Adsorption isotherms were calculated via batch experiments. The adsorbent was mixed with aqueous solutions containing different concentrations of 8 REEs ranging from 1 to 20 mg L⁻¹ and stirred at 298 K for 24 h. The sorbent was subsequently separated with a magnet, and the supernatant was analyzed to determine the remaining concentration (C_e, mg L⁻¹) using ICP-OES.

3. Results and discussion

3.1 Characterization of Fe₃O₄, Fe₃O₄@SiO₂, and Fe₃O₄@mSiO₂–DODGA

The morphological features of the nanomaterial were characterized by TEM to observe its specific shape and appearance characteristics. As shown in Fig. 1, the hollow Fe₃O₄ nanoparticles had spherical shapes and small sizes with a mean diameter of 200 nm (Fig. 1a and b). Single nanocrystals were analyzed by SAED, as shown in Fig. 1c. The diffraction patterns exhibited a distribution comprising a series of points, which was consistent with a face-centred crystal pattern, and the diffraction points corresponded to the (220) crystal planes of the crystal. The layer of SiO₂ was coated by a sol–gel reaction on the surface of the Fe₃O₄ particles. Under the same TEM characterization conditions as were used for the hollow Fe₃O₄ nanoparticles, the mean diameter of the Fe₃O₄@SiO₂ particles increased from 200 nm to 300 nm. Well-defined core–shell structures can be clearly observed in a TEM image of Fe₃O₄@SiO₂ particles (Fig. 1d). The core with dark contrast represented an Fe₃O₄ particle; the outer layer with light contrast represented the SiO₂ shell. The outer layer of mesoporous silica was constructed by a sol–gel reaction with the help of the surfactant CTAB. The outer mesoporous SiO₂ layer was lighter in color and looser in structure than the inner SiO₂ layer (Fig. 1e and f). The construction of the mesoporous structure on Fe₃O₄ particles was carried out to increase the specific surface area of the material. To characterize the mesoporous structure, a BET experiment was performed. As shown in Fig. S9,† the pore diameter of Fe₃O₄@mSiO₂–DODGA was about 6 nm. Its specific surface area was 707.181 m² g⁻¹. In contrast, no pore structures existed in Fe₃O₄@SiO₂ (Fig. S10†). Its specific surface area was 16.284 m² g⁻¹, which was much smaller than that of Fe₃O₄@mSiO₂–DODGA.

Fig. 1 TEM images of hollow Fe₃O₄ (a and b), SAED pattern (c), and TEM images of Fe₃O₄@SiO₂ (d) and Fe₃O₄@mSiO₂ (e and f).

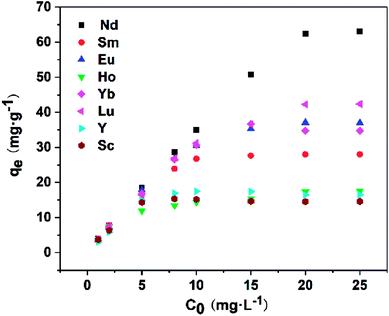
The crystal structure of Fe₃O₄ was characterized by XRD. The X-ray diffraction pattern of Fe₃O₄ nanoparticles prepared via the solvothermal method exhibited six typical diffraction peaks corresponding to (220), (311), (400), (422), (511) and (440) planes. As shown in Fig. 2A, six peaks were observed by analyzing the Fe₃O₄, Fe₃O₄@mSiO₂ and Fe₃O₄@mSiO₂–DODGA nanoparticles, which indicated that the crystal structure of the magnetite core was not changed by coating with the SiO₂ or mesoporous silica layer or chemical modification with DODGA.

Fig. 2 XRD patterns (A), FT-IR spectra (B), TGA curves (C) and VSM curves (D) of Fe₃O₄ nanoparticles.

To characterize the chemical compositions of the bare Fe₃O₄ nanoparticles, SiO₂- and mesoporous silica-coated Fe₃O₄ nanoparticles, and DODGA-modified Fe₃O₄ nanoparticles, their FT-IR spectra were recorded, as shown in Fig. 2B. Firstly, an absorption band at 606 cm⁻¹ attributed to the characteristic stretching vibrations of Fe–O bonds in Fe₃O₄ appeared in the spectra of these nanoparticles, which indicated that the chemical structure of Fe₃O₄ was not changed by chemical modification. Owing to the coatings of SiO₂ and mesoporous silica layers on the surface of the bare Fe₃O₄ nanoparticles, the strength of the Fe–O stretching band underwent a relative decrease. Secondly, after the SiO₂ layer was coated, peaks appeared at 1089 cm⁻¹, which were attributed to the stretching vibrations of Si–O–Si bonds. Thirdly, after the final modification with DODGA, the appearance of two new peaks at 1730 cm⁻¹ and 2955 cm⁻¹ confirmed that DODGA was successfully covalently bonded to the surface of Fe₃O₄@mSiO₂, and these were attributed to the stretching vibrations of C=O and C–H bonds.

To quantify the DODGA present on the chemically modified Fe₃O₄ nanoparticles, thermogravimetric analysis was used to estimate the content of DGA ligands. As shown in Fig. 2C, in the TGA curves of Fe₃O₄@mSiO₂, Fe₃O₄@mSiO₂@NH₂ and Fe₃O₄@mSiO₂–DODGA in the temperature range of 30–750 °C there was an obvious change in the loss of mass from Fe₃O₄@mSiO₂–DODGA. Owing to the physical adsorption of water by Fe₃O₄@mSiO₂, there was a slight mass loss during the heating process. At 750 °C, the weight loss for Fe₃O₄@mSiO₂ was 0.31 wt%. After the modification with amino groups and DODGA ligands of the surface of the magnetic nanoparticles, an obvious weight loss was detected. DODGA on the nanoparticles began to decompose thermally at about 200 °C. This process did not stop until the temperature reached 500 °C. Finally, the weight loss for Fe₃O₄@mSiO₂–DODGA at 750 °C reached 21.3%, whereas the weight loss for Fe₃O₄@mSiO₂@NH₂ was 8.2%. According to the results of the TGA analysis, the weight percentage of DODGA on the modified nanoparticles was about 13.1%, which indicated that the content of the DODGA ligand on the modified adsorbent was approximately 367 μmol g⁻¹.

The magnetic properties of magnetic nanoparticles are an important aspect of their properties and ensure the rapid separation of adsorbents from a complex matrix. VSM was utilized to investigate the magnetic properties of Fe₃O₄, Fe₃O₄@mSiO₂ and Fe₃O₄@mSiO₂–DODGA nanoparticles. As shown in Fig. 2D, because it was coated with SiO₂ and DODGA layers the saturation magnetization of Fe₃O₄ decreased from the initial value of 58.5 emu g⁻¹ to 37.3 emu g⁻¹. This result for the magnetic response of Fe₃O₄@mSiO₂–DODGA nanoparticles showed that they still possessed high magnetization and could be rapidly and completely separated from the mixture by an external magnetic field within 30 s. These three kinds of nanoparticle displayed no magnetic hysteresis and exhibited superparamagnetic behaviour, which made them disperse homogeneously without an external magnet and aggregate quickly in the presence of a magnet during practical applications.

3.2 Adsorption experiments

The material, namely, Fe₃O₄@mSiO₂–DODGA, that was prepared and used in this study displayed some advantages over former materials. Firstly, magnetic Fe₃O₄ particles were chosen as the inner supporting core. Their excellent superparamagnetic characteristics were beneficial for their rapid collection from real samples. Secondly, the nanosized dimensions of this material guaranteed a large specific surface area for chemical modification for further anchoring the functional ligand DODGA. Thirdly, DODGA, which has a high coordination ability for REEs, was chemically bonded to the Fe₃O₄ particles to create a bifunctional adsorbent.

3.2.1 Effects of the concentration of HNO₃. The nitric acid concentration affected the formation of metal chelates and played an essential role in the adsorption of REEs on Fe₃O₄@mSiO₂–DODGA.

The adsorption rate (AR%) was calculated by:

AR% = (C₀ − C_e) × 100/C₀

where C₀ and C_e are the concentration of the REE in the aqueous phase before and after adsorption, respectively.

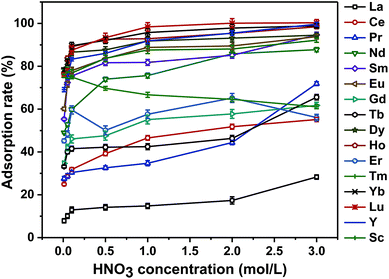
The adsorption results are shown in Fig. 3. When the concentration of the HNO₃ solution was 0.01 mol L⁻¹, the adsorbent displayed different adsorption capabilities for all 16 REEs. All the adsorption rates for each REE were low. With an increase in the concentration of the HNO₃ solution, the adsorption rates for 15 REEs, other than Tm, all increased. The adsorption rates of Fe₃O₄@mSiO₂–DODGA for 9 REEs (namely, Nd, Sm, Eu, Dy, Ho, Yb, Lu, Y and Sc) exceeded 80% when the concentration of the HNO₃ solution was 1.0 mol L⁻¹. However, when the concentration of nitric acid was increased to 3.0 mol L⁻¹, the increase in the adsorption rate of the Fe₃O₄@mSiO₂–DODGA nanoparticles for 9 rare earth elements was not obvious. During the adsorption procedure, a high concentration of HNO₃ could potentially cause damage to instruments. Therefore, a 2.0 mol L⁻¹ HNO₃ solution was used in the following adsorption experiments. In these conditions, the adsorption rates for all 16 rare earth elements ranged from 17.3% to 100.1% (Table 1). Among these elements, the adsorption rates for Nd, Sm, Eu, Dy, Ho, Yb, Lu, Y and Sc ranged from 85.12% to 100.10%.

Fig. 3 Effect of different concentrations of HNO₃ on the adsorption rate.

Table 1 Adsorption and desorption rates for 16 rare earth elements under optimal conditions

Element	AR (%)	DR (%)	Element	AR (%)	DR (%)
La	17	17	Dy	93	67
Ce	52	94	Ho	95	98
Pr	44	45	Er	65	48
Nd	86	88	Tm	65	83
Sm	85	96	Yb	98	98
Eu	90	93	Lu	100	100
Gd	58	64	Y	95	99
Tb	46	43	Sc	88	93

---

Moreover, the ligand has two carbonyl groups and an ether bond of which the oxygen atoms donate electrons to REE ions. It has been reported that⁴⁷ nitrogen donor ligands have higher coordination affinities for trivalent actinide ions in comparison with trivalent lanthanide ions. The adsorption results shown in Table 1 are in agreement with the above conclusion. Furthermore, according to the literature^48,49 cited in the above research article, DODGA exhibited different adsorption behaviour for REEs when it was used in liquid–liquid extraction. As the functional ligand for the adsorption of REEs, the anchoring of DODGA on Fe₃O₄@mSiO₂–DODGA made it display the same adsorption properties. The difference in the amount of each REE adsorbed by Fe₃O₄@mSiO₂–DODGA proved the above conclusion. Moreover, when each REE had the same concentration in the solution, the adsorption behaviour of each REE on Fe₃O₄@mSiO₂–DODGA was competitive. In particular, if the same amount of Fe₃O₄@mSiO₂–DODGA was used for adsorption, the amount of each REE adsorbed was different.

3.2.2 Effects of EDTA concentration on desorption rate. The REEs adsorbed on the Fe₃O₄@mSiO₂–DODGA nanoparticles were recovered by eluting the nanoparticles with an EDTA solution.

The desorption rate (DR%) was calculated by:

DR% = C_d × 100/(C₀ − C_e)

where C_d, C₀ and C_e are the concentration of the REE eluted from Fe₃O₄@mSiO₂–DODGA and the concentrations of the REE in the aqueous phase before and after adsorption, respectively.

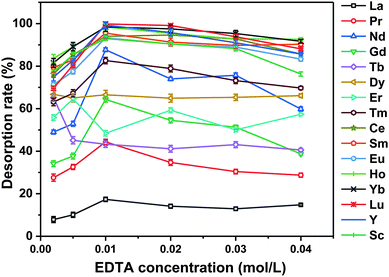
As shown in Fig. 4, when the concentration of EDTA was 0.01 mol L⁻¹ the desorption rate for each REE ion reached its maximum value. The desorption rates for some REEs (namely, Nd, Ce, Sm, Eu, Ho, Yb, Lu, Y, and Sc) were greater than 85% (Table 1). When the concentration of EDTA continued to increase, the desorption rates for the REEs decreased. Therefore, 0.01 mol L⁻¹ EDTA was selected as the optimal concentration in the following experiments.

Fig. 4 Effect of EDTA concentration on desorption rate.

3.2.3 Stability of Fe₃O₄@mSiO₂–DODGA in HNO₃. To determine whether the Fe₃O₄@mSiO₂–DODGA nanoparticles could withstand contact with HNO₃ for the adsorption of REEs, the relative stability of Fe₃O₄@mSiO₂–DODGA in an HNO₃ solution was investigated. Fe₃O₄@mSiO₂–DODGA nanoparticles were immersed in an HNO₃ solution with a concentration of 2 mol L⁻¹ for different times (1, 2, and 3 days). Then, their adsorption capacities for REEs were tested. As shown in Fig. 5, after 3 days the adsorption rate did not decrease significantly, which implied that Fe₃O₄@mSiO₂–DODGA retained its adsorption ability. This also indicated that Fe₃O₄@mSiO₂–DODGA was stable after long-term contact with 2 mol L⁻¹ HNO₃ and could hence be used for the adsorption of rare earth elements in a strongly acidic environment.

Fig. 5 Adsorption rates of Fe₃O₄@mSiO₂–DODGA after being immersed in an HNO₃ solution for different numbers of days.

3.2.4 Reusability of Fe₃O₄@mSiO₂–DODGA for adsorption of REEs. After the stability of Fe₃O₄@mSiO₂–DODGA nanoparticles was tested, their reusability was also examined. The adsorbent was regenerated with 0.01 mol L⁻¹ EDTA 4 times, and the adsorption effect after regeneration was expressed as a percentage of the original adsorption rate. As shown in Table 2, after 4 adsorption–desorption cycles the Fe₃O₄@mSiO₂–DODGA nanoparticles retained 88.25–92.63% of their initial adsorption rate for REEs.

Table 2 Experimental results for reusability of Fe₃O₄@mSiO₂–DODGA

Element	Adsorption rate (%)
	1	2	3	4
La	99	95	92	90
Ce	100	95	92	89
Pr	99	95	92	90
Nd	100	97	94	93
Sm	100	95	92	89
Eu	99	96	92	90
Gd	99	95	92	89
Tb	99	93	90	89
Dy	100	96	92	89
Ho	100	95	92	90
Er	99	94	90	88
Tm	99	96	93	91
Yb	99	96	94	91
Lu	100	95	92	89
Y	99	95	93	91
Sc	100	96	93	92

---

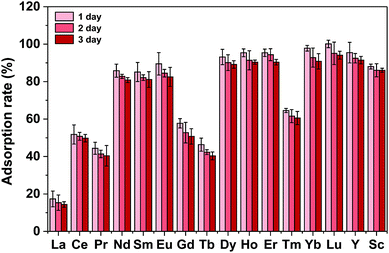
Several kinds of material used for recycling REEs are listed in Table S10.† The materials prepared with magnetic particles as the inner core and a functional ligand are usually employed for recycling one or two kinds of REE ion. After being used for 5 or more cycles, these materials still exhibited high adsorption abilities for REE ions, whereas Fe₃O₄@mSiO₂–DODGA displayed great advantages over these materials.

3.2.5 Effects of coexisting ions on adsorption of REEs. Coexisting ions are ubiquitous in real sample systems and might have a negative effect on the adsorption of REEs. The effects of coexisting cations and anions on the adsorption of REEs were investigated. The effects of fifteen kinds of ion (namely, K⁺, Na⁺, Ca²⁺, Mg²⁺, Fe³⁺, Co²⁺, Ni²⁺, Al³⁺, Zn²⁺, Cu²⁺, Ag⁺, SO₄²⁻, Cl⁻, NO₃⁻, and HPO₄²⁻) on the adsorption capacity were investigated. If the content of a coexisting ion was not higher than the value in Table 3, the adsorption of REEs by these nanoparticles would not be affected. By comparison with the concentrations of coexisting ions in other works,^18,19,23 it was obvious that the Fe₃O₄@mSiO₂–DODGA nanoparticles had excellent anti-interference abilities and the potential to adsorb rare earth ions in complex samples.

Table 3 Tolerance limits for coexisting ions

Coexisting ion	Tolerance limit mg L^−1	Tolerance limit mg L^−1	Tolerance limit mg L^−1	Tolerance limit mg L^−1
K^+	5000	200	—	—
Na^+	5000	200	—	1610
Ca^2+	2000	—	5	200
Mg^2+	2000	—	—	120
Fe^3+	50	—	5	—
Co^2+	50	—	5	—
Ni^2+	50	50	—	—
Al^3+	150	—	—	135
Zn^2+	100	—	—	—
Cu^2+	50	50	—	—
Ag^+	100	67	5	—
SO4^2−	2000	—	—	500
Cl^−	5000	—	—	200
NO3^−	12 000	—	—	200
HPO4^2−	2000	—	—	500
Reference	This work	18	19	23

---

3.2.6 Adsorption kinetics. Considering both the adsorption rate and the desorption rate of Fe₃O₄@mSiO₂–DODGA for all 16 REEs, the nanoparticles exhibited a high binding capacity for 8 rare earth ions (Nd, Sm, Eu, Ho, Yb, Lu, Y and Sc), and could be regenerated easily when EDTA was used as the eluent. Therefore, these 8 REEs were selected for use in the following adsorption kinetics and adsorption isotherm experiments.

The adsorption rate of a material for REEs is commonly considered to be an important criterion for evaluating potential applications of the adsorbent. The adsorption capacity (Q, mg g⁻¹) and the equilibrium adsorption capacity (Q_e, mg g⁻¹) were calculated according to the following equation:

where C₀ (mg L⁻¹) is the initial concentration of REEs in the aqueous phase; C_t (mg L⁻¹) is the initial and remaining concentration of REEs in the aqueous phase at different sampling intervals; V (L) is the volume of the solution; and m (g) is the weight of the adsorbent.

As shown in Fig. 6, the adsorption of REEs by Fe₃O₄@mSiO₂–DODGA could reach adsorption equilibrium in 100 min. It could be calculated that the maximum adsorption capacity of Fe₃O₄@mSiO₂–DODGA was 60.80, 27.54, 36.86, 17.16, 34.36, 42.15, 16.29, and 14.28 mg g⁻¹ for Nd, Sm, Eu, Ho, Yb, Lu, Y, and Sc, respectively.

Fig. 6 Adsorption kinetics of 8 REEs.

On the basis of the data that were obtained, four kinetic models were used to analyze the adsorption behaviour of Fe₃O₄@mSiO₂–DODGA for the 8 REEs. According to the equations in Table 4, the original data were processed and fitted. The corresponding kinetic constants, equilibrium capacities, and correlation coefficients of each adsorption kinetics model are listed in Tables 5 and 6, and the kinetic model equations are listed in the ESI (Tables S1–S4†).

Table 4 Equations of the kinetic models

Kinetic model	Equation	Parameter
Pseudo-first-order^37	qt = qe(1 − e^−k1t)	qe (mg g^−1)	Amount of REEs adsorbed at equilibrium time
		k1 (min^−1)	Pseudo-first-order reaction rate constant
Pseudo-second-order^38		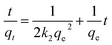k2 (g mg^−1 min^−1)	Pseudo-second-order reaction rate constant
Intra-particle diffusion^39		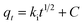ki (mg g^−1 min^−1/2)	Intra-particle diffusion rate constant
		C	Boundary layer diffusion effect
Elovich^40		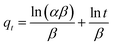α (mg g^−1 min^−1)	Initial adsorption rate constant
		β (mg g^−1 min^−1)	Parameter related to the surface coverage of the adsorbent

---

Table 5 Parameters of pseudo-first-order and pseudo-second-order models

Element	Pseudo-first-order			Pseudo-second-order
	R^2	qe (mg g^−1)	k1 (min^−1)	R^2	qe (mg g^−1)	k2 (g mg^−1 min^−1)
Nd	0.9000	57.36	0.0891	0.9997	61.76	282.73
Sm	0.9755	26.65	0.0665	0.9998	28.01	123.03
Eu	0.7948	35.39	0.1882	1.0000	37.04	56.79
Ho	0.9561	16.43	0.0927	0.9997	17.30	61.47
Yb	0.9761	33.16	0.1052	0.9999	34.60	90.69
Lu	0.5491	39.29	0.2851	0.9998	42.19	84.57
Y	0.9592	15.61	0.1032	0.9999	16.45	51.42
Sc	0.9106	13.85	0.0881	0.9997	14.56	53.58

---

Table 6 Parameters of intra-particle diffusion and Elovich models

Element	Intra-particle diffusion			Elovich
	R^2	ki (mg g^−1 min^−1/2)	C	R^2	α (mg g^−1 min^−1)	β (mg g^−1 min^−1)
Nd	0.6592	1.4109	35.99	0.9612	45.6711	0.03711
Sm	0.5851	0.7398	14.79	0.9266	17.5533	0.06792
Eu	0.5898	0.4675	28.68	0.9298	89.1700	0.10771
Ho	0.4838	0.3864	10.43	0.8744	12.38142	0.12171
Yb	0.5001	0.6897	22.53	0.8899	29.0774	0.06873
Lu	0.8311	0.4466	33.57	0.9867	284.1745	0.12994
Y	0.4985	0.3384	10.42	0.8782	13.1118	0.14076
Sc	0.4386	0.3277	8.76	0.8181	13.0943	0.14125

---

Kinetics plots were obtained by taking Nd as a representative element and are shown in Fig. 7. The pseudo-first-order kinetic model and pseudo-second-order model indicated that adsorption was determined by diffusion and chemical adsorption, respectively. Because the value of R² of the pseudo-second-order model for each REE was 0.999, this model was a better fit than the pseudo-first-order kinetic model. This result indicated that the adsorption of the 8 REEs on the Fe₃O₄@mSiO₂–DODGA nanoparticles mainly occurred in two ways, i.e., physical and chemical adsorption. Chemical adsorption determined the adsorption process.

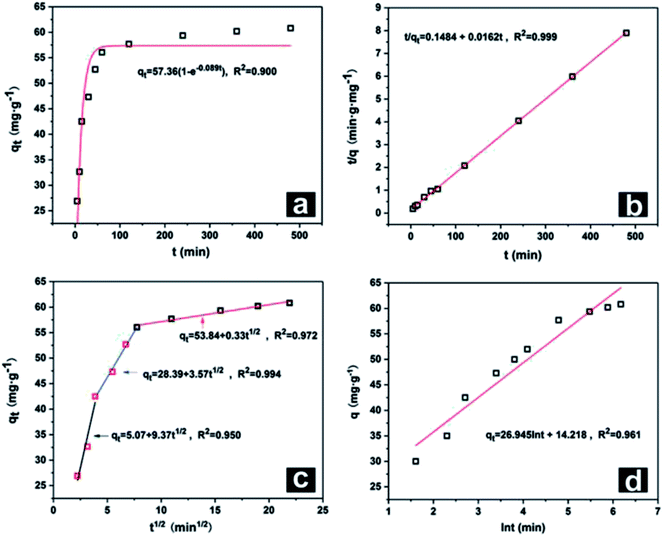Fig. 7 Kinetic plots for Nd as a representative element: (a) pseudo-first-order, (b) pseudo-second-order, (c) intra-particle diffusion, and (d) Elovich models.

After data processing according to the intra-particle diffusion kinetic model, the plot displayed three typical linear relationships. Each linear relationship corresponded to a stage of the adsorption process. The first stage was surface diffusion, which explained the diffusion of REEs from the solution to the surface of Fe₃O₄@mSiO₂–DODGA. The second stage was intra-particle diffusion of REEs between the Fe₃O₄@mSiO₂–DODGA nanoparticles. The third stage was retention of the adsorbate on the active sites, which was considered to be a stage of instantaneous entrapment. This stage could be regarded as negligible.

The Elovich model was used to describe the adsorption process on the surface of a non-uniform solid, which was based on the theoretical assumption that adsorption increased exponentially with the number of adsorption sites, which described the kinetics of a chemical adsorption process. The value of R² of this model was about 0.900, which indicated that the adsorption process of REEs tended to comprise chemical adsorption on an uneven surface, which was consistent with the structural characteristics of the mesoporous layer of nanoparticles.

The adsorption capacity of Fe₃O₄@mSiO₂–DODGA for REEs was mainly reflected by the adsorbed amount. The total amount of REEs adsorbed by the material was 249.44 mg g⁻¹ (Table 7). The highest adsorbed amount for a single REE was 60.8 mg g⁻¹ for Nd(III), which was close to the reported amount.²⁸ Other reported magnetic nanomaterials were used for the adsorption of single rare earth elements, usually Eu or Ce. In this study, the diglycolamide ligand was used to modify the magnetic nanomaterials for the further investigation of the adsorption properties for all 16 REEs and the adsorption kinetics of 8 REEs. The maximum adsorption capacities (Q_max) for 8 REEs of Fe₃O₄@mSiO₂–DODGA in a 2 mol L⁻¹ nitric acid solution are listed in Table 7. As shown, Q_max for Eu(III) was 36.86 mg g⁻¹. This value is higher than those of a series of adsorbent materials such as an Fe₃O₄/sepiolite composite,²¹ Fe₃O₄@CD-MCs²² and Fe₃O₄@HA-MNPs.²³ Fe₃O₄@mSiO₂–DODGA could be used as an effective adsorbent for the adsorption of REEs.

Table 7 Comparison of the adsorption capacities of Fe₃O₄@mSiO₂–DODGA for REEs with those of other magnetic adsorbents

MSPE material	Element	Qmax (mg g^−1)	Reference
SBA-15-BSEA-Fe3O4-NPs	Ce(III)	49.00	18
Fe3O4@SBA-15-Ce(III)-IIP	Ce(III)	87.42	19
Fe3O4@CMC	Eu(III)	42.24	20
Fe3O4/sepiolite	Eu(III)	30.85	21
Fe3O4@CD-MCs	Eu(III)	12.69	22
Fe3O4@HA-MNPs	Eu(III)	10.56	23
Fe@CS-DGA	Pb(II)	70.57	28
Fe3O4@MC-DGA	Am(III)	—	29
Fe3O4@TODGA	Am(III)	—	30
	Pu(IV)	—
Fe3O4@mSiO2–DODGA	Nd(III)	60.80	This work
	Sm(III)	27.54
	Eu(III)	36.86
	Ho(III)	17.16
	Yb(III)	34.36
	Lu(III)	42.15
	Y(III)	16.29
	Sc(III)	14.28

---

3.2.7 Adsorption isotherms. With the aim of understanding the adsorption mechanism during the adsorption process, it was necessary to carry out adsorption equilibrium experiments.

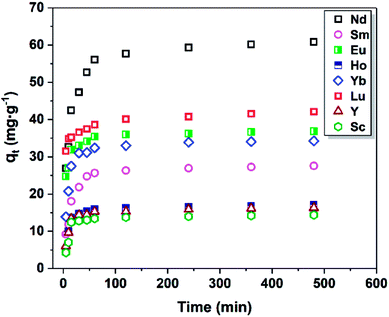
As shown in Fig. 8, the equilibrium adsorption capacity of Fe₃O₄@mSiO₂–DODGA for REEs increased markedly with an increase in the initial REE concentration. When the concentration of REEs was 20 mg L⁻¹, the adsorption capacity reached its maximum value. This result indicated that the main driving force generated by the initial concentration of REEs could significantly affect the mass transfer of REEs from the solution to the surface of Fe₃O₄@mSiO₂–DODGA. Therefore, four kinds of adsorption model (Table 8, namely, Langmuir, Freundlich, Dubinin-Radushkevich (D-R) and Temkin) were utilized to quantify the adsorption capacity and investigate the specific adsorption characteristics of Fe₃O₄@mSiO₂–DODGA. The constants, parameters, and correlation coefficients of the 4 adsorption models are listed in Tables 9 and 10, and the kinetic model equations are listed in the ESI (Tables S5–S8†).

Fig. 8 Adsorption isotherms for the adsorption of REEs on Fe₃O₄@mSiO₂–DODGA.

Table 8 Equations of the adsorption isotherm models

Isotherm model	Equation	Parameters
Langmuir^41		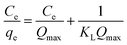KL (L mg^−1)	Constant related to the free energy of adsorption
		Qm (mg g^−1)	Langmuir monolayer adsorption capacity
Freundlich^42		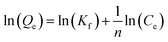Kf	Constant indicative of the relative sorption capacity
		n	Constant indicative of the heterogeneity factor
D-R^43	ln Qe = ln Qm − βε^2	Qm (mg g^−1)	Maximum adsorption capacity in D-R model
		β (mol^2 J^−2)	Constant related to the adsorption energy
Temkin^44	Qe = BT ln KT + BT ln Ce	BT = (RT)/bT	Constant related to the heat of adsorption
		KT (L g^−1)	Polanyi potential, Temkin equilibrium binding constant

---

Table 9 Isotherm parameters of Langmuir and Freundlich models for the adsorption of REEs onto Fe₃O₄@mSiO₂–DODGA

Element	Langmuir			Freundlich
	R^2	Qmax (mg g^−1)	KL (L mg^−1)	R^2	Kf	n
Nd	0.9327	68.96	1.33	0.9972	31.79	2.18
Sm	0.9987	28.57	3.43	0.9366	16.31	3.40
Eu	0.9981	40.16	1.18	0.9838	26.21	6.48
Ho	0.9892	17.27	1.31	0.9950	10.27	5.53
Yb	0.9911	38.75	1.09	0.9828	18.55	1.29
Lu	0.9900	45.45	0.99	0.9444	17.60	2.06
Y	0.9919	17.60	1.78	0.9025	8.83	1.52
Sc	0.9983	14.83	6.41	0.9429	9.87	2.52

---

Table 10 Isotherm parameters of D-R and Temkin models for the adsorption of REEs onto Fe₃O₄@mSiO₂–DODGA

Element	Temkin			D-R
	R^2	BT	KT (L g^−1)	R^2	β (mol^2 J^−2)	E (kJ mol ^−1)
Nd	0.8545	9.08	63.97	0.9543	8.001 × 10^−9	15.81
Sm	0.9702	3.89	153.23	0.9574	1.137 × 10^−8	13.26
Eu	0.9665	7.73	16.24	0.9530	2.801 × 10^−8	8.45
Ho	0.9805	2.24	101.69	0.9603	1.200 × 10^−8	12.91
Yb	0.9395	8.06	12.33	0.9578	3.197 × 10^−8	7.91
Lu	0.9650	7.91	18.79	0.9569	2.000 × 10^−8	10.00
Y	0.8066	3.48	17.40	0.9555	4.001 × 10^−8	7.07
Sc	0.8240	2.30	82.71	0.9666	1.600 × 10^−8	11.18

---

Upon comparing the R² values of the Langmuir and Freundlich models (Fig. 9), it was obvious that the adsorption data were more suitable for fitting with the Langmuir isotherm model than with the Freundlich isotherm model, which demonstrated that the adsorption of REEs by Fe₃O₄@mSiO₂–DODGA comprised single-layer adsorption. Furthermore, the Langmuir dimensionless separation factor R_L was used to predict the affinity between Fe₃O₄@mSiO₂–DODGA and REEs:

RL = 1/(1 + K_LC₀)

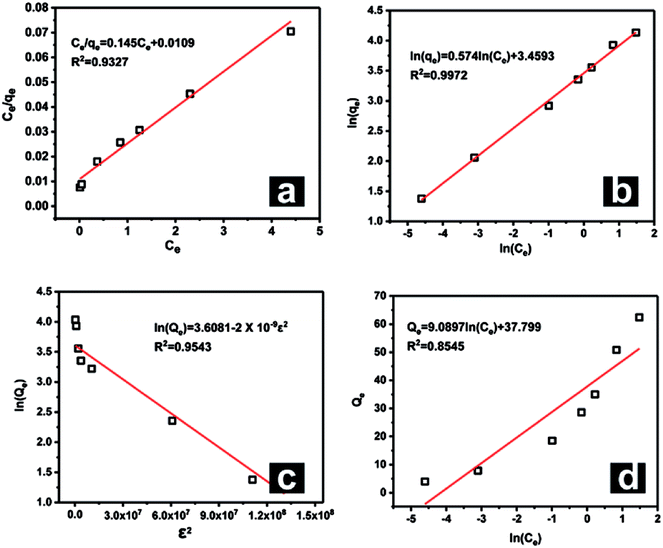Fig. 9 Adsorption model plots for Nd as a representative element: (a) Langmuir, (b) Freundlich, (c) Temkin, and (d) D-R models.

The K_L values for each REE are listed in Table S5.† Because all the K_L values for the 8 REEs were positive, all the R_L values were in the range of 0–1 for all the tested REE concentrations, which indicated that the adsorption process for each REE on Fe₃O₄@mSiO₂–DODGA was favorable.

When the data were fitted with the D-R model, the E values were obtained from this model to explain that the adsorption process was mainly dominated by chemical ion exchange or physical forces.^45,46 The E values for Yb and Y were less than 8 kJ mol⁻¹, which indicated that physical forces dominated the adsorption mechanism. The E values for the other REEs were greater than 8 kJ mol⁻¹, which suggested that chemical ion exchange was the major adsorption mechanism.

Otherwise, the Temkin isotherm model was used to process the data. The R² values were all greater than 0.95. This result indicated that the binding energy distribution for each REE during the adsorption process was homogeneous. This was in agreement with the conclusion drawn from the Langmuir model.

4. Conclusions

In this study, magnetic mesoporous nanoparticles functionalized with the REE-adsorbing ligand DODGA were prepared. The nanoparticles of Fe₃O₄@mSiO₂–DODGA that were obtained were characterized by the corresponding techniques. The results showed that Fe₃O₄@mSiO₂–DODGA had a nanosized spherical shape and mesoporous structure, and the content of the DODGA ligand was about 367 μmol g⁻¹. Moreover, the adsorption performance for 16 rare earth ions was measured using Fe₃O₄@mSiO₂–DODGA as an adsorbent. In 2 mol L⁻¹ HNO₃, the adsorption rate for the 16 rare earth ions reached its maximum value. A 0.01 mol L⁻¹ EDTA solution was selected as the eluent to make the rare earth ions adsorbed on Fe₃O₄@mSiO₂–DODGA undergo effective desorption. The nanoparticles were stable in 2 mol L⁻¹ nitric acid and could be reused 5 times. Moreover, the Fe₃O₄@mSiO₂–DODGA nanoparticles had excellent anti-interference ability and the potential to adsorb rare earth ions in complex samples. The adsorption kinetics and adsorption isotherms of 8 rare earth ions that exhibited good performance in the adsorption and desorption experiments were investigated. An analysis of the kinetic model and adsorption isotherms indicated that the adsorption process of REEs by Fe₃O₄@mSiO₂–DODGA comprised single-layer adsorption via two ways, namely, physical forces and chemical adsorption. The adsorption process was controlled by chemical adsorption and also the synergistic effect of diffusion. The Fe₃O₄@mSiO₂–DODGA nanoparticles showed great potential for applications in the adsorption of REEs in high-salinity media.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was financially supported by the National Key R&D Program of China (No. 2017YFB0702100) and the Major Science and Technology Program for Water Pollution Control and Treatment (No. 2017ZX07402001).

References

1. S. Yasuoka, J. Ishida, K. Kishida and H. Inui, J. Power Sources, 2017, 346, 56–62.
2. X. Cao, L. Chen, S. Guo, F. Fan, R. Chen and A. Yan, Scr. Mater., 2017, 131, 24–28.
3. G. G. Peng, D. Y. Zheng, C. Cheng, J. Zhang and H. Zhang, J. Alloys Compd., 2017, 693, 1250–1256.
4. A. Rout and K. Binnemans, Dalton Trans., 2014, 43, 1862–1872.
5. T. V. Hoogerstraete and K. Binnemans, Green Chem., 2014, 16, 1594–1606.
6. A. Bhattacharyya, P. K. Mohapatra, T. Gadly, D. R. Raut, S. K. Ghosh and V. K. Manchanda, J. Hazard. Mater., 2011, 1951, 238–244.
7. B. Srivastava, M. K. Barman, M. Chatterjee, D. Roy and B. Mandal, J. Chromatogr. A, 2016, 1451, 1–14.
8. X. Chen, Q. Chen, F. Guo, Y. Liao and Z. Zhao, Hydrometallurgy, 2018, 175, 326–332.
9. X. W. Huang, J. S. Dong, L. S. Wang, Z. Y. Zong, Q. N. Xue and X. L. Meng, Green Chem., 2017, 19, 1345–1352.
10. J. Liu, K. Huang, X. Wu, W. Liu, W. Song and H. Liu, Hydrometallurgy, 2018, 175, 340–347.
11. M. K. Jha, A. Kumari, R. Panda, J. R. Kumar, K. Yoo and Y. L. Jin, Hydrometallurgy, 2016, 165, 2–26.
12. D. Li, S. Egodawatte, D. I. Kaplan, S. C. Larsen, S. M. Serkiz and J. C. Seaman, J. Hazard. Mater., 2016, 317, 494–502.
13. D. Xiao, P. Dramou, N. Xiong, H. He, H. Li, D. Yuan and H. Dai, J. Chromatogr. A, 2013, 1274, 44–53.
14. Q. L. Fang, S. D. Duan, J. F. Zhang, J. X. Li and K. C. F. Leung, J. Mater. Chem. A, 2017, 5, 2947–2958.
15. J. J. Wang and J. Wei, J. Mater. Chem. A, 2017, 5, 4651–4659.
16. R. Zhou, N. F. Shen, J. Zhao, Y. Su and H. J. Ren, J. Mater. Chem. A, 2018, 6, 1275–1283.
17. J. Xu, Z. Cao, X. Liu, H. Zhao, X. Xiao, J. P. Wu, X. H. Xu and J. L. Zhou, J. Hazard. Mater., 2016, 317, 656–666.
18. K. Dashtian and R. Zaredorabei, J. Colloid Interface Sci., 2017, 494, 114–123.
19. Y. Liu, J. Qiu, Y. H. Jiang, Z. C. Liu, M. J. Meng, L. Ni, C. C. Qin and J. B. Peng, Microporous Mesoporous Mater., 2016, 234, 176–185.
20. Y. W. Cai, F. Yuan, X. M. Wang, Z. Sun, Y. Chen, Z. Y. Liu, X. K. Wang, S. T. Yang and S. A. Wang, Cellulose, 2016, 24, 1–16.
21. S. M. Yu, X. G. Liu, G. J. Xu, Y. Qiu and L. L. Cheng, Desalin. Water Treat., 2015, 57, 1–12.
22. Z. Q. Guo, Y. Li, S. H. Pan and J. Z. Xu, J. Mol. Liq., 2015, 206, 272–277.
23. S. T. Yang, P. F. Zong, X. M. Ren, Q. Wang and X. K. Wang, ACS Appl. Mater. Interfaces, 2012, 4, 6891–6900.
24. E. A. Mowafy and D. Mohamed, Sep. Purif. Technol., 2014, 128, 18–24.
25. K. Shimojo, K. Kurahashi and H. Naganawa, Extraction behavior of lanthanides using a diglycolamide derivative TODGA in ionic liquids, Dalton Trans., 2008, 252, 5083–5088.
26. F. K. Li, A. J. Gong, L. N. Qiu, W. W. Zhang, J. R. Li, Y. Liu, Y. N. Liu and H. T. Yuan, PLoS One, 2017, 12, e0185302.
27. H. T. Yuan, W. X. Hong, Y. S. Zhou, B. S. Pu, A. J. Gong, T. Xu, Q. S. Yang, F. K. Li, L. N. Qiu, W. W. Zhang and Y. N. Liu, J. Rare Earths, 2018, 336, 624–627.
28. R. X. Bai, Y. Zhang, Z. G. Zhao, Q. X. Liao, P. Chen, P. P. Zhao, W. H. Guo, F. Yang and L. C. Li, J. Ind. Eng. Chem., 2018, 59, 416–424.
29. S. Ojha, S. Chappa, A. M. Mhatre, K. K. Singh, V. Chavan and A. K. Pandey, J. Radioanal. Nucl. Chem., 2017, 312, 675–683.
30. V. Chavan, V. Thekkethil, A. K. Pandey, M. Iqbal, J. Huskens, S. S. Meena, A. Goswami and W. Verboom, React. Funct. Polym., 2014, 74, 52–57.
31. S. W. Cao, Y. J. Zhu and J. Chang, New J. Chem., 2008, 32, 1526–1530.
32. D. Liu, Y. Li, J. Deng and W. Yang, React. Funct. Polym., 2011, 71, 1040–1044.
33. J. P. Yang, F. Zhang, Y. R. Chen, S. Qian, P. Hu, W. Li, Y. H. Deng, Y. Fang, L. Han, M. Luqman and D. Y. Zhao, Chem. Commun., 2011, 47, 11618–11620.
34. Y. H. He, Y. Y. Huang, Y. L. Jin, X. J. Liu, G. Q. Liu and R. Zhao, ACS Appl. Mater. Interfaces, 2014, 6, 9634–9642.
35. G. Kantin, E. Chupakhin, D. Dar'in and M. Krasavin, Tetrahedron Lett., 2017, 58, 3160–3163.
36. M. Bessodes and N. Mignet, Nanotechnology for Nucleic Acid Delivery, 2013, vol. 948, pp. 67–84.
37. N. A. Oladoja, C. O. Aboluwoye and Y. B. Oladimeji, Turk. J. Eng. Environ. Sci., 2008, 32, 303–312.
38. Y. S. Ho and G. McKay, Sorption of dye from aqueous solution by peat, Chem. Eng. J., 1998, 70, 115–124.
39. M. K. Sureshkumar, D. Das, M. B. Mallia and P. C. Gupta, J. Hazard. Mater., 2010, 184, 65–72.
40. S. H. Chein and W. R. Clayton, Soil Sci. Soc. Am. J., 1980, 44, 265–268.
41. E. Repo, J. K. Warchol, T. A. Kurniawan and M. E. T. Sillanpää, Chem. Eng. J., 2010, 161, 73–82.
42. M. Jain, V. K. Garg and K. Kadirvelu, J. Hazard. Mater., 2009, 162, 365–372.
43. X. J. Hu, J. S. Wang, Y. G. Liu, X. Li, G. M. Zeng, Z. L. Bao, X. X. Zeng, A. W. Chen and F. Long, J. Hazard. Mater., 2011, 185, 306–314.
44. A. Sari and M. Tuzen, J. Hazard. Mater., 2009, 164, 1004–1011.
45. S. Ricodel, S. Tahaa, I. Cisseb and G. Dorange, Sep. Purif. Technol., 2001, 24, 389–401.
46. M. Arias, M. T. Barral and J. C. Mejuto, Chemosphere, 2002, 48, 1081–1088.
47. E. A. Mowafy and D. Mohamed, Sep. Purif. Technol., 2014, 128, 18–24.
48. E. A. Mowafy and H. F. Aly, Solvent Extr. Ion Exch., 2006, 24, 677–692.
49. S. A. Ansari, P. K. Mohapatra, D. R. Raut, V. C. Adya, S. K. Thulasidas and V. K. Manchanda, Sep. Purif. Technol., 2008, 63, 239–242.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra07762b

---