Open Access Article
Open Access ArticleUnderstanding the effects of vicinal carbon substituents and configuration on organofluorine hydrogen-bonding interaction†
Qingqing Jiaa,
Qingzhong Li b,
Mo Luoa and
Hai-Bei Li
b,
Mo Luoa and
Hai-Bei Li *a
*a
aSchool of Ocean, Shandong University, Weihai 264209, People's Republic of China. E-mail: lihaibei@sdu.edu.cn
bThe Laboratory of Theoretical and Computational Chemistry, School of Chemistry and Chemical Engineering, Yantai University, Yantai 264005, People's Republic of China
First published on 20th November 2018
Abstract
An investigation of C–F⋯H–O hydrogen bonds in the complexes CHnXCHnF⋯H2O (n = 0, 1, 2; X = H, F, Cl, Br) was performed at the MP2/aug-cc-pVTZ level. We found that the electron-withdrawing halogen substituents on the vicinal carbon cause the fluorine atom, participating in the hydrogen bond formation, to be less negatively charged. Thus, the halogen groups weaken the strength of organofluorine hydrogen bond by inductive effect. The position of the substituents on the vicinal carbon affects the strength of the C–F⋯H–O interaction. Compared with that in other isomers, the electron withdrawing substituent in 1-fluoro-ethane with stagger conformation as well as in 1-fluoro-ethene with trans configuration much weakens the interaction of C–F⋯H–O due to the hyperconjugative interaction between σ(C–F) and 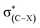 . By analogy, the electron-donating ones could largely strengthen it. We found that there is a good linear relationship between electron density at the BCP of F⋯H and Wiberg bond indexes (WBI) as well as between natural bond-bond polarizability (NBBP) and WBI, which indicates that the magnitude of NBBP and WBI could be a good indicator of the hydrogen bond strength.
. By analogy, the electron-donating ones could largely strengthen it. We found that there is a good linear relationship between electron density at the BCP of F⋯H and Wiberg bond indexes (WBI) as well as between natural bond-bond polarizability (NBBP) and WBI, which indicates that the magnitude of NBBP and WBI could be a good indicator of the hydrogen bond strength.
1. Introduction
The organofluorine compounds play important role in many aspects of the chemical industry, such as drug design, fine chemicals, and agrochemicals.1–3 They are also important intermediates in organic syntheses.4 The high electronegativity of fluorine leads to the organic fluorine, that is, δ+C–δ−F bond being highly polarized with more electrostatic character rather than covalent one.5 Thus, in the past three decades, whether or not C–F bond can act as a hydrogen-bond acceptor has long been a controversial issue.6–9 Some points of view prefer the polarized C–F bond interacting with other molecules through electrostatic or dipole interactions.5 The lone pairs of fluorine are held tightly due to its high electronegativity, thus they are reluctant to interact as hydrogen bond acceptor. Until to 2011, IUPAC revised the definition of hydrogen bond and reset the criteria for it.10 Upon the basis of the new criteria, it has been proved that the C–F bond can act as a hydrogen bond acceptor. The low polarizability and tightly held lone pairs make fluorine a weaker hydrogen-bond acceptor compared with oxygen or nitrogen.Karanam and Choudhury reported that the fluorinated azobenzenes prefer to pack in the lattice by forming C–H⋯F–C(sp2) hydrogen bonds rather than by C–F⋯F–C, C–F⋯π, and π⋯π interactions, while the chlorinated and brominated analogues favor the latter interactions.11 This indicates that the strength of hydrogen bonds involving organic halogen atom is in the order of F > Cl > Br, whereas it is in the reverse order for the halogen bonds. And their studies show that the strength of C–H⋯F–C(sp2) is very small in the range from −0.8 to −1.0 kcal mol−1. Dalvit and Vulpetti discovered a correlation between the NMR chemical shift of 19F and the strength of C–F⋯H–X interaction by running a statistical analysis of the CSD X-ray crystal structures of fluorinated molecules.12 Upon the basis of this correlation, they pointed out the organofluorine hydrogen bond is relevant for the molecular recognition mechanism and the stabilization of a preferred conformation. Undoubtedly, the strength of hydrogen bond is related to the nature of the hydrogen-bond donor and acceptor. Panini and Chopra have confirmed that the interaction of C(sp2)–H⋯F–C(sp2/sp3) is stronger than that of C(sp3)–H⋯F–C(sp2/sp3), which indicates C(sp2)–H is a better donor than C(sp3)–H; Similarly, they also found that C(sp2/sp3)–H⋯F–C(sp3) is more stable than C(sp2/sp3)–H⋯F–C(sp2), implying C(sp3)–F is a better acceptor than C(sp2)–F.13 Paquin group14 thoroughly reviewed the characteristics and properties of the intermolecular and intramolecular C–F⋯H–X interactions with C(sp2/sp3)–F as hydrogen-bond acceptor and O–H, N–H, C(sp2/sp3)–H as donor. In their studies, the presence of the organofluorine hydrogen bonds has been proved by spectroscopic experimental techniques and theoretical analysis. They figured out that organofluorine hydrogen bonds would have an impact on the chemical behaviors, like some measurable chemical equilibrium, such as acidity/basicity, preferential conformation, and reactivity.
As early as 1996, the hybridization of carbon atom in C–F bond affecting the strength of hydrogen bonds has been raised. Howard et al.6 performed a theoretical calculation of C–F⋯H–O hydrogen bonds between H2O and CH3F/CH2CHF. They found that the C(sp3)–F fluorine is a better hydrogen bonds acceptor than C(sp2)–F fluorine. Subsequently, the hybridization effect of C atom on the strength of C(spn)–F⋯H–F (n = 1, 2, and 3) hydrogen bonds was studied in the complexes CH3F⋯HF, CH2CHF⋯HF and CHCF⋯HF, which confirms that the hydrogen-bond acceptor ability of C–F increases in the order: C(sp)–F < C(sp2)–F < C(sp3)–F.15 Masoodi et al.16 further studied the effects of carbon hybridization and halogen-acceptor type on some NMR data of HF which is hydrogen bond donor in the complex. They found that the proton shielding tensor of HF increases as C(sp3) < C(sp2) < C(sp), while this trend for fluorine in HF depends on the halogen-acceptor type. For organofluorine hydrogen bond, it is in the order of C(sp3) > C(sp2) > C(sp). Giuffredi et al.17 provided the experimental evidence demonstrating that the group –CHF is a better hydrogen bond acceptor than –CF2. This indicates that the proximal withdrawing electronic substituents weaken the strength of the organofluorine hydrogen bond, which illustrates the strength of the organofluorine hydrogen bond could be modulated by the proximal substituents. However, it is possible for the proximal substituent to largely influence the properties of C–F bond, and then affects the other processes involving fluorine, such as chemical reactions and drug design. Until now, the investigation about the effects of the vicinal substituents on the properties of C(spn)–F⋯H–X interaction is scarce. Exploring the role of the vicinal substituents on this interaction is necessary to fully understand the nature of organofluorine hydrogen bonds, especially for the modulation of its strength via the substitution at the vicinal carbon.
In the present work, we take water as proton donor and the derivatives of 1-fluoro-ethane, 1-fluoro-ethene, and 1-fluoro-ethyne as proton acceptor, that is, the complexes are CHnXCHnF⋯H2O (n = 0, 1, 2; X = H, F, Cl, Br). We carried out ab initio calculations to place a particular emphasis on understanding the effect of the vicinal substituents on the interaction of C(spn)–F⋯H–O hydrogen bond. Furthermore, through the study of cis/trans isomer in CHXCHF and gauche/stagger isomer in CH2XCH2F, we evaluate the effect of the position of vicinal substituents on the interaction, and this will play important roles in many chemical processes,18 such as chemical enantiomeric selectivity and molecular recognition.
2. Theoretical methods
All structures were fully optimized at the level of MP2/aug-cc-pVTZ using the Gaussian 09 program, Revision D.01.19 The frequency calculations were performed to confirm the optimized structures being the local minimum on the potential surfaces. To eliminate the effects of basis set superposition error (BSSE), the approach of counterpoise proposed by Boys and Bernardi20 was performed in the optimization as well as in the calculation of the interaction energy. Upon the basis of Bader's atoms in molecules (AIM) theory,21 the properties of bond critical points (BCPs) referring to the organofluorine hydrogen bond were calculated using AIM2000 program22 at the same level with optimization. The natural bond orbital (NBO)23 analysis was applied to evaluate the hyperconjugation energy, natural bond-bond polarization (NBBP), and Wiberg bond index (WBI) related to the region of the hydrogen bond interaction using the NBO 6.0 program24 at the HF/aug-cc-pVTZ level. Non-covalent interaction (NCI) index and molecular electrostatic potential analyses were finished via the Multiwfn program25 with the isosurface maps rendered by VMD1.9.3 software.263. Results and discussion
3.1 Geometrical parameters and interaction energy
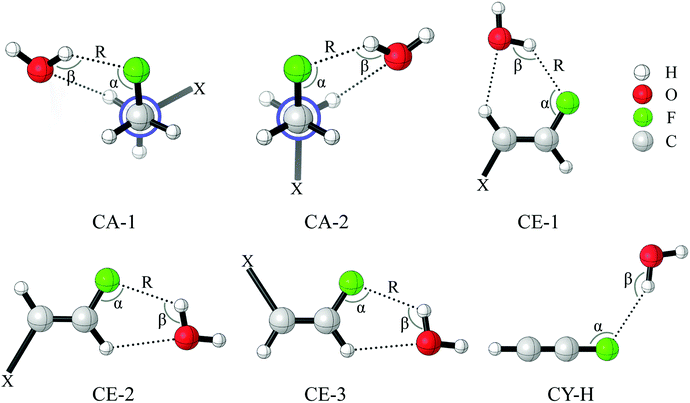
Fig. 1 presents the optimized geometries of the complexes CHnXCHnF⋯H2O (n = 0, 1, 2; X = H, F, Cl, Br). Here, CA, CE, and CY stand for the complexes of 1-fluoro-ethane, 1-fluoro-ethene, and 1-fluoro-ethyne, respectively. Depending on the position of the vicinal substituents, the derivative of 1-fluoro-ethane has gauche and stagger conformations, and that of 1-fluoro-ethene with cis and trans configurations. This leads to the formation of two and three structures for complexes CA and CE, respectively. It is evident from Fig. 1 that the C–F⋯H–O and C–H⋯O–H hydrogen bonds coexist in the CA and CE complexes. The distances of C–F⋯H–O for CA-1-H, CE-1-H, and CE-2-H are 2.011, 2.130, and 2.198 Å (Table 1), respectively, which is much less than the sum of the van der Waals atomic radius of F (1.47 Å) and H (1.20 Å).27 In CA-1-H and CE-1-H, the angle of O–H⋯F is close to 150°. This value decreases to ∼130° in CE-2-H due to the steric effect, where the proton acceptor of C–F⋯H–O and proton donor of C–H⋯O–H connect to the same carbon atom (Fig. 1). The interaction of C–F⋯H–O results in the redshift of O–H stretching vibrational frequency. All these geometrical parameters figure out that the C–F⋯H–O interaction belongs to the conventional hydrogen bond.| Complexes | X | α | β | R(F⋯H) | Δν(O–H) | ΔE |
|---|---|---|---|---|---|---|
| a α is for ∠C–F⋯H, and β is for ∠O–H⋯F, bond angles in degree; bond lengths in Å; frequencies in cm−1. | ||||||
| CA-1-X | H | 102.4 | 147.2 | 2.011 | −46.2 | −4.37 |
| F | 101.1 | 135.0 | 2.087 | −35.3 | −4.66 | |
| Cl | 102.0 | 134.8 | 2.088 | −35.4 | −4.78 | |
| Br | 102.2 | 135.4 | 2.086 | −35.5 | −4.81 | |
| CH3 | 103.4 | 149.2 | 2.001 | −47.8 | −4.34 | |
| NH2 | 104.3 | 147.5 | 2.000 | −50.8 | −4.75 | |
| NO2 | 101.1 | 126.6 | 2.177 | −26.9 | −4.97 | |
| CA-2-X | H | 102.4 | 147.2 | 2.011 | −46.2 | −4.37 |
| F | 103.2 | 135.0 | 2.099 | −29.3 | −4.07 | |
| Cl | 103.1 | 134.8 | 2.099 | −31.3 | −4.33 | |
| Br | 102.8 | 135.0 | 2.098 | −32.3 | −4.41 | |
| CE-1-X | H | 114.9 | 148.1 | 2.130 | −23.2 | −3.25 |
| F | 116.3 | 135.6 | 2.209 | −17.8 | −3.54 | |
| Cl | 116.2 | 135.0 | 2.223 | −17.9 | −3.48 | |
| Br | 115.8 | 135.3 | 2.225 | −18.5 | −3.50 | |
| CE-2-X | H | 102.1 | 130.2 | 2.198 | −18.1 | −3.20 |
| F | 100.9 | 121.0 | 2.309 | −13.1 | −3.10 | |
| Cl | 101.1 | 119.1 | 2.334 | −12.6 | −3.11 | |
| Br | 101.2 | 118.9 | 2.336 | −12.8 | −3.12 | |
| CE-3-X | H | 102.1 | 130.2 | 2.198 | −18.1 | −3.20 |
| F | 100.5 | 122.0 | 2.299 | −14.4 | −3.33 | |
| Cl | 100.9 | 120.2 | 2.322 | −13.9 | −3.34 | |
| Br | 101.0 | 119.9 | 2.327 | −14.0 | −3.34 | |
| CY-X | H | 122.9 | 153.2 | 2.375 | −2.8 | −0.56 |
| CH3 | 118.6 | 166.6 | 2.301 | −4.8 | −0.93 | |
In the complexes CA-1-H, CE-1-H, and CE-2-H, the C–H⋯O–H interaction is confirmed by the presence of the bond critical point (BCP) between H⋯O contact based on the AIM analysis (see Section 3.3), and its weak strength is illustrated by non-covalent interaction analysis (see Section 3.2). Thus, the C–H⋯O–H interaction makes a limited contribution to the total interaction energy. From Table 1, the total interaction energy of the complexes is larger than 3.00 kcal mol−1 in CA and CE. This indicates that the sp3- and sp2-C–F bonds in the fluorinated compounds are likely to form the organofluorine hydrogen bond with medium strength. In comparison with sp3- and sp2-C–F, sp-C–F bond in CHCF is a very poor hydrogen bond acceptor according to the interaction energy (0.56 kcal mol−1) and the magnitude of Δν(O–H), which is consistent with the previous studies.15 This indicates that in the fluorinated compounds involving sp-C–F, the possibility to form the organofluorine hydrogen bond is small. Although the strength of the sp-C–F⋯H–O interaction increases by the addition of the electron-donating vicinal substituents, such as CH3 (Table 1), the addition of the electron-withdrawing vicinal halogen substituents results in the parallel arrangement of O–H and C–F bonds. This implies that there is no sp-C–F⋯H–O hydrogen bond formation between CXCF (X = F, Cl, Br) and H2O. Thus, in the following section, we do not discuss the complexes involving CXCF (X = F, Cl, Br).
The halogen substituents at the vicinal carbon weaken the C–F⋯H–O interaction, which is evidenced by the longer distance of F⋯H contact, the smaller angle of ∠C–F⋯H, and the less redshift of O–H stretching vibrational frequencies compared with that of no vicinal halogen substituents (Table 1). This illustrates that the vicinal halogen substituents, like the proximal ones,17 weaken the ability of C–F to act as a weak hydrogen-bond acceptor. We further add –NO2, –CH3, and –NH2 groups at the vicinal carbon in CA-1. As anticipated, with the more electron-withdrawing –NO2 substituent at the vicinal carbon, the C–F bond is a weaker hydrogen-bond acceptor than that with halogen. On the contrary, the electron-donating groups strengthen the ability of C–F to be a better hydrogen-bond acceptor. The position of halogen atom, such as the gauche and stagger conformations in 1-fluoro-ethane, has slightly different effect on the C–F⋯H–O interaction. The magnitudes of the distance of F⋯H contact and the redshift of O–H stretching vibrational frequencies indicate that the C–F⋯H–O interaction in the stagger conformation is slightly weaker than that in the gauche one. We attribute this to the hyperconjugative interaction28–30 between σ(C–F) and 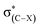 , which delocalizes the electron density of fluorine atom. The similar trend is found for the trans and cis configuration in the 1-fluoro-ethene complexes, CE-2 and CE-3, respectively.
, which delocalizes the electron density of fluorine atom. The similar trend is found for the trans and cis configuration in the 1-fluoro-ethene complexes, CE-2 and CE-3, respectively.
The halogen substituent plays duel role in the total interaction strength of the complexes. For C–F⋯H–O organofluorine hydrogen bonds, the vicinal halogen reduces its interaction strength. On the contrary, for C–H⋯O–H interaction, the electron-withdrawing halogen group is the proximal carbon substituent for proton donor C–H, and they increases the strength of C–H⋯O–H interaction.31 It is evident from Table 1 that the interaction energy is slightly larger in CA-1-X, CE-1-X, and CE-3-X (X = F, Cl, and Br) than that in its no vicinal halogen substituent complex. This indicates that the influence of the halogen substituent on the strength of C–H⋯O–H is greater than that on C–F⋯H–O. Differently, in CA-2-X and CE-2-X, the effect of the vicinal electron-withdrawing substituents on the strength of C–F⋯H–O is more significant than that on C–H⋯O–H, due to the hyperconjugative interaction between bonding and antibonding orbitals of C–F and C–X bonds.
3.2 Molecular electrostatic potential and non-covalent interaction analysis
Electrostatic potential (ESP) analysis is useful to study noncovalent interactions.32–34 A good correlation between the ability of hydrogen-bond acceptor and its molecular ESP minimum value (Vmin) has been confirmed.35 Fig. 2 presents the ESP maps for the optimized monomers of CHnXCHnF (n = 0, 1, 2; X = H, Cl) on the van der Waals surface,36 in which MA, ME, and MY stand for the monomers, 1-fluoro-ethane, 1-fluoro-ethene, and 1-fluoro-ethyne, respectively. The surfaces were colored on a blue-white-red scale according to the values of ESP. It is evident that the local Vmin of fluorine atom shows the dramatic decrease from −24.44, −16.40 to −2.06 kcal mol−1 (MA-H, ME-H, and MY-H in Fig. 2, respectively) with the increase of s-character for sp3-, sp2-, and sp-C atom. The variation of these local Vmin values on fluorine atom are consistent with that of the spn-C–F⋯H–O interaction strength. As anticipated, the electron withdrawing characteristic of the halogen groups decreases the local EPS of F, especially in the stagger conformation, MA-2, and trans configuration, ME-1 (Fig. 2). On the contrary, the electron-donating groups increases it (Fig. S1†). This correlation illustrates the electrostatic character of the organofluorine hydrogen bonds.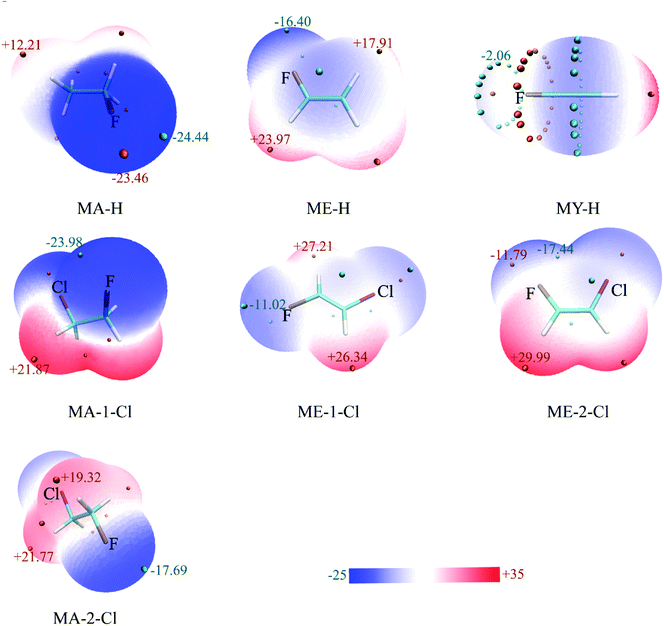 | ||
| Fig. 2 ESP-mapped molecular vdW surface of optimized monomers, in kcal mol−1. The elements of F and Cl were represented as ochre and purple, respectively. | ||
The non-covalent interaction approach, proposed by Yang et al.37 is widely used to study hydrogen bond interactions38–40 by the isosurface of the reduced density gradient (RDG). It has been confirmed that the result is insensitive to the computational level.37 The RDG analysis has been performed via Multiwfn program at B3LYP/6-31G* level. The scatter diagrams, sign(λ2)ρ versus RDG, have shown in Fig. 3 and 4. The spikes representing C–F⋯H–O interaction were marked by arrows, and the left ones with sign(λ2)ρ smaller than zero stand for the interaction of C–H⋯O–H. It is apparent from Fig. 3 and 4 that the strength of C–F⋯H–O organofluorine hydrogen bond is much stronger than that of the C–H⋯O–H in the complexes, particularly in the CH3CH2F⋯H2O. The spike values for spn-C–F⋯H–O interaction implies the hybridization of carbon atom significantly affects the interaction strength (Fig. 3a). The ability of F atom as proton acceptor is in the order: C(sp3)–F > C(sp2)–F > C(sp)–F. Similarly, the position of the spikes for vicinal Cl-substituent complexes (Fig. 3b and c) is consistent with the strength of C–F⋯H–O in the gauche and stagger isomers CA-1-Cl and CA-2-Cl, respectively, as well as in the trans and cis isomers CE-1-Cl, CE-2-Cl, and CE-3-Cl. The same case is for other halogen-substituents (see Fig. S2†). The vicinal halogen-substituents generally weaken the interaction of C–F⋯H–O, indicated by the right shift of spikes for F-, Cl-, and Br-substituent complexes compared with that in CA-1-H and CE-1-H (Fig. 4a and b). And in CA-1-X and CE-1-X, the close spike values for C–F⋯H–O interaction with vicinal F-, Cl-, and Br-substituent illustrate that the effect of vicinal halogen-substituent on the strength of C–F⋯H–O is similar. This is in accordance with the approximately equal values of both Δν(O–H) and the distance of F⋯H contact, respectively, in CA-1-X and CE-1-X (Table 1). This demonstrates that the electron withdrawing halogen group at the vicinal carbon affects the strength of the C–F⋯H–O interaction by inductive effect. However, due to the long distance transmission of electron, the inductive effect of F-, Cl-, and Br-substituent on the strength of C–F⋯H–O is comparative.
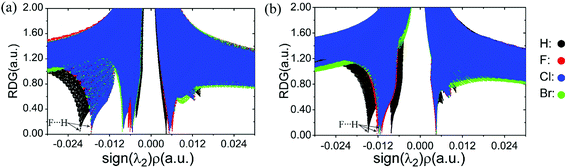 | ||
| Fig. 4 Plots of the reduced density gradient, RDG, versus the electron density multiplied by the sign of the second Hessian eigenvalue, sign(λ2)ρ for complexes (a) CA-1-X and (b) CE-1-X. | ||
3.3 AIM and NBO analysis
The quantum theory of atoms in molecules (QTAIM) proposed by Bader21 provides a powerful tool to investigate the properties of hydrogen bonds. A set of criteria have been proposed to characterize hydrogen bonds.41,42 The molecular graphs involving the BCPs in the complexes were presented in Fig. S3.† The local properties at the BCPs of C–F⋯H–O were listed in Table 2. Koch and Popelier41 proposed that the most important indicator to assess the existence of hydrogen bonds is the values of electron density and its Laplacian (∇2ρ(r)) at the BCPs. They proposed that the electron density falls within 0.002 to 0.04 a.u. and the ∇2ρ(r) ranges from 0.02 to 0.15 a.u. for the evidence of the existence of hydrogen bonds. In this work, the electron density at the BCPs is in the range from 0.007 to 0.018 a.u., and the ∇2ρ(r) is from 0.03 to 0.076 a.u. (Table 2), both of which lie within the range proposed by Koch and Popelier. Moreover, the ∇2ρ(r) as well as the total electronic energy density, H, is positive, indicating that C–F⋯H–O interaction is weak hydrogen bond upon the basis of the hydrogen bond classification proposed by Rozas et al.42| Complexes | X | ρ(r)a | ∇2ρ(r)a | Ha | NBBPb | E(2)b | WBI (F⋯H)b |
|---|---|---|---|---|---|---|---|
a Electron density, ρ(r), the Laplacian of the electron density, ∇2ρ(r) and the total electron energy density H at BCP of F⋯H. All are in a.u.b Natural bond-bond polarizability (NBBP, in a.u.) between O–H and C–F as well as the lone pairs of F, Wiberg bond index (WBI, in a.u.) of F⋯H, second-order perturbation energy (E(2), kcal mol−1) containing 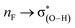 and and 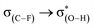 . . |
|||||||
| CA-1-X | H | 0.0180 | 0.076 | 0.0015 | 0.0087 | 3.16 | 0.0086 |
| F | 0.0154 | 0.070 | 0.0024 | 0.0059 | 1.90 | 0.0058 | |
| Cl | 0.0153 | 0.070 | 0.0025 | 0.0057 | 1.87 | 0.0058 | |
| Br | 0.0154 | 0.070 | 0.0024 | 0.0058 | 1.91 | 0.0059 | |
| CH3 | 0.0184 | 0.078 | 0.0018 | 0.0092 | 3.45 | 0.0091 | |
| NH2 | 0.0185 | 0.078 | 0.0019 | 0.0093 | 3.43 | 0.0091 | |
| NO2 | 0.0128 | 0.060 | 0.0025 | 0.0034 | 1.08 | 0.0036 | |
| CA-2-X | H | 0.0180 | 0.076 | 0.0020 | 0.0087 | 3.16 | 0.0086 |
| F | 0.0149 | 0.067 | 0.0025 | 0.0051 | 1.76 | 0.0053 | |
| Cl | 0.0149 | 0.068 | 0.0025 | 0.0053 | 1.75 | 0.0054 | |
| Br | 0.0150 | 0.068 | 0.0024 | 0.0053 | 1.78 | 0.0055 | |
| CE-1-X | H | 0.0130 | 0.057 | 0.0023 | 0.0043 | 1.55 | 0.0048 |
| F | 0.0110 | 0.051 | 0.0022 | 0.0025 | 0.85 | 0.0031 | |
| Cl | 0.0107 | 0.049 | 0.0021 | 0.0023 | 0.76 | 0.0029 | |
| Br | 0.0106 | 0.049 | 0.0021 | 0.0023 | 0.76 | 0.0029 | |
| CE-2-X | H | 0.0117 | 0.055 | 0.0015 | 0.0029 | 0.94 | 0.0034 |
| F | 0.0095 | 0.045 | 0.0021 | 0.0015 | 0.45 | 0.0021 | |
| Cl | 0.0091 | 0.043 | 0.0020 | 0.0013 | 0.38 | 0.0019 | |
| Br | 0.0091 | 0.043 | 0.0020 | 0.0013 | 0.37 | 0.0019 | |
| CE-3-X | H | 0.0117 | 0.055 | 0.0015 | 0.0029 | 0.94 | 0.0034 |
| F | 0.0097 | 0.046 | 0.0021 | 0.0016 | 0.47 | 0.0021 | |
| Cl | 0.0093 | 0.044 | 0.0020 | 0.0014 | 0.41 | 0.0019 | |
| Br | 0.0092 | 0.044 | 0.0020 | 0.0014 | 0.39 | 0.0019 | |
| CY-X | H | 0.0066 | 0.030 | 0.0015 | 0.0008 | 0.33 | 0.0013 |
| CH3 | 0.0080 | 0.036 | 0.0015 | 0.0014 | 0.60 | 0.0019 | |
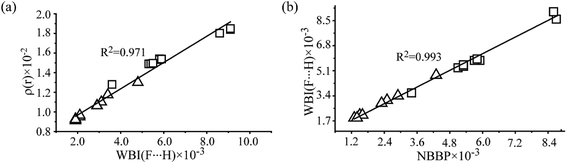
The second-order perturbation energy E(2) of the NBO analysis in Table 2 is the sum of interaction energy from the lone pairs of F and the bonding orbital of C–F, σ(C–F), to the antibonding orbital of O–H, 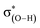 . It is evident from Table 2 that the E(2) in the complexes with vicinal halogen substituent is nearly one time less than that with no vicinal substituent. This implicates that the vicinal substituents largely affect the charge transfer from orbitals of the proton acceptor to ones of the proton donor. We calculate the WBI and NBBP indices referring to the region of hydrogen bond formation by the NBO analysis. WBI is a parameter to measure the strength between two atoms, and NBBP is a quantitative descriptor for the electronic delocalization effect. In this work, WBI is referred to the F⋯H, and the magnitude of NBBP is the sum of nF ↔ σ(O–H) and σ(C–F) ↔ σ(O–H). Fig. 5 depicts the relationships among the WBI, electron density and NBBP. As this figure illustrates, the electron density at the BCPs of F⋯H and WBI, as well as the NBBP and WBI, have good linear relationships. This indicates that like the electron density, the magnitude of WBI and NBBP, in which the latter is the sum of NBBPs referred to the bonds directly participating in the hydrogen bond formation, could be a good indicator of the hydrogen bond strength. This would be useful for the estimation of the intramolecular hydrogen bond strength as well as the single intermolecular hydrogen bond strength in the system, where several hydrogen bonds coexist.
. It is evident from Table 2 that the E(2) in the complexes with vicinal halogen substituent is nearly one time less than that with no vicinal substituent. This implicates that the vicinal substituents largely affect the charge transfer from orbitals of the proton acceptor to ones of the proton donor. We calculate the WBI and NBBP indices referring to the region of hydrogen bond formation by the NBO analysis. WBI is a parameter to measure the strength between two atoms, and NBBP is a quantitative descriptor for the electronic delocalization effect. In this work, WBI is referred to the F⋯H, and the magnitude of NBBP is the sum of nF ↔ σ(O–H) and σ(C–F) ↔ σ(O–H). Fig. 5 depicts the relationships among the WBI, electron density and NBBP. As this figure illustrates, the electron density at the BCPs of F⋯H and WBI, as well as the NBBP and WBI, have good linear relationships. This indicates that like the electron density, the magnitude of WBI and NBBP, in which the latter is the sum of NBBPs referred to the bonds directly participating in the hydrogen bond formation, could be a good indicator of the hydrogen bond strength. This would be useful for the estimation of the intramolecular hydrogen bond strength as well as the single intermolecular hydrogen bond strength in the system, where several hydrogen bonds coexist.
4. Conclusions
The C–F⋯H–O hydrogen bonds in the complexes CHnXCHnF⋯H2O (n = 0, 1, 2; X = H, F, Cl, Br) have been studied at the MP2/aug-cc-pVTZ level. In the derivatives of 1-fluoro-ethane and 1-fluoro-ethene, besides the C–F⋯H–O hydrogen bonds, the C–H⋯O–H interaction also exist. We found that the halogen substituents at the vicinal carbon, similarly with that at the proximal carbon, reduce the ability of the F atom to act as a hydrogen bond acceptor. Differently, the influence of the vicinal carbon substituents to a certain degree is less than that of the proximal ones. Our results show that the halogen group at the vicinal carbon affects the interaction strength of C–F⋯H–O by inductive effect, and due to the long distance transmission of electron, the inductive effect of the vicinal F-, Cl-, and Br-substituent on the interaction strength is comparative. Compared with other structures, the stagger conformation in 1-fluoro-ethane and the trans configuration in 1-fluoro-ethene more affect the interaction of the C–F⋯H–O due to the hyperconjugative interaction between σ(C–F) and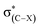 . We found that the magnitude of both Wiberg bond indexes and natural bond-bond polarizability could be a good indicator of the strength of the hydrogen bond.
. We found that the magnitude of both Wiberg bond indexes and natural bond-bond polarizability could be a good indicator of the strength of the hydrogen bond.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Science Foundation of China (21403127) and the Natural Science Foundation of Shandong Province, China (ZR2014BQ015). Hai-Bei Li thanks the fund of Young Scholars Program of Shandong University (Weihai), YSPSDUWH, and the supercomputing system in the Supercomputing Center, Shandong University, Weihai.References
- S. Purser, P. R. Moore, S. Swallow and V. Gouverneur, Chem. Soc. Rev., 2008, 37, 320–330 RSC.
- R. Berger, G. Resnati, P. Metrangolo, E. Weber and J. Hulliger, Chem. Soc. Rev., 2011, 40, 3496–3508 RSC.
- T. Furuya, A. S. Kamlet and T. Ritter, Nature, 2011, 473, 470–477 CrossRef CAS PubMed.
- H. Amii and K. Uneyama, Chem. Rev., 2009, 109, 2119–2183 CrossRef CAS PubMed.
- D. O'Hagan, Chem. Soc. Rev., 2008, 37, 308–319 RSC.
- J. A. K. Howard, V. J. Hoy, D. O'Hagan and G. T. Smith, Tetrahedron, 1996, 52, 12613–12622 CrossRef CAS.
- J. D. Dunitz and R. Taylor, Chem.–Eur. J., 1997, 3, 89–98 CrossRef CAS.
- V. R. Thalladi, H. C. Weiss, D. Blaser, R. Boese, A. Nangia and G. R. Desiraju, J. Am. Chem. Soc., 1998, 120, 8702–8710 CrossRef CAS.
- J. D. Dunitz, ChemBioChem, 2004, 5, 614–621 CrossRef CAS PubMed.
- E. Arunan, G. R. Desiraju, R. A. Klein, J. Sadlej, S. Scheiner, I. Alkorta, D. C. Clary, R. H. Crabtree, J. J. Dannenberg, P. Hobza, H. G. Kjaergaard, A. C. Legon, B. Mennucci and D. J. Nesbitt, Pure Appl. Chem., 2011, 83, 1619–1636 CAS.
- M. Karanam and A. R. Choudhury, Cryst. Growth Des., 2013, 13, 4803–4814 CrossRef CAS.
- C. Dalvit and A. Vulpetti, ChemMedChem, 2011, 6, 104–114 CrossRef CAS PubMed.
- P. Panini and D. Chopra, CrystEngComm, 2013, 15, 3711 RSC.
- P. A. Champagne, J. Desroches and J. F. Paquin, Synthesis, 2015, 47, 306–322 CAS.
- L. Chęcińska and S. J. Grabowski, Chem. Phys., 2006, 327, 202–208 CrossRef.
- H. R. Masoodi, A. Ebrahimi and M. Habibi, Chem. Phys. Lett., 2009, 483, 43–48 CrossRef CAS.
- G. T. Giuffredi, V. Gouverneur and B. Bernet, Angew. Chem., Int. Ed., 2013, 52, 10524–10528 CrossRef CAS PubMed.
- M. Guizado-Rodriguez, A. Ariza-Castolo, G. Merino, A. Vela, H. Noth, V. I. Bakhmutov and R. Contreras, J. Am. Chem. Soc., 2001, 123, 9144–9152 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, J. R. C. M. A. Robb, G. Scalmani, V. Barone, B. Mennucci, H. N. G. A. Petersson, M. Caricato, X. Li, H. P. Hratchian, J. B. A. F. Izmaylov, G. Zheng, J. L. Sonnenberg, M. Hada, K. T. M. Ehara, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, O. K. Y. Honda, H. Nakai, T. Vreven, J. A. Montgomerya Jr, F. O. J. E. Peralta, M. Bearpark, J. J. Heyd, E. Brothers, V. N. S. K. N. Kudin, T. Keith, R. Kobayashi, J. Normand, A. R. K. Raghavachari, J. C. Burant, S. S. Iyengar, J. Tomasi, N. R. M. Cossi, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, C. A. V. Bakken, J. Jaramillo, R. Gomperts, R. E. Stratmann, A. J. A. O. Yazyev, R. Cammi, C. Pomelli, J. W. Ochterski, K. M. R. L. Martin, V. G. Zakrzewski, G. A. Voth, J. J. D. P. Salvador, S. Dapprich, A. D. Daniels, J. B. F. O. Farkas, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Inc., Wallingford CT, 2013 Search PubMed.
- S. F. Boys and F. Bernardi, Mol. Phys., 2006, 19, 553–566 CrossRef.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, Oxford, 1994 Search PubMed.
- F. Biegler-Konig and J. Schonbohm, J. Comput. Chem., 2002, 23, 1489–1494 CrossRef CAS PubMed.
- A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926 CrossRef CAS.
- E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2013, 34, 1429–1437 CrossRef CAS PubMed.
- T. Lu and F. W. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- A. Bondi, J. Phys. Chem., 1964, 68, 441–451 CrossRef CAS.
- I. V. Alabugin, K. M. Gilmore and P. W. Peterson, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 109–141 CAS.
- L. Goodman, H. B. Gu and V. Pophristic, J. Phys. Chem. A, 2005, 109, 1223–1229 CrossRef CAS PubMed.
- S. Wolfe, Acc. Chem. Res., 1972, 5, 102–111 CrossRef CAS.
- S. Scheiner, S. J. Grabowski and T. Kar, J. Phys. Chem. A, 2001, 105, 10607–10612 CrossRef CAS.
- G. Narayszabo and G. G. Ferenczy, Chem. Rev., 1995, 95, 829–847 CrossRef CAS.
- P. Politzer, J. S. Murray and T. Clark, Phys. Chem. Chem. Phys., 2010, 12, 7748–7757 RSC.
- J. S. Murray and P. Politzer, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 7, e1326 Search PubMed.
- J. S. Murray, S. Ranganathan and P. Politzer, J. Org. Chem., 1991, 56, 3734–3737 CrossRef CAS.
- R. F. W. Bader, M. T. Carroll, J. R. Cheeseman and C. Chang, J. Am. Chem. Soc., 1987, 109, 7968–7979 CrossRef CAS.
- E. R. Johnson, S. Keinan, P. Mori-Sanchez, J. Contreras-Garcia, A. J. Cohen and W. Yang, J. Am. Chem. Soc., 2010, 132, 6498–6506 CrossRef CAS PubMed.
- J. Contreras-Garcia, W. T. Yang and E. R. Johnson, J. Phys. Chem. A, 2011, 115, 12983–12990 CrossRef CAS PubMed.
- A. Otero-de-la-Roza, E. R. Johnson and J. Contreras-Garcia, Phys. Chem. Chem. Phys., 2012, 14, 12165–12172 RSC.
- R. Chaudret, B. de Courcy, J. Contreras-Garcia, E. Gloaguen, A. Zehnacker-Rentien, M. Mons and J. P. Piquemal, Phys. Chem. Chem. Phys., 2014, 16, 9876–9891 RSC.
- U. Koch and P. L. A. Popelier, J. Phys. Chem., 1995, 99, 9747–9754 CrossRef CAS.
- I. Rozas, I. Alkorta and J. Elguero, J. Am. Chem. Soc., 2000, 122, 11154–11161 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra08122k |
| This journal is © The Royal Society of Chemistry 2018 |