Using batch reactor results to calculate optimal flow rates for the scale-up of UV photochemical reactions†
L. D.
Elliott‡
a,
J. P.
Knowles‡
a,
C. S.
Stacey‡
a,
D. J.
Klauber
b and
K. I.
Booker-Milburn
 *a
*a
aSchool of Chemistry, University of Bristol, Cantock's Close, Bristol, BS8 1TS, UK. E-mail: k.booker-milburn@bristol.ac.uk
bEarly Chemical Development, Pharmaceutical Sciences, IMED Biotech Unit, AstraZeneca, Macclesfield, SK10 2NA, UK
First published on 3rd January 2018
Abstract
The perceived difficulty of the scale-up of photochemistry is one of the main obstacles preventing its widespread use. Herein, we take three different challenging reactions and show that they can be reliably scaled, from immersion well batch reactors to higher power FEP flow reactors. Key to the success has been the development of a powerful calculation methodology which enables the accurate calculation of reactor flow rates from these and previously optimised batch reactions. Despite the challenging nature of these systems, in all cases tens of grams of material was obtained.
Introduction
UV photochemistry has an impressive history of transforming simple starting materials to highly complex structures in a single step.1 As such it has formed the basis of a great number of natural product syntheses,2 demonstrating its power to rapidly generate key synthetic intermediates, pre-functionalised with required reactivity. When scale-up is required, however, one problem that can occur in batch is over-irradiation as a reaction nears completion, leading to degradation and limiting yields.3We have previously reported the use of fluorinated ethylene propylene (FEP) flow reactors in reaction scale-up, and shown that the photon efficiency of such systems compares favourably with immersion-well batch alternatives.4 Herein we demonstrate the versatility of these FEP flow systems in the scale-up of three, dilute and difficult UVC photochemical processes, generating multi-gram quantities of otherwise inaccessible and synthetically useful products. This has been aided by the development of a powerful new calculation methodology, enabling the accurate calculation of reactor flow rates from optimised batch results. We have applied this methodology very successfully to 5 other historic reactions at different UV wavelengths, lamp powers and reactor and reaction types.
Results and discussion
Photochemistry of N-substituted succinimides
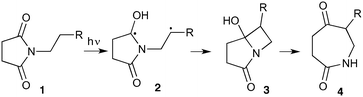
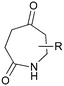
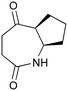
The UVC-promoted Norrish–Yang cyclisation of N-alkyl succinimides 1, proceeding via unstable cyclobutanol 3 to yield ring-expanded azepines 4, was first reported by Kanaoka5 in 1976 and the substrate scope subsequently expanded (Scheme 1).6,7 Whilst the simplicity of the reaction makes it an attractive method for the synthesis of keto-caprolactams, a fact noted by Kanaoka, a later study by Mooney concluded7 that “the general usefulness for the synthesis of 6-substituted caprolactams is limited to the isolation of small quantities for rather specific biological evaluation.” The reaction is further complicated by an alternative competing pathway involving β-scission of the diradical 2 to give succinimide and alkene by-products. This difficulty in scaling the reaction is made more frustrating by the very simple access to the starting material: simply heating the appropriate amine with succinic anhydride gives access to the desired imides on greater than mole scale.Our interest in keto-caprolactams 4 arose through our desire to use highly substituted azepine ring systems as scaffolds in drug discovery. We considered that such programmes would be greatly facilitated by access to large amounts of these photochemically produced 7-membered rings. We therefore decided to investigate whether our FEP flow reactors might enable access to much larger quantities than previously reported in the literature.
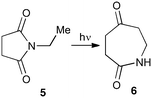
With this in mind, N-ethyl succinimide 5, the simplest possible substrate, was chosen for initial studies. The batch reaction was investigated first of all, employing a half immersed 36 W UVC lamp in a 450 mL quartz immersion well. The reaction was found to give essentially identical yields and productivities at the two concentrations investigated (Table 1, entries 1 vs. 3 and 2 vs. 4); however, the formation of insoluble by-product was observed towards the end of the reaction at the higher concentration and it was decided not to increase the concentration further.
These results compare very favourably with those of Mooney using a Rayonet reactor,7 and are a demonstration of the more efficient reactor topology of the immersion well setup. The only way to increase the productivity of this optimised reaction further is to increase the power of the lamps driving the reaction. Low-pressure lamps offer excellent electrical efficiency but the power density is low. Constructing a larger quartz immersion well reactor, which can receive the entire length of a 36 W lamp would double the productivity but would be an expensive endeavour and the scale would be fixed. A cheaper and more versatile solution is to construct FEP flow reactors around a series of lamps. Consequently, we moved to the FEP flow system we have previously reported, employing 3 × 36 W UVC lamps. Determination of flow rate in UV photochemistry is one of the key aspects of flow optimisation, and when performed using a flow reactor can often require multiple, time-consuming experiments, although recent work from the Jensen labs shows promise with visible-light flow photocatalysis.8 Herein we describe a simple and efficient way to do this on a preparative scale by extrapolating the productivity results from batch. We have previously demonstrated that both immersion-well and FEP flow reactors are highly efficient at capturing UV light, leading to similar productivities per watt4 This allows for the accurate calculation of flow rate based on the increased power of the flow reactor set-up (see later for details of calculation method). Thus, for a 6-fold increase in power a flow rate of 7.5 mL min−1 was calculated which was in excellent agreement with the experimental values obtained in Table 2.
| Entry | Flow rate/mL min−1 | Scale/g | 6 yield/% |
|---|---|---|---|
| All reaction performed in 3 × FEP quartz flow reactors connected in series with 3 × 36 W UVC lamps in MeCN. | |||
| 1 | 6 | 1.5 | 60 |
| 2 | 7 | 1.5 | 60 |
| 3 | 8 | 1.5 | 56 |
| 4 | 8 | 38 | 55 |
Confident with our reaction scoping, we optimised the flow reaction (2.5 L, 300 mmol) at 8 mL min−1 through the reactor array and were pleased to obtain 21.0 g of product in 5.2 h (55%). This increase in productivity (4 g h−1vs. the previously reported7 0.09 g h−1) comes from two factors: efficient light capture due to reactor design, a key consideration for any type of UV photochemistry; and the ability to increase power output through the use of a modular flow reactor set-up (see ESI†). A key point to note is that the flow reactor does not lead to an increase in reaction efficiency, as evidenced from our calculation of flow rate; rather, moving to flow allows an increase in reactor power whilst retaining the efficient light capture of batch.
In order to demonstrate this further, we investigated the scale-up for a range of substrates, leading to the results shown in Table 3. In all cases, the flow reactor allowed the synthesis of multi-gram quantities of material, and the simple nature of the starting materials meant that in most cases it proved possible to produce more than 20 g of material in a single run.
Photochemistry of pyridinium salts
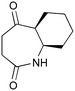
Our interest in the synthesis of novel drug scaffolds led us to also investigate the photochemistry of pyridinium salts 9, forming vinyl aziridine 10 as first reported by Kaplan9 in 1972 and subsequently extended by the work of Mariano10,11 and Burger12 (Scheme 2). Such products are ideally functionalised for multi-directional derivatisation, making them an appealing starting point for library synthesis; indeed this ease of functionalization has already been taken advantage of, as demonstrated by their recurrent use in natural product total synthesis. This work has culminated in the synthesis of a number of biologically active aminocyclopentitols13 and alkaloids,14,15Despite the proven synthetic potential of these aziridines, their more widespread use has been hindered by difficulties in scaling-up the photochemistry (10 mmol at best). Indeed, Mariano acknowledged the limitations of scale-up14b despite the power of the Rayonet reactor (RPR-100, 16 × 8 W) employed.14c
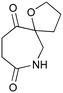
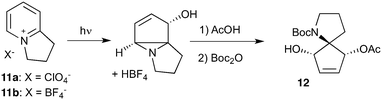
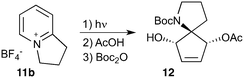
Given our interest in making larger quantities of these materials, we again considered whether our FEP flow technology would facilitate an increase in reaction scale. Of particular interest to us was the cyclopenta-fused pyridinium perchlorate salt 11a, which after irradiation and ring opening gives highly functionalised spirocycle 12, a key intermediate in the formal synthesis of (−)-cephalotaxine16 (Scheme 3).
Concerned by the potential hazards of perchlorate salts, we considered a change of counterion. Having initially explored the use of chloride and finding it led to reactor fouling, we elected to use tetrafluoroborate17 salt 11b which proved to be much more successful.
Reaction of 11b necessarily forms an equivalent of acid, in this case HBF4, which Mariano reported to promote product hydration or reaction reversal and relied upon the presence of KOH to neutralise. However, we were surprised to find photochemical reaction proceeded more cleanly in the absence of base; indeed, in its presence a deep purple polymeric material was formed during evaporation which made subsequent purification problematic.§ This product instability was however noted on storage, with polymerisation occurring, even when stored at low temperature. For this reason we elected to isolate the acetate ring-opened product, and to assist with purification the nitrogen was Boc-protected to give spirocycle 12 before the final photochemical yield was calculated.
With the initial substrate synthesis and purification method chosen, we again chose an 18 W batch immersion well set-up for our batch investigations, giving the results shown in Table 4. It can be seen that the yield plateaus at around 45% and that this can be achieved in 16 h, giving a significant improvement in both yield and productivity compared to previous results despite the lamp used being 7-times less powerful. Attempting to increase the reaction concentration led to a decrease in productivity (entry 4), and thus all further studies were performed at 0.02 M.
As with the succinimide photochemistry above our method of extrapolating batch results to flow gave a calculated flow rate of 2.8 mL min−1 (Table 5, entry 2). This again proved to be optimal: reducing to 2 ml min−1 did little to improve the yield (entry 1), whilst increasing to 4 ml min−1 reduced the yield due to incomplete conversion (entry 3). This then enabled the production of 10.3 g of spirocycle 12 in under 24 h, a significant improvement over the previous16 best of 1 g in a similar period using a Rayonet reactor. The shortcomings of the multi-lamp chamber topology are again highlighted by the observation that even the 18 W immersion well reaction gave a higher isolated mass (1.2 g vs. 1.0 g) in a shorter time period (16 h vs. 24 h) despite the multitude of lamps used in the Rayonet reactor (16 × 8 W = 128 W).
| Entry | Scale/mmol | Flow rate/ml min−1 | Yield/% | Productivity/g h−1 |
|---|---|---|---|---|
| All flow reactions performed in water (0.02 M) with 3 × 36 W FEP reactors connected in series with UVC lamps. | ||||
| 1 | 50 | 2 | 44 | 0.31 |
| 2 | 80 | 3 | 43 | 0.46 |
| 3 | 100 | 4 | 36 | 0.51 |
Pyrrole photochemistry
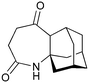
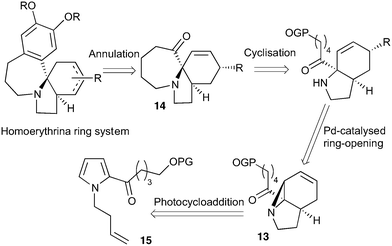
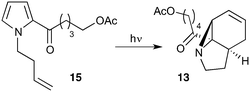
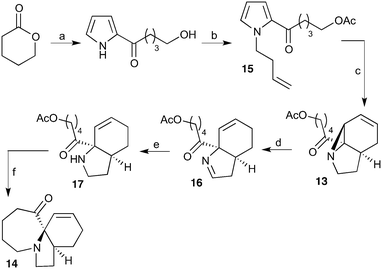
Our recently reported conversion of N-butenyl pyrroles to tricyclic aziridines18 bears several similarities to the photochemical rearrangement/hydration of pyridinium salts: both cases involve the photochemical excitation of a planar heteroaromatic using UVC irradiation, and result in the formation of a strained vinyl aziridine. In addition, we have found these reactions to suffer from similar issues during scale-up, with the reactions performing better at low concentration and thus requiring the irradiation of large solvent volumes.Our interest in the synthesis of the erythrina alkaloids19 led us to explore the retrosynthesis described in Scheme 4. We reasoned that Pd-catalysed Tsujii–Trost type ring-opening20 of aziridine 13 followed by alcohol activation–cyclisation would give the tricyclic azepine 14. This would serve as an advanced intermediate for the synthesis of homoerythrina alkaloids where the ketone moiety in 14 would allow us to explore the installation of the aromatic ring by various annulation strategies. Key to this would be the photocycloaddition of the pyrrole 15 to the aziridine 13 on a large enough scale that would us to explore a linear synthetic route towards these alkaloids.
Pyrrole 15 proved simple to synthesise on large scale using a modification of a procedure developed by Nicolaou.21 Thus 2-acylation of pyrrole with a δ-valerolactone followed by acetyl protection of the alcohol gave 15 in multigram quantities, enabling us to study the photochemistry of the system in batch. Two solvent systems initially seemed promising: our usual choice of MeCN, and a binary mixture of EtOAc and cyclohexane. As seen previously, low concentrations were required in both solvent systems to avoid a decrease in both productivity and yield (e.g. entry 4 vs. 5). We were particularly pleased to see excellent results with the cyclohexane/EtOAc system, which gave the highest yield observed so far for this kind of photochemical process as well as shorter reaction times (Table 6).
Moving to our flow system to investigate the reaction's potential for scale-up, we initially used the cyclohexane/EtOAc solvent system due to its better yield and greater productivity in batch. As can be seen in Table 7, early results were promising with the yield of the batch system being replicated and a 6-fold increase in productivity observed due to the 6-fold increase in lamp power. This therefore represents another case where flow rate can easily be determined from a single batch reaction (see discussion of calculation method). Indeed this also holds for lower concentration batch reactions (Table 6, entry 3).
| Entry | Solvent | Flow rate/ml min−1 | Scale/g | Yield/% | Productivity/g h−1 |
|---|---|---|---|---|---|
| All flow reactions were performed at 14.6 mM using 3 × 36 W FEP reactors connected in series with UVC lamps. | |||||
| 1 | EtOAc/CyH | 7.6 | 3.0 | 72 | 1.3 |
| 2 | EtOAc/CyH | 7.6 | 9.0 | 52 | 0.79 |
| 3 | MeCN | 6.6 | 5.0 | 64 | 0.95 |
| 4 | MeCN | 6.6 | 11.3 | 60 | 0.89 |
Prolonged runs in this solvent system proved less successful, with the apolar solvent leading to reactor fouling, reducing light absorption and therefore yield. Consequently we returned to using MeCN as solvent. This resulted in a small reduction in yield and productivity, however the greater solvent polarity avoided reactor fouling, permitting scale-up through longer runs. Through this approach it was therefore possible to synthesise 10.9 g of the photoproduct in a 13 h run (Table 7, entry 4).
With this material in hand, our attention turned to the proposed homoerythrina alkaloid synthesis. A thermal retroene reaction22 of aziridine 13 yielded imine 16, which was subsequently reduced to amine 17. Deprotection and activation of the alcohol was performed in a single step and telescoped with the cyclisation, leading to the formation of tricycle 14 in up to 24% yield and 5.6 g scale from δ-valerolactone over 6 steps (Scheme 5).
Calculation of reactor flow-rate from optimised batch results
As mentioned earlier the optimisation of preparative UV photochemical reactions in flow can be very time consuming, requiring a single run for each flow rate investigated. On the other hand a single batch reaction can be optimised rapidly by following the reaction over time. Over the years we have observed a striking linearity in the relationship between lamp power and productivity in UV photochemical reactions once these have been optimised in batch or flow. Indeed, we had demonstrated in a previous study that carefully optimised batch immersion well and FEP flow reactors had very similar if not identical productivities for a given lamp power.4 During the present study we reasoned that it should be possible to use an optimised immersion-well batch result to calculate the flow rate in FEP reactors. This would allow rapid estimation of optimal flow rate, saving both time and material.After some consideration we reasoned that dividing the irradiated batch volume by the optimised batch time would represent an effective calculated flow rate. To take into account any variation in lamp power between batch and flow we also introduced a power correction factor, leading to eqn (1).
Calculation of flow rate from the results of an optimised batch reactor
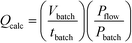 | (1) |
Q calc = Calculated flow rate/mL min−1
V batch = Batch volume/mL
t batch = Batch reaction time/min
P batch = Batch lamp power/W
P flow = Flow lamp power/W
Importantly this calculation was applied to the three photochemical results discussed above before they were carried out in flow. For example irradiation of N-ethyl succinimide was optimised in batch (Table 8, entry 1) and the results used with eqn (1) to calculate a flow rate of 7.5 ml min−1. When this reaction was transferred to flow an optimised result of 8 ml min−1 was obtained, representing a difference of just 6% between calculated and observed. As described previously, entry 2 represents an extremely challenging photochemical reaction, yet the optimised batch results were used to calculate the optimal flow rate with very little difference to that observed. Likewise entry 3 describes an example of the low quantum efficiency photochemistry of pyrroles. Again this formula was able to accurately calculate the flow rate of the FEP reactor from the optimised batch result at 14.6 mM.
| Entry | Substrate | Product | Batch conc./mM | Batch time/h | Batch yield/% | Flow conc./mM | Flow yield/% | Calculated flow rate/mL min−1 | Experimental flow rate/mL min−1 | Calculated vs. optimised flow rate/% |
|---|---|---|---|---|---|---|---|---|---|---|
| a Performed on 450 mL scale. b Performed on 400 mL scale. c Performed on 150 mL scale. d Using 50% of a 36 W UVC lamp (18 W). e Using 3 × 36 W UVC lamps. f Using 1 × 125 W medium pressure lamp. g Using 1 × 3 kW medium pressure lamp. h Using 1 × 400 W medium pressure lamp. i Using 50% of a 36 W UVA lamp (18 W). j Using 2 × 36 W UVA lamps. | ||||||||||
| 1 |
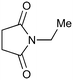
|
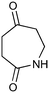
|
120a,d | 6 | 62 | 120e | 55 | 7.5 | 8.0 | 6 |
| 40a,d | 2 | 61 | 120e | 55 | 7.5 | 8.0 | 6 | |||
| 2 |
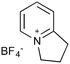
|
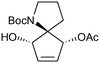
|
20a,d | 16 | 45 | 20e | 43 | 2.8 | 3 | 7 |
| 3 |
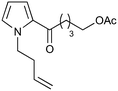
|
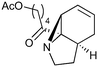
|
14.6a,d | 6 | 74 | 14.6e | 72 | 8.4 | 7.6 | 11 |
| 2.5a,d | 0.92 | 71 | 14.6e | 72 | 7.9 | 7.6 | 4 | |||
| 4 |
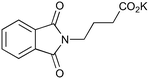
|
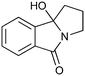
|
200c,f | 2 | 81 | 200g | 88 | 30 | 30 | 0 |
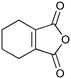
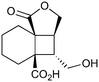
| 5 |
|
|
400c,f | 2 | 77 | 400g | 80 | 30 | 36 | 20 |
| 6 |
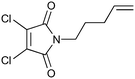
|
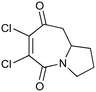
|
100b,h | 1.67 | 62 | 100h | 60 | 4.0 | 4.2 | 5 |
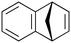
| 7 |
|
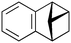
|
600b,h | 2.25 | 90 | 600h | 89 | 3.0 | 3.3 | 9 |
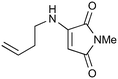
| 8 |
|
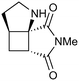
|
100a,i | 1.66 | 80 | 100j | 77 | 18 | 16 | 11 |
We were intrigued to see if this calculation could be extended to changes in concentration, allowing for small-scale batch reactions to accurately calculate optimal flow rates. For instance, applying the same calculation¶ to a 2.5 mM run in entry 3 predicted a flow rate of 7.9 mL min−1. Pleasingly this compared very well to the optimised rate of 7.6 mL min−1. Further corroboration of this was achieved when entry 1 was re-run at 40 mM concentration where an excellent calculated/observed agreement was obtained.
Perhaps the strongest endorsement of this calculation methodology was its application to batch and flow results obtained sometime before this calculation was conceived. The batch and flow results for entries 4–8 (Table 8) have all been obtained previously.4 These involve various reaction types running under a wide range of conditions, concentrations (0.1 to 0.6 M), powers (36 W to 3000 W), scales (up to 1.5 kg) as well as at 3 distinct parts of the UV spectrum: UVA (entry 8), UVB (entries 5, 6, 7) and UVC (entry 4). All but entry 5 show outstanding agreement between the calculated and experimental flow rates. In particular it is prudent to highlight entries 4 and 8. The former is an electron transfer decarboxylation/cyclisation irradiated with UVC whereas the latter is a [2 + 2] cycloaddition at 365 nm. Both use different reactors, lamps and power: entry 4 used a Firefly23 reactor and a 3000 W medium pressure mercury lamp whereas entry 8 used an FEP reactor and 2 × 36 W low-pressure mercury lamps. For two such different reactions and flow experimental set ups to give such good agreement with their batch generated calculations is a real testimony to the robustness of this new calculation methodology. Entry 5 is a highly efficient, sensitised [2 + 2] reaction which when carried out on the Firefly reactor at 3 kW power gave 1.5 kg of product in just 9 h. The flow rate calculated from batch (30 mL min−1) is about 20% less than that obtained in the Firefly, which although very good is less accurate than the other entries. A likely explanation is that when the batch reaction was run at higher concentrations (>0.1 M) significant crystallisation of the product was observed during the reaction. Therefore, due to less consistent light penetration this reaction was likely to be under-performing slightly in batch compared to flow and hence the calculated flow result has slightly more error than the other results in Table 8. Importantly this highlights that in order to get reliable results from this calculation methodology any batch experiments must be carefully optimised with maximum photon capture.
Conclusions
We have shown that our FEP flow reactor technology allows the scale-up of three UV photochemical reactions that have previously been very difficult in batch. Tens of grams of material can be produced in all three cases, allowing for their conversion into significant quantities of material of further synthetic utility. FEP flow reactors have the additional advantage that they are simple and cheap to construct, bringing the possibility of performing large-scale photochemical reactions to many synthetic laboratories.We have also shown that in all three cases optimal flow rates can be accurately calculated from the initial performance of the same reactions in batch. Eqn (1) represents a strikingly simple and effective method for solving the often-encountered problem of how to convert preparative UV batch results to flow, or how to optimise a preparative reaction in flow without carrying out multiple experiments. The power of this methodology was highlighted when it was applied retrospectively to 5 other UV photochemical reactions optimised previously in both batch and flow. These all gave excellent agreement between calculated and observed flow rates despite the fact that all the reactions differed in mechanism, key UV wavelengths, lamp types, lamp powers and reaction concentrations.
This ability to calculate flow rates from individual UV batch reactions highlights a previous4 conclusion: the productivity per W of batch and FEP flow reactors for preparative UV photochemistry is essentially identical provided they are performed in a way that maximises light capture. In our experience immersion wells and wrapped flow reactors have proved optimal. We have shown that these UV flow reactors can clearly outperform their batch counterparts where solvent volumes are high due to either reaction scale or low concentration. It remains the case however that classic immersion well batch reactors offer excellent photon capture and simplicity for smaller scale reactions. Consequently, batch can be employed with no loss of yield or efficiency for exploring new reactions or when only small amounts of material are required. For scale-up in the UV there is no doubt that flow is the best approach for most reactions, and now conditions can be predicted accurately from those optimised in batch using eqn (1). Given the current interest in synthetic photochemistry we believe such calculations will be of great use to practitioners the field.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to the Engineering and Physical Sciences Research Council (EPSRC) for funding this work (EP/P013341/1 & EP/L003325/1) and AstraZeneca and EPSRC for funding a studentship (CSS), and Novartis for additional funding.Notes and references
- (a) A. B. Beeler, Chem. Rev., 2016, 116, 9629–9630 CrossRef CAS PubMed; (b) S. Poplata, A. Tröster, Y.-Q. Zou and T. Bach, Chem. Rev., 2016, 116, 9748–9815 CrossRef CAS PubMed.
- M. D. Kärkäs, J. A. Porco Jr and C. R. J. Stephenson, Chem. Rev., 2016, 116, 9683–9747 CrossRef PubMed.
- S. Protti, D. Ravelli and M. Fagnoni, in Photochemical Processes In Continuous-flow Reactors: From Engineering Principles To Chemical Applications, ed. T. Noel, World Scientific Europe Ltd, 1st edn, 2017, ch 1 Search PubMed.
- L. D. Elliott, J. P. Knowles, P. J. Koovits, K. G. Maskill, M. J. Ralph, G. Lejeune, L. J. Edwards, R. I. Robinson, I. R. Clemens, B. Cox, D. D. Pascoe, G. Koch, M. Eberle, M. B. Berry and K. I. Booker-Milburn, Chem. – Eur. J., 2014, 20, 15226–15232 CrossRef CAS PubMed.
- Y. Kanoaka and Y. Hatanaka, J. Org. Chem., 1976, 41, 400–401 CrossRef.
- M. Machida, K. Oda and Y. Kanoaka, Chem. Pharm. Bull., 1984, 32, 950–956 CrossRef CAS.
- B. M. Mooney, R. H. Prager and A. D. Ward, Aust. J. Chem., 1981, 34, 2695–2700 CrossRef CAS.
- For an interesting microfluidic platform for the in situ optimization of visible-light photochemical reactions in flow see: C. W. Coley, M. Abolhasani, H. Lin and K. F. Jensen, Angew. Chem., Int. Ed., 2017, 56, 9847–9850 CrossRef CAS PubMed.
- L. Kaplan, J. W. Pavlik and K. E. Wilzbach, J. Am. Chem. Soc., 1972, 94, 3283–3284 CrossRef CAS.
- (a) U. C. Yoon, S. L. Quillen and P. S. Mariano, Tetrahedron Lett., 1982, 23, 919–922 CrossRef CAS; (b) U. C. Yoon, S. L. Quillen, P. S. Mariano, R. Swanson, J. L. Stavinoha and E. Bay, J. Am. Chem. Soc., 1983, 105, 1204–1218 CrossRef CAS.
- R. Ling, M. Yoshida and P. S. Mariano, J. Org. Chem., 1996, 61, 4439–4449 CrossRef CAS PubMed.
- (a) F. Glarner, S. R. Thorton, D. Schärer, G. Bernardinelli and U. Burger, Helv. Chim. Acta, 1997, 80, 121–127 CrossRef CAS; (b) F. Glarner, B. Acar, I. Etter, T. Damiano, E. A. Acar, G. Bernardinelli and U. Burger, Tetrahedron, 2000, 56, 4311–4316 CrossRef CAS.
- (a) E. A. Acar, F. Glarner and U. Burger, Helv. Chim. Acta, 1998, 81, 1095–1104 CrossRef CAS; (b) R. Ling and P. S. Mariano, J. Org. Chem., 1998, 63, 6072–6076 CrossRef CAS PubMed; (c) X. Feng, E. N. Duesler and P. S. Mariano, J. Org. Chem., 2005, 70, 5618–5623 CrossRef CAS PubMed.
- (a) Z. Zhao, L. Song and P. S. Mariano, Tetrahedron, 2005, 61, 8888–8894 CrossRef CAS; (b) Z. Zhao and P. S. Mariano, Tetrahedron, 2006, 62, 7266–7273 CrossRef CAS; (c) C. Colombo, B. M. Pinto, A. Bernardi and A. J. Bennet, Org. Biomol. Chem., 2016, 14, 6539–6553 RSC.
- (a) T. Damiano, D. Morton and A. Nelson, Org. Biomol. Chem., 2007, 5, 2735–2752 RSC; (b) J. Zou and P. S. Mariano, Photochem. Photobiol. Sci., 2008, 7, 393–404 CAS.
- Z. Zhao, E. Duesler, C. Wang, H. Guo and P. S. Mariano, J. Org. Chem., 2005, 70, 8508–8512 CrossRef CAS PubMed.
- C. S. Penkett and I. D. Simpson, Tetrahedron, 1999, 55, 6183–6204 CrossRef CAS.
- K. G. Maskill, J. P. Knowles, L. D. Elliott, R. W. Alder and K. I. Booker-Milburn, Angew. Chem., Int. Ed., 2013, 52, 1499–1502 CrossRef CAS PubMed.
- E. E. Blackham and K. I. Booker-Milburn, Angew. Chem., Int. Ed., 2017, 56, 6613–6616 CrossRef CAS PubMed.
- E. E. Blackham, J. P. Knowles, J. Burgess and K. I. Booker-Milburn, Chem. Sci., 2016, 7, 2302–2307 RSC.
- K. C. Nicolaou, D. P. Papahatjis, D. A. Claremon, R. L. Magolda and R. E. Dolle, J. Org. Chem., 1985, 50, 1440–1456 CrossRef CAS.
- J. P. Knowles and K. I. Booker-Milburn, Chem. – Eur. J., 2016, 22, 11429–11434 CrossRef CAS PubMed.
- L. D. Elliott, M. Berry, B. Harji, D. Klauber, J. Leonard and K. I. Booker-Milburn, Org. Process Res. Dev., 2016, 20, 1806–1811 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available: Full experimental procedures and characterisation for all compounds. See DOI: 10.1039/c7re00193b |
| ‡ These authors contributed equally and are listed alphabetically. |
| § Samples for quantitative NMR analysis could be concentrated without neutralising the generated HBF4 although for preparative work-up K2CO3 was added prior to evaporation. |
¶ To allow for changes in concentration, eqn (1) can be expanded to: 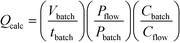 where Qcalc = calculated flow rate/mL min−1; Vbatch = batch volume/mL; tbatch = batch reaction time/min; Pbatch = batch lamp power/W; Pflow = flow lamp power/W; Cbatch = batch concentration/M and Cflow = flow concentration/M. where Qcalc = calculated flow rate/mL min−1; Vbatch = batch volume/mL; tbatch = batch reaction time/min; Pbatch = batch lamp power/W; Pflow = flow lamp power/W; Cbatch = batch concentration/M and Cflow = flow concentration/M. |
| This journal is © The Royal Society of Chemistry 2018 |