Temperature dependent chiroptical response of sigmoidal gold clusters: probing the stability of chiral metal clusters

Abstract

The stability of chiral metal clusters is of great importance for their practical applications. Herein we select three structurally well-defined gold cluster compounds to probe how structural factors influence the stability of chiral metal clusters upon heating. Through monitoring the variation of CD, UV-vis and NMR spectra at elevated temperatures, the biased chiroptical response of three sigmoidal Au₆ clusters is finally ascribed to the synergistic effect of the distinct structural tunability of central diamino ligands, inter-cluster aurophilic interactions and steric hindrance. The rigid skeleton of chiral ligands and the strong metal–metal interaction effectively enhance the stability of asymmetric structural motifs in chiral metal clusters. In addition, some central diamino ligands lead to a destructive decomposition of corresponding chiral clusters in the heating process due to the reduction of Au(I) to Au(0). The relationship between structural characteristics and the stability of chiral clusters addressed in this study will facilitate our understanding on how to achieve stable chiral metal clusters and potentiate their practical applications.

---

Introduction

Recent studies on the chirality of metal nanoparticles (NPs) and nanoclusters (NCs)¹ have attracted intense interest due to their promising applications in many interdisciplinary areas including enantioselective catalysis,² chiral recognition and separation,³ polarization-sensitive devices,⁴ and nonlinear optics.⁵ Exploration of the origin of chirality in these nano-objects will promote the comprehension of fundamental questions on the transfer and propagation of chirality at the nanoscale.⁶ Despite still being mysterious and complicated, chirality in metal NCs can be geometrically classified into three major categories: (1) chirality from an intrinsically chiral metal core, (2) chirality from an asymmetric arrangement of achiral ligands or metal–ligand motifs on the surface, and (3) extrinsic chirality induced by peripheral chiral ligands. In the past decade, by means of increasingly powerful structural analysis techniques such as X-ray crystallography and high resolution mass spectroscopy, a plethora of chiral metal NCs with nuclearity numbers up to hundreds have been structurally characterized at the atomic level despite most of them being racemic mixtures.⁷ Recent efforts on the acquisition of enantio-pure or enantio-rich metal NCs based on HPLC separation,⁸ chiral phase transfer,⁹ chiral ion pairing¹⁰ and chiral ligand induction¹¹ have resulted in a few sophisticated chiral metal clusters, which would boost in-depth studies on the rational design and application of chiral cluster compounds.

Despite such great progress in the synthesis and structural characterization of chiral metal clusters and NCs, an important aspect concerning the stability of chiral structural motifs remains unclear to date. Possible conformational changes of coordinative ligands or metal–ligand motifs, adjustment of inter-metallic interactions or asymmetric arrangement of metal atoms on the surface and inversion of the whole metal kernel upon various external stimuli (e.g. heating^12a,b and light irradiation^12c,d) all affect the chirality of metal clusters and consequently interfere with their practical applications. Bürgi and co-workers once studied the racemization process of a chiral nanocluster Au₃₈(SCH₂CH₂Ph)₂₄,^12a which possesses an asymmetric arrangement of achiral thiolate-gold staples on the surface. They showed that the Au–S chiral interface had a low activation barrier for racemization and consequently the interface was very sensitive to heating. They further found that the gold–sulfur interface can be strengthened through the introduction of a chiral dithiol ligand.^11b As to the ligand-decorated chiral metal clusters and NCs,^11,13 the adsorbed chiral ligands would not only break the reflection symmetry of the cluster surface, but also distort the arrangement of surface metal atoms or even the whole metal core and consequently strengthen the asymmetry of the whole cluster. The combination of the inherent chirality of ligands and the induced chirality of metallic cores possibly enhances the stability of the resulting chiral metal clusters and potentiate their practical applications. Therein, an important but very challenging task is to examine how chiral ligands influence the chiral stability of metal clusters. However, formidable structural complexity arising from a plethora of possible combinations between metal atoms and peripheral ligands makes the stability investigation very complicated.

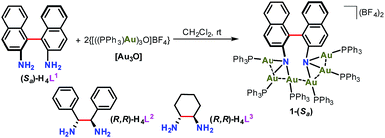
In this regard, our recently reported sigmoidal Au₆ cluster compounds may provide a simplified and convenient model.¹⁴ As shown in Scheme 1, different chiral diamino ligands can guide distinct intermetallic interactions between two NAu₃ cluster aggregates and manipulate the relative motion of such two NAu₃ units. These conformational variations will surely affect the chiroptical response of chiral clusters. In this work, we report the temperature-dependent chiroptical response of three sigmoidal Au₆ clusters that contain different chiral diamino centers. Through monitoring the variation of CD, UV-vis and NMR spectra at elevated temperatures together with theoretical simulation, we finally ascribe the distinct chiroptical response of the sigmoidal Au₆ clusters to the synergistic effect of the distinct structural tunability of the central diamino ligands, inter-cluster aurophilic interactions and steric hindrance of peripheral phosphine ligands.

Scheme 1 Possible intramolecular interaction and conformational change in diamino-centered chiral Au₆ clusters.

Results and discussion

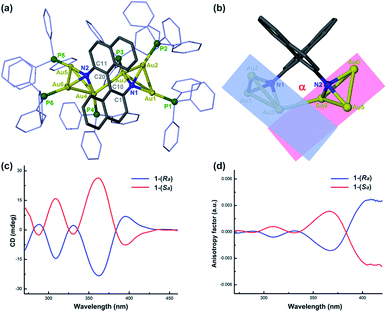
We purposefully selected three chiral diamine ligands (H₄L¹, H₄L², and H₄L³ as shown in Scheme 2) in view of different energy barriers required for their conformational change via rotation around the central carbon–carbon bonds. Theoretically, the single carbon–carbon bond between two naphthalene rings in the axial chiral compound H₄L¹ can be tuned from 0 to 180° with increasing N–N separation. In H₄L², the N–N separation is smaller than that of H₄L¹, but the bond between two stereogenic carbon atoms rotates more freely due to the lack of significant steric hindrance. As a contrast example, the presence of a rigid cyclohexane skeleton in H₄L³ makes the N–C–C–N dihedral angle vary within a very small range. With reference to our previous synthesis¹⁴ of chiral Au₆ cluster compounds 2 and 3 by the reaction of enantiopure diamine ligands H₄L² and H₄L³ with the gold-oxo cluster [O(AuPPh₃)₃](BF₄) ([Au₃O]), we successfully obtained a chiral gold cluster compound 1-(S_a) using (S_a)-H₄L¹ as a starting material (Scheme 2). 1-(S_a) crystallizes in a chiral space group of P2₁2₁2₁ with a Flack parameter of 0.008(14) and has a molecular formula of [(AuPPh₃)₆((S_a)-L¹)](BF₄)₂·Et₂O (Fig. 1a). X-ray crystallographic analysis reveals that the tetraanionic L¹ in 1-(S_a) adopts a μ₆-η³,η³ mode to bind with six gold(I) atoms by means of two μ₃-amino nitrogen centers (Au–N: 2.064(9)–2.118(10) Å). Along the shortest aurophilic connections (2.907(1)–3.223(1) Å),¹⁵ the gold chain Au1–Au2–Au3–Au4–Au5–Au6 constitutes an asymmetric sigmoidal pattern as similar as in 2-(R,R) and 3-(R,R).¹⁴ However, the separation between two amino nitrogen atoms in 1-(S_a) (4.063 Å) is much larger than that of 2-(R,R) (2.921 Å) and 3-(R,R) (3.008 Å). Consequently, the Au⋯Au contact between two NAu₃ aggregates in 1-(S_a) at Au3⋯Au4 = 3.211(1) Å is longer than the values of 2-(R,R) (3.054(1) and 3.188(1) Å) and 3-(R,R) (3.082(1) Å). In addition, the characteristic dihedral angle α defined by two Au₃ planes in 1-(S_a) is 67.4° (Fig. 1b), in sharp contrast to the α angle of 2-(R,R) (108.9°) and 3-(R,R) (106.0°). The small α angle suggests a loose arrangement of the peripheral PPh₃ ligands.

Scheme 2 Molecular structures of substrates and synthesis of chiral gold clusters.

Fig. 1 (a) Crystal structure of 1-(S_a) with tetrafluoroborate anions, hydrogen atoms and a diethyl ether solvent molecule omitted for clarity. (b) Schematic diagram for the dihedral angle (α) that is determined by two Au₃ planes. (c) CD spectra and (d) anisotropy factors of 1-(S_a) and 1-(R_a) in DMSO (c = 3.0 × 10⁻⁵ M).

We next utilized the same synthetic procedure but with (R_a)-H₄L¹ in place of (S_a)-H₄L¹ to obtain 1-(R_a). 1-(S_a) and 1-(R_a) can keep their structures intact in solution as evidenced by high-resolution ESI mass spectrometry (Fig. S1†). As shown in Fig. 1c, the circular dichroism (CD) spectra of 1-(S_a) and 1-(R_a) show an intense Cotton effect and an excellent mirror image relationship in the 250–450 nm range. Five signals at 288(−), 309(+), 331(−), 361(+), and 398(−) nm are observed in the CD spectrum of 1-(S_a). The anisotropy factor analysis over the spectral range on the basis of the equation g = ΔA/A = θ [mdeg]/(32 980 × A) reveals the highest g value of 3 × 10⁻³ at the maximal wavelength of 398 nm (Fig. 1d), which is smaller than the g value of 2-(R,R) (6 × 10⁻³ at 372 nm) and 3-(R,R) (4 × 10⁻³ at 373 nm) in CHCl₃.

To gain further insight into the structural and CD spectral difference between 1-(S_a) and 2-(R,R)/3-(R,R), we conducted a simulation of the UV-vis and CD spectra of 1-(S_a) and detailedly analyzed transition-related HOMO and LUMO orbitals in the 250–500 nm range according to the same analytical method for 2-(R,R) and 3-(R,R).¹⁴ The calculated UV-vis and CD spectra of 1-(S_a) agree quite well with the measured spectra (Fig. S2†). The Mulliken population analysis of 1-(S_a) shows that the HOMO to HOMO-3 and the LUMO to LUMO + 1 orbitals primarily lie on the binaphthalene moiety, and the LUMO + 2 to LUMO + 3 orbitals almost all arise from the phenyl groups of PPh₃ (Fig. S3 and Table S1†). Unlike 2-(R,R) and 3-(R,R), the Au atoms in 1-(S_a) have little contribution to the near-frontier transition-related orbitals. This should be ascribed to the weak Au–Au interactions in the core structure of 1-(S_a) and the dominant π-conjugated electronic configuration of the central binaphthalene moiety.

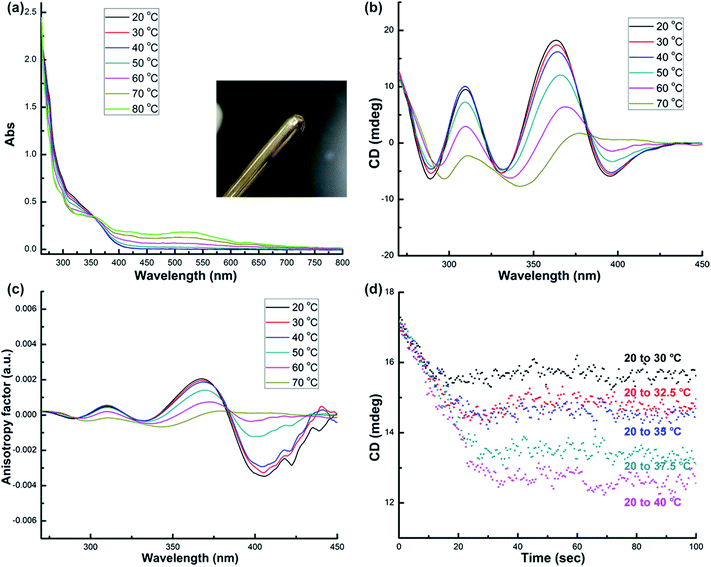
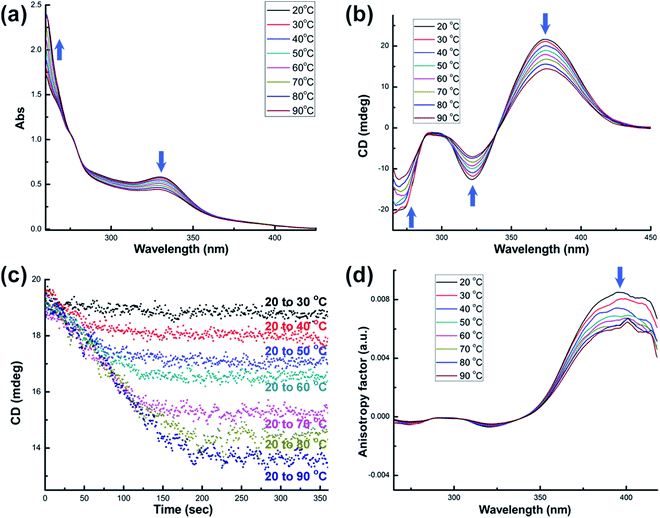
Systematic structural variation from 1-(S_a) through 2-(R,R) to 3-(R,R) in the aspects of the N_amino–N_amino separation, the inter-cluster Au–Au interaction and the structural adjustment behavior of diamino ligands makes them suitable candidates to study the thermal stability of chiral structural motifs. We subsequently prepared a diluted dimethyl sulfoxide (DMSO) solution (2.5 × 10⁻⁵ M) of corresponding enantiopure cluster compounds 1-(S_a), 2-(R,R) and 3-(R,R) and monitored their variation in UV-vis, CD and NMR spectra upon heating. As the temperature rises from 20 to 80 °C, the UV-vis spectra of 1-(S_a) show different types of variation below and above 40 °C. From 20 to 40 °C, the major absorption band in the range of 250–400 nm gradually decreases (Fig. 2a) and the presence of an isosbestic point at 365 nm implies a simple conformational transformation rather than a destructive decomposition in the heating process. When the temperature is above 40 °C, a new broad absorption band in the range of 400–700 nm appears and gradually increases. Remarkably, upon heating the solution of 1-(S_a) at 80 °C for several minutes, a gold mirror is finally observed on the surface of glassware (as shown in the inset of Fig. 2a). This experimental fact indicates that 1-(S_a) easily decomposes at high temperature through the reduction of Au(I) to Au(0). The reduction of metal atoms leads to the formation of gold nanoparticles in dispersed sizes which accounts for the new broad absorption band (Fig. S4†).

Fig. 2 (a) UV-vis and (b) CD spectra of DMSO solution (c = 2.5 × 10⁻⁵ M) of 1-(S_a) at elevated temperatures. Inset: the image of the gold mirror generated by heating the DMSO solution of 1-(S_a) at 80 °C for several minutes. (c) Unsynchronized variation of the anisotropy factors for different CD signals of 1-(S_a). (d) CD response of 1-(S_a) at 361 nm reaches a steady state at different temperatures.

Accordingly, the CD response of 1-(S_a) at different temperature ranges is differentiated as well. The decrease of CD signal intensity without any wavelength shift is observed below 40 °C (Fig. 2b). This process is accompanied by an unsynchronized decrease of the anisotropy factors for different CD signals (Fig. 2c). The g value of the peak at 398 nm experiences a remarkable decrease upon heating relative to the other peaks. The detailed variation of the chiroptical response upon heating was then monitored by following the CD peak intensity at 361 nm (Fig. 2d). It is notable that the CD signals at different temperatures finally reach a steady state and vary from 17.3 mdeg at 20 °C to 12.5 mdeg at 40 °C. The variation of CD signal intensity at elevated temperature is totally recovered upon cooling the solution back to 20 °C (Fig. S5†). When the temperature is above 40 °C, every CD peak experiences both the decrease of signal intensity and the simultaneous red-shift. Such variation together with the change of the anisotropy factor cannot be recovered when the temperature is back to 20 °C.

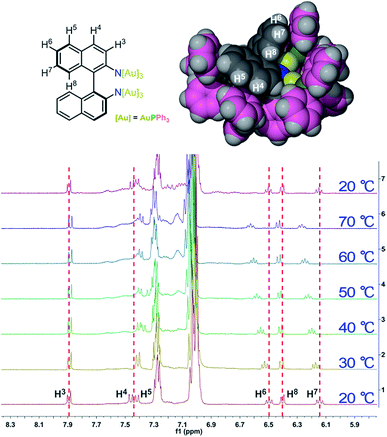
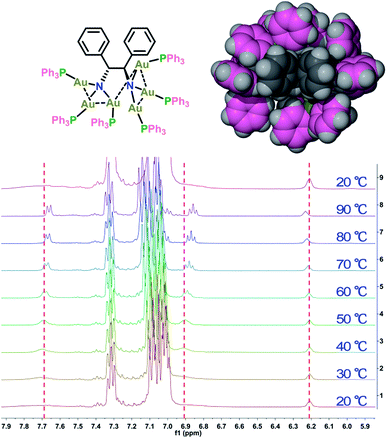
To further elucidate the details of the structural change in the heating process, we next examined the ¹H and ³¹P NMR (Fig. S6†) variation of 1-(S_a) upon increasing the temperature from 20 to 70 °C and then cooling back to 20 °C. The ¹H NMR spectrum of 1-(S_a) at 20 °C shows a set of well-resolved doublets and triplets (Fig. 3), which can be assigned to H³–H⁸ by 2D H–H COSY NMR (Fig. S7†). When the solution sample of 1-(S_a) was heated from 20 to 70 °C, the signals of H⁶, H⁷ and H⁸ underwent a down-field shift while H⁴ experienced an up-field shift. The rest of the proton atoms of the binaphthalene of L¹ almost keep their chemical shifts unchanged. As shown in the space-filling model of the crystal structure of 1-(S_a), H⁸ is located above the shielding area of another naphthalene ring. Thus the down-field shift of H⁸ indicates that one naphthalene ring of L¹ moves far away from another one through the rotation of the central carbon–carbon single bond in the binaphthalene. In addition, such rotation also brings about the change of the relative positioning between the N(AuPPh₃)₃ moiety and the three peripheral proton atoms H⁴, H⁶ and H⁷. As shown in the space-filling model structure of 1-(S_a), H⁴, H⁶ and H⁷ are all close to the phenyl rings of PPh₃ ligands. Therefore, the rotation-based conformational change of L¹ would accordingly make H⁴, H⁶ and H⁷ close to or apart from their corresponding phenyl rings, thus causing an up- or down-field shift as observed in experimental results. The present understanding of the influence of the axially chiral diamino ligand L¹ on the chiroptical properties of gold cluster 1 is reminiscent of a previous study concerning the stabilizing effect of an axially chiral dithiol ligand for a Au₃₈ nanocluster.^11b Therein, the chirality of the Au₃₈ nanocluster mainly arises from an asymmetric arrangement of thiolate-gold staples on the surface. The introduction of a single dithiol ligand reduces the flexibility of the gold–sulfur interface of the Au₃₈ cluster, thus hindering the inversion of the whole cluster. In contrast, the chirality of the Au₆ cluster in 1 is generated and stabilized by the coordination and electrostatic attraction of the central axially chiral diamino ligand L¹, whose subtle conformational change thus causes a significant change of the chiroptical response.

Fig. 3 Variable temperature ¹H NMR spectra (DMSO-d₆) of 1-(S_a) from 20 to 70 °C and back to 20 °C. The environment of different protons on the binaphthalene of L¹ is shown in a space-filling model based on the crystal structure of 1-(S_a).

We next studied the spectral variation of 2-(R,R) as the temperature rises from 20 to 90 °C. As shown in Fig. 4a, the major peak at 330 nm in the UV-vis absorption spectra of 2-(R,R) gradually decreases. This variation is accompanied by the rise of the absorption band in the ultraviolet region (<275 nm). This change is similar to the scenario of 1-(S_a) below 40 °C. Furthermore, the observation of an isosbestic point at 278 nm suggests a simple conformational transformation in the heating process. This is also substantiated by an annealing experiment. When the heated solution of 2-(R,R) is cooled to 20 °C, the CD and UV-vis absorption spectra are completely recovered (Fig. S8†). As the temperature rises, the shape of the CD spectrum of 2-(R,R) is well conserved, but the intensity of signals at 273, 316 and 372 nm all diminishes step by step (Fig. 4b). Two isosbestic points at 286 and 340 nm are observed in the variable temperature CD spectra. The detailed variation of the chiroptical response upon heating was monitored by tracking the CD peak intensity at 372 nm (Fig. 4c). As the temperature rises from 20 to a specific temperature up to 90 °C, the CD signal finally reaches a steady state that varies from 19.2 mdeg at 20 °C to 13.6 mdeg at 90 °C. This variation is vice versa from elevated temperatures to 20 °C (Fig. S9†). However, the variation of the anisotropy factors of different CD signals is unsynchronized. The g value of the peak at 372 nm experiences a remarkable decrease upon heating, which is in sharp contrast to a negligible change of the other two peaks (Fig. 4d). Notably, the DMSO solution of 2-(R,R) can be heated up to 110 °C with reversible CD and UV-vis spectral variation. Above 110 °C, 2-(R,R) gradually decomposes as similar as 1-(S_a).

Fig. 4 (a) UV-vis and (b) CD spectra of DMSO solution (c = 2.5 × 10⁻⁵ M) of 2-(R,R) at elevated temperatures. (c) CD response of 2-(R,R) at 372 nm reaches a steady state at different temperatures. (d) Unsynchronized variation of the anisotropy factors for different CD signals of 2-(R,R).

The variable temperature ¹H NMR spectra of 2-(R,R) were then collected to clarify its conformational change upon heating. As shown in Fig. 5, at 20 °C the NMR peaks corresponding to the phenyl protons of the chiral diamino ligand L² show very broad signals in the range of 7.60–7.80 and 6.80–7.00 ppm, which is due to the densely distributed PPh₃ ligands around L² (see the space-filling model structure of 2-(R,R) in Fig. 5). When the temperature is gradually elevated to 90 °C, the phenyl proton signals appear as a set of well-resolved doublet and triplet peaks along with a bit upfield shift of approximately 0.02–0.05 ppm. This NMR spectral change indicates that the two phenyl rings of L² rotate more freely arising from the spatial distance between L² and the surrounding PPh₃ ligands. In addition, the proton signals of PPh₃ ligands (6.95–7.40 ppm) and the tertiary hydrogen atoms attached on the stereogenic carbon centers (6.21 ppm) all experience a downfield shift of 0.02 ppm. When the solution cools back to 20 °C, the proton NMR is totally recovered (Fig. 5). Accordingly, the variable temperature ³¹P NMR also exhibits a downfield shift upon heating (Fig. S10†). Such unsynchronized and bi-directional variation of different proton signals is similar to the scenario in the variable temperature NMR of 1-(S_a), suggesting that the dominant conformational change arises from the rotation of the single bond between two stereogenic carbon atoms in L² plus the rotation of the phenyl rings of L².

Fig. 5 Variable temperature ¹H NMR spectra (DMSO-d₆) of 2-(R,R) from 20 to 90 °C and back to 20 °C. The environment of the central diamino ligand L² is shown in a space-filling model based on the crystal structure of 2-(R,R).

Upon heating the solution of 3-(R,R) to 90 °C, we observed a gradual decrease of the absorption peaks at 300 and 330 nm and the rise of the absorption band in the ultraviolet region (<275 nm) in the UV-vis spectra (Fig. 6a). There is an isosbestic point at 269 nm. However, when the temperature is above 70 °C, a broad absorption peak centered at 520 nm appears, suggesting the formation of gold nanoparticles as similar as in 1-(S_a)vide supra. Therefore, the thermal stability of 3-(R,R) was studied below 70 °C. As similar as the variation of CD spectra in 2-(R,R), heating the DMSO solution of 3-(R,R) results in the diminishing of CD signal intensity at 278, 311 and 373 nm (Fig. 6b). An isosbestic point at 337 nm is observed in such variable temperature CD spectra. In addition, the CD signal intensity at 373 nm stepwise reaches a steady state from 20 °C to a specific temperature and varies from 12.4 mdeg at 20 °C to 10.5 mdeg at 70 °C (Fig. S11†). The variation of the anisotropy factors of different CD signals is still unsynchronized. The anisotropy factor of the peak at 373 nm undergoes a dramatic decline upon heating, in sharp contrast to the negligible variation for the other two peaks at 278 and 311 nm (Fig. S12†). In the NMR monitoring of 3-(R,R) from 20 to 70 °C, the signals corresponding to the proton atoms of the central cyclohexane skeleton in L³ and the peripheral PPh₃ ligands are almost unchanged upon heating (Fig. S13 and S14†). This is because the small cyclohexane skeleton is too far away from the peripheral PPh₃ ligands to form substantial interaction (as shown in the space-filling model structure in Fig. S13†). Despite no obvious NMR signal variation, in view of the structural similarity between 2-(R,R) and 3-(R,R), we speculate that 3-(R,R) has a similar conformational change for the central L³ ligand.

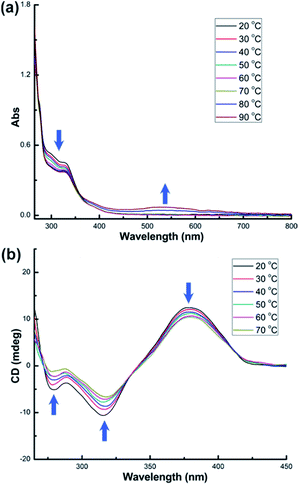Fig. 6 (a) UV-vis and (b) CD spectra of DMSO solution (c = 2.5 × 10⁻⁵ M) of 3-(R,R) at elevated temperatures.

The above experimental findings clearly indicate that 1-(S_a), 2-(R,R) and 3-(R,R) exhibit different chiroptical responses upon heating. This difference can be roughly quantified by the variation rate of CD intensity for the corresponding strongest signal (Fig. 7). It is clear that 1-(S_a) is more sensitive to heating than 2-(R,R) and 3-(R,R). In view of the similar structural tunability of L¹ and L² but remarkably different Au–Au interactions between two NAu₃ segments in 1-(S_a) and 2-(R,R), we speculate that short aurophilic interactions should be conducive to enhancing the stability of chiral clusters. This is reminiscent of a recent study that reported a substantial lowering of the racemization energy upon doping two palladium atoms in a chiral gold cluster.¹⁶ The doping may lead to the weakening of metal–metal interactions. In addition, the small α angle in 1-(S_a) relative to 2-(R,R) and 3-(R,R) implies a loose arrangement of PPh₃, which has been substantiated by well-resolved NMR signals of L¹ in 1-(S_a), but broad signals of corresponding diamino ligands in 2-(R,R) and 3-(R,R). Such an incompact structure of peripheral phosphine ligands in 1-(S_a) may also account for its high structural fluxionality and the resulting low stability.

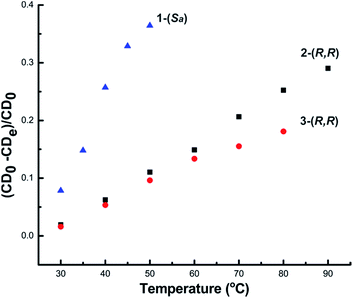Fig. 7 The variation rate of CD signal intensity for 1-(S_a) at 361 nm, 2-(R,R) at 372 nm and 3-(R,R) at 373 nm.

Although 3-(R,R) decomposes above 70 °C, it shows better stability than 2-(R,R) below 70 °C as shown in Fig. 7. Previous theoretical studies based on Mulliken population analysis have reported that the HOMO and near frontier HOMO-n orbitals of 2-(R,R) and 3-(R,R) mainly lie on the sigmoidal gold clusters and the two amino nitrogen atoms.¹⁴ Garzón and co-workers' recent theoretical investigation on the geometric quantification of the chirality origins also proved that asymmetric arrangements of metal atoms make a phenomenal contribution to the chirality of the whole cluster.¹⁷ Therefore, the stability difference between 2-(R,R) and 3-(R,R), especially reflected by the remarkable change of the anisotropy factor at maximal wavelengths (372 nm for 2-(R,R) and 373 nm for 3-(R,R)), may arise from the conformation tuning of the sigmoidal Au₆ cluster core. This was substantiated by a calculated cluster model based on the crystal structure of 2-(R,R). Upon varying the N–C–C–N dihedral angle of L² but keeping the integrity of two [N(AuPPh₃)₃] moieties, the simulated UV-vis and CD spectra indeed show the variation of CD and UV-vis peaks in the aspects of the intensity and wavelength position (Fig. S15†). In contrast, when just rotating the N(AuPPh₃)₃ moiety around a C–N bond, the variation of the CD signals is not very significant (Fig. S16†). In view of high structural similarity between 2-(R,R) and 3-(R,R) in the aspects of the N_amino–N_amino separation, the inter-cluster Au–Au interaction and the α angle, we assume such a stability difference between 2-(R,R) and 3-(R,R) should be ascribed to the rigidity difference of the central diamino ligands. It is clear that the rigid cyclohexane skeleton of L³ has low structural tunability in comparison with L². Lastly, our investigation further explores that the three diamino ligands L¹, L² and L³ have different reductive potentials at elevated temperature. 1-(S_a) and 3-(R,R) readily decompose to generate gold nanoparticles when the temperature is up to 40 °C and 70 °C, respectively, while 2-(R,R) is stable up to 90 °C.

Conclusions

In conclusion, we have studied the temperature dependent chiroptical response of three sigmoidal gold clusters with the aim at probing the stability of chiral metal clusters. The three gold cluster compounds have different diamino centers, which lead to the structural difference of acquired chiral gold clusters in the aspects of the inter-cluster Au–Au interaction, the compactness of surrounding phosphorous ligands and different modes of motion upon heating. Through monitoring the variation of CD, UV-vis and NMR spectra upon the rise of temperature, we finally ascribe the distinct chiroptical response of the sigmoidal Au₆ clusters to a synergistic effect of the distinct structural tunability of central diamino ligands, inter-cluster aurophilic interactions and steric hindrance of peripheral phosphine ligands. Moreover, different reductive potentials of the three diamino ligands at elevated temperature finally result in the decomposition of chiral clusters by forming gold nanoparticles and metallic gold. The present study offers a promising approach to enhance the stability of chiral cluster structures by using more rigid templates and strengthening intermetallic interactions. The comprehension of detailed structures and stability of chiral cluster motifs may deepen our understanding of the origin of chirality and chirality transfer in chiral metal nanomaterials, which should be conducive to their practical application in the future.

Experimental

Materials and methods

All commercially available chemicals were used without further purification. The solvents used in this study were dried by standard procedures. All reactions were carried out under a nitrogen atmosphere unless otherwise noted. [O(AuPPh₃)₃](BF₄),¹⁸2-(R,R)¹⁴ and 3-(R,R)¹⁴ were prepared according to the published methods. ¹H and ³¹P NMR experiments were carried out on a JEOL ECX-400 MHz instrument. The samples were heated to the target temperature for 10 min and ¹H and ³¹P NMR experiments were carried out in situ. CD and UV-vis measurements were carried out on a Jasco J-815 circular dichroism spectropolarimeter, using 1 cm cuvettes and with pre-dried dimethyl sulfoxide as solvent. The samples were heated to the target temperature for 10 min and the CD and UV-vis spectra were monitored in situ. For the CD measurements, two accumulations of standard sensitivity at a scan rate of 100 nm min⁻¹ and data pitch of 0.5 nm were averaged. Anisotropy factors were calculated according to g = θ [mdeg]/(32 980 × A) using the UV-vis spectrum data measured by the CD spectrometer. For time-course measurements, the change of temperature begins to detect the change of the CD response at specific wavelengths, which was followed in 0.5 s intervals at different temperatures. Mass spectra were obtained using a Thermo Scientific Exactive Orbitrap instrument.

Synthesis of 1-(S_a)

At room temperature, (S_a)-1,1′-binaphthyl-2,2′-diamine ((S_a)-BINAM) (2.8 mg, 0.01 mmol) in 1 mL of CH₂CH₂ was added to a CH₂CH₂ (1 mL) solution of [O(AuPPh₃)₃](BF₄) (29.6 mg, 0.02 mmol) under vigorous stirring. The solution underwent a gradual color change from colorless to bright yellow. After 10 h, removing the solvent finally gave a yellow crude product. Colorless plate crystals of 1-(S_a) were acquired by diffusion of diethyl ether into the concentrated CH₃OH solution of 1-(S_a). Yield: 70% (23.0 mg). ¹H NMR (400 MHz, DMSO-d₆): δ 7.92 (d, 2H), 7.49 (d, 2H), 7.45 (d, 2H), 7.35–7.27 (m, 18H), 7.15–6.98 (m, 72H), 6.53 (t, 2H), 6.43 (d, 2H), 6.18 (t, 2H). ³¹P NMR (162 MHz, DMSO-d₆): δ 27.00. HR-MS (ESI): calcd. For [M − 2BF₄]²⁺ (C₁₂₈H₁₀₂Au₆N₂P₆) 1517.7242, found 1517.7201; calcd. For [M − BF₄]⁺ (C₁₂₈H₁₀₂Au₆B₁F₄N₂P₆) 3122.4519, found 3122.44908.

X-ray crystallography

Single-crystal X-ray data for 1-(S_a) (CCDC number: 1818253†) were collected at 173 K with Cu Kα radiation (λ = 1.54178 Å) on a Rigaku Oxford Diffraction SuperNova diffractometer. The selected crystal was mounted onto a nylon loop in polyisobutene and immersed in a low-temperature (173 K) stream of dry nitrogen gas during data collection. The structure was solved by direct methods, and non-hydrogen atoms were located from difference Fourier maps. Non-hydrogen atoms, except three carbon atoms of the diethyl ether solvent molecule, were subjected to anisotropic refinement by full-matrix least-squares on F² by using the SHELXTL program¹⁹ and Olex² program.²⁰ All figures were drawn by using the X-seed program.²¹ Crystal data for 1-(S_a): C₁₃₂H₁₁₂Au₆B₂F₈N₂OP₆, M = 3283.56, orthorhombic, space group P2₁2₁2₁, a = 13.7644(1) Å, b = 24.8987(2) Å, c = 35.6022(2) Å, V = 12 201.43(15) ų, Z = 4, T = 173 K, D_c = 1.788 g cm⁻³. The structure, refined on F², converged for 25 357 unique reflections (R_int = 0.0862) and 24 837 observed reflections with I > 2σ(I) to give R₁ = 0.0605 and wR₂ = 0.1554 and a goodness-of-fit = 1.062. A tetrafluoroborate anion is disordered at two positions with the occupancy ratio of 0.65 : 0.35.

Computational details

Theoretical calculations of 1-(S_a) and the 2-(R,R)-based model clusters were performed using the Gaussian 09 program. Structures of 1-(S_a) and 2-(R,R) for calculation were built up on the basis of corresponding single-crystal structures. The Becke three-parameter hybrid functional accompanied by the Lee–Yang–Parr correlation functional (B3LYP)²² was employed in the TD-DFT calculation without any symmetry constraints on molecular structures. The Hay and Wadt effective core potentials with a double-ζ basis set (LanL2DZ)²³ were applied for all atoms. Sixty singlet states (n_states = 60, singlet) are chosen in the calculations of the UV-vis absorption and CD spectra of 1-(S_a) and the 2-(R,R)-based model clusters. The root is set as 1 in all of the TD-DFT calculations. Data for orbital composition analysis with Mulliken partition are from Gaussian 09 calculations and processed with Multiwfn software.²⁴ Plots of theoretically calculated UV-vis and CD spectra are obtained by using Multiwfn software.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support by the National Natural Science Foundation of China (21522206, 21772111 and 21661132006) is gratefully acknowledged. We are grateful to Prof. Mei-Xiang Wang (THU) and Gao-Quan Shi (THU) for their kind help in measurements. Prof. Gao-Quan Shi sadly passed away in February.

References

1. For recent reviews, see: (a) C. Gautier and T. Bürgi, ChemPhysChem, 2009, 10, 483; (b) A. Ben-Moshe, B. M. Maoz, A. O. Govorov and G. Markovich, Chem. Soc. Rev., 2013, 42, 7028; (c) S. Knoppe and T. Bürgi, Acc. Chem. Res., 2014, 47, 1318; (d) J. Kumar, K. G. Thomas and L. M. Liz-Marzan, Chem. Commun., 2016, 52, 12555; (e) W. Ma, L. Xu, A. F. de Moura, X. Wu, H. Kuang, C. Xu and N. A. Kotov, Chem. Rev., 2017, 117, 8041.
2. (a) T. Yasukawa, H. Miyamura and S. Kobayashi, Chem. Soc. Rev., 2014, 43, 1450; (b) E. Gross, J. H. Liu, S. Alayoglu, M. A. Marcus, S. C. Fakra, F. D. Toste and G. A. Somorjai, J. Am. Chem. Soc., 2013, 135, 3881; (c) Q.-Y. Zhang and L. Zhao, Tetrahedron Lett., 2018, 59, 310.
3. (a) N. Shukla, M. A. Bartel and A. J. Gellman, J. Am. Chem. Soc., 2010, 132, 8575; (b) L. Xu, Z. Xu, W. Ma, L. Liu, L. Wang, H. Kuang and C. Xu, J. Mater. Chem. B, 2013, 1, 4478; (c) Z. Chen, Q. Wang, X. Wu, Z. Li and Y.-B. Jiang, Chem. Soc. Rev., 2015, 44, 4249.
4. (a) A. Baev, M. Samoc, P. N. Prasad, M. Krykunov and J. Autschbach, Opt. Express, 2007, 15, 5730; (b) V. A. Fedotov, A. S. Schwanecke, N. I. Zheludev, V. V. Khardikov and S. L. Prosvirnin, Nano Lett., 2007, 7, 1996.
5. (a) V. K. Valev, A. V. Silhanek, N. Verellen, W. Gillijns, P. V. Dorpe, O. A. Aktsipetrov, G. A. E. Vandenbosch, V. V. Moshchalkov and T. Verbiest, Phys. Rev. Lett., 2010, 104, 127401; (b) S. Knoppe, A. Dass and T. Bürgi, Nanoscale, 2012, 4, 4211; (c) S. Knoppe, H. Hakkinen and T. Verbiest, J. Phys. Chem. C, 2015, 119, 27676.
6. D. B. Amabilino, Chirality at the Nanoscale, WILEY-VCH, Weinheim, 2009.
7. (a) P. D. Jadzinsky, G. Calero, C. J. Ackerson, D. A. Bushnell and R. D. Kornberg, Science, 2007, 318, 430; (b) H. Qian, Y. Zhu and R. Jin, ACS Nano, 2009, 3, 3795; (c) H. Qian, W. T. Eckenhoff, Y. Zhu, T. Pintauer and R. Jin, J. Am. Chem. Soc., 2010, 132, 8280; (d) O. Lopez-Acevedo, H. Tsunoyama, T. Tsukuda, H. Häkkinen and C. M. Aikens, J. Am. Chem. Soc., 2010, 132, 8210; (e) C. Zeng, T. Li, A. Das, N. L. Rosi and R. Jin, J. Am. Chem. Soc., 2013, 135, 10011; (f) X.-K. Wan, S.-F. Yuan, Z.-W. Lin and Q.-M. Wang, Angew. Chem., Int. Ed., 2014, 53, 2923; (g) D. Crasto, S. Malola, G. Brosofsky, A. Dass and H. Häkkinen, J. Am. Chem. Soc., 2014, 136, 5000; (h) Y. Chen, C. Zeng, C. Liu, K. Kirschbaum, C. Gayathri, R. R. Gil, N. L. Rosi and R. Jin, J. Am. Chem. Soc., 2015, 137, 10076; (i) C. Zeng, Y. Chen, K. Kirschbaum, K. Appavoo, M. Y. Sfeir and R. Jin, Sci. Adv., 2015, 1, e1500045; (j) S. Wang, S. Jin, S. Yang, S. Chen, Y. Song, J. Zhang and M. Zhu, Sci. Adv., 2015, 1, e1500441.
8. I. Dolamic, S. Knoppe, A. Dass and T. Bürgi, Nat. Commun., 2012, 3, 798.
9. S. Knoppe, O. A. Wong, S. Malola, H. Häkkinen, T. Bürgi, T. Verbiest and C. J. Ackerson, J. Am. Chem. Soc., 2014, 136, 4129.
10. J. Yan, H. Su, H. Yang, C. Hu, S. Malola, S. Lin, B. K. Teo, H. Häkkinen and N. Zheng, J. Am. Chem. Soc., 2016, 138, 12751.
11. (a) H. Yang, J. Yan, Y. Wang, G. Deng, H. Su, X. Zhao, C. Xu, B. K. Teo and N. Zheng, J. Am. Chem. Soc., 2017, 139, 16113; (b) S. Knoppe, S. Michalet and T. Burgi, J. Phys. Chem. C, 2013, 117, 15354; (c) Y. Yanagimoto, Y. Negishi, H. Fujihara and T. Tsukuda, J. Phys. Chem. B, 2006, 110, 11611.
12. (a) S. Knoppe, I. Dolamic and T. Bürgi, J. Am. Chem. Soc., 2012, 134, 13114; (b) Z. Li, Z. Zhu, W. Liu, Y. Zhou, B. Han, Y. Gao and Z. Tang, J. Am. Chem. Soc., 2012, 134, 3322; (c) M. Mathews, R. S. Zola, S. Hurley, D.-K. Yang, T. J. White, T. J. Bunning and Q. Li, J. Am. Chem. Soc., 2010, 132, 18361; (d) L. Óvári, M. Wolf and P. Tegeder, J. Phys. Chem. C, 2007, 111, 15370.
13. (a) T. G. Schaaff, G. Knight, M. N. Shafigullin, R. F. Borkman and R. L. Whetten, J. Phys. Chem. B, 1998, 102, 10643; (b) Y. Yanagimoto, Y. Negishi, H. Fujihara and T. Tsukuda, J. Phys. Chem. B, 2006, 110, 11611; (c) C. Gautier and T. Bürgi, J. Am. Chem. Soc., 2008, 130, 7077.
14. X. He, Y. Wang, H. Jiang and L. Zhao, J. Am. Chem. Soc., 2016, 138, 5634.
15. (a) P. Pyykkö, Chem. Rev., 1997, 97, 597; (b) H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2008, 37, 1931; (c) H. Schmidbaur and A. Schier, Chem. Soc. Rev., 2012, 41, 370.
16. N. Barrabés, B. Zhang and T. Bürgi, J. Am. Chem. Soc., 2014, 136, 14361.
17. J. J. Pelayo, R. L. Whetten and I. L. Garzón, J. Phys. Chem. C, 2015, 119, 28666.
18. A. N. Nesmeyanov, E. G. Perevalova, Y. T. Struchkov, M. Y. Antipin, K. I. Grandberg and V. P. Dyadchenko, J. Organomet. Chem., 1980, 201, 343.
19. G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112.
20. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339.
21. J. L. Atwood and L. J. Barbour, Cryst. Growth Des., 2003, 3, 3.
22. (a) A. D. Becke, J. Chem. Phys., 1993, 98, 5648; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785.
23. (a) W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284; (b) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270; (c) P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299.
24. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580.

---

Footnote

† Electronic supplementary information (ESI) available: Supporting figures, high-resolution ESI-MS, NMR, crystal refinement details and computational results. CCDC 1818253. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc00344k

---