DOI:
10.1039/C8SC01889H
(Edge Article)
Chem. Sci., 2018,
9, 6509-6515
Size-dependent rate acceleration in the silylation of secondary alcohols: the bigger the faster†
Received
25th April 2018
, Accepted 27th June 2018
First published on 29th June 2018
Abstract
Relative rates for the reaction of secondary alcohols carrying large aromatic moieties with silyl chlorides carrying equally large substituents have been determined in organic solvents. Introducing thoroughly matching pairs of big dispersion energy donor (DED) groups enhanced rate constants up to four times, notably depending on the hydrogen bond donor ability of the solvent. A linear correlation between computed dispersion energy contributions to the stability of the silyl ether products and experimental relative rate constants was found. These results indicate a cooperation between solvophobic effects and DED-groups in the kinetic control of silylation reactions.
Introduction
Aromatic interactions1 play a central role in diverse fields such as organic synthesis,2 supramolecular self-assembly,3–5 molecular recognition6 or protein and peptide structures.7 They mainly result from the sum of three terms:8,9 (1) an electrostatic component due to the electronic nature of the substituents at the interacting surfaces,10 (2) London dispersion interaction11–14 as the attractive component of van der Waals forces, which arise due to interactions between induced dipoles,15 and (3) the solvophobic or hydrophobic effect, which results from a balance between solvent–solvent and solvent–solute interactions.16–18 Whereas numerous studies have detailed the nature of the electrostatic component,19–24 it is still a challenge to quantify individual dispersive and solvophobic effects in solution.25 Recent studies by Cockroft et al.26–29 and Shimizu et al.30,31 employ torsional molecular balances32 to measure these effects through the quantification of conformational equilibria. Most of the studies conclude that the dispersive interactions are of minor importance in solution33 and that the major contribution to the stabilization of the folded state results from the balance of solvent–solvent and solute–solvent interactions. The conceptually similar idea of using sizeable (rigid) dispersion energy donor groups (DED-group) in reagents and/or ligands in the development of stereoselective catalytic processes has also been explored recently,2,34 where it has been found that the appropriate placement of interacting DED-moieties in a system can lead to higher selectivity. Interactions between DED groups in bimolecular (associative) reactions were recently analysed for acylation reactions of alcohols.34,36 For this latter class of reactions we have found that acylations mediated by TCAP (9-azajulolidine, marked in red in Fig. 1a) are fastest for pyrenyl-substituted secondary alcohols (marked in green Fig. 1) as compared to alcohols carrying smaller aromatic or even aliphatic substituents.35 In contrast, reaction rates hardly vary for acylation reagents of different size, which can most easily be accommodated in the general transition state structure shown in Fig. 1a. In the following we explore the question whether the silylation of secondary alcohols with silyl chloride reagents can be accelerated in a similarly targeted fashion through the use of sufficiently large DED substituents in the reagents and substrates. The silylation of alcohols is of outstanding importance in protection group strategies for the synthesis of complex molecular targets,37,38 and any extension of the currently available toolset will obviously be helpful for organic synthesis in general. The base-catalysed silylation of alcohols is commonly assumed to follow a Lewis base- rather than a general base-catalysed mechanism.39–42 In contrast to acylation reactions, silyl group transfer reactions proceed along an SN2-like pathway, which implies the relative orientation of catalyst, reagent and substrate shown in the transition state cartoon in Fig. 1b. For this type of transition state structure, stabilizing interactions between appropriately placed DED substituents are expected between the alcohol and the reagent, but not between the alcohol and the catalyst. In order to probe this hypothesis, we have studied the reaction rates for the reaction of secondary alcohols with silyl chloride reagents carrying alkyl and aryl substituents of varying size. In addition, the influence of reaction temperature and solvent on the reaction rate was studied. The thermochemical stability of the products was explored by theoretical methods in an effort to quantify the dispersion energy contribution to the overall reaction driving force.
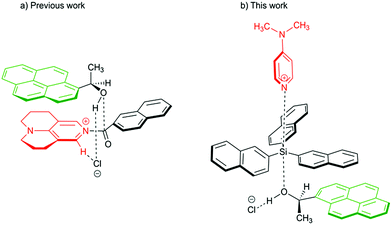 |
| | Fig. 1 Proposed transition structures for catalysed acylation (left) and silylation reaction (right) of 1-(1-pyrenyl)ethanol. | |
Results and discussion
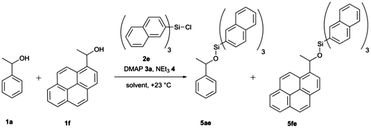
Relative rate constants krel for the Lewis base-catalysed silylation of alcohols 1a–1f with silyl chlorides 2a–2f were determined in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
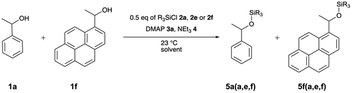
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 competition experiments employing 1-phenylethanol (1a) as the reference system (Scheme 1 and Fig. 2). The other substrate alcohols derived from 1a through annulation of one (as in 1b and 1c), two (as in 1d and 1e) or three (as in 1f) benzene rings to its phenyl group. Depending on the particular position of annulation, this generates no additional repulsive 1,5-interaction with the alcohol oxygen atom (as in 1c and 1e), one additional 1,5-interaction (as in 1b and 1f), or two such interactions in 1d. The peri positions responsible for the repulsive 1,5-interactions are marked by grey circles in Fig. 2. The silyl chloride reagents chosen here grow in size from trimethylsilyl chloride 2a to substituted trinaphthylsilyl chloride 2f (see Fig. 2 and S1 of the ESI†). The competition experiments described in Scheme 1 involve equal amounts of reference alcohol 1a and of one of the substrate alcohols 1b–f, a quantity of one of the silyl chlorides 2 sufficient enough to obtain between 20–80% turnover of the substrate alcohols 1, a catalytic amount (0.15 eq. relative to alcohols 1) of N,N-dimethylaminopyridine (3, DMAP), and triethylamine (4) as the auxiliary base, in deuterated chloroform at a constant temperature of +23 °C. The relative rate constant krel defined as the ratio of effective rate constants k2 (1b–f) over k1 (1a) was used as main control parameter and obtained from the mole distribution of reactants and products after completion of the reaction as determined by 1H NMR spectroscopy (for full details see ESI†). The resulting rate constant values are shown in Fig. 2 and in Tables S1–S5 of the ESI.†
1 competition experiments employing 1-phenylethanol (1a) as the reference system (Scheme 1 and Fig. 2). The other substrate alcohols derived from 1a through annulation of one (as in 1b and 1c), two (as in 1d and 1e) or three (as in 1f) benzene rings to its phenyl group. Depending on the particular position of annulation, this generates no additional repulsive 1,5-interaction with the alcohol oxygen atom (as in 1c and 1e), one additional 1,5-interaction (as in 1b and 1f), or two such interactions in 1d. The peri positions responsible for the repulsive 1,5-interactions are marked by grey circles in Fig. 2. The silyl chloride reagents chosen here grow in size from trimethylsilyl chloride 2a to substituted trinaphthylsilyl chloride 2f (see Fig. 2 and S1 of the ESI†). The competition experiments described in Scheme 1 involve equal amounts of reference alcohol 1a and of one of the substrate alcohols 1b–f, a quantity of one of the silyl chlorides 2 sufficient enough to obtain between 20–80% turnover of the substrate alcohols 1, a catalytic amount (0.15 eq. relative to alcohols 1) of N,N-dimethylaminopyridine (3, DMAP), and triethylamine (4) as the auxiliary base, in deuterated chloroform at a constant temperature of +23 °C. The relative rate constant krel defined as the ratio of effective rate constants k2 (1b–f) over k1 (1a) was used as main control parameter and obtained from the mole distribution of reactants and products after completion of the reaction as determined by 1H NMR spectroscopy (for full details see ESI†). The resulting rate constant values are shown in Fig. 2 and in Tables S1–S5 of the ESI.†
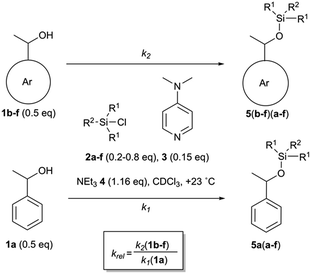 |
| | Scheme 1 Competition experiments between alcohol 1a and 1b–f with silyl reagents 2a–f. | |
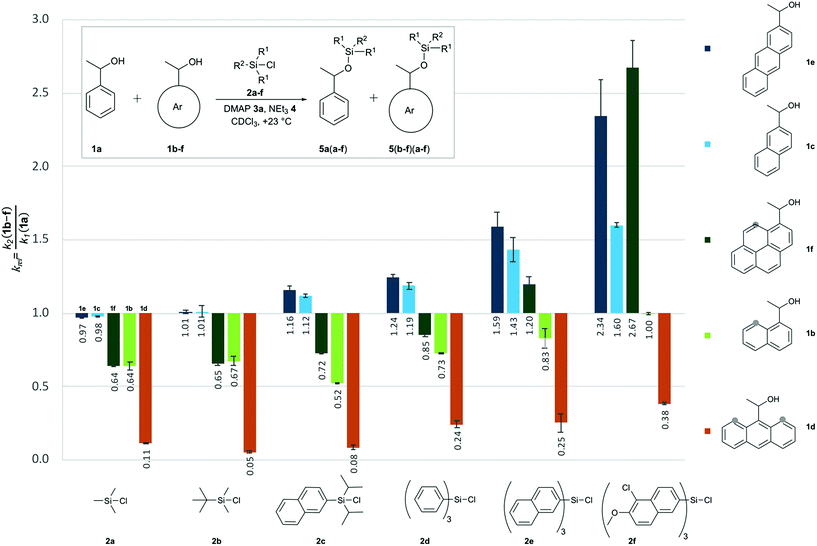 |
| | Fig. 2 Relative rate constants (krel) for competition experiments between reference alcohol 1a and selected secondary alcohols 1b–1f with silyl chlorides 2a–f. | |
Relative reaction rates for the small trimethylsilyl chloride 2a (TMSCl) reagent show no response to the size of the alcohol π-systems, but are sensitive to the number of repulsive 1,5-interactions. Reaction rates are therefore quite similar for alcohols 1a, 1c and 1e, then drop notably for alcohols with one 1,5-interaction (1b and 1f), and drop more strongly for the most hindered alcohol 1d, which reacts nine times slower than 1a. Moving to tert-butyldimethylsilyl chloride 2b (TBDMSCl) as a sterically more hindered and overall larger reagent we find practically no change in relative rate constants krel, except for the most hindered alcohol 1d, whose reactivity drops by another factor of two. With the results for smaller silyl chloride reagents in hand, we next investigated symmetrical silyl reagents 2d–2f containing sizeable aromatic substituents.
Reactions with triphenylsilyl chloride (2d, TPSCl) differ from those with TMSCl in two key aspects. First, all krel values for silyl chloride 2d are larger than those for TMSCl (2a), the sterically unhindered alcohols 1c and 1e now reacting even faster than the reference alcohol 1a. Second, silyl chloride 2d differentiates more strongly between alcohols of different size, but identical degree of steric hindrance. Reaction rates for alcohols 1b and 1f, for example, are quite similar for TMSCl (2a) and also for TBSCl (2b), but differ systematically for triphenylsilyl chloride (2d) in that the larger alcohol 1f (krel = 0.85) reacts faster than alcohol 1b (krel = 0.73). Both factors can be seen at work in an enhanced way in reactions of the even larger trinaphthylsilyl chloride 2e, where the sterically hindered, but pyrenyl-substituted alcohol 1f now reacts faster than the unhindered reference alcohol 1a (krel = 1.20). Polar substituents were then added to the 5,6-positions of the naphthyl groups in silyl chloride 2e in order to increase its overall polarizability and the contact surface with alcohol reagents. Relative reaction rates for the resulting silyl chloride 2f (TN*SCl) are all significantly larger than those for trinaphthylsilyl chloride 2e and appear to be mainly dominated by the size of the alcohol π-system. This makes pyrenyl-substituted alcohol 1f the most reactive substrate, closely followed by the less hindered anthracenyl-substituted alcohol 1e. A final test was performed with diisopropylnaphthylsilyl chloride 2c (DINSCl), which combines a single naphthyl with two α-branched isopropyl substituents. The results obtained for this reagent are basically those for trinaphthylsilyl chloride 2e, but scaled down towards the results obtained for the trialkylsilyl chlorides 2a and 2b (Fig. 2). The spatial disposition of the substituents in the crystal structure of product 5fc shows no direct interaction between the naphthyl and pyrenyl surfaces (see ESI†). Assuming a similar structure in the transition state, relative rates seem to be influenced by the isopropyl as well as the naphthyl substituents. The results presented in Fig. 2 can also be analysed from the point of view of each reacting alcohol (see Fig. S2†). While the 9-anthracenyl alcohol 1d containing two peri hydrogen atoms is for all silyl chlorides much slower than 1a, the sterically not hindered alcohols 1c and 1e react with all silyl reagents 2 equally fast or faster than 1a. In the 1-pyrenyl- and 1-naphthyl-substituted alcohols (1f and 1b) the relative rate constants are determined by a balance between interactions of the two aromatic surfaces and repulsive steric effects, the former one being dominant in the case of TN*SCl 2f. In all of the pairs krel increases with the growth of the DED-substituent at the silicon centre, which confirms that the size of interacting aromatic surfaces located at the alcohol and silyl substrates determine the chemoselectivity of the silylation reaction.
With the purpose of quantifying the influence of the reaction medium on the relative rate constants, the competition experiment between the reference alcohol 1a and the biggest alcohol 1f with TNSCl 2e was carried out in different solvents. This choice was motivated by two main considerations: (1) both alcohol 1f and TNSCl 2e carry the biggest non-substituted DED-substituents and (2) using alcohol 1f the balance between attractive aromatic interactions and repulsive steric effects can be studied in different solvents. The krel values measured in different solvents span a range from 0.59 in tetrahydrofuran to 1.38 in dichloromethane (Table 1, for details see ESI†). Strikingly, relative rates for the reaction of alcohol 1f with the naphthyl-substituted silyl chloride 2e were found to be in several solvents (entries 1–3) very similar to krel of the reaction of this alcohol 1f in the reference solvent CDCl3 with TMSCl 2a in which no aromatic interactions between alcohol and silyl moiety occur. Therefore, those solvents seem to cancel aromatic interactions almost completely and repulsive steric effects solely govern the relative rates. In contrast, krel for the silylation of alcohol 1f increases up to 2.3 times in other solvents like acetone, chloroform and dichloromethane. In order to prove that those solvent effects are causally related to aromatic interactions, reactions between alcohols 1a and 1f with silyl reagents of various sizes were explored by competition experiments in CDCl3 as the reference solvent, and in tetrahydrofuran and dichloromethane as the solvents with the smallest and largest krel values in Table 1 (Fig. 3). For TMSCl (2a) as the smallest reagent, only a negligible solvent sensitivity of krel was found (Fig. 3), while for the largest reagent TN*SCl 2f an increase in solvent sensitivity as compared to the relatively smaller TNSCl 2e is observed. Hence, the observed solvent effects are due to the significant impact of solvents on size-dependent effects, which was also reported in other studies.26,27,43–46 Distinguishing the different contributions of polarizability (π* and δ), hydrogen-bond donor (α) and acceptor ability (β) via the linear solvation energy relationship developed by Kamlet and Taft47,48 revealed that solvent effects are widely independent of the polarizability of the solvent, but correlate strongly with the hydrogen bond donor ability of the solvent (see eqn (S12) of ESI†). This can actually be further condensed to a direct correlation of the experimental krel values with the general α parameter proposed by Hunter (Fig. 4).17 Considering that the hydrogen-bond donor ability of aromatic C–H groups is commonly found to be in the range of α = 1.0–1.4 the origin of solvent effects can be clarified. Thus, for solvents with α < 1 such as THF and CS2 hydrogen bonds of aromatic C–H-bonds with solvent molecules dominate the system whereas interactions of the aromatic surfaces of the alcohol and silyl moieties are minimized. Therefore, reaction rates are barely influenced by the different size of the aromatic systems of the two competing alcohols. As H-bonds between the aromatic C–H-bonds and the solvent get less relevant in solvents with α > 1 such as chloroform and dichloromethane, desolvation of the alcohol and silyl substrates occurs and as a consequence solvent–solvent as well as aromatic solute–solute interactions become more dominant.17 Both the solvophobic effect of solvent molecules forming additional hydrogen bonds among each other and the attractive dispersion forces between the DED-groups can then enhance the rate of the reaction dependent on the size of the aromatic surfaces.
Table 1 Relative rate constants (krel) for competition experiments between alcohol 1a and 1f with silyl chloride 2e in different solvents
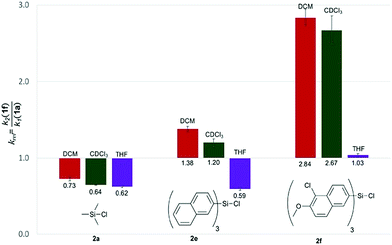 |
| | Fig. 3 Relative rate constants krel for the reaction of alcohols 1a and 1f with silyl chlorides 2a, 2e and 2f in different solvents. | |
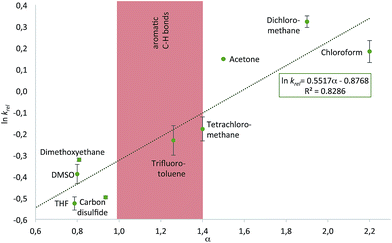 |
| | Fig. 4 Plot of experimental ln krel for the reaction of alcohols 1a and 1f with silyl chloride 2e in different solvents against the solvent hydrogen bond donor parameter α defined by Hunter.17 | |
Differentiating the contributions of the aforementioned two types of effects is one main focus of the ongoing debate on aromatic stacking. The ln krel determined in different solvents listed in Table 1 were therefore also analysed in terms of the solvent cohesive energy density (ced) as key parameter for the strength of the solvophobic effect of a solvent.27 Whether a higher ced value leads to an increase or a decrease of relative rates appears to depend on the hydrogen bond donor ability of the solvent (Fig. S14 of ESI†): in solvents with a low α (e.g. THF) higher ced values lead to a reduction in relative rates, possibly through the reinforcement of unfavourable solvent–solute interactions. In contrast, for solvents with a higher H-bond donor ability (e.g. DCM) higher ced values lead to an increase in krel. Correlations are, however, not very strong in both cases and the ced is thus insufficient to explain the observed differences in krel. The influence of London dispersion interactions on the experiment shown in Table 1 was subsequently probed through selectivity measurements in CDCl3 at different temperatures, as these interactions are known to be less temperature dependent than dipole-dominated interactions.11 Measurements in the temperature range from −10 °C to +23 °C lead to similar krel values for the 1a/1f substrate pair, but the accuracy of these measurements was not high enough for the reliable extraction of activation parameters (see ESI†).
In how far the relative reaction rates measured experimentally simply reflect the stability of the silyl ether products formed was explored by the calculation of reaction free energies in chloroform solution. Geometry optimizations were performed at the SMD(CHCl3)/B3LYP-D3/6-311+G(2d)/6-31+G(d)49–53 level of theory, followed by single point energy calculations at DLPNO-CCSD(T)/def2-TZVPP54–56 level. Solvation free energies were obtained from single point calculations with the SMD(CHCl3)/B3LYP-D3/6-311+G(2d)/6-31+G(d) model and added to the gas phase results in order to obtain the reaction free energies in solution ΔG298,sol compiled in Fig. 5 (see ESI† for details). Focusing on the results obtained for pyrenyl-substituted alcohol 1f, we find small and positive reaction energies for the smaller silyl chloride reagents. The positive sign for the reaction energy seen here derives from the fact that the calculated energies exclude the acid/base reaction between HCl and the auxiliary base NEt3. This is in full agreement with experimental results showing basically no turnover between TBDMSCl (2b) and secondary alcohols in the absence of the auxiliary base.39,40 Reaction energies become more favourable and eventually also negative on increasing the size of the silyl chloride reagent. Interestingly, the tert-butyldimethylsilyl ether 5fb is less stable than the trimethylsilyl ether 5fa, most likely due to repulsive steric interactions between the tert-butyl and the pyrenyl substituents. Although the two interacting aromatic surfaces are the same in the products 5fc and 5fe, the last one is 18.2 kJ mol−1 more stable than 5fc. This energetic difference is possibly associated to the smaller polarizability of the isopropyl substituents than the naphthyl moiety at the Si atom in 5fc. Regarding those results no significant correlations were found between the experimental krel and the differences between the ΔG298,sol of the respective silyl ethers (see ESI†), which indicates that the krel are purely kinetic phenomena. At this point, we were interested in computing the contribution of the dispersion component to the thermochemical stability of the products. Single point energy calculations were therefore performed at the B3LYP level lacking the D3 dispersion correction over the optimized structures at B3LYP-D3 level (third group, Fig. 5). It was found that ΔG298,sol decreases dramatically (larger positive values) even indicating that these products would be thermodynamically unstable. The smallest dispersion contributions were found in the silyl ethers 5fa and 5fb with non-polarizable methyl and tert-butyl substituents. However, in the case of silyl ethers carrying bigger aromatic substituents at the Si centre, the dispersion component increases notably up to −85.7 kJ mol−1 (5ff). Conformational analysis of silyl ether 5fe as the silyl ether with the largest unsubstituted aromatic substituents reveals that aromatic surfaces for the best conformers are slightly twisted toward each other so that most non-covalent interactions57 arise between the interacting Π-surfaces with a small contribution of Σ–Π interactions (see Fig. 5 and ESI† for full details). Interestingly, linear correlations appear to exist between experimental krel values and differences in dispersion contributions between the respective substrate pairs ΔΔD298,sol, grouped by the number of 1,5-interactions at the alcohol substrate (Fig. 6). The similar slope reveals that sizeable DED-groups (higher ΔΔD298,sol) increases ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel equally in both alcohol groups by 0.2 units per 10 kJ mol−1 of additional dispersion contribution. That the data points for the unhindered alcohols 1c and 1e fall onto the same correlation line implies that it is irrelevant for the increase of krel whether the increase in ΔΔD298,sol derives from growing the substrate alcohol or the silyl chloride reagent. The presence of one repulsive 1,5-interaction reduces the relative rate by 1.6 times with respect to the non-hindered alcohols represented by the gap between the two correlation lines in Fig. 6. This analysis demonstrates that the experimentally measured relative rate constants krel directly relate to the size of the interacting surfaces and to repulsive steric effects in the alcohol substrates, whereby the dispersion energy component increases together with substrate size.
krel equally in both alcohol groups by 0.2 units per 10 kJ mol−1 of additional dispersion contribution. That the data points for the unhindered alcohols 1c and 1e fall onto the same correlation line implies that it is irrelevant for the increase of krel whether the increase in ΔΔD298,sol derives from growing the substrate alcohol or the silyl chloride reagent. The presence of one repulsive 1,5-interaction reduces the relative rate by 1.6 times with respect to the non-hindered alcohols represented by the gap between the two correlation lines in Fig. 6. This analysis demonstrates that the experimentally measured relative rate constants krel directly relate to the size of the interacting surfaces and to repulsive steric effects in the alcohol substrates, whereby the dispersion energy component increases together with substrate size.
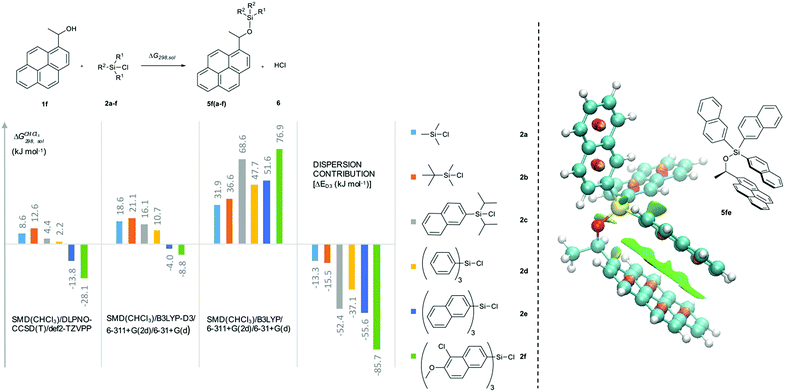 |
| | Fig. 5 Reaction free energies (kJ mol−1) for the reaction of 1f with the silyl reagent 2a–f at different levels of theory. Computed non-covalent interaction surfaces (green) of the silyl ether 5fe. | |
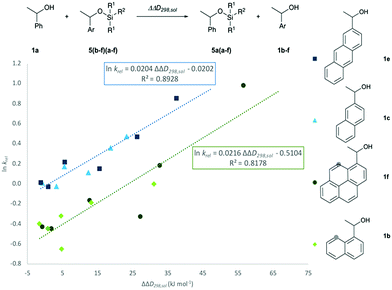 |
| | Fig. 6 Correlation of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel with calculated differences in the dispersion energy contributions, ΔΔD298,sol. krel with calculated differences in the dispersion energy contributions, ΔΔD298,sol. | |
Conclusions
In summary, we have experimentally determined relative rates between two secondary alcohols bearing sizeable aromatic surfaces in silylation experiments designed as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 competition experiments. In experiments with the comparatively small silyl chloride reagents TMSCl and TBDMSCl the relative rate constants are exclusively governed by repulsive steric effects provoked by the peri hydrogen atoms of the alcohol substrates. However, krel increases with the size of the DED groups at the silyl reagent, and aromatic interactions eventually dominate the silylation reactions with reagents as large as TN*SCl. No significant impact of the reaction temperature on krel has been found. In contrast, krel depends notably on the solvent used in the competition experiments. While size effects of the interacting aromatic surfaces appear to be cancelled in solvents with poor hydrogen bond donor abilities like tetrahydrofuran, they magnify as solvent–solute interactions get less important in halogenated solvents such as chloroform or dichloromethane depending to a notable extent on the higher solvophobic effect. Computed reaction free energies for the formation of silyl ether products predict that the dispersion component plays a key role in their thermochemical stability. Furthermore, linear correlations were found between experimental krel values and the dispersion contribution to the silyl ether formation energy. Therefore, the interplay of attractive dispersion forces and the solvophobic effect enhances relative rates for the silylation of a secondary alcohol up to 4.5 times. In this sense, the combination of sterically less hindered alcohols, tailor-made silyl chloride reagents with bigger DED groups and thoroughly chosen solvents could enhance rate constants even further than in the systems presented here.
1 competition experiments. In experiments with the comparatively small silyl chloride reagents TMSCl and TBDMSCl the relative rate constants are exclusively governed by repulsive steric effects provoked by the peri hydrogen atoms of the alcohol substrates. However, krel increases with the size of the DED groups at the silyl reagent, and aromatic interactions eventually dominate the silylation reactions with reagents as large as TN*SCl. No significant impact of the reaction temperature on krel has been found. In contrast, krel depends notably on the solvent used in the competition experiments. While size effects of the interacting aromatic surfaces appear to be cancelled in solvents with poor hydrogen bond donor abilities like tetrahydrofuran, they magnify as solvent–solute interactions get less important in halogenated solvents such as chloroform or dichloromethane depending to a notable extent on the higher solvophobic effect. Computed reaction free energies for the formation of silyl ether products predict that the dispersion component plays a key role in their thermochemical stability. Furthermore, linear correlations were found between experimental krel values and the dispersion contribution to the silyl ether formation energy. Therefore, the interplay of attractive dispersion forces and the solvophobic effect enhances relative rates for the silylation of a secondary alcohol up to 4.5 times. In this sense, the combination of sterically less hindered alcohols, tailor-made silyl chloride reagents with bigger DED groups and thoroughly chosen solvents could enhance rate constants even further than in the systems presented here.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was financially supported by the Deutsche Forschungsgemeinschaft (DFG) through the Priority Program “Control of London Dispersion Interactions in Molecular Chemistry” (SPP 1807), grant ZI 436/17-1. Marta Marin-Luna thanks Xunta de Galicia for her postdoctoral contract (ED481B 2016/166-0). We also want to thank the reviewers for their insightful comments and suggestions.
Notes and references
- C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Chem. Soc., Perkin Trans. 2, 2001, 5, 651–669 RSC.
- E. H. Krenske and K. N. Houk, Acc. Chem. Res., 2013, 46, 979–989 CrossRef PubMed.
- J. K. Klosterman, Y. Yamauchi and M. Fujita, Chem. Soc. Rev., 2009, 38, 1714–1725 RSC.
- F. Biedermann and H.-J. Schneider, Chem. Rev., 2016, 116, 5216–5230 CrossRef PubMed.
- A. Lamouroux, L. Sebaoun, B. Wicher, B. Kauffmann, Y. Ferrand, V. Maurizot and I. Huc, J. Am. Chem. Soc., 2017, 139, 14668–14675 CrossRef PubMed.
- C. Hunter, Chem. Soc. Rev., 1994, 23, 101–109 RSC.
- M. L. Waters, Biopolymers, 2004, 76, 435–445 CrossRef PubMed.
- J. W. Hwang, P. Li and K. D. Shimizu, Org. Biomol. Chem., 2017, 15, 1554–1564 RSC.
- C. R. Martinez and B. L. Iverson, Chem. Sci., 2012, 3, 2191–2201 RSC.
- S. E. Wheeler, Acc. Chem. Res., 2013, 46, 1029–1038 CrossRef PubMed.
- J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296 CrossRef PubMed.
- S. Grimme, R. Huenerbein and S. Ehrlich, ChemPhysChem, 2011, 12, 1258–1261 CrossRef PubMed.
- S. Grimme and P. R. Schreiner, Angew. Chem., Int. Ed., 2011, 50, 12639–12642 CrossRef PubMed.
- S. Rösel, C. Balestrieri and P. R. Schreiner, Chem. Sci., 2017, 8, 405–410 RSC.
- J. N. Israelachvilli, Contemp. Phys., 1974, 15, 159–178 CrossRef.
-
Y. Zhao and J. S. Moore, in Foldamers: Structure, Properties, and Applications, ed. S. Hecht and I. Huc, Wiley-VCH Verlag GmbH & Co. KGaA, 2007, ch. 3, pp. 75–108 Search PubMed.
- C. A. Hunter, Angew. Chem., Int. Ed., 2004, 43, 5310–5324 CrossRef PubMed.
- S. Otto, Chem. Sci., 2013, 4, 2953–2959 RSC.
- F. Cozzi, F. Ponzini, R. Annunziata, M. Cinquini and J. S. Siegel, Angew. Chem., Int. Ed. Engl., 1995, 34, 1019–1020 CrossRef.
- S. L. Cockroft, C. A. Hunter, K. R. Lawson, J. Perkins and C. J. Urch, J. Am. Chem. Soc., 2005, 127, 8594–8595 CrossRef PubMed.
- S. L. Cockroft, J. Perkins, C. Zonta, H. Adams, S. E. Spey, C. M. R. Low, J. G. Vinter, K. R. Lawson, C. J. Urch and C. A. Hunter, Org. Biomol. Chem., 2007, 5, 1062–1080 RSC.
- S. E. Wheeler and K. N. Houk, J. Am. Chem. Soc., 2008, 130, 10854–10855 CrossRef PubMed.
- J. Hwang, P. Li, W. R. Carroll, M. D. Smith, P. J. Pellechia and K. D. Shimizu, J. Am. Chem. Soc., 2014, 136, 14060–14067 CrossRef PubMed.
- H. Gardarsson, W. B. Schweizer, N. Trapp and F. Diederich, Chem.–Eur. J., 2014, 20, 4608–4616 CrossRef PubMed.
- H.-J. Schneider, Acc. Chem. Res., 2015, 48, 1815–1822 CrossRef PubMed.
- L. Yang, C. Adam, G. S. Nichol and S. L. Cockroft, Nat. Chem., 2013, 5, 1006–1010 CrossRef PubMed.
- L. Yang, C. Adam and S.
L. Cockroft, J. Am. Chem. Soc., 2015, 137, 10084–10087 CrossRef PubMed.
- C. Adam, L. Yang and S. L. Cockroft, Angew. Chem., Int. Ed., 2015, 54, 1164–1167 CrossRef PubMed.
- L. Yang, J. B. Brazier, T. A. Hubbard, D. M. Rogers and S. L. Cockroft, Angew. Chem., Int. Ed., 2016, 55, 912–916 CrossRef PubMed.
- J. Hwang, B. E. Dial, P. Li, M. E. Kozik, M. D. Smith and K. D. Shimizu, Chem. Sci., 2015, 6, 4358–4364 RSC.
- J. Hwang, P. Li, M. D. Smith and K. D. Shimizu, Angew. Chem., Int. Ed., 2016, 55, 8086–8089 CrossRef PubMed.
- B. Bhayana and C. S. Wilcox, Angew. Chem., Int. Ed., 2007, 46, 6833–6836 CrossRef PubMed.
- R. Pollice, M. Bolt, I. J. Kobylianskii, I. Shenderovich and P. Chen, J. Am. Chem. Soc., 2017, 139, 13126–13140 CrossRef PubMed.
- E. H. Krenske, K. N. Houk and M. Harmata, Org. Lett., 2010, 12, 444–447 CrossRef PubMed.
- J. Helberg, M. Marin-Luna and H. Zipse, Synthesis, 2017, 49, 3460–3470 CrossRef.
- E. Procházková, A. Kolmer, J. Ilgen, M. Schwab, L. Kaltschnee, M. Fredersdorf, V. Schmidts, R. C. Wende, P. R. Schreiner and C. M. Thiele, Angew. Chem., Int. Ed., 2016, 55, 15754–15759 CrossRef PubMed.
-
T. W. Green and P. G. M. Wuts, in Protective Groups in Organic Synthesis, John Wiley & Sons, Inc, 3rd edn, 2002 Search PubMed.
-
P. J. Kocienski, Protecting Groups, Thieme, Stuttgart, 3rd edn, 2005 Search PubMed.
- P. Patschinski and H. Zipse, Org. Lett., 2015, 17, 3318–3321 CrossRef PubMed.
- P. Patschinski, C. Zhang and H. Zipse, J. Org. Chem., 2014, 79, 8348–8357 CrossRef PubMed.
- M. Marin-Luna, P. Patschinski and H. Zipse, Chem.–Eur. J., 2018 Search PubMed , submitted.
- R. K. Akhani, M. I. Moore, J. G. Pribyl and S. L. Wiskur, J. Org. Chem., 2014, 79, 2384–2396 CrossRef PubMed.
- M. S. Cubberley and B. L. Iverson, J. Am. Chem. Soc., 2001, 123, 7560–7563 CrossRef PubMed.
- S. L. Cockroft and C. A. Hunter, Chem. Commun., 2006, 0, 3806–3808 RSC.
- B. U. Emenike, S. N. Bey, B. C. Bigelow and S. V. S. Chakravartula, Chem. Sci., 2016, 7, 1401–1407 RSC.
- A. S. Rury, C. Ferry, J. R. Hunt, M. Lee, D. Mondal, S. M. O. O'Connell, E. N. H. Phan, Z. Peng, P. Pokhilko, D. Sylvinson, Y. Zhou and C. H. Mak, J. Phys. Chem. C, 2016, 120, 23858–23869 CrossRef.
- M. J. Kamlet, J. M. Abboud and R. W. Taft, J. Am. Chem. Soc., 1977, 99, 6027–6038 CrossRef.
- M. J. Kamlet, J. M. Abboud, M. H. Abraham and R. W. Taft, J. Org. Chem., 1983, 48, 2877–2887 CrossRef.
- S. Y. Park, J.-W. Lee and C. E. Song, Nat. Commun., 2015, 6, 7512 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef.
- W. Y. C. Lee and R. G. Parr, Phys. Rev. B, 1988, 37, 785–789 CrossRef.
- S. Grimme, J. Chem. Phys., 2006, 124, 034108 CrossRef PubMed.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396 CrossRef PubMed.
- C. Riplinger and F. Neese, J. Chem. Phys., 2013, 138, 034106 CrossRef PubMed.
- C. Riplinger, B. Sandhoefer, A. Hansen and F. Neese, J. Chem. Phys., 2013, 139, 134101 CrossRef PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- J. Contreras-Garcia, E. R. Johnson, S. Keinan, R. Chaudret, J.-P. Piquemal, D. N. Beratan and W. Yang, J. Chem. Theory Comput., 2011, 7, 625–632 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Protocol for competition experiments, experimental procedures, characterization data, NMR spectra, computational data. CCDC 1839390 and 1839391. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc01889h |
|
| This journal is © The Royal Society of Chemistry 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article ,
Benjamin
Pölloth
,
Benjamin
Pölloth
 ,
Fabian
Zott
,
Fabian
Zott
 and
Hendrik
Zipse
and
Hendrik
Zipse
 *
*

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 competition experiments employing 1-phenylethanol (1a) as the reference system (Scheme 1 and Fig. 2). The other substrate alcohols derived from 1a through annulation of one (as in 1b and 1c), two (as in 1d and 1e) or three (as in 1f) benzene rings to its phenyl group. Depending on the particular position of annulation, this generates no additional repulsive 1,5-interaction with the alcohol oxygen atom (as in 1c and 1e), one additional 1,5-interaction (as in 1b and 1f), or two such interactions in 1d. The peri positions responsible for the repulsive 1,5-interactions are marked by grey circles in Fig. 2. The silyl chloride reagents chosen here grow in size from trimethylsilyl chloride 2a to substituted trinaphthylsilyl chloride 2f (see Fig. 2 and S1 of the ESI†). The competition experiments described in Scheme 1 involve equal amounts of reference alcohol 1a and of one of the substrate alcohols 1b–f, a quantity of one of the silyl chlorides 2 sufficient enough to obtain between 20–80% turnover of the substrate alcohols 1, a catalytic amount (0.15 eq. relative to alcohols 1) of N,N-dimethylaminopyridine (3, DMAP), and triethylamine (4) as the auxiliary base, in deuterated chloroform at a constant temperature of +23 °C. The relative rate constant krel defined as the ratio of effective rate constants k2 (1b–f) over k1 (1a) was used as main control parameter and obtained from the mole distribution of reactants and products after completion of the reaction as determined by 1H NMR spectroscopy (for full details see ESI†). The resulting rate constant values are shown in Fig. 2 and in Tables S1–S5 of the ESI.†
1 competition experiments employing 1-phenylethanol (1a) as the reference system (Scheme 1 and Fig. 2). The other substrate alcohols derived from 1a through annulation of one (as in 1b and 1c), two (as in 1d and 1e) or three (as in 1f) benzene rings to its phenyl group. Depending on the particular position of annulation, this generates no additional repulsive 1,5-interaction with the alcohol oxygen atom (as in 1c and 1e), one additional 1,5-interaction (as in 1b and 1f), or two such interactions in 1d. The peri positions responsible for the repulsive 1,5-interactions are marked by grey circles in Fig. 2. The silyl chloride reagents chosen here grow in size from trimethylsilyl chloride 2a to substituted trinaphthylsilyl chloride 2f (see Fig. 2 and S1 of the ESI†). The competition experiments described in Scheme 1 involve equal amounts of reference alcohol 1a and of one of the substrate alcohols 1b–f, a quantity of one of the silyl chlorides 2 sufficient enough to obtain between 20–80% turnover of the substrate alcohols 1, a catalytic amount (0.15 eq. relative to alcohols 1) of N,N-dimethylaminopyridine (3, DMAP), and triethylamine (4) as the auxiliary base, in deuterated chloroform at a constant temperature of +23 °C. The relative rate constant krel defined as the ratio of effective rate constants k2 (1b–f) over k1 (1a) was used as main control parameter and obtained from the mole distribution of reactants and products after completion of the reaction as determined by 1H NMR spectroscopy (for full details see ESI†). The resulting rate constant values are shown in Fig. 2 and in Tables S1–S5 of the ESI.†

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v/v).
1 (v/v).


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel equally in both alcohol groups by 0.2 units per 10 kJ mol−1 of additional dispersion contribution. That the data points for the unhindered alcohols 1c and 1e fall onto the same correlation line implies that it is irrelevant for the increase of krel whether the increase in ΔΔD298,sol derives from growing the substrate alcohol or the silyl chloride reagent. The presence of one repulsive 1,5-interaction reduces the relative rate by 1.6 times with respect to the non-hindered alcohols represented by the gap between the two correlation lines in Fig. 6. This analysis demonstrates that the experimentally measured relative rate constants krel directly relate to the size of the interacting surfaces and to repulsive steric effects in the alcohol substrates, whereby the dispersion energy component increases together with substrate size.
krel equally in both alcohol groups by 0.2 units per 10 kJ mol−1 of additional dispersion contribution. That the data points for the unhindered alcohols 1c and 1e fall onto the same correlation line implies that it is irrelevant for the increase of krel whether the increase in ΔΔD298,sol derives from growing the substrate alcohol or the silyl chloride reagent. The presence of one repulsive 1,5-interaction reduces the relative rate by 1.6 times with respect to the non-hindered alcohols represented by the gap between the two correlation lines in Fig. 6. This analysis demonstrates that the experimentally measured relative rate constants krel directly relate to the size of the interacting surfaces and to repulsive steric effects in the alcohol substrates, whereby the dispersion energy component increases together with substrate size.

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) krel with calculated differences in the dispersion energy contributions, ΔΔD298,sol.
krel with calculated differences in the dispersion energy contributions, ΔΔD298,sol.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 competition experiments. In experiments with the comparatively small silyl chloride reagents TMSCl and TBDMSCl the relative rate constants are exclusively governed by repulsive steric effects provoked by the peri hydrogen atoms of the alcohol substrates. However, krel increases with the size of the DED groups at the silyl reagent, and aromatic interactions eventually dominate the silylation reactions with reagents as large as TN*SCl. No significant impact of the reaction temperature on krel has been found. In contrast, krel depends notably on the solvent used in the competition experiments. While size effects of the interacting aromatic surfaces appear to be cancelled in solvents with poor hydrogen bond donor abilities like tetrahydrofuran, they magnify as solvent–solute interactions get less important in halogenated solvents such as chloroform or dichloromethane depending to a notable extent on the higher solvophobic effect. Computed reaction free energies for the formation of silyl ether products predict that the dispersion component plays a key role in their thermochemical stability. Furthermore, linear correlations were found between experimental krel values and the dispersion contribution to the silyl ether formation energy. Therefore, the interplay of attractive dispersion forces and the solvophobic effect enhances relative rates for the silylation of a secondary alcohol up to 4.5 times. In this sense, the combination of sterically less hindered alcohols, tailor-made silyl chloride reagents with bigger DED groups and thoroughly chosen solvents could enhance rate constants even further than in the systems presented here.
1 competition experiments. In experiments with the comparatively small silyl chloride reagents TMSCl and TBDMSCl the relative rate constants are exclusively governed by repulsive steric effects provoked by the peri hydrogen atoms of the alcohol substrates. However, krel increases with the size of the DED groups at the silyl reagent, and aromatic interactions eventually dominate the silylation reactions with reagents as large as TN*SCl. No significant impact of the reaction temperature on krel has been found. In contrast, krel depends notably on the solvent used in the competition experiments. While size effects of the interacting aromatic surfaces appear to be cancelled in solvents with poor hydrogen bond donor abilities like tetrahydrofuran, they magnify as solvent–solute interactions get less important in halogenated solvents such as chloroform or dichloromethane depending to a notable extent on the higher solvophobic effect. Computed reaction free energies for the formation of silyl ether products predict that the dispersion component plays a key role in their thermochemical stability. Furthermore, linear correlations were found between experimental krel values and the dispersion contribution to the silyl ether formation energy. Therefore, the interplay of attractive dispersion forces and the solvophobic effect enhances relative rates for the silylation of a secondary alcohol up to 4.5 times. In this sense, the combination of sterically less hindered alcohols, tailor-made silyl chloride reagents with bigger DED groups and thoroughly chosen solvents could enhance rate constants even further than in the systems presented here.