Open Access Article
Open Access ArticleReversible π-system switching of thiophene-fused thiahexaphyrins by solvent and oxidation/reduction†
Tomohiro
Higashino
 *a,
Atsushi
Kumagai
a,
Shigeyoshi
Sakaki
*a,
Atsushi
Kumagai
a,
Shigeyoshi
Sakaki
 b and
Hiroshi
Imahori
b and
Hiroshi
Imahori
 *ac
*ac
aDepartment of Molecular Engineering, Graduate School of Engineering, Kyoto University, Nishikyo-ku, Kyoto 615-8510, Japan. E-mail: t-higa@scl.kyoto-u.ac.jp; imahori@scl.kyoto-u.ac.jp
bFukui Institute for Fundamental Chemistry, Kyoto University, Sakyo-ku, Kyoto 606-8103, Japan
cInstitute for Integrated Cell-Material Sciences (WPI-iCeMS), Kyoto University, Sakyo-ku, Kyoto 606-8501, Japan
First published on 14th August 2018
Abstract
The concept of chemical topology has generated considerable interest among chemists and one of the state-of-the-art topics is Möbius topology in cyclic π-conjugated molecules. In this regard, expanded porphyrins have been extensively studied because of their facile topological interconversions and attractive optoelectronic properties. A typical example involves [28]hexaphyrins: they show topological conversion between planar Hückel and twisted Möbius topologies owing to their flexible structure. With this in mind, we designed a [28]hexaphyrin where one dimethine pyrrole unit was replaced with dithieno[3,4-b:3′,4′-d]thiophene (β-DTT), aiming at a reversible switching between macrocyclic and cross-conjugated π-systems by a change in molecular topologies. Considering that the β-DTT unit can offer both macrocyclic and cross-conjugated π-circuits, we envisioned that a combination of the topological interconversion of [28]hexaphyrin with the two π-circuits of the β-DTT unit would enable a reversible switching between macrocyclic and cross-conjugated π-circuits on Möbius and Hückel topologies, respectively, by a simple conformational change. Unexpectedly, the hexaphyrin revealed a unique, unprecedented π-system switching between a Möbius cross-conjugated π-system and a Hückel antiaromatic π-system, which was fully supported by both experimental and theoretical investigations. Meanwhile, the [28]hexaphyrin was also found to be redox interconvertible with the corresponding [26]hexaphyrin with a Hückel cross-conjugated π-system. These results demonstrate that the β-DTT unit is a new effective motif to realize π-system switching by changing molecular and π-system topologies. Importantly, external stimuli, i.e., solvent, as well as oxidation/reduction can be used to trigger the topological changes in expanded porphyrins with the help of the β-DTT unit.
Introduction
The concept of chemical topology, which was defined by Frisch and Wasserman in 1961,1 has evoked considerable interest among chemists. To date, various molecular knots, links,2 and polymers3 have been synthesized as topological molecules. Among the chemical topologies, Möbius topology is one of the important topics in aromaticity, which is essential for understanding the energetic stability of cyclic π-conjugated molecules. In general, the Hückel rule can be applied to predict whether a cyclic molecule is aromatic or antiaromatic. If the cyclic molecule has [4n+2]π or [4n]π electrons, it should be aromatic or antiaromatic, respectively. On the other hand, for the singly half-twisted cyclic molecule as a Möbius strip, Heilbronner predicted that the [4n+2]π and [4n]π electron rules should be reversed.4 Namely, the cyclic molecules with [4n]π and [4n+2]π electrons on Möbius topology are aromatic and antiaromatic, respectively. Much attention has been devoted to this Möbius aromaticity; however, the synthesis of Möbius aromatic molecules has been a challenge because of the difficulty in balancing between their twisted structure and cyclic π-conjugation. Nevertheless, Herges and co-workers reported the synthesis of the first Möbius aromatic molecule in 2003.5 After this seminal work, various porphyrinoids have been found to be Möbius aromatic6,7 and antiaromatic8 molecules.Compared to typical porphyrins possessing four pyrrole units, expanded porphyrins, which consist of more than four pyrrole units, exhibit a flexible structure. They have attracted significant attention because of their fascinating properties such as intense absorption in the near-infrared region, large two-photon absorption (TPA) cross section, and facile aromatic–antiaromatic switching upon two-electron oxidation/reduction or topological interconversions.9,10 In particular, noteworthy are their optical and photophysical properties that can be altered greatly by their topologies and π-systems.11 In addition, topology and aromaticity switches based on expanded porphyrins have attracted much interest.11d,e Thus, expanded porphyrins could be ideal platforms for exploring novel functions as well as addressing fundamental aspects of chemical topology by rational molecular design. To date, protonation has been one of the effective means to achieve topological interconversions,7b,d,i,12 while solvent-dependent topological switching is still rare.7a,13
Recently, we synthesized octaphyrins where two dimethine pyrrole units were replaced with two dithieno[3,4-b:3′,4′-d]thiophene (β-DTT) units. We found that the β-DTT unit could yield two types of π-circuits depending on the oxidation state of the sulfur atom.14 One is a macrocyclic π-circuit with incorporation of the lone pair of the central sulfur atom, and the other is a cross-conjugated π-circuit without incorporation of the lone pair (Fig. 1a). As a result, octaphyrin 1 revealed a macrocyclic 36π-electron circuit, whereas octaphyrin 2 possessed a cross-conjugated π-circuit (Fig. 1b). Namely, the optical and electrochemical properties of the octaphyrins can be altered by the corresponding change from the macrocyclic to the cross-conjugated π-system. This transformation is basically similar to that of N-confused porphyrins, which exhibit reversible π-system switching between 18π aromatic and cross-conjugated systems by NH tautomerism (Fig. 1c).15 However, it is impossible to achieve reversible π-switching between 1 and 2 because the transformation of 1 to 2 is based on chemical oxidation on the sulfur atom. We also examined the redox interconversions of 1 between 36π and 34π-electrons, or 36π and 38π-electrons, but the attempts failed probably due to the presence of the two β-DTT units, which is consistent with no examples of core-modified expanded porphyrins exhibiting reversible redox interconversions.16
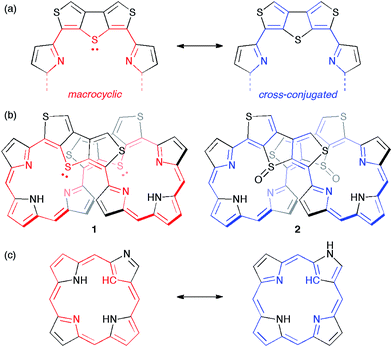 | ||
| Fig. 1 (a) Two types of π-circuits of the β-DTT unit. (b) Representation of π-circuits of the octaphyrins with the β-DTT unit. (c) Two NH tautomers of the N-confused porphyrin (NCP). | ||
Herein, to realize the reversible switching between macrocyclic and cross-conjugated π-systems on expanded porphyrins, we designed a [28]hexaphyrin where one dimethine pyrrole unit was replaced with one β-DTT unit. Typical [28]hexaphyrins are known to exhibit topological conversion between planar Hückel and twisted Möbius topologies because of their flexible structure (Fig. 2a).6b The Hückel and Möbius topologies lead to the antiaromatic and aromatic character, respectively. In general, aromatic systems are energetically favorable compared to antiaromatic ones. Indeed, the typical [28]hexaphyrin shows a distinct aromatic character in solution. On the basis of the two topologies of [28]hexaphyrin and the two types of π-circuits of the β-DTT unit, we envisioned the following four π-system topologies (Fig. 2b): (1) Möbius macrocyclic (28MM), (2) Möbius cross-conjugated (28MC), (3) Hückel macrocyclic (28HM), and (4) Hückel cross-conjugated (28HC) π-systems. On the Möbius topology, a macrocyclic 28π-circuit gains Möbius aromatic stabilization, but a cross-conjugated π-circuit weakens the aromatic stabilization. Accordingly, the Möbius topology would prefer the macrocyclic 28π-electron circuit. In contrast, a macrocyclic π-circuit on the Hückel topology is unfavorable because of the Hückel antiaromaticity, whereas a cross-conjugated π-circuit decreases the antiaromatic destabilization. Namely, the cross-conjugated π-circuit would be suitable on the Hückel topology. Overall, we predicted reversible switching between the macrocyclic π-circuit on the Möbius topology and the cross-conjugated π-circuit on the Hückel topology by a simple conformational change. Meanwhile, hexaphyrins can exhibit reversible redox interconversions between 28π and 26π-electron systems (Fig. 2a). Typical [26]hexaphyrins take a planar Hückel topology, but [26]hexaphyrins with the Möbius topology have not been reported because of the plausible instability of their Möbius antiaromaticity.6c,f Although the Möbius topology is unfavorable for [26]hexaphyrins, we can also make a list of the four π-system topologies, as proposed for [28]hexaphyrin (Fig. 2b). Taking into account that typical [26]hexaphyrins prefer the Hückel topology, we anticipated that a [26]hexaphyrin with the β-DTT unit would possess a macrocyclic π-system on the Hückel topology (26HM), and if possible, cross-conjugated π-system on the Möbius topology (26MC). Thus, a combination of the redox interconversions between [28]hexaphyrin and [26]hexaphyrin with the change in molecular topologies would accomplish the three-component reversible π-system switching between (1) 28π Möbius macrocyclic (28MM), (2) 28π Hückel cross-conjugated (28HC), and (3) 26π Hückel macrocyclic (26HM) π-systems. In this work, we describe the synthesis and characterization of hexaphyrins with the β-DTT unit and unexpected, unprecedented π-system switching with full support of theoretical calculations.
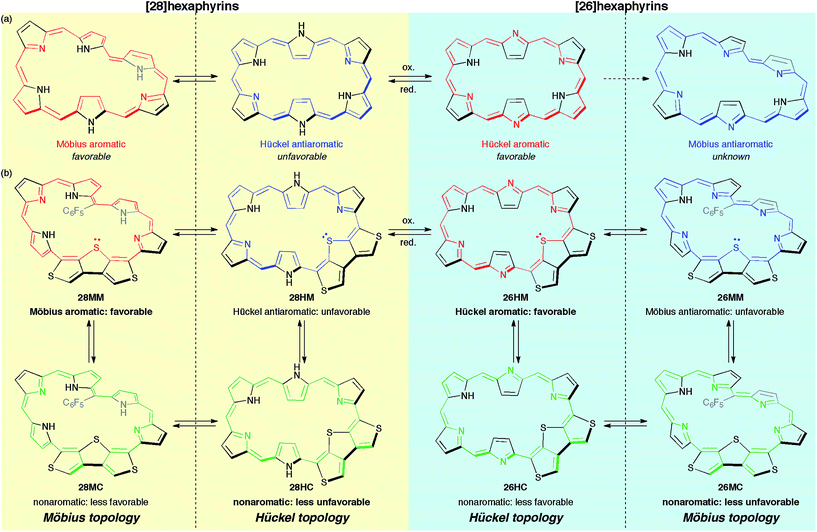 | ||
| Fig. 2 (a) Molecular topologies of [28]hexaphyrin and [26]hexaphyrin. (b) Possible π-system topologies of hexaphyrins with the β-DTT unit on Hückel and Möbius topologies. | ||
Results and discussion
Synthesis and characterization
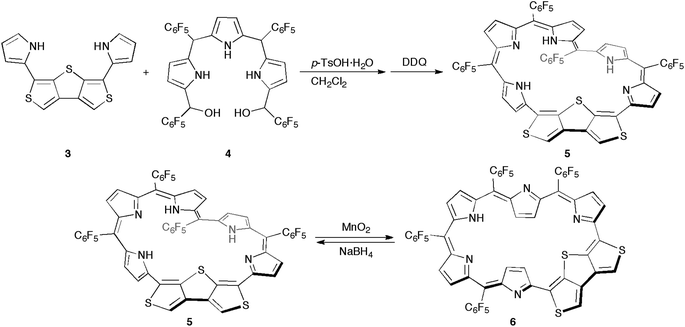
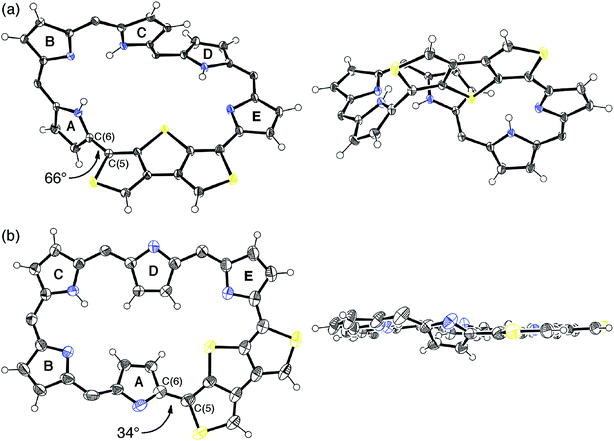
Synthetic schemes of the hexaphyrins with the β-DTT unit are shown in Scheme 1. The acid-catalyzed condensation of bis(pyrrolyl)dithienothiophene 314 and tripyrrane dicarbinol 4,17 followed by oxidation with 2,3-dichloro-5,6-dicyanobenzoquinone (DDQ), afforded [28]hexaphyrin 5 in 6.9% yield. The high-resolution mass spectrum (HRMS) of 5 exhibits an ion peak at m/z = 1234.0210 (calcd for C56H16N5F20S3, [M + H]+: 1234.0243), which matches with its 28π electronic state (Fig. S1†). Then, we attempted the redox interconversion and found that [28]hexaphyrin 5 and [26]hexaphyrin 6 were quantitatively interconvertible through oxidation with MnO2 and reduction with NaBH4. To the best of our knowledge, 6 is the first example of thia[26]hexaphyrin.18 It is noteworthy that further reduction of 5 and oxidation of 6 resulted in decomposition without formation of the corresponding [30]hexaphyrin and [24]hexaphyrin.Fortunately, we obtained single crystals suitable for X-ray diffraction analysis by vapor diffusion of n-hexane into a CH2Cl2 solution of 5. The structure of 5 was revealed to be a twisted Möbius structure (Fig. 3a and S5†).‡ The structure of 5 also showed bond length alternation to a certain extent. Although this suggests the antiaromatic or nonaromatic character of 5, it is difficult to distinguish between the antiaromatic macrocyclic π-circuit and nonaromatic cross-conjugated π-circuit from the X-ray crystal structure of 5. Because of the rigidity of the β-DTT unit, the pyrrole A neighboring the β-DTT unit is significantly tilted. Consequently, the torsion angle at C(5)–C(6) is the largest value (66°). Although the largest torsion angle in the conjugation circuit of 5 is larger than those of typical Möbius aromatic [28]hexaphyrins (26–49°),6 it is virtually identical to that of a [28]hexaphyrin monophosphorus complex (65°).8b The 1H NMR spectra of 5 were measured in various solvents. The 1H NMR spectrum in CDCl3 displays the signals from β-protons at δ = 6.94–6.24 ppm, two signals from thiophene protons at δ = 7.67 and 7.62 ppm, and three signals from NH protons at δ = 13.09, 12.25, and 9.97 ppm (Fig. 4a). Contrary to our expectation from the crystal structure, the 1H NMR spectrum implies the nonaromatic character of 5 because those of nonaromatic acyclic π-conjugated oligopyrromethenes show the characteristic signals of pyrrolic β-protons in the range of 6.0–6.7 ppm.9c,19 On the other hand, the [28]hexaphyrin monophosphorus complex exhibits a moderate 28π Möbius aromatic character even with a large torsion angle.8b Namely, the large torsion angle (66°) of 5 would not interrupt the macrocyclic π-circuit. Therefore, the nonaromatic character of 5 indicates that the cross-conjugated π-network arising from the β-DTT unit is dominant despite its Möbius structure. Remarkably, we found a dramatic solvent effect on the 1H NMR spectra of 5. In DMF-d7, the spectrum displays four significantly deshielded signals from β-protons at δ = 10.14, 9.45, 8.80, and 8.30 ppm (Fig. 4b). The downfield shifts of β-protons imply a weak diatropic ring current effect originating from the weak 28π Möbius aromaticity with retention of the Möbius structure, or a weak paratropic ring current effect originating from the weak 28π Hückel antiaromaticity on the different structures with Hückel topology.9c This means that the π-system of 5 can be switched between cross-conjugated and macrocyclic 28π-electron systems by solvent. In addition, the spectrum in acetone-d6 at 25 °C shows two sets of peaks, the major one similar to those in DMF-d7, and the minor one similar to those in CDCl3 (Fig. S3†). The intensities of the minor peaks are increased at 50 °C, suggesting the equilibrium between two conformations. Therefore, [28]hexaphyrin 5 should adopt two conformations in solution. Namely, 5 takes a Möbius conformation as the crystal structure (obtained from a CH2Cl2 solution) with the cross-conjugated π-system in CDCl3, whereas it takes a different conformation with a macrocyclic 28π-system in DMF-d7. Unfortunately, we could not obtain single crystals from a solution in polar solvents (i.e., DMF and acetone) to reveal the conformation despite extensive trials. Finally, by analyzing the results of density functional theory (DFT) calculations and simulated 1H chemical shifts judiciously, we assigned the conformation in DMF-d7 to a planar conformation exhibiting a 28π Hückel antiaromatic character (vide infra). Consequently, unexpectedly, the 1H NMR spectra displayed the switching between cross-conjugated and macrocyclic π-circuits on Möbius and Hückel topologies, respectively, both of which were anticipated to be unfavorable energetically. It should be emphasized that we confirmed the reversibility by repeated measurements in both nonpolar and polar solvents.
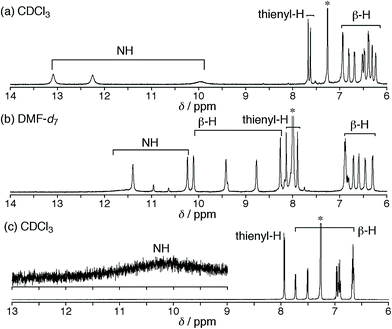 | ||
| Fig. 4 1H NMR spectra of 5 in (a) CDCl3 at 50 °C and (b) DMF-d7 at 25 °C, and (c) 6 in CDCl3 at 25 °C. | ||
Meanwhile, the structure of 6 was revealed to be a planar rectangular structure on the basis of X-ray diffraction analysis (Fig. 3b and S6†).‡ Basically, the bond length alternation also suggests the nonaromatic or antiaromatic character of 6. Taking into account that a macrocyclic π-circuit on planar [26]hexaphyrin provides a 26π aromatic character, the bond alternation of 6 implies a nonaromatic cross-conjugated π-circuit. Although pyrrole A is tilted by 33° with respect to the mean-plane (core 36 atoms), the mean-plane deviation is rather small (ca. 0.20 Å), which can be ascribed to the rigid β-DTT unit. In the packing structure, the β-DTT unit and pyrrole E form one-dimensional π–π stacking motifs and the separation distance between the two planes is approximately 3.5 Å (Fig. S7†). The 1H NMR spectrum of 6 in CDCl3 displays ten signals of β-protons at δ = 7.73–6.67 ppm, two signals of thiophene protons at δ = 7.95 and 7.93 ppm, and one broad signal of NH proton at 10.11 ppm (Fig. 4c). This spectrum indicates the almost nonaromatic character of 6, which is similar to those of cross-conjugated quinonoidal hexaphyrins.20 Thus, the dominant π-circuit of 6 is a cross-conjugated π-network derived from the β-DTT unit, which is also contrary to our initial intuitive expectation. Compared to 5, 6 displays a minor solvent effect on the 1H NMR spectra, which suggests no significant conformational change in solution (Fig. S4†). Therefore, hexaphyrins with the β-DTT unit achieved three-component reversible π-system switching between 28π Möbius cross-conjugated, 28π Hückel macrocyclic, and 26π Hückel cross-conjugated π-systems by solvent-dependent topological or redox interconversions.
Optical and electrochemical properties
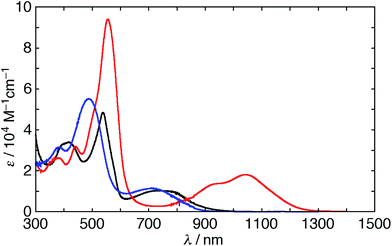
The UV/vis/NIR absorption spectra of 5 and 6 were measured in various solvents (Fig. 5). The spectrum of 5 in CH2Cl2 has a weak Soret-like band and weak and broad Q-like bands at 539 and 734 nm, respectively. The spectrum of 6 in CH2Cl2 also displays a weak Soret-like band at 487 nm and a broad Q-like band at 712 nm. These features are analogous to those of nonaromatic20,21 and phlorin-type porphyrinoids,22 which are consistent with the dominant nature of their cross-conjugated π-networks. In addition, as observed in the 1H NMR spectra, the absorption spectra of 5 also exhibit the remarkable solvent effect (Fig. S8 and S9†). In polar solvents, the Q-like bands are red-shifted in the order of THF (837 nm) < methanol (965 nm) < acetone (1032 nm) < DMSO ≈ DMF (1044 nm). This trend suggests that hydrogen bonds of the NH protons with solvent molecules induce a π-system switching to the macrocyclic 28π-electron system. A moderate solvent effect in acetone can be rationalized by the equilibrium between the two conformations, which is seen in 1H NMR spectroscopy. The spectrum of 5 in DMF displays an intense Soret-like band at 556 nm and Q-like bands at 940 and 1044 nm. Then, we also measured the steady-state fluorescence spectra of 5 and 6. It should be noted that 5 exhibits no fluorescence in DMF, while 5 and 6 exhibit weak fluorescence at 955 and 930 nm in CH2Cl2, respectively (Fig. S10†). The weak fluorescence of 5 and 6 in CH2Cl2 is consistent with the cross-conjugated π-networks.14 The optical properties of expanded porphyrins empirically enable us to judge whether they are aromatic or antiaromatic.11c,23 Intriguingly, the intense Soret- and Q-like bands in DMF imply an aromatic character, whereas no fluorescence implies an antiaromatic character. Although the reason for these conflicting features is not clear at this stage, the replacement of one dimethine pyrrole with the β-DTT unit in [28]hexaphyrin plays an important role in the unusual optical properties. As described below, DFT calculations support the moderate 28π antiaromatic character of 5 in DMF and as far as we know, [28]hexaphyrin 5 is the sole exception among antiaromatic expanded porphyrins with both intense Soret- and Q-like bands, whereas antiaromatic porphyrinoids with only an intense Soret-band have been reported.24The electrochemical properties of 5 and 6 were studied by using cyclic voltammetry (CV) and differential pulse voltammetry (DPV) in CH2Cl2versus ferrocene/ferrocenium ions (Fc/Fc+) with tetrabutylammonium hexafluorophosphate (Bu4NPF6) as an electrolyte (Fig. S11†). [28]Hexaphyrin 5 exhibits three irreversible reductions at −1.19, −1.41, and −1.83 V and two reversible oxidations at −0.03 and +0.28 V. These values are similar to those of a typical [28]hexaphyrin.22e On the other hand, [26]hexaphyrin 6 shows three reversible reductions at −0.13, −0.59 and −0.91 V, while no oxidation peak is observable. The more positive reduction potentials of 6 than those of the typical [26]hexaphyrin (−0.55 and −0.88 V)20 can be rationalized by the cross-conjugated character.
DFT calculations
DFT calculations were carried out to shed light on the unique π-system switching of [28]hexaphyrin 5. We performed optimization at the B3LYP/6-31G(d,p) level in the gas phase and obtained the optimized structure of 5a using the crystal structure as the initial geometry (Fig. 6a). Assuming that 5 adopts different conformations in DMF, we explored metastable conformations by structural optimization using various initial geometries in which the tilt angles of pyrroles A and D were varied. Finally, we obtained three metastable conformations, planar Hückel conformations 5b and 5c (Fig. 6b and c) and Möbius conformation 5d (Fig. 6d). The largest torsion angles in the conjugation circuit of 5b (46°) and 5c (44°) are smaller than that of 5a (60°). On the other hand, the largest torsion angle of 5d (63°) is slightly larger than that of 5a. The relative total energies of 5b, 5c, and 5d are calculated at the B3LYP/6-311G(d,p) level to be +18.4, +39.3, and +39.5 kJ mol−1, respectively. The relative total energies calculated at CAM-B3LYP/6-311G(d,p) and M06-2X/6-311G(d,p) levels are consistent with those at B3LYP/6-311G(d,p) (Table S2†).25 While conformations 5b and 5d possess one inverted pyrrole ring (pyrrole A), conformation 5c possesses two inverted pyrrole rings (pyrroles A and D).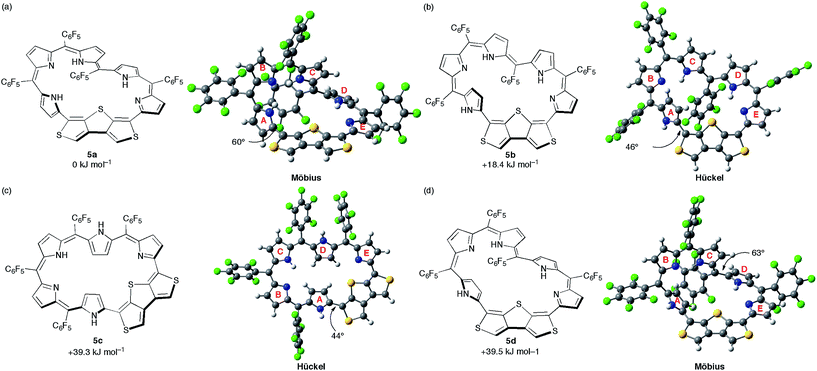 | ||
| Fig. 6 The calculated conformations and relative total energies of [28]hexaphyrin: (a) 5a, (b) 5b, (c) 5c, and (d) 5d. The torsion angles at the most distorted points are indicated. | ||
Then, we simulated 1H chemical shifts on the three conformations 5a–d using the gauge-including atomic orbital (GIAO) method at the B3LYP/6-311G(d,p) level (Fig. S12 and S13†). The 1H chemical shift values were calculated with reference to CHCl3 (δ = 7.26 ppm). The simulated 1H chemical shifts of the β-protons and two thiophene protons on 5a are 7.27–6.51, and 7.88 and 7.83 ppm, respectively, which are in good agreement with the 1H NMR spectrum of 5 in CDCl3. For 5d, the 1H chemical shifts of the β-protons and two thiophene protons are 7.35–5.03, and 7.80 and 7.69 ppm, respectively. The upfield shifts of the β-protons on pyrrole A (6.32 and 5.03 ppm) are probably due to a local ring current effect induced by the pentafluorophenyl ring (Fig. S14†). Accordingly, these results predict the nonaromatic character of 5d. In the case of 5b, the simulated 1H chemical shifts appear at 8.46–6.29 ppm for β-protons and 7.59 and 7.51 ppm for the two thiophene protons. It is noteworthy that β-protons on pyrrole A show clear downfield shifts (8.46 and 7.83 ppm), although the difference between the chemical shifts of the most shielded and deshielded β-protons is moderate (Δδ = 2.17 ppm). These downfield shifts largely agree with the 1H NMR spectrum of 5 in DMF-d7 (Δδ = 3.80 ppm). Since the β-protons on pyrrole A are located on the inside of the macrocycle, these chemical shifts suggest the 28π Hückel antiaromatic character on the planar conformation 5b. Meanwhile, the simulated 1H chemical shifts of β-protons for 5c are 11.79–6.02 ppm. The β-protons on pyrroles A and D clearly exhibit a downfield shift (10.35 and 8.99 ppm for pyrrole A, 11.79 and 9.83 ppm for pyrrole D), which suggests the distinct 28π Hückel antiaromatic character. However, the large Δδ values of the β-protons (5.77 ppm) and two NH protons on pyrroles A and D (6.42 and 5.64 ppm) imply the mismatch with the 1H NMR spectrum of 5 in DMF-d7. Furthermore, we attempted to evaluate the antiaromatic character on 5b and 5c.10b,26 Since the magnetic properties are sensitive to the aromaticity, we calculated the nucleus-independent chemical shift (NICS) values at the gravity centers of 36 core atoms (Table S3†).27 The NICS value of 5b is −0.14 ppm, which is less negative than those of 5a (−0.57 ppm) and 5d (−0.68 ppm). The NICS value of 5b is almost zero due to the small Δδ value relative to those of typical antiaromatic [28]hexaphyrins (Δδ > 10 ppm).6i,28 On the other hand, the small positive NICS value of 5c (+2.48 ppm) implies the weak antiaromatic character, as suggested by the simulated 1H chemical shifts. In addition, we also calculated the harmonic oscillator model of aromaticity (HOMA)29 of 5a–d to be −0.544, −0.651, −0.109, and −0.440, respectively. The negative HOMA values can be ascribed to their bond alternations, suggesting their almost nonaromatic character.
We also performed time-dependent DFT (TD-DFT) calculations to predict the absorption spectra at the B3LYP/6-311G(d,p) level on the optimized structures 5a–d in the gas phase because the PCM solvation model exhibited negligible differences in excitation energies in various solvents (Fig. S15†). The calculated excitation energies and oscillator strengths for 5a largely match with the absorption spectrum of 5 in CH2Cl2. If [28]hexaphyrin 5 has a macrocyclic π-circuit with zwitterionic character, the excitation energies should be increased in polar solvents. Thus, zwitterionic species of 5 should be excluded, although zwitterionic pyridinium-substituted [28]hexaphyrin was reported by Osuka and co-workers (Fig. 7).30 The calculated excitation energies and oscillator strengths of 5b and 5c may reproduce intense Soret- and Q-like bands of 5 in DMF. The lowest excitation energies of 5b (937 nm) and 5c (1005 nm) are smaller than that of 5a (829 nm), which is in good accordance with the red-shifted Q-like bands. On the other hand, the lowest excitation energy of 5d (770 nm) is larger than that of 5a, which is in contrast to the red-shifted Q-like bands of 5 in DMF. In addition, the Soret-like bands of 5b and 5c can be assigned to two excitations with large oscillator strengths (f > 0.4), which originate mainly from HOMO−1/LUMO and HOMO/LUMO+2 transitions. The high-energy transitions for the Soret-like bands of 5b and 5c are consistent with the fingerprints of antiaromaticity on the photophysical properties of expanded porphyrins.24b However, the distinct Q-like bands for the allowed HOMO/LUMO transitions are inconsistent with the fingerprints, as seen in the distinct Q-like band of 5 in DMF. Although the reason for the appearance of the distinct Q-like bands is not clear at this stage, the β-DTT unit in [28]hexaphyrin may play an important role in the unique photophysical properties. Combined with the relative total energies and the simulated 1H chemical shifts, we can finally conclude that 5b is the most probable conformation observed in DMF.
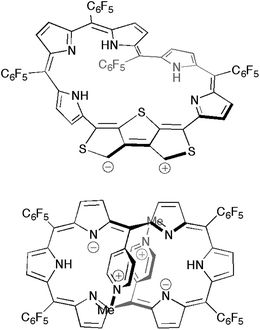 | ||
| Fig. 7 Possible zwitterionic structures of [28]hexaphyrin 5 (top) in comparison to the methylpyridinium-substituted analogue (bottom). | ||
Nevertheless, it is rather difficult for 5 to take the conformation 5b in solution considering the high relative total energy of 5b (+18.4 kJ mol−1). Given the stabilization by polar solvents, we conducted calculations for 5a and 5b using the PCM solvation model, but the relative total energy of 5b was still large even in DMSO (ca. +14 kJ mol−1). Surprisingly, the calculations of 5 in the presence of an explicit DMF molecule afford the negative relative total energy of 5b (−6.2 kJ mol−1) in comparison with 5a (Fig. 8). The conformation 5b is stabilized by a hydrogen bond of the NH proton of pyrrole A with the oxygen atom of the DMF molecule. The broad signal of the NH proton observed in the 1H NMR spectrum is attributable to this hydrogen bond. Moreover, the relative total energy of 5b in the presence of an acetone molecule is −0.4 kJ mol−1 (Fig. S16†). This small energy difference coincides with the equilibrium observed in the 1H NMR spectra in acetone-d6. The calculations using CAM-B3LYP and M06-2X as DFT functionals also afforded negative relative total energies of 5b (Table S4†). Consequently, these calculations demonstrate that the hydrogen bond of the NH protons with polar solvent molecules induces the conformational change between Möbius conformation 5a and planar conformation 5b. The theoretical conclusion is contrary to our initial intuitive prediction that switching would occur between the Möbius aromatic π-system and Hückel cross-conjugated π-system. Indeed, the calculation supports the unique π-system switching of 5 between the Möbius cross-conjugated π-system and Hückel antiaromatic π-system on the basis of the change in molecular topologies, which is triggered by external stimuli (i.e., solvent).
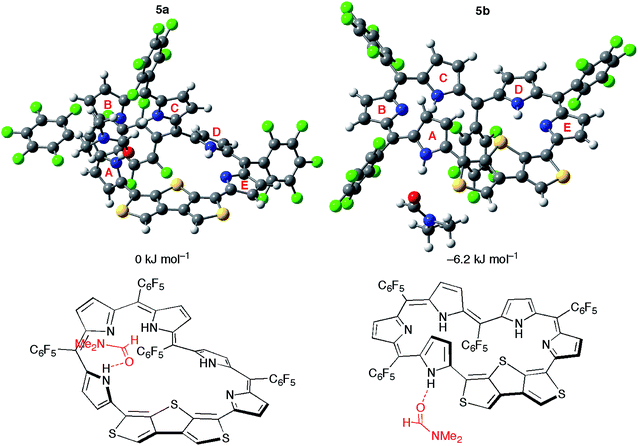 | ||
| Fig. 8 The optimized structures and relative total energies of [28]hexaphyrin conformations 5a and 5b in the presence of one DMF molecule. | ||
Meanwhile, we also performed DFT calculations for [26]hexaphyrin 6. The 1H chemical shifts of the β-protons and two thiophene protons are 7.94–6.29, and 8.36 and 8.28 ppm, respectively (Fig. S17†). The NICS value at the gravity center is −2.52 ppm. Thus, the NMR calculation supports the almost nonaromatic character of 6. The calculated excitation energies and oscillator strengths reproduce the absorption spectrum of 6 (Fig. S18†). These results also verify the nonaromatic character, which is consistent with the cross-conjugated nature of 6.
Finally, we sought to elucidate the origin of the dominant π-circuits of hexaphyrins 5 and 6. To gain insight into the structural parameters, we calculated the bond lengths and Wiberg bond indices based on NAO (natural atomic orbital) on the β-DTT unit, but these values turned out to be almost the same (Table S5†). Thus, it is impossible to predict the dominant π-circuits from the structural parameters and bond orders on the β-DTT unit.31 Then, we conducted DFT calculations of 3 as a model of the β-DTT unit (Fig. S19†). The HOMO of 3 has an orbital distribution on the central sulfur atom, which indicates the involvement of the pz orbital of the sulfur atom (Fig. 9). In contrast, the HOMO−1 has no orbital distribution on the central sulfur atom, indicating no contribution of the pz orbital. Additionally, the orbital phases on the two pyrrole rings are identical for the HOMO, or opposite for the HOMO−1. Notably, the HOMO of 5b originates from the HOMO of 3, while the HOMOs of 5a and 6 from the HOMO−1 of 3 (Fig. 9 and S20†). For 5a and 5b, the orbital exchanges of the HOMO and HOMO−1 are probably induced by topologies of their π-systems. The planar conformation 5b stabilizes the HOMO−1 of 3, while the singly half-twisted conformation 5a stabilizes the HOMO of 3 because the orbital phase is inverted by the twisted structure. Since the pz orbital of the central sulfur atom is involved in the HOMO of 5b, the cyclic 28π-system through the sulfur atom results from the HOMO. In contrast, the HOMOs of 5a and 6 provide linear π-systems owing to a disruption of the cyclic π-systems at the central sulfur atom. In accordance with the interpretation, the HOMOs of 5c and 5d also indicate the cyclic 28π-system and linear π-system, respectively, although we have no experimental evidence of these conformations (Fig. S21†). In addition, the energy gaps between HOMO−1 and HOMO−2 of 5b and 5c (ca. 0.2 eV) are smaller than those of 5a, 5d, and 6, which also implies an antiaromatic character originating from the macrocyclic π-circuit.24b As a result, the HOMO orbital distributions determine whether the hexaphyrins with the β-DTT unit possess a macrocyclic π-circuit or cross-conjugated π-circuit. Therefore, these calculation results imply that the orbital distribution of the HOMO is an important factor to determine the dominant π-circuit for expanded porphyrins. However, it is unclear at this stage why hexaphyrins 5 and 6 prefer a cross-conjugated π-circuit rather than an aromatic π-circuit.
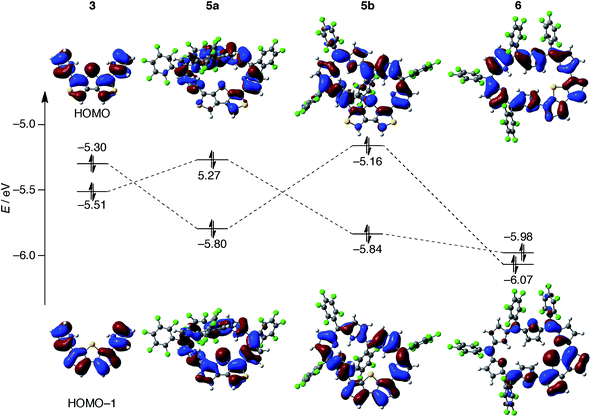 | ||
| Fig. 9 Selected Kohn–Sham orbitals for 3, 5a, 5b, and 6 that were calculated at the B3LYP/6-311G(d,p) level. | ||
Conclusion
We synthesized and characterized new hexaphyrins 5 and 6 where the dimethine pyrrole unit was replaced with the β-DTT unit. The structure of [28]hexaphyrin 5 was determined to be the twisted Möbius conformation in the single crystal obtained from the CH2Cl2 solution. Despite its Möbius topology, the 1H NMR and UV/vis/NIR absorption spectra of 5 in nonpolar solvents (i.e., CDCl3 and CH2Cl2) exhibited nonaromatic character, indicating a cross-conjugated π-circuit. In contrast, the 1H NMR and UV/vis/NIR absorption spectra of 5 in polar solvents (i.e., DMF and DMSO) were completely different, which suggests the unexpected unique π-system switching from the cross-conjugated π-circuits in the nonpolar solvent to macrocyclic π-circuits in the polar solvents (and vice versa). This π-system switching stems from the change in their molecular topologies with the help of the hydrogen bonds of the NH protons with the polar solvent molecules, which was validated by DFT calculations. More importantly, the DFT calculations provided a theoretical verification of the unprecedented, unique π-system switching of 5 between the Möbius cross-conjugated π-system and the Hückel antiaromatic π-system based on their molecular topologies induced by the solvents (Fig. 10). Although this conclusion was contrary to our initial simple prediction that the switching occurs between the Möbius aromatic π-system and the Hückel cross-conjugated π-system, we successfully corroborated that the β-DTT unit was the effective motif to achieve the π-system switching based on molecular topologies induced by the external stimuli (i.e., solvent). Meanwhile, the 1H NMR and UV/vis/NIR absorption spectra of [26]hexaphyrin 6 exhibited nonaromatic character because of the dominant cross-conjugated π-system despite its planar conformation, which was also supported by DFT calculations. In contrast to 5, 6 displayed minor solvent effects, suggesting no significant change in its molecular topology. Collectively, hexaphyrins 5 and 6 achieved three-component reversible π-system switching between 28π Möbius cross-conjugated, 28π Hückel macrocyclic, and 26π Hückel cross-conjugated π-systems by solvent-dependent topological or redox interconversions (Fig. 10). Finally, we explored the origin of the dominant π-circuits of hexaphyrins 5 and 6. The calculation results suggested that the orbital distribution of the HOMO was the important factor to determine the dominant π-circuit for expanded porphyrins. However, the next challenge is to elucidate the reason why hexaphyrins 5 and 6 prefer a cross-conjugated π-circuit rather than a macrocyclic π-circuit with aromaticity. Furthermore, the insight would provide a hint for novel 26π Möbius antiaromatic systems because 5 prefers a macrocyclic π-circuit despite its antiaromaticity. Overall, this study will open an avenue to create topological molecules of interest by integrating cyclic π-conjugated molecules with the β-DTT unit, where their molecular and π-system topologies are controlled by external stimuli such as solvent as well as conventional protonation and oxidation/reduction.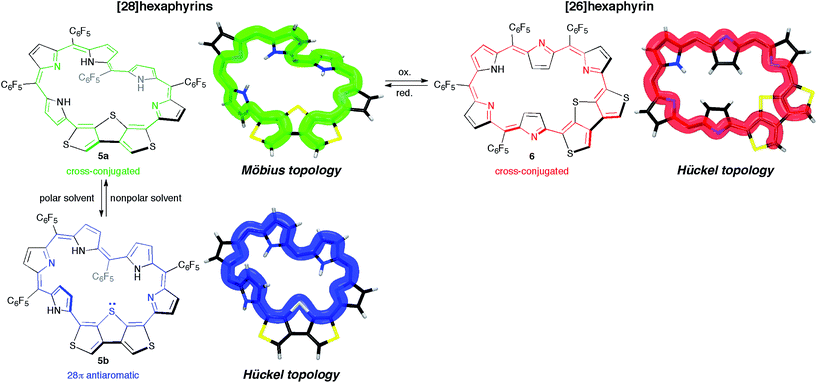 | ||
| Fig. 10 Schematic representation of reversible π-system switching between hexaphyrins 5a, 5b, and 6. meso-Aryl substituents are omitted for clarity. | ||
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the JSPS (KAKENHI grant numbers JP18K14198 (T. H.) and JP18H03898 (H. I.)).Notes and references
- H. L. Frisch and E. Wasserman, J. Am. Chem. Soc., 1961, 83, 3789–3795 CrossRef.
- (a) J. E. Beves, B. A. Blight, C. J. Campbell, D. A. Leigh and R. T. McBurney, Angew. Chem., Int. Ed., 2011, 50, 9260–9327 CrossRef PubMed; (b) R. S. Forgan, J.-P. Sauvage and J. F. Stoddart, Chem. Rev., 2011, 111, 5434–5464 CrossRef PubMed; (c) J.-F. Ayme, J. E. Beves, C. J. Campbell and D. A. Leigh, Chem. Soc. Rev., 2013, 42, 1700–1712 RSC; (d) J.-P. Sauvage, Angew. Chem., Int. Ed., 2017, 56, 11080–11093 CrossRef PubMed.
- (a) Y. Okumura and K. Ito, Adv. Mater., 2001, 13, 485–487 CrossRef; (b) Y. Tezuka and H. Oike, J. Am. Chem. Soc., 2001, 123, 11570–11576 CrossRef PubMed; (c) Z. Guan, Chem.–Asian J., 2010, 5, 1058–1070 CrossRef PubMed; (d) Y. Tezuka, Acc. Chem. Res., 2017, 50, 2661–2672 CrossRef PubMed; (e) E. M. Benetti, M. Divandari, S. N. Ramakrishna, G. Morgese, W. Yan and L. Trachsel, Chem.–Eur. J., 2017, 23, 12433–12442 CrossRef PubMed.
- E. Heilbronner, Tetrahedron Lett., 1964, 5, 1923–1928 CrossRef.
- (a) D. Ajami, O. Oeckler, A. Simon and R. Herges, Nature, 2003, 426, 819–821 CrossRef PubMed; (b) D. Ajami, K. Hess, F. Köhler, C. Näther, O. Oeckler, A. Simon, C. Yamamoto, Y. Okamoto and R. Herges, Chem.–Eur. J., 2006, 12, 5434–5445 CrossRef PubMed.
- (a) Y. Tanaka, S. Saito, S. Mori, N. Aratani, H. Shinokubo, N. Shibata, Y. Higuchi, Z. S. Yoon, K. S. Kim, S. B. Noh, J. K. Park, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2008, 47, 681–684 CrossRef PubMed; (b) J. Sankar, S. Mori, S. Saito, H. Rath, M. Suzuki, Y. Inokuma, H. Shinokubo, K. S. Kim, Z. S. Yoon, J. Shin, J. M. Lim, Y. Matsuzaki, O. Matsushita, A. Muranaka, N. Kobayashi, D. Kim and A. Osuka, J. Am. Chem. Soc., 2008, 130, 13568–13579 CrossRef PubMed; (c) S. Tokuji, J.-Y. Shin, K. S. Kim, J. M. Lim, K. Youfu, S. Saito, D. Kim and A. Osuka, J. Am. Chem. Soc., 2009, 131, 7240–7241 CrossRef PubMed; (d) M. Inoue, K. S. Kim, M. Suzuki, J. M. Lim, J.-Y. Shin, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2009, 48, 6687–6690 CrossRef PubMed; (e) T. Higashino, M. Inoue and A. Osuka, J. Org. Chem., 2010, 75, 7958–7961 CrossRef PubMed; (f) M. Inoue and A. Osuka, Angew. Chem., Int. Ed., 2010, 49, 9488–9491 CrossRef PubMed; (g) M. Inoue, T. Yoneda, K. Youfu, N. Aratani and A. Osuka, Chem.–Eur. J., 2011, 17, 9028–9031 CrossRef PubMed; (h) S. Ishida, T. Tanaka, J. M. Lim, D. Kim and A. Osuka, Chem.–Eur. J., 2014, 20, 8274–8278 CrossRef PubMed; (i) T. Higashino, T. Soya, W. Kim, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2015, 54, 5456–5459 CrossRef PubMed; (j) H. Ruffin, G. N. M. Boussambe, T. Roisnel, V. Dorcet, B. Boitrel and S. Le Gac, J. Am. Chem. Soc., 2017, 139, 13847–13857 CrossRef PubMed; (k) M. Izawa, T. Kim, S. Ishida, T. Tanaka, T. Mori, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2017, 56, 3982–3986 CrossRef PubMed.
- (a) M. Stepień, L. Latos-Grażyński, N. Sprutta, P. Chwalisz and L. Szterenberg, Angew. Chem., Int. Ed., 2007, 46, 7869–7873 CrossRef PubMed; (b) S. Saito, J.-Y. Shin, J. M. Lim, K. S. Kim, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2008, 47, 9657–9660 CrossRef PubMed; (c) J. K. Park, Z. S. Yoon, M. Yoon, K. S. Kim, S. Mori, J. Shin, A. Osuka and D. Kim, J. Am. Chem. Soc., 2008, 130, 1824–1825 CrossRef PubMed; (d) J. M. Lim, J.-Y. Shin, Y. Tanaka, S. Saito, A. Osuka and D. Kim, J. Am. Chem. Soc., 2010, 132, 3105–3114 CrossRef PubMed; (e) S. Gokulnath, M. Toganoh, K. Yamaguchi, S. Mori, H. Uno and H. Furuta, Dalton Trans., 2012, 41, 6283–6290 RSC; (f) T. Yoneda, Y. M. Sung, J. M. Lim, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2014, 53, 13169–13173 CrossRef PubMed; (g) B. Szyszko, N. Sprutta, P. Chwalisz, M. Stępień and L. Latos-Grażyński, Chem.–Eur. J., 2014, 20, 1985–1997 CrossRef PubMed; (h) A. Ghosh, A. Chaudhary, A. Srinivasan, C. H. Suresh and T. K. Chandrashekar, Chem.–Eur. J., 2016, 22, 3942–3946 CrossRef PubMed; (i) A. Mallick, J. Oh, M. A. Majewski, M. Stępień, D. Kim and H. Rath, J. Org. Chem., 2017, 82, 556–566 CrossRef PubMed.
- (a) E. Pacholska-Dudziak, J. Skonieczny, M. Pawlicki, L. Szterenberg, Z. Ciunik and L. Latos-Grazyński, J. Am. Chem. Soc., 2008, 130, 6182–6195 CrossRef PubMed; (b) T. Higashino, J. M. Lim, T. Miura, S. Saito, J.-Y. Shin, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2010, 49, 4950–4954 CrossRef PubMed; (c) T. Higashino, B. S. Lee, J. M. Lim, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2012, 51, 13105–13108 CrossRef PubMed.
- (a) T. D. Lash, Angew. Chem., Int. Ed., 2000, 39, 1763–1767 CrossRef; (b) J. L. Sessler and D. Seidel, Angew. Chem., Int. Ed., 2003, 42, 5134–5175 CrossRef PubMed; (c) S. Saito and A. Osuka, Angew. Chem., Int. Ed., 2011, 50, 4342–4373 CrossRef PubMed; (d) M. Stępień, N. Sprutta and L. Latos-Grażyński, Angew. Chem., Int. Ed., 2011, 50, 4288–4340 CrossRef PubMed; (e) T. Tanaka and A. Osuka, Chem. Rev., 2017, 117, 2584–2640 CrossRef PubMed; (f) B. Szyszko, M. J. Białek, E. Pacholska-Dudziak and L. Latos-Grażyński, Chem. Rev., 2017, 117, 2839–2909 CrossRef PubMed.
- (a) E. Marcos, J. M. Anglada and M. Torrent-Sucarrat, J. Phys. Chem. C, 2012, 116, 24358–24366 CrossRef; (b) M. Alonso, P. Geerlings and F. de Proft, Chem.–Eur. J., 2012, 18, 10916–10928 CrossRef PubMed; (c) E. Marcos, J. M. Anglada and M. Torrent-Sucarrat, J. Org. Chem., 2014, 79, 5036–5046 CrossRef PubMed; (d) M. Alonso, B. Pinter, P. Geerlings and F. De Proft, Chem.–Eur. J., 2015, 21, 17631–17638 CrossRef PubMed.
- (a) A. Osuka and S. Saito, Chem. Commun., 2011, 47, 4330–4339 RSC; (b) M. Pawlicki and L. Latos-Grażyński, Chem.–Asian J., 2015, 10, 1438–1451 CrossRef PubMed; (c) Y. M. Sung, J. Oh, W.-Y. Cha, W. Kim, J. M. Lim, M.-C. Yoon and D. Kim, Chem. Rev., 2017, 117, 2257–2312 CrossRef PubMed; (d) M. Torrent-Sucarrat, S. Navarro, E. Marcos, J. M. Anglada and J. M. Luis, J. Phys. Chem. C, 2017, 121, 19348–19357 CrossRef; (e) T. Stuyver, M. Perrin, P. Geerlings, F. De Proft and M. Alonso, J. Am. Chem. Soc., 2018, 140, 1313–1326 CrossRef PubMed.
- (a) T. Koide, K. Youfu, S. Saito and A. Osuka, Chem. Commun., 2009, 6047–6049 RSC; (b) J.-Y. Shin, J. M. Lim, Z. S. Yoon, K. S. Kim, M.-C. Yoon, S. Hiroto, H. Shinokubo, S. Shimizu, A. Osuka and D. Kim, J. Phys. Chem. B, 2009, 113, 5794–5802 CrossRef PubMed; (c) M. Stępień, B. Szyszko and L. Latos-Grażyński, J. Am. Chem. Soc., 2010, 132, 3140–3152 CrossRef PubMed; (d) S. Ishida, T. Higashino, S. Mori, H. Mori, N. Aratani, T. Tanaka, J. M. Lim, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2014, 53, 3427–3431 CrossRef PubMed; (e) K. Naoda, H. Mori, J. Oh, K. H. Park, D. Kim and A. Osuka, J. Org. Chem., 2015, 80, 11726–11733 CrossRef PubMed; (f) T. Soya, H. Mori, Y. Hong, Y. H. Koo, D. Kim and A. Osuka, Angew. Chem., Int. Ed., 2017, 56, 3232–3236 CrossRef PubMed.
- (a) M.-C. Yoon, J.-Y. Shin, J. M. Lim, S. Saito, T. Yoneda, A. Osuka and D. Kim, Chem.–Eur. J., 2011, 17, 6707–6715 CrossRef PubMed; (b) T. Higashino and A. Osuka, Chem. Sci., 2013, 4, 1087–1091 RSC.
- T. Higashino, A. Kumagai and H. Imahori, Chem. Commun., 2017, 53, 5091–5094 RSC.
- (a) M. Toganoh and H. Furuta, Chem. Commun., 2012, 48, 937–954 RSC; (b) H. Furuta, T. Ishizuka, A. Osuka, H. Dejima, H. Nakagawa and Y. Ishikawa, J. Am. Chem. Soc., 2001, 123, 6207–6208 CrossRef PubMed; (c) M. Toganoh, T. Yamamoto, T. Hihara, H. Akimaru and H. Furuta, Org. Biomol. Chem., 2012, 10, 4367–4374 RSC; (d) C. J. Ziegler, N. R. Erickson, M. R. Dalby and V. N. Nemykin, J. Phys. Chem. A, 2013, 117, 11499–11508 CrossRef PubMed; (e) R. Sakashita, Y. Oka, H. Akimaru, P. E. Kesavan, M. Ishida, M. Toganoh, T. Ishizuka, S. Mori and H. Furuta, J. Org. Chem., 2017, 82, 8686–8696 CrossRef PubMed.
- (a) T. K. Chandrashekar and S. Venkatraman, Acc. Chem. Res., 2003, 36, 676–691 CrossRef PubMed; (b) N. Shivran, S. C. Gadekar and V. G. Anand, Chem.–Asian J., 2017, 12, 6–20 CrossRef PubMed; (c) T. Chatterjee, A. Srinivasan, M. Ravikanth and T. K. Chandrashekar, Chem. Rev., 2017, 117, 3329–3376 CrossRef PubMed.
- V. G. Anand, S. Saito, S. Shimizu and A. Osuka, Angew. Chem., Int. Ed., 2005, 44, 7244–7248 CrossRef PubMed.
- Quite recently, Osuka and co-workers reported decaphyrin with the contribution of the Möbius aromatic thia[28]hexaphyrin segment. See ref 11e.
- B. Koszarna and D. T. Gryko, J. Org. Chem., 2006, 71, 3707–3717 CrossRef PubMed.
- K. Naoda, Y. M. Sung, J. M. Lim, D. Kim and A. Osuka, Chem.–Eur. J., 2014, 20, 7698–7705 CrossRef PubMed.
- (a) L. K. Frensch, K. Pröpper, M. John, S. Demeshko, C. Brückner and F. Meyer, Angew. Chem., Int. Ed., 2011, 50, 1420–1424 CrossRef PubMed; (b) E. Ganapathi, W.-Z. Lee and M. Ravikanth, J. Org. Chem., 2014, 79, 9603–9612 CrossRef PubMed; (c) Z. Zhou, Y. Chang, S. Shimizu, J. Mack, C. Schütt, R. Herges, Z. Shen and N. Kobayashi, Angew. Chem., Int. Ed., 2014, 53, 6563–6567 CrossRef PubMed.
- (a) A. J. Pistner, G. P. A. Yap and J. Rosenthal, J. Phys. Chem. C, 2012, 116, 16918–16924 CrossRef PubMed; (b) A. J. Pistner, D. A. Lutterman, M. J. Ghidiu, E. Walker, G. P. A. Yap and J. Rosenthal, J. Phys. Chem. C, 2014, 118, 14124–14132 CrossRef PubMed; (c) A. M. Bruce, E. S. Weyburne, J. T. Engle, C. J. Ziegler and G. R. Geier, J. Org. Chem., 2014, 79, 5664–5672 CrossRef PubMed; (d) A. S. Aslam, J.-H. Hong, J.-H. Shin and D.-G. Cho, Angew. Chem., Int. Ed., 2017, 56, 16247–16251 CrossRef PubMed; (e) T. Higashino and A. Osuka, Chem.–Asian J., 2013, 8, 1994–2002 CrossRef PubMed; (f) J. Kong, J. Shao, C. Li, D. Qi, M. Li, X. Liang, W. Zhu, J. Jiang and Y. Xie, Org. Lett., 2017, 19, 650–653 CrossRef PubMed.
- J.-Y. Shin, K. S. Kim, M.-C. Yoon, J. M. Lim, Z. S. Yoon, A. Osuka and D. Kim, Chem. Soc. Rev., 2010, 39, 2751–2767 RSC.
- (a) W.-Y. Cha, T. Soya, T. Tanaka, H. Mori, Y. Hong, S. Lee, K. H. Park, A. Osuka and D. Kim, Chem. Commun., 2016, 52, 6076–6078 RSC; (b) T. Woller, P. Geerlings, F. De Proft, B. Champagne and M. Alonso, Molecules, 2018, 23, 1333 CrossRef PubMed.
- M. Torrent-Sucarrat, S. Navarro, F. P. Cossío, J. M. Anglada and J. M. Luis, J. Comput. Chem., 2017, 38, 2819–2828 CrossRef PubMed.
- I. Casademont-Reig, T. Woller, J. Contreras-García, M. Alonso, M. Torrent-Sucarrat and E. Matito, Phys. Chem. Chem. Phys., 2018, 20, 2787–2796 RSC.
- (a) P. v. R. Schleyer, C. Maerker, A. Dransfeld, H. Jiao and N. J. R. v. E. Hommes, J. Am. Chem. Soc., 1996, 118, 6317–6318 CrossRef PubMed; (b) Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. v. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef PubMed.
- (a) S. Mori and A. Osuka, J. Am. Chem. Soc., 2005, 127, 8030–8031 CrossRef PubMed; (b) H. Rath, N. Aratani, J. M. Lim, J. S. Lee, D. Kim, H. Shinokubo and A. Osuka, Chem. Commun., 2009, 3762–3764 RSC; (c) T. Yoneda, T. Kim, T. Soya, S. Neya, J. Oh, D. Kim and A. Osuka, Chem.–Eur. J., 2016, 22, 4413–4417 CrossRef PubMed.
- T. M. Krygowski and M. K. Cyrański, Chem. Rev., 2001, 101, 1385–1420 CrossRef PubMed.
- K. Naoda and A. Osuka, Chem.–Asian J., 2016, 11, 2849–2853 CrossRef PubMed.
- Although bond lengths and bond orders are not sufficient to understand the dominant π-circuits of our compounds, recently proposed electronic indices26 and special ring current density32 could provide understanding of conjugation pathways in expanded porphyrins. However, at this stage these calculations cannot be performed on commercial programs such as Gaussian33 that we can use currently. The special ring current density calculation could be used to distinguish from cross-conjugated to macrocyclic networks because the antiaromatic character can be evaluated by magnetically induced currents. Such challenging calculations will be done separately and reported elsewhere in the future..
- H. Fliegl, D. Sundholm, S. Taubert and F. Pichierri, J. Phys. Chem. A, 2010, 114, 7153–7161 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision D.01, Gaussian, Inc., Wallingford, CT, 2013 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Synthesis, high-resolution mass spectra, NMR spectra, X-ray crystallographic details, absorption spectra, cyclic voltammograms, and DFT calculations. CCDC 1841655 and 1841656. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8sc02448k |
‡ Crystallographic data for 5: C56H15F20N5S3·3.5(CH2Cl2), Mr = 1531.15, triclinic, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (no. 2), a = 13.890(2), b = 14.794(2), c = 16.218(2) Å, α = 96.6694(14), β = 96.1744(14), γ = 112.8223(16)°, V = 3007.7(7) Å3, ρcalcd = 1.691 g cm−3, Z = 2, 24673 reflections measured, 13239 unique (Rint = 0.0300), R1 = 0.0621 [I > 2σ(I)], wR2 = 0.1921 [all data], GOF = 1.096, CCDC 1841655. Crystallographic data for 6: 2(C56H13F20N5S3)·3(chlorobenzene), Mr = 2793.4, triclinic, space group P (no. 2), a = 13.890(2), b = 14.794(2), c = 16.218(2) Å, α = 96.6694(14), β = 96.1744(14), γ = 112.8223(16)°, V = 3007.7(7) Å3, ρcalcd = 1.691 g cm−3, Z = 2, 24673 reflections measured, 13239 unique (Rint = 0.0300), R1 = 0.0621 [I > 2σ(I)], wR2 = 0.1921 [all data], GOF = 1.096, CCDC 1841655. Crystallographic data for 6: 2(C56H13F20N5S3)·3(chlorobenzene), Mr = 2793.4, triclinic, space group P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) (no. 2), a = 13.765(3), b = 17.271(3), c = 24.190(5) Å, α = 94.738(3), β = 102.606(4), γ = 93.061(5)°, V = 5577.7(19) Å3, ρcalcd = 1.665 g cm−3, Z = 2, 44377 reflections measured, 23504 unique (Rint = 0.0567), R1 = 0.1121 [I > 2σ(I)], wR2 = 0.3578 [all data], GOF = 1.077, CCDC 1841656. (no. 2), a = 13.765(3), b = 17.271(3), c = 24.190(5) Å, α = 94.738(3), β = 102.606(4), γ = 93.061(5)°, V = 5577.7(19) Å3, ρcalcd = 1.665 g cm−3, Z = 2, 44377 reflections measured, 23504 unique (Rint = 0.0567), R1 = 0.1121 [I > 2σ(I)], wR2 = 0.3578 [all data], GOF = 1.077, CCDC 1841656. |
| This journal is © The Royal Society of Chemistry 2018 |