Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Surfactant mediated particle aggregation in nonpolar solvents
Mojtaba
Farrokhbin
 ab,
Biljana
Stojimirović
ab,
Biljana
Stojimirović
 a,
Marco
Galli
a,
Mohsen
Khajeh Aminian
b,
Yannick
Hallez
c and
Gregor
Trefalt
a,
Marco
Galli
a,
Mohsen
Khajeh Aminian
b,
Yannick
Hallez
c and
Gregor
Trefalt
 *a
*a
aDepartment of Inorganic and Analytical Chemistry, University of Geneva, Sciences II, 30 Quai Ernest-Ansermet, 1205 Geneva, Switzerland. E-mail: gregor.trefalt@unige.ch
bDepartment of Physics, Faculty of Sciences, Yazd University, Yazd 89195-741, Iran
cLaboratoire de Génie Chimique, Université de Toulouse, CNRS, INPT, UPS, Toulouse, France
First published on 8th August 2019
Abstract
The aggregation behavior of particles in nonpolar media is studied with time-resolved light scattering. At low surfactant concentrations particles are weakly charged and suspensions are not stable. The suspensions become progressively more stable with increasing surfactant concentration as particles become more highly charged. At high concentrations the particles become neutralized and aggregation is again fast. The theory of Derjaguin, Landau, Verwey, and Overbeek (DLVO) is able to predict the stability ratios quantitatively by using the experimentally measured surface charges, screening lengths and van der Waals forces.
I. Introduction
Charging of particles in nonpolar media is important for many practical applications, for example, the development of electrophoretic displays,1,2 airborne drug delivery systems,3 and toner technologies.4 In addition to being important for applications, nonpolar colloids are also extremely interesting from a fundamental point of view. The understanding of the charging and stability mechanisms of particles in nonpolar media is far from being completely achieved. Furthermore, comparisons with aqueous systems could give new insights into possible charging mechanisms.The generation of charges in solutions typically occurs via the mechanism of dissociation of salt. The important parameter in this context is the Bjerrum length, which is the distance between two elementary charges for which the electrostatic energy is equal to the thermal energy. For water, the Bjerrum length is smaller than 1 nm and is comparable to the size of the hydrated ions; therefore the dissociation of salt is spontaneous. In nonpolar media with very low dielectric constants, such as alkanes, the Bjerrum length becomes large and can reach values of few tens of nanometers. In such solutions the ions stay paired and do not dissociate spontaneously. However, with the addition of ionic5–9 or even non-ionic surfactants,10–14 charged species are formed, which can be observed in terms of an increased conductivity of surfactant solutions. These surfactants form inverse micelles, which are much bigger than simple ions. The charge is then formed by charge disproportionation, where two neutral micelles exchange a charge, forming two oppositely charged species.5,7–9 Another possibility is to use electrolytes with large, bulky ions, which also dissociate partly in nonpolar solvents.15,16
When solid surfaces or colloidal particles are immersed in nonpolar solvents, they typically do not become charged. However, surface charge can be acquired by the introduction of surfactants. Surface charging mechanisms in nonpolar liquids mediated by surfactants were studied with various methods.5,6 Both the nature of the surface and the properties of the surfactants are important in this process. Different charging mechanisms have been described. The charge can form by dissolution of surface ions into reverse micelles,17 preferential adsorption of charged micelles onto the surface,5,8 or adsorption of individual surfactant molecules and their subsequent dissociation.18–20 In the case of non-ionic surfactants the charging can be explained by acid–base mechanisms.5,6,11–14,21,22 Specifically designed particles can charge also without addition of surfactants by surface dissociation of bulky ionic liquid like ions.23,24
Charging of colloids in nonpolar liquids leads to electrostatic repulsive forces between them. These repulsive forces were measured by different techniques, such as surface force apparatus,17 colloidal probe technique,20 total internal reflection microscopy,25 optical tweezers,9,26–29 and pair correlation function measurements.7,14 The majority of these experiments measured a long-ranged tail of the electrostatic interaction, and interpreted the measured profiles with screened Coulomb potentials, also known as Yukawa potentials. The parameters entering the Yukawa interaction extracted from the forces were found to be consistent with conductivity and electrokinetic measurements,7,9,14 although some recent force measurements showed deviations of Debye screening lengths from values extracted from conductivity measurements.15
The particle interactions drive the stability of colloidal particles in suspensions. Typically colloids are not stable in pure nonpolar liquids, but suspensions become stabilized upon addition of surfactants. While stability in nonpolar suspensions has been observed qualitatively,7,14,30 no quantitative data on aggregation kinetics are available. Such data would first quantify the stability of nonpolar suspensions and second enable extracting further information about the electrostatic and van der Waals interactions in these systems. For aqueous suspensions the simultaneous measurements of aggregation kinetics and particle interactions on the same particles showed that the interaction forces extracted from the colloidal probe technique can be used to evaluate quantitatively stability ratios.31–33 Conversely, information about the interactions, such as surface charge regulation properties, can be extracted from the aggregation rate measurements.34–37
Here we present the measurements of aggregation rates for three different particle suspensions in decane in the presence of a surfactant. In combination with the results from direct-force measurements and electrophoresis we were able to elucidate the aggregation mechanisms in nonpolar suspensions. We further pinpointed the most important factors affecting the aggregation process and extracted some information about surface charge regulation effects.
II. Experimental methods
A. Materials
Aqueous suspensions of silica particles (5.0 wt%, Corpuscular Inc.) and two types of surfactant-free polystyrene latex particles, namely sulfate latex (SL) (8.0 wt%) and amidine latex (AL) (4.0 wt%) (both from Invitrogen Corporation), were used to study the aggregation mechanism in nonpolar media. The sign of the surface charge of these particles in water is dictated by their surface chemistry. Silica and SL particles are negatively charged in water, while AL is positively charged. The average particle size determined and polydispersity measured by the manufacturer with transmission electron microscopy (TEM) and dynamic light scattering (DLS) are given in Table 1.| Particles | Radius (nm) | Polydispersity indexa | Fast rate in waterc | Fast rate in decane | |
|---|---|---|---|---|---|
| TEMa | DLSb | CV (%) | k fast (×10−18 m3 s−1) | k fast (×10−18 m3 s−1) | |
| a Measured by the producer with electron microscopy, except for silica, which was measured with DLS. b Measured by dynamic light scattering in water at 25 °C. c Measured at concentrations of KCl above 600 mM. d Measured in the 0.002–0.01 mM AOT concentration range. e Measured in the 0.02–0.4 mM AOT concentration range. f Measured in the 0.3–0.5 mM AOT concentration range. | |||||
| Silica | 100 | 103 | 22 | 1.0 ± 0.2 | 1.0 ± 0.2d |
| Sulfate latex (SL) | 150 | 155 | 4.7 | 2.8 ± 0.3 | 2.3 ± 0.3e |
| Amidine latex (AL) | 110 | 117 | 4.3 | 2.8 ± 0.3 | 2.3 ± 0.2f |
Additional DLS measurements were performed in house for all three samples. The average size measured by DLS is slightly larger than the values obtained by TEM, probably due to polydispersity effects. The supplied polystyrene particle suspensions were first dialyzed in cellulose ester (SL particles) or polyvinylidene fluoride membranes (AL particles) against Milli-Q water (Millipore) for about one week until the conductivity reached about 70 μS m−1. After dialysis the particle concentration of the suspension was determined with static light scattering by comparing the scattered intensities of dialyzed suspensions and non-dialyzed suspensions with known concentrations.
In order to study charging and aggregation in nonpolar media, the particles from aqueous suspensions had to be transferred into decane, which was achieved in two steps. First, small amounts of dialyzed particle suspensions were injected into isopropyl alcohol (99.5%, Sigma-Aldrich), resulting in suspensions with concentrations of 5 g L−1 and 0.4 g L−1 for silica and polystyrene particles, respectively. The isopropanol suspensions were used in the second step to prepare samples in decane. Dioctyl sodium sulfosuccinate with the commercial name Aerosol-OT (AOT) (>95%, Fisher Chemical) was dissolved in decane (Sigma-Aldrich, ≥99%) and filtered through 0.1 μm syringe filters. Finally, isopropanol suspensions were injected into decane/AOT, reaching the final particle concentrations of 100 mg L−1 and 10 mg L−1 for silica and polystyrene particles, respectively. Note that the amount of isopropanol in the final suspensions was typically below 1 vol% and therefore these small amounts do not significantly change the properties of the solvent.
B. Electrophoresis
Phase analysis light scattering (PALS) was used to measure electrophoretic mobility on a Zetasizer Nano ZS instrument (Malvern). A dip cell ZEN 1002 appropriate for non-aqueous solutions was used. This cell employs two planar palladium electrodes separated by 2 mm, dipped into a glass cuvette with a square cross-section. The cell electrodes and glass cuvettes were cleaned and rinsed with decane. Suspensions were prepared by mixing a stock solution of AOT surfactant in decane to get the desired surfactant concentration and then particles were injected from stock isopropanol suspensions. The final particle concentration used for electrophoresis measurement was 100 mg L−1 for silica and 10 mg L−1 for polystyrene particles. The mobility values were measured under different electric fields and extrapolated to zero-field values.14 In general, the deviations of the zero-field extrapolated values and values measured under finite fields were below 5 × 10−11 m2 V−1 s−1, which corresponds to deviation in the electrokinetic potential below 5 mV. The electrophoretic mobilities were converted into electrokinetic potentials by employing the Hückel expression suitable for the systems under investigation.C. Karl Fischer titration
Karl Fischer titration (736 GP Titrino, Metrohm) with methanol as the solvent was used to measure the water content of decane/AOT suspensions. The water content depended on the AOT concentration and it was in the range of 0.1–0.4 wt% for silica suspensions and 0.05–0.1 wt% for polystyrene suspensions. The higher water content for silica samples can be explained by the larger concentration of silica particles, which introduces more water into the final decane suspension.D. Conductivity measurements
A High Precision Conductivity Meter (Model 1154, Emcee Electronics, Inc.) was used to measure the conductivity of the suspensions. Conductivities below 1 pS m−1 were measured for the pure solvent (decane). The conductivity values were used to estimate the inverse Debye length, κ.E. Force measurements
The van der Waals forces between spherical silica particles (Bangs Laboratories Inc.) in decane were measured using the colloidal probe technique based on atomic force microscopy (AFM) in a symmetric sphere–sphere geometry. First, a single silica particle with a diameter reported to be 4.07 μm was glued on a tipless cantilever (MikroMasch, Tallinn, Estonia). A small drop of glue (Araldite 2000+) and some silica particles were placed on a glass slide next to each other. The cantilever was mounted inside the AFM head and manipulated to touch the glue and immediately after to pick up a single particle. The substrate was prepared separately by spreading silica particles on a quartz microscope slide (Plano GmbH, Wetzlar, Germany), previously cleaned in piranha solution (a 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 mixture of H2SO4 (98%) and H2O2 (30%)). Both the cantilever with the glued particle and the prepared substrate were placed in an oven for 2 h at 1200 °C. After this sintering process, the particles were firmly attached to the substrate/cantilever and the glue was burned away.
1 mixture of H2SO4 (98%) and H2O2 (30%)). Both the cantilever with the glued particle and the prepared substrate were placed in an oven for 2 h at 1200 °C. After this sintering process, the particles were firmly attached to the substrate/cantilever and the glue was burned away.
Force measurements were performed at room temperature 23 ± 2 °C with a closed loop AFM (MFP-3D, Asylum Research) mounted on an inverted optical microscope (Olympus IX70). The substrate and the cantilever were cleaned in ethanol and water, and plasma-treated for 20 min. The substrate with particles was mounted into the fluid cell. Decane (Acros Organics, 99%) was kept on molecular sieves to reduce the water content, and filtered through a 0.02 μm syringe filter (Whatman Anotop 25) before measurement. The particle on the cantilever was centered above the selected particle on the substrate with a precision of about 100 nm. The deflection of the cantilever was recorded for 150 approach–retract cycles, and the cantilever speed was 400 nm s−1. The deflection was converted to force using Hooke's law, where the spring constant of the cantilever was determined by the Sader method, and was 0.345 N m−1. The approach part of the recorded curves was averaged to obtain final force-curves.
F. Light scattering
A time-resolved light scattering technique was used to study the particle aggregation mechanism by using a goniometer setup (ALV/CGS-3). This instrument uses a He/Ne laser with a wavelength of 633 nm. A stock solution of AOT surfactant in decane was diluted to the desired concentration in 2 mL borosilicate cuvettes. Then, an appropriate amount of suspension of particles in isopropanol was injected into the cuvette and the suspension was rapidly mixed. The final concentrations of particles in the samples were 100 mg L−1 for silica and 10 mg L−1 for polystyrene particles. A higher concentration of silica particles had to be used due to their lower refractive index, which results in a lower scattering signal. Before use, the borosilicate cuvettes were cleaned in a hot piranha solution for one day, then washed with Milli-Q water and dried in a dust-free oven at 60 °C. The scattering intensity was accumulated at an angle of 90° for 20 s to build a correlation function, which was analyzed with a second-order cumulant fit in order to obtain the diffusion coefficient. The Stokes–Einstein relation was used for the conversion of the diffusion coefficient to hydrodynamic radius, where the viscosity of pure decane of 0.86 mPa s was used.In order to determine the aggregation rate constants for singlet particles forming a doublet, the time evolution of the hydrodynamic radius was followed for typically 1 h.38 The apparent dynamic rate coefficient, Δ, was determined from the initial increase of the hydrodynamic radius, Rh,
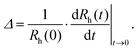 | (1) |
The stability ratio, W, was determined as
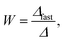 | (2) |
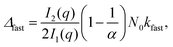 | (3) |
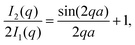 | (4) |
III. Results and discussion
The aggregation of colloids in decane in the presence of AOT surfactant was investigated. In order to understand the aggregation process, we first measured the charging of silica, sulfate latex (SL), and amidine latex (AL) in decane as a function of AOT concentration. All the particles are practically uncharged in pure decane and become charged upon the addition of the surfactant. We were further able to estimate the interaction forces between the particles, which in turn enabled us to calculate the aggregation rate constants. A comparison between the theoretically calculated and experimentally measured aggregation rates confirms that the electrostatic and vdW interactions are the main drivers of the aggregation process.A. Charging of colloidal particles
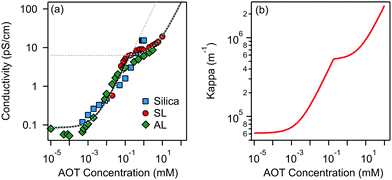
Charging of colloidal particles was determined indirectly by measuring electrophoretic mobility. The electrophoretic mobility can be further converted to an electrokinetic potential and electrokinetic charge. This conversion depends on the thickness of the double-layer compared to the size of the particle. The double-layer thickness, which is equal to the inverse Debye length, κ−1, is dependent on the concentration of charged species in the solution. The charge in the nonpolar solutions containing AOT stems from inverse micelles. However, only a small fraction ∼ 1 × 10−5 of these micelles are charged.7 Electrical conductivity measurements in the nonpolar solutions give an accurate estimation of the Debye lengths.7,9,14 By knowing the size of charge carriers, κ can be calculated from conductivity, σ, by using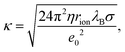 | (5) |
Below the CMC the charge in solution is created by the dissociation of individual AOT molecules, complexation of charged impurities by AOT, and formation of pre-micellar complexes.9,10 Above the CMC the conductivity is dominated by charged reverse micelles. The majority of micelles are neutral; however, during collisions between them, the charge can be transferred through the charge disproportionation mechanism,7,9,10 which can be described in the framework of charge fluctuation theory.42
The Debye lengths estimated from the conductivity are found in the range of κ−1 = 1–10 μm, see Fig. 1b. Compared to the radii, a, of the investigated colloids, which are between 0.10 and 0.15 μm, the double-layer thickness is much larger and therefore our measurements are performed in the κa ≪ 1 limit.
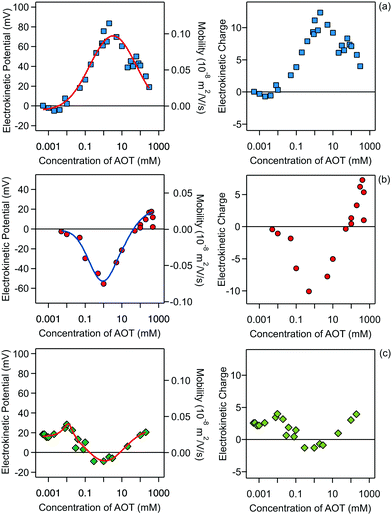
The electrophoresis results for all three systems are presented in Fig. 2.
The electrophoretic mobilities, μ, were converted into the electrokinetic potential, ζ, also called the zeta potential, using the Hückel theory:
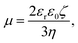 | (6) |
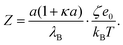 | (7) |
Note that this charge represents the number of charged species on the surface of one particle. The maximum absolute number of charges is relatively low as it reaches values of only about 10 charges per particle. However, due to the low dielectric constant of the medium, this low charge translates into rather high maximal electrostatic potentials of about 80 mV. Eqn (7) is valid in fact only when the Debye–Hückel theory is valid, in practice for potentials lower than 40–50 mV in dilute suspensions. We use (7), however, as ζ rarely exceeds this threshold in the present experiments. All the particles are only weakly charged at low surfactant concentrations and the sign of the charge is consistent with their surface chemistry in water, namely negative for silica and SL (silanol and sulfate groups), and positive for AL (amidine groups). In all the systems charge reversal is observed upon addition of AOT. Note that the magnitude of the charge of the silica is extremely low at small AOT concentrations and therefore the particles are practically neutral under these conditions.
The electrokinetic potential of silica particles is almost neutral below 0.01 mM AOT and at this concentration the silica surface becomes positively charged. After this point the potential increases and reaches a maximum value of about 80 mV at 3 mM AOT. At high concentrations of AOT, the mobility again decreases and approaches zero at concentrations of several hundreds of mM. Similar behavior was observed for larger silica particles in decane/AOT suspensions by Keir et al.43 They speculated that the charge reversal is caused by adsorption of positively charged AOT micelles. Such behavior could also be explained by the specific adsorption of sodium ions to the silica surface.
Compared to the silica particles, the situation is reversed for the SL particles. The opposite behavior of the silica and latex particles is possibly due to the different affinities of AOT for the adsorption for the two surfaces. For SL particles the electrokinetic potential first decreases with concentration and reaches a pronounced minimum of −55 mV at 1 mM. At higher concentrations the SL particles become neutralized again. This neutralization at higher concentrations is very reminiscent of the charging of SL particles in water.21,34,44,45 One can argue that the main driver for the charging in water and in decane/AOT is the charging of the sulfate groups present on the surface of the particle. In the case of decane the particle counterions can be solubilized by AOT micelles and this process would produce negatively charged sulfate groups on the surface.21 However, looking at the electrokinetic charge profile in decane (Fig. 2, right), a clear difference with aqueous suspensions is revealed. First, the number of surface charges on a similar particle in water is typically at least three orders of magnitude greater than the values in nonpolar media. Second, while in the case of aqueous suspensions the charge of SL particles at higher concentrations is constant and the reduction in the magnitude of the potential is caused by double-layer screening with salt, in the decane/AOT system, the charge is not constant, and the magnitude of charge first decreases and after 1 mM increases. Therefore in the latter case it seems that there are two adsorption regimes which control the charge and consequently the potential. The behavior at lower concentrations is consistent with the mechanism of AOT adsorption and its subsequent ionization, which was inferred from scattering measurements for PMMA particles.19 At higher concentrations positive species are adsorbed, which could possibly be solubilized sodium ions.
The results for AL particles, shown in Fig. 2c, reveal that this type of surface remains weakly charged in the whole concentration regime, consistent with the earlier measurements of AL charge in the presence of AOT.21 The particles are positively charged at low AOT concentrations and become neutralized at concentrations between 0.1 and 10 mM, where even a slight charge inversion is observed. At concentrations above 10 mM the particles become slightly positively charged again. Compared to the silica and SL particles the magnitude of the charge of the AL particles is smaller. For AL the maximal number of charges reached is about two times smaller than the maximal values for the other two surfaces. It seems that adsorption of charged micelles or solubilization of surface groups is much less pronounced for AL surfaces.
B. Interactions between particles
In order to understand the aggregation mechanisms in decane/AOT suspensions, we next focus on the particle interactions in these systems. The interactions are modelled with the DLVO theory as a sum of van der Waals, UvdW, and double-layer, Udl, interaction energies:| Udlvo = UvdW + Udl. | (8) |
The van der Waals interaction is calculated using the non-retarded expression for two spherical particles,46,47
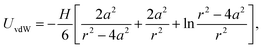 | (9) |
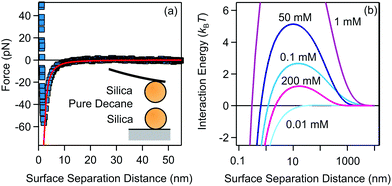 | ||
| Fig. 3 (a) van der Waals interaction measured between two 4 μm silica spheres measured in pure decane. The line represents the fit to non-retarded van der Waals expression with the Hamaker constant H = (1.8 ± 0.2) × 10−21 J. (b) DLVO interaction energies for 200 nm silica particles in decane for different AOT concentrations, calculated with eqn (8). The measured Hamaker constant was used to calculate the van der Waals interaction, while electrokinetic potential and conductivity measurements were used to calculate the double-layer interaction. | ||
We have fitted the force curve with the expression FvdW = −Ha/(12h2),46 where h = r − 2a is the surface separation distance. Note that this expression can be derived from eqn (9) for a ≪ h and it is valid for the large 4 μm silica particles. The force measurements enabled us to extract the Hamaker constant, H = (1.8 ± 0.2) × 10−21 J, for two silica surfaces interacting through decane. This constant is slightly smaller than the value measured for similar silica particles across water48 and close to the calculated value of two interacting silica surfaces across dodecane.47 The Hamaker constant extracted from the force measurements was later used to estimate the van der Waals interaction energy between aggregating silica particles in suspensions.
The other contribution to the DLVO interaction is the double-layer interaction energy, which is approximated by the Yukawa potential:
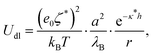 | (10) |
In order to make an estimation of the double-layer forces, ζ* and κ* have to be estimated. The screening lengths estimated from electrical conductivity usually match well the decay lengths determined directly from experimental pair interaction curves.7,9,14 Indeed, such experiments are conducted with two particles in an otherwise empty electrolyte, whereas κ* essentially differs from the inverse Debye length at finite volume fractions. Therefore we have used the screening length values shown in Fig. 1b for our calculations. Note that the Yukawa potential form (10) has been demonstrated only for weakly charged, well separated, colloids as a result of the DH theory. However, the electric field generated by highly charged colloids decays away from their surfaces so that at large enough distance it can be matched by a fictitious field obeying the DH equation and that would be generated by colloids with a so-called renormalized surface potential ζ*. This fitting procedure is termed a renormalization method and can be undertaken for example with the recipe proposed by Trizac et al.50 Under these conditions, it is not unreasonable to assume that colloids interact with a potential with form (10) provided the renormalized potential value is used. Experiments reveal that the electrokinetic, or zeta, potential value is usually quite consistent with the renormalized potential value, probably because using the Hückel formula (6) to convert the true mobility into a potential is akin to a renormalization method. Therefore we have used directly the electrokinetic potentials, ζ, in eqn (10) for the calculations of the DLVO potential.
The DLVO pair interactions for 200 nm silica particles in decane/AOT solutions at several AOT concentrations are shown in Fig. 3b. At 0.01 mM AOT the charge of the silica is practically zero and only the van der Waals force is present. The energy barrier increases for 0.1 and 1 mM AOT as the charge of the particles increases. At larger concentrations of 50 and 200 mM, the re-entrant behavior is observed as the energy barrier is lowered again. Interactions are dominated by the charging of the silica surfaces.
The interactions for silica, SL, and AL particles were calculated in the full concentration range and were used to predict the stability of particle suspensions, presented below.
C. Particle aggregation
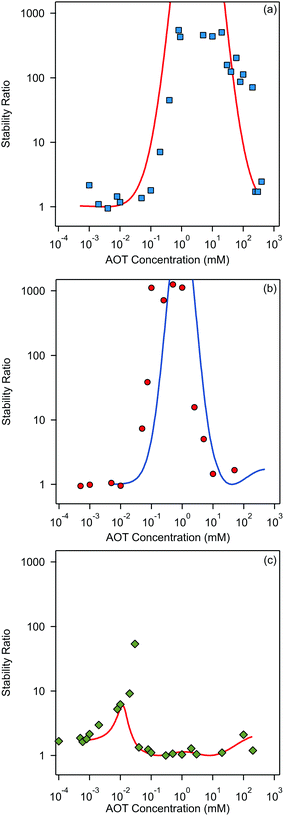
Finally, we focus on particle aggregation in decane/AOT solutions. We have measured the kinetics of aggregation with light scattering and extracted the aggregation rate constant. We have further determined the absolute aggregation rates for rapidly aggregating suspensions in both water and decane, which are given in Table 1. These fast rates are measured under conditions where the repulsive electrostatic forces are weak and attractive van der Waals interactions are dominant. For aqueous suspensions, this regime can be achieved by adding a sufficient amount of monovalent salt (KCl), which screens the electrostatic interactions. In the case of decane suspension we determined the fast rate at an AOT concentration for which the charge of the particles is close to zero. The fast rates in water are comparable to the values measured earlier for similar systems,44,45,51 although we measured slightly lower rates for silica suspension. The fast rates measured in decane solutions are also comparable to the values obtained in water, see Table 1. The viscosity of decane is slightly lower than that of water so the rates in decane should be a few percent higher; however, this difference is small compared to the measurement errors. The fast rates in decane for latex particles are slightly lower than those obtained in water, and this difference could be related to weaker van der Waals forces in decane solutions, due to the smaller difference in the refractive indices of decane and the particles.The apparent dynamic rate constants measured in decane for the wide concentration range of AOT were converted into the stability ratios viaeqn (2). The stability ratio, W, is a measure of the stability of suspensions, with W = 1 corresponding to fast aggregation where only attractive forces are present, and with large values of W corresponding to slow aggregation due to repulsive interactions. The stability ratios in decane as a function of AOT concentration for silica, SL, and AL particles are shown in Fig. 4.
All three systems exhibit a similar qualitative behavior. The stability ratio is equal to unity at low AOT concentrations, and the suspensions are not stable. At intermediate concentrations a peak in the stability ratio is observed corresponding to stable dispersions. The stability again decreases at high concentrations and the suspensions start to aggregate rapidly again. While silica and SL reach high stability with W ∼ 1000 at intermediate concentrations, the AL particles only reach maximal stability ratios between 10 and 100. This lower stability of AL particles can be explained by the lower magnitude of the surface charge of AL as compared to the other two systems. The qualitative stability behavior of all three suspensions can be understood by looking at the particle charging presented in Fig. 2. At low AOT concentrations particles are not charged and suspensions are not stable, at intermediate concentrations the magnitude of the surface charge increases and thus the stability ratio increases, and at high concentrations the particles become neutralized again and this process leads to unstable suspensions.
A better understanding of aggregation can be gained by calculating the stability ratios from particle interactions. To that end, we have used DLVO interactions to model the aggregation behavior. The aggregation rate constants can be calculated by solving the diffusion equation for particles interacting via the pair potential:46,52
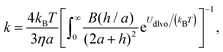 | (11) |
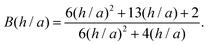 | (12) |
The stability ratio is then calculated with W = kfast/k, where kfast is calculated with eqn (11) and by setting Udl to zero. The calculations of the stability ratios for all three systems were first performed by utilizing the DLVO interaction energy given by (8)–(10). This is justified by the use of effective parameters in (10) and by the low volume fraction (<4 × 10−5) of all the suspensions considered.
For calculating the van der Waals interaction energy, the Hamaker constant values of 1.8 × 10−21 J and 3 × 10−21 J were used for silica and polystyrene particles, respectively. Note that the first value was measured with direct force measurement, while the second was chosen based on the values measured for SL and AL particles in water. The theoretical values of the Hamaker constant for latex particles interacting across water are 9–13 × 10−21 J.47 However, experimentally substantially lower values 2–4 × 10−21 J have been measured, due to roughness effects.54,55 The Hamaker constant for latex particles interacting across decane should be lower than its value for an aqueous suspension and higher than the silica–decane–silica value.47 Therefore the value of 3 × 10−21 J was chosen for the polystyrene–decane–polystyrene system. Furthermore, the precise choice of the Hamaker constant does not substantially affect the calculated stability ratios as will be shown below.
The double-layer interaction energies were calculated by employing the interpolated values of electrokinetic potentials shown in Fig. 2 and by inserting them into eqn (10).
The stability ratios calculated by employing DLVO interaction energies are shown alongside experimentally measured values in Fig. 4. The calculations can reproduce the observed behavior surprisingly well. There are slight shifts on the concentration axis and the peak magnitude of the stability ratio is not well predicted, but this simple model is able to predict quite quantitatively the AOT concentration range in which the suspension is effectively stabilized. This reasonable agreement could be considered as rather surprising, since some recent results suggested that the Yukawa model should fail in nonpolar suspensions.15,30,56 We will come back to this apparent discrepancy later. From our results on aggregation one can conclude that DLVO forces are the principle drivers of aggregation in the decane/AOT solutions.
Let us now discuss the most important factors affecting the stability of nonpolar suspensions. We will focus on a silica system. In Fig. 5 we show the stability ratios, where we vary the inverse Debye length and the Hamaker constant in the calculation.
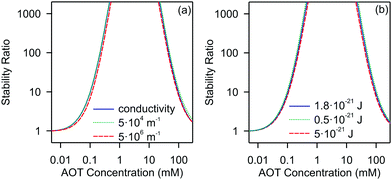 | ||
| Fig. 5 Calculated stability ratios for silica in decane as a function of AOT concentration. (a) Effect of the inverse Debye length on the stability ratio. (b) Effect of the Hamaker constant on the stability ratio. In (a) the solid line represents values extracted from the conductivity values shown in Fig. 1b, and the dotted and dashed lines use the constant values of κ = 5 × 104 m−1 and κ = 5 × 106 m−1, respectively. In (b) the solid line represents results for the experimentally measured Hamaker constant of 1.8 × 10−21 J, and the dotted and dashed lines use values of H = 0.5 × 10−21 J and H = 5 × 10−21 J. | ||
For the inverse Debye length we show three cases. In the first one we use the κ determined experimentally for the calculation, the second represents the lower bound, and the third the upper bound as determined from the conductivity, see Fig. 1. Note that in the second and third cases we fix κ and do not change it as a function of the concentration. Interestingly, the calculated stability ratios are practically independent of the choice of the screening length. This behavior is different from those of the aqueous systems, where the screening length is an extremely important factor for determining the stability.34,35 This insensitivity to the screening length shows that AOT influences aggregation by acting on the surface charge density rather than by setting the screening length of the double-layer. This is not surprising since all the systems investigated (whatever the AOT concentration) are in the κa ≪ 1 limit for which electrostatics converge to those of the salt-free regime where the only ions in the suspension are the counterions of the colloids. This observation is also consistent with electrokinetic measurements, which show that the change in the electrokinetic potential is caused by the change of the charge and not by the double-layer screening, see Fig. 2.
Next, we focus on the effect of the van der Waals forces on the aggregation. Although attractive van der Waals forces cause the particles to aggregate, the choice of the value of the Hamaker constant does not significantly affect the stability ratio, as shown in Fig. 5b. By changing the Hamaker constant from 0.5 to 5 × 10−21 J the stability ratio remains practically unaffected.
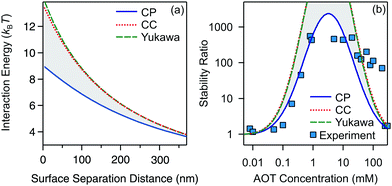
Let us finally focus on the influence of charge regulation effects on aggregation in the present system. Here we refer to charge regulation as the variation of charge as a function of the distance between two interacting particles.57,58 In addition, the charge of the particles can also vary with salt or particle concentration, and pH and the two phenomena are closely related to each other.57,59,60 While charge regulation in aqueous media has been thoroughly studied,57,60 recent measurements also showed the importance of charge regulation in nonpolar suspensions.56 It is important to realize that charge regulation effects cannot be accounted for with the Yukawa potential (10) for a constant ζ* because in this case the same numerical value of the prefactor of the exponential can result from a constant charge condition or a constant potential condition, among the other more sophisticated conditions. In order to address the influence of charge regulation on the stability of colloidal particles in decane/AOT, we compare the stability ratios based on exact interaction potentials stemming from constant potential (CP) and constant charge (CC) boundary conditions used to compute the exact solution of the Debye–Hückel equation for a pair of spheres,61 see Fig. 6.
The interaction energies between two silica particles under conditions corresponding to 4.7 mM AOT are shown in Fig. 6a. They show that the CC matches the Yukawa profile, which is expected for small κa.61,62 The CP curve is below the CC and Yukawa ones and the three curves converge to the same value at large separations. The stability ratios calculated with CC and CP boundary conditions are presented in Fig. 6b. The experimental values and Yukawa calculations are also added for comparison. The CC and Yukawa models predict stronger stability as compared to the CP solution, and such behavior is expected from the corresponding interaction potentials. Most interestingly, the CP curve matches very nicely with experimental measurements. This result suggests that silica surfaces regulate strongly and become progressively neutralized upon approach. The adjustment of the charge upon approach is regulated by adsorption/desorption equilibria, which involves AOT surfactant in a peculiar way that seems to maintain a roughly constant surface potential. Recent electrophoretic mobility measurements have also shown strong charge regulation upon increasing the particle concentration for polymeric colloids in AOT/dodecane suspensions56 and in pure isopropanol.63 It seems that for both the colloidal stability and charging of particles at elevated concentrations charge regulation is driven by similar adsorption/desorption mechanisms.
Let us finally discuss why the DLVO theory is quite appropriate for describing the stability of particles in the present decane/AOT system. We have used the linear DH approximation for calculating double-layer interactions, with electrokinetic potentials considered as some kind of effective potential. This is a classical and reasonable method per se that allows the mapping of true non-linear electrostatics due to high surface potentials on a linear theory suited for low potentials. However, we have also used the charge renormalization procedure introduced by Trizac et al.50 to estimate what would be the true surface potential ψs that would lead to the effective, measured, electrokinetic potential ζ*. The maximum difference was never larger than a few percent, showing that in the present case charges were always small enough to permit DH linearization. Further, the concentration of particles in our experiments is low enough to avoid many-body forces27 and the non-monotonic dependence of surface charge at high particle concentrations described by Hallett et al.56 Additionally, our results in Fig. 5a show that the stability does not depend on the value of screening length. Therefore, our stability ratio results do not contradict recent findings of discrepancies between measured and predicted screening lengths in nonpolar media,15 but the aggregation behavior is simply not sensitive to the changes in the screening length.
Although the DLVO predictions for our three systems shown in Fig. 4 are in general good, the remaining discrepancies are probably due to charge regulation effects. Indeed, the surface charge variation upon approach of two particles affects the stability ratios as shown in Fig. 6a with the use of potentials extracted from the exact DH solution. Further inconsistencies between theory and experiment could be connected to the non-uniformity of surface charge. Since the surface charge is at most on the order of 10 charges per particle (Fig. 2), the distance between the charges on the particle surface is large and therefore charged patches exist. Such non-uniformity of charge can lead to additional non-DLVO forces.64,65 At high AOT concentrations the stability of the silica is underestimated by the theory. This discrepancy could be caused by steric effects due to the adsorbed surfactant at high concentrations.66
IV. Conclusions
We have measured the stability of silica and polystyrene latex particles in decane/AOT suspensions. Upon addition of AOT surfactant, particles become charged and the suspensions become stable in the intermediate surfactant concentration range. At higher concentrations of AOT the particles are neutralized and the suspensions aggregate rapidly again. The DLVO theory based on a simple Yukawa potential is able to predict the surfactant concentration range in which the suspension is stabilized and to recover the re-entrant behavior observed experimentally. The aggregation behavior is driven by surface charging through adsorption/desorption processes, while screening of the double-layer does not play an important role in destabilization. On the other hand, charge regulation effects are an important factor affecting the value of the stability ratio. The silica particles in the decane/AOT system follow the model predictions calculated by using constant potential boundary conditions. As yet, stability has to be calculated with potentials extracted from the exact DH solution since no simple Yukawa-like model accounting for charge regulation and suited for the κa ≪ 1 case is known. Building such a model would be highly valuable for applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Swiss National Science Foundation through grant 162420 and the University of Geneva. The authors are thankful to Michal Borkovec for providing access to the instruments in his laboratory and to Plinio Maroni for help with AFM measurements. M. F. also acknowledges the support of the Iran Ministry of Science, Research and Technology.References
- B. Comiskey, J. D. Albert, H. Yoshizawa and J. Jacobson, Nature, 1998, 394, 253–255 CrossRef CAS
.
- Y. Chen, J. Au, P. Kazlas, A. Ritenour, H. Gates and M. McCreary, Nature, 2003, 423, 136 CrossRef CAS PubMed
.
- S. A. Jones, G. P. Martin and M. B. Brown, J. Pharm. Sci., 2006, 95, 1060–1074 CrossRef CAS PubMed
.
- M. D. Croucher, K. P. Lok, R. W. Wong, S. Drappel, J. M. Duff, A. L. Pundsack and M. L. Hair, J. Appl. Polym. Sci., 1985, 30, 593–607 CrossRef CAS
.
- I. D. Morrison, Colloids Surf., A, 1993, 71, 1–37 CrossRef CAS
.
- G. N. Smith and J. Eastoe, Phys. Chem. Chem. Phys., 2012, 15, 424–439 RSC
.
- M. F. Hsu, E. R. Dufresne and D. A. Weitz, Langmuir, 2005, 21, 4881–4887 CrossRef CAS PubMed
.
- G. S. Roberts, R. Sanchez, R. Kemp, T. Wood and P. Bartlett, Langmuir, 2008, 24, 6530–6541 CrossRef CAS PubMed
.
- S. K. Sainis, J. W. Merrill and E. R. Dufresne, Langmuir, 2008, 24, 13334–13337 CrossRef CAS PubMed
.
- Q. Guo, V. Singh and S. H. Behrens, Langmuir, 2009, 26, 3203–3207 CrossRef PubMed
.
- S. Poovarodom and J. C. Berg, J. Colloid Interface Sci., 2010, 346, 370–377 CrossRef CAS PubMed
.
- M. Gacek, D. Bergsman, E. Michor and J. C. Berg, Langmuir, 2012, 28, 11633–11638 CrossRef CAS PubMed
.
- J. Lee, Z.-L. Zhou and S. H. Behrens, Langmuir, 2016, 32, 4827–4836 CrossRef CAS PubMed
.
- C. E. Espinosa, Q. Guo, V. Singh and S. H. Behrens, Langmuir, 2010, 26, 16941–16948 CrossRef CAS PubMed
.
- F. Waggett, M. D. Shafiq and P. Bartlett, Colloids Interfaces, 2018, 2, 51 CrossRef CAS
.
- S. D. Finlayson and P. Bartlett, J. Chem. Phys., 2016, 145, 034905 CrossRef PubMed
.
- W. H. Briscoe and R. G. Horn, Langmuir, 2002, 18, 3945–3956 CrossRef CAS
.
- P. G. Smith, M. N. Patel, J. Kim, T. E. Milner and K. P. Johnston, J. Phys. Chem. C, 2006, 111, 840–848 CrossRef
.
- R. Kemp, R. Sanchez, K. J. Mutch and P. Bartlett, Langmuir, 2010, 26, 6967–6976 CrossRef CAS PubMed
.
- C. E. McNamee, Y. Tsujii and M. Matsumoto, Langmuir, 2004, 20, 1791–1798 CrossRef CAS
.
- Q. Guo, J. Lee, V. Singh and S. H. Behrens, J. Colloid Interface Sci., 2013, 392, 83–89 CrossRef CAS PubMed
.
- M. Gacek, G. Brooks and J. C. Berg, Langmuir, 2012, 28, 3032–3036 CrossRef CAS PubMed
.
- G. Hussain, A. Robinson and P. Bartlett, Langmuir, 2013, 29, 4204–4213 CrossRef CAS PubMed
.
- R. Sánchez and P. Bartlett, Soft Matter, 2011, 7, 887–890 RSC
.
- D. C. Prieve, J. D. Hoggard, R. Fu, P. J. Sides and R. Bethea, Langmuir, 2008, 24, 1120–1132 CrossRef CAS PubMed
.
- S. K. Sainis, V. Germain and E. R. Dufresne, Phys. Rev. Lett., 2007, 99, 018303 CrossRef PubMed
.
- J. W. Merrill, S. K. Sainis and E. R. Dufresne, Phys. Rev. Lett., 2009, 103, 138301 CrossRef PubMed
.
- J. W. Merrill, S. K. Sainis, J. Bławzdziewicz and E. R. Dufresne, Soft Matter, 2010, 6, 2187–2192 RSC
.
- D. E. Masri, P. V. Oostrum, F. Smallenburg, T. Vissers, A. Imhof, M. Dijkstra and A. V. Blaaderen, Soft Matter, 2011, 7, 3462–3466 RSC
.
- G. N. Smith, S. D. Finlayson, S. E. Rogers, P. Bartlett and J. Eastoe, J. Phys. Chem. Lett., 2017, 8, 4668–4672 CrossRef CAS PubMed
.
- P. Sinha, I. Szilagyi, F. J. Montes Ruiz-Cabello, P. Maroni and M. Borkovec, J. Phys. Chem. Lett., 2013, 4, 648–652 CrossRef CAS PubMed
.
- F. J. Montes Ruiz-Cabello, G. Trefalt, Z. Csendes, P. Sinha, T. Oncsik, I. Szilagyi, P. Maroni and M. Borkovec, J. Phys. Chem. B, 2013, 117, 11853–11862 CrossRef PubMed
.
- F. J. Montes Ruiz-Cabello, G. Trefalt, T. Oncsik, I. Szilagyi, P. Maroni and M. Borkovec, J. Phys. Chem. B, 2015, 119, 8184–8193 CrossRef CAS PubMed
.
- T. Cao, T. Sugimoto, I. Szilagyi, G. Trefalt and M. Borkovec, Phys. Chem. Chem. Phys., 2017, 19, 15160–15171 RSC
.
- T. Cao, G. Trefalt and M. Borkovec, Langmuir, 2018, 34, 14368–14377 CrossRef CAS PubMed
.
- P. Rouster, M. Pavlovic and I. Szilagyi, J. Phys. Chem. C, 2017, 121, 6749–6758 CrossRef CAS PubMed
.
- P. Rouster, M. Pavlovic, T. Cao, B. Katana and I. Szilagyi, J. Phys. Chem. C, 2019, 123, 12966–12974 CAS
.
- H. Holthoff, S. U. Egelhaaf, M. Borkovec, P. Schurtenberger and H. Sticher, Langmuir, 1996, 12, 5541–5549 CrossRef CAS
.
- P. Galletto, W. Lin, M. I. Mishchenko and M. Borkovec, J. Chem. Phys., 2005, 292, 139–147 Search PubMed
.
- M. Kotlarchyk, J. S. Huang and S. H. Chen, J. Phys. Chem., 1985, 89, 4382–4386 CrossRef CAS
.
- T. K. De and A. Maitra, Adv. Colloid Interface Sci., 1995, 59, 95–193 CrossRef CAS
.
- H. F. Eicke, M. Borkovec and B. Das-Gupta, J. Phys. Chem., 1989, 93, 314–317 CrossRef CAS
.
- R. I. Keir, Suparno and J. C. Thomas, Langmuir, 2002, 18, 1463–1465 CrossRef CAS
.
- T. Oncsik, A. Desert, G. Trefalt, M. Borkovec and I. Szilagyi, Phys. Chem. Chem. Phys., 2016, 18, 7511–7520 RSC
.
- T. Sugimoto, T. Cao, I. Szilagyi, M. Borkovec and G. Trefalt, J. Colloid Interface Sci., 2018, 524, 456–464 CrossRef CAS PubMed
.
-
M. Elimelech, J. Gregory and X. Jia, Particle Deposition and Aggregation: Measurement, Modelling and Simulation, Butterworth-Heinemann, 2013 Search PubMed
.
-
J. Israelachvili, Intermolecular and Surface Forces, Academic Press, London, 3rd edn, 2011 Search PubMed
.
- B. Uzelac, V. Valmacco and G. Trefalt, Soft Matter, 2017, 13, 5741–5748 RSC
.
- S. K. Sainis, V. Germain, C. O. Mejean and E. R. Dufresne, Langmuir, 2007, 24, 1160–1164 CrossRef PubMed
.
- E. Trizac, L. Bocquet, M. Aubouy and H. H. von Grünberg, Langmuir, 2003, 19, 4027–4033 CrossRef CAS
.
- M. Kobayashi, M. Skarba, P. Galletto, D. Cakara and M. Borkovec, J. Colloid Interface Sci., 2005, 292, 139–147 CrossRef CAS PubMed
.
-
W. B. Russel, D. A. Saville and W. R. Schowalter, Colloidal Dispersions, Cambridge University Press, Cambridge, 1989 Search PubMed
.
- E. P. Honig, G. J. Roebersen and P. H. Wiersema, J. Colloid Interface Sci., 1971, 36, 97–102 CrossRef CAS
.
- M. Moazzami-Gudarzi, G. Trefalt, I. Szilagyi, P. Maroni and M. Borkovec, Phys. Chem. Chem. Phys., 2016, 18, 8739–8751 RSC
.
- M. Elzbieciak-Wodka, M. Popescu, F. J. Montes Ruiz-Cabello, G. Trefalt, P. Maroni and M. Borkovec, J. Chem. Phys., 2014, 140, 104906 CrossRef PubMed
.
- J. E. Hallett, D. A. J. Gillespie, R. M. Richardson and P. Bartlett, Soft Matter, 2018, 14, 331–343 RSC
.
- G. Trefalt, S. H. Behrens and M. Borkovec, Langmuir, 2016, 32, 380–400 CrossRef CAS PubMed
.
- N. Adžić and R. Podgornik, Eur. Phys. J. E: Soft Matter Biol. Phys., 2014, 37, 49 CrossRef PubMed
.
- R. Podgornik, J. Chem. Phys., 2018, 149, 104701 CrossRef PubMed
.
- Y. Avni, D. Andelman and R. Podgornik, Curr. Opin. Electrochem., 2019, 13, 70–77 CrossRef CAS
.
- S. L. Carnie and D. Y. C. Chan, J. Colloid Interface Sci., 1993, 161, 260–264 CrossRef CAS
.
- A. B. Glendinning and W. B. Russel, J. Colloid Interface Sci., 1983, 93, 95–104 CrossRef CAS
.
- L. Teulon, Y. Hallez, S. Raffy, F. Guerin, E. Palleau and L. Ressier, J. Phys. Chem. C, 2019, 123, 783–790 CrossRef CAS
.
- R. M. Adar, D. Andelman and H. Diamant, Adv. Colloid Interface Sci., 2017, 247, 198–207 CrossRef CAS PubMed
.
- N. Adži and R. Podgornik, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2015, 91, 022715 CrossRef PubMed
.
- I. Szilagyi, G. Trefalt, A. Tiraferri, P. Maroni and M. Borkovec, Soft Matter, 2014, 10, 2479–2502 RSC
.
| This journal is © the Owner Societies 2019 |