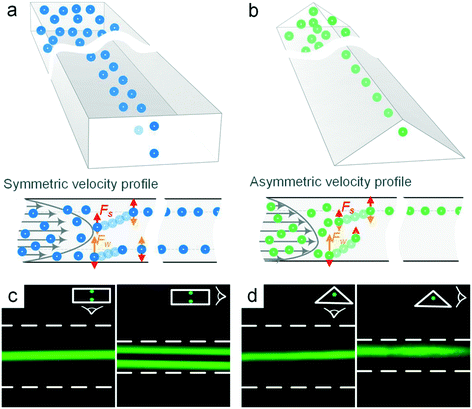
Single stream inertial focusing in low aspect-ratio triangular microchannels
Prithviraj
Mukherjee
a,
Xiao
Wang
b,
Jian
Zhou
 a and
Ian
Papautsky
a and
Ian
Papautsky
 *ac
*ac
aDepartment of Bioengineering, University of Illinois at Chicago, 851 S. Morgan Street, 218 SEO, Chicago, IL 60607, USA. E-mail: papauts@uic.edu; Tel: +1 312 413 3800
bBioMEMS Resource Center, Department of Surgery, Massachusetts General Hospital, Boston, MA 02115, USA
cUniversity of Illinois Cancer Center, Chicago, IL 60612, USA
First published on 29th November 2018
Abstract
A wide range of microfluidic devices for single stream focusing of cells and particles has emerged in recent years, based on both passive and active methods. Inertial microfluidics offers an attractive alternative to these methods, providing efficient and sheathless passive focusing of cells and beads. Nevertheless, in rectangular microchannels, the presence of multiple equilibrium positions necessitates complicated solutions involving manipulation of the 3D structure in order to achieve single stream flows. Here, we present a new approach to single-stream inertial focusing based on a triangular microchannel geometry. Changing the channel cross-sectional shape leads to asymmetry in the velocity profile, resulting in a size-dependent single stable equilibrium position near the channel apex. We demonstrate that soft lithography masters for such microchannels can be fabricated using PMMA through micromilling, and 15 μm diameter beads can be efficiently focused into a single stream. Confocal microscopy was used to confirm the focusing positions in the microchannel cross-section. We further integrated this device with a laser counting system to form a sheathless flow cytometer and demonstrated the counting of beads with an ∼326 s −1 throughput. The use of a triangular cross-section offers a number of benefits, including simplicity of the fundamental principle and geometry, control of design, a small footprint, and ease of integration, as well as high-precision single position focusing.
Introduction
Flow cytometry is a powerful lab automation technique for sorting and counting cells in biomedical research and theranostics.1 In a flow cytometer, fluorescently labeled cells are first focused into a narrow stream in the fluid and then sequentially studied using a laser beam, with the fluorescent and scattered light from each cell collected for counting or analysis. One of the critical components is a flow cell, which focuses cells into a tightly ordered stream to ensure that they pass the laser beam one at a time at the same focal position. In a conventional flow cytometer, such focusing is achieved using sheath flow to pinch cells in the sample flow into a single stream. In today's commercial flow cytometer systems, a flow cell is expensive to manufacture, costing hundreds to thousands of dollars. Furthermore, bench-top cytometers can be bulky and expensive instruments that require an additional fluid source for the sheath. A number of groups have attempted to miniaturize this useful tool using microfluidics2–10 to make it more compact, or even handheld.3 The key advantage of using microfluidics is the precise manipulation and focusing of cells through various microchannel geometries, which in turn makes it possible to build miniature systems for sorting, counting, single cell analysis, and other bioanalytical applications.9–15Cell focusing in microfluidic flow cells is based on two-dimensional (2D) or three-dimensional (3D) hydrodynamic confinement,16 typically accomplished using sheath flows.17,18,26 The first microfluidic demonstration was by McClain et al. who injected fluorescently-labeled E. coli into a channel flanked by two symmetric sheath flows from each side for 2D focusing.19 This configuration became a standard design for many subsequent studies in micro-flow cytometry.20,21 Generally, in 2D focusing, confinement may be vertical or horizontal, where cells or particles may still span the height or the width of the microchannel, respectively, which may lead to inaccurate counting of cell samples.22,23 These drawbacks are generally addressed in 3D focusing, where cells or particles are no longer stacked along a band, but rather are focused in a single position, in both the vertical and horizontal axes.
Microfluidic 3D focusing is accomplished using both active and passive systems. Active systems, such as dielectrophoresis24 or acoustic transducers,25 require external force fields, complex control circuitry, power, and often complex microfluidic chip design and usability. Conversely, passive systems rely on channel geometry and do not require any external components (other than a syringe pump). For example, 3D focusing can be achieved using multiple sheath flows and grooves (chevrons), which isolate the top and bottom flows.27 But these systems require complex fabrication with multiple alignment steps and as well as additional geometrical considerations for sheath flow inputs.
Attractive alternatives are passive, sheathless, 3D focusing systems, where single stream focusing is achieved at well-defined points of lateral equilibrium of the internally-induced inertial forces. There are two significant effects of inertial forces on the flow in a microchannel, inertial migration due to lift forces as shown by us29 and Di Carlo et al.,2,22 and geometry induced secondary flows in curved or spiral microchannels, as shown by Martel et al.,15 Oakey et al.30 and our group.32 These approaches simplify the flow cell as they rely only on hydrodynamic forces and cell focusing in serpentine microchannels, offering a significant improvement over the sheath flow systems with throughputs of 49![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles per s at Rep = 6, with a concentration of 2 × 106 particles per mL. Di Carlo et al.6 demonstrated sheathless single stream inertial focusing with 99% focusing efficiency, utilizing “local helical secondary flows”, arising from steps in the channel height, with significantly high throughputs as high as 36
000 particles per s at Rep = 6, with a concentration of 2 × 106 particles per mL. Di Carlo et al.6 demonstrated sheathless single stream inertial focusing with 99% focusing efficiency, utilizing “local helical secondary flows”, arising from steps in the channel height, with significantly high throughputs as high as 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles per s for a variety of different sized particles. However, this approach relies on multi-step photolithography, which significantly complicates fabrication. Wang et al.45 demonstrated sheathless, single position focusing of particles and cells in a straight channel, with a rectangular cross-section, about 3.5 cm in length, with the use of inertial forces only, with 95–100% efficiency, and a count rate of 2200 s−1. Others showed single stream focusing using viscoelastic flows in rectangular and circular channels.28 However, the throughput in these channels is significantly lower due to higher fluid viscosity which necessitates lower flow rates. Recently, Kim et al.33,34 reported single stream inertial focusing with 99% efficiency by combining channels with rectangular, triangular and semi-circular cross-sections. While successful, all these systems either use long microchannels, which increase the pressure drop and shear stress on cells, or a large on-chip real estate which makes system integration challenging.
000 particles per s for a variety of different sized particles. However, this approach relies on multi-step photolithography, which significantly complicates fabrication. Wang et al.45 demonstrated sheathless, single position focusing of particles and cells in a straight channel, with a rectangular cross-section, about 3.5 cm in length, with the use of inertial forces only, with 95–100% efficiency, and a count rate of 2200 s−1. Others showed single stream focusing using viscoelastic flows in rectangular and circular channels.28 However, the throughput in these channels is significantly lower due to higher fluid viscosity which necessitates lower flow rates. Recently, Kim et al.33,34 reported single stream inertial focusing with 99% efficiency by combining channels with rectangular, triangular and semi-circular cross-sections. While successful, all these systems either use long microchannels, which increase the pressure drop and shear stress on cells, or a large on-chip real estate which makes system integration challenging.
In this work, we introduce an approach that has the potential to overcome challenges associated with single stream focusing in microchannels. The design is based on manipulation of the inertial forces within a microchannel by altering the cross-sectional geometry to achieve single stream focusing in a shorter downstream length. Our system uses a single straight channel with a triangular cross-section with a tip angle of 120°, and offers focusing in less than 3 cm at a flow rate of 100 μL min−1. Confocal microscopy was used to confirm the particle focusing positions in the cross-section of the channel. Ultimately, we show that it is possible to focus particles at a single position using these low aspect ratio channels with triangular cross-sections, at relatively low flow rates (Re = 29–44) and thus a low fluidic shear. Using polymer beads as surrogates for cells, we demonstrate that counting can be performed with these channels by integrating a simple laser counting system. Since the flow cell is simply a straight microfluidic channel, it can be easily integrated with automated particle or cell preparation and counting or in high-throughput parallel systems already reported in the literature.
Results and discussion
Channels with a triangular cross-section
Before discussing triangular channels, we first briefly review inertial focusing in low-aspect-ratio rectangular microchannels. In general, inertial focusing of cells and particles occurs when the particle/cell Reynolds number Rep > 1, which is given as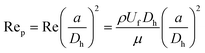 | (1) |
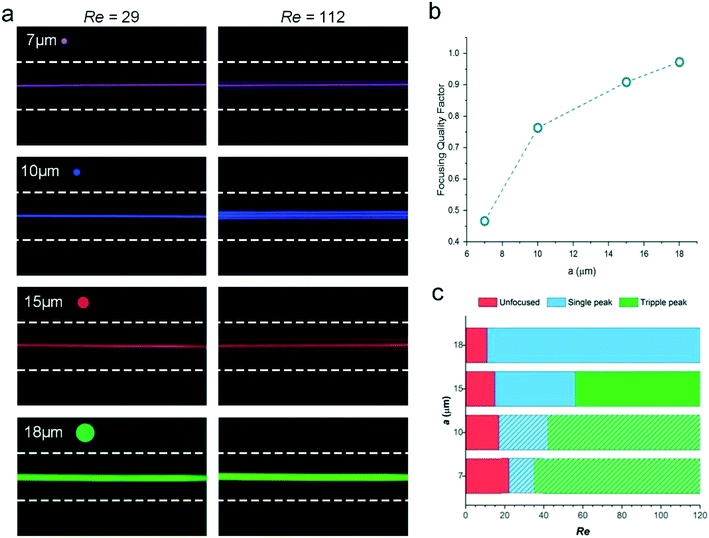
While three focusing positions are expected, the inertial equilibria are counterintuitive in the low aspect ratio triangular channels. Since square microchannels exhibit equilibrium positions centered at its four walls upon completion of both migration stages, one might expect a similar behavior in triangular channels and thus three equilibrium positions near the center of each wall. This indeed has been reported in recent work by Kim et al.33 However, in our low aspect-ratio (AR) triangular microchannel a single focusing position emerges as evidenced by the bottom- and side-view images (Fig. 1b and d).
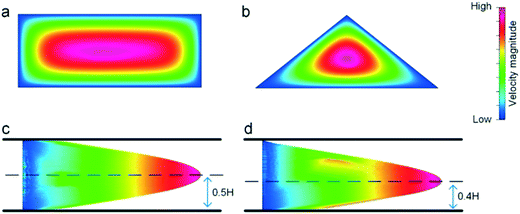
In a low AR rectangular microchannel, the point of maximum velocity is at half of the channel height, H□= H/2, as illustrated by the numerical model in Fig. 2a. In contrast, the point of maximum velocity shifts to approximately 40% of the channel height (HΔ= 2H/5) in our low-AR triangular microchannel (Fig. 2b and d). This shift is about 16 μm, which is comparable to the size of the suspended particles (15.5 μm). In such a circumstance, the particles at the lower portion of the channel cross-section (below the point of maximum velocity) are already so close to the bottom wall, even without the stage I migration observed in rectangular microchannels and that the wall-induced lift force increases considerably as Fw inversely scales with the distance between the particles and the wall.29 This augmented wall force subsequently displaces the particles upward, causing them to cross the point of maximum velocity toward the apex of the triangular cross-section. As a result, the focusing position at the bottom wall is eliminated. This peculiar migration dynamics also suggests that the particle size serves as a determining factor of focusing positions in triangular microchannels (e.g., particles smaller than 15 μm still occupy the bottom focusing position), which will be demonstrated and discussed later in this work.
In the upper portion of the channel cross-section above the point of maximum velocity, the balance of forces is similar to that of a rectangular microchannel and particles first undergo stage I migration toward the channel sidewalls. Previous work by Kim et al.33 has shown that particles in an equilateral triangular microchannel (AR = 1) follow a two-stage migration and are focused into three positions centered at each wall. As the AR decreases (tip angle increases), the two positions near the sidewalls move toward the channel apex due to the disruption of the cross-sectional symmetry. Similar focusing behavior was reported in a follow-up study by Kim et al.34 using a system that combines rectangular and triangular cross-section channels, where a single position near the apex emerged for large particles.
In this work, we observed the merging of the two side-positions into a single focusing position near the apex in our simple triangular channel with a tip angle of ∼120°. This position is stable as all the forces can be balanced, leading to a zero net-force on the particles. The shear-induced lift force Fs acts down the velocity gradient and pushes the particles into the channel apex, where the Fs is balanced by the vertical component of the two wall-induced lift forces (Fw) arising from both angled sidewalls. The horizontal components of the two forces are in opposite directions due to symmetry, and thus balance each other.
Fabrication of channels with a triangular cross-section
Multiple methods were considered for the fabrication of the triangular channels in this work, since microfluidic systems are generally fabricated using lithography-based techniques that yield channels with rectangular cross-sections. Anisotropic wet etching of silicon is one such approach, but is generally limited to few cross-sectional geometries due to crystallography, although Kim et al.33 has fabricated triangular channels with 70.6° and 90° tip angles for investigation of particle focusing. Recently, the same group34 reported a scribing method with a diamond tipped tool for fabricating triangular channel masters. This method is straightforward as only a single step is required and greatly simplifies the channel fabrication compared to their original approach. Nevertheless, scribing creates a negative master mold and double-casting is required to fabricate a sealed microchannel. Secondly, this approach makes it challenging to integrate these triangular channels with other channels or structures.CO2 laser ablation is another method capable of generating triangular cross-sections.35–37,42 Even though this technique can generate triangular geometry, it is effective for creating high aspect ratio negative masters, which requires double casting and significantly adds to fabrication complexity and suffers from melting and re-deposition issues with PMMA substrates, which is undesirable for our application.40 Liu et al.38 used a 10 kHz repetition rate, Yb:CaF2 chirped pulse amplification system, which produces 200 fs pulses to fabricate triangular channels of varying width and height, but it mostly produced high aspect ratio channels.
3D printing is an attractive alternative, with a potential to fabricate a wide range of cross-sectional shapes. However, while today's mainstream commercial printers offer a minimum layer height as small as 10 μm (e.g., 3D Pro2 Plus from Raise3D, XCEL or XEED from Leapfrog), their lateral resolution is limited to the laser spot size (generally > 100 μm) and are not suitable for small channels. Further, fabricating slanted geometries may lead to stepped sidewalls due to layered deposition, which would be detrimental to the focusing behavior in the microchannels. Custom 3D printing solutions39–41 exist, such as multi-photon 3D printers, but require extensive instrument development and can be costly. Photonic Professional GT from Nanoscribe GmbH offers sub-micron resolution for 3D printing but is much more expensive compared to other fabrication methods and requires substantial printing times for larger scale devices.
Micromilling was ultimately selected for the fabrication of triangular channels considering cost and design flexibility in obtaining different tip angles. Micromilling is a fast prototyping technique, as the design can be made using a CNC software and the fabrication is fully automated using a computer generated G-code. Low-cost tabletop milling machines are available with reasonable precision (e.g., Minitech Mini-Mill 3).41 The smallest end mills available in the market are about 25 μm in diameter, making it possible to mill devices with features at that scale or smaller. Moreover, these tools are available in different materials, such high-speed steel, carbide or cobalt, with different coatings such as titanium nitride, titanium carbo-nitride, and diamond,45 making it easy to work on any material stock (e.g., aluminum, acrylic) with high precision and ease.
A number of milling approaches were attempted to form triangular channels on the PMMA stock. Using a tapered end mill to form a negative master did not yield good results due to an apex width of at least 10 μm arising from the radius of curvature at the tip of the mill, and the limited options with respect to the side taper angles (0.5° to 15°) and thus the resulting triangle apex angle. Also, lidding of the PMMA channels can be challenging, as thermocompression bonding can lead to distortion of channel features, while solvent bonding can lead to channel flooding that also results in the loss of desired channel features.
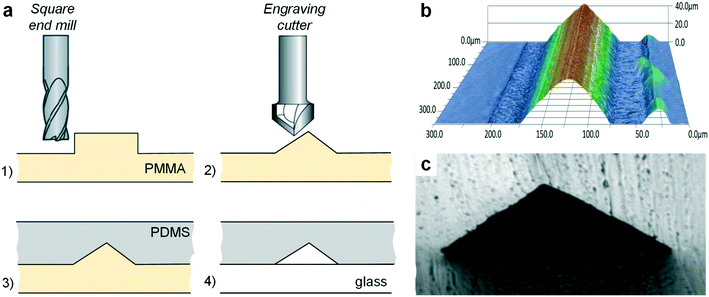
Ultimately, milling with an engraving cutter yielded consistent results and channels with a wider range of options for low aspect ratio triangles. The steps for positive master fabrication on a PMMA substrate using an engraving cutter are shown in Fig. 3a. Similar to the tapered end mill, the cutter width at the tip (arising from tip curvature) was >100 μm, and thus this mill could not be used to generate trenches directly on the PMMA stock. Instead, we first used a standard flat end mill to form a ridge and subsequently removed corners with the engraving cutter. Simply tilting the work stage and using a square end mill did not prove to be effective, primarily due to registration issues, which resulted in either a trapezoidal cross-section or in cross-sectional variations throughout the channel. By using an engraving cutter, a wider variety of side angles could be accessed (from 30° to 120°), while removing corners from a ridge negated any effects of the web thickness. Considering these advantages, we milled a positive PMMA master for PDMS casting.41 The surface finish of the PMMA master was a few hundred nm45 and can be further improved by controlling the spindle speed and the feed rate parameters.
Fig. 3b shows a representative optical profile of the positive PMMA master generated in this work. One of the issues faced in milling with an engraving tool was burring along the sides of the channels, which is visible in the profile scan. But this was solved by adjusting the Z-axis height, spindle speed and feed rate. The tip of the channels fabricated in the positive master was much sharper compared to those fabricated through the negative master. The width and height of the channels were both uniform along the length, with the apex angle measuring ∼115 ± 4°.
PDMS can be cast and cured on a PMMA master to generate replicas. Repeated curing and peeling did not cause any visible damage. At this point in the fabrication process, PDMS replicas can be plasma bonded to either a glass slide to complete channel fabrication, or to a thin PDMS slab for generating devices that can be cut next to the sidewall. The completed device consisted of LAR triangular channels (channel width w > channel height h), with a base width of 100 μm and a height of 40 μm, with a total length of 5 cm.
Optimizing 3D focusing with high efficiency
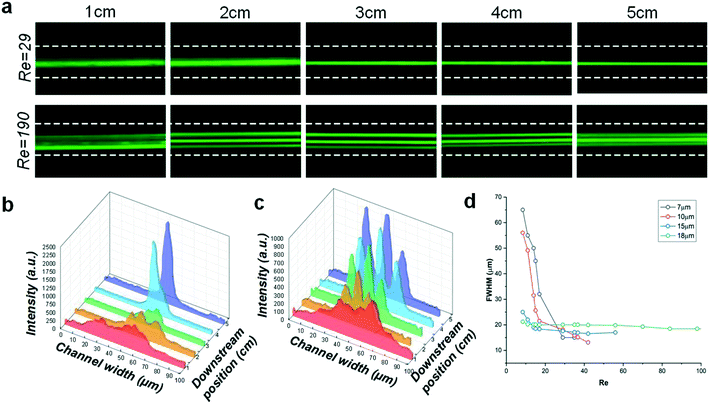
We investigated the inertial focusing of microbeads of different sizes to better understand the feasible size range for the triangular channel. To mimic the size range of cells, we prepared bead suspensions with diameters of 18 μm, 15 μm, 10 μm and 7.32 μm and individually pumped each sample into the channel at flow rates ranging from Q = 30 μL min−1 (Re ∼8.4) to Q = 650 μL min−1 (Re = 190). We used concentrations of about 2 × 105 particles per mL, since our earlier work28,32,45 showed that bead or cell samples with concentrations of ≤106 particles per mL yielded the highest focusing efficiency and better quality (tighter) fluorescent streams. Fluorescence images were taken at 1 cm intervals.Our results reveal that at lower flow rates (Re < 29), the 15 μm diameter particles did not achieve 3D focusing throughout the 5 cm downstream length of the microchannel, as the inertial lift forces were not sufficiently high. At Re = 29, the 15 μm diameter particles randomly distributed at the inlet begin to migrate toward the top of the channel under the influence of FS and FW, as discussed previously. At 1 cm downstream, the beads appear to be focused, and complete focusing is achieved at approx. 4 cm downstream (Fig. 4a). As the flowrate increases to Re > 100, two additional equilibrium positions emerge near the side walls and evolve into three bands along the sidewalls of the channel. At Re = 190, the formation of three distinct particle streams is clearly visible (Fig. 4a). It was not possible to achieve higher flow rates (Re > 190) as channels began to deform and bonding at the inlet came apart due to the increase in pressure. By fabricating channels in thermoplastic or OSTE,43 this problem can be potentially addressed, in order to investigate higher Re flows in the future.
The line scans of the fluorescence intensity peaks at 1 mm downstream positions show the evolution of a single stream at Re = 29 (Fig. 4b) to three streams at Re = 190 (Fig. 4c). The full width at half maximum (FWHM) of the fluorescence intensity peaks obtained from fluorescent streak velocimetry (FSV) images decreases from ∼60 μm at 1 cm downstream until either a single peak of ∼15 μm wide emerges at Re = 29 or three distinct peaks emerge at Re = 190. Examining the focusing behavior of four different particle sizes at 5 cm downstream as a function of flowrate (Fig. 4d) indicates that high quality, tight focusing for 15 μm particles is achieved in our design, for Re > 29 where the peak FWHM saturates at approx. 15 μm. Similar behavior is observed for the 18 μm diameter beads, which also saturate at Re > 20 with a FWHM of approx. 20 μm. The smaller 7.32 and 10 μm diameter beads, while able to focus in the channel, never achieved full single stream focusing. At Re > 45, the 7.32 μm particles form an ∼16 μm wide stream, while the lowest FWHM achieved by the 10 μm beads is ∼14 μm at Re = 42. Smaller channel dimensions are necessary to further compress the velocity profile for focusing smaller particles.
Fluorescence images taken at 5 cm downstream (Fig. 5a) show that all particle sizes are capable of forming a single, focused streak at low flowrates. However, at high flow rates, all but the 18 μm diameter particles transitioned into three streams. To evaluate the focusing quality,44 we measured the FWHM of the fluorescence intensity peaks and defined the Focusing Quality Factor (FQF) as the ratio of the particle diameter and FWHM (a/FWHM).38 Thus, the FQF is close to unity in full focusing, and approaches zero if there is no focusing. As Fig. 5b illustrates, FQFs for the 15 μm and 18 μm diameter beads are both >0.9, indicating high focusing quality. For the 10 μm diameter beads, the ratio decreases to ∼0.75, suggesting poor confinement while still maintaining a single stream. It further decreases to ∼0.47 for the 7.32 μm diameter beads, indicating incomplete poor-quality focusing of a single stream or the manifestation of two parallel, closely-spaced streams. The latter phenomenon was indeed observed by Lee et al. in their recent work.34 This is because the inertial lift forces decrease with the size of the particle, leading to a much slower inertial migration towards the equilibrium positions. Further improvement of the focusing quality may be achieved using a microchannel with a smaller cross-section.
Fig. 5c illustrates the gradual transition from a random distribution to a single stream, and finally to triple stream positions. Although all four particles appear to be focused in a single-stream in Fig. 5a, the smaller particles (10 μm and 7.32 μm) did not achieve single-position focusing near the apex. Rather, these particles were focused in two positions, centered on the bottom wall and the apex of the channel. Two streams of these smaller particles were observed in the side view images, while only a single stream was captured in the bottom view images. Similarly, these particles do not necessarily achieve three position focusing despite evolving into three fluorescent streams observed at higher flowrates. Since the bottom focusing position cannot be eliminated, it is possible that these particles focus in four positions and further studies are needed to be conclusive. As discussed previously, the point of maximum velocity shifts closer to the bottom wall (16 μm instead of 20 μm), leading to size-dependent focusing positions in our low AR triangular microchannel. While particles larger than 16 μm will naturally migrate toward the apex as the bottom focusing position is excluded by their size, smaller particles will continue to occupy that position. To facilitate the single position 3D focusing for smaller particles, a further decrease in the AR is required to shift the Pmaxv downward.
Particle focusing along the cross-section
Confocal microscopy was used to investigate the cross-sectional location of the focused particle streams. Streak velocimetry aggregates the fluorescence signal from flowing particles and is an excellent tool for visualization of lateral focusing positions but does not provide information on the vertical positioning. Fig. 6a shows the position of the fluorescent particles in the channel cross-section 5 cm downstream at Re = 29. No fluorescence was observed at the bottom half of the channel, which suggests that the particles are focused near the apex. This can be attributed to the compression of the velocity profile as suggested by the numerical model. As discussed previously, the compression of the velocity profile in our low-aspect ratio system, results in asymmetric values of the negative lift co-efficient (CL−) across the channel axis. Near the bottom channel wall, CL− > 0 always, which eliminates the equilibrium position and causes the particles to focus near the apex. Increasing the flow to Re > 190, two additional focusing positions emerge near the channel sidewalls, as indicated in Fig. 6b. This behavior seems to be analogous to the rectangular microchannels, where a higher number of equilibrium positions emerge at higher flow velocities. Indeed, this also correlated with our streak velocimetry results in Fig. 4.The confocal imaging results were further confirmed by performing the experiments in side-view profiled channels as shown in Fig. 6c and d. The focusing positions of the particle along the sidewalls do not further separate as there is a competition for space near the base. We used 15 μm particles, so the particle can only focus up to a region where the cumulative height is greater than 15 μm. With the effect of the wall forces, the particle will also be pushed away from the walls, which confines the three positions into a tight profile, along the perimeter of the channel cross-section.
Sheathless flow cytometry
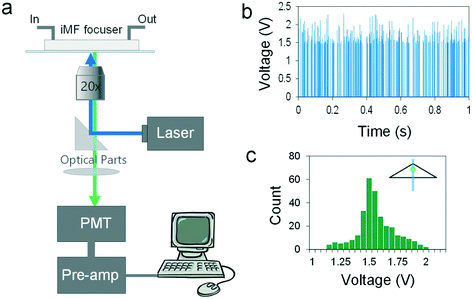
The triangular cross-section microchannel can be integrated with a laser counting system for high-throughput counting of fluorescently labeled microbeads or cells. As Fig. 7a shows, a laser with a spot size of ∼20 μm was aimed at the apex of the channel near the outlet at about 5 cm downstream. As each fluorescently labeled bead or cell traverses the laser spot, light is emitted and is collected by a photomultiplier tube (PMT), amplified and converted into a voltage signal, and recorded with a LabView data acquisition system. Fig. 7b demonstrates the counting of FITC-labeled 15 μm diameter polystyrene particles. At Re = 29, focusing of the 15 μm particles is optimized for a single stream and yields 326 voltage peaks during the 1 s time window at 2 × 105 particles per mL. This throughput of 326 particles per s is not especially high, considering we previously demonstrated throughputs of 1370 particles per s.35 Nevertheless, considering that no sheath flows were involved and the channel is rather short and occupies little real estate (in comparison with our spiral chips32–34), these results are quite promising and serve as a proof-of-concept. While 105 particles per mL is a typical concentration used with cells; increasing the concentration 10-fold to 106 particles per mL would increase the throughput accordingly (as we have demonstrated in the past49). The lower throughput is also due to the system inlet design, which abruptly transitioned from a rectangular input port to a triangular microchannel cross-section, resulting in some particle trapping and aggregation. This can be observed in Fig. 7b as rather broad gaps between some signal peaks. Improved design of the inlet system, by creating a draft angle similar to the channel angle, prior to the channel entry, may lead to easier passage of particles, increasing the throughput and accuracy.The histogram of the voltage signal shows a Gaussian-like distribution with a coefficient of variation (CV) of ∼18% (Fig. 7c), indicating the high precision of the 3D focusing in the channel. This is comparable to a rectangular LAR channel. However, our recent work with a helical capillary arranged in a spiral35 shows that a CV of ∼12% is possible, with the improvement due to, in a large part, the elimination of scattering of the excitation light in the sidewall interface. Herein, however, while the bottom of the microchannel was glass and yielded minimal scattering, the angled sidewalls of the triangular channel reflected light, yielding greater variability in the signal.
Conclusions
In summary, we described a simple approach to sheathless 3D focusing of particles in a straight channel. In our system, single-position focusing is achieved using a unique velocity profile in a low-aspect ratio triangular channel. The channel consisted of a uniform cross-section, devoid of the complexities of multiple cross-sections used by other groups. This also permitted simple fabrication via micromilling and PDMS casting, sparing the need for complex fabrication steps described in previous works, such as wet etching of Si, CO2 laser ablation, or double casting of PDMS, thereby reducing cost and time. Though the cytometry throughput is ∼326 s−1, and is lower than our previous work,35 it can be improved with further optimization. Ultimately, we believe this work is significant as it reveals that focusing positions merge into a single point near the apex, which was unexpected, and improves our understanding of how inertial migration evolves in channels with asymmetric velocity profiles.A limitation of this work is that we did not demonstrate focusing of a heterogeneous particle sample. However, our goal was to highlight the focusing positions that emerge due to the unique velocity profile in a low aspect ratio triangular microchannel and to demonstrate a potential application in flow cytometry. In future studies, we plan to explore a wider range of Reynolds numbers and experiment with a range of particle sizes to improve our understanding of the physics of inertial focusing in these triangular channels and thus control of the focusing positions. Given the rapid developments in 3D printing, we expected that channels with triangular cross-sections could be soon fabricated in this manner. Then, considering the simple nature of the device and its powerful 3D focusing performance, we expect this device concept to create new opportunities for inertial focusing in laboratory research.
Materials and methods
Device fabrication
The triangular channels used in the experiments were 5 cm in length, 100 μm in width and 40 μm in height. A positive master with triangular ridges was milled on a PMMA stock (63.5 × 63.5 × 5 mm) using a high precision micro-milling machine (Microlution 5100, Microlution Inc., IL, USA). The positive PMMA master was fabricated in four steps. A 6.35 mm flat end STD mill (Motion Industries, OH, USA) was first used to face mill the PMMA to get a new working height (Z = 0) for the mill. Rectangular ridges were then made using a 1.35 mm STD flat end mill. An engraving tool (Motion Industries, OH, USA) with a tip angle of 120° (Shank Diameter – 1/8′′, OAL – 1–1/2′′, Split Length – 3′8′′) was then used to make the triangular ridges on the PMMA. Trenches were milled 100 μm apart and 40 μm deep. A 1.35 mm STD flat end mill was used to clear the excess PMMA around the triangular ridges up to the base of the channels. Mastercam-X8 (CNC Software, Inc., CT, USA) was used to first simulate the milling process and generate the G-code which was uploaded into the mill. A schematic of the fabrication process is shown in Fig. 2a.Microchannels were then formed using the standard soft lithography process. Polydimethylsiloxane (PDMS, Dow Corning) was mixed with a curing agent in the ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (w/w), degassed, poured over the positive PMMA master and cured for 2 h at 80 ° C. For the top-view channels, the PDMS replicas were then peeled and bonded to 1′′ × 3′′ glass slides using O2 plasma (O2 flow low rate ∼15 cc min−1) for 20 s. Inlet and outlet ports were punched in the PDMS replicas with a 1/16′′ flat head needle prior to bonding. These bonded chips were then left on a hot plate for 90 min at 80 ° C to improve bonding strength. Side-view profile channels were fabricated in the same way as above, but rather than using glass, the PDMS replicas were bonded to another PDMS substrate.31 The bonded device was then cut laterally to have a uniform base, flipped and fixed sideways to a petri dish by pouring and curing PDMS around it for stability during imaging and to match the refractive index.
1 (w/w), degassed, poured over the positive PMMA master and cured for 2 h at 80 ° C. For the top-view channels, the PDMS replicas were then peeled and bonded to 1′′ × 3′′ glass slides using O2 plasma (O2 flow low rate ∼15 cc min−1) for 20 s. Inlet and outlet ports were punched in the PDMS replicas with a 1/16′′ flat head needle prior to bonding. These bonded chips were then left on a hot plate for 90 min at 80 ° C to improve bonding strength. Side-view profile channels were fabricated in the same way as above, but rather than using glass, the PDMS replicas were bonded to another PDMS substrate.31 The bonded device was then cut laterally to have a uniform base, flipped and fixed sideways to a petri dish by pouring and curing PDMS around it for stability during imaging and to match the refractive index.
Sample preparation, operation and imaging
Flow experiments were performed using FITC labeled 7.32, 10, 15 and 18 μm diameter polystyrene beads (Bangs Lab Inc., IN, USA). Microbead suspensions with a concentration of 1 × 105 particles per mL were prepared in deionized water, with 0.01% v/v Tween20 added as the surfactant to prevent particle aggregation and channel clogging. A 1/16′′ peek tubing and fittings (IDEX) were connected to a 5 mL luer lock syringe. The particle solution was flowed into the device through the syringe using a syringe pump (KD Scientific, MA, USA). Flow rates were varied from 5–650 μL min−1 and images were taken using an inverted microscope (Olympus IX-71) fitted with a 12-bit CCD camera (Retiga EXi, QImaging). Fluorescence images were obtained using a FITC filter. At least 30 images were taken, every 1 cm, at an exposure of 200 ms and stacked using ImageJ®. Intensity line scans were taken and the FWHMs were calculated using Excel.Confocal experiments
Cross-sectional images of the particle positions at different flow rates (Re ≈ 29 and Re ≈ 190) were obtained using a Zeiss LSM 710 confocal microscope (Carl Zeiss Meditec, Inc. CA, USA). The total Z-axis range was set with ±25 μm at the top and bottom, to span the microchannel 40 μm height. A 2 × 105 particles per mL solution of the 15 μm particles (Bangs Lab Inc., IN, USA) was used in this case to increase the number of events captured by the camera. A FITC channel (488![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 525 nm) was used as the fluorescence filter. The images were then converted into TIFF using Zen lite software (Carl Zeiss Meditec, Inc. CA, USA) and stacked using ImageJ®.
525 nm) was used as the fluorescence filter. The images were then converted into TIFF using Zen lite software (Carl Zeiss Meditec, Inc. CA, USA) and stacked using ImageJ®.
Particle counting
Particle counting experiments were performed using a custom laser counting system consisting of an inverted microscope (TE2000U, Nikon Inc., Melville, NY, USA) with a 20× objective. A 2 × 105 particles per mL 15 μm particle solution was used in the particle counting experiments. The particles were excited using a 488 nm argon laser (50 mW, CVI Melles Griot, Albuquerque, NM, USA) with a corresponding neutral density filter (Thorlabs, Newton, NJ, USA) for power adjustment. A photomultiplier tube (H6780-20, Hamamatsu, Bridgewater, NJ, USA) was used to collect the emitted light. The signal collected from the PMT was processed with a current-to-voltage preamplifier (SR570, Stanford Research Systems, Sunnyvale, CA, USA) and then further recorded using a custom LabVIEW data acquisition system (NI PCI 6036E National Instruments, Austin, TX, USA).Data analysis
Fluorescent line scans were obtained to measure the intensities along the width of the channel, and later exported to Excel to generate the intensity graphs. Data from the laser counting system was also exported to Excel to measure the count, CV and standard deviation (σ) of the focusing of the particles.Numerical models
Numerical models of the triangular channels were developed using the Multiphysics software CFD-ACE+ (ESI-CFD Inc., Huntsville, AL, USA). A straight triangular microchannel, with dimensions of 100 μm × 40 μm was used to simulate the flow profile in the channels. The FLOW module was used, with the physical properties of water being applied to the fluid in the simulation (density ρ = 1000 kg m−1 and dynamic viscosity μ = 10−3 kg m−1 s −1). The velocity of the x-direction (ms−1) calculated from the flow rate was applied to the initial inlet velocity. The convergence limit was set to 10−6 which results in approximately 300 iterations. The simulation was then visualized using CFD-VIEW.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by the Department of Bioengineering at the University of Illinois at Chicago.References
- J. P. Nolan and L. A. Sklar, Nat. Biotechnol., 1998, 16, 633 CrossRef CAS PubMed
.
- H. Amini, W. Lee and D. Di Carlo, Lab Chip, 2014, 14, 2739–2761 RSC
.
- J. Wang, Z. Fan, Y. Zhao, Y. Song, H. Chu, W. Song, Y. Song, X. Pan, Y. Sun and D. Li, Reports, 2016, 6, 23165 CAS
.
- A. A. S. Bhagat, S. S. Kuntaegowdanahalli and I. Papautsky, Lab Chip, 2008, 8, 1906–1914 RSC
.
- X. Cheng, A. Gupta, C. Chen, R. G. Tompkins, W. Rodriguez and M. Toner, Lab Chip, 2009, 9, 1357–1364 RSC
.
- A. J. Chung, D. R. Gossett and D. Di Carlo, Small, 2013, 9, 685–690 CrossRef CAS PubMed
.
- D. Di Carlo, J. F. Edd, K. J. Humphry, H. A. Stone and M. Toner, Phys. Rev. Lett., 2009, 102, 094503 CrossRef PubMed
.
- P. B. Howell Jr, J. P. Golden, L. R. Hilliard, J. S. Erickson, D. R. Mott and F. S. Ligler, Lab Chip, 2008, 8, 1097–1103 RSC
.
- T. D. Chung and H. C. Kim, Electrophoresis, 2007, 28, 4511–4520 CrossRef CAS PubMed
.
- D. A. Ateya, J. S. Erickson, P. B. Howell Jr, L. R. Hilliard, J. P. Golden and F. S. Ligler, Anal. Bioanal. Chem., 2008, 391, 1485–1498 CrossRef CAS PubMed
.
- G. Goddard, J. C. Martin, S. W. Graves and G. Kaduchak, Cytometry, Part A, 2006, 69, 66–74 CrossRef PubMed
.
- N. Pamme, Lab Chip, 2007, 7, 1644–1659 RSC
.
- J. Godin, C. H. Chen, S. H. Cho, W. Qiao, F. Tsai and Y. H. Lo, J. Biophotonics, 2008, 1, 355–376 CrossRef CAS PubMed
.
- J. Zhou, P. V. Giridhar, S. Kasper and I. Papautsky, Lab Chip, 2013, 13, 1919–1929 RSC
.
- J. M. Martel and M. Toner, Annu. Rev. Biomed. Eng., 2014, 16, 371–396 CrossRef CAS PubMed
.
- S. M. Imaad, N. Lord, G. Kulsharova and G. L. Liu, Lab Chip, 2011, 11, 1448–1456 RSC
.
- A. A. Bhagat, S. S. Kuntaegowdanahalli, N. Kaval, C. J. Seliskar and I. Papautsky, Biomed. Microdevices, 2010, 12, 187–195 CrossRef PubMed
.
- A. Wolff, I. Perch-Nielsen, U. D. Larsen, P. Friis, G. Goranovic, C. R. Poulsen, J. P. Kutter and P. Telleman, Lab Chip, 2003, 3, 22–27 RSC
.
- M. A. McClain, C. T. Culbertson, S. C. Jacobson and J. M. Ramsey, Anal. Chem., 2001, 73, 5334–5338 CrossRef CAS PubMed
.
- X. Xuan and D. Li, Electrophoresis, 2005, 26, 3552–3560 CrossRef CAS PubMed
.
- G.-B. Lee, C.-C. Chang, S.-B. Huang and R.-J. Yang, J. Micromech. Microeng., 2006, 16, 1024 CrossRef
.
- D. Di Carlo, D. Irimia, R. G. Tompkins and M. Toner, Proc. Natl. Acad. Sci. U. S. A., 2007, 104, 18892–18897 CrossRef CAS PubMed
.
- C. Grenvall, C. Antfolk, C. Z. Bisgaard and T. Laurell, Lab Chip, 2014, 14, 4629–4637 RSC
.
- H. Chu, I. Doh and Y. H. Cho, Trans. Korean Soc. Mech. Eng. A, 2009, 33(3), 261–264 CrossRef
.
- Y. Chen, A. A. Nawaz, Y. Zhao, P. Huang, J. P. McCoy, S. J. Levine, L. Wang and T. J. Huang, Lab Chip, 2014, 14, 916–923 RSC
.
- M. G. Lee, S. Choi and J. Park, Lab Chip, 2009, 9, 3155–3160 RSC
.
- Y. Chiu, S. H. Cho, Z. Mei, V. Lien, T. Wu and Y. Lo, Lab Chip, 2013, 13, 1803–1809 RSC
.
- D. Yuan, Q. Zhao, S. Yan, S. Y. Tang, G. Alici, J. Zhang and W. Li, Lab Chip, 2018, 18(4), 551–567 RSC
.
- J. Zhou and I. Papautsky, Lab Chip, 2013, 13, 1121–1132 RSC
.
- J. Oakey, R. W. Applegate, E. Arellano, D. Di Carlo, S. W. Graves and M. Toner, Anal. Chem., 2010, 82, 3862–3867 CrossRef CAS PubMed
.
- N. Nivedita and I. Papautsky, Biomicrofluidics, 2013, 7, 54101 CrossRef PubMed
.
- X. Wang, H. Gao, N. Dindic, N. Kaval and I. Papautsky, Biomicrofluidics, 2017, 11, 014107 CrossRef PubMed
.
- J. Kim, J. Lee, C. Wu, S. Nam, D. Di Carlo and W. Lee, Lab Chip, 2016, 16, 992–1001 RSC
.
- J. A. Kim, J. R. Lee, T. J. Je, E. C. Jeon and W. Lee, Anal. Chem., 2018, 90, 1827–1835 CrossRef CAS PubMed
.
- S. Darvishi, T. Cubaud and J. P. Longtin, Opt. Lasers Eng., 2012, 50, 210–214 CrossRef
.
- S. J. Zhang and Y. C. Shin, Int. J. Adv. Des. Manuf. Technol., 2017, 93, 1079–1094 CrossRef
.
- G. Shao, J. Wu, Z. Cai and W. Wang, Sens. Actuators, A, 2012, 178, 230–236 CrossRef CAS
.
- Y. Liu, A. Hansen, E. Block, N. R. Morrow, J. Squier and J. Oakey, J. Colloid Interface Sci., 2017, 507, 234–241 CrossRef CAS PubMed
.
- N. Bhattacharjee, A. Urrios, S. Kang and A. Folch, Lab Chip, 2016, 16, 1720–1742 RSC
.
- H. Gong, B. P. Bickham, A. T. Woolley and G. P. Nordin, Lab Chip, 2017, 17, 2899–2909 RSC
.
- D. J. Guckenberger, T. E. De Groot, A. M. D. Wan, D. J. Beebe and E. W. K. Young, Lab Chip, 2015, 15, 2364–2378 RSC
.
- K. J. Land, M. B. Mbanjwa, K. Govindasamy and J. G. Korvink, Biomicrofluidics, 2011, 5, 036502 CrossRef PubMed
.
- C. F. Carlborg, T. Haraldsson, K. Öberg, M. Malkoch and W. van der Wijngaart, Lab Chip, 2011, 11, 3136 RSC
.
- A. E. Reece and J. Oakeya, Phys. Fluids, 2016, 28(4), 043303 CrossRef PubMed
.
- X. Wang, M. Zandi, C. Ho, N. Kaval and I. Papautsky, Lab Chip, 2015, 15, 1812–1821 RSC
.
| This journal is © The Royal Society of Chemistry 2019 |