Controlling the distance of highly confined droplets in a capillary by interfacial tension for merging on-demand

Abstract

Droplet microfluidics is a powerful technology that finds many applications in chemistry and biomedicine. Among different configurations, droplets confined in a capillary (or plugs) present a number of advantages: they allow positional identification and simplify the integration of complex multi-steps protocols. However, these protocols rely on the control of droplet speed, which is affected by a complex and still debated interplay of various physico-chemical parameters like droplet length, viscosity ratio between droplets and carrier fluid, flow rate and interfacial tension. We present here a systematic investigation of the droplet speed as a function of their length and interfacial tension, and propose a novel, simple and robust methodology to control the relative distance between consecutive droplets flowing in microfluidic channels through the addition of surfactants either into the dispersed and/or into the continuous phases. As a proof of concept application, we present the possibility to accurately trigger in space and time the merging of two confined droplets flowing in a uniform cross-section circular capillary. This approach is further validated by monitoring a conventional enzymatic reaction used to quantify the concentration of H₂O₂ in a biological sample, showing its potentialities in both continuous and stopped assay methods.

---

Introduction

Droplet microfluidics is a fast developing subfield of microfluidics, dealing with emulsions of aqueous droplets (or dispersed phase) in oil (or continuous phase). It has been drawing a lot of attention, due to its interesting applications in biomedical and chemical fields.^1–4 Droplets are generated by specific channel geometries⁵ or by pipetting.⁶ Surfactants,⁷ which reduce the interfacial tension between the continuous and dispersed phases, are usually added to facilitate the droplet generation and, in some cases, to prevent their merging by steric repulsion.⁷ Among different implemented platforms, the “plug format”, in which droplets are highly confined in a capillary^8,9 are particularly suitable in applications requiring multi-step assays.^9,10 In detail, since they are bigger than the channel diameter, droplets assume an elongated shape and flow as independent wagons in a train, which may contain different reagents, preserving the deterministic order of production and allowing their identification without requiring any complicated barcoding. In this context, circular capillaries are extensively used to transport droplets between the different moduli of platforms devoted to complex protocols, such as ELISA,^11,12 chemical synthesis,¹³ incubation^14,15 and purification reactions.¹⁶

Importantly, even if confined, droplets are never in contact with the channel wall because, under suitable conditions,¹⁷ they are surrounded by a thin lubrication film of the continuous phase.¹⁸ This film is essential to reduce cross-contamination risks and it also plays a fundamental role on the droplet motion. In detail, in circular tubings the droplet is always faster than the continuous phase^19,20 and its speed depends on the thickness of the lubrication layer surrounding the droplet: the thicker the film, the faster the droplet. Starting from this observation, recent theoretical studies have investigated in more detail this phenomen, focusing on the role of the viscosity ratio between the continuous and the dispersed phases.^21–23 A few experimental works have measured the thickness of the lubrication film,^24–27 yielding contradictory results. These are typically justified assuming the presence of unwanted molecules in the fluids,²⁸ which may act as surfactants that modify the interfacial tension and, especially, introduce Marangoni's stresses due to a non-homogenous distribution at the interfaces.⁷ The effect of surfactants on the lubrication film thickness in confined geometries has been addressed, both numerically^29–31 and experimentally.²⁵ These investigations show that surfactants cause an elongation of the moving droplet, which leads to a thicker lubrication film and thus to a higher speed.²⁸ Other works focusing on the speed ratio between the dispersed and continuous phases have identified different regimes depending on the viscosity ratio between the two liquids.^32,33 Although these results suggest that both droplet length and viscosity ratio may affect the droplet speed, a comprehensive understanding of these phenomena is still lacking. More importantly, no study has directly addressed the role played by the interfacial tension. The latter is especially relevant in bioanalytical assays, in which numerous agents contained in the droplets are surface-active. They may involve surfactants⁷ or ethanol,³⁴ used e.g. for cleaning or stabilization purposes, and biomolecules themselves. These surface-active molecules may induce large variations in interfacial tensions between the droplet and the oil.³⁵

Given such a complex scenario, controlling the separation distance between confined droplets, essential to prevent or promote their contact and the eventual merging, is not a trivial task. Actually, among the different operations that can be performed with droplets, merging (or coalescence) of two (or more) droplets represents a fundamental step for triggering a variety of chemical and biological applications, e.g., kinetic studies, chemical synthesis, screening of biological contents and bio-medical diagnosis.³⁶ Merging strategies can be conveniently divided into passive and active ones. In the former case, droplets are not sterically stabilized by the surfactant¹⁶ (such as PFD, PFO), therefore they spontaneously coalesce upon contact. Active merging is instead preferred when the carrier fluid contains surfactants, such as Krytox-PEG, that prevent merging by steric interactions at the interface; the fusion must be thus achieved by applying an external perturbation (pressure drop,³⁷ electric field,³⁸ mechanical vibration,³⁹ local heating⁴⁰) or, in case of non-confined droplets, endowing microchannels with specific geometric features,⁴¹ tuning contact time and surfactant concentration.⁴² Regardless of the adopted approach, the merging of two droplets requires the contact between their interfaces. When droplets are flowing in separated channels, this can be achieved by synchronizing them using ladder-like geometries,⁴³ droplet on demand generators⁴⁴ or railroad-like microstructures.⁴⁵ Differently, when confined droplets flow in a linear sequence along the same channel, specific geometrical architectures, like channel expansions, must be used to vary the local speed of a droplet and to allow its merging with the subsequent one.^46–48 All these methods require the use of exclusive and specifically engineered microfluidic chips, which generally need dedicated and long fabrication procedures in clean room facilities. A simpler alternative is to induce an intrinsic difference in speed between two consecutive droplets. In this work we demonstrate that the speed difference induced by the interfacial tension between two or more confined droplets, transported by a constant flow rate of carrier fluid in a straight circular capillary, can be exploited to precisely trigger their meeting point, and therefore the eventual merging, without the need of any specific microchannel feature or external equipment. As a proof of concept, we apply this strategy to the implementation of a well established enzymatic reaction⁸ for the detection of the H₂O₂ released from biological samples. In order to fully characterize the relative droplets motion, we have systematically investigated the speed of a single confined droplet in a circular capillary having uniform cross-section, and its dependence on i) the viscosity ratio between dispersed and continuous phase, ii) the droplet length, iii) the oil flow rate and, especially, iv) the interfacial tension. The latter is varied by: i) using different hydro-organic solutions and ii) adding a commonly used surfactant (Tween20) in the dispersed phase. As expected, both approaches lead to a decrease in the interfacial tension, however a different behavior is found between the two systems due to the presence of Marangoni's stress in the case of Tween20. The latter case is particularly relevant since surfactants are typically present in most of the commercial available biological reagents, such as PCR mix, cell culture medium or protein buffers. Since in most applications surfactants are added in the continuous phase,⁷ we have also investigated the contribution of the oil-dispersed surfactant to the droplet speed.

Materials and methods

Continuous and dispersed liquid phases

Table 1 lists all the liquids used in this study and their main physical properties (see also Table S1 in ESI†). FC-40 oil (by 3M) is used as continuous phase either pure (labeled as FC40) or with 2% (w/w) of surfactant. Two different surfactants are used: 1H,1H,2H,2H-perfluoro-1-decanol (labeled as FC40 + PFD, by Fluorochem) and PEG-Krytox (labeled as FC40 + PK, by RAN Biotechnologies). The dispersed phase consists of MilliQ-water in different combinations: pure, in solution with various concentrations of glycerol (by Sigma-Aldrich) to modify the viscosity ratio λ between the dispersed and the continuous phases, and with ethanol or Tween20 (by Sigma-Aldrich) to tune the interfacial tension γ. The interfacial tension and the viscosity are measured by the pending drop method⁴⁹ and by an Ostwald's viscometer, respectively.

Table 1 List of the liquids used as continuous and dispersed phases during the experiments, with the corresponding interfacial tension γ and viscosity ratio λ between the dispersed and the continuous phases (FC40 and FC40 + PFD). All dilutions are measured as % w/w

FC40 (viscosity: 4.14 ± 0.02 mPa s)			FC40 + PFD (viscosity: 4.25 ± 0.03 mPa s)
Dispersed phase	γ (mN m^−1)	λ	Dispersed phase	γ (mN m^−1)	λ
MilliQ water	51.2 ± 0.3	0.243 ± 0.003	MilliQ water	14.9 ± 0.2	0.243 ± 0.003
Glycerol 49%	48.3 ± 0.5	1.230 ± 0.004	Glycerol 49%	14.3 ± 0.3	1.201 ± 0.004
Glycerol 67%	46.2 ± 0.6	3.402 ± 0.009	Glycerol 67%	13.9 ± 0.3	3.310 ± 0.008
EtOH 4%	40.4 ± 0.5	0.252 ± 0.003	EtOH 12%	13.1 ± 0.1	0.279 ± 0.003
EtOH 8%	33.1 ± 0.5	0.256 ± 0.004	EtOH 25%	7.4 ± 0.1	0.414 ± 0.003
EtOH 15%	27.3 ± 0.2	0.329 ± 0.003	EtOH 50%	4.0 ± 0.1	0.514 ± 0.003
EtOH 31%	17.6 ± 0.2	0.500 ± 0.003	Tween20–0.001%	13.1 ± 0.4	0.241 ± 0.003
Tween20–0.00125%	40.9 ± 0.1	0.241 ± 0.003	Tween20–0.01%	7.3 ± 0.2	0.241 ± 0.003
Tween20–0.01%	26.7 ± 0.2	0.242 ± 0.003	Tween20–0.1%	5.6 ± 0.1	0.242 ± 0.003
Tween20–0.1%	18.8 ± 0.2	0.244 ± 0.003	Tween20–1%	5.2 ± 0.1	0.249 ± 0.003
Tween20–0.5%	17.9 ± 0.1	0.246 ± 0.003	Tween20–6%	4.7 ± 0.1	0.251 ± 0.003
Tween20–1%	17.6 ± 0.2	0.249 ± 0.003
Tween20–6%	17.3 ± 0.1	0.251 ± 0.003
Tween20–12%	16.5 ± 0.2	0.252 ± 0.003

---

The liquids solutions are chosen to investigate the dependence of the droplet speed for variable surface tensions γ, while keeping λ constant and, vice versa, to study the effect of the viscosity ratio for a fixed interfacial tension.⁵⁰ As a matter of fact, as shown in Table 1, the presence of glycerol in water does not strongly affect the value of γ, while it causes a variation of one order of magnitude in λ (from λ ≃ 0.24 to λ ≃ 3.40). Differently, adding ethanol or Tween20 to the aqueous phase does not induce significant variations in λ, while γ drastically changes. Similarly, the introduction of surfactants in the oil phase causes a drop in γ, while λ values are not affected (see Tables 1 and S1 in ESI†). The apparent critical micelle concentration (CMC_app) of the water/Tween20 mixture with the oil phases, evaluated from the measured equilibrium interfacial tensions,⁵¹ are found to be about 0.05%, 0.02% and 0.01% in FC40, FC40 + PFD and FC40 + PK cases, respectively (see Fig. S1 in ESI† for more details).

Finally, the Amplex Red Hydrogen Peroxide/Peroxidase Assay kit (by Thermofisher) is used for the enzymatic reaction. Fresh substrate solutions of the supplied H₂O₂ in reaction buffer are prepared the day of the experiment, in a range between about 3.90 × 10⁻¹ μM and 7.62 × 10⁻² μM. Then a mixture containing 97% reaction buffer (with 0.01% w/w Tween20 detergent added), 2% of the horseradish peroxidase enzyme (HRP, 0.25 U mL⁻¹) and 1% of the Amplex Red probe (10 mM) is prepared as enzymatic solution. All the relative preparations, as well as the experiments, are performed in a dark room to avoid exposure of the Amplex Red to light.⁵²

Experimental setups

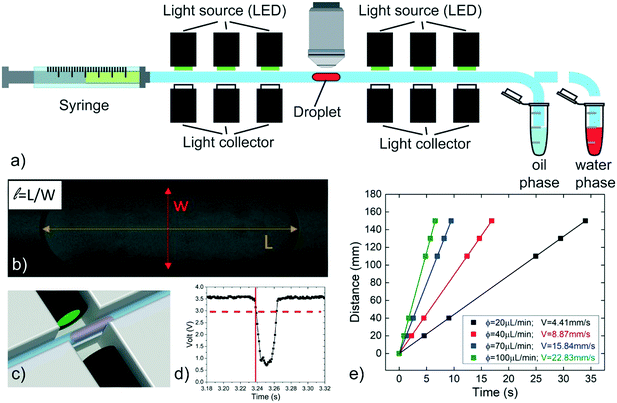
Two customized experimental setups have been developed with the aim of: i) measuring the speed of a single confined droplet in a circular capillary (or tube) (see setup 1) and ii) demonstrating the feasibility of passive droplet merging-on-demand and its capability in the implementation of enzymatic reactions (setup 2).

Setup 1 is schematically shown in Fig. 1a. A single water-phase droplet is generated in a circular PTFE tube (inner nominal diameter 0.3 mm, outer nominal diameter 0.6 mm) by pipetting¹⁶ (at a flow rate of 0.2 μL s⁻¹), using a 100 μL syringe (by SGE) mounted on a syringe pump (PHD 22/2000, by Harvard apparatus) and pre-filled with the oil phase. Negligible oscillations in the generated flow are observed during the measurements (see Fig. S2 and Table S2 in ESI†). One extremity of the tube is connected to the syringe, while the other is moved between two conventional Eppendorf tubes containing the oil and the water-phase solutions to be investigated. By this approach, droplets having volumes between 15 nL and 300 nL are generated with a dispersion of about 2%.¹⁶ The length L of each droplet (Fig. 1b) is measured at rest by transmission microscopy (Nikon Eclipse Ci, with 4× and 10× objectives, MiKrotron camera) before and after every run of measurements. The acquired images are analyzed by ImageJ software. The estimated droplet volume⁵³ is compared to the expected pipetted volumes in order to verify the reliability of both the pipetting and the measured droplet length. The tube is held in a 3D printed structure (see Fig. S3 in ESI†), designed to integrate six optical detectors, placed at fixed positions along the tube length to record the droplet passage. Each detector is composed of two optical fibres facing each other across the tube. These fibres are respectively coupled with a LED (L-7113GC by Kingbright) and a photodiode (OPT101, by Texas Instruments), used to emit and collect the light passing through the tube, respectively (see Fig. 1c). The droplet crossing the detection region defocuses the optical beam, causing a typical decrease in the transmitted intensity (see Fig. 1d). This signal is processed by an Arduino board controlled by a customized LabVIEW (National Instruments) program, which allows to record the crossing time of the droplet at each photodetector. The crossing time is defined as the time at which the signal decreases below a defined threshold (dashed line in Fig. 1d). Then, the detector positions are plotted in terms of the crossing times and the droplet speed is evaluated as the slope of the linear fit of these data points (see Fig. 1e). During a typical run, a single droplet is flown at least 6 times back and forth along the tube, then the oil phase flow rate ϕ is changed and the operation is repeated. The normalized speed β is calculated as the speed of the droplet V divided by the average speed of the oil phase U = ϕ/πr², where r is the inner tube radius. In order to estimate the accuracy of the syringe pump, selected values of ϕ are compared with those deduced by weighing the mass of the liquid flown out the capillary in fixed amounts of time.³³ The discrepancy is found to be systematic and less than 1% (see Table S3 in ESI†). Additionally, for a more accurate estimate of U, the inner radius (r) of the tube is evaluated by repeated direct measurements with a transmission microscope (Nikon Eclipse Ti) (see Fig. S4 in ESI†), yielding r = 145 ± 1 μm. Finally, all measurements are performed in a constantly monitored air-conditioned room (RT = 22 °C with a maximum oscillation of 1.5 °C during different days).

Fig. 1 Scheme of the experimental setup used to measure the droplet speed. (a) A single droplet is generated by pipetting alternatively the water and the oil phase solutions. The droplet is moved in front of the objective to evaluate its length (b) and then is flowed along the tube. Six pairs of optical fibers (c) are used to detect the droplet crossing signal, recording the time of this event (red lines in d). The droplet speed is evaluated as the slope of linear fits of its travelled distance as a function of time (e).

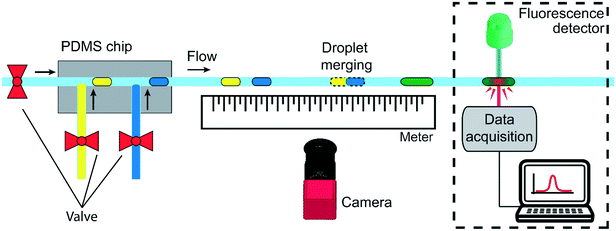
A second experimental setup (setup 2) is designed to demonstrate the passive droplet merging approach based on precise surface tension tuning. The same setup is also exploited for the implementation of an enzymatic reaction, as a proof-of-concept application. It is composed by a microfluidic PDMS device produced by conventional double replica molding^54,55 of a master fabricated by micromilling³⁷ (see Fig. S5 in ESI†). As sketched in Fig. 2, the chip presents two consecutive T-junctions to generate pairs of droplets containing two different solutions. The inlets of the device are also connected to a pressure controller (MFCS, by Fluigent) and the flows are regulated by 3 customized micro-valves, described in ref. 56, for droplet-on-demand generation.⁵⁷ The pressure used for the droplets generation is 200 mbar, while for the oil flow is between 150 and 300 mbar.

Fig. 2 Scheme of the experimental setup for the droplet merging study. Pairs of droplets containing pure water (blue) and Tween20 aqueous solution (yellow) are generated in a PDMS chip by a sequence of T-junctions using the droplet-on-demand approach. The three inlets of the junctions are connected to a pressure controller. The distance between the droplets and the oil phase flow can be easily tuned by acting on the valves actuation time and applied pressure. After generation, the droplets flow in the capillary that is placed in correspondence of a meter. A camera is used to acquire the position of the merging event. In the case of the enzymatic reaction (dashed rectangle), the emitted fluorescence intensity is measured by a detector connected to a computer.

This approach allows the independent control of the droplet volumes, their frequency, the oil gap separating two consecutive droplets and the flow rate of the continuous phase. Droplets pairs are then flown out of the device in the circular PTFE tube, which is fixed above a meter to measure the merging position by a movable camera (Nikon D3300). Finally, in the case of the enzymatic reaction experiments (dashed square in Fig. 2), the tube passes through a customized fluorescence detector.¹²

Results and discussion

In this work we present a novel method for achieving the passive merging of droplets flowing in a circular channel. It relies on the tuning of the droplet speed via the control of several parameters of the system: i) the normalized droplet length [small script l] = L/w (where L is the droplet length and w the tube diameter), ii) the viscosity ratio λ between the dispersed and the continuous phase, iii) the interfacial tension γ between the dispersed and the continuous phase, iv) the flow rate ϕ of the continuous phase. In the following, the influence of these physical quantities will be presented and discussed in separated sections for the sake of clarity.

Variation of the droplet speed with the continuous phase flow rate ϕ and the viscosity ratio λ

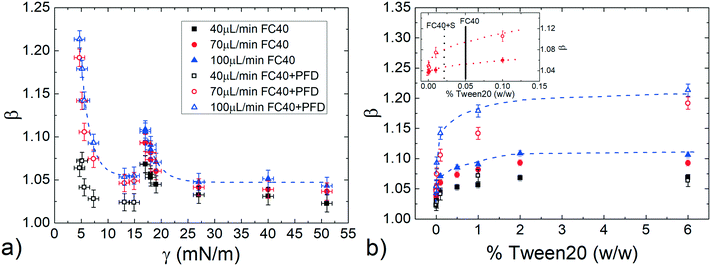
At first, the influence of the normalized droplet length [small script l] and of the carrier oil flow rate ϕ on the speed of a pure water droplet is evaluated, keeping constant both γ and λ. In detail, Fig. 3a shows the normalized droplet speed (or droplet mobility) β as a function of [small script l], for different ϕ. In agreement with earlier results,²⁸ the droplet speed V is always larger than the average oil speed U, i.e. β = V/U > 1. Furthermore, the data corresponding to different ϕ exhibit the same trend: upon increasing the droplet length, β decreases up to a critical length (about [small script l] = 5), then increases reaching a plateau. Similar trends have been observed in numerical simulations,^21,58 although at higher capillary numbers (Ca) than those used in our work (Ca = 10⁻⁴ ÷ 10⁻³). Considering that the speed depends on the thickness of the lubrication film and that the droplet is deformed during the flow,^21,58 we suggest that the plateau is due to the fact that, above a certain length, the [small script l]-dependence of the average value of the film thickness saturates, while for shorter droplet, yet still confined, the average film thickness is significantly affected by the deformation of the droplet frontal and rear meniscii. Furthermore, the data show that an increase in the flow rate of the continuous phase ϕ leads to an increase in the droplet mobility ratio β (see inset Fig. 3a). This was expected considering that the lubrication film around the droplet increases with ϕ,²² leading to higher values of β. Finally, similar trends, slightly enhanced by about 1–2%, can be observed by adding PFD to the continuous phase (see Fig. S6 in ESI† for more details).

Fig. 3 (a) Normalized droplet speed β as a function of the normalized droplet length [small script l] using pure water as the dispersed phase and pure FC40 as the continuous phase, for different flow rates ϕ. The inset shows β as a function of ϕ for two different values of [small script l]. (b) Dependence of β on [small script l] at different viscosity ratios λ between the dispersed and the continuous phase, for a fixed flow rate ϕ = 40 μL min⁻¹. Dashed lines are only a guide to the eyes.

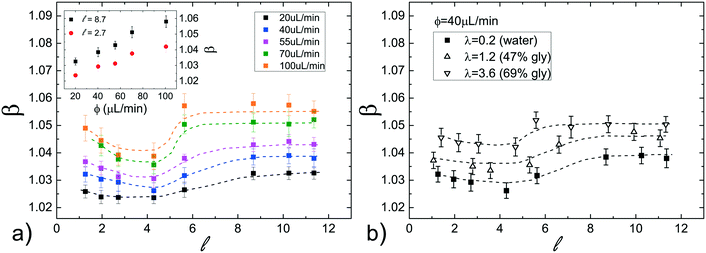
We have also evaluated the effect of the viscosity ratio λ between the dispersed and the continuous phase on the droplet speed. In detail, to vary the viscosity without affecting the surface tension, we have used three glycerol/water mixtures⁵⁰ at different concentrations as the dispersed phase, achieving a variation of more than one order of magnitude in λ (from 0.23 to 3.6, see Table 1). Fig. 3b shows the droplet mobility β plotted as a function of the droplet length [small script l] for the three λ values considered and for a specific oil flow rate (ϕ = 40 μL min⁻¹). Despite the large variation of λ, the graph presents a maximum oscillation in β of about 1.5%, barely above the sensitivity of our experiment. We can then safely conclude that for [small script l] > 1, β is very weakly affected by the viscosity ratio.

Variation of the droplet speed with γ by modifying the hydro-organic composition of the dispersed phase

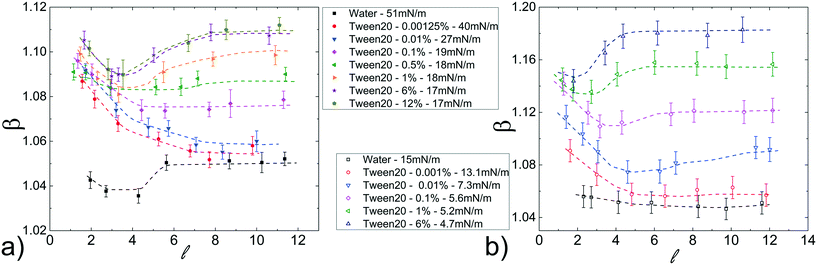
The effect of the surface tension on the droplet speed is studied by considering different hydro-organic (water/ethanol mix) solutions as the dispersed phase. An increase in ethanol concentration leads to a decrease of γ, while keeping almost constant the viscosity ratio⁵⁰ (see Table 1).

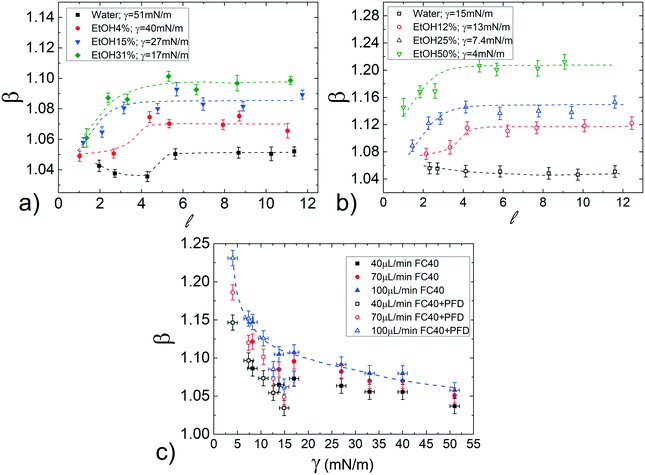
Considering that β slightly varies with the normalized droplet length [small script l] (see Fig. 3a), we first evaluate the influence of γ for various [small script l]. Fig. 4a displays the normalized droplet speed β as a function of [small script l] for various γ (between 51 and 17mN), using FC40 oil as the continuous phase. At first, it is clearly shown that the droplet speed increases as the interfacial tension γ decreases. Furthermore, independently from γ, the droplet mobility assumes a value of about β = 1.05 for [small script l] close to 1. Then, β increases for longer droplets and reaches a plateau above a critical length ([small script l] ≃ 5). Moreover, the final constant values increase with ethanol concentration and thus, with decreasing interfacial tensions. This behaviour may be explained considering that β increases with the average thickness of the lubrication film,¹⁹ which is affected by the local droplet deformation. In fact, the drainage of the oil surrounding the droplet, which tends to get thinner the film, is expected to be easier for shorter droplets. This results in an increase of the droplet mobilities β with [small script l] (up to [small script l] ≃ 5). Then, for sufficiently long droplets (about [small script l] > 5), the results indicate that β, thus the film thickness, is constant with [small script l], as found in ref. 21 and 58.

Fig. 4 Normalized droplet mobility β as a function of the droplet length [small script l] for droplets of ethanol–water solutions of different concentrations carried out by pure FC40 oil (a) or by FC40 oil added with PFD surfactant (b) at a fixed flow rate (ϕ = 70 μL min⁻¹). The vertical scales are different in the two graphs for a better data visualization. (c) β as a function of the static interfacial tension γ obtained by varying the ethanol concentration in the droplet phase. The data refer to droplets having [small script l] = 8 and different flow rates. Dashed lines are reported as a guide to the eyes.

Since in most applications, surfactants are dispersed in the continuous phase, we evaluate their influence by repeating the same study in FC40 + PFD conditions (see Materials and methods). The results, reported in Fig. 4b, show similar trends as in the previous case (pure FC40); nevertheless, data are distributed on a wider range of β, meaning that a smaller variation in γ leads to a more important variation in the droplet mobility. This represents an interesting effect from the application point of view: the merging of two consecutive droplets can be passively achieved acting on their difference in interfacial tensions.

Remarkably, these observations hold not only in the presence and absence of surfactants in the continuous phase, but also for different flow rates (see Fig. S7 in ESI†). To better evaluate the influence of the interfacial tension on droplet speed differences, in Fig. 4c, β is plotted against γ for a fixed droplet length in the plateau region ([small script l] = 8), with both FC40 (full symbols) and FC40 + PFD (empty symbols) carrier phases, and for different flow rates (ϕ = 40, 70 100 μL min⁻¹). As previously observed, the graph shows that the decrease of the interfacial tension leads to an increase in the droplet speed β (see dashed line). Overall, the graph indicates that decreasing γ by one order of magnitude causes a variation in the droplet speed between pure water and ethanol solution as high as 16%. This variation increases with the flow rate and it reaches 25% when γ = 5 mN m⁻¹ and ϕ = 100 μL min⁻¹. Similar trends have been observed in the case of FC40 + PK (see Fig. S9a in ESI†). Finally, the effect of viscosity ratio on the droplet speed (see Fig. 3b) is found to be significantly smaller than that due to changes in the interfacial tension (Fig. 4a).

Variation of the droplet speed with γ by adding surfactant to the dispersed phase

Differently from the case discussed above, in which the interfacial tension is modified acting on the hydro-organic composition of the dispersed phase, we further investigate the dependence on γ by considering the addition of various concentration of a surfactant (Tween20) to the dispersed phase.

In particular, the Tween20 concentrations in water are chosen to obtain values of γ similar to those of the hydro-organic solutions above discussed. As in the previous case, solutions of FC40 oil, both pure and in presence of surfactant (FC40 + PFD or FC40 + PK), are used as continuous phases.

Fig. 5a shows β as a function of [small script l], for a fixed flow rate of the continuous phase (ϕ = 70 μL min⁻¹). The results present a strong dependence on the Tween20 concentration. Below the critical micellar concentration, CMC_app (≃0.05%), β decreases with [small script l], reaching a plateau for long droplets ([small script l] > 5); above the CMC_app, β initially decreases with [small script l] and then, for longer droplets ([small script l] > 3), increases, reaching a plateau as well for [small script l] > 5. By adding the surfactant to the continuous phase (FC40 + PFD, CMC_app ≃ 0.02%), β exhibits the same behaviour as with pure FC40 however, as for the hydro-organic mixtures, the values of β are now distributed on a wider range of values (see Fig. 5b). As in the previous case, this represents an interesting feature for the final merging applications. Finally, the same general trends are also found for different oil flow rates (see Fig. S8 in ESI†) and in the case of FC40 + PK (see Fig. S9b and c in ESI†).

Fig. 5 Normalized droplet mobility β as a function of the droplet length [small script l] varying the Tween20 concentration in the dispersed phase using different liquids as continuous phase (a) FC40 and (b) FC40 + PFD. The flow rate is the same: ϕ = 70 μL min⁻¹.

To better clarify the influence of the Tween20 in the dispersed phase, Fig. 6a shows the normalized speed β as a function of γ, for different ϕ and for a fixed droplet length [small script l] = 8, which guarantees to work in the asymptotic region. In both FC40 and FC40 + PFD, β increases by decreasing γ. However, there is no overlap between the two sets of data because γ ≈ 15 mN m⁻¹ corresponds to the smallest (for FC40) and the highest (for FC40 + PFD) obtainable values, respectively. For a given ϕ, the maximum β variation, corresponding to a decrease in γ of one order of magnitude, is about 14%. In Fig. 6b, the same data are plotted versus Tween20 concentration, showing that β initially increases with the surfactant concentration even beyond the CMC_app point, and eventually reaches an asymptotic value that depends on the applied ϕ. Similar behaviors for the FC40 + PK case are discussed in ESI† (see point 8). Therefore, the addition of Tween20 to the dispersed phase leads to a more complex behaviour than the one observed for the hydro-organic solutions. In order to discuss the experimental results, different effects must be considered. On the one side, it is known that an increasing concentration of surfactants makes the droplet interface less compressible (or more incompressible)⁵⁹ due to the compact arrangement of the molecules, thus the droplet tends to be elongated instead of being deformed in the rear part. This leads to a thicker lubrication film, thus to a higher speed.²⁹ On the other side, due to the internal recirculation flows associated with the droplet motion, the surfactant distribution at the interface is not homogenous: molecules are more concentrated at the rear meniscus than at the front one, and almost absent in the central region.⁷ This generates an interfacial tension gradient (∇γ) that creates a Marangoni's stress acting against the droplet motion.²⁹ However, the inhomogeneous distribution of the surfactants decreases with their concentration,²⁹ leading to a reduction in Marangoni's stress for high concentrations. We expect that the resulting droplet speed is a combination of these different contributions. In fact, for short droplets ([small script l] < 3), ∇γ may be neglected with respect to the incompressibility⁵⁹ of the interface, leading to a droplet speed which mainly depends on the surfactant concentration: higher concentration leads to higher incompressibility, thus higher elongation and speed. Differently, for longer droplets ([small script l] > 3), β is influenced by both ∇γ and concentration. In fact, as shown in Fig. 5, for low concentrations of surfactant (<CMC_app), β decreases with [small script l], suggesting that the contribution of ∇γ is dominant. Differently, for high concentrations (>CMC_app), ∇γ is less effective than the surface incompressibility, which increases with the surfactant concentration leading to higher β.

Fig. 6 Droplet mobility β as a function of (a) the static surface tension γ and (b) the Tween20 concentration, in both FC40 and FC40 + PFD case. The inset represents a magnification of the same graph at small concentrations, indicating the CMC_app for FC40 (solid line) and FC40 + PFD (dashed line) condition.

Passive on demand droplet merging and enzymatic reaction

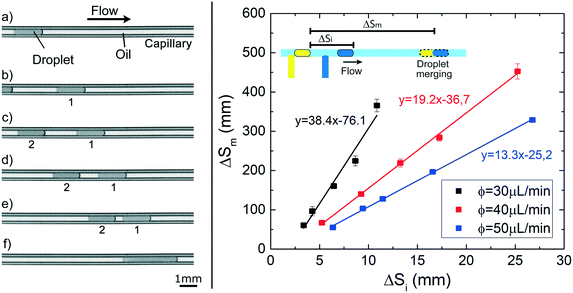
We show here that the observed variation in droplet speed with interfacial tension can be exploited to induce the merging between droplets in a channel of constant circular cross-section. By using the experimental setup 2, pairs of droplets of about 130 nL ([small script l] ≃ 7), separated by a tunable initial distance (ΔS_i), are generated in FC40 + PFD. The first droplet containing pure water moves slower than the second one, containing a water phase solution with 1% of Tween20. They eventually merge after a certain distance (ΔS_m), as shown in the sequence of images of Fig. 7 and in the Movie S1.† Additionally, the graph in Fig. 7 shows that ΔS_m is linearly proportional to ΔS_i, and that higher flow rates lead to faster merging events. Both results are expected considering the previously presented results: i) droplets show uniform motions and ii) higher flow rate of the continuous phase leads to higher droplet speed. Thus, the merging of two droplets based on their difference in interfacial tension can be easily achieved, and for a given composition of droplets, the position of the merging along the capillary can be precisely tuned in space and time without the need of any specific geometrical features or external equipment, by simply varying ΔS_i or/and the flow rate of the continuous phase, as shown in the Movie S2–4.† Therefore, the merging point can be easily predicted, facilitating the design and the integration of this on-demand merging step in a microfluidic platform.

Fig. 7 Droplet merging experiments. (left) Sequence of images showing two droplets (130 nL) containing 1) pure water and 2) Tween20 solution (at 1%) flowing in the capillary; even if they are initially separated (a and b) of about 2.5 mm, they progressively get closer (c–e) and finally merge (f). (right) Graph of the distance travelled by the droplet before the merging (ΔS_m) as function of the initial generation space (ΔS_i), for three different flow rate ϕ of the continuous phase (FC40 + PFD). The solid lines are the linear fits of the data.

This innovative on-demand merging approach is validated by implementing, in a droplet microfluidic device, an enzymatic reaction aimed to quantify the hydrogen peroxide content in a solution.⁶⁰ In conventional format, these assays, characterized by a time-dependent readout, are affected by operator-dependent variability due to the multiple steps required.^12,61 Integration and automation are, therefore, fundamental to improve processing time, reproducibility and sensitivity.^62,63 In order to measure the enzymatic activity or detect a target analyte, precise triggering of the fusion step between the sample and the reagent droplet, as well as a reproducible and reliable monitoring of the product formation are mandatory, in both continuous and stopped assay methods.⁶⁴

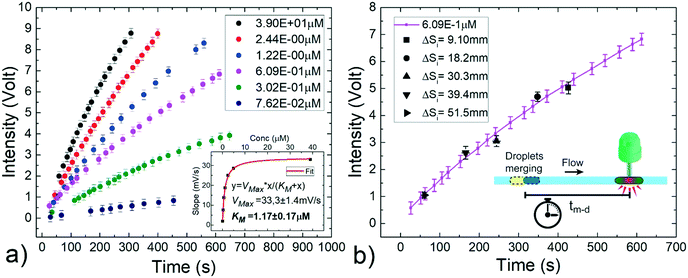
Using the same experimental setup 2 as above, two droplets (200 nL volume) are generated containing i) different concentrations of hydrogen peroxide (from 3.90 × 10⁻¹ μM to 7.62 × 10⁻² μM) and ii) the enzymatic solution including 0.01% Tween20 (see Material and methods). The initial separation between the two droplets (ΔS_i) is fixed at a constant distance and each pair is transported at a constant flow rate of 15 μL min⁻¹. In these conditions, the merging point is expected at about 14 cm from the detector. Upon coalescence, the enzymatic reaction starts and the HRP enzyme catalyses the reduction of hydrogen peroxide to convert the non-fluorescent Amplex Red molecules into resorufin, a red-fluorescent oxidation product, proportionally to the content of hydrogen peroxide.^60,65 The fluorescence signal is monitored by flowing the merged droplet back and forth several times across the detector during the reaction period,¹² as performed in a continuous assay. As commonly carried out in batch, the resulting signal from a negative assay, obtained by using a sample droplet containing only the buffer solution (without H₂O₂), is subtracted to the one corresponding to the droplet containing hydrogen peroxide. Fig. 8a reports the time evolution of the fluorescent intensity during the reaction for different hydrogen peroxide concentrations of interest. Each point of the graph represents the average of three independent measurements and the error bars represent standard deviations. As expected, the amount of formed products increases with time and is dependent on the H₂O₂ concentration. From these curves, the enzyme kinetics can be investigated by plotting the slope of the curve at the beginning of the reaction against the H₂O₂ concentration (see inset of Fig. 8a). The enzymatic activity follows the Michaelis–Menten model,⁶⁶ a typical description of the kinetic properties of a wide class of enzymes, characterized by an initial linear increase with the substrate concentration and by a levelling off at higher substrate concentrations. Additionally, the Michaelis constant K_M obtained as fitting parameter results 1.17 ± 0.17 μM in good agreement with the value obtained for the same substrate/enzyme combination in batch.⁶⁷ This assures that the efficiency of the enzymatic reaction under investigation is not affected by the fact of being performed in small volumes (nL ranges) and in presence of a small amount of surfactants. Indeed, surfactants are often added in conventional reactions buffers, to prevent non-specific binding in immunoassays, to promote cell lysis, to solubilize the released intracellular materials or to denature proteins and other macromolecules.^68–71

Fig. 8 Implementation of an enzymatic reaction for the detection of hydrogen peroxide in a solution based on the passive merging between a sample droplet and an enzymatic solution one. a) Continuous assay: temporal evolution of the resulting fluorescence intensity for different peroxidase concentrations (ranging from about 7.62 × 10⁻² μM to 3.90 × 10⁻¹ μM). The initial slopes of these curves are plotted in the inset as a function of the respective hydrogen peroxide concentrations to determine the enzyme activity. The experimental points (in black) follow the Michaelis–Menten model for enzymes kinetics (red fit curve). b) Stopped assay: fixing the hydrogen peroxide concentration (6.09 × 10⁻¹ μM) and varying the initial spacing ΔS_i between the droplets, it is possible to define different incubation times by delaying the merging. The enzymatic reaction curve (full purple line) is successfully recovered (black points). Each point is an average of three independent measurements and standard deviations are taken as error bars.

Alternatively, the enzymatic reaction product can be evaluated by measuring the fluorescent readout after a fixed incubation time from the beginning of the reaction. This method, known as stopped assay, provides one single point and typically requires the introduction of an additional solution to quench the reaction.⁶⁴ Differently, our approach allows to precisely define the space between the merging point and the detector, thus the incubation time (t_m–d) for the reaction, without any quenching solution. With this aim, a fixed H₂O₂ concentration of 6.09 × 10⁻¹ μM is chosen and several pairs of droplets with the same composition as above described are generated varying their initial distance ΔS_i from 1.0 cm to 51.5 cm to define five different incubation times, between about 61 s and 427 s. In this way, as shown in Fig. 8b, the temporal enzymatic reaction curve previously obtained (solid purple curve) is successfully recovered within the experimental errors. This result confirms the robustness of the on-demand merging approach, and provides a simplification in the detection protocol of a common enzymatic reaction, allowing a reliable observation time without additional steps to quench the reaction, as needed in conventional batch methods.

Conclusion

In this paper, we present an innovative microfluidic method for tuning the separation distance of pairs of confined droplets (or plugs) flowing in capillaries, by suitably varying the interfacial tension. The method requires standard equipment and circular tubings without the need of any microfabrication steps. It has been achieved after an extensive investigation of the droplet speed in a capillary as a function of several physico-chemical parameters, notably the droplet interfacial tension. Interestingly, different trends are observed by varying the droplet length ([small script l]) and by adding surfactants to either the continuous or dispersed phases. Correspondingly, the variation of the relative droplet speed can be as high as 25%. Thanks to this, we prove that the merging of droplets transported by the same carrier fluid can be easily and precisely triggered in space and time, in an on-demand fashion, by selecting the initial droplet distance and the carrier phase flow rate. As a proof of concept, we successfully applied this method to perform a standard enzymatic reaction for the detection of hydrogen peroxide in a solution, in both continuous and stopped assay configurations. More generally, our method can be easily extended to any protocol in which a reliable and/or time-resolved merging is required to start or stop a reaction. In particular, differently from a previous work,⁸ it allows triggering several different types of reactions in a row after a predefined incubation time. Furthermore, it can be exploited to bring into contact two droplets stabilized by surfactants that guarantee a steric stabilization of the droplet interfaces (e.g.: PEG-Krytox⁷²), which can be merged by an external stimulus.³⁸ Finally, we point out that the investigated dependence of droplet speed on the interfacial tension can also be exploited to increase or maintain the distance between consecutive droplets of different contents. This represents an interesting alternative to the introduction of air bubbles^12,73 to prevent undesired coalescence in trains of droplets.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We thank Marie-Caroline Jullien for the scientific discussion, Vélan Taniga and INOREVIA for support in the optical detectors development, Giogio Delfitto for developing the electronic components. This work was supported by the French National Research Agency (ANR) as part of the “Investissements d'Avenir” program (reference: ANR 10-NANO-0207), by the Labex and Equipex IPGG (references: 10-LABX-0031 and 10-EQPX-0034), by ERC “CellO” (FP7-IDEAS-ERC-321107) and by the ARC foundation for young researcher fellowship (DF). MS was supported by a Curie Institute International PhD fellowship. DF, MS, J-LV and SD are coinventors of a patent application filed by Institut Curie and CNRS, encompassing some of the technologies described in this article.

References

1. M. T. Guo, A. Rotem, J. A. Heyman and D. A. Weitz, Lab Chip, 2012, 12, 2146.
2. T. S. Kaminski and P. Garstecki, Chem. Soc. Rev., 2017, 46, 6210–6226.
3. M. Serra, D. Ferraro, I. Pereiro, J.-L. Viovy and S. Descroix, Lab Chip, 2017, 17, 3979–3999.
4. T. S. Kaminski, O. Scheler and P. Garstecki, Lab Chip, 2016, 16, 2168–2187.
5. R. Seemann, M. Brinkmann, T. Pfohl and S. Herminghaus, Rep. Prog. Phys., 2012, 75, 016601.
6. K. D. Dorfman, M. Chabert, J.-H. Codarbox, G. Rousseau, P. de Cremoux and J.-L. Viovy, Anal. Chem., 2005, 77, 3700–3704.
7. J.-C. Baret, Lab Chip, 2012, 12, 422–433.
8. J. D. Tice, H. Song, A. A. D. Lyon and R. F. Ismagilov, Langmuir, 2003, 19, 9127–9133.
9. H. Song, D. L. Chen and R. F. Ismagilov, Angew. Chem., Int. Ed., 2006, 45, 7336–7356.
10. A. M. Nightingale, T. W. Phillips, J. H. Bannock and J. C. de Mello, Nat. Commun., 2014, 5, 3777.
11. A. Ali-Cherif, S. Begolo, S. Descroix, J.-L. Viovy and L. Malaquin, Angew. Chem., Int. Ed., 2012, 51, 10765–10769.
12. T. D. Mai, D. Ferraro, N. Aboud, R. Renault, M. Serra, N. T. Tran, J.-L. Viovy, C. Smadja, S. Descroix and M. Taverna, Sens. Actuators, B, 2018, 255, 2126–2135.
13. D. Ferraro, Y. Lin, B. Teste, D. Talbot, L. Malaquin, S. Descroix and A. Abou-Hassan, Chem. Commun., 2015, 51, 16904–16907.
14. L. Baraban, F. Bertholle, M. L. M. Salverda, N. Bremond, P. Panizza, J. Baudry, J. A. G. M. de Visser and J. Bibette, Lab Chip, 2011, 11, 4057.
15. M. Horka, S. Sun, A. Ruszczak, P. Garstecki and T. Mayr, Anal. Chem., 2016, 88, 12006–12012.
16. D. Ferraro, J. Champ, B. Teste, M. Serra, L. Malaquin, J.-L. Viovy, P. de Cremoux and S. Descroix, Sci. Rep., 2016, 6, 25540.
17. O. Shingo, T. Nisisako, T. Torii and T. Higuchi, Langmuir, 2004, 20, 9905–9908.
18. C. N. Baroud, F. Gallaire and R. Dangla, Lab Chip, 2010, 10, 2032.
19. F. P. Bretherton, J. Fluid Mech., 1961, 10, 166.
20. G. I. Taylor, J. Fluid Mech., 1961, 10, 161.
21. E. Lac and J. D. Sherwood, J. Fluid Mech., 2009, 640, 27.
22. S. R. Hodges, O. E. Jensen and J. M. Rallison, J. Fluid Mech., 2004, 501, 279–301.
23. G. F. Teletzke, H. T. Davis and L. E. Scriven, Rev. Phys. Appl., 1988, 23, 989–1007.
24. J.-D. Chen, J. Colloid Interface Sci., 1986, 109, 341–349.
25. A. Huerre, O. Theodoly, A. M. Leshansky, M.-P. Valignat, I. Cantat and M.-C. Jullien, Phys. Rev. Lett., 2015, 115, 064501.
26. P. Aussillous and D. Quéré, Phys. Fluids, 2000, 12, 2367.
27. I. Beresnev, W. Gaul and R. D. Vigil, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84, 026327.
28. A. Huerre, V. Miralles and M.-C. Jullien, Soft Matter, 2014, 10, 6888–6902.
29. R. M. Carroll and N. R. Gupta, Phys. Fluids, 2014, 26, 122102.
30. U. Olgac and M. Muradoglu, Int. J. Multiphase Flow, 2013, 48, 58–70.
31. K. J. Stebe and D. Barthès-Biesel, J. Fluid Mech., 1995, 286, 25.
32. L. W. Schwartz, H. M. Princen and A. D. Kiss, J. Fluid Mech., 1986, 172, 259.
33. S. Jakiela, S. Makulska, P. M. Korczyk and P. Garstecki, Lab Chip, 2011, 11, 3603.
34. D. F. B. Miller, P. S. Yan, A. Buechlein, B. A. Rodriguez, A. S. Yilmaz, S. Goel, H. Lin, B. Collins-Burow, L. V. Rhodes, C. Braun, S. Pradeep, R. Rupaimoole, M. Dalkilic, A. K. Sood, M. E. Burow, H. Tang, T. H. Huang, Y. Liu, D. B. Rusch and K. P. Nephew, Methods, 2013, 63, 126–134.
35. J. M. Rodríguez Patino, J. M. Navarro García and M. R. Rodríguez Niño, Colloids Surf., B, 2001, 21, 207–216.
36. S.-Y. Teh, R. Lin, L.-H. Hung and A. P. Lee, Lab Chip, 2008, 8, 198.
37. B. Teste, N. Jamond, D. Ferraro, J.-L. Viovy and L. Malaquin, Microfluid. Nanofluid., 2015, 19, 141–153.
38. M. Chabert, K. D. Dorfman and J.-L. Viovy, Electrophoresis, 2005, 26, 3706–3715.
39. M. Sesen, T. Alan and A. Neild, Lab Chip, 2014, 14, 3325–3333.
40. C. N. Baroud, M. Robert de Saint Vincent and J.-P. Delville, Lab Chip, 2007, 7, 1029.
41. L. Mazutis, J.-C. Baret and A. D. Griffiths, Lab Chip, 2009, 9, 2665.
42. L. Mazutis and A. D. Griffiths, Lab Chip, 2012, 12, 1800.
43. B. Ahn, K. Lee, H. Lee, R. Panchapakesan and K. W. Oh, Lab Chip, 2011, 11, 3956.
44. K. Churski, P. Korczyk and P. Garstecki, Lab Chip, 2010, 10, 816.
45. L. Xu, H. Lee, R. Panchapakesan and K. W. Oh, Lab Chip, 2012, 12, 3936.
46. N. Bremond, A. R. Thiam and J. Bibette, Phys. Rev. Lett., 2008, 100, 024501.
47. E. Um and J.-K. Park, Lab Chip, 2009, 9, 207–212.
48. X. Niu, S. Gulati, J. B. Edel and A. J. deMello, Lab Chip, 2008, 8, 1837.
49. A. Daerr and A. Mogne, J. Open Res. Softw., 2016, 4, e3.
50. P. Sartori, D. Quagliati, S. Varagnolo, M. Pierno, G. Mistura, F. Magaletti and C. M. Casciola, New J. Phys., 2015, 17, 113017.
51. E. C. Wijaya, F. Separovic, C. J. Drummond and T. L. Greaves, Phys. Chem. Chem. Phys., 2016, 18, 24377–24386.
52. F. A. Summers, B. Zhao, D. Ganini and R. P. Mason, in Methods in enzymology, 2013, vol. 526, pp. 1–17.
53. M. Musterd, V. van Steijn, C. R. Kleijn and M. T. Kreutzer, RSC Adv., 2015, 5, 16042–16049.
54. Y. Xia and G. M. Whitesides, Annu. Rev. Mater. Sci., 1998, 28, 153–184.
55. D. Ferraro, C. Semprebon, T. Tóth, E. Locatelli, M. Pierno, G. Mistura and M. Brinkmann, Langmuir, 2012, 28, 13919–13923.
56. D. Ferraro, M. Serra, I. Ferrante, J.-L. Viovy and S. Descroix, Sens. Actuators, B, 2018, 258, 1051–1059.
57. K. Churski, J. Michalski and P. Garstecki, Lab Chip, 2010, 10, 512–518.
58. M. J. Martinez and K. S. Udell, J. Fluid Mech., 1990, 210, 565.
59. I. Cantat, Phys. Fluids, 2013, 25, 031303.
60. V. Mishin, J. P. Gray, D. E. Heck, D. L. Laskin and J. D. Laskin, Free Radical Biol. Med., 2010, 48, 1485–1491.
61. B. S. Lee, J.-N. Lee, J.-M. Park, J.-G. Lee, S. Kim, Y.-K. Cho and C. Ko, Lab Chip, 2009, 9, 1548.
62. D. M. Rissin, C. W. Kan, T. G. Campbell, S. C. Howes, D. R. Fournier, L. Song, T. Piech, P. P. Patel, L. Chang, A. J. Rivnak, E. P. Ferrell, J. D. Randall, G. K. Provuncher, D. R. Walt and D. C. Duffy, Nat. Biotechnol., 2010, 28, 595–599.
63. J. Shim, R. T. Ranasinghe, C. A. Smith, S. M. Ibrahim, F. Hollfelder, W. T. S. Huck, D. Klenerman and C. Abell, ACS Nano, 2013, 7, 5955–5964.
64. H. Bisswanger, Perspect. Sci., 2014, 1, 41–55.
65. B. Kalyanaraman, V. Darley-Usmar, K. J. A. Davies, P. A. Dennery, H. J. Forman, M. B. Grisham, G. E. Mann, K. Moore, L. J. Roberts and H. Ischiropoulos, Free Radical Biol. Med., 2012, 52, 1–6.
66. J. M. Berg, J. L. Tymoczko, L. Stryer and L. Stryer, Biochemistry, W.H. Freeman, 2002.
67. G. H. Seong, J. Heo and R. M. Crooks, Anal. Chem., 2003, 75, 3161–3167.
68. E. T. Maggio, J. Excipients Food Chem., 2016, 3, 1108.
69. M. Johnson, Mater. Methods, 2013, 3, 163.
70. M. R. Arkin, M. A. Glicksman, H. Fu, J. J. Havel and Y. Du, Inhibition of Protein-Protein Interactions: Non-Cellular Assay Formats, Eli Lilly & Company and the National Center for Advancing Translational Sciences, 2004.
71. M. Lever, Anal. Biochem., 1977, 83, 274–284.
72. C. Holtze, A. C. Rowat, J. J. Agresti, J. B. Hutchison, F. E. Angilè, C. H. J. Schmitz, S. Köster, H. Duan, K. J. Humphry, R. A. Scanga, J. S. Johnson, D. Pisignano and D. A. Weitz, Lab Chip, 2008, 8, 1632.
73. S. P. Damodaran, S. Eberhard, L. Boitard, J. G. Rodriguez, Y. Wang, N. Bremond, J. Baudry, J. Bibette and F.-A. Wollman, PLoS One, 2015, 10, e0118987.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8lc01182f

---