Transferable coarse-grained MARTINI model for methacrylate-based copolymers†
Gerardo
Campos-Villalobos
 ,
Flor R.
Siperstein
,
Flor R.
Siperstein
 and
Alessandro
Patti
and
Alessandro
Patti
 *
*
School of Chemical Engineering and Analytical Science, The University of Manchester, Sackville Street, M13 9PL, Manchester, UK. E-mail: alessandro.patti@manchester.ac.uk
First published on 17th December 2018
Abstract
A versatile and transferable coarse-grained (CG) model was developed to investigate the self-assembly of two ubiquitous methacrylate-based copolymers: poly(ethylene oxide-b-methylmethacrylate) (PEO-b-PMMA) and poly(ethylene oxide-b-butylmethacrylate) (PEO-b-PBMA). We derive effective CG potentials that can reproduce their behaviour in aqueous and organic polymer solutions, pure copolymer systems, and at the air–water interface following a hybrid structural–thermodynamic approach, which incorporates macroscopic and atomistic-level information. The parameterization of the intramolecular CG potentials results from matching the average probability distributions of bonded degrees of freedom for chains in solution and in pure polymer systems with those obtained from atomistic simulations. Potential energy functions for the description of effective intra- and intermolecular interactions are selected to be fully compatible with the MARTINI force-field. The optimized models allow for an accurate prediction of the structural properties of a number of methacrylate-based copolymers of different length over a well-defined range of thermodynamic state points. In addition, we propose a single-segment model for tetrahydrofuran (THF), an organic solvent commonly used in methacrylate-based polymer processing. This model exhibits a fluid phase behaviour close to that observed experimentally and predicted by more sophisticated molecular models and can reproduce the experimental free energy of transfer between water and octanol.
Design, System, ApplicationNovel routes for the synthesis of hierarchical porous materials have recently highlighted the relevance of methacrylate-based block copolymers, which are able to self-assemble into a variety of ordered mesophases, including bicontinuos nanospheres. Nevertheless, the phase behaviour of this family of structure directing agents is only partially understood, most likely due to the lack of efficient molecular models able to mimic their self-assembly in solution. It is therefore of paramount importance to develop coarse-grained models that can bridge this gap and provide useful guidelines for experiments. To this end, we have built a transferable coarse-grained (CG) model that can mimic the behaviour of poly(ethylene oxide-b-methylmethacrylate) and poly(ethylene oxide-b-butylmethacrylate) in aqueous and organic solutions, pure polymer systems and at the air–water interface. Our hybrid structural–thermodynamic design consists in matching a number of key structural properties calculated by fully-atomistic models with those obtained by our coarse-grained model, which is then optimised by recursive parameterization. We are currently employing the CG model proposed in this work to map the phase diagrams of methacrylate-based copolymers and observing the formation of novel vesicular morphologies that have not yet been found experimentally. |
1 Introduction
Recognizing the rich variety of opportunities deriving from the bottom-up self-assembly of amphiphilic molecules in solution has allowed the synthesis of porous materials with uniform and tunable pore dimensions and large surface areas.1,2 These materials, resulting from the cooperative templating with a silica precursor, have been successfully applied in catalysis,3 adsorption4 and clean energy technologies, such as biofuels production.5 Crucial for their synthesis is the fundamental understanding of the phase and aggregation behaviour of the amphiphilic building blocks, which determines the existence of suitable mesophases and controls their internal organization.Amphiphilic diblock copolymers are macromolecules consisting of two connected blocks, which exhibit very different behaviour in a solvent: one block is solvophilic and can be solvated by the solvent, while the other is solvophobic. If the solvent is water, the former is referred to as the hydrophilic block and the latter as the hydrophobic block. This functional ambivalence with the solvent explains why block copolymers have acquired a central role in nanomaterials science and engineering. Specifically, in order to limit the contact between their solvophobic blocks and the solvent, at sufficiently large concentrations a number of copolymer's molecules aggregate into complex nanostructures, where solvophilic and solvophobic moieties are clearly separated. This spontaneous aggregation or self-assembly, which has captured the interest of a wide scientific community for its tremendous impact in e.g. nanomedicine (drug delivery and nanoreactors),6 materials science (templated synthesis of porous solids),7 and environmental protection (water remediation),8 stems from the ceaseless competition between enthalpic and entropic contributions to the system free energy. This delicate equilibrium, which determines the morphology of the aggregates, can be easily altered by almost intangible thermal fluctuations of few kBT, with T the absolute temperature and kB ≃ 1.38 × 10−23 J K−1 the Boltzmann constant.
At the critical micellar concentration (CMC), isolated amphiphilic molecules start to merge together in aggregates of spherical or cylindrical shape, usually referred to as micelles, consisting of a solvophobic core surrounded by a solvophilic corona. Block copolymers have also been observed to form vesicles (or polymersomes),9,10 being hollow, lamellar structures resulting from the interdigitation of the solvophobic moieties of two curved monolayers. At larger copolymer concentrations, well above the CMC, mesophases with a significant degree of internal organization, such as cubic, hexagonally-packed, and lamellar liquid crystals, can form. Bicontinuous phases, where the solvophilic and solvophobic moieties are clearly separated, but do not necessarily show a significant long-ranged order, have also been observed in experiments,11 predicted by theory12 and by molecular simulations.13
Block copolymers incorporating methacrylate-based blocks, such as poly(ethylene oxide-b-methylmethacrylate) (PEO-b-PMMA) and poly(ethylene oxide-b-butylmethacrylate) (PEO-b-PBMA), are currently being employed in a wide spectrum of practical applications, including the preparation of macroporous polymer electrolytes14,15 and nanoporous membranes,16,17 and in the templated synthesis of ordered porous solids.18–20 In particular, by employing blends of poly(vinylidene fluoride) (PVDF) and PEO-b-PMMA, Zhang and co-workers obtained macroporous polymer electrolytes that exhibit very good electrochemical stability and high ionic conductivity at ambient temperature, properties that make these materials especially suitable for applications in lithium ion batteries.14 PEO-b-PBMA has been used to fabricate PVDF ultrafiltration membranes with enhanced separation performance and resistance to fouling.17 The authors indicate the presence of copolymer micelles, induced by a PEO-metal ion complex, as the main factor causing an increased porosity in the selective membrane layer. The presence of these micelles, however, would not fully explain the better anti-fouling properties, which are most probably due to the organization of the copolymer's hydrophilic blocks at the membrane/water interface.
In addition, methacrylate-based block copolymers have also been employed to synthesize self-assembled complex nanostructures such as micelles, multi-lamellar vesicles and bicontinuous polymer nanospheres (BPNs) via the solvent switch (or co-solvent) method.21 In this technique, copolymer chains (usually at a concentration below 10 wt%) are firstly dissolved in a common solvent for both blocks (e.g. THF, DMF and DMSO) and then, a selective solvent such as water is added until aggregation starts.22 It has been observed that the aggregates undergo morphological transitions as the ratio of common and selective solvents is varied23 and that the final structures strongly depend on the nature of the common solvent. For example, Sommerdijk and co-workers investigated the effect of the relative length of PEO and PBMA blocks and their degree of affinity with the organic solvent on the formation of BPNs.24 Their study revealed an intriguing change of morphology, from BPNs to lamellae, when dioxane, rather than THF, was employed as nonselective organic solvent.
One can therefore infer that a full insight into the solvent/copolymer interactions is crucial to predict and control the formation of the desired mesophase. Nevertheless, unravelling the nature of these interactions and their relative impact on the self-assembly process is anything but trivial, especially because of their multifaceted nature, which harmoniously determines the final morphology of the aggregates. By precisely controlling the physico-chemical parameters and boundary conditions of a self-assembly process, molecular simulation can be especially effective to overcome this challenge and provide a clear insight into the physical laws underpinning the associated kinetics and equilibrium.
High-resolution atomistic models are in general highly accurate and offer a very detailed insight into interesting phenomena operating at relatively short time- and length-scales. However, if the interest is to study biological or soft-matter systems, which require a description beyond the nanometre and nanosecond scales, they become extremely computationally demanding. Therefore, a simplified or coarse-grained (CG) approach, where a number of interactions sites are merged together, is key to enhance our ability to disclose the self-assembly pathway by molecular simulation. Lattice CG models have been successfully applied to investigate the phase behaviour of diblock copolymers in dilute13,25,26 and concentrated27,28 aqueous solutions. Larson and co-workers proposed the use of a lattice model to investigate the self-assembly of block copolymers in an implicit solvent and observed the formation of different liquid crystals, including hexagonal and lamellar phases.13 This model was then modified to study ternary systems containing also an inorganic precursor to mimic the templated synthesis of hybrid organic–inorganic materials.29–33 Although these models allow for a qualitative understanding of the self-assembly process and can reproduce the formation of micelles and liquid crystal phases, their level of chemical detail is often not sophisticated enough to attempt a precise quantitative comparison with the experimental observations. Off-lattice CG models, with an explicit representation of the solvent and an ad hoc parameterization, offer an excellent compromise between the computational efficiency of lattice models and the complexity of fully atomistic models. They have been applied to describe the self-assembly pathway of proteins,34 surfactants,35,36 polymer solutions,37 and block copolymers.38
Despite the practical impact of methacrylate-based copolymers in the formulation of hierarchical porous materials, there are no available CG models to describe their self-assembly. In this work, we propose an off-lattice CG model for PEO-b-PMMA and PEO-b-PBMA, which in principle can be extended to other methacrylate-based block copolymers in solution. We also parameterize an efficient monomeric CG model for THF, an organic molecule commonly used as a co-solvent in the preparation of self-assembled aggregates from methacrylate-based copolymers in solution. The hybrid thermodynamic–structural method followed here relies on the combination of top-down and bottom-up approaches of coarse-graining and the resulting model is compatible with the MARTINI force-field.39 To validate our CG model, we perform extensive molecular dynamics (MD) simulations of either single chains dissolved in THF, where inter-chain interactions are virtually absent, or pure polymer systems, where these interactions become dominant, and compare our results with those obtained with an atomistic model. Additionally, to test the transferability of our CG model to different chemical environments, we calculate the monolayer surface pressure–area isotherm of a PEO-b-PBMA copolymer at the air–water interface, which is found to be in very good agreement with that measured experimentally. The parameterized models capture to a good approximation the properties that are critical in self-assembly and therefore a detailed study of the formation and stability of complex morphologies is possible and will be the subject of future works.
2 Computational details
All simulations, both atomistic and coarse-grained, were performed by employing the GROMACS 5.0.4 molecular dynamics package.402.1 Atomistic simulations
We used well-defined classical intra and intermolecular potentials of the GROMOS41 force-field family to describe interatomic forces of the molecular systems represented as united-atom structures. This force-field has been used to simulate structural and thermodynamic properties of PEO/PEG chains in combination with other biomolecules42 as well as short chains of PMMA and PBMA.43 It was also recently employed to parameterize intramolecular interactions for the CG MARTINI model of polyoxyethylene alkyl ether surfactants.44 Herein, parameters of the 54A7 version were adopted45 (details on the force-field can be consulted in the ESI†). Initial cubic simulation cells with periodic boundaries were constructed by random spatial distribution and rotation of solvent and/or copolymer molecules using the PACKMOL package.46 The species were initially arranged in the simulation box at relatively low densities to avoid overlap and energy minimization was performed by applying the steepest descent method. Subsequently, the system was allowed to achieve the equilibrium density in the isothermal–isobaric (NPT) ensemble at 300 K and 1 bar. All simulations were performed by integrating the classical equations of motion using the leapfrog MD algorithm47 with a time step of 2 fs. The temperature was kept constant by the stochastic velocity rescale thermostat48 with a relaxation time of 0.5 ps. Isotropic pressure coupling was employed using the Berendsen algorithm49 with a barostat relaxation constant of 3.0 ps and compressibility of 4.5 × 10−5 bar−1. The cut-off for the non-bonded (dispersion and electrostatic) interactions was set to 1.4 nm excluding standard long-range corrections to the energy and pressure. Finally, a reaction-field approach was applied to handle long-range electrostatic interactions. Details on the simulated systems are given below.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 THF molecules. The total simulation time was 300 ns, with the last 250 ns used for production of results.
000 THF molecules. The total simulation time was 300 ns, with the last 250 ns used for production of results.
2.2 Coarse-grained simulations
CG simulations were performed in the NPT ensemble, where the equations of motion were numerically integrated using the standard MARTINI time step of 20 fs.39 The ensemble temperature was set to 300 K using the stochastic velocity rescale thermostat with a relaxation time of 1.0 ps and the pressure was maintained at 1 bar by means of the Berendsen barostat with isotropic pressure coupling characterized with a relaxation constant of 3.0 ps and a compressibility of 5 × 10−5 bar−1. Three-dimensional periodic boundary conditions were applied. The shift function for dispersion interactions starting from 0.9 nm was employed with a cut-off of 1.2 nm. Initial configurations for CG simulations were created by mapping the centres of mass of the equivalent atomistic systems according to our CG approach.2.3 Thermodynamic integration
In the optimization of the monomeric CG model of THF, we select the Lennard-Jones (LJ) parameters for cross-interactions with water and octanol to reproduce the experimental free energy of partitioning between these two fluids. The free energy change upon transferring a THF molecule from octanol to water (ΔGow) was approximated as the difference between the free energy of solvation of the molecule in pure octanol (ΔGsolvo) and pure water (ΔGsolvw):| ΔGow ≈ ΔGsolvw − ΔGsolvo | (1) |
The individual free energies of solvation were determined by employing the thermodynamic integration (TI) method,50 in which the Gibbs free energy difference between two macroscopic states is computed by integrating out the ensemble average of the first order derivative of the Hamiltonian of the system, ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (qN, pN; λ), with respect to the coupling parameter λ. In particular, in the configurational part of
(qN, pN; λ), with respect to the coupling parameter λ. In particular, in the configurational part of ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , only non-bonded dispersion interactions were coupled to λ and the two characteristic states of the system were specified as follows: with λ = 0, all the interactions were present and with λ = 1 the molecule did not interact with the solvent. Therefore, assuming reversibility, the energy of solvation of the individual molecule in each solvent was determined by:
, only non-bonded dispersion interactions were coupled to λ and the two characteristic states of the system were specified as follows: with λ = 0, all the interactions were present and with λ = 1 the molecule did not interact with the solvent. Therefore, assuming reversibility, the energy of solvation of the individual molecule in each solvent was determined by:
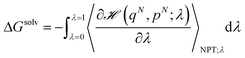 | (2) |
In order to enhance phase space sampling and to better capture variations in the curve ∂![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) (qN, pN; λ)/∂λ along the pathway connecting the initial and final states of the system, we performed 11 simulations of a duration of 500 ns, corresponding to equally-spaced intermediate values of λ. The simulations were carried out by inserting a single THF molecule in a cubic box containing either 750 water beads (≈3000 real water molecules) or 500 octanol molecules, which were modelled using the MARTINI force-field. All simulations were performed in the NPT ensemble at 300 K and 1 bar. In order to avoid singularities in the potential due to the removal or addition of non-bonded interaction sites, the LJ pair potential was modified into a soft-core interaction.51
(qN, pN; λ)/∂λ along the pathway connecting the initial and final states of the system, we performed 11 simulations of a duration of 500 ns, corresponding to equally-spaced intermediate values of λ. The simulations were carried out by inserting a single THF molecule in a cubic box containing either 750 water beads (≈3000 real water molecules) or 500 octanol molecules, which were modelled using the MARTINI force-field. All simulations were performed in the NPT ensemble at 300 K and 1 bar. In order to avoid singularities in the potential due to the removal or addition of non-bonded interaction sites, the LJ pair potential was modified into a soft-core interaction.51
3 Development of the coarse-grained models
While deriving CG potential functions with specific parameters for a molecular model, one typically has to identify the targeted properties to measure and integrate out the less relevant degrees of freedom of the higher-resolution reference system. The parameterization of the CG force-field performed here aims to capture thermodynamic, interfacial, and structural properties of real methacrylate-based copolymers. In the design of our CG model, the link with the atomistic representation for the different molecules has been established in line with the MARTINI force-field,39 which is a versatile model that has been widely used for studying condensed phases of proteins,52,53 lipids,54 carbohydrates55 and polymers.56–58Within the group-contribution MARTINI approach, non-bonded interactions using the spherically symmetrical LJ potential were originally parameterized to allow for the reproduction of densities and free energies of partitioning between water and organic phases of a collection of 18 different resembling chemical groups. In the case of PEO-b-PMMA and PEO-b-PBMA, we have additionally included structural properties as target for the optimization of the force-field. Probability distributions of bond distances and angles obtained from atomistic simulations are used to derive parameters for the effective bonded interactions. In all the cases, the CG bonded potentials are expressed in terms of simple analytical functions compatible with the MARTINI force-field. The approach presented here provides a systematic means to develop computationally efficient and specific high-level CG potentials incorporating information from both top-down (experimental) and bottom-up (atomistic) approaches.
3.1 Single-segment coarse-grained model for THF
Although THF is a solvent ubiquitously used in a broad spectrum of applications including polymer processing, limited work has been directed to the development of CG models for the prediction of its thermodynamic properties by direct molecular simulation. Interestingly, there is not available model for this molecule within the MARTINI force-field. Therefore, the parameterization of a new single-site interaction model of THF fully compatible with the MARTINI force-field was necessary. It is important to mention that other recent models such as those based on the SAFT-γ approach59 cannot be consistently coupled to the MARTINI framework due to differences in the functional form of the pair potentials (Mie and LJ, respectively) and their truncation, as well as the methodology for obtaining the force-field parameters.Our model of THF, just as many other MARTINI solvent models (e.g. water), does not incorporate any electronic charges at the CG level and consequently, it does not allow for the description of the fluid molecules in the presence of electrostatic fields or polarization effects. Although it is well-known that THF exhibits a net dipole moment, our aim here is not reproducing the dielectric properties of the solvent nor the molecular orientational correlations because, at least at this stage, our model is not intended to be used in combination with ionic or partially charged species. In contrast, by following the MARTINI philosophy, the parameterization of the new CG particle was based on the accurate estimation of the bulk fluid density and partition free energy between water and octanol liquid phases, whose experimental value is ΔGow = 2.64 kJ mol−1.60 In principle, the MARTINI CG sites of non-polar species, Na, could be used to reproduce this feature within a statistical accuracy of ±1 kJ mol−1. Nevertheless, the length- and energy-scale parameters for the self-interaction lead to an underestimation of the bulk density of THF at room conditions. In order to overcome this problem, the segment diameter of the like interaction was increased from the standard value of 0.47 nm to 0.48 nm. We coined this new interaction site containing five heavy atoms as TH. Additionally, the unlike interaction with the water beads was systematically modified to better reproduce the experimental value of ΔGsolvw and therefore ΔGow. Cross-interactions between THF and octanol were not altered. The free energy calculations were performed on the basis of the TI technique described in section 2.3.
The vapour–liquid phase equilibrium envelope and interfacial properties of the new CG model of THF were also determined by direct coexistence simulations in the canonical (NVT) ensemble. In particular, we first equilibrated a liquid phase of N = 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 THF beads in the NPT ensemble. After equilibration, the simulation box was expanded to three times its original size along the z direction, and the system was allowed to achieve, in the NVT ensemble, a new equilibrium state, where two liquid/vapour interfaces were formed. The properties of these coexisting phases were then measured at different temperatures by averaging the simulation trajectories over the last 300 ns.
500 THF beads in the NPT ensemble. After equilibration, the simulation box was expanded to three times its original size along the z direction, and the system was allowed to achieve, in the NVT ensemble, a new equilibrium state, where two liquid/vapour interfaces were formed. The properties of these coexisting phases were then measured at different temperatures by averaging the simulation trajectories over the last 300 ns.
The diagonal components of the pressure tensor, P, were used in order to estimate the vapour–liquid interfacial tension, γ, and the equilibrium vapour pressure, Pvap. While the latter corresponds to the normal component of P, i.e. Pvap = Pzz, the former was calculated using the normal and tangential components:
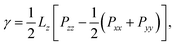 | (3) |
3.2 Coarse-grained models for PEO-b-PMMA and PEO-b-PBMA
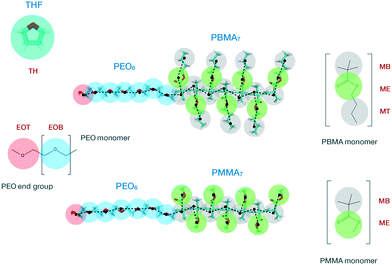
The low molecular weight diblock copolymers PEO6-b-PMMA7 and PEO6-b-PBMA7 were used as reference systems to build our CG model. Experimentally, this type of copolymers are usually synthesized via atom transfer radical polymerization (ATRP),63,64 which causes the final molecular structures to have a residual group from the macroinitiator linking the two blocks. In this work, for the sake of simplicity, the methacrylate and PEO blocks are assumed to be directly bonded in both copolymers. In the following, we present the two stages for the development of our MARTINI-based CG model: (i) mapping of the high-resolution atomistic structure to the CG representation along with the definition of non-bonded interactions, and (ii) derivation of intramolecular (bonded) potentials.Our mapping scheme is schematically sketched in Fig. 1, where we show the CG representation of the species studied in this work, indicated by transparent beads, along with its atomistic counterpart, represented by solid segments in the background. The hydrophilic PEO block consists of one terminal and six bridging beads, mimicking, respectively, the ending HO–CH2– group, here referred to as EOT (ethylene oxide terminal), and the repeating –CH2–O–CH2– monomers, here referred to as EOB (ethylene oxide bridging). EOT and EOB correspond, respectively, to the SPh and SP0 sites of the PEO MARTINI model proposed by Rossi et al.44 The repeating units of the hydrophobic PMMA and PBMA blocks display similar molecular structures as they only differ in the length of the aliphatic side-chain group attached to the methacrylate group. In particular, both methacrylate blocks incorporate seven backbone beads, each mimicking a group of three carbon atoms and here referred to as MB (methacrylate backbone). The MT (methacrylate terminal) site employed to describe the terminal group in the side chain of the PBMA block is identical to the MB bead. Additionally, the side chains of PMMA and PBMA also incorporate an ester group, which is denoted as ME (methacrylate ester) and occupies a terminal position in the former and a bridging position in the latter block. The MB and MT beads correspond to the SC1 site of the original MARTINI force-field,39 while the ME bead to an Na MARTINI site. Finally, in the same figure, we also show the CG representation of a THF molecule, referred to as TH, which incorporates four carbon and one oxygen atoms. In the case of the copolymers, the energy- and length-scale parameters for the interaction between pairs of LJ particles were not altered in order to retain the interfacial properties of the original CG MARTINI optimization.
In order to generate the atomistic target probability distributions, extensive atomistic simulations consisting of either single chains dissolved in THF (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 solvent molecules) or pure polymer systems (consisting of 300 chains) were performed using the GROMOS force-field. The resulting trajectories were converted into the CG representation by mapping the centres of mass (COMs) of groups of constituent atoms according to the approach illustrated in Fig. 1. From the mapped trajectories, probability distributions of bond distances and angles were computed for each copolymer in each environment. Using BI, the initial average potentials for every type of bond and angle were estimated as follows
000 solvent molecules) or pure polymer systems (consisting of 300 chains) were performed using the GROMOS force-field. The resulting trajectories were converted into the CG representation by mapping the centres of mass (COMs) of groups of constituent atoms according to the approach illustrated in Fig. 1. From the mapped trajectories, probability distributions of bond distances and angles were computed for each copolymer in each environment. Using BI, the initial average potentials for every type of bond and angle were estimated as follows
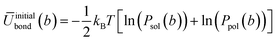 | (4) |
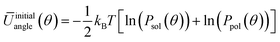 | (5) |
Since the initial potentials derived with eqn (4) and (5) implicitly incorporate many-body effects, they can be considered as potentials of mean force, thus, CG simulations using these potentials did not reproduce the atomistic target distributions and therefore a refinement procedure was implemented. In order to keep the model compatible with the MARTINI force-field, the initial inverted probability distributions for the different bonded interactions were fitted to classical harmonic potential functions
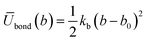 | (6) |
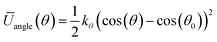 | (7) |
The characteristic force constants and equilibrium bond lengths and angles were then systematically tuned until a reasonable agreement between atomistic and CG distributions was achieved.
4 Results and discussion
4.1 Thermodynamic and interfacial properties of CG THF
In this section, we present the simulation results obtained with our monomeric CG model of THF. We assess and validate the performance of the parameterized model in reproducing the experimental bulk density and free energy of partition between water and octanol in the liquid state. As a secondary test, we examine the vapour–liquid interfacial properties and compare our results with literature simulation data obtained with other more sophisticated molecular models. The calculated average equilibrium bulk density of our CG model of THF at 1 bar and 300 K matches to a high accuracy the experimental value. Likewise, the potential optimization for describing cross-interactions with other CG particles based on TI calculations allow for a close reproduction of the free energy of partition between water and octanol. The optimized LJ parameters for the like and unlike interactions are reported in Table 1. Parameters for like interactions of water and octanol can be consulted in the ESI.† In Table 2 the thermodynamic data obtained with our model are summarized and compared with experimental results.60,72| Pair | ε (kJ mol−1) | σ (nm) |
|---|---|---|
| TH–TH | 4.000 | 0.480 |
| TH–W | 4.120 | 0.470 |
| TH–OA | 4.500 | 0.470 |
| TH–OC | 2.700 | 0.470 |
The vapour–liquid phase equilibrium of the CG model was studied by direct coexistence simulations in the NVT ensemble. In order to characterize the liquid and vapour phases in equilibrium at a given temperature, density profiles (ρ(z)) along the z direction perpendicular to the interface were determined by discretizing the simulation box in 250 slabs. The bulk liquid and vapour densities were then estimated by averaging ρ(z) away from the interface. The VLE envelope for the CG model presented in this work is depicted in Fig. 2. Coexistence curves obtained with other molecular models and experimental values reported in the work by Garrido et al.73 are also included for comparison. As can be observed, our model is able to closely predict the correct temperature-density phase diagram, although it slightly overestimates the actual vapour and liquid densities in the whole range of temperatures. In particular, positive deviations in the predicted fluid density become more important in the vapour branch as the temperature increases. Such a discrepancy has been identified as one of the limitations of the MARTINI force-field,39 in which the vaporization free energies of different compounds although well approximated, do not match quantitatively the real values due to the low stability of the condensed fluid with respect to the vapour phase. This effect can also be noticed in the vapour pressure (Pvap) and surface tension (γ) curves illustrated in Fig. 12 of the ESI.†
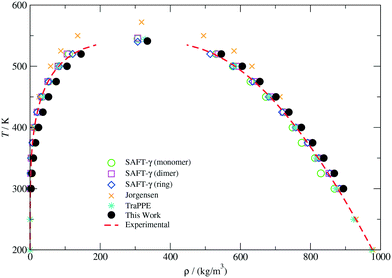 | ||
| Fig. 2 Temperature-density vapour–liquid coexistence envelope for THF. Experimental values (dashed lines) and data points indicated for the SAFT-γ (monomer), SAFT-γ (dimer), SAFT-γ (ring), Jorgensen and TraPPE models are compiled from ref. 73. | ||
The lack of a full agreement between our results and those displayed in Fig. 2 can also be due to the substantial sensitivity of the interfacial properties to the potential truncation.73,74 As previously mentioned, we have used the standard MARTINI truncation procedure, which restricts the calculation of dispersion interactions up to about 2.5σ without real-space long-range corrections. However, it has been established that a cut-off larger than six diameters is necessary to provide a reliable description of interfacial properties.74 Despite these limitations, our model describes very well the thermodynamic properties of the condensed phase (ΔGow and ρbulk) as well as the equilibrium structure (see ESI†) at the state point selected to parameterize the CG potentials for the copolymers and no further calibration was performed.
4.2 Coarse-grained potentials for copolymers
A major limitation in coarse-graining is the lack of thermodynamic and structural consistency between various representation levels.75 Due to the presence of many-body effects, which are implicitly incorporated into simple CG potentials, the derived parameters tend to be generally temperature, composition and density dependent. Thus, in principle, for the two studied systems, a pure polymer and a dilute solution, two different parameterizations should be performed. In the approach adopted here, we instead have defined the target distributions as the average probability density of bonded conformations across the two environments in pursuit of capturing the foremost features of each of them. In the following, we check the validity of this assumption for the two methacrylate-based copolymers. In order to retain the interfacial properties of the original MARTINI optimization, the energy- and length-scale parameters for the intermolecular pair interactions of the chain beads were not altered. The complete list of parameters for all the non-bonded interaction between CG beads, including the new model for THF, is given in Table 3.| Pair | ε (kJ mol−1) | σ (nm) | Pair | ε (kJ mol−1) | σ (nm) |
|---|---|---|---|---|---|
| TH–TH | 4.000 | 0.480 | EOT–EOB | 3.375 | 0.430 |
| EOT–EOT | 3.750 | 0.430 | EOT–MB | 2.025 | 0.430 |
| EOB–EOB | 3.375 | 0.430 | EOT–MT | 2.025 | 0.430 |
| MB–MB | 2.625 | 0.430 | EOT–ME | 4.500 | 0.470 |
| MT–MT | 2.625 | 0.430 | |||
| ME–ME | 4.000 | 0.470 | EOB–MB | 2.025 | 0.430 |
| EOB–MT | 2.025 | 0.430 | |||
| TH–EOT | 4.500 | 0.470 | EOB–ME | 4.500 | 0.470 |
| TH–EOB | 4.500 | 0.470 | |||
| TH–MB | 2.700 | 0.470 | MB–MT | 2.625 | 0.430 |
| TH–MT | 2.700 | 0.470 | MB–ME | 2.700 | 0.470 |
| TH–ME | 4.500 | 0.470 | |||
| MT–ME | 2.700 | 0.470 |
The LJ parameters describing the non-bonded interactions of the copolymers' methacrylate blocks have been set to reproduce, within a reasonably good approximation, the experimental densities of their repeating units, namely methylmetacrylate (MMA) and butylmethacrylate (BMA). In Table 4, we report the MMA and BMA densities as measured experimentally76 along with those estimated by simulation using our CG model. Differences in the order of ≈6% are comparable to those obtained in the MARTINI-based parameterization of the PEO block by Lee et al.37
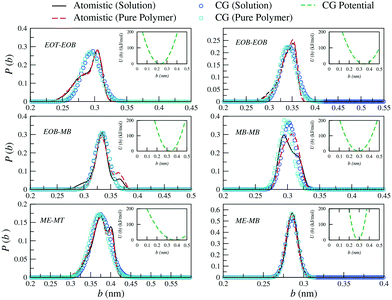 | ||
| Fig. 3 Probability distributions of bond lengths (b) between the different CG sites of a PEO6-b-PBMA7 chain. Distributions obtained from atomistic simulations of single chains in THF (black solid curves) and pure polymer systems (red dashed curves) are included along with the CG distributions (empty symbols). In the insets, the corresponding effective potentials as calculated from eqn (4) are reported. | ||
Similarly, for the derivation of the average angle bending potentials, the direct Boltzmann-inverted atomistic distributions (eqn (5)) were taken as initial guess and fitted to the potential function given by eqn (7). The equilibrium angles and force constants were systematically modified in order to reproduce the average probability distributions of the atomistic systems. In Fig. 4, we present these distributions along with the resulting effective potentials. The angles between segments MB–MB–ME and EOB–MB–ME (see Fig. 1) were not included in the parameterization, because their distributions were defined by the remaining angle types. To limit the complexity of the problem, we decided to neglect the effect of the dihedral angles at the CG level. In the case of the methacrylate block of the copolymers, the computed atomistic distributions for the backbone beads (MB) are comparable to those obtained in other previous PMMA CG parameterizations,71,77,78 where distinct atomistic force-fields have been used and different mappings have been adopted. In particular, the width of the angle distribution with non-zero probability extending from θ ≈ 80° to θ ≈ 160° and with the maximum located at θ ≈ 120°, agrees with the results by Keten and co-workers,71 which were obtained by employing the general-purpose Dreiding force-field. The bond distance distribution for MB–MB is however slightly shifted to larger distances, with the mean value at about b = 0.30 nm instead of b = 0.28 nm. This small difference reflects the different mapping strategy adopted by the other authors, in which, the backbone bead center is located and fixed at the quaternary carbon atom in the methacrylate group, whereas in our case, the bead center, calculated as the center of mass of the group with three carbon atoms, can fluctuate as explained above.
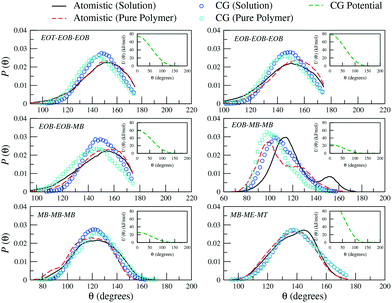 | ||
| Fig. 4 Probability distributions of angles (θ) between the different CG sites comprising a PEO6-b-PBMA7 chain. Distributions obtained from atomistic simulations of single chains in THF (black solid curves) and pure polymer systems (red dashed curves) are included along with the CG distributions (empty symbols). In the insets, the corresponding effective potentials as calculated from eqn (5) are reported. | ||
As observed for the bond length distributions, the angle distributions calculated in a polymer solution does not significantly differ from that obtained in a pure polymer. Interestingly, the main discrepancy is found for the angle formed by the beads across the hydrophilic and hydrophobic blocks, that is EOB–MB–MB. The secondary peak found in solution at approximately θ = 150° is not observed in a pure polymer system, where this probability distribution appears to be restricted to smaller angles. As a result, our CG model is not able to simultaneously reproduce both distributions and clearly misses this secondary peak in solution. The remaining CG mapping shows a reasonably good agreement, although the occurrence of configurations with relatively small angles is slightly underestimated.
In general, the reference atomistic distributions for bond lengths and angles are similar regardless of the chemical environment and therefore the average behaviour can be adequately reproduced with the unique parameterized CG analytical potential functions. This behaviour arises because THF is a thermodynamically good solvent for the two copolymer blocks. We additionally observe that the derived set of intramolecular parameters can be applied to model the copolymer PEO6-b-PMMA7 (see ESI†) as well as methacrylate-based copolymers of different architecture, as we will show in the following sections. The full set of parameters employed to describe the bonded interactions are reported in Table 5.
| Bonded interaction | b 0 (nm)/θ0 (deg) | k b (kJ mol−1 nm−2)/kθ (kJ mol−1) |
|---|---|---|
| Bonds | ||
| EOT–EOB | 0.299 | 12![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
| EOB–EOB | 0.348 | 8500 |
| EOB–MB | 0.335 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 300 300 |
| MB–MB | 0.289 | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
| MB–ME | 0.282 | 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| MT–ME | 0.383 | 5000 |
| Angles | ||
| EOT–EOB–EOB | 180 | 37 |
| EOB–EOB–EOB | 170 | 40 |
| EOB–EOB–MB | 180 | 30 |
| EOB–MB–MB | 139 | 15 |
| MB–MB–MB | 175 | 13 |
| MB–ME–MT | 144 | 67 |
4.3 Structural properties
To test the extent of validity of our CG model, we estimate the size and chain conformation of a number of methacrylate-based copolymers, keeping the length of one of the blocks to 6 monomers and varying the length of the other block between 3 and 18 monomers. To this end, we calculate the radius of gyration, Rg, and compare the results with atomistic simulations in THF solution and in pure polymer systems at 300 K. In particular, the radius of gyration is calculated as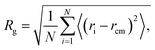 | (8) |
| PEO6-b- | Solution | Pure polymer | ||
|---|---|---|---|---|
| CG (nm) | Atomistic (nm) | CG (nm) | Atomistic (nm) | |
| MMA3 | 0.787 ± 0.081 | 0.743 ± 0.088 | 0.781 ± 0.001 | 0.760 ± 0.003 |
| MMA7 | 0.841 ± 0.085 | 0.800 ± 0.109 | 0.851 ± 0.001 | 0.829 ± 0.001 |
| MMA14 | 0.939 ± 0.088 | 0.988 ± 0.106 | 0.908 ± 0.001 | 0.937 ± 0.004 |
| MMA18 | 1.050 ± 0.117 | 1.060 ± 0.158 | 0.970 ± 0.001 | 1.012 ± 0.001 |
| BMA3 | 0.829 ± 0.075 | 0.787 ± 0.090 | 0.821 ± 0.001 | 0.784 ± 0.002 |
| BMA7 | 0.884 ± 0.062 | 0.835 ± 0.081 | 0.864 ± 0.002 | 0.824 ± 0.001 |
| BMA14 | 0.991 ± 0.068 | 1.013 ± 0.093 | 0.970 ± 0.001 | 0.966 ± 0.004 |
| BMA18 | 1.070 ± 0.090 | 1.092 ± 0.091 | 1.072 ± 0.001 | 1.082 ± 0.002 |
In general, we notice that our CG model tends to slightly overestimate the size of smaller chains and, by contrast, underestimates the size of larger chains, both in solution and in the pure polymer. Nevertheless, this tendency is very light and often within the estimated error. As a matter of fact, the associated standard deviations show that the distribution of the copolymer's chain conformation at the two representation levels overlap, suggesting that the derived CG potentials allow for a sampling of the phase space configurations accessible to the atomistic models. Substantial differences in atomistic chain conformation in the dilute solution and pure polymer systems are not observed and the mean values of the radius of gyration are reproduced with the unique set of CG parameters, showing the universality and transferability of the potentials to work under the constraints imposed by the two different chemical environments.
| Temperature (K) | Solution | |
|---|---|---|
| CG (nm) | Atomistic (nm) | |
| 300 | 0.884 ± 0.062 | 0.835 ± 0.081 |
| 310 | 0.883 ± 0.059 | 0.829 ± 0.078 |
| 320 | 0.886 ± 0.070 | 0.838 ± 0.080 |
| 330 | 0.886 ± 0.068 | 0.833 ± 0.076 |
4.4 Copolymer monolayer adsorption at the air–water interface
Due to their amphiphilic nature, PEO-b-PBMA copolymers are interfacially active molecules and can act as compatibilizing agents for two-phase systems, such as air–water systems. At relatively low concentrations, most of the molecules tend to migrate from the bulk to the interface, with the PEO block preferentially in the liquid phase and the PBMA block trying to minimize its contact with water and thus pointing towards the gas phase. At increasing concentration, but still below the CMC, a monolayer is formed. Monolayers of several PEO-b-PBMA copolymers have been observed experimentally and characterized by their Langmuir pressure–area (Π − AL) isotherms as well as by X-ray reflectivity (XR) measurements.80In general, it has been observed that, at a fixed temperature, non-fluorinated copolymers exhibit a succession of phase transitions, from gas to solid, as the area per molecule is decreased. At low to moderate densities, the monolayers are found in the so-called liquid-expanded (LE) state,81,82 where the PEO blocks behave like random coils in solution (pancake configuration).80 By contrast, at larger densities, the system is in a liquid-condensed (LC) phase and the polymer enters the “brush” regime, where the individual chains tend to reorient and adopt stretched conformations. For copolymers of different PBMA/PEO block-length ratio, defined as f = NBMA/NEO, where NBMA and NEO are, respectively, the number of repeating units in the PBMA and PEO blocks, Li et al. obtained Langmuir isotherms with similar features, and well-defined phases and phase transitions.80 A full insight into the structure of the copolymer chains within the self-assembled monolayer can, however, only be achieved by molecular simulation.
To this end, we performed CG simulations at different values of the monolayer surface tension (γm) in water–air systems containing PEO15-b-PBMA5 at 300 K. The block-length ratio of this copolymer, f ≈ 0.3, is similar to that of PEO113-b-PBMA30 employed in the experimental calculation of the Langmuir adsorption isotherms.80 A number of configurations obtained from these simulations are shown in Fig. 5, where we show the LE and LC phases that have also been observed experimentally.80 In particular, the transition from the LE phase to the coexistence LE + LC region and then to the LC phase is promoted by an increasing lateral compression exerted on the monolayer at constant normal pressure.
To compare our results with experiments, we notice that in PEO-based copolymers adsorbed at the air–water interface, the surface area per molecule has been found to increase with the number of monomers, NEO, in the PEO block according to the scaling law AL ≈ NEO1/2.83,84 By applying this scaling law, we can rescale the results obtained experimentally by Li to the case of a smaller copolymer with the same block-length ratio and NEO = 15. In particular:
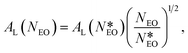 | (9) |
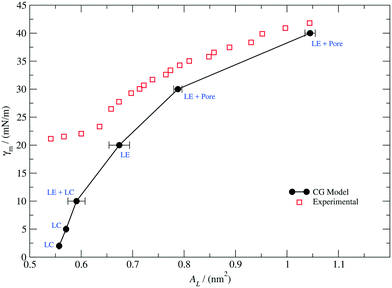 | ||
| Fig. 6 Monolayer surface tension–molecular area isotherm at 300 K. The solid black dots correspond to our simulation results for a PEO15-b-PBMA5 monolayer (f ≈ 0.3). The solid line, which is a guide for the eye, exhibits perforated LE, LE, LC and coexisting LC and LE phases. The red empty squares correspond to the experimental data points measured for a PEO113-b-PBMA15 monolayer (f ≈ 0.3) and rescaled according to eqn (9) (adapted and reprinted with permission from [J. Phys. Chem. B113, 35, 11841–11847]. Copyright 2009 American Chemical Society). | ||
As it can be observed, the CG model qualitatively predicts the correct trend of the monolayer surface tension as a function of the molecular area for values of AL above 0.65 nm2, but it deviates significantly at high densities, where the system exhibits an LC phase. Additionally, the slope of our calculated isotherm appears to be steeper in comparison to that of the experimental curve, suggesting that our model would overestimate the area compressibility modulus of the monolayer. In general, the model perform well for describing the interfacial properties of the real system in the LE region and a correction can be attempted in further work so as to better reproduce the behaviour at high packing fractions.
5 Conclusions
In summary, we have designed and discussed a CG potential derivation for THF and two methacrylate-based copolymers, namely, PEO-b-PMMA and PEO-b-PBMA using a hybrid structural–thermodynamic approach within the framework of the MARTINI force-field. To represent THF as a monomeric fluid, we introduced a new bead type, coined as TH, which is able to reproduce the experimental values of the bulk density and free energy of partitioning between water and octanol in the liquid state. This model can be further refined by incorporating orientational polarizability to the CG beads in order to accurately describe the interactions between THF and charged particles. To enhance the transferability of the intramolecular CG potentials and capture the distinguishing features of different chemical environments, our copolymer models were successfully parameterized by matching the average probability distributions of the chain conformation in very dilute THF solutions and in pure polymer systems as obtained from atomistic simulations.Our multi-phase parameterization has proven to perform well in describing PEO-b-PMMA and PEO-b-PBMA copolymers of various chain-length in the two chemical environments over the well-defined range of thermodynamic state points studied here. Just by including bond stretching and angle bending potentials for the description of intramolecular interactions, the model allows for an accurate representation of copolymer chains with NEO and NNMA (or NBMA) ≤18. From these observations, one could expect the model to be valid for copolymers of different molecular weight at any concentration in THF at the reported temperatures, however, a more detailed study on the properties of the models at varying polymer composition and chain length would be required to further test the representability and robustness of the derived potentials. As a case study and in order to test the transferability of the force-field to a different solvent, we have investigated the adsorption of a PEO-b-PBMA monolayer at the air–water interface showing that our model correctly predicts the experimental trend in the surface tension–molecular area isotherm for intermediate values of surface coverage. Thus, properties not easily accessible by experimental techniques such as the monolayer thickness and conformation of the single polymer chains within the monolayer can be obtained. Our reduced order CG models are computationally efficient as they can be used with the standard MARTINI time step of 20 fs, allowing one to overcome spatiotemporal limitations encountered in all-atom models and investigate interesting slow phenomena such as peptide and protein diffusion in model membranes and the phase and aggregation behaviour of the amphiphilic block-copolymers in selective solvents.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project leading to these results has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 676045 (MULTIMAT). The authors acknowledge the assistance given by IT Services and the use of the Computational Shared Facility at the University of Manchester as well as Prof Felipe J. Blas (University of Huelva) for providing the experimental data on the interfacial properties of THF.Notes and references
- J. S. Beck, J. C. Vartuli, W. J. Roth, M. E. Leonowicz, C. T. Kresge, K. D. Schmitt, C. T. W. Chu, D. H. Olson, E. W. Sheppard, S. B. McCullen, J. B. Higgins and J. L. Schlenker, J. Am. Chem. Soc., 1992, 114, 10834–10843 CrossRef CAS.
- Q. Huo, D. I. Margolese, U. Ciesla, P. Feng, T. E. Gier, P. Sieger, R. Leon, P. M. Petroff, F. Schüth and G. D. Stucky, Nature, 1994, 368, 317–321 CrossRef CAS.
- Q. Yang, J. Liu, L. Zhang and C. Li, J. Mater. Chem., 2009, 19, 1945–1955 RSC.
- M. Kruk, M. Jaroniec and A. Sayari, J. Phys. Chem. B, 1997, 101, 583–589 CrossRef CAS.
- N. Linares, A. M. Silvestre-Albero, E. Serrano, J. Silvestre-Albero and J. García-Martínez, Chem. Soc. Rev., 2014, 43, 7681–7717 RSC.
- A. Rösler, G. W. M. Vandermeulen and H.-A. Klok, Adv. Drug Delivery Rev., 2012, 64, 270–279 CrossRef.
- Q. Huo, D. I. Margolese, U. Ciesla, D. G. Demuth, P. Feng, T. E. Gier, P. Sieger, A. Firouzi, B. Chmelka, F. Schüth and G. D. Stucky, Chem. Mater., 1994, 6, 1176–1191 CrossRef CAS.
- Y. Zhu, L. Fan, B. Yang and J. Du, ACS Nano, 2014, 8, 5022–5031 CrossRef CAS PubMed.
- B. M. Discher, D. A. Hammer, F. S. Bates and D. E. Discher, Curr. Opin. Colloid Interface Sci., 2000, 5, 125–131 CrossRef CAS.
- P. Alexandridis, J. F. Holzwarth and T. A. Hatton, Macromolecules, 1994, 27, 2414–2425 CrossRef CAS.
- C. G. Vonk, J. F. Billman and E. W. Kaler, J. Chem. Phys., 1988, 88, 3970–3975 CrossRef CAS.
- Y. Talmon and S. Prager, J. Chem. Phys., 1978, 69, 2984 CrossRef CAS.
- R. G. Larson, J. Chem. Phys., 1989, 91, 2479–2488 CrossRef CAS.
- Q. Xiao, X. Wang, W. Li, Z. Li, T. Zhang and H. Zhang, J. Membr. Sci., 2009, 334, 117–122 CrossRef CAS.
- R. Sengwa, P. Dhatarwal and S. Choudhary, Electrochim. Acta, 2014, 142, 359–370 CrossRef CAS.
- S. Chaudhury, J. Gaalken, J. Meyer and M. Ulbricht, Polymer, 2018, 139, 11–19 CrossRef CAS.
- J. Meyer and M. Ulbricht, J. Membr. Sci., 2018, 545, 301–311 CrossRef CAS.
- E. J. W. Crossland, M. Kamperman, M. Nedelcu, C. Ducati, U. Wiesner, D. M. Smilgies, G. E. S. Toombes, M. A. Hillmyer, S. Ludwigs, U. Steiner and H. J. Snaith, Nano Lett., 2009, 9, 2807–2812 CrossRef CAS PubMed.
- B. E. McKenzie, F. Nudelman, P. H. H. Bomans, S. J. Holder and N. A. J. M. Sommerdijk, J. Am. Chem. Soc., 2010, 132, 10256–10259 CrossRef CAS PubMed.
- I. Vukovic, S. Punzhin, Z. Vukovic, P. Onck, J. T. M. De Hosson, G. ten Brinke and K. Loos, ACS Nano, 2011, 5, 6339–6348 CrossRef CAS PubMed.
- B. E. McKenzie, H. Friedrich, M. J. M. Wirix, J. F. de Visser, O. R. Monaghan, P. H. H. Bomans, F. Nudelman, S. J. Holder and N. A. J. M. Sommerdijk, Angew. Chem., Int. Ed., 2015, 54, 2457–2461 CrossRef CAS PubMed.
- Y. Mai and A. Eisenberg, Chem. Soc. Rev., 2012, 41, 5969–5985 RSC.
- A. Choucair and A. Eisenberg, Eur. Phys. J. E: Soft Matter Biol. Phys., 2003, 10, 37–44 CrossRef CAS PubMed.
- B. E. McKenzie, J. F. de Visser, H. Friedrich, M. J. M. Wirix, P. H. H. Bomans, G. de With, S. J. Holder and N. A. J. M. Sommerdijk, Macromolecules, 2013, 46, 9845–9848 CrossRef CAS.
- A. D. Mackie, A. Z. Panagiotopoulos and S. K. Kumar, J. Chem. Phys., 1995, 102, 1014–1023 CrossRef CAS.
- A. Z. Panagiotopoulos, M. A. Floriano and S. K. Kumar, Langmuir, 2002, 18, 2940–2948 CrossRef CAS.
- R. G. Larson, Macromolecules, 1994, 27, 4198–4203 CrossRef CAS.
- Q. Wang, P. F. Nealey and J. J. de Pablo, Macromolecules, 2002, 35, 9563–9573 CrossRef CAS.
- F. R. Siperstein and K. E. Gubbins, Langmuir, 2003, 19, 2049–2057 CrossRef CAS.
- A. Patti, F. R. Siperstein and A. D. Mackie, J. Phys. Chem. C, 2007, 111, 16035–16044 CrossRef CAS.
- A. Patti, A. D. Mackie and F. R. Siperstein, Langmuir, 2007, 23, 6771–6780 CrossRef CAS PubMed.
- A. Patti, A. D. Mackie, V. Zeleňak and F. R. Siperstein, J. Mater. Chem., 2009, 19, 724–732 RSC.
- A. Patti, A. D. Mackie and F. R. Siperstein, J. Mater. Chem., 2009, 19, 7848–7855 RSC.
- L. Monticelli, S. K. Kandasamy, X. Periole, R. G. Larson, D. P. Tieleman and S.-J. Marrink, J. Chem. Theory Comput., 2008, 4, 819–834 CrossRef CAS PubMed.
- S. J. Marrink, A. H. de Vries and A. E. Mark, J. Phys. Chem. B, 2004, 108, 750–760 CrossRef CAS.
- W. Shinoda, R. DeVane and M. L. Klein, Soft Matter, 2008, 4, 2454–2462 RSC.
- H. Lee, A. H. de Vries, S.-J. Marrink and R. W. Pastor, J. Phys. Chem. B, 2009, 113, 13186–13194 CrossRef CAS PubMed.
- M. Hatakeyama and R. Faller, Phys. Chem. Chem. Phys., 2007, 9, 4662–4672 RSC.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. De Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. Berendsen, J. Comput. Chem., 2005, 26, 1701–1718 CrossRef CAS PubMed.
- C. Oostenbrink, A. Villa, A. E. Mark and W. F. Van Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676 CrossRef CAS PubMed.
- Y. Xue, M. L. O'Mara, P. P. Surawski, M. Trau and A. E. Mark, Langmuir, 2010, 27, 296–303 CrossRef PubMed.
- Y. Lv, Z. Lin, T. Tan, W. Feng, P. Qin and C. Li, Sens. Actuators, B, 2008, 133, 15–23 CrossRef CAS.
- G. Rossi, P. Fuchs, J. Barnoud and L. Monticelli, J. Phys. Chem. B, 2012, 116, 14353–14362 CrossRef CAS PubMed.
- N. Schmid, A. P. Eichenberger, A. Choutko, S. Riniker, M. Winger, A. E. Mark and W. F. van Gunsteren, Eur. Biophys. J., 2011, 40, 843 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- C. K. Birdsall and A. B. Langdon, Plasma physics via computer simulation, CRC press, 2004 Search PubMed.
- G. Bussi, D. Donadio and M. Parrinello, J. Chem. Phys., 2007, 126, 014101 CrossRef.
- H. J. Berendsen, J. v. Postma, W. F. van Gunsteren, A. DiNola and J. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef CAS.
- D. Frenkel and B. Smit, Understanding molecular simulation: from algorithms to applications, Academic Press, 2001, vol. 1 Search PubMed.
- T. C. Beutler, A. E. Mark, R. C. van Schaik, P. R. Gerber and W. F. van Gunsteren, Chem. Phys. Lett., 1994, 222, 529–539 CrossRef CAS.
- P. J. Bond, J. Holyoake, A. Ivetac, S. Khalid and M. S. Sansom, J. Struct. Biol., 2007, 157, 593–605 CrossRef CAS.
- R. A. Mansbach and A. L. Ferguson, J. Phys. Chem. B, 2017, 121, 1684–1706 CrossRef CAS PubMed.
- R. S. Davis, P. Sunil Kumar, M. M. Sperotto and M. Laradji, J. Phys. Chem. B, 2013, 117, 4072–4080 CrossRef CAS.
- C. A. López, A. H. de Vries and S. J. Marrink, PLoS Comput. Biol., 2011, 7, e1002020 CrossRef PubMed.
- S. Nawaz and P. Carbone, J. Phys. Chem. B, 2014, 118, 1648–1659 CrossRef CAS PubMed.
- G. Rossi, L. Monticelli, S. R. Puisto, I. Vattulainen and T. Ala-Nissila, Soft Matter, 2011, 7, 698–708 RSC.
- G. Rossi, I. Giannakopoulos, L. Monticelli, N. K. Rostedt, S. R. Puisto, C. Lowe, A. C. Taylor, I. Vattulainen and T. Ala-Nissila, Macromolecules, 2011, 44, 6198–6208 CrossRef CAS.
- V. Papaioannou, T. Lafitte, C. Avendaño, C. S. Adjiman, G. Jackson, E. A. Müller and A. Galindo, J. Chem. Phys., 2014, 140, 054107 CrossRef PubMed.
- E. M. Duffy and W. L. Jorgensen, J. Am. Chem. Soc., 2000, 122, 2878–2888 CrossRef CAS.
- J. S. Rowlinson and F. Swinton, Liquids and liquid mixtures: Butterworths monographs in chemistry, Butterworth-Heinemann, 2013 Search PubMed.
- B. Smit, J. Chem. Phys., 1992, 96, 8639–8640 CrossRef CAS.
- J. Meyer and M. Ulbricht, J. Membr. Sci., 2018, 545, 301–311 CrossRef CAS.
- B. E. McKenzie, J. F. de Visser, H. Friedrich, M. J. Wirix, P. H. Bomans, G. de With, S. J. Holder and N. A. Sommerdijk, Macromolecules, 2013, 46, 9845–9848 CrossRef CAS.
- T. Bereau and K. Kremer, J. Chem. Theory Comput., 2015, 11, 2783–2791 CrossRef CAS PubMed.
- Z. Zhang, L. Lu, W. G. Noid, V. Krishna, J. Pfaendtner and G. A. Voth, Biophys. J., 2008, 95, 5073–5083 CrossRef CAS PubMed.
- Z. Zhang, J. Pfaendtner, A. Grafmüller and G. A. Voth, Biophys. J., 2009, 97, 2327–2337 CrossRef CAS PubMed.
- E. A. Müller and G. Jackson, Annu. Rev. Chem. Biomol. Eng., 2014, 5, 405–427 CrossRef PubMed.
- D. Reith, M. Pütz and F. Müller-Plathe, J. Comput. Chem., 2003, 24, 1624–1636 CrossRef CAS PubMed.
- T. C. Moore, C. R. Iacovella and C. McCabe, J. Chem. Phys., 2014, 140, 06B606_1 Search PubMed.
- D. D. Hsu, W. Xia, S. G. Arturo and S. Keten, J. Chem. Theory Comput., 2014, 10, 2514–2527 CrossRef CAS PubMed.
- W. Hayduk, H. Laudie and O. H. Smith, J. Chem. Eng. Data, 1973, 18, 373–376 CrossRef CAS.
- J. Garrido, J. Algaba, J. Míguez, B. Mendiboure, A. Moreno-Ventas Bravo, M. Piñeiro and F. Blas, J. Chem. Phys., 2016, 144, 144702 CrossRef CAS PubMed.
- A. Trokhymchuk and J. Alejandre, J. Chem. Phys., 1999, 111, 8510–8523 CrossRef CAS.
- J. McCarty, A. Clark, J. Copperman and M. Guenza, J. Chem. Phys., 2014, 140, 204913 CrossRef CAS PubMed.
- D. R. Lide, CRC Handbook of chemistry and physics, B&T, 2007 Search PubMed.
- W. Xia, S. Mishra and S. Keten, Polymer, 2013, 54, 5942–5951 CrossRef CAS.
- C. Chen, P. Depa, J. K. Maranas and V. Garcia Sakai, J. Chem. Phys., 2008, 128, 124906 CrossRef PubMed.
- S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801–6822 RSC.
- Z. Li, V. Schön, P. Huber, J. Kressler and K. Busse, J. Phys. Chem. B, 2009, 113, 11841–11847 CrossRef CAS PubMed.
- Z.-W. Yu, J. Jin and Y. Cao, Langmuir, 2002, 18, 4530–4531 CrossRef CAS.
- E. Ruckenstein and B. Li, J. Phys. Chem., 1996, 100, 3108–3114 CrossRef CAS.
- P. Alexandridis, V. Athanassiou, S. Fukuda and T. A. Hatton, Langmuir, 1994, 10, 2604–2612 CrossRef CAS.
- Y. Nikas, S. Puvvada and D. Blankschtein, Langmuir, 1992, 8, 2680–2689 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8me00064f |
| This journal is © The Royal Society of Chemistry 2019 |