Direct probe of the nuclear modes limiting charge mobility in molecular semiconductors†
Thomas F.
Harrelson
 a,
Varuni
Dantanarayana
b,
Xiaoyu
Xie
c,
Correy
Koshnick
d,
Dingqi
Nai
a,
Varuni
Dantanarayana
b,
Xiaoyu
Xie
c,
Correy
Koshnick
d,
Dingqi
Nai
 a,
Ryan
Fair
e,
Sean A.
Nuñez
f,
Alan K.
Thomas
g,
Tucker L.
Murrey
a,
Ryan
Fair
e,
Sean A.
Nuñez
f,
Alan K.
Thomas
g,
Tucker L.
Murrey
 d,
Michael A.
Hickner
f,
John K.
Grey
d,
Michael A.
Hickner
f,
John K.
Grey
 g,
John E.
Anthony
g,
John E.
Anthony
 h,
Enrique D.
Gomez
h,
Enrique D.
Gomez
 e,
Alessandro
Troisi
e,
Alessandro
Troisi
 c,
Roland
Faller
c,
Roland
Faller
 a and
Adam J.
Moulé
a and
Adam J.
Moulé
 *ab
*ab
aDepartment of Chemical Engineering, University of California, Davis, CA, USA. E-mail: amoule@ucdavis.edu
bDepartment of Chemistry, University of California, Davis, CA, USA
cDepartment of Chemistry, University of Liverpool, Liverpool, UK
dDepartment of Materials Science and Engineering, University of California, Davis, CA, USA
eDepartment of Chemical Engineering, Pennsylvania State University, University Park, PA, USA
fDepartment of Materials Science and Engineering, Pennsylvania State University, University Park, PA, USA
gDepartment of Chemistry & Chemical Biology, University of New Mexico, Albuquerque, NM, USA
hDepartment of Chemistry, University of Kentucky, Lexington, KY, USA
First published on 23rd October 2018
Abstract
Recent theories suggest that low frequency dynamic intramolecular and intermolecular motions in organic semiconductors (OSCs) are critical to determining the hole mobility. So far, however, it has not been possible to probe these motions directly experimentally and therefore no unequivocal and quantitative link exists between molecular-scale thermal disorder and macroscale hole mobility in OSCs. Here we use inelastic neutron scattering to probe thermal disorder directly by measuring the phonon spectrum in six different small molecule OSCs, which we accurately reproduce with first principles simulations. We use the simulated phonons to generate a set of electron–phonon coupling parameters. Using these parameters, the theoretical mobility is in excellent agreement with macroscopic measurements. Comparison of mobility between different materials reveals routes to improve mobility by engineering phonon and electron–phonon coupling.
Conceptual insightsThe charge mobility in molecular semiconductors is limited by significant nonlocal electron–phonon coupling caused by intermolecular vibrations, otherwise known as phonons. To engineer new molecular materials with superior functional properties and performance, we need to gain fundamental understanding of how these phonons cause dynamic localization of charge carriers. Here we directly measure the phonon spectrum using high-resolution inelastic neutron scattering (INS) experiments. INS provides a more complete phonon spectrum than analogous optical experiments, such as FTIR or Raman. We demonstrate the accurate computation of nonlocal electron–phonon coupling parameters for six different molecular semiconductors using density functional theory simulations of phonons over the full Brillouin zone, experimentally validated by inelastic neutron scattering experiments. Our coupling parameters were then used to compute charge mobilities which quantitatively agree with literature values, demonstrating our ability to accurately predict functional properties of a variety of molecular semiconductors. Thus, our measured results coupled with computational methodology can be used to screen molecular semiconductors to predict a set of high-performance materials, significantly accelerating the navigation through chemical design space for next-generation materials. |
1 Introduction
The key to creating sustainable electronics for the future hinges on our ability to effectively rationalize, predict, and improve material properties from atomistic structure. This is particularly true for organic semiconductors (OSCs) for which the power of synthetic chemistry can be used to deliver solution processable materials for a vast range of applications, including chemical and biological sensors, light emitting diodes (OLED) for lighting and display, photovoltaics (OPV), bioelectronics, and field-effect transistor (OFET) technologies.1–6 Specifically for transistor technologies, OSCs have already exceeded the performance of amorphous silicon,7 and now must compete with polycrystalline silicon and emerging oxide materials to become more industrially relevant. For FETs with p-type active layers, hole mobility (μh) is the figure of merit of the material,7 and a common research goal is to find means to improve μh of OSCs (1–10 cm2 V−1 s−1) to compete with polycrystalline silicon (>20–50 cm2 V−1 s−1).It is natural to expect that μh can be optimized by exploring the materials space with suitable computational models coupling the atomic scale material properties (describing electron, phonon, and electron–phonon interactions) with a macroscopic theory of charge transport. This has not been realized so far because of challenges on both the computational and the theoretical side of the problem. Boltzmann (band) transport theory is the standard theory to describe charge carriers in inorganic semiconductors. Band theory fails to describe molecular semiconductors with experimental mobilities of the order of few cm2 V−1 s−1 because it predicts a mean free path of just few Angstroms, which is inconsistent with the carrier delocalization assumed by band transport. In contrast, incoherent hopping models fail to be physically reasonable because they predict a hopping rate that is too fast (>1013 s−1). Several recent reviews summarize the problems and the common approach emerging to address them.8,9 The new approach describes the interaction between molecular orbitals localized on different molecules with a transfer integral J, which is modulated by thermal motions. For molecular semiconductors, the standard deviation of the thermal modulation (σ) is of the same order of magnitude as J and takes place with a timescale of ≈1 ps. The thermal fluctuations are a manifestation of non-local electron–phonon coupling but, unlike other simpler cases, the fluctuations of J are too large to be treated as a small perturbation (as in band transport), too slow to be averaged out (e.g. renormalized), and too fast to be treated as static disorder. A variety of numerical approaches have been proposed to deal with this scenario often described as “dynamic disorder”, where the electron–phonon coupling is responsible for a transient localization of the carrier.8,10–13
For any model, it is impossible to predict charge mobility without high quality experimental information about the phonons responsible for the dynamic localization, e.g. mostly low frequency motions with a large intermolecular component. While high energy phonons can be routinely probed via FTIR and/or Raman spectroscopy,14–16 low energy phonons can only be measured using a specialized Raman spectroscopy setup and/or terahertz spectroscopy.17 Even then, the selection rules for Raman limit the measurement to the observation of gamma point phonons, which is of limited use for μh calculations because the symmetry of gamma point phonons minimize the relative displacements between molecules in neighboring cells. Phonons at the Brillouin zone boundaries are most important for the computation of μh. Also terahertz spectroscopy of OSCs is dominated by the dielectric response of free or loosely bound charge carriers present in OSCs, which mask the weaker response of phonons. Diffuse electron scattering has been used to measure the cumulative disorder caused by phonons,18 but this method does not resolve the dynamic disorder into its frequency dependent components and cannot directly inform the charge transport model. This lack of information has so far prevented a quantitative test of dynamic transport theories and the validation of any computed phonon spectra at low frequency. Thus measurement of the full phonon spectrum has been a central blocking point for the development of organic electronics.
To measure the phonons that lead to dynamic disorder, we use inelastic neutron scattering (INS), a technique that probes the atomic dynamics of a material. INS has been used to infer a variety of materials properties including the local structure of polymers,19,20 binding interactions in porous materials,21,22 and protein folding in response to a stimulus. INS is particularly well suited for studying dynamic disorder in OSCs because spectroscopy with neutrons does not have any selection rules (every phonon mode in the Brillouin zone is observable) and neutrons interact with atomic nuclei only (not the free charge carriers).19,23 The low energy vibrations are not convoluted with the dielectric response of the material because there is no neutron-charge carrier interaction. Also the inelastic scattering cross-section is largest for protons, so we observe the weighted density of states of proton motions. Since nearly every carbon motion in an OSC is coupled to the motion of 1H atoms, the INS spectrum contains energy-resolved information of all atomic motions in the OSC crystal. Given an experimentally well-defined crystal structure, the INS instrument at Oak Ridge National Laboratory called VISION characterizes vibrational dynamics with high resolution over a broad energy range (1–600 meV or 8–5000 cm−1) better than other available instruments because the specific instrument design and high incident neutron flux maximizes the signal-to-noise ratio and count rate.24,25
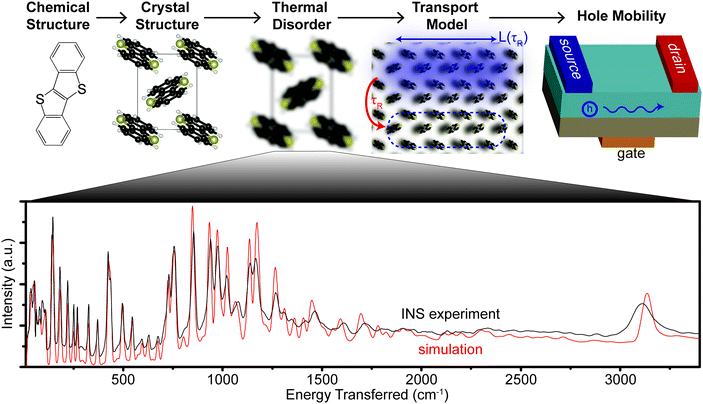
An accurate simulation of the spectrum, e.g. via density functional theory (DFT), provides the most detailed picture of phonon modes in the OSC crystal across all measured energy scales. As van der Waals (vdW) forces strongly impact the crystal structure of molecular semiconductors, and therefore the phonons, we simulate each material with a functional that explicitly includes vdW forces. We use the experimentally verified set of phonons to create a parameter-free model of hole transport in six different OSCs. The model connects structure at the atomic length scale to observable phenomena at the device length scale using information obtained entirely from first principles as shown in Fig. 1, which fits into any computational scheme that that searches through chemical design space to optimize μh.
A numerically efficient method to compute μh is provided by transient localization theory (TLT).8 We chose to use this technique because the theory was specifically designed for modeling high-mobility molecular semiconductors, but any other appropriate theory could be used in conjunction with the computed EP parameters. TLT has been shown to qualitatively reproduce μh for a wide variety of OSCs,26 but has not been applied to materials in which the phonon spectrum is known.
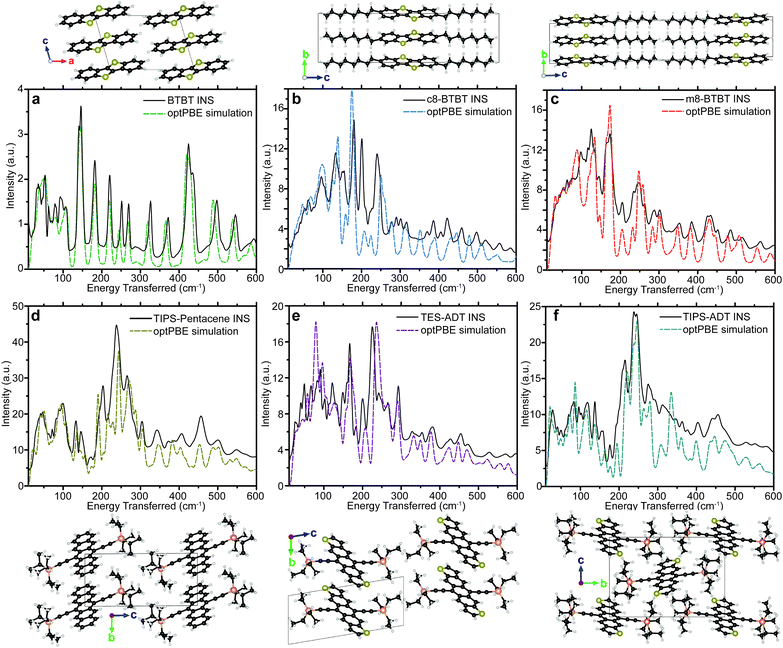
The six materials studied exhibit either high μh, or have slight chemical variations that reduce μh (see crystal structures in Fig. 2 and chemical names in methods section) and can be grouped into two series of homologous compounds. The first group is BTBT, m8-BTBT, and c8-BTBT, with an identical conjugated core and a very similar herring-bone crystal structure in the high mobility plane. The only difference is the inclusion of one (m8-BTBT), or two (c8-BTBT) octyl chains along the longitudinal axis of the BTBT core. Nevertheless, μh of c8-BTBT is much higher than m8-BTBT or BTBT.27 It has been suggested that the octyl side chains reduce the dynamic disorder (σ) of the BTBT repeat unit by preventing lateral vibrations.18 We also study a series of three substituted acenes: TIPS-PN, TES-ADT, and TIPS-ADT to test how changing the conjugated core and side chain structure affects the phonon spectrum. TES-ADT has a nearly identical brickwork crystal structure as TIPS-PN,28,29 but has a higher μh.18,28,29 TES-ADT substituted the terminal benzenes of the core of TIPS-PN with thiophenes, and has smaller side chains than TIPS-PN and TIPS-ADT. A recent article by Illig et al.18 suggested that the charge mobility in TES-ADT is higher due to reduced dynamic motion of the backbone. We also study TIPS-ADT, which assumes a slipped-stack crystal packing and typically displays much lower μh.29,30 Both sets of OSCs are designed to show how differences in crystal structure and side chain attachment affect the phonon spectrum, and therefore the EP coupling.
2 Results and discussion
The measured spectra are reported in Fig. 1, to illustrate the resolution across all relevant energies for BTBT, and Fig. 2, which focuses on the more relevant low energy region for all six materials. For each INS spectrum in Fig. 2, the error bars are smaller than the width of the plotted curves. We simulated the phonons using plane-wave DFT starting from previously published crystal structures,31–34 which we optimized by screening different functionals, electronic k-point sampling densities, convergence criteria, basis set size, supercell size, and phonon q-point sampling (see ESI,† Section S4 for selection of functional and tests of convergence). We ultimately chose the optPBE-vdW functional because it resulted in a simulated spectrum for BTBT that demonstrated the best agreement with the experimental spectrum at low energy amongst the tested vdW density functionals. We chose to limit our supercell screening (see ESI,† Fig. S17) to the vdW-DF class of functionals because the simulated lattice parameters demonstrated the best agreement with prior literature values, which is necessary for computing accurate transfer integrals (see ESI,† Table S3). The simulated phonon energies in Fig. 1 were scaled by 1.015 to better agree with measured data at high energy, but comparisons between simulated and INS spectra in all other figures were not scaled. The agreement in peak position, width, and intensity is remarkable across the entire spectrum demonstrating excellent correspondence between measurement and simulation over energies spanning two orders of magnitude. All other comparisons between experimental and simulated spectra are compared over the full energy range (cf. ESI,† Section S2).Most importantly for μh calculations, we accurately simulate the phonon spectrum at energies below kBT at room temperature (<200 cm−1). Fig. 2 shows a comparison between the measured and simulated phonons for each of the six OSCs studied from 10–600 cm−1. The agreement between measurement and simulation is excellent down to the linewidth of the elastic peak (∼10 cm−1) for five of the six samples, particularly below 200 cm−1, indicating that we accurately simulated the interactions between the conjugated cores. Many of the peaks above 200 cm−1 primarily contain motions of side chains, which are expected to display increased structural heterogeneity leading to minor disagreements between the experiments and our simulations.
Our INS results, combined with XRD data in ESI,† Section S1, identify a low temperature polymorphism in c8-BTBT causing an apparent disagreement between the INS and simulated spectra. Since the simulated structure of c8-BTBT agrees with room temperature XRD measurements,35 the simulated phonons correspond to the room temperature motions. The c8-BTBT phonon predictions without experimental INS verification is justified by the quality of agreement for the other five materials.
In addition to the INS data, we measured Raman and FTIR spectra for each of the substituted acene materials (see ESI,† Section S3). Both, FTIR and Raman spectra substantially differ from their INS counterparts, which demonstrates the complementarity between the three measurements. Despite the limitations of Raman and FTIR due to the selection rules, the observed peaks are not heavily weighted by the motions of hydrogens as in INS, and, thus, contain more carbon–carbon, carbon–silicon, carbon–sulfur information than the associated INS spectra. For each substituted acene material, our simulated phonons nicely agree with the FTIR spectra (see ESI,† Section S4), indicating that the simulated phonons accurately describe the full range of motions.
To assess the impact of the phonons on transfer integrals between different pairs of molecules, we computed the non-local electron–phonon coupling, which is a measure of how the transfer integral Jij between molecules i and j is modulated by the displacement QI along phonon mode I. Assuming a linear coupling, the non-local EP coupling parameters gij,I are defined by the relation,
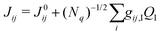 | (1) |
Because of the very large number of modes, a convenient way to report the computed EP coupling is by defining a spectral density,
 | (2) |
We see that each material contains many peaks in Bij(ω) over a very large energy range indicating that many different types of modes contribute to the dynamic disorder. Some materials show the largest peaks in the low energy region of the spectrum (lower than 200 cm−1), indicating that those phonons can be treated classically when considering their impact on charge transport, in agreement with prior studies.10,11,13,36 However, every material contains a non-negligible contribution from high energy modes to total EP coupling, even when considering the phonon occupation numbers at 300 K (see Table 1). The high energy peaks (∼1500 cm−1) in the EP spectra of all materials are the result of carbon–carbon stretch modes in the conjugated core, leading to disruption of the bonding order causing large shifts in the frontier orbital density. The intensity of high energy peaks in the substituted BTBT's appears to be greater than the same peaks in the substituted acenes, in which EP coupling is dominated by acoustic modes.
| Material | J (cm−1) | σ 300K (cm−1) | Low freq. (%) | Pair | 1/m* (a.u.−1) | μ theory (cm2 V−1 s−1) | μ exp |
|---|---|---|---|---|---|---|---|
| c8-BTBT | −728 | 367 | 70 | B and C | 2.21 | 4.86 | 6.0 ± 1.1 |
| 802 | 210 | 62 | A | ||||
| m8-BTBT | −625 | 547 | 76 | B | 2.11 | 1.43 | 2.9 ± 1.1 |
| −706 | 535 | 76 | C | ||||
| 769 | 254 | 67 | A | ||||
| BTBT | 1.03 | 39.0 | 96 | B and C | 0.45 | 0.963 | 0.024 ± 0.007 |
| 765 | 256 | 77 | A | ||||
| TES-ADT | −1339 | 439 | 87 | C | 3.40 | 4.22 | 1.0 ± 0.5 |
| −462 | 223 | 94 | B | ||||
| TIPS-PN | 587 | 311 | 88 | B | 0.71 | 1.34 | 0.65 ± 0.35 |
| 19.1 | 124 | 74 | C | ||||
| TIPS-ADT | −486 | 279 | 97 | A | 0.61 | 0.545 | 0.30 ± 0.25 |
To get an aggregate picture of how phonons impact μh, we find the variance of the transfer integral (σij,T2) at a given temperature using eqn (3).37
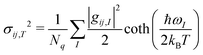 | (3) |
While σij,T in Table 1 were computed from the phonons sampled over the full Brillouin zone, we also compute σij,T from only the gamma point phonons (see ESI,† Section S4). These gamma point σij,T values differ from the corresponding values in Table 1 by −40% to 25%. Thus, gamma point phonons and measurements that only probe the gamma point (e.g. Raman) are insufficient to describe quantitatively the dynamic disorder in OSCs. To better appreciate the different relevance of the information provided by Raman and INS spectroscopy, we report both experimental spectra along with Bij(ω) in Fig. 3. There are a few peaks in Bij(ω) that are present in the Raman spectra and absent in the corresponding INS spectra. However, the dominant contributions to EP coupling come from the large, broad peak <50 cm−1, which is only captured by INS because INS contains information on phonons over the entire Brillouin zone, whereas Raman scattering only probes gamma point phonons. Each of the six materials displays considerable phonon dispersion at low energy (see ESI,† Section S4). Therefore, INS can be used to probe dynamic disorder in crystalline OSCs, but INS and Raman should be used together to obtain complete information of the low energy phonons.
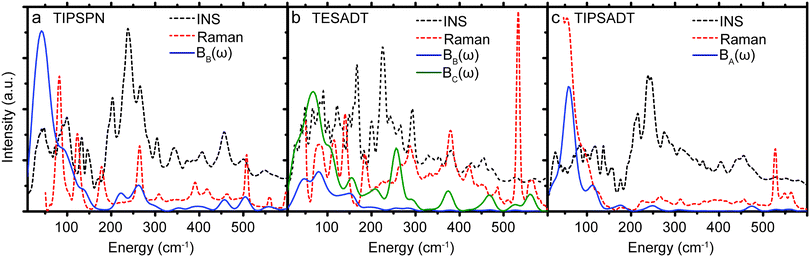 | ||
| Fig. 3 Comparison between INS, Raman, and EP coupling spectra (Bij(ω)) for the substituted acene materials (TIPS-PN, TES-ADT, TIPS-ADT). | ||
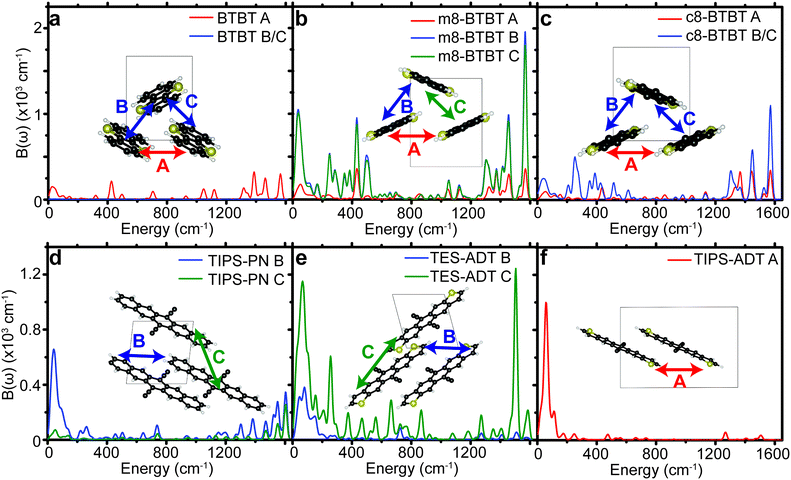 | ||
| Fig. 4 Spectral decomposition of the EP coupling parameter for different pairs of molecules (A, B, or C) for all molecules studied. Sketches of pairs of molecules are shown in the insets of (a–f). | ||
Our experimentally verified EP couplings were used to parameterize the TLT models of μh for each material. The input for the model are the transfer integrals (Jij) and their standard deviation in the high mobility plane (σij) with a single characteristic fluctuation time, τR (which is extracted from the spectral density as detailed in the ESI,† Section S5). In comparing theoretical and experimental μh one must consider that defects and surface effects coming from different substrates make the measurement of the intrinsic single crystal μh extremely challenging. Also, μh can be highly anisotropic in the high-mobility plane (ESI,† Section S6), meaning that the crystalline orientation with respect to the substrate strongly impacts the measured μh. Each of the materials has been heavily studied in the literature except for BTBT, and the reported μh in Table 1 represents reasonable averages from recent publications that performed transistor measurements to measure μh.28,30,34,38 Since there is no available evidence of intrinsic, band-like transport in BTBT in the literature (e.g. experiments showing a decrease in mobility with temperature), it is possible that the value in Table 1 may be indicative of thermally activated transport and thus not comparable with our theoretical results. In addition, these experimental μhs do not hold for every processing condition/device architecture; they are used as a qualitative guide to determine the accuracy of our simulations.
Since TLT treats all phonons classically, but the role of quantum high frequency modes varies across the materials considered, an improved model should be introduced to differentiate between the effect of low and high frequency phonons. The only phonons able to localize the charge are those with characteristic fluctuation time similar to or slower than the quantum delocalization dynamics of the charges. Faster phonons can eventually re-normalize J but this has only a minor effect on μh.26 To introduce a first phonon quantum correction to transient localization theory, we have recomputed μh assuming that the σij on J is only due to low frequency modes, which agrees with another recent theoretical approach on naphthalene.39
For the BTBT-based materials, our simulated μhs qualitatively match the measured values (see μtheory, and μexp in Table 1), in that the theory appropriately ranks the materials in order of highest μh. The temperature dependence of μh for all materials follows a power law, μh ∼ T−a, where the exponent ranges from 0.835–1.19 (see ESI,† Section S6), which agrees with literature reports of “band-like” mobility in OSCs.40,41 The extremely low μh value for BTBT is likely due to extrinsic defects within the crystal that are very effective in disrupting the quasi one-dimensional transport. Since there is no conclusive evidence for band-like transport for BTBT in the literature, it is likely that the reported BTBT μh in Table 1 is more indicative of thermally activated transport, and thus not applicable to our theoretical predictions. However, the predictions for c8-BTBT and m8-BTBT demonstrate excellent quantitative agreement with experimental results.
The simulated μhs for the substituted acene materials are also captured accurately, again properly ranking the materials. Assuming that each experimental μh is comprised of multiple measurements across multiple domains that are isotropically averaged over the high mobility plane, then the experimental mobility should match the average theoretical μh. However, each average theoretical μh overpredicts the experimental μh, which potentially provides information on the impact of defects on μh. Such information might be valuable as future studies can investigate how different types of defects impact μh, which can guide how to optimize processing conditions for OSC thin films. While the experimental μhs in Table 1 represent reasonable averages found in the literature,26 there are examples of μh measurements for materials with potentially fewer extrinsic defects than average. For TIPS-PN, ref. 38 show that devices can exceed 1 cm2 V−1 s−1 (reaching as high as 1.8 cm2 V−1 s−1). For TIPS-ADT, ref. 30 show devices with μh as high as 0.6 cm2 V−1 s−1. In both cases, our TLT results are in quantitative agreement.
Amongst the substituted acenes studied, TES-ADT demonstrates the poorest agreement between μtheory and μexp. The reason is because we only consider one chemical polymorph, and one crystal polymorph, but we know that this material exhibits multiple chemical/crystalline polymorphs.28,29 Such polymorphs don't disrupt the crystal packing as the ADT core has the same orientation, only the sulfurs are positioned at different positions on the backbone. Inclusion of these polymorphs in mobility simulations would introduce disorder in the equilibrium transfer integrals (acting as extrinsic defects), which would decrease the simulated mobility. We expect that TES-ADT films have a greater density of extrinsic defects than c8-BTBT, which would result in a greater disparity between simulated and experimental μhs.
In addition to TLT, we compute the effective masses of each material, to demonstrate how band theory (without nonlocal EP coupling) predicts μh. Without nonlocal EP coupling to scatter charge carriers, the observed μh is determined by the impurity scattering in the film. Assuming a constant impurity scattering relaxation time for all materials, the values for μh predicted by band theory correlate with the inverse of the effective mass. In Table 1, we show that the inverse effective mass (1/m*) for c8-BTBT is equal to m8-BTBT, 1/m* for TIPS-PN is nearly equivalent to TIPS-ADT, and that 1/m* for TES-ADT is more than 1.5-fold greater than any other material. None of these trends are consistent with experimental values. In all cases, TLT improves on these predictions through the inclusion of nonlocal EP coupling, demonstrating the importance of properly accounting for nonlocal EP coupling in any theory that computes μh.
One of the goals of a detailed description of the system Hamiltonian is the identification of useful paths to improve OSC performance. We can, for example, investigate the chemical origin of the different mobility (and dynamic disorder) in m8- and c8-BTBT to establish principles for designing new materials. Low dynamic disorder can be associated with a smaller gradient of the transfer integral (∇Jij), but this is not the case for these molecules, as shown in Fig. 5 where this quantity is represented graphically for the relevant molecular pair. We conclude (with further details given in ESI,† Section S5) that it is the phonon mode polarization that causes the μh difference between these two materials. One can envision a materials discovery approach where molecular arrangement with the smallest ∇Jij are identified first and phonon calculations are used to verify if dynamic disorder will be sufficiently small.
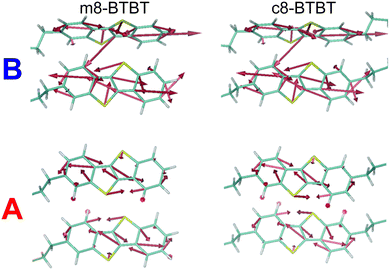 | ||
| Fig. 5 Graphical representation of the transfer integral gradient in transport directions A and B for m8-BTBT and c8-BTBT. | ||
3 Conclusions
The identification of the electron–phonon interactions in OSCs has been a longstanding barrier to accurately computing hole mobility in OSCs without empirical parameterization. We have demonstrated that INS can resolve the low energy phonon spectrum relevant to charge transport and the results agree with Raman data where comparable. In addition, we have demonstrated that EP coupling parameters resolved from accurate simulations of phonon modes (verified by INS and Raman) yields high quality theoretical predictions of μh for OSCs. With the computational barrier removed, we expect that our EP coupling results will drive further advancement in theoretical treatment of OSCs. Specifically, computational approaches can now begin to assess the impact of extrinsic defects, such as grain boundaries, on observed μh of thin film OSCs. Alternative theories of transport can be tested more effectively thanks to the knowledge of virtually exact phonons and EP couplings. We have identified that μh in OSC materials can be improved by finding materials with configurations that minimize the transfer integral gradient.Although our work is most related to charge transport in organic transistor materials, vibrational dynamics are also important to other branches of OSC technology such as exciton separation in OPVs, dynamical processes in triplet emitters, and heat/charge transport in low temperature thermoelectrics. In addition to OSC technologies, our methodology can be applied to diverse fields ranging from topics in catalysis such as reactant binding isomerism/kinetics in MOFs and biological enzymes, to transport mechanisms in energy storage technologies such as fuel cells, CO2 electrolyzers, and artificial photosynthesis. More generally, we have demonstrated a way of integrating phonon measurements and modeling to drive discovery in any field that requires low energy dynamical information.
4 Methods
[1]Benzothieno[3,2-b][1]benzothiophene (BTBT), 2-octyl[1]benzothieno[3,2-b][1]benzothiophene (m8-BTBT), and 2-7-dioctyl[1]benzothieno[3,2-b][1]benzothiophene (c8-BTBT) were synthesized, and purified via silica chromatography. The chemical purity of the samples were determined by NMR spectroscopy. Further details regarding the synthesis, purification, and characterization of BTBT-based materials are in ESI,† Section S1. Concentrated solutions (ca. 75 mg mL−1) in anhydrous toluene (99.99%, Sigma-Aldrich) were made at 50 °C, and further heated to 60 °C to ensure dissolution. Solutions were cooled to 5 °C, and held for five hours to induce crystallization. Crystals were recovered through filtering.6,13-Bis(triisopropylsilylethynyl)pentacene (TIPS-PN) was dissolved in boiling acetone, then filtered and re-boiled before covering and allowing solvent to evaporate over several days in a chemical fume hood. The crystals were collected by vacuum filtration, then washed with 0 °C acetone. 5,11-Bis(triethylsilylethynyl)anthradithiophene (TES-ADT) was dissolved in boiling hexanes, then covered, and allowed the solvent to evaporate over several days in a chemical fume hood. The crystals were collected after complete evaporation of the solvent. 5,11-Bis(triisopropylsilylethynyl)anthradithiophene (TIPS-ADT) was prepared and purified as described in ref. 42.
The inelastic neutron scattering spectra were obtained from the VISION spectrometer24,25 at the Spallation Neutron Source at Oak Ridge National Laboratory. The samples were made up of crystalline powders with crystal dimensions of 10s–100s of μm. Each data set is a powder spectrum with no orientational effects. The samples were cooled down to 5 K before collected scattering data to minimize the effect of the Debye–Waller factor on the final results. Measured neutron data for all 6 samples is publicly available in an archive.43
Phonon calculations were performed using plane-wave density functional theory using the Vienna Ab initio Software Package (VASP)44,45 with projector augmented-wave pseudopotentials.46 Unit cell simulations were performed on BTBT to find the appropriate functional, basis size, k-point sampling density, and convergence tolerances (see ESI,† Section S4). The optPBE van der Waals density functional was chosen with a basis size of 520 eV. The appropriate electronic k-point sampling density was 0.5 Å−1. The electronic energy was converged to 10−8 eV, and the interatomic forces to less than 2 × 10−3 eV Å−1 to consider the molecular geometry fully optimized. The unit cell simulations were performed using the MedeA 2.20.2 software suite with VASP 5.4.1 built in. To perform supercell simulations, we prepared the input files using MedeA, then simulated the supercells on the Edison and Cori supercomputers provided by the National Energy Resource Scientific Computing Center (NERSC). Once the supercells were optimized, we used Phonopy47 to calculate the vibrational modes and energies over a specified phonon k-point sampling grid (different for each material) using the finite difference method in which the atoms were perturbed by 0.01 Å. The vibrational modes, and energies were converted to simulated INS spectra using the oCLIMAX tool provided by Oak Ridge National Laboratory.48 We sampled the phonon Brillouin zone densely enough to achieve convergence in the simulated INS spectrum for each material.
Electron–phonon coupling parameters for each phonon mode of every material are computed via numerical differentiation. The variances of all transfer integrals (Jij) for a particular material are computed according to eqn (3) in the text. These variances are used as an input for hole mobility computation using a tight-binding Hamiltonian approach called transient localization theory. A Hamiltonian is constructed for a finite 2D lattice of 5000 localized sites in which the values for Jij are randomly selected from a Gaussian distribution centered on the equilibrium value of Jij with the variance defined above. The Hamiltonian is diagonalized, and the eigenvectors and eigenvalues are used to compute a localization length for the given snapshot of disorder in the system. The Hamiltonian is reconstructed and diagonalized 25 times to achieve convergence in the computed localization lengths. Full details of transient localization theory is available in ESI,† Section S6.
4.1 Data availability
All neutron data collected in this work is available at https://doi.org/10.25338/B81015.43Author contributions
TFH, AT, R. Faller, and AJM wrote the paper. AJM performed the INS measurements. TFH, VD, and DN computed DFT simulated spectra, and TFH analyzed the results. AT and XX computed electron–phonon coupling. AT computed hole mobilities. R. Fair performed XRD on c8-BTBT. EDG, MAH, and SN synthesized, characterized, and crystallized the BTBT-based materials. CK crystallized TIPS-PN, and TES-ADT using methods obtained from JEA. JEA synthesized, characterized, and crystallized TIPS-ADT. TLM performed FTIR measurements. JG and AKT performed Raman measurements.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the Department of Energy – Basic Energy Sciences, Award DE-SC0010419, including salary for TFH, VD and AJM. This research used resources of the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. AT acknowledges the support of ERC and EPSRC (grant EP/N021754/2 and ARCHER supercomputing time) for electron–phonon simulations. SN, MAH and EDG acknowledge financial support from the Dow Chemical Company and RFair and EDG also acknowledge financial support from DMR-1629006 for synthesis and measurement of BTBTs. JEA thanks the National Science Foundation (DMREF-1627428) for support of organic semiconductor exploration of substituted acenes. AKT and JKG acknowledge financial support from the National Science Foundation (CHE-1506558) for Raman measurements. AT wishes to thank Sergio Ciuchi (L'Aquila) for his help with transient localization theory.References
- S. R. Forrest, The path to ubiquitous and low-cost organic electronic appliances on plastic, Nature, 2004, 428, 911–918 CrossRef CAS PubMed.
- C. D. Muller, A. Falcou, N. Reckefuss, M. Rojahn, V. Wiederhirn, P. Rudati, H. Frohne, O. Nuyken, H. Becker and K. Meerholz, Multi-colour organic light-emitting displays by solution processing, Nature, 2003, 421(6925), 829–833 CrossRef PubMed.
- S. Reineke, F. Lindner, G. Schwartz, N. Seidler, K. Walzer, B. Lussem and K. Leo, White organic light-emitting diodes with fluorescent tube efficiency, Nature, 2009, 459(7244), 234–U116 CrossRef CAS PubMed.
- J. W. Chen and Y. Cao, Development of novel conjugated donor polymers for high-efficiency bulk-heterojunction photovoltaic devices, Acc. Chem. Res., 2009, 42(11), 1709–1718 CrossRef CAS PubMed.
- H. Usta, A. Facchetti and T. J. Marks, n-channel semiconductor materials design for organic complementary circuits, Acc. Chem. Res., 2011, 44(7), 501–510 CrossRef CAS PubMed.
- Y. Mei, M. A. Loth, M. Payne, W. Zhang, J. Smith, C. S. Day, S. R. Parkin, M. Heeney, I. McCulloch, T. D. Anthopoulos, J. E. Anthony and O. D. Jurchescu, High mobility field-effect transistors with versatile processing from a small-molecule organic semiconductor, Adv. Mater., 2013, 25(31), 4352–4357 CrossRef CAS PubMed.
- H. Sirringhaus, 25th anniversary article: organic field-effect transistors: the path beyond amorphous silicon, Adv. Mater., 2014, 26(9), 1319–1335 CrossRef CAS PubMed.
- S. Fratini, D. Mayou and S. Ciuchi, The transient localization scenario for charge transport in crystalline organic materials, Adv. Funct. Mater., 2016, 26(14), 2292–2315 CrossRef CAS.
- H. Oberhofer, K. Reuter and J. Blumberger, Charge transport in molecular materials: an assessment of computational methods, Chem. Rev., 2017, 117(15), 10319–10357 CrossRef CAS PubMed.
- H. Oberhofer and J. Blumberger, Revisiting electronic couplings and incoherent hopping models for electron transport in crystalline c60 at ambient temperatures, Phys. Chem. Chem. Phys., 2012, 14, 13846–13852 RSC.
- L. Wang and D. Beljonne, Flexible surface hopping approach to model the crossover from hopping to band-like transport in organic crystals, J. Phys. Lett., 2013, 4(11), 1888–1894 CAS.
- W. Si and C.-Q. Wu, Decoherence and energy relaxation in the quantum-classical dynamics for charge transport in organic semiconducting crystals: an instantaneous decoherence correction approach, J. Chem. Phys., 2015, 143(2), 024103 CrossRef PubMed.
- A. Heck, J. J. Kranz, T. Kubař and M. Elstner, Multi-scale approach to non-adiabatic charge transport in high-mobility organic semiconductors, J. Chem. Theory Comput., 2015, 11(11), 5068–5082 CrossRef CAS PubMed.
- D. Di Nuzzo, C. Fontanesi, R. Jones, S. Allard, I. Dumsch, U. Scherf, E. von Hauff, S. Schumacher and E. Da Como, How intermolecular geometrical disorder affects the molecular doping of donor-acceptor copolymers, Nat. Commun., 2015, 6, 6460 CrossRef PubMed.
- Y. Q. Gao, T. P. Martin, A. K. Thomas and J. K. Grey, Resonance raman spectroscopic- and photocurrent imaging of polythiophene/fullerene solar cells, J. Phys. Chem. Lett., 2010, 1(1), 178–182 CrossRef CAS.
- Y. Furukawa, K. Seto, K. Nakajima, Y. Itoh, J. Eguchi, T. Sugiyama and H. Fujimura, Infrared and raman spectroscopy of organic thin films used for electronic devices, Vib. Spectrosc., 2012, 60, 5–9 CrossRef CAS.
- A. Brillante, I. Bilotti, R. G. Della Valle, E. Venuti and A. Girlando, Probing polymorphs of organic semiconductors by lattice phonon raman microscopy, CrystEngComm, 2008, 10, 937–946 RSC.
- S. Illig, A. S. Eggeman, A. Troisi, L. Jiang, C. Warwick, M. Nikolka, G. Schweicher, S. G. Yeates, Y. Henri Geerts, J. E. Anthony and H. Sirringhaus, Reducing dynamic disorder in small-molecule organic semiconductors by suppressing large-amplitude thermal motions, Nat. Commun., 2016, 7, 10736 CrossRef CAS PubMed.
- T. F. Harrelson, Y. Q. Cheng, J. Li, I. E. Jacobs, A. J. Ramirez-Cuesta, R. Faller and A. J. Moulé, Identifying atomic scale structure in undoped/doped semicrystalline p3ht using inelastic neutron scattering, Macromolecules, 2017, 50(6), 2424–2435 CrossRef CAS.
- C. Bousige, C. M. Ghimbeu, C. Vix-Guterl, A. E. Pomerantz, A. Suleimenova, G. Vaughan, G. Garbarino, M. Feygenson, C. Wildgruber, F.-J. Ulm, R. J. M. Pellenq and B. Coasne, Realistic molecular model of kerogen's nanostructure, Nat. Mater., 2016, 15(5), 576–582 CrossRef CAS PubMed.
- X. Han, H. G. W. Godfrey, L. Briggs, A. J. Davies, Y. Cheng, L. L. Daemen, A. M. Sheveleva, F. Tuna, E. J. L. McInnes, J. Sun, C. Drathen, M. W. George, A. J. Ramirez-Cuesta, K. M. Thomas, S. Yang and M. Schröder, Reversible adsorption of nitrogen dioxide within a robust porous metal-organic framework, Nat. Mater., 2018, 17, 691–696 CrossRef CAS PubMed.
- C. Cuadrado-Collados, J. Fernandez-Catala, F. Fauth, Y. Q. Cheng, L. L. Daemen, A. J. Ramirez-Cuesta and J. Silvestre-Albero, Understanding the breathing phenomena in nano-zif-7 upon gas adsorption, J. Mater. Chem. A, 2017, 5, 20938–20946 RSC.
- P. C. H. Mitchell, S. F. Parker, A. J. Ramirez-Cuesta and J. Tomkinson, Vibrational Spectrocopy with Neutrons, 3 of Neutron Techniques and Applications, World Scientific, 2005 Search PubMed.
- P. A. Seeger, L. L. Daemen and J. Z. Larese, Resolution of vision, a crystal-analyzer spectrometer, Nucl. Instrum. Methods Phys. Res., Sect. A, 2009, 604(3), 719–728 CrossRef CAS.
- S. F. Parker, A. J. Ramirez-Cuesta and L. Daemen, Vibrational spectroscopy with neutrons: recent developments, Spectrochim. Acta, Part A, 2018, 190, 518–523 CrossRef CAS PubMed.
- S. Fratini, S. Ciuchi, D. Mayou, G. T. de Laissardière and A. Troisi, A map of high-mobility molecular semiconductors, Nat. Mater., 2017, 16, 998 CrossRef CAS PubMed.
- J. M. Adhikari, P. Zhan, B. D. Calitree, W. Zhang, I. E. Jacobs, A. J. Moulé, S. T. Milner, J. K. Maranas, M. A. Hickner and E. D. Gomez, Side chain addition suppresses lattice fluctuations and enhances charge mobilities in benzothienobenzothiophenes, submitted.
- A. K. Hailey, A. J. Petty, J. Washbourne, K. J. Thorley, S. R. Parkin, J. E. Anthony and Y.-L. Loo, Understanding the crystal packing and organic thin-film transistor performance in isomeric guest–host systems, Adv. Mater., 2017, 29(23), 1700048 CrossRef PubMed.
- J. E. Anthony, Functionalized acenes and heteroacenes for organic electronics, Chem. Rev., 2006, 106(12), 5028–5048 CrossRef CAS PubMed.
- K. Schulze, T. Bilkay and S. Janietz, Triisopropylsilylethynyl-functionalized anthradithiophene derivatives for solution processable organic field effect transistors, Appl. Phys. Lett., 2012, 101(4), 043301 CrossRef.
- V. S. Vyas, R. Gutzler, J. Nuss, K. Kern and B. V. Lotsch, Optical gap in herringbone and[small pi]-stacked crystals of[1]benzothieno[3,2-b]benzothiophene and its brominated derivative, CrystEngComm, 2014, 16, 7389–7392 RSC.
- T. Izawa, E. Miyazaki and K. Takimiya, Molecular ordering of high-performance soluble molecular semiconductors and re-evaluation of their field-effect transistor characteristics, Adv. Mater., 2008, 20(18), 3388–3392 CrossRef CAS.
- J. E. Anthony, J. S. Brooks, D. L. Eaton and S. R. Parkin, Functionalized pentacene: improved electronic properties from control of solid-state order, J. Am. Chem. Soc., 2001, 123(38), 9482–9483 CrossRef CAS PubMed.
- M. M. Payne, S. R. Parkin, J. E. Anthony, C.-C. Kuo and T. N. Jackson, Organic field-effect transistors from solution-deposited functionalized acenes with mobilities as high as 1 cm2 V−1 s−1, J. Am. Chem. Soc., 2005, 127(14), 4986–4987 CrossRef CAS PubMed.
- S. Shinamura, E. Miyazaki and K. Takimiya, Synthesis, properties, crystal structures, and semiconductor characteristics of naphtho[1,2-b:5,6-b′]dithiophene and -diselenophene derivatives, J. Org. Chem., 2010, 75(4), 1228–1234 CrossRef CAS PubMed.
- A. Troisi and G. Orlandi, Charge-transport regime of crystalline organic semiconductors: diffusion limited by thermal off-diagonal electronic disorder, Phys. Rev. Lett., 2006, 96, 086601 CrossRef PubMed.
- V. Coropceanu, R. S. Sánchez-Carrera, P. Paramonov, G. M. Day and J.-L. Brédas, Interaction of charge carriers with lattice vibrations in organic molecular semiconductors: naphthalene as a case study, J. Phys. Chem. C, 2009, 113(11), 4679–4686 CrossRef CAS.
- S. K. Park, T. N. Jackson, J. E. Anthony and D. A. Mourey, High mobility solution processed 6,13-bis(triisopropyl-silylethynyl) pentacene organic thin film transistors, Appl. Phys. Lett., 2007, 91(6), 063514 CrossRef.
- N.-E. Lee, J.-J. Zhou, L. A. Agapito and M. Bernardi, Charge transport in organic molecular semiconductors from first principles: the bandlike hole mobility in a naphthalene crystal, Phys. Rev. B, 2018, 97, 115203 CrossRef.
- T. Sakanoue and H. Sirringhaus, Band-like temperature dependence of mobility in a solution-processed organic semiconductor, Nat. Mater., 2010, 9, 736 CrossRef CAS PubMed.
- Y. Mei, P. J. Diemer, M. R. Niazi, R. K. Hallani, K. Jarolimek, C. S. Day, C. Risko, J. E. Anthony, A. Amassian and O. D. Jurchescu, Crossover from band-like to thermally activated charge transport in organic transistors due to strain-induced traps, Proc. Natl. Acad. Sci. U. S. A., 2017, 114(33), E6739–E6748 CrossRef CAS PubMed.
- M. M. Payne, S. A. Odom, S. R. Parkin and J. E. Anthony, Stable, crystalline acenedithiophenes with up to seven linearly fused rings, Org. Lett., 2004, 6(19), 3325–3328 CrossRef CAS PubMed.
- T. Harrelson, V. Dantanarayana, R. Faller and A. Moule, Vibrational neutron spectroscopy data for small molecule organic semiconductors, UC Davis Dash, 2017, dataset Search PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6(1), 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- A. Togo and I. Tanaka, First principles phonon calculations in materials science, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- A. Ramirez-Cuesta, aclimax 4.0.1, the new version of the software for analyzing and interpreting ins spectra, Comput. Phys. Commun., 2004, 157(3), 226–238 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8mh01069b |
| This journal is © The Royal Society of Chemistry 2019 |