Contrasting motif preferences of platinum and gold nanoclusters between 55 and 309 atoms

Abstract

The atomic structure of size-selected Pt clusters in the range 10–600 atoms is investigated with aberration-corrected scanning transmission electron microscopy and reveals significantly different behaviour from the existing data for Au clusters. The Pt clusters show a dominance of the FCC motif from relatively small sizes, whereas traditionally for Au multiple motifs – the icosahedron, decahedron and FCC motifs (and related structures) compete. The new data motivates a comprehensive computational investigation to better understand similarities and differences in the structures and energetics of the two different metallic clusters. Low energy structures of Pt and Au clusters with 55, 101, 147, 228 and 309 atoms (±2%) are identified using a global optimisation algorithm, and the relative energies found by local minimisation using density functional theory. Our computational results support the experimental observations; for Au clusters all motifs are comparably stable over the whole size range, whereas for Pt, the motifs only compete at the smallest sizes, after which the FCC motif is the most stable. Structural analysis suggests the greater tendency of Au towards amorphisation enables the icosahedron and decahedron to remain competitive at larger sizes.

---

1 Introduction

Nanoclusters are finding increasing use in a wide range of fields from sustainable energy production and storage¹ to biomedical applications.² The properties of nanoclusters are highly dependent on size and atomic-scale morphology. For example, despite being inert in the bulk,³ Au nanoclusters present interesting catalytic properties such as high activity for CO oxidation^4–6 and selective oxidation of hydrocarbons.⁷ Pt nanoclusters are used extensively as catalysts in the green energy sector; in particular in fuel cells^8,9 and electrochemical hydrogen formation.¹⁰ The recently developed synthetic technique of cluster beam deposition enables precise control over size and deposition energy such that a population of supported clusters with a narrow size distribution can be generated.^11,12 To understand the properties of these nanoclusters it is necessary to elucidate their atomic-scale structure.

A number of experimental investigations have sought to probe the morphology of Au clusters. While many small (<100 atoms) Au clusters are rather disordered,¹³ a high-symmetry, tetrahedral isomer of Au₂₀ has been identified (amongst others).^14,15 Au₅₅ clusters are found to exhibit low-symmetry morphologies, and a hybrid, chiral isomer was observed experimentally (again, among other structures),¹⁶ in accordance with theoretical predictions.^17–19 For larger clusters (several hundred atoms) higher symmetry structures are observed, such as the truncated decahedral motif, identified by X-ray powder diffraction²⁰ and HRTEM.²¹ For Au₃₀₉, observed clusters can be assigned to distinct structural classifications commonly observed in nanoclusters, namely decahedral (Dh), octahedral (FCC) or icosahedral (Ih) motifs.²²

All three motifs have also been observed at 561, 742 and 923 atoms, although the proportion of metastable Ih clusters can be limited by control of the cluster source parameters.²³ For 561 atoms, at high temperatures both Dh and FCC clusters are observed but at lower temperatures the metastable Dh isomer transforms to FCC.²⁴ From the high-temperature data, the energy difference between the isomers is determined experimentally to be only 0.040 ± 0.020 eV.

Relatively little is known experimentally about the morphology of Pt clusters, particularly bare or unsupported clusters. Non-crystalline to crystalline transitions have been observed using HRTEM and EXAFS for supported Pt clusters.²⁵ The size at which the transition occurs is dependent on the support but is in the vicinity of 1.5 nm. Dh nanoclusters were rarely observed. A preference for ordered structures has been observed for polymer-capped Pt²⁶ and Pt–Pd core–shell particles, where the presence of Pt atoms in the core tended to facilitate ordering.²⁶

Experimental determination of the most thermodynamically stable structures of deposited clusters is not a trivial task. The process can be hampered by heating under the electron beam as well as kinetic trapping during growth. Gas phase formation conditions can be tuned to reduce the formation of far-from equilibrium structures,²³ but this does not completely eliminate other factors. Theoretical calculations can aid in deducing the equilibrium structure of clusters by quantifying the relative energies of clusters, as well as by explicitly considering the effects of temperature and by simulating growth processes.^27,28

A variety of calculations have been performed for both Au and Pt clusters, from survey calculations over a large cluster size range using an empirical potential²⁹ to detailed global optimisations at a few selected sizes.^17,18,30,31 Many studies have provided support for the notion of a crossover (either gradual or abrupt) from Ih to Dh to FCC as the cluster size is increased.^{20,29,32–36} However, it should be noted that both Dh and FCC have been shown to be competitive structures over a wide range of sizes;^29,37 recently, it has been found that Dh and FCC motif preference continues to oscillate even at sizes up to 4000 atoms.³⁸ Furthermore, small changes to the theoretical description can have a large impact on the relative energies of these motifs.

Detailed theoretical studies of Au clusters at selected sizes have shown the close competition between the Dh and FCC structures. Global optimisations of Au clusters with 315 ± 15 atoms found predominantly Ih-like clusters, although FCC-like clusters were also observed.³⁹ This study also found that energy differences between motifs were small (<1 meV) and that the lowest energy structural motif changed over the size range considered (300–330 atoms). A wider size range was considered by Bao et al. (13–318 atoms); again, it was found that the most stable motif often changed with the addition of a single atom.⁴⁰

Molecular dynamics simulations have recently been employed to study the growth of Au clusters from 13 to 923 atoms at several growth temperatures.²⁷ Here it was observed that, after solidification, the vast majority of clusters retained their underlying motif for the remainder of the simulation. This suggests that the structures observed experimentally for Au clusters are usually due to kinetic trapping, rather than energetic stability.

Theoretical calculations for Pt are relatively scarce. An early global optimisation study of Pt clusters, with up to 60 atoms using an empirical potential, found low-symmetry clusters to be the most stable.⁴¹ This was confirmed using density functional theory (DFT), where a reconstruction of the five-fold vertices of an Ih cluster results in a more stable cluster than the perfect Mackay Ih cluster.⁴² DFT calculations investigated the energetics of competing isomers of Pt clusters, largely focussed on clusters with fewer than 38 atoms.⁴³ FCC structures were observed for sizes smaller than 21 atoms, then again from 24–38 atoms. The study is less comprehensive for clusters larger than 38 atoms but suggests continued dominance of the FCC motif.

In the current study, we present experimental results showing the FCC motif dominance of Pt clusters, which contrast with the rather different behaviour of Au clusters documented in the literature. A systematic computational investigation into both Au and Pt clusters is therefore performed. Low energy structures for a range of cluster sizes are determined using a combination of global and local optimisation techniques using empirical potentials and density functional theory. The result is a comprehensive overview of the structures and energies of Pt and Au clusters, within a common theoretical framework. Analysis of the calculated energies and structures rationalise some of the observed experimental structural similarities and differences between these two kinds of clusters.

2 Methodology

2.1 Experimental methods

2.1.1 Production of nanoclusters. Pt clusters were produced with a magnetron sputtering, gas condensation beam source^44,45 and selected in size with a lateral time-of-flight mass selector⁴⁶ prior to deposition, with a resolving power of M/ΔM ∼ 20. Two kinds of samples were generated: clusters of a single mass (55, 147 and 309 atoms) and also a size range (10–600 atoms) for which the mass selector was run over size selected ranges. Argon gas was used to create a DC plasma that sputters Pt atoms from a pure Pt target (99.95%, from PI-KEM, U.K.) at an average pressure of 10⁻⁷ Torr. The hot atoms were condensed into clusters in a mixture of argon and helium gas, the walls of which were cooled by liquid nitrogen. Ar and He flow rates were both 200 sccm. Clusters were produced under “slow growth” conditions²³ (250 mm condensation length, 150 W magnetron power) and deposited onto holey carbon TEM films supported on copper grids. The deposition energy was approximately 1 eV per atom to ensure the clusters were soft-landed.

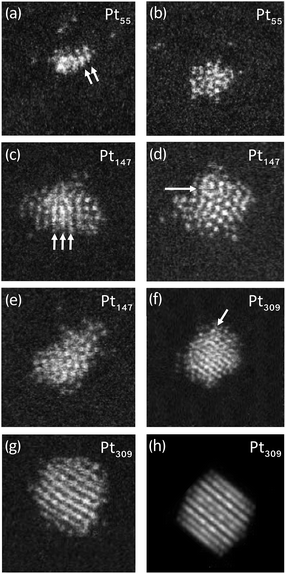
Initially samples of a range of cluster sizes were made so that the distribution of cluster motifs could be investigated across a wide mass range. Specifically, three samples were made covering the 10 to 600 atom range: 10–147, 147–309 and 309–600 atoms. 700 clusters were imaged in total and there was an approximately even distribution of each cluster size. Three samples were made (rather than one) so that the density of clusters could be kept low, preventing aggregation, whilst still having enough clusters of each size to image. For these samples, the cluster size was determined based on the HAADF intensity (vide infra). To investigate the structures in more detail, single sized clusters were produced with 55, 147 and 309 atoms, where the cluster size was determined by the mass selector; the mass resolution was approximately ±2.5%.

2.1.2 Characterisation using STEM. The imaging of the clusters was performed using a 200 keV (JEOL 2100F) STEM with a spherical aberration corrector (CEOS) and resulting probe size of 0.1 nm. The HAADF detector's inner and outer collection angles were 62 and 164 mrad, respectively. This enabled the intensity of the images of the clusters to be used to calculate the number of atoms in each cluster,⁴⁷ whilst using the background measurements to normalise between grids.

Multiple electron scattering simulations were performed for model Ih, Dh and FCC clusters with 55, 147, 309 and 561 atoms using the QSTEM software.⁴⁸ Simulations included the full range of possible orientations of the clusters, generating a “simulation atlas”.⁴⁹ Imaged clusters were then compared with the simulation atlas to determine the atomic structure of the cluster. Distinctive patterns were noted e.g. the images in the FCC atlas exhibit parallel lines, while the Ih atlas shows five fold symmetry often with rings present. These characteristic features made it possible to identify the structural motifs of clusters that did not have exactly the same size as the simulation atlas.

2.2 Computational methods

Clusters at the so-called magic number sizes, 55, 147 and 309 atoms were chosen as a focus for study, as well as two cluster sizes between these, 101 and 228 atoms. The magic numbers represent cluster sizes at which a closed-shell structure is possible for each of the three motifs (Dh, FCC and Ih). The intermediate regions were chosen to explore size regimes between the sizes that have traditionally dominated the literature, as well as to allow for the possibility of clusters that are structurally different from those at the magic sizes. Clusters with mass ± ∼2% were considered around each of these sizes chosen, to reflect size variation typical in an experiment. The studied cluster sizes were: 55 ± 1, 101 ± 2, 147 ± 3, 228 ± 4 and 309 ± 6 atoms.

In this study we employ a workflow in which we (i) manually construct an ensemble of low-energy starting clusters, (ii) explore the surrounding potential energy surface using a global optimisation algorithm then (iii) refine the resulting clusters using DFT. This yields low energy, often asymmetric or distorted Ih, Dh and FCC clusters. All calculations here neglect the influence of temperature and support.

2.2.1 Generating the initial ensemble of structures. The ensemble of initial structures was constructed using a recently-developed interpolation scheme³⁸ to estimate the lowest energy clusters of each motif for any size. This scheme is based on the premise that asymmetric FCC or Dh or Ih clusters that may have incomplete (stepped/kinked) surfaces or present adatoms are relatively stable if their “parent”, symmetric clusters are themselves stable. For a given number of atoms, surrounding symmetric clusters were constructed and the requisite number of atoms removed to reach the desired cluster size. This was repeated for all nearby symmetric structures yielding an ensemble of asymmetric clusters of a given size. More details can be found in the ESI.†

All ensemble structures were generated using the Atomic Simulation Environment⁵⁰ (ASE) version 3.9.0 and locally minimised using the software package EON⁵¹ and the RGL interatomic potential with parameters from Baletto et al.²⁹ (hereafter referred to as the empirical potential (EP) approach). The RGL potential, and this particular parametrisation, was chosen as it is widely used for metallic clusters.

2.2.2 Global optimisation. Global optimisation (GO) calculations were performed using the recently-developed “global optimisation using saddle traversals” (GOUST) algorithm⁵² as implemented in EON with the RGL potential for interatomic interactions. The method explores the potential energy surface by locating first-order saddle points and their connected minima, applying the minimum-mode following method^53,54 with the bowl breakout extension.⁵⁵ From the initial local minimisation carried out on each of the ensemble structures, GO calculations were performed for each of the lowest energy Ih, four lowest energy Dh and four lowest energy FCC nanoclusters and run until at least 130 minima were found in each case. A second GO run was initiated for each of the lowest energy structures, with a larger initial displacement to attempt a wider exploration of the potential energy surface near each initial structure. Verification of the GOUST algorithm was undertaken through comparison with results obtained from a genetic algorithm where it was found to perform equal to or better than the genetic algorithm. For discussion and validation of the global optimisation techniques, see the ESI.†

2.2.3 DFT refinement. Structures from all GO runs for each cluster motif of a given number of atoms were combined and the three lowest energy clusters of each motif, FCC, Dh and Ih, were then re-optimized using DFT. The DFT calculations were performed with the PBE⁵⁶ exchange–correlation functional. Each cluster was placed in a cubic supercell and separated from its nearest replica by at least 10 Å in each dimension. The Brillouin zone sampling was restricted to the gamma point only. A plane wave basis set with an energy cutoff of 229 eV was used to describe the valence electrons, while the core electrons were treated using the PAW^57,58 representation. All DFT calculations were performed using the VASP software package.⁵⁹

3 Results and discussion

3.1 Experimental results for Pt clusters soft-landed on carbon films

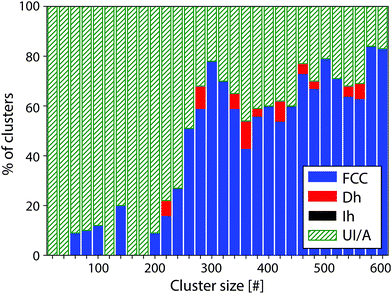
The identification of the cluster structures was performed by comparison of the experimental images to simulated QSTEM atlases, allowing for characteristic features in the experimental clusters to be identified, and for these clusters to be assigned a motif. This laborious manual process is more effective than automated image recognition at the present time. FCC clusters exhibit parallel planes of atoms that show up as parallel lines in the QSTEM atlas. Dh clusters often show curved lines as well as areas of more distinct dots, while Ih clusters show more circular contours often with the patterns radiating out from the centre of the cluster. These distinct patterns allow clusters of any size to be identified, which avoids the need to generate a QSTEM atlas for every size cluster investigated, and allows us to assign clusters over a wide size range. If no positive identification can be made, the cluster is classed as unidentified/amorphous (UI/A). Clusters that are UI/A do not match any of the three candidate structures considered, but do sometimes exhibit distinctive features.

The proportion of Pt clusters assigned to each motif between 10 and 600 atoms is shown in Fig. 1 and tabulated in the ESI.† At large sizes (>300 atoms) FCC is the dominant motif (66%), while 31% of the clusters are UI/A and 3% of the clusters were found to be Dh and no Ih structures were found. However, for smaller clusters (<300 atoms) most clusters are UI/A (80%). The FCC motif was also present (19%) but only a minimal appearance of the Dh structure was seen (1%); again, no Ih clusters were seen. Due to the high proportion of UI/A clusters in this region, exact isomer proportions in Fig. 1 should be treated with caution as our assignments are rather conservative.

Fig. 1 Overview of the dominant motif for Pt clusters between 10 and 600 atoms, classified as either FCC (blue), Dh (red), Ih (black) or unidentified/amorphous (UI/A, green). 700 clusters were imaged in total. The bin size is chosen for ease of viewing and does not represent the experimental uncertainty in cluster size.

To investigate in more detail the high proportion of UI/A clusters, size-selected clusters containing 55, 147 and 309 atoms were produced and imaged; representative images can be found in Fig. 2. When these clusters were imaged a more conservative approach was taken in motif assignment when comparing to QSTEM atlases. For both 55 and 147 atoms, all clusters were identified as UI/A but some distinct features such as parallel lines, characteristic of FCC clusters (Fig. 2a) and the appearance of rings with dots, characteristic of Ih clusters (Fig. 2d) could be seen. These patterns suggest the possibility of ordered regions within glassy overall structures, which do not extend sufficiently to match simulations to allow for assignment of these clusters as traditional FCC, Dh or Ih motif. For the 309 atom clusters, 34% of clusters were assigned as UI/A. However, some of these could be assigned as twinned FCC clusters, with non-continuous planes (Fig. 2f).

Fig. 2 Representative HAADF STEM images of Pt clusters (a): UI/A Pt₅₅ cluster showing parallel lines; (b) UI/A Pt₅₅ with no discernible structure; (c) UI/A Pt₁₄₇ cluster showing a parallel lines; (d) UI/A Pt₁₄₇ cluster showing a ring-dot pattern; (e) UI/A Pt₁₄₇ cluster with no discernible structure; (f) Pt₃₀₉ cluster showing a possible twin plane; (g) FCC Pt₃₀₉ cluster; (h) Pt₃₀₉ electron scattering simulation, corresponding to the cluster seen in (g).

3.2 Theoretical results for Pt and Au clusters

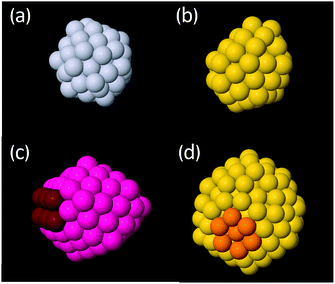
Cluster structures were found using global optimisation methods with an empirical potential (EP) and then refined using DFT before reporting the final structures and energies. Refinement of the EP structures was found to be necessary as the EP often predicted (i) the wrong ordering of the energies of clusters within a structural motif (e.g. the wrong truncation of a given motif) and (ii) the wrong energy ordering between the Ih, Dh and FCC motifs. Furthermore, notable differences in the structures were also observed between EP starting structures and relaxed DFT structures. For a full discussion of the results obtained using the EP, see the ESI.† Henceforth, only DFT structures and energies will be discussed. While this study refined the energies of several low-lying clusters of each motif, rather than just the lowest energy isomer, the use of an EP followed by refinement by DFT is not equivalent to direct exploration of the DFT potential energy surface therefore some low energy isomers may be missed by the present approach. Regrettably, DFT-based global optimisation is prohibitive for clusters of this size.

3.2.1 Cluster morphology. Clusters were assigned to a given motif by eye, based on a majority of structural features such that none of the clusters in the computational study were assigned to be UI/A.
3.2.1.1 Icosahedral clusters. Examples of the types of low energy Ih structures calculated are shown in Fig. 3. For Pt and Au clusters in the 54–56 atom bracket, the structures are rather distorted (Fig. 3a and b, respectively), especially for Au, in agreement with previous literature.⁶⁰ We assign these structures to the Ih motif here due to the appearance of Ih-like features but we note that the heavy distortion of the clusters makes this assignment somewhat subjective.

Fig. 3 Examples of low energy icosahedral (Ih) clusters as calculated using DFT. (a) Distorted lowest energy Ih structure of Pt₅₅; (b) distorted lowest energy Ih structure of Au₅₅; (c) distorted Ih cluster common in 99–103 atom bracket for both Pt and Au, exhibiting both Ih (pink) and Dh features (red). (d) Distorted Ih Au₁₄₇ with a highlighted rosette surface feature (orange). Grey: Pt; yellow: Au; pink: structures common to both Au and Pt.

For clusters between 144 and 150 atoms, the lowest energy Ih clusters for both Pt and Au exhibit predominantly ordered structures with some surface reconstruction; perfect Ih are not the most stable structure for either metal. A common reconstruction is the so-called rosette reconstruction, where six atoms form a ring with a central atom slightly depressed within the ring (Fig. 3d).⁴² The rosette feature is typically more pronounced in Au than Pt. Other surface reconstructions include the appearance of small (100)-like facets. Previous computational studies have also concluded that distorted Ih structures are more stable than perfect Ih structures at a cluster size of 147 atoms.^30,61 For the largest clusters considered between 303 and 315 atoms, similar reconstructions are also observed but they tend to be more localised and the remainder of the cluster is ordered.

The 99–103 atom and the 224–232 atom size brackets are interesting size ranges as they lie directly between magic sizes, i.e. they are as far as possible from a closed shell Ih. Accordingly, the Ih structures that are observed in these regions are distorted. A common feature is a severely truncated Ih, where a significant portion of the cluster is missing. This causes the Ih features of these clusters to distort and strong Dh features can also be seen, such as (100) facets and re-entrant edges typical of a Marks decahedron (Fig. 3c).

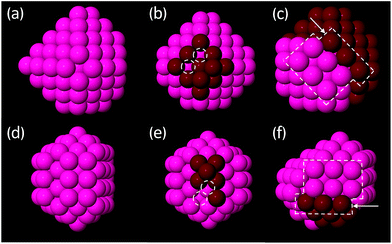
3.2.1.2 Decahedral and FCC clusters. The calculated low energy Dh and FCC structures of Au and Pt are common across both metals and are typically quite ordered. Across all size brackets, the features observed within each motif for both metals form three distinct categories: (1) perfect, closed-shell clusters (Fig. 4a and d) (2) open-shell clusters with incomplete facets and/or with adatoms (Fig. 4b and e) or (3) clusters with a stacking fault, which may, in addition to this, be open-shell (Fig. 4c and f). The perfect, closed-shell structures (1) are not necessarily symmetric with respect to the size of the facets/depths of the corners but all facets are complete and the surfaces do not contain adatoms, nor do these clusters have any stacking faults.

Fig. 4 Examples of low energy decahedral (Dh) and octahedral (FCC) clusters typical of both Au and Pt, in all size brackets, as calculated with DFT. (a) Closed-shell FCC: deeper truncation at one corner but all exposed facets are complete; (b) open-shell FCC: missing atoms on a (100) facet; (c) FCC with stacking fault; (d) closed-shell Dh: Marks Dh with one (100) facet larger than the others; (e) open-shell Dh: atoms missing on a (100) facet; (f) Dh with stacking fault. Dark red atoms indicate either facets that are incomplete (b and e) or are used to illustrate the two parts of the cluster either side of the stacking fault (c and f). Dashed white circles indicate missing atoms and arrows indicate stacking faults.

Stacking faults (Fig. 4c and f) are quite common in the smaller clusters but are rarely observed for clusters greater than 100 atoms. Stacking faults are a bulk (rather than a surface) defect and have an associated energy penalty that increases with the amount of bulk.⁶² Due to the high surface area to bulk ratio of small clusters, bulk energy penalties are of little consequence at small sizes. As the size of the cluster increases, bulk effects dominate more and stacking faults destabilise the clusters, explaining their absence in the low-energy structures of the larger clusters.

For all size brackets, the most stable structures within a given motif are very similar for both metals. For example, the lowest energy Dh clusters around 147 atoms, for both Pt and Au, are based on a Dh cluster with (100) facets that contain 6 atoms and Marks edges with a depth of 1 atom. This further emphasises the similarity in structure of the Pt and Au clusters. The change in structure upon increasing the cluster size by one atom is typically the simple addition of one more atom to a (100) facet of the same base structure.

3.2.2 Cluster energetics. The calculated energy of the most stable cluster of each motif (Ih, Dh and FCC) for each metal is shown in Fig. 5, for all of the size ranges considered here, enabling comparison of the calculated motif dominance for Au and Pt clusters as a function of size.

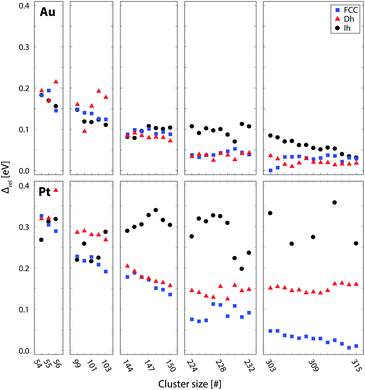Fig. 5 Lowest energy structures from each structural motif for Au (top) and Pt (bottom) clusters, as calculated using DFT; FCC (blue), Dh (red), and Ih (black). Stability of clusters is represented by the quantity Δ = (E_tot − NE_bulk)/N^2/3, where E_tot is the energy of the cluster, N the number of atoms and E_bulk is the energy per atom in the bulk FCC crystal. Δ essentially divides the excess energy of the cluster by the approximate number of surface atoms, thereby enabling facile comparison of stability of clusters of different sizes. However, this has no effect on the relative stability of the motifs (see ESI†). Values of Δ are given relative to the most stable cluster for each metal (Au or Pt). Due to the high instability of the Ih clusters > 300 atoms, only selected Ih clusters were calculated in this region.

For both Pt and Au, the smaller clusters (54–56 and 99–103 brackets) show competition between the (distorted) Ih and FCC motifs. In these size brackets, Pt shows more FCC dominance than Au, while for Au, Ih is more stable more often. The Dh motif is only found to be the lowest energy motif once, for Au₁₀₀. The dominance of Ih clusters for Au at small sizes is expected from general arguments of cluster stability; Ih clusters have the most favourable surface packing of the three motifs and at small sizes the high internal strain of the Ih is not severe enough to offset this. The stability of Pt FCC clusters at small sizes is less intuitive as it has the least favourite surface packing. However, previous theoretical work by Kumar and Kawazoe found FCC clusters to be the dominant motif for Pt from sizes of around 40 atoms.⁴³ They postulated that the stability of the FCC isomer was due to growth from stable triangular Pt₆ and square planar Pt₉ clusters, such that larger clusters rich in these features (such as the FCC motif) are particularly stable.

For medium-sized clusters (144–150 atom size bracket), Au exhibits close competition between all three motifs, suggesting the presence of multiple motifs for clusters generated in this size range. Au does, however, have a slight preference for Dh at this size, with 5 out of 7 of the clusters in this bracket finding the Dh motif to be the most stable. For Pt, within this same size bracket, the Dh and FCC motifs compete while the Ih clusters are very unstable.

For Au clusters of 224–232 atoms, the energetics of Ih clusters lie well above the realm of the lowest energy clusters. However, between the FCC and Dh motifs there remains strong competition, with the lowest energy clusters fluctuating between the two motifs. For Pt clusters in this same size bracket, there is a strong preference for the FCC motif. The Dh clusters in this bracket are relatively unstable (with the possible exception of Pt₂₂₇), and the instability of the Ih clusters persists.

For the largest Au clusters considered (303–315 atoms), the competition between Dh and FCC motifs, as witnessed for medium-sized clusters, is still apparent, with slight preference once more for the Dh motif for all except Au₃₀₃ and Au₃₀₄. The Ih gain stability in this bracket, such that the energy difference between all three motifs is small, particularly for the larger clusters (>309 atoms). Conversely, Pt behaves very differently to Au in this bracket. The separation of energy between the motifs is now clear; FCC is the most stable structure while the Dh and Ih clusters are very unstable in contrast.

3.3 Comparison of experiment and theory

3.3.1 Structure. The calculated cluster structures presented here can be compared with experimental observations of structural features in Au and Pt clusters. The lowest energy structure of Au₅₅ found here is in good agreement with previous computational^17–19,31 and experimental¹⁶ studies that identify the lowest energy isomers of Au₅₅ to be a family of distorted, chiral clusters. The exact structure of the global minimum depends highly on the theoretical description of the atomic interactions (see ESI† for detailed discussion). For larger clusters, literature on the specific structural features of Ih structures is scant and we are unable to compare our calculated structures to experiment for these sizes. In the intermediate size brackets (99–103 and 224–232 atoms), our calculated Ih structures were generally rather distorted or severely truncated and strong Dh features were observed. Mixed Ih–Dh Au structures have also been observed experimentally, albeit synthesised with non-size selected chemical methods on a carbon support.⁶³

Three families of Dh and FCC clusters were identified in the calculations, (i) closed-shell clusters, (ii) open-shell clusters with adatoms or incomplete facets and (iii) clusters with stacking faults. Examples of all three of these types of clusters have been observed experimentally; Dh Au₉₂₃ clusters have been observed to exhibit partial Marks corners²³ and FCC Au₉₂₃ clusters have demonstrated adatoms on both (111) and (100) facets.⁶⁴ Stacking faults are possibly observed in our experimental Pt data, in which some of the UI/A experimental Pt₃₀₉ clusters exhibited features that could be due to twinned particles or particles with stacking faults (see Fig. 2f for an example).

3.3.2 Energetics. Comparison of experimental and calculated data of the relative energies of different cluster motifs is somewhat difficult for many of the clusters considered here. To our knowledge, there is no size-selected experimental data on motif preference for Au at sizes between 99 and 103 and 224 and 232 atoms. For Au₁₄₇ clusters relatively little experimental data exists. Available data is either for specific sized clusters but synthesised by ligand templating⁶⁵ or clusters with a rather large size distribution. Hence, we refrain from making any specific comparisons between our theoretical motif dominance and experimental observations for Au clusters smaller than 300 atoms.

Experimentally, size-selected Au clusters with >300 atoms have been studied extensively. An early study found that, for Au clusters with 309 ± 6 atoms, no single motif dominates the observed distribution of clusters; Dh clusters were found to make up about a third of the observed clusters, FCC about a quarter and Ih less than 10%.²² The remaining clusters could not be confidently assigned. However, it should be recognised that clusters are inherently metastable and the observed isomeric population is not necessarily representative of the equilibrium structures; instead, the structures observed can be due to kinetic trapping/growth effects. Wang and Palmer developed a method of deducing the most stable isomer by irradiating the cluster sample under the electron beam, i.e. annealing inside the electron microscope.⁴⁹ Less stable clusters are transformed into more stable clusters under the electron beam. The structure of Au₃₀₉ was recently revisited using electron beam irradiation experiments.⁶⁶ For this size, rather than observing the majority of clusters transforming to one motif, the structures tended to oscillate back and forth between motifs under the electron beam. Frame-by-frame analysis,^14,16 was therefore used to monitor the relative occurrence of each isomer; it was found that FCC clusters were observed most often (56%), followed by Dh (37%) and Ih clusters (7%), respectively, concluding that the FCC motif was the most stable, followed by Dh and Ih. Our computational results show that the energies of all motifs are rather close in energy, which is reflected in the ease with which the clusters transform back and forth between motifs under the electron beam. Our simulated results indicate that the Dh clusters are the most stable, rather than FCC as seen in the experiments. However, there were a large number of clusters that were not able to be identified in the experiments, which could affect the exact proportions of each isomer observed.

Comparison of calculated and experimental motif dominance for the smaller (<250 atoms) Pt clusters is difficult. Experimentally, most of the clusters in this region could not be assigned to any particular motif. Those structures that could be identified were determined to be FCC. Our calculated results support the absence of Ih clusters and presence of FCC clusters, but the large proportion of UI/A clusters complicates the situation somewhat. To further identify some of the UI/A clusters, QSTEM atlases were generated using some of the low energy clusters obtained from the GO simulations. These clusters were either distorted Ih clusters or Dh and FCC with stacking faults and/or incomplete facets. This allowed some additional clusters to be assigned to one of the motifs. For example, for the 55 atom clusters, this led to 15 more clusters from a total of 100 clusters being positively identified (6 Ih, 4 Dh and 5 FCC) and an additional 7 clusters from a total of 100 for the 147 atom clusters (6 Dh, 1 FCC, see ESI† for the new QSTEM atlases and reassigned clusters). While the majority of clusters remained unidentified this demonstrates how inclusion of imperfect clusters in the QSTEM atlas can aid in identification of clusters that are further from the traditional perfect motifs.

For Pt clusters with >300 atoms, the calculated data are in broad accordance with the experimental results. FCC clusters make up 66% of the observed clusters in the experiments, with a small proportion (3%) of Dh clusters and no Ih clusters. Indeed, our calculated data in this region show that Ih are very unstable and that FCC is clearly the dominant structure, save for few specific sizes where Dh clusters are competitive.

We acknowledge that our calculations are temperature free, the inclusion of which would likely alter the precise proportions of each motif. It should also be noted that the experimental clusters are soft-landed on carbon films. However, the low deposition energy means that clusters are not fragmented or coalesced on impact²² and the conducting nature of the carbon film leads to efficient dissipation of energy and charge.⁶⁷ Furthermore, the electronic structure of clusters,⁶⁸ as well as the melting point⁶⁹ have been shown to be only minimally perturbed by a carbon support.

3.4 Rationalisation of differences between Pt and Au

Both the experimental and theoretical results for Pt and Au in this work reveal clear differences in the trends in motif dominance with size. Trends in cluster motifs are commonly rationalised in terms of competition between surface and bulk effects. Ih is favoured at low sizes due to low surface energy. However, it has high internal strain, which becomes more significant as the size of the cluster increases. Therefore, Dh is favoured next before eventually, FCC, which is stable in the bulk limit. From Fig. 5, it can be seen that Pt clusters roughly follow this trend, where the Ih clusters are the first motif to become unstable, followed by the Dh clusters until, at the largest size considered (∼309 atoms), the FCC motif is the only stable motif. In contrast, for Au the Dh and, to a lesser extent, Ih motifs remain competitive at ∼309 atoms. This is a counterintuitive result as one would expect the FCC motif to gain in dominance as size is increased, which is clearly not the case here. Furthermore, experimental results for Au clusters of larger sizes suggest that the motif competition between Dh and FCC isomers of Au persists even up to at least 900 atoms.^23,24,27 This is clearly in contrast to the more expected behaviour of Pt clusters.

To gain some insight into these contrasting trends, the structures of selected clusters are examined in more detail. Low energy closed shell clusters around 309 atoms, locally-minimised with DFT, are considered. These are the 309 atom Mackay Ih, a 318 Marks Dh and a 314 atom truncated octahedron FCC cluster. The relative energies of these clusters are similar to the relative energies of the global minimum Ih, Dh and FCC clusters in the 303–315 atom size bracket (see ESI†), but without the added complexity of large-scale structural distortions. At the smallest size (∼55 atoms) there is more difference in the relative energies between the global minimum and closed-shell clusters, which is discussed in more detail in the ESI.†

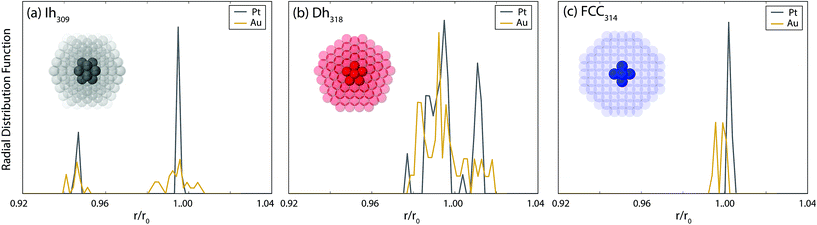
Given the aforementioned importance of internal strain for cluster stability, in Fig. 6 the radial distribution functions (rdf) of the nearest neighbours in the core region of the closed shell clusters are analysed. For Pt, the rdf reveals a very ordered core for all motifs; only a few sharp peaks are observed. In contrast, for Au, disorder in the core region is evident (especially for the Ih) where the peaks in the rdf are broadened. It has been shown that amorphisation of the core of Au clusters leads to a significant lowering of the energy of the core atoms, thus reducing the strain.⁷⁰ This lowering more than compensates the concomitant gain in energy of the surface atoms due to increased disorder, leading to a more stable cluster.^42,70 Accordingly, we propose that for Au, the disorder evident in the core of the Ih and Dh clusters reduces the internal strain and stabilises these clusters, thus allowing them to remain competitive with the FCC clusters at the largest size here. For Pt there is a lesser tendency towards amorphisation as shown in the ordered core atoms and consequently the Ih and Dh clusters are rather unstable at the largest size considered here.

Fig. 6 Top: radial distribution function, of core atoms in closed shell (a) Ih₃₀₉, (b) Dh₃₁₈ and (c) FCC₃₁₄ Au and Pt clusters, locally minimised with DFT. Interatomic distances are normalised with respect to the nearest neighbour distance in the bulk, r₀. Cluster structures are shown in the insets to each plot, where the atoms defined as the core are opaque. For FCC₃₁₄, the core is defined as the innermost 6 atoms, for Dh₃₁₈ it is 19 atoms and for Ih₃₀₉ it is 13 atoms. The core is defined as the smallest region that has the same symmetry as the overall cluster.

The tendency of Au to amorphise has been discussed in detail previously by Soler et al.⁷⁰ There, the tendency of metallic bonds to contract at the surface of clusters, and the low energy cost to bond length and coordination disorder, were cited as key factors to favouring amorphisation. These were quantified by comparing the ratio of the elastic energy to the enthalpy of melting. Pt has a higher elastic energy, which should therefore favour amorphisation. However, this is offset by the enthalpy of melting, which is significantly smaller in Au, thereby enabling more facile amorphisation for Au than for Pt. Factors favouring amorphisation are enhanced from left to right and down the d-block such that Au has the highest tendency towards amorphisation.⁷⁰ However, the metal with the next highest tendency towards amorphisation is Pt, which has also been noted in another study.⁴² This explains why, while the final motif trends are somewhat different between Pt and Au, there are still very strong structural similarities between the two types of clusters. Notably, the morphology of the most stable clusters of Pt and Au are often very similar, with similar defects observed. Furthermore, somewhat disordered clusters are always lower in energy than their closed-shell counterparts.

4 Conclusions

This study investigates the structural differences observed between Pt and Au nanoclusters. Experimental Pt clusters up to 600 atoms were synthesised in a cluster beam source, soft landed on carbon films and imaged using aberration-correction scanning transmission electron microscopy. The resulting clusters were found to be largely amorphous/glassy at sizes less than 200 atoms. From approximately 200 atoms, a large proportion of FCC clusters is seen. Very few Dh clusters are observed experimentally over the range studied. In contrast, Au clusters show close competition between Ih, Dh and FCC motifs at all sizes up to ∼300 atoms.

We have used a combined computational approach to explore the energies of Pt and Au clusters of sizes 54–56, 99–103, 144–150, 224–232 and 303–315 atoms. First, an ensemble of clusters was generated using recently developed methodology that estimates the structure of low energy asymmetric clusters of a given size based on the energies of nearby symmetric clusters. These clusters were then subjected to a global optimisation that located the lowest energy structures of each competing motif using the RGL empirical potential description of the atomic interactions. Finally the energies of the most stable clusters were refined using DFT. This refinement was necessary as the empirical potential was often found to predict the wrong energetic ordering of clusters both within a given motif and between motifs.

None of the most stable calculated Ih clusters were the high-symmetry Mackay icosahedron but were somewhat distorted, for both Pt and Au; in the smallest size bracket (54–56 atoms) the distortion was rather pronounced. At larger sizes closer to the traditional “magic” sizes (144–150, 303–315), Ih structures are less distorted, with surface reconstruction being the predominant feature. Ih clusters in the size ranges between magic sizes (144–150 and 303–315) were interesting as they exhibited both Ih and Dh features. FCC and Dh clusters generally fell into one of three categories (i) closed-shell, (ii) open-shell with adatoms or incomplete facets and (iii) clusters with stacking faults. In terms of individual structures, Pt and Au showed strong similarity.

Despite the observed structural similarity of Pt and Au clusters within each motif, energetic analysis of the two types of clusters revealed notable differences. For Au we find all three motifs to be competitive in energy at all sizes. Conversely, Pt only finds all three motifs to be competitive at small sizes (54–56 and 99–103) after which size the distinction between motifs becomes clear. From sizes of 144 atoms the Ih motif is not competitive and the relative instability increases with size. Dh is competitive in the 144–150 size bracket but from the 224–232 size brackets it also becomes unstable such that by the 303–315 bracket the FCC motif is clearly the most dominant motif. These results are in broad occurence with experimental results.

Structural analysis reveals possible reasons for the differences in motif dominance of the two types of clusters. Au clusters show a greater tendency towards amorphisation, which is able to lessen the energy penalty arising from the strained core of the non-crystalline Ih and Dh clusters. As a result, these motifs remain competitive for Au whereas for Pt they quickly become disfavoured due to the lesser tendency towards amorphisation.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. G. L, G. R. W and A. L. G. are grateful for financial contributions from the Marsden Fund administered by the Royal Society of New Zealand and a University of Otago Research Grant. The experimental work was kindly supported by the EPSRC. The authors acknowledge the contribution of the NeSI high-performance computing facilities to the results of this research. NZ's national facilities are provided by the NZ eScience Infrastructure and funded jointly by NeSI's collaborator institutions and through the Ministry of Business, Innovation & Employment's Research Infrastructure programme. URL: https://www.nesi.org.nz.

Notes and references

1. E. Serrano, G. Rus and J. García-Martínez, Renewable Sustainable Energy Rev., 2009, 13, 2373–2384.
2. Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167.
3. A. Sanchez, S. Abbet, U. Heiz, W.-D. Schneider, H. Häkkinen, R. N. Barnett and U. Landman, J. Phys. Chem. A, 1999, 103, 9573–9578.
4. C. Xu, X. Xu, J. Su and Y. Ding, J. Catal., 2007, 252, 243–248.
5. M. Haruta, N. Yamada, T. Kobayashi and S. Iijima, J. Catal., 1989, 115, 301–309.
6. T. S. Kim, J. D. Stiehl, C. T. Reeves, R. J. Meyer and C. B. Mullins, J. Am. Chem. Soc., 2003, 125, 2018–2019.
7. M. D. Hughes, Y.-J. Xu, P. Jenkins, P. McMorn, P. Landon, D. I. Enache, A. F. Carley, G. A. Attard, G. J. Hutchings, F. King, E. H. Stitt, P. Johnston, K. Griffin and C. J. Kiely, Nature, 2005, 437, 1132–1135.
8. B. C. H. Steele and A. Heinzel, Nature, 2001, 414, 345–352.
9. A. F. Ghenciu, Curr. Opin. Solid State Mater. Sci., 2002, 6, 389–399.
10. J. Greeley, T. Jaramillo, J. Bonde, I. Chorkendorff and J. K. Nørskov, Nat. Mater., 2006, 5, 909–913.
11. K. Bromann, C. Félix, H. Brune, W. Harbich, R. Monot, J. Buttet and K. Kern, Science, 1996, 274, 956–958.
12. R. E. Palmer, S. Pratontep and H.-G. Boyen, Nat. Mater., 2003, 2, 443–448.
13. W. Huang, M. Ji, C.-D. Dong, X. Gu, L.-M. Wang, X. G. Gong and L.-S. Wang, ACS Nano, 2008, 2, 897–904.
14. Z. W. Wang and R. E. Palmer, Nanoscale, 2012, 4, 4947–4949.
15. J. Li, X. Li, H.-J. Zhai and L.-S. Wang, Science, 2003, 299, 864–867.
16. Z. W. Wang and R. E. Palmer, Nano Lett., 2012, 12, 5510–5514.
17. I. L. Garzón, J. A. Reyes-Nava, J. I. Rodríguez-Hernández, I. Sigal, M. R. Beltrán and K. Michaelian, Phys. Rev. B, 2002, 66, 073403.
18. I. L. Garzón, M. R. Beltrán, G. González, I. Gutíerrez-González, K. Michaelian, J. A. Reyes-Nava and J. I. Rodríguez-Hernández, Eur. Phys. J. D, 2003, 24, 105–109.
19. X. López-Lozano, L. A. Pérez and I. L. Garzón, Phys. Rev. Lett., 2006, 97, 233401.
20. C. L. Cleveland, U. Landman, T. G. Schaaff, M. N. Shafigullin, P. W. Stephens and R. L. Whetten, Z. Phys. D, 1997, 40, 503–508.
21. K. Koga, H. Takeo, T. Ikeda and K. Ohshima, Phys. Rev. B, 1998, 57, 4053–4062.
22. Z. Y. Li, N. P. Young, M. Di Vece, S. Palomba, R. E. Palmer, A. L. Bleloch, B. C. Curley, R. L. Johnston, J. Jiang and J. Yuan, Nature, 2008, 451, 46–48.
23. S. R. Plant, L. Cao and R. E. Palmer, J. Am. Chem. Soc., 2014, 136, 7559–7562.
24. D. M. Foster, R. Ferrando and R. E. Palmer, Nat. Commun., 2018, 9, 1323.
25. L. Li, L.-L. Wang, D. D. Johnson, Z. Zhang, S. I. Sanchez, J. H. Kang, R. G. Nuzzo, Q. Wang, A. I. Frenkel, J. Li, J. Ciston, E. A. Stach and J. C. Yang, J. Am. Chem. Soc., 2013, 135, 13062–13072.
26. S. I. Sanchez, M. W. Small, E. S. Bozin, J.-G. Wen, J.-M. Zuo and R. G. Nuzzo, ACS Nano, 2013, 7, 1542–1557.
27. D. M. Wells, G. Rossi, R. Ferrando and R. E. Palmer, Nanoscale, 2015, 7, 6498–6503.
28. M. J. Cuddy, K. P. Arkill, Z. W. Wang, H.-P. Komsa, A. V. Krasheninnikov and R. E. Palmer, Nanoscale, 2014, 6, 12463–12469.
29. F. Baletto, R. Ferrando, A. Fortunelli, F. Montalenti and C. Mottet, J. Chem. Phys., 2002, 116, 3856–3863.
30. H. Li, L. Li, A. Pedersen, Y. Gao, N. Khetrapal, H. Jónsson and X. C. Zeng, Nano Lett., 2015, 15, 682–688.
31. K. Sukata, M. Van den Bossche, A. Pedersen and H. Jónsson, Nanosyst.: Phys., Chem., Math., 2017, 8, 723–731.
32. G. Grochola, I. K. Snook and S. P. Russo, J. Chem. Phys., 2007, 127, 224704.
33. C. L. Cleveland, U. Landman, M. N. Shafigullin, P. W. Stephens and R. L. Whetten, Phys. Rev. Lett., 1997, 79, 1873–1876.
34. J. Uppenbrink and D. J. Wales, J. Chem. Phys., 1992, 96, 8520–8534.
35. F. R. Negreiros, E. A. Soares and V. E. de Carvalho, Phys. Rev. B, 2007, 76, 205429.
36. A. S. Barnard, N. P. Young, A. I. Kirkland, M. A. van Huis and H. Xu, ACS Nano, 2009, 3, 1431–1436.
37. J. M. Rahm and P. Erhart, Nano Lett., 2017, 17, 5775–5781.
38. A. L. Garden, A. Pedersen and H. Jónsson, Nanoscale, 2018, 10, 5124–5132.
39. B. C. Curley, R. L. Johnston, N. P. Young, Z. Y. Li, M. Di Vece and R. E. Palmer, J. Phys. Chem. C, 2007, 111, 17846–17851.
40. K. Bao, S. Goedecker, K. Koga, F. Lançon and A. Neelov, Phys. Rev. B, 2009, 79, 041405.
41. A. Sachdev, R. I. Masel and J. B. Adams, Catal. Lett., 1992, 15, 57–64.
42. E. Aprà, F. Baletto, R. Ferrando and A. Fortunelli, Phys. Rev. Lett., 2004, 93, 065502.
43. V. Kumar and Y. Kawazoe, Phys. Rev. B, 2008, 77, 205418.
44. I. M. Goldby, B. von Issendorff, L. Kuipers and R. E. Palmer, Rev. Sci. Instrum., 1997, 68, 3327–3334.
45. S. Pratontep, S. J. Carroll, C. Xirouchaki, M. Streun and R. E. Palmer, Rev. Sci. Instrum., 2005, 76, 045103.
46. B. von Issendorff and R. E. Palmer, Rev. Sci. Instrum., 1999, 70, 4497–4501.
47. Z. W. Wang, Z. Y. Li, S. J. Park, A. Abdela, D. Tang and R. E. Palmer, Phys. Rev. B, 2011, 84, 073408.
48. C. Koch, PhD thesis, Arizona State University, Tuscon, Arizona, 2002.
49. Z. W. Wang and R. E. Palmer, Phys. Rev. Lett., 2012, 108, 245502.
50. H. Larsen, J. Mortensen, J. Blomqvist, I. Castelli, R. Christensen, M. Dułak, J. Friis, M. Groves, B. Hammer and C. Hargus, et al. , J. Phys.: Condens. Matter, 2017, 29, 273002.
51. S. T. Chill, M. Welborn, R. Terrell, L. Zhang, J.-C. Berthet, A. Pedersen, H. Jónsson and G. Henkelman, Model. Simul. Mater. Sci. Eng., 2014, 22, 055002.
52. M. Plasencia, A. Pedersen, A. Arnaldsson, J.-C. Berthet and H. Jónsson, Comput. Geosci., 2014, 65, 110–117.
53. G. Henkelman and H. Jónsson, J. Chem. Phys., 1999, 111, 7010–7022.
54. A. Pedersen, S. F. Hafstein and H. Jónsson, SIAM J. Sci. Comput., 2011, 33, 633–652.
55. A. Pedersen and M. Luiser, J. Chem. Phys., 2014, 141, 024109.
56. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
57. P. E. Blöchl, Phys. Rev. B, 1994, 50, 17953.
58. G. Kresse and J. Joubert, Phys. Rev. B, 1999, 59, 1758.
59. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169.
60. J. L. F. Da Silva, H. G. Kim, M. J. Piotrowski, M. J. Prieto and G. Tremiliosi-Filho, Phys. Rev. B, 2010, 82, 205424.
61. S. Jindal, S. Chiriki and S. S. Bulusu, J. Chem. Phys., 2017, 146, 204301.
62. K. Manninen and M. Manninen, Eur. Phys. J. D, 2002, 20, 243–249.
63. J. A. Ascencio, M. Pérez and M. José-Yacamán, Surf. Sci., 2000, 447, 73–80.
64. Z. W. Wang and R. E. Palmer, Nano Lett., 2012, 12, 91–95.
65. S. T. Chill, R. M. Anderson, D. F. Yancey, A.-T. Frenkel, R. M. Crooks and G. Henkelman, ACS Nano, 2015, 9, 4036–4042.
66. D. M. Foster, PhD thesis, University of Birmingham, Birmingham, U.K., 2017.
67. S. Iijima and T. Ichihashi, Phys. Rev. Lett., 1986, 56, 616–619.
68. M. G. Mason, Phys. Rev. B, 1983, 27, 748–762.
69. J. Lee, T. Tanaka, J. Lee and H. Mori, Calphad, 2007, 31, 105–111.
70. J. M. Soler, M. R. Beltrán, K. Michaelian, I. L. Garzón, P. Ordejón, D. Sánchez-Portal and E. Artacho, Phys. Rev. B, 2000, 61, 5771–5780.

---

Footnote

† Electronic supplementary information (ESI) available: Details on generation of the initial cluster ensemble, performance and verification of the global optimisation algorithm, detailed motif dominance of Pt clusters soft-landed on carbon films, comparison of empirical potential and density functional theory results, comparison of stability measures, detailed morphology of icosahedral and FCC clusters around 55 atoms, new QSTEM atlases built on computationally-derived clusters, energies of selected closed-shell clusters. See DOI: 10.1039/c9na00122k

---