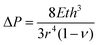An atomically thin molecular aperture: two-dimensional gallium phosphate

Abstract

Unlocking true size- and shape-selectivity in membranes requires new materials design paradigms. In this work, a novel two-dimensional GaPO₄ material is presented that can act as an adjustable and switchable molecular sieve for small molecule separations. Two-dimensional GaPO₄ is constructed of a bilayer of alternating corner-sharing GaO₄ and PO₄ tetrahedra arranged in six-membered rings. Density functional theory calculations indicate the tetrahedra rotate in the minimum energy structure to create impenetrably small openings. In response to modest tensile stresses, however, the tetrahedra act as molecular hinges, rotating against each other to open apertures sufficient for small molecules to pass through. The result is a membrane structure with a high porosity and a relatively broad range of effective pore sizes for precise and switchable control over gas permeation. Simulations for He, Ne, and H₂O reveal the ability to control the permeability over nine orders of magnitude. To achieve this adjustable separation in a scalable, practical manner, a pressure-driven device is outlined which uses small pressure differences between the permeate and retentate sides to apply the tensile stress, highlighting the simplicity of utilizing two-dimensional GaPO₄ for tunable and switchable separation of small gas phase molecules.

---

Conceptual insights

Achieving dynamically tunable and switchable membranes for separating, storing and releasing small molecules based on their size and shape has been a long-standing challenge. While thinning two-dimensional (2D) materials down to their atomic limits has promised ultimate permeance membranes, the structural openings in the common 2D materials are too small to allow any molecules to pass and thus intricate defect engineering is required that is either non-scalable or severely restricts the permeance. Here it is shown that a 2D form of GaPO₄ intrinsically includes hinges that allow the openings in its honeycomb structure to reversibly and controllably vary from smaller than any molecule to the size of small molecules as modest tensile strains are applied. Simulations indicate that this can allow the permeance to be controlled over nine orders of magnitude to effectively allow passage through the material to be switched on and off and to precisely tune the pore size to achieve difficult separations. A simple device is proposed and modeled in which pressure differences across the membrane supply the tensile strain. The structural motif that includes natural hinges offers a design principal to extend dynamically tunable and switchable membranes to larger molecules.

Achieving true size-and shape-based separation of small molecules is a longstanding challenge for developing effective membranes.¹ While thin metal organic frameworks (MOFs) and zeolite-based membranes have gained much attention,^2–6 the diffusion lengths through practical membranes of this type are quite long and much of the separations are driven by adsorption differences, limiting both the maximum permeance and selectivity. At the fundamental level, two-dimensional van der Waals (2D-VDW) materials have been explored to minimize the diffusion lengths and move towards so-called “ultimate permeation”.^7–13 Most commonly, graphene-based membranes with milled holes, tears, or engineered defects have been tested, although these methods are difficult to scale to practical implementation and the overall permeance per unit area is very low. Recently, effective small molecule separation has been demonstrated for single-layer graphene with spontaneously-formed nanopores;¹⁴ however, the total gas flow is limited to the density of these larger holes as the six-membered C rings in monolayer graphene are impermeable, even to He,¹⁵ and precise pore size control has not yet been achieved experimentally.

An atomically thin membrane with true ultimate permeation characteristics should also have a high density of accessible pores to achieve practical gas flow during operation (high overall permeance), and ideally could be tuned to effectively separate a target gas mixture. Bilayer silica, which consists of linked layers of six-membered rings of corner-sharing SiO₄ tetrahedra in a crystalline state or four- to nine-membered rings of SiO₄ tetrahedra in an amorphous state,^16–19 has been explored as a candidate material due to ring sizes appropriate for small molecule separations and its chemical inertness.^20,21 However, the structural characteristics of this material are controlled by a limited choice of metallic substrates,²² and additional tunability would be preferred. In our recent work, we catalogued the structures of 2D-VDW bilayer group III phosphates (2D-T_IIIPO₄), which consist of alternating T_IIIO₄ and PO₄ tetrahedra in place of the SiO₄ tetrahedra in bilayer silica.²³ Of these T_IIIPO₄ layers, AlPO₄ and GaPO₄ were found to be the most stable, and the favored GaPO₄ structure featured alternately rotated tetrahedra. While the initial observation was that this distortion would restrict the pores to the point where no gases could permeate, here it will be shown that inducing tensile strain causes the tetrahedra to reversibly rotate to expand the effective pore size. Harnessing this effect in gas separation would match all the ideal criteria for ultimate permeation through an atomic-scale membrane, while supplying the additional benefits of dynamic pore size control which can allow pore size tuning during operation for specific separations and the ability to turn the membrane on and off.

In this work, we investigate 2D GaPO₄'s potential as a new membrane material with strain-adjustable pore sizes. The intrinsic rotations of GaO₄ and PO₄ tetrahedra within the unstrained structure act as molecular hinges, swinging through a 1.37 Å range of pore sizes with modest applied strains. Calculated barriers for transmission of small gases suggest precise control over gas permeation selectivity with room temperature operation, with the ability to balance selectivity and permeance as a function of strain in the membrane. Furthermore, we show the simplicity of using this atomically thin ultimate membrane in a pressure-driven device, demonstrating the promise of scalable, switchable gas separation.

The FHI-AIMS code package was used for all density functional theory calculations in this work.^24,25 The specifics follow details provided in a previous paper focused on the structure, stability and prospects for forming 2D-VDW group III phosphates.²³ The one significant difference here is the inclusion of long range van der Waals interactions, modeled using the Tkatchenko–Scheffler approach,²⁶ which is essential to capture the interactions of the noble gas atoms and small molecules, in this case H₂O, with the 2D-VDW materials. Compared to the prior work, inclusion of the VDW interactions reduces the lattice constants of 2D GaPO₄ and AlPO₄ by ≈0.01 Å. The activation energies and transition state configurations for permeation through 2D GaPO₄ were calculated using a climbing image version of the string method converged to a residual force of less than 60 meV Å⁻¹.^27,28 To reduce possible cooperative interactions between molecules permeating adjacent unit cells, the adsorption and transition state search calculations presented here were performed using a 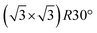superstructure of the primitive 2D unit cell. All atoms in the superstructure were allowed to relax during the transition state calculations.

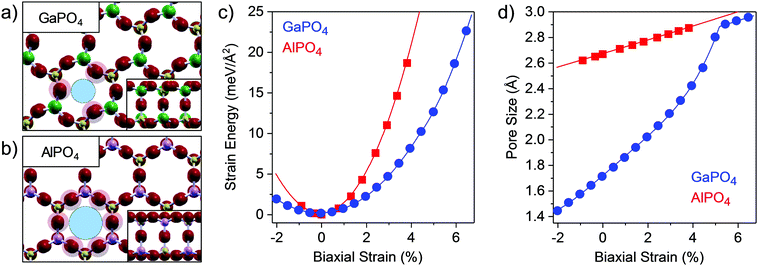
The atomic structure of bilayer GaPO₄ is shown in Fig. 1a, with the structure of the similar bilayer AlPO₄ provided in Fig. 1b for comparison. Both consist of PO₄ and T_IIIO₄ tetrahedra, and despite the considerable distortion in the relaxed GaPO₄ material, both are joined into a bilayer through nearly 180° interlayer T_III–O–P bonds. Due to this interlayer connection the T_III and P atoms are four-coordinated throughout, and the structure is fully closed, which is analogous to 3D zeolitic forms of these materials.^29,30 As observed in our previous study,²³ the alternating rotations of the neighboring tetrahedra in GaPO₄ results in a lattice constant which is smaller than AlPO₄, despite Ga's larger size (a_GaPO4 = b_GaPO4 = 5.30 Å, a_AlPO4 = b_AlPO4 = 5.37 Å). The tetrahedral rotations in GaPO₄ may be in-phase layer-to-layer, as shown in Fig. 1a, or out-of-phase, as shown in Fig. S1 (ESI†) and as initially reported; in this work, we report characteristics for the in-phase structure as its relaxed configurations are consistently ≈1 meV per primitive unit cell lower in energy. For GaPO₄, the tetrahedral distortion causes three of the upper layer O atoms to extend further into the pore, resulting in an opening which is smaller than for AlPO₄ and defined by those three O atoms. As the lattice constant expands, the GaO₄ and PO₄ tetrahedra rotate and increase the size of the opening between O atoms – it will be demonstrated that this behavior opens a new pathway for tensile strain relief, allowing for expansion without distorting the tetrahedra or stretching bonds.

Fig. 1 Calculated structural properties of bilayer GaPO₄ and AlPO₄. Top-down views of the structures of (a) GaPO₄ and (b) AlPO₄ (side view inset). Red, yellow, green, and light magenta represent oxygen, phosphorous, gallium, and aluminum atoms. Lighter red halos represent the O ionic radii (1.35 Å) in the upper layer, creating effective pore sizes taken as the diameters of the blue circles. (c) Strain energy vs. biaxial strain for GaPO₄ and AlPO₄ bilayers. Solid lines indicate equation of state polynomial fits used to extract 2D bulk moduli. (d) Effective pore size vs. biaxial strain for GaPO₄ and AlPO₄ bilayers. Solid lines indicate best fits to the calculated values.

The strain energy as a function of stress-induced biaxial strain (ε) is shown in Fig. 1c. The biaxial strain values given in this paper are expressed in terms of strain along one unit cell axis while the materials are stretched along both axes simultaneously; both materials are isotropic, as demonstrated for GaPO₄ in Fig. S2 (ESI†). Fitting over the full range for GaPO₄ yields a 2D bulk modulus of 2.39 eV Å⁻², considerably softer than AlPO₄ which has a 2D bulk modulus of 6.10 eV Å⁻². However, it is clear from the plot of dE/dε as a function of ε (Fig. S3, ESI†) that there are two independent linear regimes for GaPO₄, indicating two mechanisms for strain relief with a change occurring around ε = 4.5%. Indeed, fitting the strain energy data separately within the two regimes reveals that the low-strain and high-strain 2D bulk moduli are 2.32 eV Å⁻² and 4.74 eV Å⁻². The linearity in both regimes indicates that the response is elastic and thus the structural changes reversible. The change in the strain-relief mechanism manifests in the geometric change in the apparent pore size of the GaPO₄ bilayer as a function of stress-induced strain (Fig. 1d), which exhibits distinct behavior below and above ε = 4.5%. Remarkably, pore sizes from 1.43 Å to 2.80 Å may be accessed with little stress-induced biaxial strain, from only 2% compressive to 5% tensile. Here, the pore size is defined as the diameter of the void created by the ionic radius of O atoms in the phosphate structure, which is similar to the zeolite membrane literature where the ionic radius of O in the silicate (1.35 Å) is used to define the pore.³¹ Note that since the pores are a natural consequence of the structure, inducing defects by processes such as ion milling is not required and the porosities (defined as the pore area to total area ratio) reach 0.23 when the pores are fully open at 5% tensile strain.

To decouple the strain relief mechanisms apparent in the GaPO₄ bilayers, the out-of-plane strain and the tetrahedral rotation angle between neighboring GaO₄ and PO₄ tetrahedra are shown as functions of the in-plane strain ε in Fig. 2a and b. From these plots, it is apparent that tensile strain relief in bilayer GaPO₄ proceeds through counter-rotation of neighboring tetrahedra until the tetrahedral rotation, θ (defined as the deviation from 180° of the angle formed by lines connecting neighboring Ga and P atoms through their bridging O), approaches 10° at ε = 4.5%. Then, further strain relief goes through a transition region where out-of-plane strain increases and the rotation is reduced to 0°. Simplified illustrations of the tetrahedral rotations are shown for ε = 0% (33°) in Fig. 2c, and for ε = 4.5% (0°) in Fig. 2d. After 5.5% strain has been induced and the effective pore size has reached 2.90 Å, GaPO₄ behaves similarly to AlPO₄ and accommodates strain though out-of-plane contraction and flattening of the tetrahedral bond angle. Up to moderate compressive strain, tetrahedral rotation is also the primary strain relief mechanism.

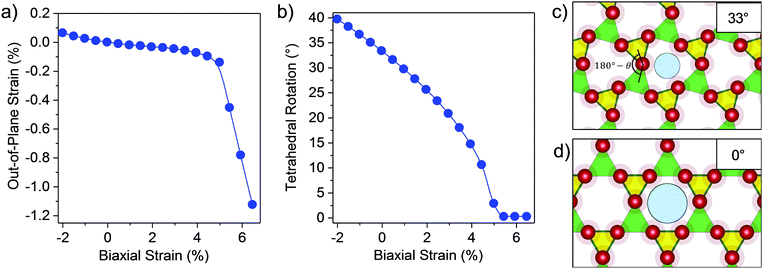Fig. 2 Strain relief mechanism of bilayer GaPO₄. Plots of (a) out-of-plane strain vs. biaxial strain and (b) rotation angle (θ) of GaO₄ and PO₄ tetrahedra vs. biaxial strain. The out-of-plane strain is defined as the change in the distance between the outer oxygen planes of the two halves of the bilayer (see inset in Fig. 1a) relative to this distance in the unstrained state. (c and d) Polyhedral representation of bilayer GaPO₄ to illustrate the tetrahedral rotation and the effective pore size calculated in Fig. 1c for (c) zero strain and (d) 5.5% biaxial strain. Green and yellow correspond to GaO₄ and PO₄ tetrahedra. Color scheme same as Fig. 1.

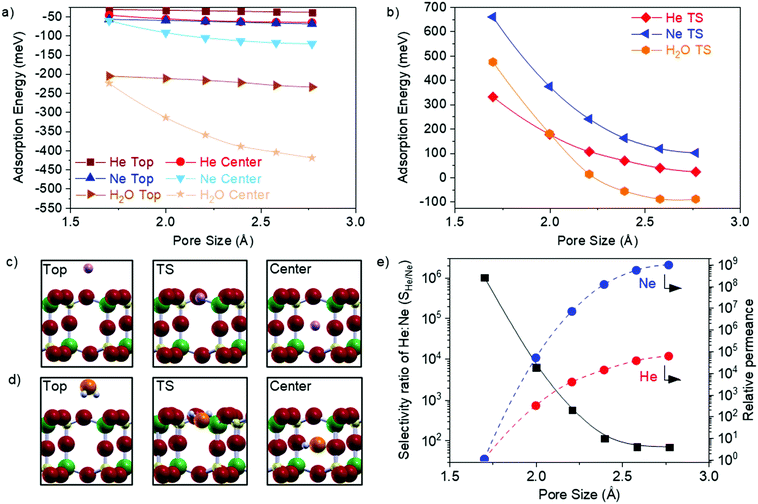
The wide range of accessible pore sizes in GaPO₄ overlap the kinetic diameters of small molecules, which makes 2D GaPO₄ a flexible new member on the small list of atomically thin gas separation membranes described to date. To further assess the feasibility of 2D GaPO₄ as a strain-tuneable gas separation membrane, we have calculated the transmission pathways and associated barriers for He, Ne, and H₂O as they pass through 2D GaPO₄ strained to achieve a range of different pore sizes. Helium and Ne were selected due to their comparatively inert nature and different kinetic diameters (2.6 Å and 2.8 Å, respectively^32,33), while H₂O (2.7 Å kinetic diameter^32,33) was selected to simulate greater complexity with internal degrees of freedom and the impact of potential hydrogen bonding. Adsorption energies of relaxed structures for the gases on top of 2D GaPO₄ and at the center of the bilayer pore are plotted as functions of pore size in Fig. 3a, and the transition state energies (referenced to the gas phase) between the two configurations in Fig. 3b. Representative atomic structures are provided for He and Ne in Fig. 3c and for H₂O in Fig. 3d. Interestingly, all gases exhibit stronger adsorption at the center of the bilayer pores which weakens as the pore size is reduced, though the effect is weaker for He and Ne than for H₂O. Rather than approaching zero adsorption energy at the transition state position, H₂O begins to exhibit “barrierless” transmission to the center of the pore from the gas phase when the pore size is above 2.25 Å. The trajectory of H₂O through GaPO₄ varies as a function of pore size (Fig. S4, ESI†), but this effect does not introduce any abrupt transitions in the adsorption or transition state energy curves. Overall, the calculated values demonstrate that changing the GaPO₄ pore size strongly affects the energies required to permeate the material.

Fig. 3 (a) Adsorption energies of He and Ne, and H₂O on top and in the center of GaPO₄ bilayers as a function of pore size changes produced by strain. (b) Transition state energies of He, Ne, and H₂O while entering or exiting GaPO₄ as a function of pore size. Relaxed, ε = 0%, structures of (c) Ne and (d) H₂O in the top, transition state (TS), and center, corresponding to energies reported in (a and b). White, red, yellow, green represent H, O, P, and Ga atoms, while pink represents Ne. The O atoms in H₂O are shown in orange for clarity. (e) Selectivity ratio of He : Ne (S_He/Ne) and permeance for He and Ne relative to their values through unstrained GaPO₄ at 298 K.

To obtain approximate selectivity for a pair of gases passing through a bilayer membrane, transmission through the membrane was modeled as adsorption on top of the material followed by activated motion to the center; once at the center the species could reemerge on either side of the membrane following the same kinetics. Adsorption/desorption on the membrane surface was assumed to follow Langmuir adsorption/desorption kinetics (see the ESI† for additional details). Within this model, the overall energy barrier of the process reduces to the transition state energy referenced to the gas phase (E_TS). This E_TS then serves as an apparent activation energy in an Arrhenius rate expression for gas permeation, and the selectivity ratio between two gases (S_X/Y) is the ratio of the rate expressions for each gas. For further simplicity, the pre-exponential factors in the Arrhenius expressions are treated as identical. Permeances for each gas through each pore size relative to the permeance at ε = 0% are calculated through the kinetic theory of gases at standard conditions and using a Maxwell distribution to model transmission probability, as has been previously described for porous graphene.³⁴ The results in Fig. 3e suggest that tensile strain can change the Ne permeance by nine orders of magnitude. Estimates of the absolute permeances were obtained by multiplying the transmission probabilities by the porosities, as defined above (see ESI† for details).

The calculated selectivity ratios for a mixture of He and Ne passing through GaPO₄ at 298 K as a function of pore size are shown in Fig. 3e. Unsurprisingly, S_He/Ne decreases as the pore size increases, due to rapidly decreasing barriers for both gases. For the smallest pore size (ε = 0%), S_He/Ne = 1.0 × 10⁶ as the permeance of Ne is vanishingly small (∼10⁻¹⁴ mol m⁻² s⁻¹ Pa⁻¹). Classical membranes may achieve 10³ selectivity,³⁵ and S_He/Ne remains above this threshold as the pore size increases up to 2.21 Å. Remarkably, this high selectivity occurs at room temperature even though He and Ne are so similar in size and chemistry. At the largest pore size of 2.77 Å, S_He/Ne = 69 and the permeance of He has increased to ∼10⁻³ mol m⁻² s⁻¹ Pa⁻¹ (S_He/Nevs. He permeance for the full range is shown in Fig. S5, ESI†). In principle, similar behavior is expected for polyatomic molecules such as H₂O, though the greater complexity makes modeling the selectivity ratio more challenging. For comparison, it has been estimated that relatively-inflexible bilayer SiO₂ can achieve a maximum of S_He/Ne = 3.2 × 10³ through its six-membered rings under similar conditions; inducing a vitreous state with a distribution of ring sizes can dramatically lower this selectivity ratio, but such a modification is permanent.²⁰ Clearly, the advantages of using 2D GaPO₄ as a gas permeation membrane are: the ability to dynamically balance selectivity and permeance to achieve an optimum value for effective separation of gas streams, which is unique to this new class of membranes; the ability to effectively turn permeation on and off which makes it interesting for storing and releasing molecules; and the high porosity that is a natural consequence of the structure.

For practical implementation of this 2D GaPO₄ material as a membrane, it is necessary to find a way to control the applied strain directly. We propose a convenient and scalable method to exploit the tunability of 2D GaPO₄: suspending layers of this material over a porous support and applying a pressure differential to induce strain. Such a device can be simple to construct and has been previously employed to create graphene “balloons”.¹⁵ Expressions relating the applied pressure differential to the physical properties of thin films have been derived for several geometries for the purposes of bulge testing.^36–39 For a film with negligible residual stress:

where ΔP is the difference between the high- and low-pressure sides of the membrane (P₂ and P₁, respectively), E is the 2D Young's modulus, ν is the 2D Poisson's ratio, t is the membrane thickness, h is the deflection at the center, and r is the radius of the support hole. For simplicity, we model the film properties only at the center of the circular hole, where the pressure-driven stress is greatest. At the center, the deflection of the film may be related to the biaxial strain by ε = 2h²/3r², from which corresponding pore sizes can be extracted from the plot in Fig. 1d. For 2D layers, E/2(1 − ν) is also known as the 2D bulk modulus, which was extracted from Fig. 1c.

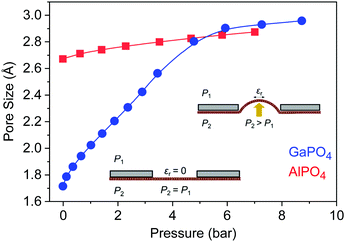
Modeling results for the effective pore size at the center of the substrate hole as a function of applied pressure are shown in Fig. 4. The chosen 10 μm circular hole radius balances readily-available mesh sieves with the need for coherent films; increasing the radius decreases the required pressure differential for a given pore size but would also require larger-area, defect-free films to maintain effective gas separation (Fig. S6a, ESI†). Since inducing a pore size change in 2D GaPO₄ is facile through the range where tetrahedral rotation is the primary expansion mechanism, only a modest pressure differential of 4.82 bar is required to achieve ε = 4.5% at the center and a pore size of 2.80 Å. When the material stiffens to ε > 4.5%, the pressure requirement rapidly increases for small changes in the pore size. As expected, AlPO₄ would require a substantially higher pressure differential to achieve a significant change in pore size, likely resulting in rupture. Pressure differentials on the order of 1 to 10 bar are readily achievable near atmospheric pressure without requiring high absolute pressures.⁴⁰

Fig. 4 Plots of pore size vs. pressure differential for 2D GaPO₄ and AlPO₄ suspended over a circular hole with r = 10 μm. Schematics of a freestanding 2D material responding to a pressure differential where P₂ = P₁ and P₂ > P₁ are inset. Dashed lines in the schematics represent the 2D material suspended over a circular hole.

If the residual internal stress, σ₀, is non-zero, a second linear term appears in the expression for ΔP which scales as 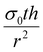. The effect of varying this parameter up to 100 GPa is shown in Fig. S6b (ESI†). For very small values of σ₀ there is negligible effect on the expected pore size as a function of ΔP, and even the largest values only shift the range of ΔP by a factor of 10. While the value of σ₀ for 2D GaPO₄ is unknown for the simulated gas separation membrane, experimental work on graphene has shown that σ₀ is only 30% of the 2D bulk modulus.⁴¹ If it is assumed that membranes of 2D GaPO₄ behave in a qualitatively similar manner, then the order of magnitude of ΔP for the full pore size range will not depend strongly on σ₀ and this effect may be neglected.

Conclusions

By exploiting the molecular hinges within GaPO₄ which arise from tetrahedral rotations as a low-energy strain relief mechanism, we have identified a new concept for controlling molecular flow across atomically thin layers. By reversibly tuning the membrane through small applied strains, the selectivity of small molecule permeation may be controlled, and we have proposed a simple way of utilizing this property in a scalable, pressure-driven device. Such a device can be tested at the laboratory scale using simple delamination of a GaPO₄ film onto porous microscopy grids,^42,43 a process which may be extended later to industrial scale mesh screens for practical implementation. Growth of bilayer GaPO₄ may be achieved through Ga and P deposition techniques already developed in the III–V semiconductor field.⁴⁴ While gas separation through GaPO₄ is limited to small molecules, the material design principle, hinged structures that can reversibly open without other structural distortions, should be further investigated to extend to separation of larger molecules with the same levels of high expected selectivity, facile tunability and switchability, unlocking a new direction for molecular sieving.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank J.-H. Jhang, C. Zhou and X. Liang for their assistance in carrying out this work. The Yale Center for Research Computing is thanked for its support of the computing infrastructure used to carry out this work. Acknowledgment is made to the Donors of the American Chemical Society Petroleum Research Fund for support of this research through grant number ND55524.

Notes and references

1. D. S. Sholl and R. P. Lively, Nature, 2016, 532, 435–437.
2. H. Furukawa, K. E. Cordova, M. O'Keeffe and O. M. Yaghi, Science, 2013, 341, 1230444.
3. M. Shah, M. C. McCarthy, S. Sachdeva, A. K. Lee and H.-K. Jeong, Ind. Eng. Chem. Res., 2012, 51, 2179–2199.
4. D. Bradshaw, A. Garai and J. Huo, Chem. Soc. Rev., 2012, 41, 2344–2381.
5. N. Rangnekar, N. Mittal, B. Elyassi, J. Caro and M. Tsapatsis, Chem. Soc. Rev., 2015, 44, 7128–7154.
6. X. Ma, P. Kumar, N. Mittal, A. Khlyustova, P. Daoutidis, K. A. Mkhoyan and M. Tsapatsis, Science, 2018, 361, 1008–1011.
7. S. P. Koenig, L. Wang, J. Pellegrino and J. S. Bunch, Nat. Nanotechnol., 2012, 7, 728–732.
8. L. Wang, L. W. Drahushuk, L. Cantley, S. P. Koenig, X. Liu, J. Pellegrino, M. S. Strano and J. Scott Bunch, Nat. Nanotechnol., 2015, 10, 785–790.
9. H. Li, Z. Song, X. Zhang, Y. Huang, S. Li, Y. Mao, H. J. Ploehn, Y. Bao and M. Yu, Science, 2013, 342, 95–98.
10. K. Celebi, J. Buchheim, R. M. Wyss, A. Droudian, P. Gasser, I. Shorubalko, J. I. Kye, C. Lee and H. G. Park, Science, 2014, 344, 289–292.
11. Y. Wang, J. Li, Q. Yang and C. Zhong, ACS Appl. Mater. Interfaces, 2016, 8, 8694–8701.
12. M. S. H. Boutilier, C. Sun, S. C. O’Hern, H. Au, N. G. Hadjiconstantinou and R. Karnik, ACS Nano, 2014, 8, 841–849.
13. L. Wang, M. S. H. Boutilier, P. R. Kidambi, D. Jang, N. G. Hadjiconstantinou and R. Karnik, Nat. Nanotechnol., 2017, 12, 509–522.
14. Z. Yuan, J. D. Benck, Y. Eatmon, D. Blankschtein and M. S. Strano, Nano Lett., 2018, 18, 5057–5069.
15. J. S. Bunch, S. S. Verbridge, J. S. Alden, A. M. van der Zande, J. M. Parpia, H. G. Craighead and P. L. McEuen, Nano Lett., 2008, 8, 2458–2462.
16. D. Löffler, J. J. Uhlrich, M. Baron, B. Yang, X. Yu, L. Lichtenstein, L. Heinke, C. Büchner, M. Heyde, S. Shaikhutdinov, H. J. Freund, R. Włodarczyk, M. Sierka and J. Sauer, Phys. Rev. Lett., 2010, 105, 146104.
17. A. Malashevich, S. Ismail-Beigi and E. I. Altman, J. Phys. Chem. C, 2016, 120, 26770–26781.
18. E. I. Altman, J. Götzen, N. Samudrala and U. D. Schwarz, J. Phys. Chem. C, 2013, 117, 26144–26155.
19. B. Yang, W. E. Kaden, X. Yu, J. A. Boscoboinik, Y. Martynova, L. Lichtenstein, M. Heyde, M. Sterrer, R. Włodarczyk, M. Sierka, J. Sauer, S. Shaikhutdinov and H.-J. Freund, Phys. Chem. Chem. Phys., 2012, 14, 11344–11351.
20. B. Yao, S. Mandrà, J. O. Curry, S. Shaikhutdinov, H.-J. Freund and J. Schrier, ACS Appl. Mater. Interfaces, 2017, 9, 43061–43071.
21. E. Emmez, B. Yang, S. Shaikhutdinov and H.-J. Freund, J. Phys. Chem. C, 2014, 118, 29034–29042.
22. X. Yu, B. Yang, J. A. Boscoboinik, S. Shaikhutdinov and H.-J. Freund, Appl. Phys. Lett., 2012, 100, 151608.
23. E. I. Altman, J. Phys. Chem. C, 2017, 121, 16328–16341.
24. V. Blum, R. Gehrke, F. Hanke, P. Havu, V. Havu, X. Ren, K. Reuter and M. Scheffler, Comput. Phys. Commun., 2009, 180, 2175–2196.
25. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
26. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
27. W. E, W. Ren and E. Vanden-Eijnden, J. Chem. Phys., 2007, 126, 164103.
28. W. E, W. Ren and E. Vanden-Eijnden, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 052301.
29. J. Yu and R. Xu, Chem. Soc. Rev., 2006, 35, 593–604.
30. A. K. Cheetham, G. Ferey and T. Loiseau, Angew. Chem., Int. Ed., 1999, 38, 3268–3292.
31. S. Kulprathipanja, Zeolites in industrial separation and catalysis, Wiley-VCH, Weinheim, 2010.
32. N. Mehio, S. Dai and D.-E. Jiang, J. Phys. Chem. A, 2014, 118, 1150–1154.
33. D. W. Breck, Molecular Sieves: Structure, Chemistry and Use, John Wiley & Sons, New York, 1974.
34. S. Blankenburg, M. Bieri, R. Fasel, K. Müllen, C. A. Pignedoli and D. Passerone, Small, 2010, 6, 2266–2271.
35. S. T. Oyama, D. Lee, P. Hacarlioglu and R. F. Saraf, J. Membr. Sci., 2004, 244, 45–53.
36. J. J. Vlassak and W. D. Nix, J. Mater. Res., 2011, 7, 3242–3249.
37. K.-T. Wan, S. Guo and D. A. Dillard, Thin Solid Films, 2003, 425, 150–162.
38. E. I. Bromley, J. N. Randall, D. C. Flanders and R. W. Mountain, J. Vac. Sci. Technol., B: Microelectron. Process. Phenom., 1983, 1, 1364–1366.
39. U. Komaragiri, M. R. Begley and J. G. Simmonds, J. Appl. Mech., 2005, 72, 203–212.
40. R. W. Baker, Ind. Eng. Chem. Res., 2002, 41, 1393–1411.
41. C. Lee, X. Wei, J. W. Kysar and J. Hone, Science, 2008, 321, 385–388.
42. P. Y. Huang, S. Kurasch, A. Srivastava, V. Skakalova, J. Kotakoski, A. V. Krasheninnikov, R. Hovden, Q. Mao, J. C. Meyer, J. Smet, D. A. Muller and U. Kaiser, Nano Lett., 2012, 12, 1081–1086.
43. C. Büchner, Z.-J. Wang, K. M. Burson, M.-G. Willinger, M. Heyde, R. Schlögl and H.-J. Freund, ACS Nano, 2016, 10, 7982–7989.
44. M. Henini, Molecular beam epitaxy: from research to mass production, Elsevier, Amsterdam, 2013.

---

Footnote

† Electronic supplementary information (ESI) available: Out-of-phase rotations in bilayer two-dimensional GaPO₄; isotropic elastic response of 2D GaPO₄; comparison of differential strain curves of 2D AlPO₄ and GaPO₄; change in the water permeation mechanism with pore size; support and residual stress effects on pressure driven pore opening; kinetic modeling of transmission through the 2D membrane (PDF). See DOI: 10.1039/c8nh00335a

---