Molecular evidence for feedstock-dependent nucleation mechanisms of CNTs†
Umedjon
Khalilov
 *,
Charlotte
Vets
*,
Charlotte
Vets
 and
Erik C.
Neyts
and
Erik C.
Neyts

PLASMANT Research Group, Department of Chemistry, University of Antwerp, Universiteitsplein 1, 2610 Antwerpen, Belgium. E-mail: umedjon.khalilov@uantwerpen.be; Fax: +32-3-265-23-43; Tel: +32-3-265-23-82
First published on 2nd January 2019
Abstract
Atomic scale simulations have been shown to be a powerful tool for elucidating the growth mechanisms of carbon nanotubes. The growth picture is however not entirely clear yet due to the gap between current simulations and real experiments. We here simulate for the first time the nucleation and subsequent growth of single-wall carbon nanotubes (SWNTs) from oxygen-containing hydrocarbon feedstocks using the hybrid Molecular Dynamics/Monte Carlo technique. The underlying nucleation mechanisms of Ni-catalysed SWNT growth are discussed in detail. Specifically, we find that as a function of the feedstock, different carbon fractions may emerge as the main growth species, due to a competition between the feedstock decomposition, its rehydroxylation and its contribution to etching of the growing SWNT. This study provides a further understanding of the feedstock effects in SWNT growth in comparison with available experimental evidence as well as with ab initio and other simulation data, thereby reducing the simulation–experiment gap.
Conceptual insightsThis work demonstrates the crucial role of carbon and non-carbon species in CNT growth from oxygen-containing hydrocarbons (CxHyOz) through atomistic simulations. Over the past two decades, many researchers have employed atomic scale simulations to study CNT growth. Nevertheless, there are no reports yet on simulated nucleation and growth from CxHyOz. Despite the fact that a vast majority of experiments use these feedstocks, most simulations so far considered pure carbon as the feedstock, assuming that the non-carbon species play little or no role of importance in CNT growth. In contrast, this work demonstrates how non-growth species have a direct impact on the CNT nucleation and growth. We distinguish three classes of growth contributors, whose formation is found to depend on a competition between feedstock decomposition, its rehydroxylation and its contribution to etching of the growing CNT. Also, we demonstrate the dependence of the tube diameter on the C incorporation rate, in excellent agreement with the in situ TEM evidence. Finally, we explain the role of oxygen and hydrogen in broadening and necking of CNTs. In summary, these simulations are the first of their kind, provide new microscopic information on the CNT nucleation nature, and assist in reducing the gap between simulations and real experiments. |
Introduction
Carbon nanotubes (CNTs) have attracted the attention of many researchers for several decades, thanks to their geometry-dependent electronic, mechanical and optical properties.1 Among the various synthesis techniques, chemical vapour deposition (CVD) is an often preferred technique due to its simplicity, high degree of control and scalability.2 In spite of tremendous efforts, the synthesis of nanotubes with controlled properties can be achieved in the CVD process only to some extent, at least in part due to our current incomplete understanding of the growth mechanism.2,3Probably the most sought-after property is chirality-controlled growth. It is often believed that control over the nucleation stage eventually also allows control of the CNT chirality.4 To support this, some transmission electron microscopy (TEM) studies have shown time-resolved details of metal catalysed single-wall CNT (SWNT) nucleation and consequent growth at the atomic level.5,6 However, the atomic scale dynamics of the CNT nucleation processes cannot be captured by current TEM resolution.3,6 Consequently, a variety of computational techniques have been applied to gain complementary information on various effects, including the importance of the carbon chemical potential7 or the metal-mediated defect healing,8 the necessity of a carbide phase,9 and the influence of the Cx growth feedstock,10,11 and all these have contributed to unravelling and explaining experimental observations. In particular, the dislocation theory of chirality-controlled nanotube growth, proposed by Ding and co-workers,12 successfully addresses the growth rate-chiral angle proportionality,13 and the axial rotation of SWNTs.14 In this kinetic approach, however, the main issue of debate is the neglect of the role of the catalyst nanoparticles, the substrate, the feedstock pressure, and temperature on the resulting (n,m) distribution of grown SWNTs.15–20
Besides these important factors in CVD-based CNT growth, the choice of the carbon feedstock is one of the main parameters for tuning the SWNT diameter15–17 and chirality.18–20 However, real growth species, including hydrocarbon and non-carbon species such as hydrogen, oxygen, and hydroxyl radicals are generally not taken into account in computer simulations, and it is still a major issue.2 Only very recently, the first dynamic simulation study on SWNT nucleation using hydrocarbons as a carbon source has been reported, investigating the decomposition of the hydrocarbon molecule,21 the appearance of carbon chains and networks22,23 and the formation of a carbon cap24 on the transition metal nanoparticle surface. These investigations revealed that the dual role of hydrogen and thus the competition between (re)hydrogenation and dehydrogenation processes during the incubation stage are critical for the dynamics of the SWNT nucleation process.24 Besides hydrocarbons, oxygen-containing hydrocarbon (CxHyOz) feedstocks are also widely used in SWNT growth and thus understanding the role of oxygen is also very important.25–27 To this end, Oguri and co-workers have very recently studied the decomposition of ethanol molecules on a Ni catalyst surface.28,29 Although such investigations are quite interesting and give useful information on the onset of SWNT nucleation, understanding the whole picture of SWNT nucleation and growth from CxHyOz species, however, still remains unclear.
In this work, we report on carbon nanotube cap nucleation and consequent SWNT growth using different CxHyOz feedstocks through combined reactive molecular dynamics and time-stamped force-bias Monte Carlo (MD/tfMC) simulations,8,24 for the first time. In particular, we found that the competition between catalytic dissociation of the CxHyOz feedstock and its hydroxylation and subsequently its etching process is critical in determining the main carbon contributors for SWNT growth.
Computational methodology
MD/tfMC simulation technique
Simulation of the Ni-catalysed SWNT growth from CxHyOz species is performed using a combined reactive MD and tfMC technique.8,24 In MD/tfMC, the impacts of the growth species on the nanocatalyst surface and the initial chemical reactions taking place during the first few picoseconds are accounted for by the MD module,24 while the tfMC module subsequently takes care of the longer time relaxation of the system after each chemical reaction. While the exact system dynamics are not reproduced in tfMC calculations, it provides a realistic (albeit not exact) dynamical path, and reproduces end configurations in full agreement with (very long) MD simulations.8ReaxFF
In order to properly describe the bond dissociation and formation processes, including the C–C bond dissociation, H2 or H2O formation and other reactions during both the MD and the tfMC cycles, the ReaxFF potential30 is applied with new force-field parameters developed by Zou et al.31 To validate the force-field quality, we evaluated test simulations carried out using new parametrized ReaxFF (ReaxFF-Zou) against results obtained using parameterization by Mueller et al. (ReaxFF-Mueller),32 and other simulations and experimental data,33–39 which are shown in Table 1. In particular, ReaxFF-Zou reproduces the cohesive energy of nickel (−4.45 eV) in excellent agreement with experiments (−4.44 eV)35 as well as DFT calculations (−4.42 eV),36 while the ReaxFF-Mueller result is somewhat off (−4.50 eV). While the heat of solution of the C atom in the Ni864 bulk (0.62 eV) is slightly higher than the experimental value of about 0.42–0.49 eV,37 the value for the Ni55 nanocluster (0.29 eV) is in the range of both experimental and other simulation results (0.2–0.4 eV).37,38 The formation volume VF quantifies the deformation of the Ni crystal upon incorporation of C in the lattice (NixC). It is defined as VF = V(NixC) − xΩ0(Ni), where V(NixC) and Ω0(Ni) are the volume of the relaxed NixC structure and the volume per atom of elemental Ni, respectively, where x is the number of Ni atoms in the system. We found that the VF/Ω0 ratio (0.78) is in close agreement with the ab initio data of Siegel et al. (0.64–0.8),37 although the value is slightly higher than the value calculated using the ReaxFF-Mueller parametrization (0.68 and 0.71 for Ni864C and Ni32C, respectively). Also, we calculated the energy barrier of H2 desorption from the Ni surface to be 1.22 eV, which is close to the range of DFT calculation results (0.42–1.19 eV)33 and in very close agreement with the experimental activation energy (1.2–1.3 eV),34 while the ReaxFF-Mueller parametrization yields a slightly too high value (1.66 eV).39 In spite of quantitative differences between ReaxFF-Mueller and ReaxFF-Zou results, our test simulations indicate that such small differences do not affect the overall growth mechanisms (see Fig. 1 in the ESI†). The overall results indicate that the new ReaxFF potential is sufficiently accurate to address catalysed CNT growth using MD/tfMC simulations.| ReaxFF | Other simulation methods | Experiment | ||
|---|---|---|---|---|
| Zou | Mueller | |||
| a For Ni864C. b For Ni55C. c For Ni32C. d For Ni(100), Ni(110) and Ni(111).33 e For T > 500 K.34 | ||||
| E coh (Ni), eV | −4.45 | −4.50 | −4.4235 | −4.4436 |
| ΔH (C), eV | 0.62a | 0.78a | 0.20–0.3637 | 0.42–0.4937 |
| 0.29b | 0.68c | 0.4038 | ||
| V F (NixC)/Ω0 | 0.78a | 0.68a | 0.64–0.97c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37 37 |
— |
| 0.71c | ||||
| E des (H2), eV | 1.22b | 1.6639 | 0.42–1.19d | 1.2–1.3e![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) 34 34 |
Simulation details
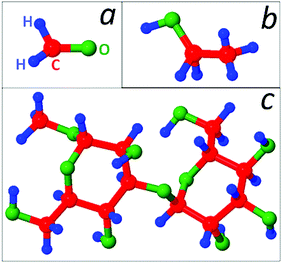
For the simulation of SWNT growth, a Ni55 nanocluster is initially equilibrated at 2000 K using the canonical Bussi thermostat.40 The nanocatalyst is physisorbed on a virtual Al surface, employing a z-integrated Lennard-Jones potential.23 In order to gain a generic understanding of the role of CxHyOz feedstocks, we use three different molecules, viz. formaldehyde (CH2O) and ethanol (C2H6O) molecules, which have double or single C–C bonds, respectively, and complex β-methyl lactoside (C13H24O11) molecule (Fig. 1).The molecules are allowed to impinge on the cluster one by one, while keeping their number density in the simulation cell constant during the simulations. Due to lower pyrolysis temperature of the C13H24O11 (∼445 K)41 and C2H6O (1050–1275 K)42 molecules, compared to CH2O (2200–2650 K),43 different molecular fractions can already be found in the gas-phase before the molecule impinges on the catalyst surface at 2000 K. However, we found that the formation rate of the pyrolysis products is very low. When a gas-phase species adsorbs on the nanocluster, the resulting structure is allowed to relax by the application of tfMC.23,24 During the relaxation, no new feedstock is allowed to enter the simulation cell.
DFT calculations
The VASP software44 is used for DFT calculations of adsorbed/dissociated/desorbed H2 and H2O molecules on/from the Ni55 nanocatalyst. Optimizations are done in the generalized gradient approximation (GGA), using the revised Perdew–Burke–Ernzerhof (RPBE) functional,45 and the projector augmented wave (PAW) method.46 Methfessel–Paxton smearing of the first order is used,47 along with a Γ-centered (1 × 1 × 1) k-point mesh. Supercells with sizes of (20 × 20 × 20) Å are employed, except for the structures where H2 and H2O are desorbed from the nanoparticle, in which case the size is (30 × 30 × 30) Å. Spin polarization with no symmetry constraints is employed. The energy cutoff is set to 500 eV, and the energy convergence to 1 × 10−6 eV. A magnetic moment is applied to the Ni atoms.Results and discussions
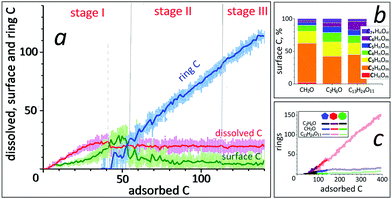
From our results we infer that SWNT nucleation and its subsequent growth from CxHyOz feedstocks can be distinguished into three stages, which are similar to SWNT growth from non-oxygen containing hydrocarbon species:24 (i) incubation, (ii) cap formation and (iii) continued (tube) growth, as illustrated in Fig. 2. We find that the SWNT nucleation from CxHyOz feedstocks is clearly different from both pure carbon (Cx)7–10,48 and hydrocarbon (CxHy) species.22–24 However, fast C dissolution after the feedstock dissociation at the onset of the incubation stage is identical for all types of growth species.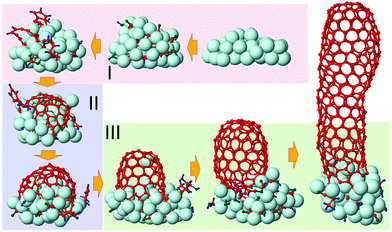 | ||
| Fig. 2 Base-growth process of SWNTs from CxHyOz species, divided into three stages. Ni, C, H and O atoms are shown in cyan, red, blue and green colours, respectively. | ||
Feedstock-catalyst reactions
As representative for all CxHyOz feedstocks, we here analyse the entire adsorption/dissolution process of the ethanol (C2H6O) molecule on/in a Ni nanocatalyst. After impingement on the cluster, the molecule typically first binds to the surface with its O-atom (Fig. 3a and b). While the feedstock sticking probability depends on the nature of the Ni facets,33 the Ni nanoparticle is amorphized at high temperature and therefore it does not contain any specific facets during the entire growth process. Consequently, all C–H, C–O and C–C bonds of the molecule are gradually broken (Fig. 3c–j). In particular, C–C bonds from the surface CHxCO fragment (e.g., HCCO in Fig. 3f) are dissociated (Fig. 3g) during the simulation, which concurs with previous ab initio MD calculation results.29 Yet, binding of another H-adatom to the remaining CO fragment leads to weakening and consequently breaking of the single C–O bond (Fig. 3i and j). In the CH2O case, however, such H binding is rather rare due to low concentration of H adatoms and consequently CO fragments remain longer on the cluster or desorb from the cluster. After C–O bond breaking, the single C atom quickly dissolves into clusters. During the feedstock dissociation, H adatoms eventually associate with a remaining OH fragment or another H adatom and desorb as a water or hydrogen molecule from the cluster surface, respectively (Fig. 3k and l).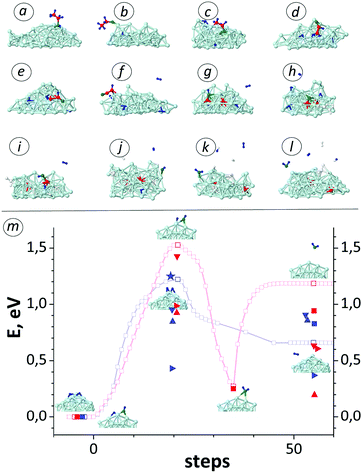 | ||
| Fig. 3 (a–l) Adsorption and dissociation steps of ethanol molecules on Ni55 clusters. The fractions or individual atoms of other adsorbed ethanol molecules are coloured in white, for the sake of clarity. (m) Association/dissociation activation barriers in desorption/adsorption of H2 (blue lines with open squares) and H2O molecules (red lines with open squares) on Ni55 nanoclusters. DFT values for H2O on Ni(111), Ni(110) and Ni(100) surfaces33 are indicated by red up, red down and red right triangles, respectively. DFT data for H2O on Ni55 is indicated by red squares. Also, DFT data for H233 are shown in blue. Furthermore, the blue star indicates the experimental activation energy barrier for H2 desorption.34 | ||
Hydrogenation vs. oxidation
Employing nudged elastic band (NEB)49 calculations (Fig. 3m), the energy barrier for the recombination of OH and H species on the Ni55 cluster is found to be 1.53 eV (red open squares in Fig. 3m). This value is slightly higher than DFT values for different nickel facets, i.e., 0.87 eV for Ni(111), 0.94 eV for Ni(110) and 1.39 eV for Ni(100) surfaces (red up triangles, red right triangles and red down triangles, respectively, in Fig. 3m).33 These species subsequently desorb as a H2O molecule from the Ni surface. The same water formation mechanism was also reported in ab initio MD studies.28 In contrast to the recombination and desorption, H2O re-adsorption is found to be barrier-less. The adsorbed molecule preferably desorbs again from the surface rather than dissociatively chemisorbing on the catalyst surface: the desorption and splitting barriers are 0.91 eV (our DFT value is 0.71 eV, see red squares in Fig. 3m) and 1.25 eV, respectively. Thus, most adsorbed H2O molecules desorb again without proceeding to decompose to OH + H species, which is in agreement with both experimental50,51 and DFT calculation results.52 As mentioned above, H adatoms freely diffuse over the cluster surface (with a maximum diffusion barrier of 0.51 eV) compared to adsorbed OH, until they recombine with either an OH species (1.53 eV) or another H adatom (1.22 eV) in order to desorb as H2O or H2 molecules, respectively. Our results show that the OH diffusion barrier is rather high, about 2 times higher than the H diffusion barrier due to its high adsorption (binding) energy, which is in agreement with DFT calculation results.33 Also, the value for the H2 desorption energy barrier (blue open squares in Fig. 3m) is in close agreement with the experimental activation energy in the range of 1.2–1.3 eV (blue star in Fig. 3m)34 and first-principle results, ranging from 0.42 eV to 1.37 eV for different nickel surfaces (blue triangles in Fig. 3m).33 While both recombination energy barriers differ somewhat from DFT values, overall DFT and MD/tfMC calculations indicate that the formation rate of OH&H pairs on the cluster surface (i.e., HO* + H* + Ni → H2O↑ + Ni) is relatively slow compared to the H&H formation rate (i.e., H* + H* + Ni → H2↑ + Ni). Furthermore, the positive reaction energies of 0.66 eV for H2 and 1.18 eV for H2O are close to first-principle values in the range of 0.36–0.90 eV for H2 (blue triangles and squares) and 0.20–0.94 eV for H2O (red triangles and squares),33 indicating the endergonic nature of both H2 and H2O desorption reactions. Therefore, both desorbed molecules preferably re-adsorb again on the catalyst surface. While the H2 adsorption barrier is non-zero (0.24 eV) unlike H2O adsorption, the chemical dissociation barrier of the H2 molecule (0.56 eV) is much lower than the dissociation barrier of the H2O molecule (1.25 eV). Comparing dissociative adsorption and associative desorption probabilities of H2 and H2O molecules, the results point out that the probability for hydrogenation is higher than for oxidation during the CNT growth from CxHyOz species. In addition, the high non-dissociative adsorption rate of H2O due to its zero-barrier can assist in the growth of defect-less SWNTs.25Super-saturation point
When a CxHyOz molecule completely dissociates, all C atoms are found as dissolved species in Ni55 nanoclusters, which is similar to simulation studies of SWNT nucleation from Cx7–10,48 and CxHy species22–24 at the onset of SWNT nucleation. This scenario of “CxHyOz adsorption/dissociation, C dissolution, as well as H2 and H2O desorption” continues until the nanocluster is saturated, i.e., no space is available in the catalyst. At this supersaturation point (indicated by the dashed line in Fig. 4a),48 the number of dissolved C atoms can gradually increase up to about 30% of the amount of Ni atoms (Fig. 4a, dissolved C). After supersaturation, the amount of dissolved C atoms reduces through the formation of different carbon species and subsequent incipient carbon nanostructures on the catalyst surface.Surface carbon species
The appearance of surface C species can be explained by decreasing the catalyst activity after its saturation. As a result, feedstock fractions preferably remain at and diffuse over the catalyst surface rather than splitting and diffusing into the catalyst.10 The results indicate that a surface carbon species is the product of the competition between the feedstock dissociation due to the saturated catalyst and its re-hydroxylation/etching caused by non-carbon surface species such as H, O and OH. Because of this competition, the number of remaining CkHnOm species increases on decreasing their carbon content, as shown in Fig. 4b. Consequently, C2HnOm species, including carbon dimers, are the predominant species found among all surface species in all feedstock cases, which is in agreement with the theoretical suggestions.11,53 Recent first-principles calculation results led to the conclusion that chiral selective CNTs can elongate through the addition of C2-fragments instead of adding C atoms one-by-one and the incorporation of C2 species into the SWNT rim continues the growth without changing its chirality.11,53 Furthermore, C6HnOm species, including C6 polyyne chains, increase when the growth feedstock contains more carbon atoms. The appearance of such six-atom chains eventually leads to hexagon formation on the catalyst surface, hence the fast network elongation. When incipient carbon rings, e.g., pentagons or hexagons, appear on the surface, the number of surface C species considerably decreases (Fig. 4a). While their amount fluctuates around a constant number in stage II, it gradually lowers in the final growth stage due to the blocking of most of the available area on the catalyst surface by the growing tube (Fig. 4c).Desorption vs. etching
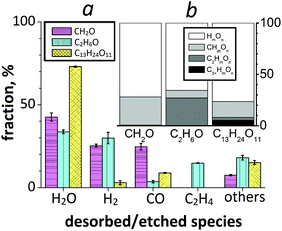
While the supply probability of surface C species to the growing carbon network is obviously very high after the supersaturation point, the contribution of desorbed or etched gas-phase species to the growth process is not negligible. In Fig. 5, desorbed and etched species, i.e., gas-phase non-C and C species are analysed. In particular, the number of desorbed HmOn species, including water and hydrogen molecules, is relatively high, i.e., it corresponds to about 70% of all desorbed species for all three cases (Fig. 5b).We find that desorption of H2O and H2 is favourable for all cases (Fig. 5a). From the NEB calculations presented in the previous sections, we find that adsorbed H2 molecules easily split to H adatoms due to the low dissociation energy barrier, whereas adsorbed H2O molecules prefer to desorb again rather than dissociate to OH and H surface species.50–52 Consequently, the concentration of desorbed H2O molecules increases in comparison to the concentration of desorbed H2 molecules. H adatoms originating from splitting H2 molecules may lead to etching of a growing cap/tube,54,55 in addition to their contributions to the etching process of surface carbon species. Also, H2O dissociative adsorption may contribute to removal of amorphous carbon from the cluster, improving defect-less tube growth.25,26 However, we do not observe SWNT oxidation and subsequent SWNT damage caused by adsorbing H2O, which is again in agreement with earlier experimental evidence.25
Besides non-carbon species, re-adsorption of etched carbon species (about 30% of all gas-phase species in Fig. 5b) can be responsible for two effects, i.e., (1) enhancing the tube growth or (2) increasing topological defects or additional structures on the grown tube.56,57Fig. 4a shows that desorption of carbon monoxide occurs in all the feedstock cases, whereas desorption of ethylene molecules is only found in the ethanol-assisted SWNT growth. Here, the high desorption rate of CO and C2H4 molecules in the CH2O and C2H6O cases, respectively, can be explained by the existence of the strong carbonyl (C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O) group in formaldehyde and the much weaker C–O linkage in ethanol molecules, respectively. The results show that the total amount of other etched species is also not minor, although their partial concentration is negligible: the ratio of CHmOn/C2HmOn/C3+HmOn desorbed species is about 27/1/0, 8/27/0 and 16/3/5 (in %) for the CH2O, C2H6O and C13H24O11 cases, respectively (Fig. 5b). Thus, the analysis of all carbon-containing species clarifies which etched carbon species have a high probability to contribute to SWNT nucleation and growth from CxHyOz feedstocks.
O) group in formaldehyde and the much weaker C–O linkage in ethanol molecules, respectively. The results show that the total amount of other etched species is also not minor, although their partial concentration is negligible: the ratio of CHmOn/C2HmOn/C3+HmOn desorbed species is about 27/1/0, 8/27/0 and 16/3/5 (in %) for the CH2O, C2H6O and C13H24O11 cases, respectively (Fig. 5b). Thus, the analysis of all carbon-containing species clarifies which etched carbon species have a high probability to contribute to SWNT nucleation and growth from CxHyOz feedstocks.
Carbon contributors
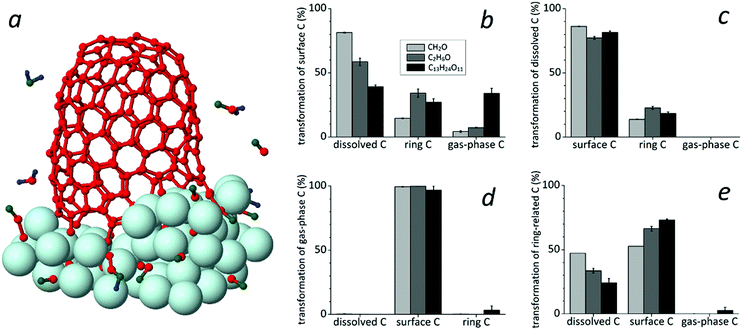
We find three types of species contributing to the growing tube, i.e., surface carbon species, dissolved carbon atoms and gas-phase (previously etched) carbon species, as shown in Fig. 6a.These contributors can directly transform to ring-related carbon atoms through their incorporation into the tube rim. Also, ring-C atoms can transform to these contributors again. Overall, these four carbon species can transform to other species during the growth process. In particular, surface C species subsequently convert or transform to all other carbon species, i.e., dissolved, ring- and gas-phase C species, as a function of the feedstock type (Fig. 6b). The conversion to the dissolved and gas-phase species depends on the carbon index in the feedstock. In particular, the transformation to dissolved C atoms increases with decreasing amount of C in the feedstock and this phenomenon can be explained by the dissociation/etching rate of the feedstock or/and its fraction(s). In contrast, the conversion to gas-phase C species increases with increasing carbon amount in the feedstock. This phenomenon can be explained by the high re-hydroxylation and etching rates of the precursor(s). Obviously, both conversion/transformation rates indicate that there is a competition between hydroxylation/etching of the remaining fraction(s) due to hydrogen/oxygen adatoms and dissociation/dissolution of the fraction(s) due to the catalyst. Also, the incorporation of both surface (Fig. 6b) and dissolved C species (Fig. 6c) to the carbon network or to the tube-end is related to the feedstock type, while these contributors mainly transform to each other. However, nearly all gas-phase (etched) carbon species transform to surface C species for all feedstock cases (Fig. 6d). Also, the transformation of ring-C to surface C species is significant, although its contribution to dissolved C is also not negligible (Fig. 6e). Both transformations strongly depend on the amount of carbon atoms in the feedstock. Obviously, the surface C species are overall the main contributors to the CNT growth for all three CxHyOz feedstocks (see Table 1 in the ESI†). Regarding DFT calculation results,11 we also suggest that dissolved carbon atoms (C1) favour change in the SWNT chirality, while surface C species (Cn) result in both chirality change and growth.
Despite the huge number of C–C association and dissociation reactions at the tube–catalyst interface, the amount of C atoms in the grown network linearly rises during the SWNT nucleation/growth (Fig. 4a, ring C). In the carbon network, the number of hexagons continuously increases, while the formation of pentagons and heptagons initially speeds up and subsequently their number remains constant during the growth (Fig. 4c). While the ring formation rates per adsorbed C atom for all feedstock cases are identical, the formation rate depends on the C sticking/incorporation rate (see the ESI,† Fig. 3b). Consequently, a high rate of hexagon formation due to carefully chosen feedstocks assures the growth of a less-defective tube with a certain diameter.58
Tube diameter vs. feedstock
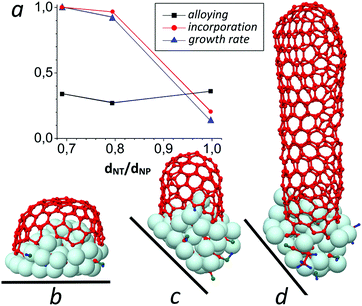
We compare the effect of small (CH2O) and large (C13H24O11) feedstock molecules, which contain a similar C/H/O ratio (∼1/2/1), resulting in two growth modes: “tangential”, when the tube and nanoparticle diameters are identical (dCNT/dNP ≈ 1) (Fig. 7b), and “perpendicular”, when the tube diameter is smaller than the nanoparticle diameter (dCNT/dNP < 0.8) (Fig. 7c and d), respectively.This feedstock effect was already reported by He and co-workers.16 In their study, Fe-catalysed-SWNTs with narrow diameter were produced by using CO as the carbon source, while large-diameter SWNTs were produced by using CH4. They explained that CO based growth leads to a high amount of dissolved carbon, resulting in a tube that is narrower than the nanoparticle diameter, while CH4 yields less dissolved C in the nanoparticle and a large diameter tube.59 In our results, the tube–nanoparticle ratio, however, seems not to significantly depend on the concentration of dissolved C in the liquefied nanoparticle, as shown in Fig. 7a. Instead, the figure clearly indicates that the C incorporation and the tube elongation (growth) rates are significantly changed when the dCNT/dNP ratio alters. While both feedstocks have the same C/H/O ratio, the carbon supply of the large feedstock allows a high C incorporation and thus results in fast tube growth with a narrow-diameter. In contrast, under low C incorporation, the wide-diameter tube grows slowly. Such growth behaviour is in agreement with recent in situ TEM observations. Zhang et al. observed a change of SWNT diameter as a function of the ratio between carbon supply (Csupply) and carbon incorporation (Cinc) rates and they found that necking and broadening of SWNTs occurs when Csupply/Cinc < 1 and Csupply/Cinc > 1, respectively.60 In particular, they proposed two reasons for necking and subsequent cessation of SWNTs, i.e., insufficient active carbon species (or fast carbon incorporation) and a certain amount of stress exerted at the tube–catalyst interface. Overall, it indicates that fast (or slow) carbon incorporation leads to SWNT growth with a narrow (or wide) diameter. This explanation completely corroborates our results in Fig. 7a: the carbon incorporation rate inversely depends on the dNT/dNP ratio. Besides, in the CxHyOz case, this phenomenon is also observed in both Cx and CxHy feedstock cases (see Fig. 2 and 3 in the ESI†).
We also find that the incorporation of hydrogen or oxygen adatoms into the grown tube leads to an increase or reduction of the tube diameter. In particular, reactive hydrogen atoms can quickly impinge on a carbon sheet or a cap-end and reduce the sheet/cap–catalyst adhesion. Consequently, the carbon cap expands over the surface by shrinking its rim diameter such that the carbon sheet can partially cover the catalyst surface. Our previous studies revealed that such carbon nanosheets can even transform to free-standing single or parallel carbon sheets at low growth temperatures due to high H and lower C concentrations.23,24 The appearance of such parallel carbon nanowalls23 may explain the nucleation onset of multi-walled CNTs (MWNTs),24 as earlier proposed by Hofmann and co-workers.5 On the other hand, such transformations are less frequent in CxHyOz based SWNT growth due to the oxygen scavenging of reactive hydrogen atoms.27 As a result, the nucleation probability of CNTs with a low-wall-number or a narrow-diameter increases during the CxHyOz-based growth.20,27 This suggestion is supported by an experimental observation of the Fe-catalysed SWNT and double-walled CNT (DWNT) growth from CxHyOz and CxHy feedstocks.20 In particular, they found SWNT/DWNT population yields (in %) of about 92/8, 89/11 and 25/75 for ethanol (C2H6O), toluene (C7H8) and methane (CH4)-based CNT growth, respectively. Such a yield sequence is also compatible with the sequence of pyrolysis temperatures of these molecules, which are ∼1025 K, ∼1050 K and ∼1470 K, respectively. Our calculation results also agree with this evidence: a large (C13H24O11) feedstock with a low pyrolysis temperature (∼445 K) yields narrow-diameter tubes (perpendicular mode) and a small (CH2O) feedstock with high pyrolysis temperature (2200–2650 K) results in large-diameter tubes (tangential mode). This indicates that the fast decomposition increases the carbon concentration and thus its incorporation rate. On the other hand, Wang and co-workers grew narrow- and wide-diameter tubes using CO and C2H2 feedstocks, respectively, while the decomposition rate of C2H2 is much higher than that of CO.15 They thus concluded that the feedstock pressure is a key factor for chirality (diameter) control. Also, Lu et al. found that the diameters of SWNTs were closely related to the carbon feeding rate by selective activation of nanoparticles.19
In general, from our calculation results and available theoretical and experimental evidence,11,15–20,27,59,60 we conclude that the tube diameter can be controlled by the incorporation rate of the aforementioned three carbon contributors. Besides the choice of catalyst, temperature and pressure, the choice of feedstock and associated growth precursors allows tuning of the formation of desirable carbon contributors due to competition between alloying catalysts and non-carbon etchant species, which can eventually steer the diameter and possibly chirality of SWNTs.
Conclusion
The nucleation of incipient SWNTs from oxygen-containing hydrocarbon feedstocks is computationally studied for the first time. All simulation results are obtained using a combined MD/tfMC simulation technique. The overall results indicate that if we can control the formation of the three main carbon contributors, i.e., dissolved C atoms, surface C species and gas-phase (etched) C species, we can control the carbon incorporation into the rim of the growing cap/tube. Our results show that the appearance of these contributors is due to catalyst and etchant species, which result either completely or partially from the dissociation of the carbon feedstock. Therefore, the choice of the growth feedstock determines the competition between these processes, and allows preferable carbon species to be selectively incorporated into a growing tube, contributing to controlled SWNT quality (defect density) and radius.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors gratefully acknowledge the financial support from the Research Foundation – Flanders (FWO), Belgium, (Grant numbers 12M1318N and 1S22516N). The work was carried out in part using the CalcUA core facility of the Universiteit Antwerpen, a division of the Flemish Supercomputer Centre VSC, funded by FWO and the Flemish Government (Department EWI). We thank Prof. A. C. T. van Duin for sharing the reax-code and force-field parameters.References
- S. Iijima, Helical microtubules of graphitic carbon, Nature, 1991, 354, 56–58 CrossRef CAS.
- V. Jourdain and C. Bichara, Current understanding of the growth of carbon nanotubes in catalytic chemical vapour deposition, Carbon, 2013, 58, 2–39 CrossRef CAS.
- J.-P. Tessonnier and D. S. Su, Recent Progress on the Growth Mechanism of Carbon Nanotubes: A Review, ChemSusChem, 2011, 4, 824–847 CrossRef CAS PubMed.
- S. Reich, L. Li and J. Robertson, Structure and formation energy of carbon nanotube caps, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 165423 CrossRef.
- S. Hofmann, et al., In situ Observations of Catalyst Dynamics during Surface-Bound Carbon Nanotube Nucleation, Nano Lett., 2007, 7, 602–608 CrossRef CAS PubMed.
- H. Yoshida, S. Takeda, T. Uchiyama, H. Kohno and Y. Homma, Atomic-Scale In-situ Observation of Carbon Nanotube Growth from Solid State Iron Carbide Nanoparticles, Nano Lett., 2008, 8, 2082–2086 CrossRef CAS PubMed.
- H. Amara, C. Bichara and F. Ducastelle, Understanding the nucleation mechanisms of carbon nanotubes in catalytic chemical vapor deposition, Phys. Rev. Lett., 2008, 100, 056105 CrossRef CAS PubMed.
- E. C. Neyts, Y. Shibuta, A. C. T. van Duin and A. Bogaerts, Catalyzed Growth of Carbon Nanotube with Definable Chirality by Hybrid Molecular Dynamics Force Biased Monte Carlo Simulations, ACS Nano, 2010, 4, 6665–6672 CrossRef CAS PubMed.
- A. J. Page, H. Yamane, Y. Ohta, S. Irle and K. Morokuma, QM/MD Simulation of SWNT Nucleation on Transition-Metal Carbide Nanoparticles, J. Am. Chem. Soc., 2010, 132, 15699–15707 CrossRef CAS PubMed.
- D. A. Gómez-Gualdrón, J. M. Beetge, J. C. Burgos and P. B. Balbuena, Effects of Precursor Type on the CVD Growth of Single-Walled Carbon Nanotubes, J. Phys. Chem. C, 2013, 117, 10397–10409 CrossRef.
- Q. Wang, M.-F. Ng, S.-W. Yang, Y. Yang and Y. Chen, The Mechanism of Single-Walled Carbon Nanotube Growth and Chirality Selection Induced by Carbon Atom and Dimer Addition, ACS Nano, 2010, 4, 939–946 CrossRef CAS PubMed.
- F. Ding, A. Harutyunyan and B. I. Yakobson, Disslocation theory of chirality-controlled nanotube growth, PNAS, 2009, 106, 2506–2509 CrossRef CAS PubMed.
- R. Rao, D. Liptak, T. Cherukuri, B. I. Yakobson and B. Maruyama, In situ evidence for chirality-dependent growth rates of individual carbon nanotubes, Nat. Mater., 2012, 11, 213–216 CrossRef CAS PubMed.
- M. Marchand, C. Journet, D. Guillot, J.-M. Benoit, B. I. Yakobson and S. T. Purcell, Growing a Carbon Nanotube Atom by Atom: “And Yet It Does Turn”, Nano Lett., 2009, 9, 2961–2966 CrossRef CAS PubMed.
- B. Wang, C. H. P. Poa, L. Wei, L.-J. Li, Y. Yang and Y. Chen, (n,m) Selectivity of Single-Walled Carbon Nanotubes by Different Carbon Precursors on Co−Mo Catalysts, J. Am. Chem. Soc., 2007, 129, 9014–9019 CrossRef CAS PubMed.
- M. He, H. Jiang, E. I. Kauppinen and J. Lehtonen, Diameter and chiral angle distribution dependencies on the carbon precursors in surface-grown single-walled carbon nanotubes, Nanoscale, 2012, 4, 7394 RSC.
- C. Z. Loebick, et al., Selective Synthesis of Subnanometer Diameter Semiconducting Single-Walled Carbon Nanotubes, J. Am. Chem. Soc., 2010, 132, 11125–11131 CrossRef PubMed.
- L. Wei, et al., Narrow-chirality distributed single-walled carbon nanotube synthesis by remote plasma enhanced ethanol deposition on cobalt incorporated MCM-41 catalyst, Carbon, 2014, 66, 134–143 CrossRef CAS.
- C. Lu and J. Liu, Controlling the Diameter of Carbon Nanotubes in Chemical Vapor Deposition Method by Carbon Feeding, J. Phys. Chem. B, 2006, 110, 20254–20257 CrossRef CAS PubMed.
- J. S. Barnard, C. Paukner and K. K. Koziol, The role of carbon precursor on carbon nanotube chirality in floating catalytic chemical vapour deposition, Nanoscale, 2016, 8, 17262–17270 RSC.
- R. Arifin, Y. Shibuta, K. Shimamura, F. Shimojo and S. Yamaguchi, Ab Initio Molecular Dynamics Simulation of Ethylene Reaction on Nickel(111) Surface, J. Phys. Chem. C, 2015, 119, 3210–3216 CrossRef CAS.
- Y. Wang, et al., Quantum chemical simulations reveal acetylene-based growth mechanisms in the chemical vapor deposition synthesis of carbon nanotubes, Carbon, 2014, 72, 22–37 CrossRef CAS.
- U. Khalilov, A. Bogaerts and E. C. Neyts, Microscopic mechanisms of vertical graphene and carbon nanotube cap nucleation from hydrocarbon growth precursors, Nanoscale, 2014, 6, 9206–9214 RSC.
- U. Khalilov, A. Bogaerts and E. C. Neyts, Atomic scale simulation of carbon nanotube nucleation from hydrocarbon precursors, Nat. Commun., 2015, 6, 10306 CrossRef CAS PubMed.
- K. Hata, D. N. Futaba, K. Mizuno, T. Namai, M. Yumura and S. Iijima, Water-Assisted Highly Efficient Synthesis of Impurity-Free Single-Walled Carbon Nanotubes, Science, 2004, 306, 1362–1364 CrossRef CAS PubMed.
- S. Maruyama, R. Kojima, Y. Miyauchi, S. Chiashi and M. Kohno, Low-temperature synthesis of high-purity single-walled carbon nanotubes from alcohol, Chem. Phys. Lett., 2002, 360, 229–234 CrossRef CAS.
- G. Zhang, et al., Ultra-high-yield growth of vertical single-walled carbon nanotubes: hidden roles of hydrogen and oxygen, PNAS, 2005, 102, 16141–16145 CrossRef CAS PubMed.
- T. Oguri, K. Shimamura, Y. Shibuta, F. Shimojo and S. Yamaguchi, Ab Initio Molecular Dynamics Simulation of the Dissociation of Ethanol on a Nickel Cluster: Understanding the Initial Stage of Metal-Catalyzed Growth of Carbon Nanotubes, J. Phys. Chem. C, 2013, 117, 9983–9990 CrossRef CAS.
- T. Oguri, K. Shimamura, Y. Shibuta, F. Shimojo and S. Yamaguchi, Bond dissociation mechanism of ethanol during carbon nanotube synthesis via alcohol catalytic CVD technique: ab initio molecular dynamics simulation, Chem. Phys. Lett., 2014, 595–596, 185–191 CrossRef CAS.
- A. C. T. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard III, ReaxFF: A Reactive Force Field for Hydrocarbons, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS.
- C. Zou, Y. K. Shin, A. C. T. van Duin, H. Fang and Z.-K. Liu, Molecular dynamics simulations of the effects of vacancies on nickel self-diffusion, oxygen diffusion and oxidation initiation in nickel, using the ReaxFF reactive force field, Acta Mater., 2015, 83, 102–112 CrossRef CAS.
- J. E. Mueller, A. C. T. van Duin and W. A. Goddard III, Development and Validation of ReaxFF Reactive Force Field for Hydrocarbon Chemistry Catalyzed by Nickel, J. Phys. Chem. C, 2010, 114, 4939–4949 CrossRef CAS.
- A. Mohsenzadeh, T. Richards and K. Bolton, DFT study of the water gas shift reaction on Ni(111), Ni(100) and Ni(110) surfaces, Surf. Sci., 2016, 644, 53–63 CrossRef CAS and references therein.
- A. L. Cabrera, Desorption studies of hydrogen and carbon monoxide from nickel surfaces using thermal desorption spectroscopy, J. Vac. Sci. Technol., A, 1990, 8, 3229–3236 CrossRef CAS.
- C. Kittel, Introduction to Solid State Physics, Wiley, New York, 8th edn, 2005 Search PubMed.
- O. Assowe, O. Politano, V. Vignal, P. Arnoux, B. Diawara, O. Verners and A. C. T. van Duin, Reactive Molecular Dynamics of the Initial Oxidation Stages of Ni(111) in Pure Water: Effect of an Applied Electric Field, J. Phys. Chem. A, 2012, 116, 11796–11805 CrossRef CAS PubMed.
- D. J. Siegel and J. C. Hamilton, First-principles study of the solubility, diffusion, and clustering of C in Ni, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 094105 CrossRef and references therein.
- H. Amara, C. Bichara and F. Ducastelle, Formation of carbon nanostructures on nickel surfaces: a tight-binding grand canonical Monte Carlo study, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 113404 CrossRef.
- W. Somers, et al., Temperature influence on the reactivity of plasma species on a nickel catalyst surface: an atomic scale study, Catal. Today, 2013, 211, 131–136 CrossRef CAS.
- G. Bussi, D. Donadio and M. Parrinello, Canonical sampling through velocity-rescaling, J. Chem. Phys., 2007, 126, 014101 CrossRef PubMed.
- F. Smith and J. W. Van Cleve, A Reinvestigation of the Preparation of β-Methyl Lactoside, J. Am. Chem. Soc., 1952, 74, 1912–1913 CrossRef CAS.
- G. Rotzoll, High-temperature pyrolysis of ethanol, J. Anal. Appl. Pyrolysis, 1985, 9, 43–52 CrossRef CAS.
- K. Saito, T. Kakumoto, Y. Nakanishi and A. Imamura, Thermal Decomposition of Formaldehyde at High Temperature, J. Phys. Chem., 1985, 89, 3109–3113 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- B. Hammer, L. Hansen and J. Nørskov, Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- M. Methfessel and A. T. Paxton, High-precision sampling for Brillouin-zone integration in metals, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616–3621 CrossRef CAS.
- F. Ding, A. Rosén and K. Bolton, Molecular dynamics study of the catalyst particle size dependence on carbon nanotube growth, Chem. Phys., 2004, 121, 2775–2779 CAS.
- G. Henkelman, B. P. Uberuage and H. A. Jonsson, Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- A. Hodgson and S. Haq, Water adsorption and the wetting of metal surfaces, Surf. Sci. Rep., 2009, 64, 381–451 CrossRef CAS.
- C. Benndorf and T. E. Madey, Adsorption of H2O on clean and oxygen-predosed Ni(110), Surf. Sci., 1988, 194, 63–91 CrossRef CAS.
- A. Mohsenzadeh, K. Bolton and T. Richards, DFT study of the adsorption and dissociation of water on Ni(111), Ni(110) and Ni(100) surfaces, Surf. Sci., 2014, 627, 1–10 CrossRef CAS.
- Y. Li, R. Ahuja and J. A. Larsson, Communication: origin of the difference between carbon nanotube armchair and zigzag ends, J. Chem. Phys., 2014, 140, 091102 CrossRef PubMed.
- F.-B. Rao, T. Li and Y.-L. Wang, Effect of hydrogen on the growth of single-walled carbon nanotubes by thermal chemical vapor deposition, Phys. E, 2008, 40, 779–784 CrossRef CAS.
- U. Khalilov, A. Bogaerts, B. Xu, T. Kato, T. Kaneko and E. C. Neyts, How the alignment of adsorbed ortho H pairs determines the onset of selective carbon nanotube etching, Nanoscale, 2017, 9, 1653–1661 RSC.
- F. Ding, K. Jiao, Y. Lin and B. I. Yakobson, How Evaporating Carbon nanotubes Retain Their Perfection?, Nano Lett., 2007, 7, 681–684 CrossRef CAS PubMed.
- A. Malesevic, S. Vizireanu, R. Kemps, A. Vanhulsel, C. Van Haesendonck and G. Dinescu, Combined growth of carbon nanotubes and carbon nanowalls by plasma-enhanced chemical vapor deposition, Carbon, 2007, 45, 2932 CrossRef CAS.
- S. Iijima, Growth Model for Carbon Nanotubes, Phys. Rev. Lett., 1992, 69, 3100–3103 CrossRef CAS PubMed.
- M. He, Y. Magnin, H. Jiang, H. Amara, E. I. Kauppinen, A. Loiseau and C. Bichara, Growth Modes and Chiral Selectivity of Single-walled Carbon Nanotubes, Nanoscale, 2018, 10, 6744–6750 RSC.
- L. Zhang, M. He, T. W. Hansen, J. Kling, H. Jiang, E. I. Kauppinen, A. Loiseau and J. B. Wagner, Growth Termination and Multiple Nucleation of Single-Wall Carbon Nanotubes Evidenced by In Situ Transmission Electron Microscopy, ACS Nano, 2017, 11, 4483–4493 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8nh00323h |
| This journal is © The Royal Society of Chemistry 2019 |