In situ structural evolution of single particle model catalysts under ambient pressure reaction conditions†
Sara
Fernández
ab,
Lu
Gao
 c,
Jan Philipp
Hofmann
c,
Jan Philipp
Hofmann
 c,
Jérôme
Carnis
c,
Jérôme
Carnis
 ab,
Stéphane
Labat
a,
Gilbert A.
Chahine
b,
Arno J. F.
van Hoof
ab,
Stéphane
Labat
a,
Gilbert A.
Chahine
b,
Arno J. F.
van Hoof
 c,
M. W. G. M. (Tiny)
Verhoeven
c,
Tobias U.
Schülli
b,
Emiel J. M.
Hensen
c,
M. W. G. M. (Tiny)
Verhoeven
c,
Tobias U.
Schülli
b,
Emiel J. M.
Hensen
 c,
Olivier
Thomas
a and
Marie-Ingrid
Richard
c,
Olivier
Thomas
a and
Marie-Ingrid
Richard
 *ab
*ab
aAix Marseille Université, CNRS, Université de Toulon, IM2NP UMR 7334, 13397, Marseille, France. E-mail: marie-ingrid.richard@im2np.fr
bID01/ESRF, 6 rue Jules Horowitz, BP220, F-38043 Grenoble Cedex, France
cLaboratory of Inorganic Materials Chemistry, Department of Chemical Engineering and Chemistry, Eindhoven University of Technology, P. O. Box 513, 5600MB Eindhoven, The Netherlands
First published on 3rd December 2018
Abstract
The catalytic activity of metal nanoparticles can be altered by applying strain, which changes the crystalline lattice spacing and modifies the electronic properties of the metal. Understanding the role of elastic strain during catalytic reactions is thus crucial for catalyst design. Here, we show how single highly faceted Pt nanoparticles expand or contract upon interaction with different gas atmospheres using in situ nano-focused coherent X-ray diffraction imaging. We also demonstrate inter-particle heterogeneities, as they differ in development of strain under CO oxidation reaction conditions. The reported observations offer new insights into the design of catalysts exploiting strain effects.
1 Introduction
Understanding how nanoparticles catalyse chemical reactions is important for the development of efficient catalytic materials for a wide range of energy and environmental applications. Among all catalytic conversions, oxidation of carbon monoxide is considered as a prototype reaction for studying fundamental concepts in heterogeneous catalysis.1 It is relevant for exhaust gas purification. Tracking the atomic scale structural re-organisation in a catalyst material in situ during a catalytic process is crucial to identify the catalytically active sites. Catalysis being a surface effect has been shown to depend on the crystallographic orientation of the surface. Furthermore, nanoparticles are known to change the crystallographic orientation of their facets when exposed to different gases in a catalytic reaction.2 Elastic strain, which has been demonstrated to alter the reactivity of metal substrates,3 can play a vital role in the adsorption and activation of molecules on nanoparticles. Controlling nanoparticle surface strain, i.e. compression (or stretch) of surface atoms, is an important approach to tune nanoparticle surface chemistry to optimise their catalytic properties. Interatomic distances at catalytic surfaces playing a crucial role for the increased reactivity and eventual dissociation of adsorbed molecules, crystallographic orientation, surface reconstruction and strain naturally are supposed to influence catalytic activity. Accommodation of elastic strain inside the crystal volume may be a particular strength of nanoparticles increasing their attractiveness for catalysis. For example, Zhang et al.4 evidence that the strain at the surface in a core/shell nanoparticle can be tuned by the core structure to improve catalytic performance. Peter et al.5 point out that Pd nanoparticles less than 8 nm in diameter are compressively strained, and this leads to weaker CO adsorption. More recently, lattice compression and tension in individual Pt nanoparticles induced using a lithium cobalt oxide substrate were observed and led to a 90% enhancement or 40% suppression in the Pt catalysed oxygen reduction reaction (ORR), respectively.6 K. Yan et al. have also demonstrated that elastic strain tunes the catalytic activity in a controlled and predictable way.7,8 During hydrogen evolution reaction (HER), they demonstrated that the activity of Pt was increased by applying a compressive mechanical loading. These examples clearly demonstrate that strain engineering via e.g. synthesis of core–shell nanoparticles, compositional segregation, substrate straining or mechanical loading has a strong impact on the catalytic properties. The effects of surface lattice strain are enhanced in nanocatalysts due to a higher ratio of surface to bulk atoms and significantly alter the adsorption properties of reactants.9 As a result, it is now well accepted that strain influences the catalytic activity of nanoparticles. However, there has been no clear demonstration of how strain evolves inside individual single nanoparticles during CO oxidation in gas phase. Lattice strain mapping is often performed ex situ using transmission electron microscopy (TEM) (see, for instance ref. 10). When used in situ (environmental TEM), in most cases, only the projections of the atomic planes are accessible, which renders the three-dimensional spatial determination of the strain field difficult. At the nanoscale, X-ray diffraction is currently the only method, which can image strain with a good resolution: at a level hardly achievable with other techniques, with a strain sensitivity better than 10−4. The technique is highly sensitive to atomic displacement and is easily deployed to realistic sample environments due to the high penetration power of hard X-rays. Recent works using nano-focused Bragg coherent diffraction imaging have demonstrated the capabilities of X-ray diffraction to measure the local strain in 3D in nanoparticles during chemical reaction.11–13 However, no investigations have shown to date both the local and average evolution of the strain distribution (with a high strain sensitivity), the lattice orientation of single nanoparticles as well as inter-particle heterogeneities during a gas-phase heterogeneous catalytic reaction.Here, we report on local and average structural changes of individual single platinum nanoparticles electrochemically synthesized on glassy carbon during catalytic reaction at near ambient pressure and elevated temperature using in situ nano-focused coherent Bragg diffraction imaging. We focus on the role of both the Pt nanoparticle surface and volume in the catalytic oxidation of carbon monoxide. Structural modifications have been induced on faceted Pt nanoparticles by interaction with O2 and CO/O2 mixtures at elevated temperatures up to 200 °C. We observe the scattered signals to change upon exposure to O2 and to stoichiometric mixtures of CO and O2, permitting us to gain insights into strain changes of a single Pt nanoparticle under realistic catalytic conditions.
2 Results and discussion
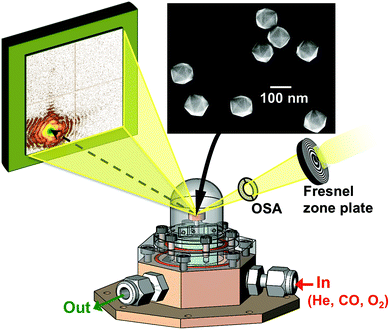
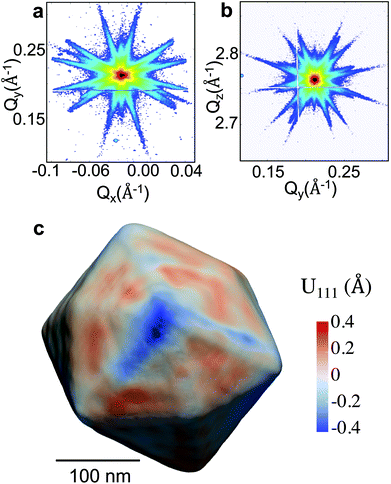
The experiment was performed at the nanodiffraction imaging beamline ID01 at the European Synchrotron (ESRF) using a dedicated reactor compatible with nano-focused X-ray diffraction and gaseous environment, as illustrated in Fig. 1. The reactor fulfills the constraints of weight and size of the three-axis piezoelectric nanopositioning stage as well as the constraints of stability and movement precision issues.14 Coherent X-rays with photon energy of 8 keV were focused to a spot size of 170 (vertically) × 465 (horizontally) nm2 by a Fresnel zone plate (FZP) in order to illuminate a single particle. Unfocused radiation transmitted by the FZP is eliminated using a combination of a 50 μm central stop placed just before the FZP and an order sorting aperture (OSA) with a 50 μm diameter positioned at 2.3 cm before the sample. The scattered X-rays were detected using a two-dimensional (2D) Maxipix pixel detector15 (516 × 516 pixels of 55 μm). The in situ X-ray studies were realized under flow conditions: a constant flux of He flowed in the reactor during the whole experiment (20 ml min−1) in order to be able to change quickly and efficiently the reactive gases present in the chamber. The sample consists of high-index faceted tetrahexahedral (THH) Pt nanocrystals randomly oriented on a glassy carbon (GC) substrate, as shown in the scanning and transmission electron microscopy images in Fig. 1 and 1S of ESI.† They have been synthesized on glassy carbon electrodes by a square-wave-potential method with a saturated calomel reference electrode (SCE) and a Pt foil counter electrode in 2 mM H2PtCl6 and 0.1 M H2SO4 electrolyte following the procedure in ref. 16. The THH shape can be described as a cube whose faces are capped by square-based pyramids, leading to 24 high-index planes of hk0 type (h ≠ k ≠ 0).17 The diameter of the Pt NCs varies from 50 to 400 nm. Fig. 2(c) displays the Bragg coherent diffraction imaging reconstruction of the three-dimensional (3D) displacement field, U111, measured along the [111] direction of a THH Pt nanoparticle with 24 {210} facets. The measurement (3D rocking curve at the 111 Pt Bragg reflection – see Fig. 2(a–b), where reciprocal space maps of the diffraction peak are displayed) has been performed at room temperature and ambient pressure. The overall shape with well defined facets is evidenced as well as displacement inhomogeneities (and thus strain inhomogeneities, as strain verifies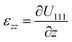 ) at the surface.
) at the surface.
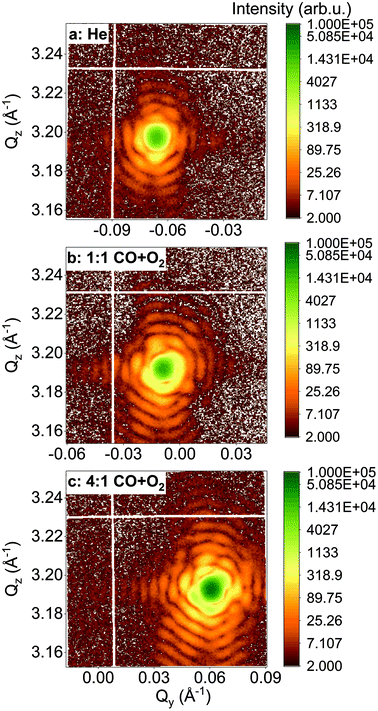
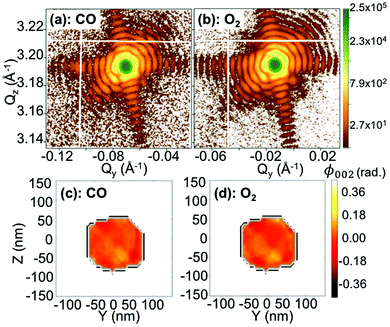
In the following, we will focus on two single Pt nanoparticles, called hereafter particles A and B with a diameter of 110 nm and 140 nm, respectively. They were tracked during reaction at a temperature of 200 °C and upon exposure to different gases. For a fast evaluation of the shape and strain evolution, only 2D detector images and fast 3D reciprocal space maps have been recorded in the following. For observation of the strain evolution, the 002 Pt Bragg peak was monitored for all process steps by fixing the detector at a scattering angle of 2θ = 46.57°, which corresponds to twice of the value of the theoretical Bragg angle (θB = 23.285°). Fig. 3 shows the evolution of the Bragg coherent diffraction patterns (acquisition time of 60 s) of the 110 nm diameter Pt THH nanocrystal (particle A) at the maximum of the rocking curve under (a) He, (b) 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 CO + O2 (c) and (c) 4
1 CO + O2 (c) and (c) 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 CO + O2. The diffraction patterns are plotted as a function of the reciprocal space coordinates Qy and Qz (both perpendicular to the X-ray beam, either in-plane or out-of-plane and in the crystal frame). Under ambient environmental conditions, well defined streaks from the Pt nanoparticle around the 002 Pt Bragg reflection show the faceted nature of the nanoparticle surface (as observed in Fig. 2). The interference fringes are a sensitive probe of changes in shape, size and strain (asymmetric intensity distribution of the diffraction pattern) of the investigated particle. Important changes are observed both on the visibility, the periodicity and the intensity distribution of the coherent diffraction patterns. Although basic interpretations are possible by just evaluating e.g. the periodicity of the fringes to extract the particle size along one crystallographic direction, the most elegant way is to extract all accessible information by a transformation of the diffraction pattern into real space.
1 CO + O2. The diffraction patterns are plotted as a function of the reciprocal space coordinates Qy and Qz (both perpendicular to the X-ray beam, either in-plane or out-of-plane and in the crystal frame). Under ambient environmental conditions, well defined streaks from the Pt nanoparticle around the 002 Pt Bragg reflection show the faceted nature of the nanoparticle surface (as observed in Fig. 2). The interference fringes are a sensitive probe of changes in shape, size and strain (asymmetric intensity distribution of the diffraction pattern) of the investigated particle. Important changes are observed both on the visibility, the periodicity and the intensity distribution of the coherent diffraction patterns. Although basic interpretations are possible by just evaluating e.g. the periodicity of the fringes to extract the particle size along one crystallographic direction, the most elegant way is to extract all accessible information by a transformation of the diffraction pattern into real space.
To visualise distinct changes, the 2D data were phased and inverted using the reconstruction code of the PyNX package.18 The following algorithms have been used to retrieve the 2D data-sets: error reduction,19 charge flipping, Fienup's hybrid-input–output,20 maximum-likelihood21 and shrink-wrap.22Fig. 4 displays the 2D reconstruction of the projected phase ϕ002 (along the direction perpendicular to the detector)23 of the retrieved object from the selected coherent diffraction patterns shown in Fig. 3. The reconstructed voxel size being 6.5 nm (vertically) × 4.9 nm (horizontally), the crystal dimensions are estimated to be ∼110 × 110 nm2. The method enables the simultaneous analysis of the evolution of the size of the particle and its structure at nanoscale resolution. As demonstrated by Labat et al.,23 in the case of phase retrieval of a 2D slice, the modulus and phase of the retrieved 2D complex-valued object (arising from the 3D object) are both intimate mixtures of the electronic density and displacement field U(x, y, z), due to the averaging along the detector direction. As here the out-of-plane 002 Pt Bragg reflection has been measured for particle A, changes in the phase are related to modification of the displacement field along the [001] direction (i.e., U002) in the particle. Interestingly, the projection maps in Fig. 4 suggest only weak changes of the shape of the particle (see the black contour in the figure) but the variations of the internal structure appear to be much more important. These drastic changes of the phase (thus of the displacement field) are observed to be dependent on the composition of the gas mixture. This implies that strain (spatial derivative of the displacement field) evolution inside the particle occurs during interaction with the introduced gases. Note that the {001} planes of particle A tilt with time (see Fig. 5(a)). As the tilt remains small (<3°), the inhomogeneities observed in the projected phase in particle A are assumed to be related to local strain effects. The strain distribution may originate from lattice distortion at edges of the nanoparticles, i.e. from the interactions forces between the reactants and the Pt catalysts as reported in ref. 13. Inhomogeneities in strain distribution are relevant for catalysis as it has been recently demonstrated that strain may affect the turnover frequency24 and boost or alter the catalytic activity of metals in heterogeneous nano-catalysts.6
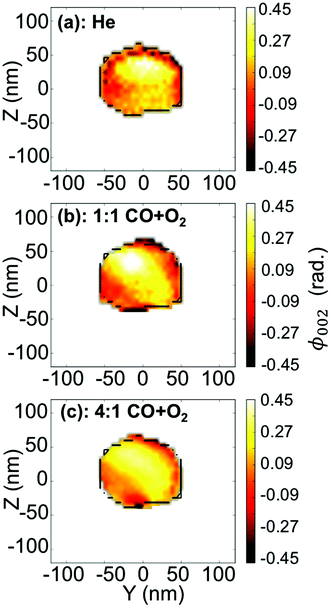 | ||
| Fig. 4 (a–c) Two-dimensional reconstruction of the projected phase, ϕ002 (projected in the detector plane), from the diffraction patterns shown in Fig. 3(a–c), respectively. The black line is a guide for the eyes and indicates the contour of the particle retrieved in figure (a). | ||
Looking closely at the X-ray reciprocal space maps displayed in Fig. 3, we can observe that the maximum of the diffraction pattern of the tracked nanoparticle is not centered at the same (Qy, Qz) positions upon exposure to different gases. This change of position in the reciprocal space can either be due to modifications of the average strain and/or of crystallographic plane orientation of the particle. It is then necessary to disentangle the strain and crystallographic lattice orientation of the tracked particle as a function of gas mixture and time.
To follow and disentangle the strain and lattice orientation evolution during reaction, fast three-dimensional (3D) reciprocal space maps (RSMs) were recorded around the 002 Pt Bragg peak. A RSM lasted 40 seconds. We successfully tracked the single particle owing to (1) a continuous gas flow ensuring a fixed flow rate and constant chamber pressure and (2) by tracking the nanoparticle position to keep the latter inside the focus of the X-ray beam utilizing the quick-mapping method developed at the ID01 beamline.25 This method consists of a two-dimensional fast mapping of a sample with a nano-focused X-ray beam and within few nanometer precision. The 3D data sets of the RSMs of the selected Pt nanoparticle give enough information to retrieve the average out-of-plane strain εzz as well as the crystallographic orientation (or tilt) of the {001} atomic planes of the single particle during its exposure to O2 and CO/O2 mixtures. The strain εhkl is related to the variation of the lattice parameter aPt and consequently to the variation of the dhkl spacing of the atomic planes. It can be retrieved using eqn (1):
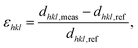 | (1) |
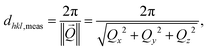 | (2) |
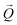 . The conversion of pixels from the detector images into
. The conversion of pixels from the detector images into 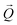 coordinates was done using the xrayutilities26 package. Gaussian fits were performed on 3D data sets to determine the
coordinates was done using the xrayutilities26 package. Gaussian fits were performed on 3D data sets to determine the 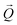 coordinates. The determination of the strain then only depends on the total length of the scattering vector
coordinates. The determination of the strain then only depends on the total length of the scattering vector 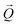 . Tilts of the {001} atomic planes (see Fig. S2 of ESI†) with respect to its first measured value were determined using the following equation:
. Tilts of the {001} atomic planes (see Fig. S2 of ESI†) with respect to its first measured value were determined using the following equation: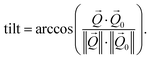 | (3) |
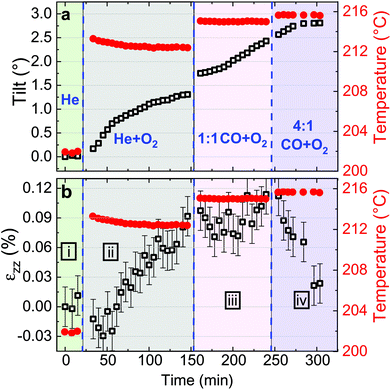
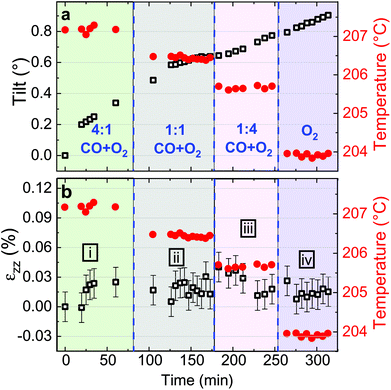
Fitting the series of Bragg peaks and applying eqn (3) yield the tilt evolution of the {001} atomic planes (shown in Fig. 5(a)) of the single Pt nanoparticle. While the temperature was kept at around 200 °C (see red dots in Fig. 5), the partial flows were set successively to: (i) fHe = 25 ml min−1, (ii) fHe = 20 ml min−1 and fO2 = 5 ml min−1, (iii) fHe = 20 ml min−1, fCO = 2.5 ml min−1 and fO2 = 2.5 ml min−1 and (iv) fHe = 20 ml min−1, fCO = 4 ml min−1 and fO2 = 1 ml min−1. An increase of temperature (the thermocouple is fixed in a close vicinity to the top of the carbon electrode inside a cylindrical holder, which maintains the sample on the button heater of the reactor) is observed while changing gas mixture (to replace part of the He support flow with either O2 or CO; the latter two having comparable heat conductivities) due to the different heat conductivities of the gases as we are working at constant heating power.
The in situ monitoring of the tilt demonstrates a rotation of the {001} atomic planes of 2.7° over a period of 3 h 40 min. Note that the Pt particles are not strongly bonded to the glassy carbon substrate and they are observed to rotate. Tilt of the particle may be explained by X-ray photoelectric effect but most probably by the roughening of the glassy carbon substrate which has been observed to be etched during reaction. As expected from the changes observed in Fig. 4, the strain inside the particle evolves as a function of the gas mixture (see Fig. 5(b)). Note that the reference strain is taken at time zero at the beginning of the experiment. As a change of temperature is observed while changing gas mixture, both thermal strain εthermal of Pt and substrate must be taken into account. In a first approximation (i.e., neglecting elastic strain and neglecting adhesion of the particle on the GC substrate), as response to the temperature change ΔT, both materials are expected to linearly expand, yielding a thermal strain that depends on the linear coefficient of thermal expansion αL as εthermal = αLΔT. While flowing O2, the maximum difference of temperature between the recorded strain is ΔT = 14 °C. Taking the tabulated values for the glassy carbon (GC) and Pt thermal expansion αGC ∼3.7 × 10−6 K−1 and αPt ∼9.457 × 10−6 K−1 (at 200 °C), a first estimation of the thermal strain yields to εthermal,Pt = 0.013% for Pt, and to εthermal,GC = 0.005% for the GC substrate. These values are much smaller than the changes we observe in our experiments. Strain caused by thermal mismatch can thus be left unconsidered when regarding the present strain values. Hence, larger shifts of the peak with respect to the reference value (first measurement under He flow) are attributed to variations of lattice parameter in the particle under gas exposure. The possible mechanisms are explained hereafter.
Indeed, after thermal stabilisation, exposure to O2 (phase ii of Fig. 5(b)) induces a tensile expansion in the nanoparticle, reaching a maximum of 0.09% strain. This value is close to what has been measured by Lamber et al., who have observed an average strain variation of about 0.13% due to surface stress in 100 nm size gold cluster embedded in plasma polymer matrices.27 Our obtained value can possibly be attributed to the influence of surface stress. According to the work of Tian et al., a difference of surface stress Δτ of −2.2 N m−1 is observed during O exposure of Pt(111) at 320 K (about 50 °C).28 The surface stress can be converted into radial strain using the following formula: Δεr = −2Δτ/(3Br), where r is the radius of the particle and B = (C11 + 2C12)/3 = 282.7 GPa is related to the elastic constants of Pt. This leads to Δεzz = Δεr/3∼ +0.0033%. The obtained value is positive and may explain the tensile strain that we have experimentally observed during exposure to O2. But this value is quite low compared to our experimental values; this can be explained by the fact that we are working at a higher temperature (200 °C instead of 50 °C) and with small surfaces with high index facets (THH Pt nanoparticles). Apart from surface stress, the lattice expansion, which is observed during exposure to a mixture of He and O2, can also be likely caused by the formation of an oxide layer at the surface (O adsorption), leading to a displacement field that propagates into the volume of the nanoparticle. PtO and/or PtO2 are known to form during oxidation.29 These oxides do not show the same structure as bulk Pt,30 and may strain (lattice mismatch) the volume of the Pt nanoparticle. Owing to our applied conditions, we first expect the formation of a surface oxide. As the oxide layer is very thin, the nano-focused coherent X-ray technique is not sensitive enough to probe small volume of materials and to detect the formation of the oxide layer. Moreover, we can demonstrate that an out-of-plane strain of 0.09% can be induced by a change of temperature of 95 °C of the Pt particle. From the knowledge of the standard enthalpy of formation of anhydrous PtO2 (ΔH = −80 kJ mol−1, from ref. 31), it is possible to calculate the heat energy released by the Pt particle: q = cmΔT, where c = 0.1256 J K−1 g−1 is the tabulated specific heat capacity of Pt, m the mass of the Pt particle and ΔT the temperature difference (i.e., 95 °C). Supposing a volume of the particle of 4πr3/3 (where r ∼55 nm) and from the volumetric mass density (ρ = 21.45 g cm−3), we get 1.49 × 10−17 kg for the mass and q = 1.79 × 10−13 J. Knowing q and ΔH, we can get information about the number of platinum oxide units participating in the thermal release. This corresponds to a volume V, of ∼21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 nm3; this leads to an oxide shell of Δr (V = 4πr2Δr) of 0.56 nm. The formation of an oxide shell of 0.56 nm around the Pt particle can then lead to a change of temperature of 95 °C and an out-of-plane strain of 0.09%. Note that we do not have the resolution to determine if hot spots with locally different temperatures are generated on the particles. It is then possible that the strain change can be explained by the formation of a platinum oxide leading to: (a) an overheat of the particle due to an insufficient thermal coupling to the GC substrate and/or (b) surface stress and/or (c) lattice mismatch induced by the formation of an oxide layer as compared to Pt metal. These effects cannot be disentangled.
140 nm3; this leads to an oxide shell of Δr (V = 4πr2Δr) of 0.56 nm. The formation of an oxide shell of 0.56 nm around the Pt particle can then lead to a change of temperature of 95 °C and an out-of-plane strain of 0.09%. Note that we do not have the resolution to determine if hot spots with locally different temperatures are generated on the particles. It is then possible that the strain change can be explained by the formation of a platinum oxide leading to: (a) an overheat of the particle due to an insufficient thermal coupling to the GC substrate and/or (b) surface stress and/or (c) lattice mismatch induced by the formation of an oxide layer as compared to Pt metal. These effects cannot be disentangled.
In a second step (phase iii of Fig. 5(b)), CO was introduced in the reactor. Once temperature is stable, small changes in the lattice parameter are observed, oscillating in a strain range of ±0.03%. When the CO/O2 mixture was changed to reducing (i.e. stoichiometric excess of CO) conditions (phase iv of Fig. 5(b)), compression takes place. In the meantime, small variations of the lattice orientation, i.e. tilt (phase iv of Fig. 5(a)), are observed.
Previous studies of catalytic reactions have suggested oscillatory behaviour even under fixed conditions.2,32 The shape of faceted Pt nanoparticles exposed to CO/O2 mixtures have been reported to show an oscillatory shape behaviour, evolving from faceted to rounded shapes according to reversible cycles of oxidation or reduction that take place every 10–20 seconds in a ∼50 nm diameter Pt particle.33 Here, the particle is larger but the strain fluctuations observed in phase iii may be linked to this oscillatory behavior attributed to dynamic changes in the catalyst structure. Surface oxide formation is known to contribute to the oscillatory CO conversion.34,35 Note that the standard enthalpy of reaction for the CO oxidation (ΔH = −283 kJ mol−1, from ref. 36) is quite large and may also contribute to the observed oscillations. Then, the drop in strain (compression) observed for particle A during phase iv (under 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 CO + O2) may be related to the reduction of the Pt oxide.
1 CO + O2) may be related to the reduction of the Pt oxide.
The same analysis has been made for a larger particle (particle B). Fig. 6 displays the Qy–Qz X-ray reciprocal space maps around the 002 Pt reflection for an individual 140 nm diameter THH nanoparticle (particle B) at 200 °C and upon exposure to different gases: (a) CO and (b) O2. The respective reconstructed projection of the out-of-plane displacement is also shown in Fig. 6(c–d). Faint changes are observed. The projection maps of the out-of-plane displacement field are also quite homogeneous contrary to the ones of particle A (see Fig. 4). The lattice tilt and average out-of-plane strain of the particle are displayed in Fig. 7. While the in situ monitoring of the tilt demonstrates a rotation of the {001} atomic planes of 0.9° over a period of 5 h, only weak variations of the average strain are observed, in contrast to particle A. This shows the stability of the measurement and experimental setup. Here, the weak variation of the average strain as well as the rather homogeneous displacement field observed in particle B (grown under the same conditions as particle A) can possibly demonstrate that the particle is non-active (i.e. poisoned). As particles A and B are different in their development of strain in response to different gas compositions, this shows inter-particle heterogeneities.37,38 The difference between particles shows the strength of nano-diffraction. The differences are often concealed by ensemble characterisation. Note that Bragg coherent X-ray diffraction experiments with metallic nanoparticles have been performed at energies close to our working energy and in gas phase and no beam damage has been revealed.12,13
3. Conclusion
In conclusion, we measured in situ under ambient pressure conditions the lattice orientation and out-of-plane strain field (at the local and average scales) in single Pt nanoparticles during their exposure to O2 and CO/O2 mixtures by Bragg coherent X-ray diffraction imaging. We were able to follow the average (volume and surface) strain of one single particle during reaction as well as its reconstructed projected displacement field using 2D phase retrieval. From the reconstructed projected displacement field, we can assume an inhomogeneous strain field inside particle A. The high strain sensitivity (Δa/a = 10−4) at high temperature (200 °C) makes it possible to determine strain fluctuations of a single Pt nanoparticle during reaction with a 1-minute time resolution. It is then possible to track a single particle in a gas phase environment and measure its strain response to different gas atmospheres at high temperature. Our report shows clear evidence that the average and local strain in nanoparticles evolves during catalytic action. The present findings demonstrate that nanoparticle strain dynamics should be taken into account for a complete description of oscillating catalytic reactions. Our results show the utility of imaging the strain field evolution during catalysis reactions. This identification can be carried out at the single particle level under operating conditions and can serve to identify the optimal morphology and size for catalysts. The reported observations offer new insights into the design of catalysts to exploit strain effects.Author contributions
S.F., L.G., J.P.H., G.C., A. van H., T. V. and M.I.R. performed the synchrotron measurements. M.I.R., S.F. and J.C. analysed the synchrotron data. L.G. prepared the samples. All contributed to data discussion and to writing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the ID01 beamline staff for excellent support during the experiment and ESRF for beamtime allocation (beamtime proposal: CH4426). Financial support to this work by ANR Charline (ANR-16-CE07-0028-01) and a NWO TOP grant to E. J. M. H. are gratefully acknowledged.References
- H.-J. Freund, G. Meijer, M. Scheffler, R. Schlögl and M. Wolf, Angew. Chem., Int. Ed., 2011, 50, 10064–10094 CrossRef CAS PubMed.
- P. Nolte, A. Stierle, N. Y. Jin-Phillipp, N. Kasper, T. U. Schulli and H. Dosch, Science, 2008, 321, 1654–1658 CrossRef CAS PubMed.
- M. Mavrikakis, B. Hammer and J. K. Nørskov, Phys. Rev. Lett., 1998, 81, 2819–2822 CrossRef.
- S. Zhang, X. Zhang, G. Jiang, H. Zhu, S. Guo, D. Su, G. Lu and S. Sun, J. Am. Chem. Soc., 2014, 136, 7734–7739 CrossRef CAS PubMed.
- M. Peter, S. Adamovsky, J. M. F. Camacho and S. Schauermann, Faraday Discuss., 2013, 162, 341–354 RSC.
- H. Wang, S. Xu, C. Tsai, Y. Li, C. Liu, J. Zhao, Y. Liu, H. Yuan, F. Abild-Pedersen, F. B. Prinz, J. K. Nørskov and Y. Cui, Science, 2016, 354, 1031–1036 CrossRef CAS PubMed.
- K. Yan, T. A. Maark, A. Khorshidi, V. A. Sethuraman, A. A. Peterson and P. R. Guduru, Angew. Chem., Int. Ed., 2016, 55, 6175–6181 CrossRef CAS PubMed.
- K. Yan, S. K. Kim, A. Khorshidi, P. R. Guduru and A. A. Peterson, J. Phys. Chem. C, 2017, 121, 6177–6183 CrossRef CAS.
- B. T. Sneed, A. P. Young and C.-K. Tsung, Nanoscale, 2015, 7, 12248–12265 RSC.
- T. Daio, A. Staykov, L. Guo, J. Liu, M. Tanaka, S. M. Lyth and K. Sasaki, Sci. Rep., 2015, 5, 13126 CrossRef CAS PubMed.
- A. Ulvestad, M. J. Welland, S. S. E. Collins, R. Harder, E. Maxey, J. Wingert, A. Singer, S. Hy, P. Mulvaney, P. Zapol and O. G. Shpyrko, Nat. Commun., 2015, 6, 10092 CrossRef CAS PubMed.
- A. Ulvestad, K. Sasikumar, J. W. Kim, R. Harder, E. Maxey, J. N. Clark, B. Narayanan, S. A. Deshmukh, N. Ferrier, P. Mulvaney, S. K. R. S. Sankaranarayanan and O. G. Shpyrko, J. Phys. Chem. Lett., 2016, 7, 3008–3013 CrossRef CAS PubMed.
- D. Kim, M. Chung, J. Carnis, S. Kim, K. Yun, J. Kang, W. Cha, M. J. Cherukara, E. Maxey, R. Harder, K. Sasikumar, S. K. R. S. Sankaranarayanan, A. Zozulya, M. Sprung, D. Riu and H. Kim, Nat. Commun., 2018, 9, 3422 CrossRef PubMed.
- M.-I. Richard, S. Fernández, J. P. Hofmann, L. Gao, G. A. Chahine, S. J. Leake, H. Djazouli, Y. De Bortoli, L. Petit, P. Boesecke, S. Labat, E. J. M. Hensen, O. Thomas and T. Schülli, Rev. Sci. Instrum., 2017, 88, 093902 CrossRef PubMed.
- C. Ponchut, J. M. Rigal, J. Clément, E. Papillon, A. Homs and S. Petitdemange, J. Instrum., 2011, 6, C01069 Search PubMed.
- N. Tian, Z.-Y. Zhou, S.-G. Sun, Y. Ding and Z. Lin Wang, Science, 2007, 316, 732–735 CrossRef CAS PubMed.
- A. A. Proussevitch and D. L. Sahagian, Comput. Geosci., 2001, 27, 441–454 CrossRef.
- O. Mandula, M. Elzo Aizarna, J. Eymery, M. Burghammer and V. Favre-Nicolin, J. Appl. Crystallogr., 2016, 49, 1842–1848 CrossRef CAS.
- J. R. Fienup, Opt. Lett., 1978, 3, 27–29 CrossRef CAS PubMed.
- J. Fienup, Appl. Opt., 1982, 21, 2758–2769 CrossRef CAS PubMed.
- P. Thibault and M. Guizar-Sicairos, New J. Phys., 2012, 14, 063004 CrossRef.
- S. Marchesini, H. He, H. N. Chapman, S. P. Hau-Riege, A. Noy, M. R. Howells, U. Weierstall and J. C. H. Spence, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 140101 CrossRef.
- S. Labat, V. Chamard and O. Thomas, Thin Solid Films, 2007, 515, 5557–5562 CrossRef CAS.
- T. Nilsson Pingel, M. Jørgensen, A. B. Yankovich, H. Grönbeck and E. Olsson, Nat. Commun., 2018, 9, 2722 CrossRef PubMed.
- G. A. Chahine, M.-I. Richard, R. A. Homs-Regojo, T. N. Tran-Caliste, D. Carbone, V. L. R. Jacques, R. Grifone, P. Boesecke, J. Katzer, I. Costina, H. Djazouli, T. Schroeder and T. U. Schülli, J. Appl. Crystallogr., 2014, 47, 762–769 CrossRef CAS.
- D. Kriegner, E. Wintersberger and J. Stangl, J. Appl. Crystallogr., 2013, 46, 1162–1170 CrossRef CAS PubMed.
- R. Lamber, S. Wetjen, G. Schulz-Ekloff and A. Baalmann, J. Phys. Chem., 1995, 99, 13834–13838 CrossRef CAS.
- Z. Tian, D. Sander, N. N. Negulyaev, V. S. Stepanyuk and J. Kirschner, Phys. Rev. B, 2010, 81, 11340 Search PubMed.
- D. J. Miller, H. Öberg, S. Kaya, H. Sanchez Casalongue, D. Friebel, T. Anniyev, H. Ogasawara, H. Bluhm, L. G. M. Pettersson and A. Nilsson, Phys. Rev. Lett., 2011, 107, 195502 CrossRef CAS PubMed.
- R. K. Nomiyama, M. J. Piotrowski and J. L. F. Da Silva, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 100101 CrossRef.
- Y. Nagano, J. Therm. Anal. Calorim., 2002, 69, 831–839 CrossRef CAS.
- R. Imbihl and G. Ertl, Chem. Rev., 1995, 95, 697–733 CrossRef CAS.
- S. B. Vendelbo, C. F. Elkjær, H. Falsig, I. Puspitasari, P. Dona, L. Mele, B. Morana, B. J. Nelissen, R. van Rijn, J. F. Creemer, P. J. Kooyman and S. Helveg, Nat. Mater., 2014, 13, 884–890 CrossRef CAS PubMed.
- J. E. Turner, B. C. Sales and M. B. Maple, Surf. Sci., 1981, 103, 54–74 CrossRef CAS.
- M. D. Ackermann, T. M. Pedersen, B. L. M. Hendriksen, O. Robach, S. C. Bobaru, I. Popa, C. Quiros, H. Kim, B. Hammer, S. Ferrer and J. W. M. Frenken, Phys. Rev. Lett., 2005, 95, 255505 CrossRef CAS PubMed.
- W. M. Haynes, CRC Handbook of Chemistry and Physics, CRC Press, 95th edn, 2014 Search PubMed.
- I. L. C. Buurmans and B. M. Weckhuysen, Nat. Chem., 2012, 4, 873–886 CrossRef CAS PubMed.
- E. Plessers, I. Stassen, S. P. Sree, K. P. F. Janssen, H. Yuan, J. Martens, J. Hofkens, D. De Vos and M. B. J. Roeffaers, ACS Catal., 2015, 5, 6690–6695 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/C8NR08414A |
| This journal is © The Royal Society of Chemistry 2019 |