Enhanced intrinsic saturation magnetization of ZnxCo1−xFe2O4 nanocrystallites with metastable spinel inversion†
Henrik Lyder
Andersen
 a,
Cecilia
Granados-Miralles‡
a,
Cecilia
Granados-Miralles‡
 a,
Matilde
Saura-Múzquiz
a,
Matilde
Saura-Múzquiz
 a,
Marian
Stingaciu§
a,
Jacob
Larsen
a,
Marian
Stingaciu§
a,
Jacob
Larsen
 b,
Frederik
Søndergaard-Pedersen
b,
Frederik
Søndergaard-Pedersen
 a,
Jakob Voldum
Ahlburg
a,
Jakob Voldum
Ahlburg
 a,
Lukas
Keller
c,
Cathrine
Frandsen
a,
Lukas
Keller
c,
Cathrine
Frandsen
 b and
Mogens
Christensen
b and
Mogens
Christensen
 *a
*a
aCenter for Materials Crystallography, Department of Chemistry and Interdisciplinary Nanoscience Centre (iNANO), Aarhus University, DK-8000 Aarhus C, Denmark. E-mail: mch@chem.au.dk
bDepartment of Physics, Technical University of Denmark, DK-2800 Kgs. Lyngby, Denmark
cLaboratory for Neutron Scattering and Imaging, Paul Scherrer Institut, 5232 Villigen, Switzerland
First published on 26th February 2019
Abstract
The magnetic properties of spinel ferrites (MFe2O4, M = Mn, Fe, Co, Ni, Zn, etc.) are largely determined by the type of divalent cation, M2+ and cation distribution between the tetrahedral and octahedral sites in the structure. Partial substitution of Zn2+ into the thermodynamically preferred tetrahedral coordination in ferrites produces an increase in magnetic saturation at room temperature. However, nanosized crystallites are known to adopt different structures compared to their bulk equivalents. Consequently, reliable characterization of the atomic structure of nanosized ferrites is essential for understanding and tailoring their magnetic properties. Here, we present a meticulous study of the crystal-, magnetic- and micro-structures of mixed ZnxCo1−xFe2O4 spinel ferrite nanocrystallites in the entire composition range (x = 0.0–1.0 in steps of 0.1). Gram-scale nanoparticle preparation was performed via the widely used hydrothermal method. Eight compositions were selected to study the effect of 4 hours vacuum annealing at 823 K. Combined Rietveld refinement of powder X-ray and neutron diffraction data along with Mössbauer analysis reveal how the as-synthesized nanocrystallites adopt metastable cation inversions, different from the well-established and thermodynamically stable inversions of the bulk equivalents. The annealing treatment causes the structure of the crystallites to relax towards a more bulk-like cation distribution. For all compositions, the smaller as-synthesized nanocrystallites with metastable cation inversion exhibit a higher saturation magnetization compared to the annealed samples. The demonstrated control over the spinel ferrite cation distribution is a key step on the way to designing cheap magnetic materials with tunable properties optimized for specific applications.
Introduction
Magnetic spinel ferrites (MFe2O4, M = Mn, Fe, Co, Ni, Zn, etc.) are among the most important magnetic materials, and have a large number of applications due to their low cost, excellent resistance to corrosion and good magnetic performance.1 In particular, nanosized spinel ferrite particles are currently being studied extensively for uses in e.g. magnetic exchange-spring nanocomposites,2,3 drug delivery,4,5 magnetically recoverable nanocatalysts,6,7 contrast agents for magnetic resonance imaging,8,9 hyperthermia cancer treatment10,11 and many more.12 In all applications, the performance of the spinel ferrite particles can be optimized by tuning or maximizing their magnetic properties, which are determined by the complex interplay between the crystal-, magnetic-, and nano-structure of the nanoparticles.13At the atomic scale, the MFe2O4 compounds all adopt the face centered cubic (fcc) spinel structure (space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m) illustrated in Fig. 1, which consists of a cubic close-packed oxygen lattice with metal ions occupying 1/8 of the tetrahedral and 1/2 of the octahedral voids. Thus, the number of tetrahedrally coordinated ionic species in the structure (8 per unit cell) is half of the octahedrally coordinated (16 per unit cell). In the normal spinel configuration, the M2+ and Fe3+ ions fully occupy the tetrahedral and octahedral site, respectively, yielding the empirical formula, [M2+]tet[Fe23+]octO4. On the other hand, the structure can also be inverse with the M2+ ions located on the octahedral sites, forcing half of the Fe3+ ions to occupy the tetrahedral sites, i.e. [Fe3+]tet[M2+Fe3+]octO4. Finally, the spinel structure can be partially inverse, [M2+1−yFey3+]tet[My2+Fe2−y3+]octO4, with a fraction of the M2+ ions, y, called the inversion degree, occupying the octahedral site. Notably, the different 3d transition metal ions exhibit different affinities for the two crystallographic sites. In the bulk, ZnFe2O4 is a normal spinel, CoFe2O4 and NiFe2O4 are inverse, and MnFe2O4 is partially inverse (y = 0.8).14 However, for nanocrystalline ferrite structures a large variety of inversion degrees have been reported.13,15–22
m) illustrated in Fig. 1, which consists of a cubic close-packed oxygen lattice with metal ions occupying 1/8 of the tetrahedral and 1/2 of the octahedral voids. Thus, the number of tetrahedrally coordinated ionic species in the structure (8 per unit cell) is half of the octahedrally coordinated (16 per unit cell). In the normal spinel configuration, the M2+ and Fe3+ ions fully occupy the tetrahedral and octahedral site, respectively, yielding the empirical formula, [M2+]tet[Fe23+]octO4. On the other hand, the structure can also be inverse with the M2+ ions located on the octahedral sites, forcing half of the Fe3+ ions to occupy the tetrahedral sites, i.e. [Fe3+]tet[M2+Fe3+]octO4. Finally, the spinel structure can be partially inverse, [M2+1−yFey3+]tet[My2+Fe2−y3+]octO4, with a fraction of the M2+ ions, y, called the inversion degree, occupying the octahedral site. Notably, the different 3d transition metal ions exhibit different affinities for the two crystallographic sites. In the bulk, ZnFe2O4 is a normal spinel, CoFe2O4 and NiFe2O4 are inverse, and MnFe2O4 is partially inverse (y = 0.8).14 However, for nanocrystalline ferrite structures a large variety of inversion degrees have been reported.13,15–22
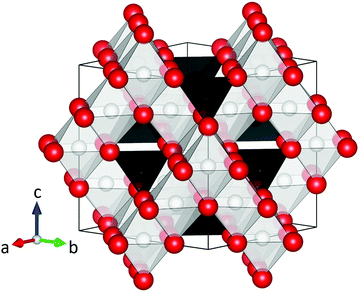 | ||
Fig. 1 Illustration of the spinel ferrite structure (space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, origin choice 2). The red spheres represent oxygen, while the black and white polyhedra show the tetrahedral and octahedral sites, respectively. The structural figure was made using the VESTA software.23 m, origin choice 2). The red spheres represent oxygen, while the black and white polyhedra show the tetrahedral and octahedral sites, respectively. The structural figure was made using the VESTA software.23 | ||
Magnetically, the spinel ferrites generally display a ferrimagnetic ordering, which is governed by a relatively strong antiparallel superexchange-coupling between the neighboring tetrahedral and octahedral magnetic species.14 As there are twice as many octahedrally as tetrahedrally coordinated transition metal ions in the structure, this generally results in a net magnetization along the octahedral moment direction. Consequently, the intrinsic magnetic properties of MFe2O4 nanoparticles are determined by the choice of divalent cation, M2+, and the distribution of the cationic species, M2+ and Fe3+, between the crystallographic sites in the spinel structure. For example, MnFe2O4 and NiFe2O4 are soft ferrimagnets (with mass-specific saturation magnetizations, σS, of 83 and 50 A m2 kg−1, respectively), CoFe2O4 is a hard ferrimagnet (with first uniaxial anisotropy constant, K1, of 0.270 MJ m−3 and σS = 75 A m2 kg−1), and ZnFe2O4 is an antiferromagnet (with a Néel temperature,TN, of 10 K, i.e. paramagnetic at room temperature) owing to the distinct magnetic natures and relative coordination affinities of the constituent transition metal cations.24 Partial elemental substitution in the isostructural MFe2O4 compounds has long been used as a handle for tuning the magnetic properties. In particular, substitution by the non-magnetic Zn2+ ion (ZnxM1−xFe2O4), which has a natural affinity for the tetrahedral site, is known to produce a significant enhancement of the saturation magnetization.14 However, an optimal degree of Zn substitution (typically x ≈ 0.4) exists, before the absence of magnetic species on the tetrahedral sites causes a breaking of the superexchange paths and a collapse of the long-range magnetic order.14
Recently, very high room temperature saturation magnetizations of 116 A m2 kg−1, 161 A m2 kg−1 and 175 A m2 kg−1 have been reported for nanosized (15–25 nm) Zn0.5Ni0.5Fe2O4, Zn0.4Fe(II)0.6Fe2O4 and Zn0.4Mn0.6Fe2O4 soft spinel ferrite nanoparticles, respectively.10,25 Saturation magnetizations of this magnitude are exceptionally high for ceramic magnets and have thus caused a surge of interest in nanostructured and Zn-substituted ferrite particles. In this context, Zn-substitution in nanosized CoFe2O4 spinel ferrite particles is particularly interesting due to the compound's hard magnetic properties. An increase of the induced magnetization could lead to a substantial improvement of the magnetic energy product and, in turn, the permanent magnetic performance of the material. Consequently, a large number of studies of Zn substituted CoFe2O4 nanoparticles have been conducted in recent years, with ZnxCo1−xFe2O4 nanoparticles of various compositions in the 0.0 < x < 1.0 range, and crystallite sizes of ≈5–35 nm, being prepared using a number of different synthesis techniques, including hydrothermal,26–28 microwave,29,30 solid-state,31 microemulsion,32 sol–gel autocombustion33,34 and thermal decomposition methods.35 The synthesis step is, in many cases, followed by either a milling and/or an annealing step in order to achieve the desired crystalline nanosized particles. Considering the above-mentioned studies, a simple correlation between composition and saturation magnetization cannot be directly determined (see Fig. S1A in the ESI†). Furthermore, very large variations in σs are observed for nanoparticles of identical compositions. These discrepancies could potentially be related to crystallite size, as small nanoparticles often exhibit a reduced saturation magnetization due to surface spin disorder, reduced crystallinity or structural defects.36–38 However, considering only the samples of identical composition, no correlation between size and σs is readily seen either (see Fig. S1B in the ESI†). Therefore, the observed differences in magnetic properties are most likely related to differences in the cation distribution in the spinel structure of the samples prepared by the various synthesis methods. Unfortunately, there is a scarcity of systematic structural studies seeking to clarify the atomic-scale structures of the ferrite crystallites prepared via the various methods, as Rietveld refinement of conventional laboratory X-ray diffraction data does not yield trustworthy results. The combination of the similar X-ray scattering powers of the 3d transition metals, the size broadening of the Bragg peaks due to the reduced crystallite sizes and the high backgrounds due to Fe fluorescence at the Cu X-ray energy, causes the site occupation fractions to fluctuate drastically during structural refinements of conventional laboratory X-ray diffraction data. Instead, different and/or supplementary characterization techniques must be employed.
In the present study, the crystal-, magnetic- and nano-structure of spinel ferrite nanoparticles in the entire ZnxCo1−xFe2O4 composition range have been examined. The ZnxCo1−xFe2O4 nanoparticles have been prepared by the flexible, green and scalable hydrothermal synthesis method,39,40 which is among the most widely used techniques for preparation of nanosized spinel ferrite particles. As demonstrated by our previous studies, the structural and microstructural characteristics of hydrothermally prepared spinel ferrite nanoparticles can be tuned by varying reaction parameters such as temperature, pressure, precursor concentration, pH, and reaction time.41–45 Furthermore, the structural consequences of a post-synthesis annealing treatment have been investigated. The as-prepared and annealed nanoparticles have been meticulously characterized by both powder X-ray diffraction (PXRD) and neutron powder diffraction (NPD). In this context, the NPD technique is particularly advantageous as the scattering length of neutrons varies erratically with the atomic number of the element probed, making it possible to obtain significantly higher contrast between Zn, Co, and Fe, than with conventional X-ray diffraction. In addition, neutrons carry a spin moment, which allows them to scatter off of the atomic magnetic moments in the material, thereby yielding information about its magnetic structure. In this work, a very robust structural analysis has been carried out by combined Rietveld refinement of a constrained structural model to the PXRD and NPD data. Furthermore, the implementation of a magnetic model in the NPD data refinement allows the change in magnetic ordering in the structure as function of Zn substitution to be followed and the variation in intrinsic saturation magnetization to be determined. In addition, characterization by Mössbauer spectroscopy, which supplements PXRD and NPD by its sensitivity to cation (Fe) site distributions and magnetic ordering, has been carried out on selected as-synthesized samples. The structural investigations are complemented by transmission electron microscopy (TEM), scanning transmission electron microscopy (STEM), energy dispersive X-ray spectroscopy (EDS), and the measurement of macroscopic magnetic properties by vibrating sample magnetometry (VSM). The present study thus both sheds light onto the fundamental atomic-, magnetic- and micro-structural features governing the magnetic properties of ZnxCo1−xFe2O4 nanoparticles, and directly relates them to the observed macroscopic magnetic performance. The flexibility added by fully understanding the structure–property relationship in spinel ferrite nanoparticles, will enable us to directly target and tailor crystallites with certain characteristics optimized for specific applications in the future.
Experimental
Sample preparation
ZnxCo1−xFe2O4 nanopowders with nominal compositions x = 0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0 were synthesized by a hydrothermal autoclave batch method. Aqueous solutions of 3.0 M Zn(NO3)2·6H2O (Sigma-Aldrich, ≥98%), 3.0 M Co(NO3)2·6H2O (Sigma-Aldrich, ≥98%) and 2.5 M Fe(NO3)3·9H2O (Sigma-Aldrich, ≥98%) were mixed in molar amounts corresponding to the desired product stoichiometry. Subsequently, an excess amount of 16.0 M NaOH solution, corresponding to 1.33 times the molar amount of NO3−, was added dropwise to the mixture under magnetic stirring causing a viscous gel to be formed. Subsequently, 75 ml of the precursor mixture were transferred to a 180 ml Teflon lined steel autoclave, which was placed in a convection oven, preheated to 513 K, for 2 hours.Following the synthesis, the hot autoclaves were removed from the oven and left to cool naturally to room temperature overnight. Subsequently, the formed aqueous nanoparticle suspensions were transferred to 500 ml centrifuge bottles, washed with demineralized water and separated from the supernatant by centrifuging at 2000 rpm for 3 minutes. This washing routine was repeated three times with demineralized water before transferring the samples to 100 ml glass beakers and drying them overnight at 333 K in a vacuum oven. The powders were then collected and agglomerates were broken in an agate mortar. Finally, any remaining adsorbed water was removed by repeated drying in a vacuum oven at 333 K.
For selected samples, i.e. x = 0.0, 0.1, 0.2, 0.3, 0.4, 0.6, 0.8, and 1.0, parts of the powders were subjected to a post-synthesis annealing treatment. The powders were put in ceramic alumina crucibles, which were placed in a large quartz tube. The tube was evacuated, sealed and inserted into a preheated Barnstead Thermolyne 21100 tube furnace. The annealing was carried out in vacuum at 823 K for 4 hours. Following the annealing treatment, the quartz tube was removed from the furnace and left to cool naturally at ambient temperature.
Characterization
Powder X-ray diffraction patterns of the samples were collected at room temperature using a Rigaku SmartLab diffractometer (Rigaku, Japan) configured with cross beam optics in Bragg–Brentano geometry and equipped with a DteX/Ultra detector. To reduce the effect of Fe fluorescence, the instrument was equipped with a diffracted beam monochromator in the receiving optics for Cu Kα1,2 radiation (λ1 = 1.5406 Å, λ2 = 1.5444 Å) or equipped with a cobalt anode (λ1 = 1.7892 Å, λ2 = 1.7931 Å). Data were collected in a 2θ-range of 15° to 125° at an angular resolution of 0.02°.The neutron powder diffraction experiments were carried out at the Cold Neutron Powder Diffractometer (DMC) instrument at the Swiss Spallation Neutron Source (SINQ), Paul Scherrer Institute (PSI), Villigen, Switzerland at 300 K using a wavelength of 2.459 Å.46 The instrument is equipped with a linear position-sensitive BF3 multidetector consisting of 400 detector channels at an angular separation of 0.2° covering a total angular range of 79.8°. The detector was moved between two positions to attain an angular resolution of 0.1°.
57Fe Mössbauer spectra were obtained by conventional constant acceleration spectrometers with sources of 57Co in rhodium foil. Approximately 50 mg of sample material (x = 0.0, 0.2, 0.4, 0.5, 0.6, 0.8, and 1.0) were mixed with boron nitride powder at a ratio of approximately 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in weight, encapsulated in flat 16 mm diameter Plexiglas containers, and measured in transmission geometry over 20–70 hours. The spectra were collected at 18 K by using a closed cycle helium refrigerator from APD Cryogenics, at 80 K by using a liquid nitrogen cryostat, and at room temperature (295 K). Isomer shifts are given relative to that of α-Fe at 295 K.
1 in weight, encapsulated in flat 16 mm diameter Plexiglas containers, and measured in transmission geometry over 20–70 hours. The spectra were collected at 18 K by using a closed cycle helium refrigerator from APD Cryogenics, at 80 K by using a liquid nitrogen cryostat, and at room temperature (295 K). Isomer shifts are given relative to that of α-Fe at 295 K.
Transmission electron microscopy micrographs were recorded on a FEI TALOS F200A analytical (S)TEM electron microscope equipped with an X-FEG electron source and a Ceta 16M camera. Spatially resolved elemental analysis was performed employing the same microscope operating in scanning transmission electron microscopy mode. STEM images were acquired using a high angle annular dark field (HAADF) detector and energy dispersive X-ray spectroscopy elemental maps were obtained using a Super-X EDS detector.
Magnetic hysteresis curves at 300 K were measured on cold pressed pellets (diameter = 2.7 mm, mass = 5–20 mg) using a Quantum Design Physical Property Measurement System (PPMS) equipped with a Vibrating Sample Magnetometer (VSM). The field dependent magnetization of the samples was measured at 300 K by scanning the external field between ±1592 kA m−1 (±2 T). The measurements were conducted at a frequency of 40 Hz and an averaging time of 2 seconds.
Structural analysis
The powder diffraction patterns were analyzed by Rietveld refinement using the Fullprof Suite software package.47 A combined simultaneous refinement of the PXRD and NPD patterns was carried out with a constrained structural model of ZnxCo1−xFe2O4 in the cubic Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. Furthermore, linear restraints on the atomic site occupation fractions on the tetrahedral, 8a (⅛,⅛,⅛), and octahedral, 16d (½,½,½), Wyckoff sites were imposed to avoid unphysical over- or under-population of the specific sites while keeping the stoichiometric ratio of 1
m space group. Furthermore, linear restraints on the atomic site occupation fractions on the tetrahedral, 8a (⅛,⅛,⅛), and octahedral, 16d (½,½,½), Wyckoff sites were imposed to avoid unphysical over- or under-population of the specific sites while keeping the stoichiometric ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 between M2+ and Fe3+. The atomic position of oxygen, (u,u,u), on the 32e Wyckoff site was refined as well as the lattice parameter, a. The site-specific isotropic Debye–Waller factors were fixed based on interpolation between end-member values from a previous high-resolution NPD study.13 For each individual powder diffraction pattern, a scale factor, zero shift and background, described using a fifth degree Chebyshev polynomial, were refined. For the NPD data, the contribution from the magnetic scattering was described using a collinear ferrimagnetic model with antiparallel magnetic moment components on the tetrahedral and octahedral sites. The magnetic structure was implemented as an additional phase of the type “Magnetic Phase” with lowest symmetry space group of the corresponding centering, i.e. F
2 between M2+ and Fe3+. The atomic position of oxygen, (u,u,u), on the 32e Wyckoff site was refined as well as the lattice parameter, a. The site-specific isotropic Debye–Waller factors were fixed based on interpolation between end-member values from a previous high-resolution NPD study.13 For each individual powder diffraction pattern, a scale factor, zero shift and background, described using a fifth degree Chebyshev polynomial, were refined. For the NPD data, the contribution from the magnetic scattering was described using a collinear ferrimagnetic model with antiparallel magnetic moment components on the tetrahedral and octahedral sites. The magnetic structure was implemented as an additional phase of the type “Magnetic Phase” with lowest symmetry space group of the corresponding centering, i.e. F![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) . The special positions of the magnetic species (Fe3+ and Co2+ on the tetrahedral and octahedral sites) were specified, from which all magnetic spins were generated by providing the first 24 symmetry operations (see ESI†) of the Fd
. The special positions of the magnetic species (Fe3+ and Co2+ on the tetrahedral and octahedral sites) were specified, from which all magnetic spins were generated by providing the first 24 symmetry operations (see ESI†) of the Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group and considering the centrosymmetry. The magnitudes of the magnetic moment components were refined as mean values of the magnetic species (Co2+ and Fe3+) on the tetrahedral and octahedral sites, respectively.
m space group and considering the centrosymmetry. The magnitudes of the magnetic moment components were refined as mean values of the magnetic species (Co2+ and Fe3+) on the tetrahedral and octahedral sites, respectively.
The peak profiles were modeled using the Thompson–Cox–Hastings formulation of the pseudo-Voigt function.48 The peak asymmetry and the instrumental contribution to the total peak broadening in the PXRD and NPD data were determined by Rietveld refinement of data from a NIST LaB6 660b line profile standard and a Na2Ca3Al2F14 standard, respectively, measured with the same instrumental configurations. The obtained instrumental resolution functions were implemented in the refinements and the remaining sample contribution to the peak broadening was modeled assuming spherical, strain-free crystallites. Notably, the peak profile modeling was constrained to yield identical crystallite sizes from the PXRD and NPD data taking into account the difference in wavelengths. The crystallite sizes were calculated by the Scherrer formula, H = (K·λ)/(〈D〉·cos(θ)),49 where 〈D〉 is the mean volume-weighted size of the coherently scattering crystalline domains, λ is the X-ray wavelength, θ is the Bragg angle, H describes the peak broadening (full width at half maximum intensity) and K is the shape factor, which was set to 0.829 assuming isotropic crystallite morphology.50
Results and discussion
Combined PXRD and NPD structural refinement
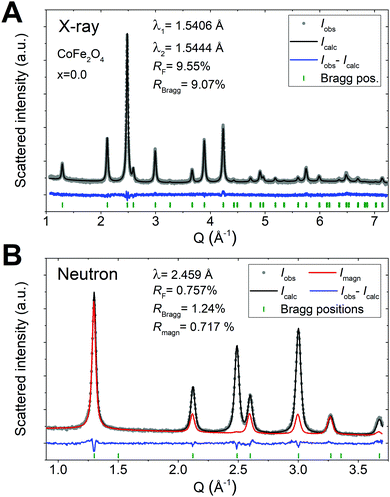
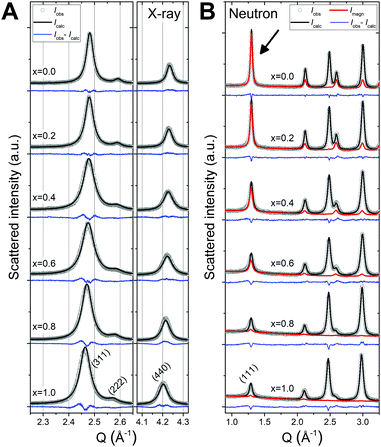
For all as-synthesized samples, the positions and relative intensities of the observed reflections in the PXRD and NPD patterns are in agreement with a single phase-pure spinel ferrite phase, showing no sign of additional crystalline phases. Furthermore, the diffraction patterns feature broad peaks indicative of nanosized crystallites. The powder diffraction data were in all cases modelled by Rietveld refinement of a constrained structural model yielding good fits to the data. The PXRD and NPD patterns, and corresponding Rietveld fits for all samples may be found in the ESI.† The two techniques have individual advantages (as discussed in the Introduction) and employing a combined refinement of a constrained structural model thus yields a very robust structural description, which has been conditioned by the merits of both techniques. Fig. 2A and B show a representative PXRD pattern and NPD pattern, respectively, and the corresponding Rietveld fit for the pure CoFe2O4 endmember (x = 0.0) sample. A strong magnetic scattering contribution is observed in the low-Q region of the NPD data of the CoFe2O4 sample, indicating the presence of long-range magnetic order in the structure. The magnetic contribution was described through implementation of a magnetic model in the refinement of the NPD data.For the as-synthesized samples, as illustrated in Fig. 3A, a gradual shift in the peak positions towards lower Q with increasing Zn-content is observed, which indicates an expansion of the crystallographic unit cell. This is in accordance with the larger lattice parameters of ZnFe2O4 compared to CoFe2O4 generally reported in the literature.27–29,32,33 The NPD data shown in Fig. 3B shows a gradual decrease in the magnetic contribution to the data with increasing Zn-content, which implies a loss of long-range magnetic order.
The powder diffraction patterns of the annealed samples exhibit only minor observable differences with respect to the corresponding as-synthesized samples. A slight sharpening of the diffraction peaks is observed for most annealed samples (see Fig. S7 in the ESI†) which suggest crystallite growth to take place as a result of the heat treatment. Very weak impurity peaks, which could be assigned to α-Fe2O3 (hematite) phase in space group R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c, were visible in the PXRD patterns of the annealed Zn0.8Co0.2Fe2O4 and pure ZnFe2O4 samples, indicating formation of a minor amount (<5%) of impurity during annealing of the Zn-rich samples. This could indicate a gradual extraction of Fe from the spinel phase, which could be facilitated by introduction of vacancies and/or Zn evaporation during the vacuum annealing. However, the present data quality does not allow reliable non-restrained refinement of correspondingly small variations in site occupation fractions. The formation of α-Fe2O3 could also be explained by crystallization of residual amorphous precursor, which might not have been removed during the post-synthesis washing. In spite of the α-Fe2O3 impurity, the powder diffraction patterns could still be fitted well with the stoichiometrically restrained model, indicating no severe degradation of the spinel phase.
c, were visible in the PXRD patterns of the annealed Zn0.8Co0.2Fe2O4 and pure ZnFe2O4 samples, indicating formation of a minor amount (<5%) of impurity during annealing of the Zn-rich samples. This could indicate a gradual extraction of Fe from the spinel phase, which could be facilitated by introduction of vacancies and/or Zn evaporation during the vacuum annealing. However, the present data quality does not allow reliable non-restrained refinement of correspondingly small variations in site occupation fractions. The formation of α-Fe2O3 could also be explained by crystallization of residual amorphous precursor, which might not have been removed during the post-synthesis washing. In spite of the α-Fe2O3 impurity, the powder diffraction patterns could still be fitted well with the stoichiometrically restrained model, indicating no severe degradation of the spinel phase.
Crystal structure and crystallite size
Satisfactory and converging Rietveld fits were obtained in the combined structural modeling of the PXRD and NPD data of both the as-synthesized and annealed ZnxCo1−xFe2O4 samples. An overview of selected refined structural parameters may be found in Table 1.| Zn-content, x | Unit cell length, a (Å) | Crystallite size, DCryst (nm) | Oxygen atomic position, u | Stoichiometric formula |
|---|---|---|---|---|
| As-synthesized | ||||
| 0.0 | 8.3897(2) | 17.6(1) | 0.2570(2) | [Co0.28Fe0.72]tet[Co0.72Fe1.28]octO4 |
| 0.1 | 8.4030(2) | 14.1(1) | 0.2575(2) | [Zn0.10Co0.20Fe0.70]tet[Zn0.00Co0.70Fe1.30]octO4 |
| 0.2 | 8.3973(2) | 14.7(1) | 0.2569(2) | [Zn0.20Co0.16Fe0.64]tet[Zn0.00Co0.64Fe1.36]octO4 |
| 0.3 | 8.4062(2) | 10.8(1) | 0.2574(2) | [Zn0.29Co0.11Fe0.60]tet[Zn0.01Co0.59Fe1.40]octO4 |
| 0.4 | 8.4025(2) | 10.7(1) | 0.2579(2) | [Zn0.39Co0.08Fe0.53]tet[Zn0.01Co0.52Fe1.47]octO4 |
| 0.5 | 8.4072(2) | 10.6(1) | 0.2574(2) | [Zn0.48Co0.06Fe0.46]tet[Zn0.02Co0.44Fe1.54]octO4 |
| 0.6 | 8.4124(2) | 9.9(1) | 0.2572(2) | [Zn0.56Co0.03Fe0.41]tet[Zn0.04Co0.37Fe1.59]octO4 |
| 0.7 | 8.4214(2) | 8.6(1) | 0.2573(2) | [Zn0.65Co0.02Fe0.33]tet[Zn0.05Co0.28Fe1.67]octO4 |
| 0.8 | 8.4280(2) | 11.8(1) | 0.2574(2) | [Zn0.75Co0.00Fe0.25]tet[Zn0.05Co0.20Fe1.75]octO4 |
| 0.9 | 8.4400(2) | 8.9(1) | 0.2573(2) | [Zn0.74Co0.00Fe0.26]tet[Zn0.16Co0.10Fe1.74]octO4 |
| 1.0 | 8.4515(2) | 11.0(1) | 0.2578(2) | [Zn0.76Fe0.24]tet[Zn0.24Fe1.76]octO4 |
| Annealed | ||||
| 0.0 | 8.38176(3) | 25.2(1) | 0.2563(1) | [Co0.20Fe0.80]tet[Co0.80Fe1.20]octO4 |
| 0.1 | 8.38152(6) | 17.4(1) | 0.2570(1) | [Zn0.10Co0.22Fe0.68]tet[Zn0.00Co0.68Fe1.22]octO4 |
| 0.2 | 8.39223(5) | 20.2(1) | 0.2566(1) | [Zn0.20Co0.11Fe0.69]tet[Zn0.00Co0.69Fe1.31]octO4 |
| 0.3 | 8.39122(8) | 14.0(1) | 0.2569(1) | [Zn0.30Co0.12Fe0.58]tet[Zn0.00Co0.58Fe1.42]octO4 |
| 0.4 | 8.39875(7) | 14.1(1) | 0.2566(1) | [Zn0.40Co0.02Fe0.58]tet[Zn0.00Co0.58Fe1.42]octO4 |
| 0.6 | 8.41206(6) | 16.5(1) | 0.2567(1) | [Zn0.56Co0.00Fe0.44]tet[Zn0.04Co0.40Fe1.56]octO4 |
| 0.8 | 8.42407(5) | 20.2(2) | 0.2568(1) | [Zn0.69Co0.00Fe0.31]tet[Zn0.11Co0.20Fe1.69]octO4 |
| 1.0 | 8.44065(5) | 17.8(1) | 0.2582(1) | [Zn0.84Fe0.16]tet[Zn0.16Fe1.84]octO4 |
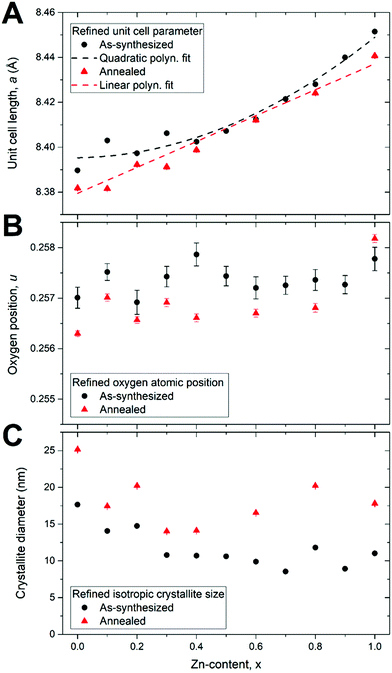
Fig. 4A shows the refined unit cell parameters as function of Zn-content. A gradual increase in the unit cell length with increasing Zn-content is observed, which is consistent with the shift in peak positions discussed above. The unit cell expansion can be understood based on the relative effective ionic radii of the cationic species in tetrahedral (Zn2+ = 60 pm > Co2+ = 58 pm > Fe3+ = 49 pm) and octahedral (Co2+ = 74.5 pm > Zn2+ = 74 pm > Fe3+ = 64.5 pm) coordination,51 and considering the general preference of Zn ions for the tetrahedral coordination and Co ions for octahedral coordination in the spinel structure. The structural expansion produced by the substitution of the larger Zn ion into the small tetrahedral site outweighs the contraction induced by the removal of Co from the octahedral site and will produce a net expansion of the structure. Notably, the lattice parameters of the as-synthesized nanocrystallites do not exhibit the strictly linear dependence on composition predicted by Vegard's law.52 This observation indicates variations of the respective inversion degrees of the cations and thus deviations from the thermodynamically favorable bulk cation distribution in the nanosized crystallites. However, the annealing treatment leads to a reduction in unit cell length for all samples, which results in a near linear dependence on Zn-content, as would generally be expected in a solid solution substitution series of isostructural compounds. This behavior corroborates the notion that the atomic structure of the as-synthesized nanocrystallites is initially trapped in a non-equilibrium state, which is relaxed by the annealing treatment. This is supported by the refined values of the oxygen atomic position parameter, u, shown in Fig. 4B. The oxygen position is affected by structural deformations and can consequently be used as a measure of the lattice distortion. For an undistorted spinel lattice u = 1/4 = 0.250, but values between 0.255–0.260 are generally reported for real spinel ferrites.14 Here, both the as-synthesized and annealed samples display lattice distortion, with oxygen positions u ≈ 0.256–258. Interestingly, the annealing treatment leads to a systematic decrease in the spinel distortion, which is likely to be related to a rearrangement of the cationic species between the crystallographic sites in the structure.
Fig. 4C shows the mean isotropic nanocrystallite dimensions as function of Zn-content. For the as synthesized samples, a decreasing trend is observed with increasing Zn substitution. The pure as-synthesized CoFe2O4 nanocrystallites have the largest refined diameter of 17.6(1) nm while the ZnFe2O4 crystallites are 11.0(1) nm. The smallest crystallite diameter of 8.6(1) nm is observed for the Zn0.7Co0.3Fe2O4 sample. The annealing treatment leads to an increase in crystallite size, which is consistent with the observed decrease in unit cell length of the annealed samples compared to the as-synthesized. In smaller nanoparticles a larger percentage of the atoms in the structure are located near the surface, where longer bonds are often present due to surface relaxations.53 The crystallite growth causes more atoms to be incorporated into the more tightly packed bulk-like structure. No obvious growth trend can be discerned, neither based on composition nor on initial crystallite size. This might be related to a dissimilar heating of the nanopowders in the employed tube furnace, as some crucibles were placed more centrally in the employed open-ended tube furnace than others, thus effectively receiving a higher temperature and more impactful annealing treatment.
Cation distribution
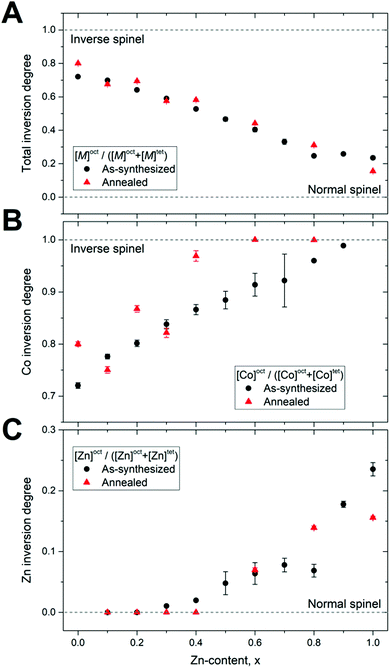
The cation distribution between the tetrahedral and octahedral sites in the crystal structure of spinel ferrites directly determines the intrinsic magnetic properties of the compounds, i.e. their Curie/Neél temperature, bulk saturation magnetization and magnetocrystalline anisotropy.14 Reliable characterization of the spinel inversion and its influence on magnetic properties is therefore crucial for the design and preparation of magnetic ferrite materials with optimal performance. It is well-established that bulk CoFe2O4 and ZnFe2O4 crystals exhibit inverse and normal spinel structures, respectively.14 However, the distribution of cations in nanocrystalline ferrites is known to differ from that of the bulk, and a broad range of inversion degrees are reported for nanoparticles with both compositions in the literature.15,17,21,22Fig. 5A shows the total M2+ (Zn2+ + Co2+) spinel inversion degree obtained by combined Rietveld refinement of the NPD and PXRD data. Total inversion degrees of 0.72(1) and 0.24(1) for the as-synthesized CoFe2O4 (x = 0.0) and ZnFe2O4 (x = 1.0) endmembers, respectively, are obtained, which are in good agreement with our recent high-resolution NPD study of non-substituted spinel ferrite nanocrystallites.13 After annealing, total inversion of degrees of 0.80(1) for the CoFe2O4 and 0.16(1) for the ZnFe2O4 samples are obtained from the refinements, indicating transitions towards more bulk-like structures.
For the intermediate compositions, the total inversion degrees shown in Fig. 5A exhibit a near-linear dependence on Zn-content for both the as-synthesized and annealed. At first glance, this could be interpreted as the constituent cations simply ordering with inversions equivalent to the corresponding endmember values. However, separating the individual refined inversion degrees of the Co and Zn ions (see Fig. 5B and C) reveals a compositional dependence of their respective affinities for the crystallographic sites. Interestingly, reducing the content of a specific ion seemingly increases its affinity for the thermodynamically preferred bulk coordination, i.e. Zn becomes more inclined to sit in a tetrahedral coordination (normal spinel) when the Zn-content is low and Co increasingly prefers the octahedral coordination (inverse spinel) when Co-content is low. Notably, the inversion of the Co ions, in particular, goes towards a more inverse configuration following the annealing treatment, while the Zn inversion is seemingly unaffected.
Nanostructure, composition and elemental distribution
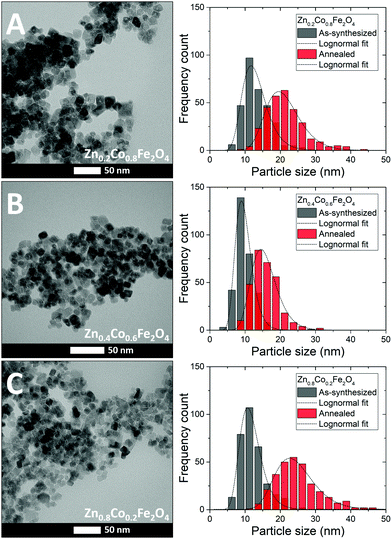
Representative TEM images of three selected as-synthesized samples (x = 0.2, 0.4 and 0.8) are shown in Fig. 6 illustrating the isotropic morphology of the nanoparticles. Additional TEM images of both as-synthesized and annealed samples may be found in the ESI.†For each of the three selected samples, size analysis of the as-synthesized and annealed particles was carried out using the software Fiji54 to measure the dimensions of over 300 individual particles for each sample in TEM micrographs collected at several different places on the grids. The resulting particle size distributions are shown in Fig. 6 next to the corresponding TEM images. The obtained histograms were fitted by a lognormal distribution from which the mean particle size and the standard deviation were determined. For comparison, a summary of the mean crystallite sizes (Dcryst) obtained from the Scherrer analysis in the combined Rietveld refinement of PXRD and NPD data and the average particle sizes (DTEM) from the TEM analysis are given in Table 2. The TEM analysis reveals a clear increase in particles size and a concurrent broadening of the size distributions following the annealing treatment, which is consistent with the size analysis of the powder diffraction data.
| x | D Cryst (nm) | D TEM (nm) | x EDS Zn2+/M2+ | Stoich. EDS M2+/Fe3+ |
|---|---|---|---|---|
| As-synthesized | ||||
| 0.2 | 14.1(1) | 13.2(1) ± 3.7(7) | 0.21(3) | 0.53(6) |
| 0.4 | 10.7(1) | 9.8(1) ± 2.4(7) | 0.40(5) | 0.51(6) |
| 0.8 | 11.8(1) | 11.9(1) ± 3.2(7) | 0.81(11) | 0.56(7) |
| Annealed | ||||
| 0.2 | 20.2(1) | 21.2(1) ± 5.1(7) | 0.20(3) | 0.53(6) |
| 0.4 | 14.1(1) | 15.8(1) ± 3.8(7) | 0.42(5) | 0.53(6) |
| 0.8 | 20.2(1) | 24.6(1) ± 5.7(7) | 0.80(10) | 0.57(7) |
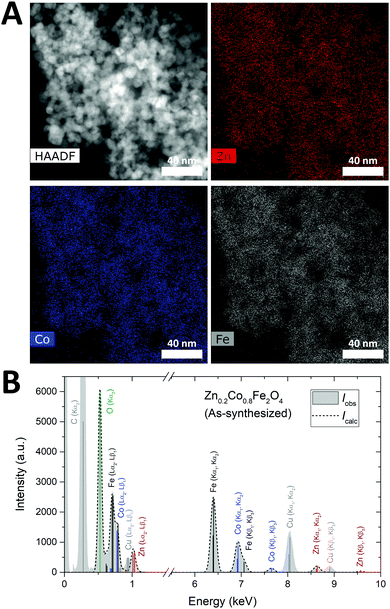
The elemental homogeneity of the nanoparticles was examined by STEM-EDS mapping. A representative, STEM-HAADF micrograph and elemental maps for Zn, Co, and Fe in the given region are shown in Fig. 7A. STEM images and elemental maps for the other samples may be found in the ESI.† Generally, a homogeneous distribution of the transition metals is observed between the particles, confirming that the samples indeed consist of a single nanocrystalline mixed ZnxCo1−xFe2O4 ferrite phase rather than a stoichiometric mixture of ZnFe2O4 and CoFe2O4 crystallites. In addition, the elemental compositions of the selected samples were determined by quantitative analysis of the overall energy-dispersive X-ray spectra using the Bruker ESPRIT software suite. Fig. 7B shows a representative spectrum for the as-synthesized Zn0.2Co0.8Fe2O4 sample and additional spectra and information may be found in the ESI.† Following subtraction of the Bremsstrahlung contribution to the measured spectrum, the relative atomic percentages were determined by fitting of the intensities of the characteristic fluorescent X-ray lines. The contributions from the carbon and copper from the TEM grids were deconvoluted in the fitting and thereby excluded from the quantitative analysis. The TEM grids also contain a substantial amount of oxygen and are thus responsible for part of the detected oxygen content. This contribution cannot be discerned from that of the sample, which leads to an overestimation of the oxygen content with respect to the amounts of Zn, Co and Fe. Consequently, the Zn-content was calculated as Znat%/(Znat% + Coat%), and the stoichiometry evaluated based on the ratio between the divalent species and iron, i.e. (Znat% + Coat%)/Feat%. The experimentally determined compositions are in good agreement with the formal stoichiometries from the synthesis (see Table 2).
Mössbauer spectroscopy
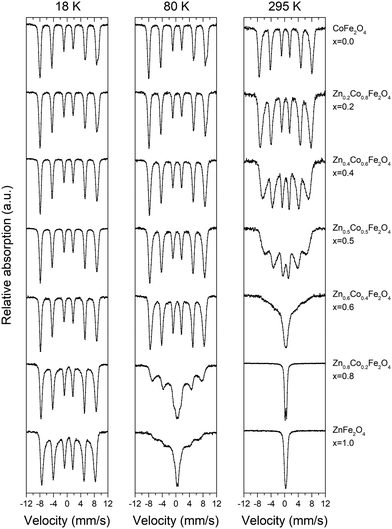
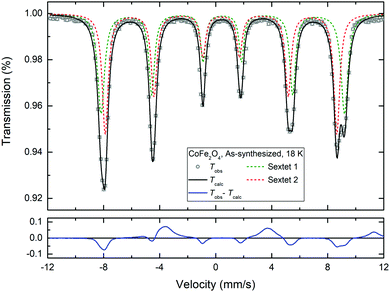
Fig. 8 shows room temperature (295 K) and low temperature (80 K and 18 K) Mössbauer spectra of selected as-synthesized ZnxCo1−xFe2O4 nanopowders. A gradual increase in magnetic relaxation is observed with increasing Zn-content, which is consistent with the NPD data. In addition, a gradually increasing asymmetry is observed in the spectra with increasing Co-content (particularly prominent in the CoFe2O4 sample at 18 K). This asymmetry can be attributed to Fe3+ occupation of two distinct sites, i.e. Fe3+ on both tetrahedral and octahedral sites, which is in agreement with the increased inversion degree in Co-rich samples observed in the powder diffraction analysis.Fig. 9 shows the 18 K Mössbauer spectrum of CoFe2O4 (top left corner in Fig. 8), which has been fitted by two sextets, respectively, with hyperfine field splittings of 51.3 T and 53.9 T, isomer shifts of 0.38 mm s−1 and 0.49 mm s−1 and zero quadrupole shifts. Typically, the isomer shift is ≈0.1 mm s−1 larger for octahedral sites than for tetrahedral sites for Fe3+.55 The fit (Fig. 9) indicates a roughly 50/50 distribution of Fe3+ between the A and B sites (i.e. indicative of an inverse spinel), however, precise determination of the occupation numbers is not straightforward due to the extensive overlap of the peaks. Substitution by Zn is seen to primarily replace Fe on one of the sites as the spectral asymmetry diminishes with increasing Zn-content. The 18 K-spectrum of ZnFe2O4 (which shows some magnetic fluctuation) was fitted by components with isomer shifts around 0.44 mm s−1 suggesting one distinct Fe3+ site. This is in good agreement with the affinity of Zn for the tetrahedral site and the reconfiguration towards normal spinel with increasing Zn content observed from the combined PXRD and NPD analysis.
Magnetic structure and properties
The constituent 3d transition metal ions of the spinel ferrites carry different magnetic moment owing to their different electron configurations, i.e. [Ar]3d5 for Fe3+, [Ar]3d7 for Co2+ and [Ar]3d10 for Zn2+. At 0 K and assuming high-spin configurations, this leads to spin moment magnitudes of Fe3+ (5 μB) > Co2+ (3 μB) > Zn2+ (0 μB). For 3d transition metals, the orbit moment contribution to the total spin–orbit moment is generally negligible due to a strong crystal-field quenching.56 However, for Co2+ the orbital magnetic moment remains unquenched by the crystalline field, which leads to an increase in the net magnetic moment of the Co2+ ion (≈3.9 μB) and gives rise to the large anisotropy (i.e. hard magnetic properties) of the CoFe2O4 compound.14The Rietveld refinement of the magnetic structure was based on the collinear model illustrated for the Zn0.2Co0.8Fe2O4 sample in Fig. 10A. An antiparallel superexchange coupling exists between octahedral and tetrahedral magnetic species in the structure. Consequently, the observed preference of non-magnetic Zn2+ ions for the tetrahedral site in the nanocrystalline structure would intuitively lead to an improvement of the magnetization due to a reduction of the antiparallel tetrahedral moment. This is indeed observed for small amounts of Zn-substitution (x = 0.2), as demonstrated by the macroscopic field-dependent magnetization curves at 300 K of selected as-synthesized and annealed samples shown in Fig. 10B. However, further substitution (x > 0.2) leads to a considerable reduction in the observed magnetization with increasing Zn content, ultimately resulting in the paramagnetic character observed for the annealed X = 1.0 powders.
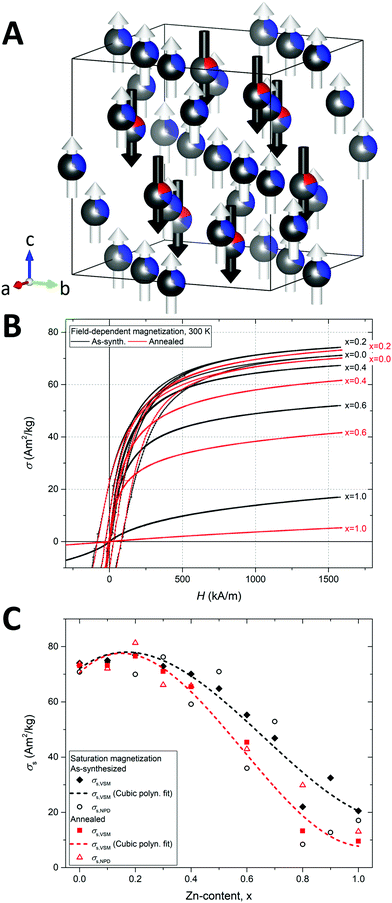 | ||
| Fig. 10 (A) Representative refined crystal and magnetic structure of the as synthesized Zn0.2Co0.8Fe2O4 nanocrystalline sample. The refined site occupation fractions of zinc (red), cobalt (blue) and iron (grey) are indicated on the spheres. The arrows indicate the relative directions and magnitudes of the refined magnetic moments on the tetrahedral (black) and octahedral (white) sites. Illustration made in VESTA.23 (B) Room temperature field-dependent magnetization curves of selected as-synthesized (black) and annealed (red) samples. A magnification of the low H region along with hysteresis curves for all samples may be found in the ESI.† (C) Refined crystallographic saturation magnetization (σs,NPD) and measured macroscopic saturation magnetization (σs,VSM) for as-synthesized and annealed samples as function of Zn-content. | ||
The macroscopic saturation magnetizations (σs,VSM) and crystallographic saturation magnetization (σs,NPD) as function of Zn-content are plotted in Fig. 10C. The σs,VSM values were obtained from the VSM hysteresis curve measurements by extrapolation using the law of approach to saturation,57 while the σs,NPD were calculated from the refined atomic magnetic moments and site occupation fractions. The general trend and the magnitudes of the macroscopic and crystallographic saturation magnetizations of the samples are in relatively good agreement. The dashed lines in the figure represent cubic polynomial fits to the σs,VSM values illustrating the reduction in saturation magnetization with increasing Zn-content. This trend can be ascribed to a breaking of the superexchange paths due to the absence of magnetic moments on the tetrahedral sites. At room temperature, this results in a loss of long-range magnetic order, as observed from the decrease in magnetic diffraction (see Fig. 3B). In ZnFe2O4, the full occupation of non-magnetic Zn2+ ions on the tetrahedral sites is known to prompt a weak antiferromagnetic coupling of the octahedral moments, which at low temperature (<9 K) facilitates the formation of a long-range antiferromagnetic structure.58
Interestingly, the annealed samples generally exhibit a lower magnetization compared to the as-synthesized samples. This observation corroborates the refined site occupancies (see Table 1), which revealed a transition into a more normal configuration for the Zn ions and inverse configuration for the Co ions as a result of the annealing treatment. The reduction in magnetization is particularly pronounced for the samples with higher Zn content highlighting the detrimental effect on the magnetic structure of the tetrahedral Zn2+. In the case of the pure Co spinel (x = 0), the small reduction in σs after annealing can be ascribed to the less magnetic Co2+ (3.9 μB) replacing Fe3+ (5 μB) on the octahedral sites (see Fig. 5). The substitution by Zn is also observed to induce a considerable magnetic softening, which is evident from the reduction in magnetic hysteresis (see Fig. 10B) and the concurrent reduction in coercive field and remanence (see Fig. S21 in the ESI†) with increasing Zn-content. The as-synthesized and annealed samples are observed to become “fully soft”, i.e. Hc ≈ 0 and Mr ≈ 0, for Zn contents above X > 0.3. The specific values of coercive fields (Hc) mass saturation magnetizations (σs,VSM) refined mean magnitudes of the magnetic moment components on tetrahedral (|μtet,NPD|) and octahedral (|μoct,NPD|) sites, and the calculated crystallographic saturation magnetizations (σs,NPD) of the samples are given in Table 3.
| Zn-content, x | H c | σ s,VSM | |μtet,NPD| | |μoct,NPD| | σ s,NPD |
|---|---|---|---|---|---|
| (kA m−1) | (A m2 kg−1) | (μB) | (μB) | (A m2 kg−1) | |
| As-synthesized | |||||
| 0.0 | 85(1) | 74.0(2) | 3.65(4) | 3.31(3) | 71(2) |
| 0.1 | 31(2) | 75.0(2) | 3.43(4) | 3.28(3) | 74(2) |
| 0.2 | 28(2) | 76.9(1) | 3.03(4) | 2.99(3) | 70(2) |
| 0.3 | 4.1(1) | 72.9(2) | 2.68(6) | 2.96(4) | 76(3) |
| 0.4 | 3.90(1) | 70.0(1) | 2.35(6) | 2.43(4) | 59(3) |
| 0.5 | 3.8(1) | 64.8(1) | 1.95(8) | 2.48(5) | 71(4) |
| 0.6 | 0.9(1) | 55.3(1) | 1.9(1) | 1.72(6) | 36(6) |
| 0.7 | 1.2(1) | 46.9(2) | 1.4(2) | 1.8(1) | 53(12) |
| 0.8 | 0.4(1) | 22.0(1) | 1.0(2) | 0.7(1) | 8(17) |
| 0.9 | 1.6(1) | 32.5(2) | 1.6(2) | 1.1(1) | 13(18) |
| 1.0 | 2.4(1) | 20.5(1) | 1.2(2) | 0.3(2) | 17(23) |
| Annealed | |||||
| 0.0 | 82(5) | 73.1(2) | 3.76(4) | 3.43(3) | 74(2) |
| 0.1 | 33(2) | 73.1(1) | 3.51(4) | 3.28(3) | 72(2) |
| 0.2 | 29(2) | 76.5(2) | 2.71(5) | 3.07(3) | 81(2) |
| 0.3 | 9.5(2) | 71.0(2) | 2.72(6) | 2.76(4) | 66(3) |
| 0.4 | 7.3(4) | 65.5(2) | 2.30(8) | 2.55(4) | 66(4) |
| 0.6 | 0.15(1) | 45.4(2) | 1.5(1) | 1.64(7) | 43(8) |
| 0.8 | 7.1(5) | 13.3(1) | 0.8(2) | 1.1(1) | 30(14) |
| 1.0 | 3.1(2) | 10(2) | 0.8(1) | 0.7(2) | 13(24) |
The VSM data on ZnxCo1−xFe2O4 are supported by the Mössbauer spectra (Fig. 8). At room temperature, the spectrum of CoFe2O4 shows a magnetically ordered material, but increasing Zn-content decreases the magnetic order. At X = 0.2–0.5, the Mössbauer lines become asymmetrically broadened in a way that is typical for fluctuations of particle magnetizations around their easy directions in systems of interacting nanoparticles.59 At X = 0.6, the spectrum is almost collapsed to a singlet, representing magnetic relaxation whereby the magnetization averages towards zero at the timescale of Mössbauer spectroscopy (≈1 ns). At X ≥ 0.8, the room temperature spectra are fully dominated by fast superpara/paramagnetic relaxation. The decrease in magnetic order (e.g. that ZnFe2O4 is paramagnetic at room temperature) is likely caused by the weakening of the exchange coupling between cations when substituting Co with non-magnetic Zn. Moreover, the reduction in Co content and the decreasing particle size also decrease the magnetic anisotropy of the nanoparticles, leading to a softer magnetic material and faster fluctuations of the magnetization.
Conclusions
The magnetic performance of spinel ferrite nanocrystallites is the product of the non-trivial interrelation between atomic structure, chemical composition, crystallite size, polydispersity, particle morphology, etc. Consequently, it is essential to reliably characterize and understand the underlying structural features in order to gain the necessary insight to rationally design and tailor ferrites with improved magnetic performance. For spinel ferrites, the distribution of the magnetic transition metal cations between tetrahedral and octahedral sites in the structure, i.e. the inversion degree, is a key structural characteristic. However, reliable experimental determinations of the spinel inversion of nanosized ferrites in the literature are scarce. In the present study, the crystal-, magnetic- and micro-structures of nanosized zinc-substituted cobalt ferrites, ZnxCo1−xFe2O4, in the entire composition range (nominal compositions x = 0.0–1.0, in steps of 0.1) have been elucidated through meticulous analysis of diffraction, microscopy and spectroscopy data and related to the macroscopic magnetic properties. It is demonstrated how the employed hydrothermal synthesis pathway allows ZnxCo1−xFe2O4 nanoparticles to be prepared with metastable cation distributions different from the well-established thermodynamically preferred bulk configurations. Annealing treatment at 823 K under vacuum induces a reordering of the Zn and Co cations into their favorable tetrahedral and octahedral coordination, respectively, which is accompanied by a reduction in macroscopic saturation magnetization. The demonstrated structural control is a key step on the way to designing and tailoring ferrite nanoparticles with tunable properties optimized for specific applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the Danish National Research Foundation (Center for Materials Crystallography, DNRF93), Innovation Fund Denmark (Green Chemistry for Advanced Materials, GCAM-4107-00008B), Independent Research Fund Denmark (Small and Smart Magnet Design) and the Danish Center for Synchrotron and Neutron Science (DanScatt). Affiliation with the Center for Integrated Materials Research (iMAT) at Aarhus University is gratefully acknowledged. The authors are grateful for the obtained beamtime at the DMC beamline, SINQ, PSI, Villigen, Switzerland.References
- J. M. D. Coey, J. Magn. Magn. Mater., 2002, 248, 441–456 CrossRef CAS.
- Q. Song and Z. J. Zhang, J. Am. Chem. Soc., 2012, 134, 10182–10190 CrossRef CAS PubMed.
- C. Granados-Miralles, M. Saura-Múzquiz, H. L. Andersen, A. Quesada, J. V. Ahlburg, A.-C. Dippel, E. Canévet and M. Christensen, ACS Appl. Nano Mater., 2018, 1, 3693–3704 CrossRef CAS PubMed.
- Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, J. Phys. D: Appl. Phys., 2003, 36, R167–R181 CrossRef CAS.
- C. C. Berry and A. S. G. Curtis, J. Phys. D: Appl. Phys., 2003, 36, R198–R206 CrossRef CAS.
- D. Guin, B. Baruwati and S. V. Manorama, Org. Lett., 2007, 9, 1419–1421 CrossRef CAS PubMed.
- R. Abu-Reziq, H. Alper, D. S. Wang and M. L. Post, J. Am. Chem. Soc., 2006, 128, 5279–5282 CrossRef CAS PubMed.
- J. H. Lee, Y. M. Huh, Y. Jun, J. Seo, J. Jang, H. T. Song, S. Kim, E. J. Cho, H. G. Yoon, J. S. Suh and J. Cheon, Nat. Med., 2007, 13, 95–99 CrossRef CAS PubMed.
- H. B. Na, I. C. Song and T. Hyeon, Adv. Mater., 2009, 21, 2133–2148 CrossRef CAS.
- J. T. Jang, H. Nah, J. H. Lee, S. H. Moon, M. G. Kim and J. Cheon, Angew. Chem., Int. Ed., 2009, 48, 1234–1238 CrossRef CAS PubMed.
- C. A. Quinto, P. Mohindra, S. Tong and G. Bao, Nanoscale, 2015, 7, 12728–12736 RSC.
- A. H. Lu, E. L. Salabas and F. Schuth, Angew. Chem., Int. Ed., 2007, 46, 1222–1244 CrossRef CAS PubMed.
- H. L. Andersen, M. Saura-Múzquiz, C. Granados-Miralles, E. Canévet, N. Lock and M. Christensen, Nanoscale, 2018, 10, 14902–14914 RSC.
- S. s. Chikazumi and C. D. Graham, Physics of ferromagnetism, Oxford University Press, Oxford, New York, 2nd edn, 2009 Search PubMed.
- E. Solano, C. Frontera, T. Puig, X. Obradors, S. Ricart and J. Ros, J. Appl. Crystallogr., 2014, 47, 414–420 CrossRef CAS.
- C. Liu, B. S. Zou, A. J. Rondinone and Z. J. Zhang, J. Phys. Chem. B, 2000, 104, 1141–1145 CrossRef CAS.
- C. Liu, A. J. Rondinone and Z. J. Zhang, Pure Appl. Chem., 2000, 72, 37–45 CAS.
- J. Jacob and M. A. Khadar, J. Appl. Phys., 2010, 107, 114310 CrossRef.
- S. M. Patange, S. E. Shirsath, G. S. Jangam, K. S. Lohar, S. S. Jadhav and K. M. Jadhav, J. Appl. Phys., 2011, 109, 053909 CrossRef.
- Z. Z. Lazarevic, C. Jovalekic, A. Milutinovic, D. Sekulic, V. N. Ivanovski, A. Recnik, B. Cekic and N. Z. Romcevic, J. Appl. Phys., 2013, 113, 187221 CrossRef.
- T. Slatineanu, A. R. Iordan, M. N. Palamaru, O. F. Caltun, V. Gafton and L. Leontie, Mater. Res. Bull., 2011, 46, 1455–1460 CrossRef CAS.
- V. Blanco-Gutierrez, E. Climent-Pascual, M. J. Torralvo-Fernandez, R. Saez-Puche and M. T. Fernandez-Diaz, J. Solid State Chem., 2011, 184, 1608–1613 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- R. Skomski, J. Phys.: Condens. Matter, 2003, 15, R841–R896 CrossRef CAS.
- S. Mukherjee, S. Pradip, A. K. Mishra and D. Das, Appl. Phys. A: Mater. Sci. Process., 2014, 116, 389–393 CrossRef CAS.
- F. Gozuak, Y. Koseoglu, A. Baykal and H. Kavas, J. Magn. Magn. Mater., 2009, 321, 2170–2177 CrossRef.
- H. Sozeri, Z. Durmus and A. Baykal, Mater. Res. Bull., 2012, 47, 2442–2448 CrossRef CAS.
- R. Topkaya, A. Baykal and A. Demir, J. Nanopart. Res., 2013, 15, 1359 CrossRef.
- E. Hema, A. Manikandan, P. Karthika, S. A. Antony and B. R. Venkatraman, J. Supercond. Novel Magn., 2015, 28, 2539–2552 CrossRef CAS.
- Y. Koseoglu, A. Baykal, F. Gozuak and H. Kavas, Polyhedron, 2009, 28, 2887–2892 CrossRef CAS.
- A. K. Azad, A. K. M. Zakaria, M. Y. Jewel, A. Khan, S. M. Yunus, I. Kamal, T. K. Datta and S. G. Eriksson, AIP Conf. Proc., 2015, 1660, 090050 CrossRef.
- H. Malik, A. Mahmood, K. Mahmood, M. Y. Lodhi, M. F. Warsi, I. Shakir, H. Wahab, M. Asghar and M. A. Khan, Ceram. Int., 2014, 40, 9439–9444 CrossRef CAS.
- T. Slatineanu, A. R. Iordan, V. Oancea, M. N. Palamaru, I. Dumitru, C. P. Constantin and O. F. Caltun, Mater. Sci. Eng., B, 2013, 178, 1040–1047 CrossRef CAS.
- R. S. Yadav, J. Havlica, M. Hnatko, P. Sajgalik, C. Alexander, M. Palou, E. Bartonickova, M. Bohac, F. Frajkorova, J. Masilko, M. Zmrzly, L. Kalina, M. Hajudchova and V. Enev, J. Magn. Magn. Mater., 2015, 378, 190–199 CrossRef CAS.
- V. Mameli, A. Musinu, A. Ardu, G. Ennas, D. Peddis, D. Niznansky, C. Sangregorio, C. Innocenti, N. T. K. Thanh and C. Cannas, Nanoscale, 2016, 8, 10124–10137 RSC.
- R. H. Kodama, A. E. Berkowitz, E. J. McNiff and S. Foner, Phys. Rev. Lett., 1996, 77, 394–397 CrossRef CAS PubMed.
- Z. Nedelkoski, D. Kepaptsoglou, L. Lari, T. L. Wen, R. A. Booth, S. D. Oberdick, P. L. Galindo, Q. M. Ramasse, R. F. L. Evans, S. Majetich and V. K. Lazarov, Sci. Rep., 2017, 7, 45997 CrossRef CAS PubMed.
- S. Morup, E. Brok and C. Frandsen, J. Nanomater., 2013, 2013, 1–8 CrossRef.
- R. I. Walton, Chem. Soc. Rev., 2002, 31, 230–238 RSC.
- M. Yoshimura and K. Byrappa, J. Mater. Sci., 2008, 43, 2085–2103 CrossRef CAS.
- H. L. Andersen and M. Christensen, Nanoscale, 2015, 7, 3481–3490 RSC.
- H. L. Andersen, K. M. Ø. Jensen, C. Tyrsted, E. D. Bøjesen and M. Christensen, Cryst. Growth Des., 2014, 14, 1307–1313 CrossRef CAS.
- C. Granados-Miralles, M. Saura-Muzquiz, E. D. Bojesen, K. M. O. Jensen, H. L. Andersen and M. Christensen, J. Mater. Chem. C, 2016, 4, 10903–10913 RSC.
- M. Schmidt, H. L. Andersen, C. Granados-Miralles, M. Saura-Muzquiz, M. Stingaciu and M. Christensen, Dalton Trans., 2016, 45, 6439–6448 RSC.
- M. Stingaciu, H. L. Andersen, C. Granados-Miralles, A. Mamakhel and M. Christensen, CrystEngComm, 2017, 19, 3986–3996 RSC.
- J. Schefer, P. Fischer, H. Heer, A. Isacson, M. Koch and R. Thut, Nucl. Instrum. Methods Phys. Res., Sect. A, 1990, 288, 477–485 CrossRef.
- J. Rodriguez-Carvajal, Phys. B, 1993, 192, 55–69 CrossRef CAS.
- P. Thompson, D. E. Cox and J. B. Hastings, J. Appl. Crystallogr., 1987, 20, 79–83 CrossRef CAS.
- P. Scherrer, Nachr. Ges. Wiss. Goettingen, Math.-Phys. Kl., 1918, 1918, 98–100 Search PubMed.
- J. I. Langford and A. J. C. Wilson, J. Appl. Crystallogr., 1978, 11, 102–113 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Found. Adv., 1976, 32, 751–767 CrossRef.
- L. Vegard, Z. Phys., 1921, 5, 17–26 CrossRef CAS.
- C. Weidenthaler, Nanoscale, 2011, 3, 792–810 RSC.
- J. Schindelin, I. Arganda-Carreras, E. Frise, V. Kaynig, M. Longair, T. Pietzsch, S. Preibisch, C. Rueden, S. Saalfeld, B. Schmid, J. Y. Tinevez, D. J. White, V. Hartenstein, K. Eliceiri, P. Tomancak and A. Cardona, Nat. Methods, 2012, 9, 676–682 CrossRef CAS PubMed.
- G. M. Bancroft, Mössbauer spectroscopy: an introduction for inorganic chemists and geochemists, Wiley, New York, 1973 Search PubMed.
- O. Eriksson, B. Johansson, R. C. Albers, A. M. Boring and M. S. S. Brooks, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 42, 2707–2710 CrossRef CAS.
- W. F. Brown, Phys. Rev., 1941, 60, 139–147 CrossRef.
- A. Kremenovic, B. Antic, P. Vulic, J. Blanusa and A. Tomic, J. Magn. Magn. Mater., 2017, 426, 264–266 CrossRef CAS.
- J. Fock, M. F. Hansen, C. Frandsen and S. Morup, J. Magn. Magn. Mater., 2018, 445, 11–21 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9qm00012g |
| ‡ Current address: Instituto de Cerámica y Vidrio, Consejo Superior de Investigaciones Científicas (CSIC), Kelsen 5, 28049 Madrid, Spain. |
| § Current address: Institute for Energy Technology, IFE Neutron Material Characterisation, Instituttveien 18, NO-2007 Kjeller, Norway. |
| This journal is © the Partner Organisations 2019 |