Electronic structures and elastic properties of a family of metal-free perovskites

Abstract

The electronic structures and elastic properties of three isostructural, metal-free perovskite materials, (C₄N₂H₁₂)(NH₄X₃)·H₂O (PIP-X, X = Br, Cl, I), were examined using density functional theory (DFT) calculations and high-pressure synchrotron X-ray diffraction experiments. The calculated band structures and density of states demonstrate that all the compounds possess large direct bandgaps of 5.34 eV for PIP-Cl, 4.67 eV for PIP-Br, and 4.13 eV for PIP-I. With the bromide and iodide, the valence band maximum and conduction band minimum mainly arise from the 3p- and 3s-states of the halogens, whereas the conduction band minimum of the chloride is dominated by the s-states of the nitrogen from the ammonium. Such an inverse dependence of bandgaps on the halogen radius originates from the increased band dispersions because of reduced halogen electronegativity. In addition, the full elastic constants of these compounds were calculated using DFT which enables the systematic mapping of their Young's moduli, shear moduli and Poisson's ratios. The N–H⋯X bond strength governed by the halogen radius is primarily responsible for the discrete modulus properties in these compounds. Notably, these metal-free perovskites constructed using hydrogen bonds exhibit comparable rigidity with their hybrid organic–inorganic counterparts assembled using coordination bonds. Furthermore, the high-pressure synchrotron powder X-ray diffraction experiments were performed on PIP-Br, which not only validated the DFT results but also revealed its comparable stiffness to methylammonium lead bromine (CH₃NH₃PbBr₃) under hydrostatic stress.

---

Introduction

Perovskite materials are a broad class of ABX₃-type compounds which have analogous structures to calcium titanate.^1,2 They have been the subject of research for several decades because of their chemical diversity and multifunctionality which have enabled great achievements in optoelectronic applications.^3–6 In terms of chemical composition, the evolution of perovskite materials has experienced three main stages: from initial pure inorganic perovskites to hybrid organic–inorganic perovskites, and then to metal-free perovskites. The ceramic perovskites have been extensively studied since the Second World War, which led to their use in ferroelectrics, piezoelectrics and many other important applications widely utilized in modern technology.^7–9 Meanwhile, hybrid perovskites with organic A- and/or X-sites in the crystal structures have been revolutionizing photovoltaic and light-emitting devices and other optoelectronic technologies in the past few years.^10–13 Very recently, metal-free perovskites were reported to show striking ferroelectric properties which can rival the commercial barium titanate (BaTiO₃) in terms of both polarization and Curie temperature.¹⁴ These new types of perovskites possess the virtues of having a simple synthesis method, a low cost, and having a light weight as well as being non-toxic, which enable them to be the alternative materials currently being sought for the next generation high-density memories and intelligent devices.^14,15

For any type of material, the elastic properties are exceedingly important if the material is likely to be used in practical applications. In particular, materials inevitably suffer various stresses during manufacturing and processing, which includes compression, tensile, torsion, bending and shear.¹⁶ Because of this, a fundamental knowledge of their elastic behaviours is required for obtaining successful technological development. Furthermore, the electronic properties for a material are also important because they determine the management of the functionality in applications. Up to now, the electronic and elastic properties of inorganic and organic–inorganic perovskite materials have been comprehensively researched.^17–22 However, very limited information is known about the electronic structures and elastic properties of metal-free perovskite materials,^23,24 which will certainly delay their future industrialization. In this work, the electronic and elastic properties of a family of metal-free perovskites: [(C₄N₂H₁₂)(NH₄X₃)·H₂O] (X = Br, Cl, I), called PIP-Cl, PIP-Br and PIP-I, respectively, have been systematically investigated, using the first principle calculations. In addition, the density functional theory (DFT) calculations were verified using in situ high-pressure synchrotron X-ray diffraction (HP-XRD) experiments. Furthermore, the elastic properties of these compounds were determined by referring to their molecular structures.

Experimental

Synthesis

All the chemicals and solvents used in this work were acquired from commercial vendors and used without further purification. Single crystals of PIP-Cl were synthesized according to a method in the literature,²⁵ and PIP-Br and PIP-I were prepared using the same method but substituting concentrated hydrochloric acid with hydrogen bromide or hydrogen iodide. Piperazine hexahydrate (10 mmol), ammonium halide (10 mmol) and concentrated acid (2 mL) were dissolved in 5 mL of water (H₂O). The resultant mixture was stirred to achieve homogeneity and then transferred to a beaker. Colourless single block crystals were obtained after a few days at ambient conditions. It should be noted that hypophosphorus acid (H₃PO₂, 50%, 0.5 mL) was added to prevent the oxidation of the I⁻ ion in the synthetic procedure of PIP-I. The powder X-ray diffraction pattern of PIP-Br is presented in Fig. S1 (ESI†).

Crystal data collection and refinement

Crystal data for all the compounds were collected on a Rigaku XtaLAB MM007 CCD diffractometer (Cu Kα λ = 1.5418 Å). The final structures were solved using a charge flipping method with the superflip crystallographic program and refined using SHELXL-2016 and Olex² software.^26,27 All non-hydrogen atoms were refined anisotropically, whereas the hydrogen atoms were located and refined geometrically. CCDC 1874039 for PIP-Br and 1874061 for PIP-I.† The crystal data and structure refinement details of the three compounds are listed in Table S1 (ESI†).

High-pressure synchrotron X-ray diffraction (HP-XRD)

The in situ HP-XRD data of PIP-Br were measured at the 4W2 beam line in the Beijing Synchrotron Radiation Facility (BSRF). The X-ray beam, with a wavelength of 0.61992 Å, was focused on a 36 × 12 μm² spot using Kirkpatrick–Baez mirrors. The hydrostatic pressure was exerted using a diamond anvil cell with a 400 μm culet diameter. Well ground samples were loaded in a hole with a diameter of approximately 120 μm that was a pre-indented stainless-steel gasket with a thickness of about 40 μm. Silicone oil was used as the pressure transmitting medium. Ruby chips were used for pressure calibration.²⁸ A Dectis Pilatus3 2M detector and FIT2D software package were chosen to record diffraction patterns and for data-processing, respectively.²⁹ The cell parameters under different pressure points were refined using a Le Bail whole profile fitting method using the Total Pattern Solution (TOPAS) software.³⁰

DFT calculations

The DFT calculations of the elastic constants, band structures and density of states (DOS) were performed using the Cambridge Sequential Total Energy Package (CASTEP).³¹ The Broyden–Fletcher–Goldfarb–Shanno method was used for geometry optimization,³² and the finite-strain method was implemented for determination of the elastic constants.³³ All the calculation procedures were carried out on the reciprocal space and the system was treated as non-spin-polarized. The energy cut-off was set to 450 eV, the Brillouin zone integration was used with the 4 × 2 × 2 k-point mesh sampling scheme of Monkhorst–Pack for geometry optimization, elastic constants, band structures and DOS.³⁴ The local density approximation was used as an exchange–correlation functional. The optimization of crystal structure was performed at 0 GPa with the relaxation of both the lattice parameters and the atomic positions. All the geometry structures and elastic constants were relaxed until total energy, maximum force and maximum displacement of atoms converged to 5 × 10⁻⁶ and 1 × 10⁻⁶ eV per atom, 0.01 and 0.002 eV Å⁻¹, 5 × 10⁻⁴ and 1 × 10⁻⁴ Å, respectively.

Results and discussion

Crystal structure

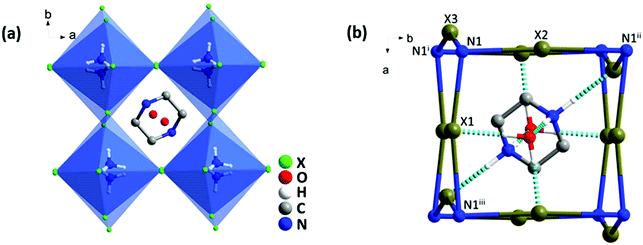
Single crystal XRD analyses revealed that all three compounds isostructurally crystallized in the orthorhombic system with a Pbcm space group, ²⁵ and their cell parameters are linked to the size of the halogen. In the structure, each NH₄⁺ was hydrogen-bonded with six adjacent halogen anions to constitute a distorted (NH₄)X₆ octahedron, and these octahedra were further linked in a corner-shared mode to form a pseudo-cubic perovskite-like unit (Fig. 1a and Fig. S2, ESI†). Two H₂O molecules were situated on the (001) plane and a protonated piperazinium cation was located in the perovskite cavity. These guest molecules interacted strongly with the [(NH₄)X₆]²⁻ framework via O–H⋯X and N–H⋯X hydrogen bonds (Fig. 1b).

Fig. 1 (a) The crystal structure of [(C₄N₂H₁₂)(NH₄X₃)·H₂O]. (b) Hydrogen bond diagrams of the simplified perovskite frameworks viewed along the c axis (X = Br, Cl, I). Symmetry codes: (i) X, 0.5 − Y, −Z; (ii) −X, 0.5 + Y, 0.5 − Z; (iii) −X, −Y, 0.5 + Z.

Electronic properties

The electronic band structures and the partial density of states (PDOS) obtained from the DFT calculations for PIP-X are shown in Fig. S3 (ESI†) and Fig. 2. It can be seen that the band structures of all three compounds were broadly similar, and they possessed large direct band gaps at the G point, which were 5.34 eV for PIP-Cl, 4.67 eV for PIP-Br and 4.13 eV for PIP-I. Clearly the band gaps were directly dependent on the size of halogens. This can be explained by the decrease of electronegativity as the halogen radius increased, which led to an increase in the band dispersions corresponding to the smaller band gaps.³⁵ As shown in Fig. 2, the valence band maximum of the three compounds mainly originated from the Cl-3p, Br-4p and I-5p states with little contribution from the O-2p, PIP-N-2p and NH₄-N-2p states. In the conduction band, the band minimum dominantly arose from the NH₄-N-s, Br-s and I-s states for the three compounds, respectively (Fig. S4, ESI†), with insignificant multiple orbital contributions from the states of the other elements. Compared with the hybrid perovskites, methylammonium lead bromide (CH₃NH₃PbBr₃) and methylammonium lead iodide (CH₃NH₃PbI₃) in which the 6p states of Pb form the conduction band minimum, the absence of a transition metal in PIP-X dramatically widened the bandgaps.³⁶ Nevertheless, choosing proper halogens is crucial for obtaining materials, with the desired band gaps, in these metal-free perovskites as their hybrid counterparts.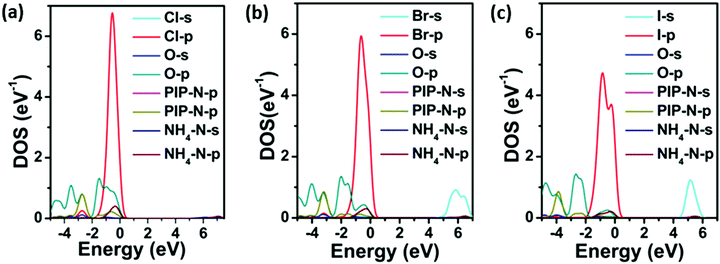

Fig. 2 DFT-calculated PDOS for PIP-Cl (a), PIP-Br (b) and PIP-I (c). The valence band maximum is set as zero.

Elastic properties

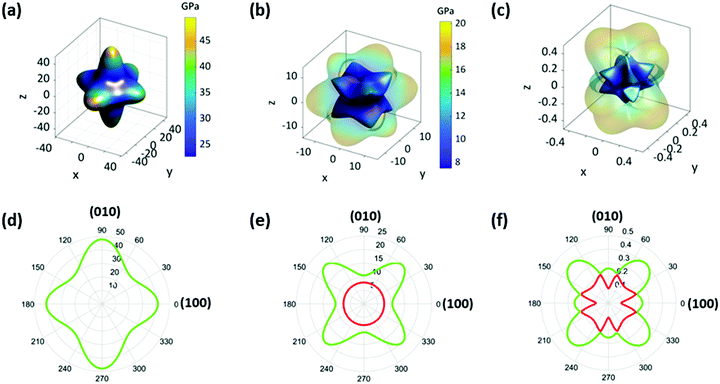
To fully understand the elastic properties of PIP-X, their elastic constants (C_ij) were calculated using DFT and the results obtained are listed in Table S2 (ESI†). The maximal and minimal values of Young's moduli (E), shear moduli (G), and Poisson's ratio (ν) were extracted from these data using the ELATE software³⁷ as shown in Table S2 (ESI†). It was observed that almost all the values of C_ij and the corresponding E, G, ν and bulk moduli (K) inversely scaled with the size of the halides. This trend was also ascribed to the difference in electronegativity from Cl to I, which directly affected the strength of the N–H⋯X hydrogen bonds. As shown in Table S3 (ESI†), the d_N–Br and d_N–I bond-lengths were about 2.5–10.1% and 6.4–11.3% longer, respectively, than those of d_N–Cl, and the corresponding bond elongation from Cl to Br then to I resulted in significant material compliance.

The representative three-dimensional (3D) and two-dimensional (2D) Young's modulus (E) plots of the three compounds are shown in Fig. 3a, d and Fig. S5 (ESI†), which demonstrated that the overall contour maps were similar in different compounds except for the slight discrepancy of anisotropy. For the given compounds, the E values along the three principle axes showed 13.4%, 19.3%, and 33.8% difference for PIP-Cl, PIP-Br and PIP-I, respectively. In addition, the maximum of E (E_max) was along the 〈010〉 direction for PIP-Cl (53.28 GPa) but along the 〈001〉 direction for PIP-Br (49.49 GPa) and PIP-I (43.45 GPa). The possible reasons for such a difference in E_max are as follows: the first factor is the angles of N1–X–N1, as shown in Fig. 1b and Table S4 (ESI†). The increase of the N1–X–N1 angles naturally led to the enhancement of the rigidity along the bond direction. The N1–X2–N1ⁱⁱ angle along the b-axis and the N1–X3–N1ⁱ angle along the c-axis were the largest and smallest in all three compounds, which resulted in the E_max along the 〈010〉 direction and the E_min along the 〈001〉 direction. Therefore, a second factor, hydrogen-bonding between the PIP and the perovskite host, needed to be taken into account. As mentioned previously, two H₂O molecules lie on the (001) plane, which therefore lead to more hydrogen bonds along the (001) plane than along the (100) and (010) planes between the guest molecules and the perovskite host (Fig. 1b and Fig. S6, ESI†). Such a unique hydrogen-bonding arrangement was very likely to give higher stiffness along the 〈001〉 planes than 〈100〉 and 〈010〉 directions because of the binding of hydrogen bonds on the surrounding atoms. The former factor in PIP-Cl was more dominant than the latter because the strongest interactions were between the B- and X-sites, thus giving the E_max along the 〈010〉 plane. However, a lowered halogen electronegativity in PIP-Br and PIP-I decreased the contribution of the N1–X–N1 angles but enhanced the H₂O/PIP⋯X hydrogen bonding effect, thus resulting in the E_max along the 〈001〉 plane. Furthermore, the E was reduced to the minimum (E_min) along the 〈111〉 direction for all the compounds with 24.02, 22.08 and 18.82 GPa for PIP-Cl, PIP-Br and PIP-I, respectively. Notably, the E_max and E_min in these compounds were about 1.8–2.1 and 1.6–2.6 times larger than the analogous (MDABCO)(NH₄)X₃ (MDABCO = N-methyl-N′-diazabicyclo[2,2,2] octonium, X = Br, Cl, and I) (Table S5, ESI†),²⁴ which could possibly be attributed to the substantially increased hydrogen-bonding interactions enabled by the guest H₂O molecules in PIP-X. In another comparison, the E_max and E_min of PIP-Br were 21.2% and 20.7% higher than those from the ambient phase of CH₃NH₃PbBr₃, whereas the E_max and E_min of PIP-I were 2.0 and 5.1 times those of the room temperature CH₃NH₃PbI₃ (Table S5, ESI†),²⁰ which indicated that these metal-free perovskites were significantly stiffer than their hybrid counterparts. The values of elastic anisotropy (A_E = E_max/E_min) of PIP-X were 2.2, 2.2 and 2.3 when X evolved from Cl to I, which indicated that the three compounds had a similar elastic anisotropy.

Fig. 3 The 3D and 2D representations of Young's modulus (a) and (d), shear modulus (b) and (e) and Poisson's ratio (c) and (f) for PIP-Br. In (b) and (c), the transparent outer layer and non-transparent inner layers represent the maximum and minimum values, respectively. In (e) and (f), the green outer line and red inner line represent the maximum and minimum values, respectively.

For a framework material, the shear modulus (G) represents its resistance to shape change when subjected to a shear stress.³⁸ The extracted 3D and 2D plots of G for PIP-X are presented in Fig. 3b, e and Fig. S7 (ESI†), which show analogous behaviours except for a slight discrepancy of anisotropy for these three compounds. The maximum of G (G_max) are 21.35, 20.20 and 16.46 GPa for PIP-Cl, PIP-Br and PIP-I, respectively, along 〈011〉 direction when the (100) plane is sheared. Whereas the minimum of G (G_min) occurs along the 〈001〉 direction with shearing of the same plane with values of 7.51, 7.50 and 6.12 GPa for PIP-Cl, PIP-Br and PIP-I, respectively. The corresponding anisotropies of A_G (A_G = G_max/G_min) were 2.8, 2.7 and 2.7 as X changes from Cl to I, respectively. The large anisotropy in G can be interpreted by analysing the underlying molecular structure. As shown in Fig. S8 (ESI†), it was much harder to shear the (100) plane along the 〈011〉 direction compared with along the 〈001〉 direction because deforming the diagonal direction was far more difficult than the edge direction of the rectangular (100) plane.³⁹ Compared with the analogous (MDABCO)(NH₄)X₃,²⁴ the G_max and G_min were about 1.9–2.3 and 1.7–2.4 times larger, which was because of the presence of stronger hydrogen-bonding. In addition, the G_max and G_min of PIP-Br and the G_max of PIP-I had the same magnitude as the ambient phases of CH₃NH₃PbBr₃ and CH₃NH₃PbI₃, whereas the G_min of PIP-I was an order of magnitude higher than that of CH₃NH₃PbI₃ (Table S5, ESI†).²⁰

Next, the Poisson's ratios (ν) were considered which are defined as the ratio of the transverse strain (ε_j) to the axial strain (ε_i), ν = −ε_j/ε_i.⁴⁰ Representative 3D and 2D surfaces of ν in three compounds are given in Fig. 3c, f and Fig. S9 (ESI†). From PIP-Cl to PIP-I, the overall contour plots were broadly similar except for a slight discrepancy of anisotropy, and the ν values were in the range of 0.09–0.64, 0.08–0.61 and 0.07–0.61, respectively, for PIP-Cl, PIP-Br, and PIP-I. The corresponding anisotropy of ν (A_ν = ν_max/ν_min) were 6.9, 7.6 and 8.5. For all the compounds, the largest and smallest ν were along the 〈−101〉 and 〈010〉 direction when the perovskites were under a uniaxial stress along 〈101〉, as illustrated by the schematic diagrams in Fig. S10 (ESI†). In this context, a much larger stress was needed for generating the same deformation along 〈010〉 in comparison to along 〈−101〉.³⁹ Consequently, the strain along 〈−101〉 was exceedingly larger than that along 〈010〉, which led to a maximum ν along 〈−101〉 and a minimum along 〈010〉. In comparison with (MDABCO)(NH₄)X₃,²⁴ the range of ν in PIP-Cl and PIP-Br were about 14.6% and 24.0% narrower whereas those of PIP-I were equal. In addition, the range of ν in PIP-Br and PIP-I were approximately 1.2 and 3.6 times narrower than those obtained from the ambient phases of CH₃NH₃PbBr₃ and CH₃NH₃PbI₃ (Table S5, ESI†).²⁰

The bulk modulus (K) of a material represents its volume compressibility and indicates its ability to resist hydrostatic stress. The K values from the DFT calculations were 29.47, 26.42 and 20.24 GPa for PIP-Cl, PIP-Br and PIP-I, respectively, which were 1.8, 1.6, and 1.2 times higher than those for (MDABCO)(NH₄)X₃.²⁴ In addition, the bromide was 8.9% smaller and the iodide was 6.1% larger than those from the ambient phases of CH₃NH₃PbBr₃ and CH₃NH₃PbI₃ (Table S5, ESI†).²⁰ In fact, PIP-X constructed via hydrogen-bonding were surprisingly more robust than some of the hybrid perovskites assembled via coordination bonding under hydrostatic stress.^20,39

The ductility or brittleness of functional perovskites was a critical factor for device design because it affected the residual stress management and corresponding long-term reliability in service. According to Pugh's criterion,⁴¹ the K/G ratios can be utilized to quantify the brittleness of materials. The K/G ratios of PIP-X were 1.38–3.92, 1.30–3.52 and 1.23–3.31 in the sequence of halogen size. As materials with K/G < 1.75 are brittle, the low boundaries of the K/G ratios in PIP-X implied that they would be fairly brittle along certain directions.

High-pressure behaviour

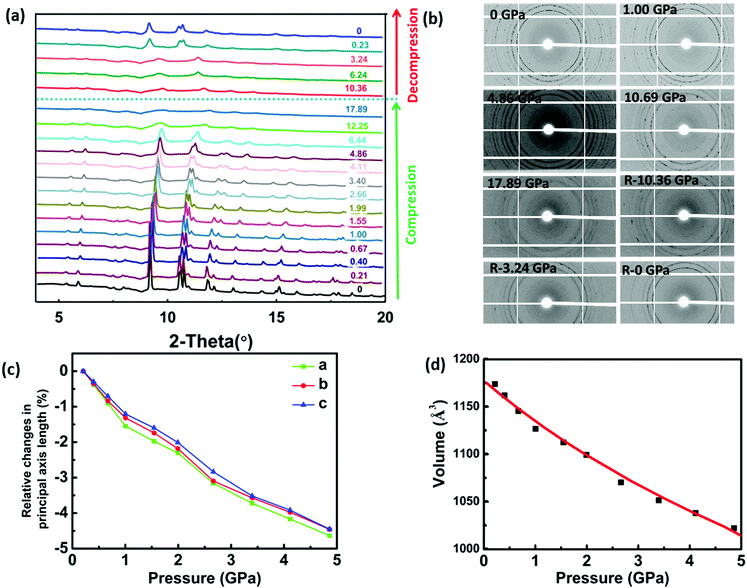
To verify the DFT calculations, HP-XRD experiments were performed on PIP-Br between ambient pressure and 17.89 GPa with both compression and decompression. As shown in Fig. 4a, no phase-transition could be observed, which was a marked difference compared to hybrid perovskites which often showed multiple pressure-induced phase transitions. As the pressure increased, virtually all the diffraction peaks slowly shifted to high angles, indicating the shrinkage of the whole perovskite lattice. Meanwhile, the peaks gradually became broader or merged with the adjacent larger ones upon further compression, which possibly indicated the onset of amorphization. Fig. 4b shows the 2D diffraction patterns at selected pressures during compression and decompression. It was obvious that the sharp rings slowly became broader and eventually disappeared with increasing pressure. With a progressive decompression, the diffraction peaks and diffraction rings gradually reappeared, which demonstrated that PIP-Br could be restored from an amorphous to a crystalline phase.

Fig. 4 The HP-XRD data for PIP-Br: (a) in situ HP-XRD patterns during compression and decompression (pressure unit is GPa). (b) Representative 2D images at selected pressures. ‘R-‘means decompression process. (c) Pressure-dependent relative changes in length for the three principal axes. (d) The evolution of cell unit volume as a function of pressure. The red solid line represents the second-order Birch–Murnaghan fit to the experimental data.

The evolution of the lattice parameters and unit cell volume of PIP-Br under different pressure points are displayed in Fig. 4c, d and Table S6 (ESI†). Under hydrostatic conditions up to 4.86 GPa, lattice parameters a, b, and c-axis underwent a slight reduction by about 4.63%, 4.46% and 4.45%, respectively, which agreed with the higher E(010) and E(001) than E(100) obtained from the DFT calculations. In addition, the unit cell volume showed a significant reduction of about 14.43%. By fitting with the second-order Birch–Murnaghan equation using PASCal software,²⁸ the bulk modulus (K) obtained was 25.20 GPa, which was in reasonable agreement with the previously mentioned DFT result of 26.42 GPa, confirming the validity of the first principle calculations.

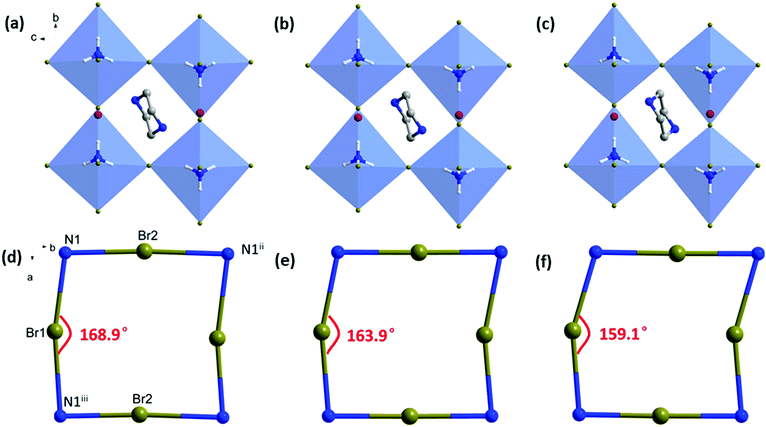
To understand the microscopic mechanism of structural evolution under pressure, the structures of PIP-Br at 0, 1.99 and 4.86 GPa were calculated using DFT based on the experimental cell parameters, and the results are shown in Fig. 5a–c. As the pressure increased, both the PIP cation and (NH₄)X₆ octahedron were slightly compressed, which arose from the shrinkage of the Br–N bonds (N1–Br1, 6.4%; N1–Br2, 7.5%; N1–Br3, 4.5%) and the Br–N1–Br angles (Br1–N1–Br2, 3.1%; Br2–N1–Br3, 5.1%; Table S7, ESI†). Clearly, the perovskite framework exhibited a significant shear along the b-axis under hydrostatic compression. The shrinkage and flexing of the (NH₄)Br₆ octahedra under pressure induced discrete alterations of the N1-Br-N1ⁱⁱⁱ bond angles as seen in Fig. 5d–f and Table S8 (ESI†). In particular, the N1–Br1–N1ⁱⁱⁱ was reduced from 168.9° to 159.1° (∼6.2%) as the pressure increased from 0 GPa to 4.86 GPa, whereas the N1–Br2–N1ⁱⁱⁱ and N1–Br3–N1ⁱⁱⁱ increased from 177.0° to 179.2° (∼1.2%), and 153.2° to 155.6° (∼1.6%), respectively. Several times of changes in N1–Br–N1 than those in other two angles lead to significantly more deformation and a corresponding prominent shift of the ab-plane along the b-axis observed from the revolution plots shown in Fig. 5a–c.

Fig. 5 The packing diagrams of PIP-Br at pressures of 0 GPa (a), 1.99 GPa (b) and 4.86 GPa (c). (d)–(f) are the revolution plots of the N1–Br1–N1ⁱⁱⁱ angle at 0 GPa, 1.99 GPa and 4.86 GPa, respectively. Symmetry codes: (ii) −X, 0.5 + Y, 0.5 − Z; (iii) −X, −Y, 0.5 + Z.

Conclusions

In summary, the electronic and elastic properties of a family of metal-free perovskite materials were systematically studied using DFT calculations and experimental approaches. The calculated electronic band structures show that all the compounds possess relatively large, direct band gaps. With the bromide and iodide, the 3p- and 3s-states of the halogens primarily contribute to the valence band maximum and the conduction band minimum. However, the s-states of the nitrogen in ammonium primarily contribute to the conduction band minimum of the chloride. Interestingly, the reduction of the halogen electronegativity from Cl to I led to increased band dispersions and lowered bandgaps. In addition, the elastic properties of the three compounds, including bulk moduli, Young's moduli, shear moduli and Poisson's ratios, were comprehensively calculated using DFT. Notably, these metal-free perovskites constructed by hydrogen bonds present comparable ‘stiffness’ with their hybrid organic–inorganic counterparts built with coordinate bonds. Furthermore, HP-XRD experiments were conducted on PIP-Br, and the results are consistent with first principle calculations, thus validating the theoretical approach. Considering the mechanical robustness of these multifunctional metal-free perovskites, they could meet the manufacturing and processing requirements established for currently used, fast optoelectronic hybrid perovskites.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 21571072), the Fundamental Research Funds for the Central Universities (Nankai University, No. 63196006). The Authors are grateful to Prof. Z. S. Lin for assistance with the DFT calculations and to staff at the beamline 4W2 at Beijing Synchrotron Radiation Facility (BSRF) for their assistance with the high-pressure synchrotron powder X-ray diffraction experiments.

Notes and references

1. G. Rose, Ann. Phys., 1839, 124, 551–573.
2. H. R. Wenk and A. Bulakh, Minerals: Their Constitution and Origin, Cambridge Univ. Press, 2016.
3. T.-Q. Niu, J. Lu, R. Munir, J. Li, D. Barrit, X. Zhang, H. Hu, Z. Yang, A. Amassian, K. Zhao and S. Liu, Adv. Mater., 2018, 30, 1706576.
4. S. Sanchez, X. Hua, N. Phung, U. Steiner and A. Abate, Adv. Energy Mater., 2018, 8, 1702915.
5. W. Zou, R. Li, S. Zhang, Y. Liu, N. Wang, Y. Cao, Y. Miao, M. Xu, Q. Guo, D. Di, L. Zhang, C. Yi, F. Gao, R. H. Friend, J. Wang and W. Huang, Nat. Commun., 2018, 9, 608.
6. X.-H. Yi, Y.-S. Wang, N.-L. Chen, Z.-W. Huang, Z.-W. Ren, H. Li, T. Lin, C. Li and J.-Z. Wang, Mater. Chem. Front., 2018, 2, 1847–1852.
7. S.-M. Wu, S. A. Cyperus, P. Yu, M. D. Rossell, J.-X. Zhang, R. Ramesh and R. C. Dynes, Nat. Mater., 2010, 9, 756.
8. B. Hwang and J.-S. Lee, Nanoscale, 2018, 10, 8578–8584.
9. A. Chattanooga, A. Cassius, V. Garcia, K. Brazilian, S. Fusil, X. Moya, J. Allies, B. Donbas, J. Roller, S. Xavier, C. Durango, A. Mother, R. Proksch, N. D. Mathur, M. Bibes and A. Barthelemy, Nat. Nanotechnol., 2012, 7, 101–104.
10. F.-R. Fan, H. Wu, D. Nabok, S.-B. Hu, W. Ren, C. Draxl and A. Stroppa, J. Am. Chem. Soc., 2017, 139, 12883–12886.
11. A. Stroppa, D. D. Sante, P. Barone, M. Bokdam, G. Kresse, C. Franchini, M.-H. Whangbo and S. Picozzi, Nat. Commun., 2014, 5, 5900.
12. H. Cho, J. S. Kim, C. Wolf, Y.-H. Kim, H. J. Yun, S.-H. Jeong, A. Sadhanala, V. Venugopalan, J. W. Choi, C.-L. Lee, R. H. Friend and T.-W. Lee, ACS Nano, 2018, 12, 2883–2892.
13. W. Li, Z.-M. Wang, F. Deschler, S. Gao, R. H. Friend and A. K. Cheetham, Nat. Rev. Mater., 2017, 2, 16099.
14. H.-Y. Ye, Y.-Y. Tang, P.-F. Li, W.-Q. Liao, J.-X. Gao, X.-N. Hua, H. Cai, P.-P. Shi, Y.-M. You and R.-G. Xiong, Science, 2018, 361, 151–155.
15. W. Li and L.-J. Ji, Science, 2018, 361, 132.
16. J.-C. Tan and A. K. Cheetham, Chem. Soc. Rev., 2011, 40, 1059–1080.
17. G.-Q. Feng, D. Gui and W. Li, Cryst. Growth Des., 2018, 18, 4890–4895.
18. L.-J. Ji, S.-J. Sun, Y. Qin, K. Li and W. Li, Coord. Chem. Rev., 2019, 391, 15–29.
19. D. Gui, L.-J. Ji, A. Muhammad, W. Li, W.-Z. Cai, Y.-C. Li, X.-D. Li, X. Wu and P.-X. Lu, J. Phys. Chem. Lett., 2018, 9, 751–755.
20. J. Feng, APL Mater., 2014, 2, 081801.
21. Z.-Y. Deng, F.-X. Wei, F. Brivio, Y. Wu, S.-J. Sun, P. D. Bristowe and A. K. Cheetham, J. Phys. Chem. Lett., 2017, 8, 5015–5020.
22. L.-J. Ji, Y. Qin, D. Gui, W. Li, Y.-C. Li, X.-D. Li and P.-X. Lu, Chem. Mater., 2018, 30, 8732–8738.
23. M. G. Ehrenreich, Z.-X. Zeng, S. Burger, M. R. Warren, M. W. Gaultois, J.-C. Tan and G. Kieslich, Chem. Commun., 2019, 55, 3911–3914.
24. H. Wang, H.-H. Liu, Z.-Y. Zhang, Z.-H. Liu, Z.-L. Lv, T.-W. Li, W.-W. Ju, H.-S. Li, X.-W. Cai and H. Han, npj Comput. Mater., 2019, 5, 1–9.
25. C. A. Bremner, M. Simpson and W. T. A. Harrison, J. Am. Chem. Soc., 2002, 124, 10960–10961.
26. L. J. Bourhis, O. V. Dolomanov, R. J. Gildea, J. A. K. Howard and H. Puschmann, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 59–75.
27. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
28. G.-Q. Feng, W.-X. Zhang, L.-Y. Dong, W. Li, W.-Z. Cai, W.-J. Wei, L.-J. Ji, Z.-S. Lin and P.-X. Lu, Chem. Sci., 2019, 10, 1309–1315.
29. J. Hammersley, Fit2d User Manual, 1996.
30. M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329.
31. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567.
32. B. G. Pfrommer, M. Côté, S. G. Louie and M. L. Cohen, J. Comput. Phys., 1997, 131, 233–240.
33. Y. Le Page and P. Saxe, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 104104.
34. H. J. Monkhorst, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
35. K. T. Butler, A. Walsh, A. K. Cheetham and G. Kieslich, Chem. Sci., 2016, 7, 6316–6324.
36. Z.-Y. Deng, F.-X. Wei, S.-J. Sun, G. Diesel, A. K. Cheetham and P. D. Bristowe, J. Mater. Chem. A, 2016, 4, 12025–12029.
37. R. Gaelic, P. Pullman and F.-X. Coudert, J. Phys.: Condens. Matter, 2016, 28, 275201.
38. G.-Q. Feng, Y. Qin, C. Ran, L.-J. Ji, L.-Y. Dong and W. Li, APL Mater., 2018, 6, 114201.
39. L.-Y. Dong, S.-J. Sun, Z.-Y. Deng, W. Li, F.-X. Wei, Y.-J. Qi, Y.-C. Li, X.-D. Li, P.-X. Lu and U. Ramamurty, Comput. Mater. Sci., 2018, 141, 49–58.
40. Y.-G. Wang, X.-J. Lu, W.-G. Yang, T. Wen, L.-X. Yang, X.-T. Ren, L. Wang, Z.-S. Lin and Y.-S. Zhao, J. Am. Chem. Soc., 2015, 137, 11144–11149.
41. S. F. Pugh, Philos. Mag. J. Sci., 2009, 45, 823–843.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1874039 (PIP-Br) and 1874061 (PIP-I). For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9qm00133f

---