Open Access Article
Open Access ArticleMolecular dynamics simulation of protein-mediated biomineralization of amorphous calcium carbonate
R. Sandya Rani and
Moumita Saharay
and
Moumita Saharay *
*
Department of Physics, Osmania University, Hyderabad, India. E-mail: saharaymou@gmail.com
First published on 16th January 2019
Abstract
The protein-mediated biomineralization of calcium carbonate (CaCO3) in living organisms is primarily governed by critical interactions between the charged amino acids of the protein, solvent, calcium (Ca2+) and carbonate (CO32−) ions. The present article investigates the molecular mechanism of lysozyme-mediated nucleation of amorphous calcium carbonate (ACC) using molecular dynamics and metadynamics simulations. The results reveal that, by acting as nucleation sites, the positively charged side chains of surface-exposed arginine residues form hydrogen bonds with carbonates and promote aggregation of ions around them leading to the formation and growth of ACC on the protein surface. The newly formed ACC patches were found to be less hydrated due to ion aggregation-induced expulsion of water from the nucleation sites. Despite favorable electrostatic interactions of the negatively charged side chains of aspartate and glutamate with calcium ions, these residues contribute minimally to the growth of ACC on protein surface. The activation barrier for the growth of partially hydrated ACC patches on lysozymes was determined from the free energy profiles obtained from metadynamics simulations.
Introduction
Calcium carbonate (CaCO3) is a commonly found biomineral in the environment. The diversity in the morphology, origin, and composition exhibited by naturally occurring CaCO3 makes it an intriguing system to investigate the mechanism, energetics and thermodynamics of biomineralization. Apart from the three anhydrous (calcite, vaterite, and aragonite) and two hydrous (monohydrocalcite, CaCO3·H2O; and ikaite, CaCO3·6H2O) crystalline polymorphs, calcium carbonate can also exist in metastable amorphous phases.1 Amorphous calcium carbonate (ACC) serves as a precursor in the biomineralization of almost all types of biogenic CaCO3.2–8In living organisms, the process of mineral formation is primarily governed by the interactions between the charged biopolymers,9–12 ionic constituents (Ca2+ and CO32−), and water. For instance, the negatively charged proteins in corals and sea urchin spicules are shown to stabilize the amorphous phase of CaCO3 even in in vitro experiments in the absence of any biological cells.13–15 A recent study on the formation of coral skeleton demonstrated that the ACC phase is indeed the metastable precursor to the crystalline CaCO3, and that the growth rate of aragonite crystals through the non-classical crystallization process11,12 involving aggregation of ACC particles is ∼100 times faster than the classical route of ion-by-ion formation of crystals.16 Earlier studies have also shown that the binding affinity of Ovocleidin-17 (OC-17), a hen eggshell protein, for ACC nanoparticles is much higher than that for the calcite surface17,18 suggesting that favorable binding of the protein to ACC is critical for biomineralization and eggshell formation. The lower calcite-protein binding affinity is leveraged for the detachment of the protein from the crystal after the ACC to crystal transition.18 Thus, OC-17 or a class of functionally similar proteins/biopolymers can be regarded as catalysts to facilitate the crystallization of CaCO3.
Although previous computer simulation studies have investigated the mechanism of the attachment of the protein19,20 to the ACC nanoparticles and CaCO3 crystal surfaces, little is known about the role of protein in promoting the formation of ACC from the ionic solution. Another key feature that is yet to be understood is the atomistic details of the mechanism and energetics of protein-ACC association/dissociation process. Some proteins/biopolymers hinder the crystallization of CaCO3 by stabilizing3,21,22 the amorphous phase, and the biomineralization is activated as and when the living organism requires it. The nucleation of CaCO3 in the presence of negatively charged biopolymers10 is thought to occur in two steps: (i) the binding of Ca2+ with the biopolymer to form Ca2+-bound globules, (ii) the diffusion and association of CO32− ions with the globules to form polymer-mediated ACC phase that then grows in size. These polymers, referred to as ‘ion sponge’, critically determine where and how the CaCO3 nucleation will take place and proceed further. However, the precise molecular details associated with these steps are still missing.
In vitro experiments have shown that the positively charged lysozyme increases the nucleation rate of CaCO3 crystals.23,24 The large negative ζ-potential (−14 mV) around this protein favors the formation of negatively charged double layers of CO32− around its surface.23 To understand the microscopic details of the onset of protein-mediated aggregation of Ca2+ and CO32− and to identify the vital molecular attributes and the key residues that govern the mineralization process,25,26 we have performed a series of atomistic molecular dynamics simulations of lysozyme, a hen eggshell protein. Our results reveal that the positively charged side chains of solvent-exposed arginine residues act as nucleation sites for the formation and growth of ACC on protein surface, while the negatively charged side chains of glutamate and aspartate residues contribute minimally to biomineralization.
Simulation details
We have investigated the following four model systems: (i) lysozyme in water (hereafter referred to as LW), (ii) hydrated ACC (hACC) having 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.67 composition of CaCO3
0.67 composition of CaCO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O, (iii) lysozyme in CaCO3 solution with two different CaCO3
H2O, (iii) lysozyme in CaCO3 solution with two different CaCO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O concentrations (S1LC and S2LC). The dimensions and the number of constituents of the simulated model systems are provided in Table 1.
H2O concentrations (S1LC and S2LC). The dimensions and the number of constituents of the simulated model systems are provided in Table 1.
| System | CaCO3 pairs | Water molecules | Orthorhombic box dimension (Å3) |
|---|---|---|---|
| LW | — | 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 284 284 |
70.0 × 70.0 × 70.0 |
| S1LC | 235 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 289 289 |
76.2 × 76.2 × 76.2 |
| S2LC | 474 | 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238 238 |
76.5 × 76.5 × 76.5 |
| hACC | 1620 | 1094 | 50.0 × 50.0 × 50.0 |
The LW model allows us to characterize the lysozyme–water interactions in the absence of Ca2+ and CO32− ions, whereas S1,2LC models are used to probe the influence of these ions on lysozyme. The initial coordinates of the hen egg-white lysozyme (PDB Id: 2cds) was taken from the X-ray crystal structure. To neutralize the net positive charge on lysozyme, 8 Cl− were added in LW system, while 4 extra CO32− were added in S1,2LC models. The initial configurations of S1,2LC were generated by randomly placing desired numbers of Ca2+ and CO32− ions in cubic water boxes of sizes specified in Table 1. The lysozyme was then solvated in this ionic solution by removing the ions and water molecules that were in hard contact with the protein using CHARMM-GUI27–29 package. CHARMM36 (ref. 30) force field (FF) parameters were used for the protein and ions (Ca2+, CO32−) together with the standard TIP3P water model.
For hACC, H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CaCO3 ratio was maintained at 0.67 to be consistent with our earlier investigation.31 The MD simulations were performed using NAMD32 package. The systems were equilibrated for 1 ns in NPT ensemble followed by 15 ns of MD simulations in NVT ensemble with the time step of 2 fs. The temperature and pressure were maintained at 303 K and 1 atm, respectively. The temperature was controlled by the Langevin thermostat using a damping coefficient of 1 ps−1. The electrostatic interactions were evaluated using particle mesh Ewald method with a grid spacing of 1 Å. Periodic boundary conditions were used and a distance cutoff of 12 Å was chosen to calculate the non-bonded interaction energies between different species.
CaCO3 ratio was maintained at 0.67 to be consistent with our earlier investigation.31 The MD simulations were performed using NAMD32 package. The systems were equilibrated for 1 ns in NPT ensemble followed by 15 ns of MD simulations in NVT ensemble with the time step of 2 fs. The temperature and pressure were maintained at 303 K and 1 atm, respectively. The temperature was controlled by the Langevin thermostat using a damping coefficient of 1 ps−1. The electrostatic interactions were evaluated using particle mesh Ewald method with a grid spacing of 1 Å. Periodic boundary conditions were used and a distance cutoff of 12 Å was chosen to calculate the non-bonded interaction energies between different species.
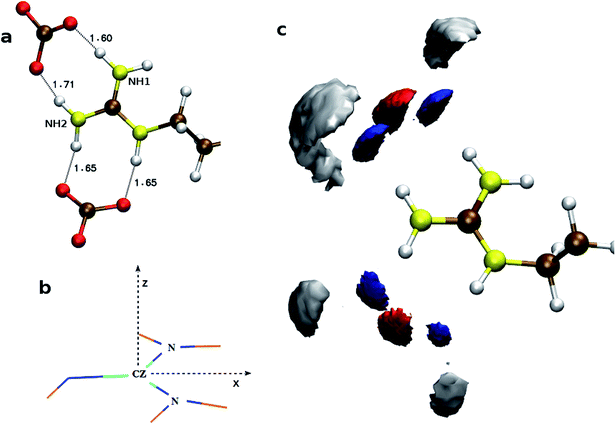
To understand the flexibility of the near neighbor environment around the positively charged side chains, we studied the evolution of hydrogen bonds formed by the side chains with the nearest CO32− and water molecules. An arginine side chain was considered to be hydrogen bonded to CO32− if the CZ–Oc (refer Fig. 1 for atom labels) distance was less than 4.5 Å or to a water molecule if the CZ–Ow distance was less than 4.0 Å.33–35 For each type of h-bond, the time correlation function, Chb(t), which is defined as follows,
| C(t) = 〈h(0)h(t)〉/〈h〉 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 〉’ represents the ensemble average.
〉’ represents the ensemble average.
 | ||
| Fig. 1 Atom names used for the descriptions of side chains in (a) arginine, (b) aspartate, and (c) glutamate. | ||
We performed well-tempered metadynamics36–38 simulations, using NAMD package, to estimate the free energy required for the association of ions and dehydration of hydrated Ca2+–CO32− clusters around selected side chains of lysozyme. The separation (rCV) between the tagged ions and the residue of interest was chosen as the collective variable (CV). The Gaussian hills were added at a regular interval of 100 fs, and the width of each Gaussian hill was 1 Å. The total run length for the metadynamics simulation was 100 ns.
Results and discussion
Ionic structure around lysozyme
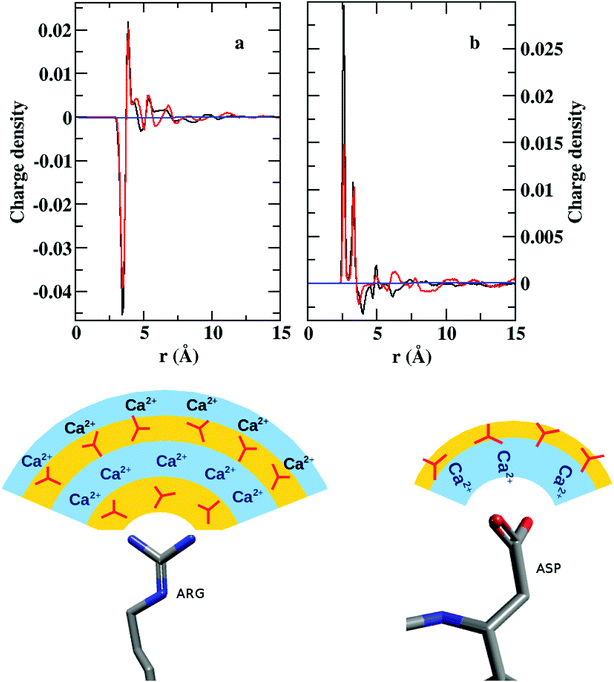
Fig. 2 compares the arrangement of ions around lysozyme in the initial configuration of S1LC with that in a snapshot taken after 15 ns of MD simulation. The ions are distributed randomly around lysozyme in the initial structure, while dense ionic patches are observed around specific surface residues of lysozyme in the equilibrated system. The aggregation of ions occur primarily around arginine residues, but to some extent also around glutamate and aspartate. The clustering of Ca2+ and CO32− at specific surface sites of the protein underscores the key role of protein-mediated aggregation of ions in the formation of biominerals. The average mass density of the dense ionic patches around arginine is ∼1.3 g cm−3, which is comparable with that of hydrated ACC.26 However, the local environment around glutamate (0.7 g cm−3) and aspartate (0.71 g cm−3) are relatively less dense than the microenvironment of arginine residues.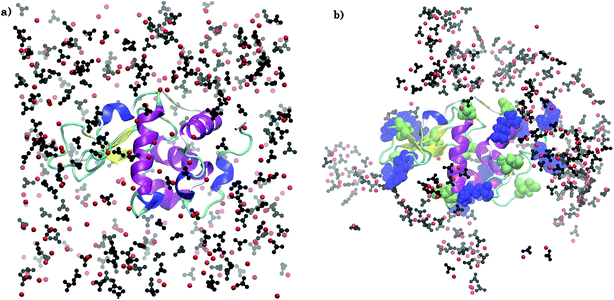 | ||
| Fig. 2 Arrangement of Ca2+ (red spheres) and CO32− (black) ions around arginine (blue), aspartate (green), and glutamate (green) residues in S1LC for (a) initial configuration and (b) after 15 ns of MD simulation. Water molecules are not shown for clarity. VMD39 software package was used for visualization. | ||
The clusters of ions are observed to grow in size during the course of MD simulation. The largest ion cluster is formed around ARG14, ARG125, and ARG128. Due to their close proximity, these three surface residues form an ‘attractive triangle’, which favors the rapid growth of amorphous calcium carbonate on lysozyme. The positively charged guanidinium (Gdm+) functional groups of arginine residues play a crucial role in the nucleation and growth25 of crystalline CaCO3 by favorably interacting with the negatively charged CO32− ions. The Gdm+–CO32− and Ca2+–CO32− interactions facilitate the ion association and further growth of amorphous CaCO3-like domains around these residues.
Radial distribution function
To further investigate the local environment around the key residues of the protein, we examined the distribution of ions and water around them by calculating the radial distribution functions (RDFs) that describes how the density of neighbors vary around a reference atom/particle as a function of radial separation between the two.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O ratio (1620
H2O ratio (1620![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1094 in hACC and 474
1094 in hACC and 474![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 14
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 238 in S2LC).
238 in S2LC).
| g(r) | S2LC | hACC | ||
|---|---|---|---|---|
| Atom pair | Peak position r (Å) | N(r) | Peak position r (Å) | N(r) |
| Cc–Cc | 4.8 | 3.0 | 4.6 | 9.2 |
| Ca–Cc | 2.6, 3.2 | 2.3 | 2.6, 3.2 | 4.6 |
| Ca–Ow | 2.2 | 3.0 | 2.2 | 0.8 |
| Ca–Ca | 3.3, 3.8 | 1.3 | 3.3, 3.7 | 4.4 |
| Ca–Oc | 2.1 | 3.2 | 2.07 | 5.4 |
| Cc–Ow | 3.3 | 12.8 | 3.1 | 4.04 |
Although the peak intensities in ion–ion RDFs are relatively higher in S2LC than in hACC, peak positions remain mostly unchanged. The ion–ion RDFs indicate that the ions are held together strongly to form a semi-rigid and well-structured coordination shells in S2LC. The present structural analysis reveals that local environment around lysozyme favors the aggregation of ions and the formation of amorphous calcium carbonate, although, the concentration of ions is much lower than the hydrated ACC (hACC) studied here.
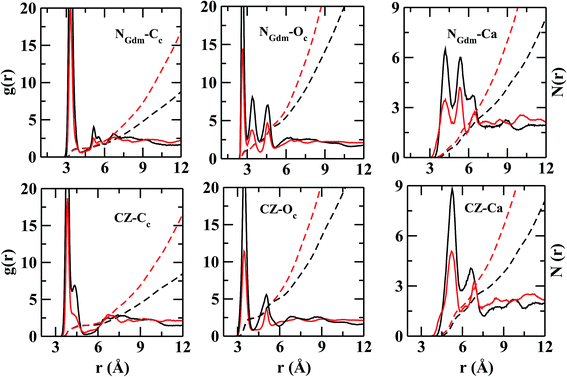
In Fig. 4, the RDFs between NGdm (guanidinium-nitrogen) and Cc (carbonate carbon) atom pair shows three maxima at 3.34, 5.18, and 7 Å. The coordination number at the first minimum is 1.24. The first and second maxima are separated by a plateau of width ∼0.7 Å with negligible intensity, showing a crystal-like ordering of Cc atoms in this region. The number of Oc (carbonate oxygen) around NGdm is ∼1.4 at the first minimum (2.9 Å) of gNGdm–Oc(r) (Fig. 4). The underlying geometry could possibly indicate a configuration where one of the H atoms of a NGdm forms single h-bond with Oc. This preferential arrangement compares well with the geometry optimized isolated cluster25 of Gdm+–CaCO3–2H2O, where the distance between NGdm and Oc is ∼2.65 Å. The second and third maxima in gNGdm–Oc(r) appear at 3.4 and 4.6 Å, respectively. The coordination numbers at the corresponding minima in S1LC are 2.3 (2.0 in S2LC) and 4.7 (4.5 in S2LC), respectively.
The first maximum in gNGdm–Ca(r) (Fig. 4) shows two sub peaks at 4.2 and 5.5 Å in both the systems. This characteristic arrangement of Ca2+ around NGdm is somewhat similar to that of Ca2+-environment around Cc in hACC (Fig. 3), where the first peak of gCa–C(r) is also divided into two sub peaks. This indicates two preferred arrangements: for longer distance, Ca2+ is coordinated with only one NGdm or Oc making a ‘monodentate’ geometry whereas for shorter distance Ca2+ is equidistant from two NGdm or Oc making a ‘bidentate’ geometry. With increased ionic concentration in S2LC, the intensity of these peaks decreases which implies a less-structured coordination shell with same number of neighboring Ca2+.
The Cc coordination number around CZ (Fig. 4) is 2 within the first coordination shell for rCZ–Cc < 5.4 Å, which indicates that each pair of NGdm atoms (NH1, NH2; and NH2, NE) of Gdm+ interacts with a single CO32−. The arrangement and density of anions up to the second coordination shell is mostly similar in both the systems while the ion density increases significantly for S2LC beyond second coordination shell.
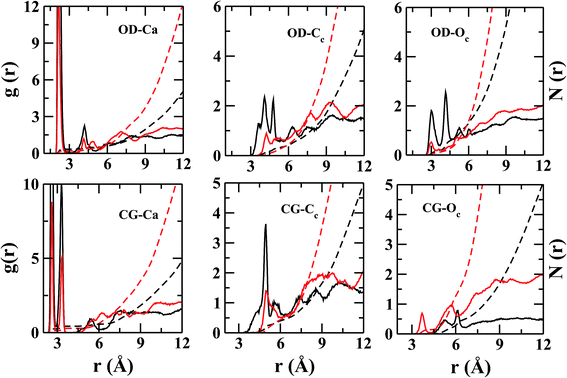
However, the near neighbor environment around the negatively charged functional groups (Fig. 5) of ASP and GLU residues are mostly populated by Ca2+. The RDF between carbonyl-oxygen (OD) of ASP and Ca2+ shows two sharp maxima at 2.2 and 4.2 Å, separated by a zero-intensity plateau of 1 Å width which signifies a crystal-like near neighbor ordered structure up to ∼5 Å from ASP. In addition, the gCG–Ca(r) (Fig. 5) also shows two high-intensity peaks at ∼2.2 and 3.2 Å signifying two preferred geometries of the cations with respect to the COO− group of ASP/GLU, bidentate and monodentate respectively. The radial distributions of Cc and Oc (Fig. 5) around COO− group of ASP/GLU are poorly structured with coordination numbers less than 1 up to the first minima at ∼5.0 Å for both the distributions.
Density map
The calculated atomic density distribution (Fig. 6), i.e. density map, of CO32− around Gdm+ shows two density peaks of Cc atoms within the CZ–Cc distance cutoff of 4.3 Å, the first minimum in gCZ–Cc(r) (Fig. 4). In contrast, Oc density map within the first minimum of gCZ–Oc(r) at 3.5 Å shows four high-density regions along the N–H bond directions.
In general, the non-polar compounds approach the arginine side chain from the directions normal to Gdm+ plane, while the polar compounds, e.g. water, carboxylates/carbonyls, form in-plane h-bonds40,41 with Gdm+. Our results reveal that in the lysozyme–CaCO3 systems, the CO32− ions replace the water molecules from the first coordination shell of arginine to form the TNTO coordination geometry. The second coordination shell is primarily formed by the Ca2+ ions with approximately three near-neighbor (NN) cations for each CO32− (Fig. 6). The observed distribution of NN Ca2+ and CO32− around arginine facilitates the formation of further layers of ions leading to their aggregation around the surface-exposed arginine side chains of lysozyme. In S1,2LC, the coordination number of water oxygen (Ow) around arginine is less than that of in LW. The aggregation of ions around Gdm+ in lysozyme–CaCO3 systems by expelling water molecules indicates that arginine residues act as nucleation sites for the formation of biominerals. The observed water expulsion at the protein-ACC interface is in-line with Freeman et al.18's work that showed that the water population at the ACC-protein interface is much less than that at the calcite-protein interface.
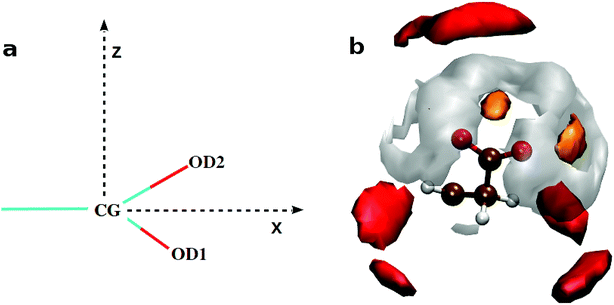
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and along the bisector vector of the angle OD1–CG–OD2. The density distribution along the bisector is similar to the most stable geometry of isolated cluster25 containing acetate (AcO−), Ca2+, and CO32−, where Ca2+ is coplanar to the COO− plane and equidistant from the oxygen atoms. However, the cation population along the lone pairs of the oxygen was not observed in the H2O containing clusters of acetate.25 The ensemble averaged coordination number of Ca2+ around CG is ∼0.9 up to CG–Ca2+ distance of 7.0 Å. Unlike arginine side chain, the first layer of ions around COO− is surrounded by water molecules (Fig. 7).
O bond and along the bisector vector of the angle OD1–CG–OD2. The density distribution along the bisector is similar to the most stable geometry of isolated cluster25 containing acetate (AcO−), Ca2+, and CO32−, where Ca2+ is coplanar to the COO− plane and equidistant from the oxygen atoms. However, the cation population along the lone pairs of the oxygen was not observed in the H2O containing clusters of acetate.25 The ensemble averaged coordination number of Ca2+ around CG is ∼0.9 up to CG–Ca2+ distance of 7.0 Å. Unlike arginine side chain, the first layer of ions around COO− is surrounded by water molecules (Fig. 7).
The binding energies of Ca2+–CO32− and Ca2+–H2O complexes are ∼520.8 kcal mol−1 (ref. 25) and 56.9 kcal mol−1,42 respectively. Among these two attractive interactions, the hydrophilic nature of calcium dominates which results in the separation of the CO32− from its Ca2+ counterpart via a water layer (Fig. 7) in between. These water molecules are ‘tightly bound’ by both types of ions. As the life time of Ca–H2O h-bond is large, the possibility of breaking this h-bond within the simulation time limit is slim. Thus, the removal of water from the nearest hydration layer and aggregation of ions around aspartate/glutamate seems unlikely.
A convoluted picture of the distribution of ions and the ion density with reference to a given side chain residue are presented here by charge density plots (Fig. 8). The average charge density (ρ) around arginine demonstrates sharp oscillations around the neutral axis, ρ = 0, up to ∼7 Å, indicating the formation of four alternating layers of cations and anions. However, the charge density around the COO− bearing groups (aspartate/glutamate) shows only one prominent positive peak with a much weaker next layer of anions before the distribution merges to the neutral axis. Thus, we can conclude that arginine may play the major role in the nucleation and growth of CaCO3 crystal in lysozyme, whereas the other two residues may facilitate the protein to bind to the positively charged surface of the CaCO3 crystal.
Hydrogen bond dynamics
Fig. 9 shows the calculated hydrogen bond time correlation functions, Chb(t), for S1LC and S2LC systems. The time correlation for water–arginine h-bonds (Cwhb(t)) decays much faster than that for CO32−–arginine h-bonds (Cchb(t)) in both the systems. The slow decay of the Cchb(t) implies that the CO32− ions remain h-bonded for an extended period of time, whereas the relatively faster decay of Cwhb(t) signifies frequent breaking and formation of h-bonds with water. The higher concentration of ions in S2LC results in further slowing down of the decay of Cchb(t) suggesting that the ions are held tightly to the protein surface. These tightly bound CO32− ions hinder water molecules to establish strong h-bonds with arginines and thereby promote faster decay of Cwhb(t) in S2LC.Each time correlation function was fitted with a multiexponential function to obtain average time constant or relaxation time (τhb, Table 3). The values of τhb for CO32− are orders of magnitude higher than those for water, which is indicative of higher residence times of CO32− ions in the vicinity of the nucleation sites. The shorter relaxation times of ‘loosely bound’ water molecules may be necessary to facilitate the dehydration of the ACC patches on the protein surface.
| System | Function | τhb (ns) |
|---|---|---|
| S1LC | Cchb(t) | 10.10 |
| Cwhb(t) | 0.69 | |
| S2LC | Cchb(t) | 154.53 |
| Cwhb(t) | 0.12 |
Free energies for the association of ions near arginine side chain
Free energy profiles were calculated to understand the energetics of ion association, growth of ion density, and the expulsion of water at the protein surface. As we have already studied the structure and energetics of ions in the first coordination shell of various side chain residues using radial distribution functions, density maps, and cluster analysis,25 our focus here is on the energetics of higher coordination shells. Since the binding affinity between arginine and CO32− depends on the thickness of the ionic-layer present on the protein surface, it is likely that the role of the ion–ion interactions would dominate over arginine–CO32− interactions in controlling the growth beyond some threshold thickness of ACC.The calculated free energy profile estimates the energy cost to bring an anion or a Ca2+–CO32− ion pair that is located away from the protein surface to the vicinity of arginine side chain. The separation (rCV) between the Cc atom of a distant CO32− and the CZ atom of ARG61 was chosen as a collective variable (CV) to describe arginine–Ca2+–CO32− association. Fig. 10 shows the calculated free energy profile as a function of rCV in the range from 6.0 Å to 20.0 Å.
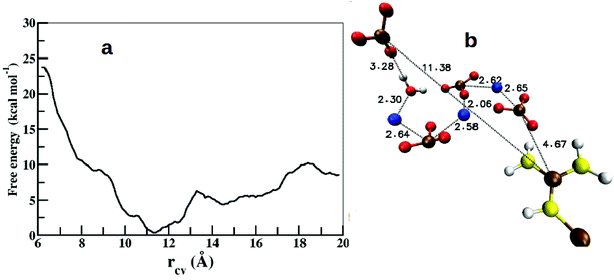 | ||
| Fig. 10 (a) Free energy profile for the association of CO32− around the arginine side chain along the reaction coordinate (rCV). (b) Snapshot from the global minimum of the free energy profile showing the arrangement of ions and water. Color scheme: same as in Fig. 6. | ||
In the initial configuration, the chosen CO32− ion pairs with a neighboring Ca2+ to form an isolated CaCO3 unit surrounded by water. This particular Ca2+ ion was observed to be bound to the selected CO32− throughout the range of rCV. The free energy profile shows a shallow and broad minimum at rCV = 11.4 Å (Fig. 10a). The binding energy (ΔF) between the dissociated state at rCV = 20 Å and the global minimum is ∼8.4 kcal mol−1. This value compares well with the binding energy (∼10 kcal mol−1) between OC-17 (a hen eggshell protein) and calcite surface, where arginine residues serve as the anchors to the crystal surface.18 However, this barrier height (ΔF) is 4 kcal mol−1 higher than that estimated for a single CO32− around a Gdm+ functional group25 and that between an isolated arginine residue and ACC,26 which can be attributed to the inhomogeneous environment of the carbonate ion in the present study. The interactions between an anchoring agent (here, arginine) and the ions (Ca2+ and CO32−) play a crucial role in the initial stages of the ion aggregation, but further growth of ACC is generally governed mainly by the interactions between ions and water molecules. Thus, the barrier height reported here is an approximate estimate on the energetics for the growth of existing ion aggregates irrespective of the anchoring agent.
Further analysis of the metadynamics trajectory shows that the addition of this single CO32− in the arginine environment increases the ion-cluster size by at least three more CaCO3 pairs via near-neighbor electrostatic interactions (Fig. 10b).
Conclusions
In this work, we report protein-mediated formation of amorphous calcium carbonate (ACC) from the free ions using molecular dynamics (MD) simulations of a hen eggshell protein, lysozyme, in ionic solutions of calcium and carbonate. Our investigation provides comprehensive understanding on the role of selected side chain residues of lysozyme that facilitate the ion association to develop a dense amorphous phase of ions driven primarily by the strong electrostatic interactions between the functional group and its respective counter ions (Ca2+ or CO32−). The radial distribution functions (RDFs) among the ions and water in the ionic clusters around lysozyme are in good agreement with that in the hydrated ACC resembling a similar local environment in both the systems. Three key residues, arginine, glutamate, and aspartate, serve as potential nucleation sites for the crystallization of CaCO3. However, the structure and energetics results indicate that the influence of arginine dominates over the rest, which could be a general scenario in all positively charged proteins, e.g. lysozyme, responsible for biomineralization.Two model systems of lysozyme were generated with different ion concentrations, and both show essentially similar results, apart from a denser ACC phase in the solution with higher concentration of ions. The three dimensional density profile of ions around arginine shows that, on the average, each arginine is coordinated by at least two CO32− ions forming four h-bonds with the Gdm–NH2-groups making a twin-nitrogen-twin-oxygen (TNTO) geometry. This strong association with the nearest neighbors initializes the foundation for the successive alternating layers of positive and negative charges replacing the solvent water molecules. Moreover, the charge density plots also confirm this layering of charges suggesting that arginine can play a pivotal role in the nucleation of CaCO3 crystals. To elucidate the growth of ionic layers around a given arginine residue, we performed metadynamics calculations to estimate the required free energy for ion association in the higher coordination shell. The computed free energy profile shows a barrier height of ∼8 kcal mol−1 between the bound and unbound states of a CO32− ion. We also observed that the addition of a single CO32− may fetch few more Ca2+ and CO32− pairs via near-neighbor electrostatic interactions and thus increases the size of the ion cluster around arginine. In contrast, the local environment around glutamate and aspartate retain the strongly bound solvent water through hydrophilic interactions with Ca2+ that inhibit the formation of next layer of CO32− ions.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the University Grants Commission-Basic Scientific Research (UGC-BSR) through Startup Grant. We thank Dr M. Krishnan for helpful discussions.References
- Y. U. Gong, C. E. Killian, I. C. Olson, N. P. Appathurai, A. L. Amasino, M. C. Martin, L. J. Holt, F. H. Wilt and P. Gilbert, Phase transitions in biogenic amorphous calcium carbonate, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6088–6093 CrossRef PubMed.
- J. Aizenberg, G. Lambert, S. Weiner and L. Addadi, Factors involved in the formation of amorphous and crystalline calcium carbonate: a study of an ascidian skeleton, J. Am. Chem. Soc., 2002, 124, 32–39 CrossRef PubMed.
- L. Addadi, S. Raz and S. Weiner, Taking advantage of disorder: amorphous calcium carbonate and its roles in biomineralization, Adv. Mater., 2003, 15, 959–970 CrossRef.
- Y. Politi, T. Arad, E. Klein, S. Weiner and L. Addadi, Sea urchin spine calcite forms via a transient amorphous calcium carbonate phase, Science, 2004, 306, 1161–1164 CrossRef PubMed.
- R. Lakshminarayanan, J. S. Joseph, R. M. Kini and S. Valiyaveettil, Structure-Function Relationship of Avian Eggshell Matrix Proteins: A Comparative Study of Two Major Eggshell Matrix Proteins, Ansocalcin and OC-17, Biomacromolecules, 2005, 6, 741–751 CrossRef PubMed.
- R. Lakshminarayanan, X. J. Loh, S. Gayathri, S. Sindhu, Y. Banerjee, R. M. Kini and S. Valiyaveettil, Formation of transient amorphous calcium carbonate precursor in quail eggshell mineralization: an in vitro study, Biomacromolecules, 2006, 7, 3202–3209 CrossRef PubMed.
- A. Radha, T. Z. Forbes, C. E. Killian, P. Gilbert and A. Navrotsky, Transformation and crystallization energetics of synthetic and biogenic amorphous calcium carbonate, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 16438–16443 CrossRef PubMed.
- J. H. Cartwright, A. G. Checa, J. D. Gale, D. Gebauer and C. I. Sainz-Díaz, Calcium carbonate polyamorphism and its role in biomineralization: how many amorphous calcium carbonates are there?, Angew. Chem., Int. Ed., 2012, 51, 11960–11970 CrossRef PubMed.
- G. Falini, S. Albeck, S. Weiner and L. Addadi, Control of aragonite or calcite polymorphism by mollusk shell macromolecules, Science, 1996, 271, 67–69 CrossRef.
- P. J. Smeets, K. R. Cho, R. G. Kempen, N. A. Sommerdijk and J. J. De Yoreo, Calcium carbonate nucleation driven by ion binding in a biomimetic matrix revealed by in situ electron microscopy, Nat. Mater., 2015, 14, 394–399 CrossRef PubMed.
- P. J. M. Smeets, Towards understanding pathway complexity in calcium carbonate mineralization, PhD thesis, Technische Universiteit Eindhoven, 2016 Search PubMed.
- P. J. Smeets, A. R. Finney, W. J. Habraken, F. Nudelman, H. Friedrich, J. Laven, J. J. De Yoreo, P. M. Rodger and N. A. Sommerdijk, A classical view on nonclassical nucleation, Proc. Natl. Acad. Sci. U. S. A., 2017, 5, E7882E7890 Search PubMed.
- T. Mass, J. L. Drake, E. C. Peters, W. Jiang and P. G. Falkowski, Immunolocalization of skeletal matrix proteins in tissue and mineral of the coral Stylophora pistillata, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 12728–12733 CrossRef PubMed.
- M. Reggi, S. Fermani, V. Landi, F. Sparla, E. Caroselli, F. Gizzi, Z. Dubinsky, O. Levy, J.-P. Cuif, Y. Dauphin, S. Goffredo and G. Falini, Biomineralization in Mediterranean corals: the role of the intraskeletal organic matrix, Cryst. Growth Des., 2014, 14, 4310–4320 CrossRef.
- G. Falini, S. Fermani and S. Goffredo, Coral biomineralization: a focus on intra-skeletal organic matrix and calcification, Semin. Cell Dev. Biol., 2015, 17–26 CrossRef PubMed.
- T. Mass, A. J. Giuffre, C.-Y. Sun, C. A. Stifler, M. J. Frazier, M. Neder, N. Tamura, C. V. Stan, M. A. Marcus and P. U. Gilbert, Amorphous calcium carbonate particles form coral skeletons, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, E7670–E7678 CrossRef PubMed.
- C. L. Freeman, J. H. Harding, D. Quigley and P. M. Rodger, How does an amorphous surface influence molecular binding?–ovocleidin-17 and amorphous calcium carbonate, Phys. Chem. Chem. Phys., 2015, 17, 17494–17500 RSC.
- C. L. Freeman, J. H. Harding, D. Quigley and P. M. Rodger, Structural control of crystal nuclei by an eggshell protein, Angew. Chem., Int. Ed., 2010, 49, 5135–5137 CrossRef.
- A. Dey, P. H. Bomans, F. A. Müller, J. Will, P. M. Frederik, G. de With and N. A. Sommerdijk, The role of prenucleation clusters in surface-induced calcium phosphate crystallization, Nat. Mater., 2010, 9, 1010 CrossRef.
- D. Gebauer and H. Cölfen, Prenucleation clusters and non-classical nucleation, Nano Today, 2011, 6, 564–584 CrossRef.
- S. Raz, P. C. Hamilton, F. H. Wilt, S. Weiner and L. Addadi, The transient phase of amorphous calcium carbonate in sea urchin larval spicules: the involvement of proteins and magnesium ions in its formation and stabilization, Adv. Funct. Mater., 2003, 13, 480–486 CrossRef.
- F. Tewes, O. L. Gobbo, C. Ehrhardt and A. M. Healy, Amorphous calcium carbonate based microparticles for peptide pulmonary delivery, ACS Appl. Mater. Interfaces, 2016, 8, 1164–1175 CrossRef.
- L. N. Hassani, F. Hindré, T. Beuvier, B. Calvignac, N. Lautram, A. Gibaud and F. Boury, Lysozyme encapsulation into nanostructured CaCO3 microparticles using a supercritical CO2 process and comparison with the normal route, J. Mater. Chem. B, 2013, 1, 4011–4019 RSC.
- A. Sergeeva, R. Sergeev, E. Lengert, A. Zakharevich, B. Parakhonskiy, D. Gorin, S. Sergeev and D. Volodkin, Composite magnetite and protein containing CaCO3 crystals. External manipulation and vaterite calcite recrystallization-mediated release performance, ACS Appl. Mater. Interfaces, 2015, 7, 21315–21325 CrossRef.
- M. Saharay and R. J. Kirkpatrick, Ab initio and metadynamics studies on the role of essential functional groups in biomineralization of calcium carbonate and environmental situations, Phys. Chem. Chem. Phys., 2014, 16, 26843–26854 RSC.
- R. Innocenti Malini, A. Finney, S. Hall, C. Freeman and J. Harding, The Water– Amorphous Calcium Carbonate Interface and Its Interactions with Amino Acids, Cryst. Growth Des., 2017, 17, 5811–5822 CrossRef.
- S. Jo, T. Kim, V. G. Iyer and W. Im, CHARMM-GUI: a web-based graphical user interface for CHARMM, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef.
- B. Brooks, et al., CHARMM: the biomolecular simulation program, J. Comput. Chem., 2009, 30, 1545–1614 CrossRef.
- J. Lee, et al., CHARMM-GUI input generator for NAMD, GROMACS, AMBER, OpenMM, and CHARMM/OpenMM simulations using the CHARMM36 additive force field, J. Chem. Theory Comput., 2015, 12, 405–413 CrossRef.
- R. B. Best, X. Zhu, J. Shim, P. E. Lopes, J. Mittal, M. Feig and A. D. MacKerell Jr, Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone φ, ψ and side-chain χ1 and χ2 dihedral angles, J. Chem. Theory Comput., 2012, 8, 3257–3273 CrossRef.
- M. Saharay, A. O. Yazaydin and R. J. Kirkpatrick, Dehydration-induced amorphous phases of calcium carbonate, J. Phys. Chem. B, 2013, 117, 3328–3336 CrossRef.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kale and K. Schulten, Scalable molecular dynamics with NAMD, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef.
- F. H. Stillinger, Theory and molecular models for water. Advances in Chemical Physics: Non-Simple Liquids, 1975, pp. 1–101 Search PubMed.
- A. Chandra, Effects of ion atmosphere on hydrogen-bond dynamics in aqueous electrolyte solutions, Phys. Rev. Lett., 2000, 85, 768 CrossRef.
- S. Balasubramanian, S. Pal and B. Bagchi, Hydrogen-bond dynamics near a micellar surface: origin of the universal slow relaxation at complex aqueous interfaces, Phys. Rev. Lett., 2002, 89, 115505 CrossRef.
- P. Raiteri, A. Laio, F. L. Gervasio, C. Micheletti and M. Parrinello, Efficient reconstruction of complex free energy landscapes by multiple walkers metadynamics, J. Phys. Chem. B, 2006, 110, 3533–3539 CrossRef.
- A. Barducci, G. Bussi and M. Parrinello, Well-tempered metadynamics: a smoothly converging and tunable free-energy method, Phys. Rev. Lett., 2008, 100, 020603 CrossRef.
- A. Barducci, M. Bonomi and M. Parrinello, Metadynamics, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843 CAS.
- W. Humphrey, A. Dalke and K. Schulten, VMD – Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS.
- C. T. Armstrong, P. E. Mason, J. R. Anderson and C. E. Dempsey, Arginine side chain interactions and the role of arginine as a gating charge carrier in voltage sensitive ion channels, Sci. Rep., 2016, 6, 21759 CrossRef CAS.
- T. Oroguchi and M. Nakasako, Influences of lone-pair electrons on directionality of hydrogen bonds formed by hydrophilic amino acid side chains in molecular dynamics simulation, Sci. Rep., 2017, 7, 15859 CrossRef.
- M. Pavlov, P. E. Siegbahn and M. Sandström, Hydration of beryllium, magnesium, calcium, and zinc ions using density functional theory, J. Phys. Chem. A, 1998, 102, 219–228 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |