Open Access Article
Open Access ArticleFirst-principles study of the electric, magnetic, and orbital structure in perovskite ScMnO3†
Guang Song *ab,
Yuting Chena,
Guannan Liac and
Benling Gaoa
*ab,
Yuting Chena,
Guannan Liac and
Benling Gaoa
aDepartment of Physics, Huaiyin Institute of Technology, Huaian 223003, China
bJiangsu Provincial Key Laboratory of Palygorskite Science and Applied Technology, Huaiyin Institute of Technology, Huaian 223003, China
cNational Laboratory of Solid State Microstructures and Department of Physics, Nanjing University, Nanjing 210093, China. E-mail: gsong@hyit.edu.cn
First published on 15th January 2019
Abstract
Perovskite ScMnO3 has been synthesized under high temperature and high pressure. The magnetic ordering of this compound was proposed to be in the E-AFM state in previous theoretical research. Such magnetic ordering would lead the Mn3+ ions to be off-centered in the MnO6 octahedra; however, this is not detected experimentally. To address this issue, we systematically investigate the magnetic, orbital, and electric structures of perovskite ScMnO3 with first-principles calculations. It is found that its magnetic ground state is G-AFM and the magnetic ordering can explain the puzzle very well. Moreover, there is an unreported three-dimensional alternating cooperative orbital ordering in perovskite ScMnO3. The antiferromagnetic coupling between the nearest-neighbor Mn3+ ions is stabilized by the strong octahedral distortions that decrease the ferromagnetic interaction between the eg orbitals of the Mn3+ ions. In addition, we find that perovskite ScMnO3 is a bipolar antiferromagnetic semiconductor in which completely spin-polarized currents with reversible spin polarization can be tuned simply by applying a gate voltage. Such controllability of the spin polarization of the current opens up new avenues for future spintronic devices. Our results not only suggest that the G-AFM phase is the ground magnetic state for perovskite ScMnO3, but also enrich research in orbital ordering in rare-earth manganites.
1. Introduction
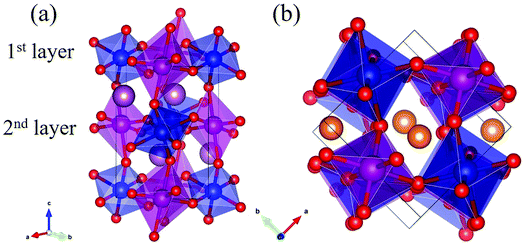
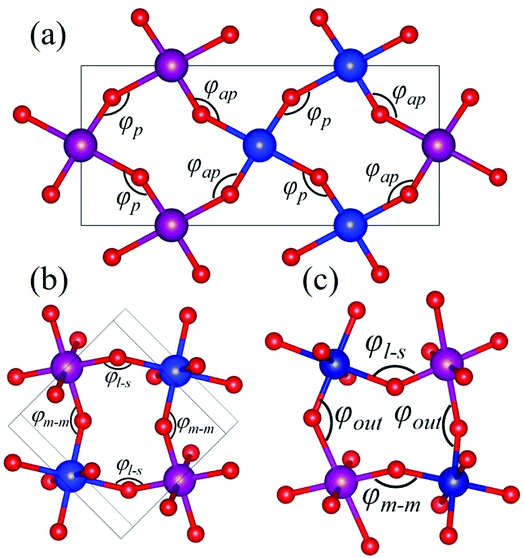
Rare-earth manganites exhibit a variety of fascinating physical phenomena, such as their unusual magnetoresistance properties, peculiar charge, spin, and orbital orderings, and spin-driven ferroelectricity.1–6 Owing to the different ionic radii of R3+ (R: rare-earth), RMnO3 can naturally form two different types of structures: one is a perovskite orthorhombic (R = La–Dy) structure7–9 and the other is a hexagonal (R = Ho–Lu, Y, Sc) structure.10–13 In particular, the hexagonal structure RMnO3 can be stabilized into the perovskite orthorhombic phase for small R3+ (R = Ho–Lu, Y) ion sizes under high temperature and high pressure.14 Additionally, as the rR (the radius of rare-earth ion R3+) changes from La to Lu, a complex magnetic phase diagram has been established for orthorhombic RMnO3 (R = La–Lu, Y) materials with the perovskite crystal structure (space group: Pnma, no. 62).15,16 The collinear A-type antiferromagnetic ordering is favored when the R3+ ions are light rare-earth cations (R = La, Pr, Nd),17–20 whereas manganites exhibit a sinusoidal magnetic structure when the R3+ ions are Tb or Dy.8,21–24 Starting at Ho, the metastable orthorhombic RMnO3 systems are proposed to be E-AFM insulators.8,14,25Recently, perovskite ScMnO3 (PSMO) has been synthesized under high temperature and high pressure.26,27 Since the Sc3+ ion has the smallest radius among rare-earth elements, PSMO has a highly distorted structure and crystallizes into the monoclinic P21/n (space group, no. 14) phase. In this phase, there are two kinds of Mn atoms denoted as Mn1 and Mn2 (see Fig. 1). Additionally, there is a small deviation in β (experimental value: 93.566°, see ref. 26) compared with other orthorhombic rare-earth manganites. Such highly distorted structures can be well understood from the Goldschmidt tolerance factor 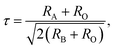 where RA, RB, and RO are the radii of ions on the A, B, and X sites, respectively.28 In PSMO, the calculated τ is 0.83 (LaMnO3: 0.902; LuMnO3: 0.840),29 indicating that PSMO has a larger lattice distortion than LuMnO3. In PSMO, the rotations and tilts of the MnO6 octahedra are the same as those of other rare-earth manganites, which can be expressed as a+b+c− in Glazer notation. However, the Mn–O–Mn bond angle in PSMO is quite different from those of other orthorhombic rare-earth manganites (see Fig. 2). Although the crystal structure of PSMO has been definitely confirmed in previous experimental studies,26,27 its ground magnetic state is still uncertain. Recently, in order to understand the effect of magnetic ordering on the distortion, a theoretical study based on density functional theory (DFT) has shown that the E-AFM phase has a lower energy than that of A-AFM.27 Moreover, it is also predicted that there are displacements of the Mn sites of ∼0.07 Å in the E-AFM phase. However, such displacements are not detected by experimental study even at low temperature,27 indicating that the E-AFM phase cannot explain the experimental observation. Therefore, the magnetic ground ordering of PSMO still calls for more accurate theoretical models to account for the controversy in such a highly perovskite compound.
where RA, RB, and RO are the radii of ions on the A, B, and X sites, respectively.28 In PSMO, the calculated τ is 0.83 (LaMnO3: 0.902; LuMnO3: 0.840),29 indicating that PSMO has a larger lattice distortion than LuMnO3. In PSMO, the rotations and tilts of the MnO6 octahedra are the same as those of other rare-earth manganites, which can be expressed as a+b+c− in Glazer notation. However, the Mn–O–Mn bond angle in PSMO is quite different from those of other orthorhombic rare-earth manganites (see Fig. 2). Although the crystal structure of PSMO has been definitely confirmed in previous experimental studies,26,27 its ground magnetic state is still uncertain. Recently, in order to understand the effect of magnetic ordering on the distortion, a theoretical study based on density functional theory (DFT) has shown that the E-AFM phase has a lower energy than that of A-AFM.27 Moreover, it is also predicted that there are displacements of the Mn sites of ∼0.07 Å in the E-AFM phase. However, such displacements are not detected by experimental study even at low temperature,27 indicating that the E-AFM phase cannot explain the experimental observation. Therefore, the magnetic ground ordering of PSMO still calls for more accurate theoretical models to account for the controversy in such a highly perovskite compound.
The focus of the present work is to clarify the magnetic ground state of monoclinic P21/n ScMnO3, in more general terms, to investigate its electric and orbital properties in depth. With first-principles calculations, we consider different magnetic alignments for the highly distorted manganite (FM, C-AFM, A-AFM, G-AFM and E-AFM, see ESI Fig. S1†) ScMnO3. It is found that the G-AFM state is the magnetic ground state for PSMO and that such a state can give correct structural information in describing the displacements of Mn3+ ions. Moreover, we reveal a new type of orbital ordering which can be expressed as a 3z2 − r2/3y2 − r2-alternating manner in the 1st layer and 3x2 − r2/3z2 − r2-alternating behavior in the 2nd layer, and along the c axis it forms 3y2 − r2/3z2 − r2-alternating and 3z2 − r2/3x2 − r2-alternating orbital orderings in a chain-like manner in the two adjacent chains. In such a three-dimensional staggered orbital ordering system, the competition between the antiferromagnetic and ferromagnetic interactions plays a relevant role in the stabilization of AFM interactions between nearest-neighbor Mn3+ ions. In addition, PSMO is identified as a bipolar antiferromagnetic semiconductor, in which completely spin-polarized currents with reversible spin polarization can be created and controlled simply by applying a gate voltage. Such controllability of the spin polarization of the current gives PSMO great potential applications in future spintronic devices. This study not only finds that the magnetic ground state of ScMnO3 is a G-AFM state, but also enlarges the field of orbital ordering in rare-earth manganites.
2. Computational methods
First-principles calculations are carried out using DFT with projector augmented wave (PAW) potentials,30 as implemented in the Vienna ab initio simulation package (VASP).31,32 The PAW potentials explicitly include three valence electrons for Sc (3d14s2), 13 for Mn (2p63d54s2), and 6 for O (2s22p4) atoms. The exchange correlation functions are represented within the generalized gradient approximation (GGA) by the PBE and PBEsol parameterizations.33,34 Meanwhile, the local density approximation exchange correlation function (LDA) represented by the Cz-Pz parameterization is also used in optimizing the structure of ScMnO3.35 Additionally, the GGA + U method is also employed to investigate the influence of +U correction. The rotationally invariant approach introduced by Dudarev et al. is used to treat the Coulomb repulsion parameter U.36 To investigate the effect of the U value on the calculated results, we use U values changing over the range 1–5 eV with a fixed exchange parameter J = 1 eV for the 3d orbital of Mn ions. The wave function is expanded in a plane wave basis with an energy cutoff of 600 eV. 6 × 6 × 4 Γ-centered k-point sampling is used for reciprocal space integrations in calculating the FM, C-AFM, A-AFM, and G-AFM magnetic states (a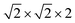 supercell is used in the calculations), and 6 × 3 × 4 Γ-centered k-point sampling is used for the E-AFM magnetic state (a
supercell is used in the calculations), and 6 × 3 × 4 Γ-centered k-point sampling is used for the E-AFM magnetic state (a 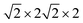 supercell is used in the calculations). We have carefully checked convergence with these settings by testing higher energy cutoffs and larger k-point meshes. Each self-consistent electronic calculation is converged to 10−6 eV and the tolerance force is converged to less than 1 meV Å−1.
supercell is used in the calculations). We have carefully checked convergence with these settings by testing higher energy cutoffs and larger k-point meshes. Each self-consistent electronic calculation is converged to 10−6 eV and the tolerance force is converged to less than 1 meV Å−1.
3. Results and discussion
The optimized lattice parameters of PSMO with different magnetic orderings are summarized in Table 1 together with the experimental data (293 K).26 The agreement between the calculated and experimental crystal parameters is perfect, and the relative errors are all within 3% when the PBE and PBEsol functions are used in the calculations, while the relative error exceeds 8% when the Cz-Pz function is used. The total energies for various possible magnetic orderings are calculated with PBE, PBEsol, and Cz-Pz parameterizations, and the calculated results are summarized in Table 1. It is found that the magnetic ordering of the ground state is G-AFM phase within the GGA method (including PBE and PBEsol functions), while the ground magnetic ordering is FM within the LDA method. It should be noted that the magnetic state of PSMO is proposed to be antiferromagnetic ordering experimentally.26 Thus the LDA method not only overly underestimates the lattice parameters, but also gives a dissimilar magnetic ordering compared with experimental data. Therefore, we do not use the LDA method in the next study and continue to use the GGA method to investigate the structure, electric, and orbital properties of ScMnO3.| Exp. | Method | G-AFM | E-AFM | C-AFM | A-AFM | FM | |
|---|---|---|---|---|---|---|---|
| a (Å) | 5.053 | PBEsol | 4.965 | 4.967 | 4.955 | 4.991 | 4.985 |
| PBE | 5.056 | 5.059 | 5.045 | 5.080 | 5.073 | ||
| Cz-Pz | 4.793 | 4.800 | 4.806 | 4.801 | 4.802 | ||
| b (Å) | 5.355 | PBEsol | 5.335 | 5.353 | 5.329 | 5.363 | 5.360 |
| PBE | 5.357 | 5.366 | 5.356 | 5.374 | 5.378 | ||
| Cz-Pz | 5.335 | 5.330 | 5.319 | 5.312 | 5.306 | ||
| c (Å) | 7.757 | PBEsol | 7.626 | 7.554 | 7.624 | 7.558 | 7.546 |
| PBE | 7.894 | 7.864 | 7.884 | 7.865 | 7.847 | ||
| Cz-Pz | 7.089 | 7.052 | 7.070 | 7.040 | 7.037 | ||
| β (°) | 93.566 | PBEsol | 94.325 | 93.648 | 93.765 | 93.672 | 92.743 |
| PBE | 94.702 | 94.785 | 94.993 | 94.780 | 94.468 | ||
| Cz-Pz | 90.088 | 90.082 | 90.085 | 90.088 | 90.075 | ||
| ΔE (meV) | — | PBEsol | −63.2 | −53.7 | −55.0 | −15.0 | 0.0 |
| PBE | −52.8 | −40.8 | −41.4 | −17.5 | 0.0 | ||
| Cz-Pz | 39.8 | 49.2 | 61.3 | 28.1 | 0.0 | ||
| HSE06 | −63.1 | 12.3 | −49.4 | −30.1 | 0.0 |
Then we discuss whether the proposed G-AFM state can explain the structural distortions observed experimentally. To obtain the distortion of the MnO6 octahedra in PSMO, we calculate the bond lengths of Mn–O of different magnetic orderings, and the results are listed in Table 2. Herein, it should be emphasized that the two calculated bond lengths are equal along the local axis of the MnO6 octahedra for the G-AFM, FM, C-AFM, and A-AFM phases; thus, the Mn3+ ions are in the center of the MnO6 octahedra. It is, therefore, indicated that there is no displacement of Mn3+ ions in PSMO with these magnetic orderings. Conversely, for the E-AFM phase, we can see that the bond lengths are different along the local axis of the MnO6 octahedra; thus, the Mn3+ ions are not in the center of the MnO6 octahedra any more. From the difference in bond lengths, one can calculate the displacements of Mn3+ ions. The calculated magnitudes of displacements away from the center are about 0.06 and 0.13 Å for the PBEsol and PBE functions, respectively. In a previous DFT study, the calculated displacements of Mn3+ ions are about 0.07 Å for the E-AFM phase. However, these displacements are not detected experimentally.27 Therefore, it is suggested that the ground magnetic ordering of PSMO is not E-AFM. Based on the calculated total energies of PSMO with different magnetic orderings, one can conclude that the magnetic ground state is G-AFM. It should also be emphasized that the G-AFM state is a new magnetic ordering in the family of rare-earth manganites.15
| Bond | Exp. | Method | G-AFM | E-AFM | C-AFM | A-AFM | FM |
|---|---|---|---|---|---|---|---|
| Mn1–O2 | 1.920 | PBEsol | 1.888 | 1.907, 1.887 | 1.909 | 1.897 | 1.932 |
| PBE | 1.902 | 1.915, 1.895 | 1.913 | 1.903 | 1.917 | ||
| Mn1–O3 | 1.967 | PBEsol | 1.942 | 1.936, 1.922 | 1.951 | 1.934 | 1.938 |
| PBE | 1.965 | 1.970, 1.958 | 1.968 | 1.969 | 1.969 | ||
| Mn1–O1 | 2.138 | PBEsol | 2.115 | 2.108, 2.071 | 2.093 | 2.102 | 2.075 |
| PBE | 2.202 | 2.208, 2.170 | 2.185 | 2.200 | 2.189 | ||
| Mn2–O1 | 1.902 | PBEsol | 1.871 | 1.891, 1.875 | 1.871 | 1.892 | 1.896 |
| PBE | 1.891 | 1.903, 1.891 | 1.889 | 1.906 | 1.905 | ||
| Mn2–O3 | 1.930 | PBEsol | 1.917 | 1.960, 1.921 | 1.914 | 1.947 | 1.953 |
| PBE | 1.925 | 1.948, 1.922 | 1.925 | 1.934 | 1.944 | ||
| Mn2–O2 | 2.320 | PBEsol | 2.283 | 2.250, 2.205 | 2.240 | 2.229 | 2.166 |
| PBE | 2.442 | 2.468, 2.371 | 2.413 | 2.422 | 2.385 |
Another interesting result is the distortions of MnO6 octahedra, which have a significant effect on the electric structures of transition metal ions. The distortion can be described by two normal modes, Q2 and Q3, which are represented by 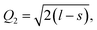 and
and 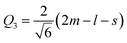 1,37, where l = long bond length, m = medium bond length, and s = short bond length. Because of the two unique Mn3+ ions in PSMO, there are two Q2 and two Q3 modes in PSMO. The calculated results are summarized in Table 3. One can see that the calculated values of the distortion mode of ScMnO3 with the G-AFM phase within the PBEsol function is quite close to the experimental data.27 Additionally, the modes of Mn1 and Mn2 are not equal. It is indicated that the local environments of the nearest-neighbor (NN) Mn ions are distinct from each other. This difference may induce a charge transfer between NN Mn ions. The electron numbers of d-orbital electrons of Mn ions have been calculated with the PBEsol function and they are 4.95 and 4.98e for Mn1 and Mn2, respectively. Obviously, a weak charge ordering of NN Mn ions exists in PSMO. Herein, the fascinating thing is that the origin of this charge order is quite different from the Mn4+/Mn3+ charge order in La0.7Ca0.3MnO3,38 in which the charge order is induced by doping the alkaline-earth metal, while in PSMO the charge transfer is just related to the distortion of the MnO6 octahedra.
1,37, where l = long bond length, m = medium bond length, and s = short bond length. Because of the two unique Mn3+ ions in PSMO, there are two Q2 and two Q3 modes in PSMO. The calculated results are summarized in Table 3. One can see that the calculated values of the distortion mode of ScMnO3 with the G-AFM phase within the PBEsol function is quite close to the experimental data.27 Additionally, the modes of Mn1 and Mn2 are not equal. It is indicated that the local environments of the nearest-neighbor (NN) Mn ions are distinct from each other. This difference may induce a charge transfer between NN Mn ions. The electron numbers of d-orbital electrons of Mn ions have been calculated with the PBEsol function and they are 4.95 and 4.98e for Mn1 and Mn2, respectively. Obviously, a weak charge ordering of NN Mn ions exists in PSMO. Herein, the fascinating thing is that the origin of this charge order is quite different from the Mn4+/Mn3+ charge order in La0.7Ca0.3MnO3,38 in which the charge order is induced by doping the alkaline-earth metal, while in PSMO the charge transfer is just related to the distortion of the MnO6 octahedra.
| Exp. | Method | G-AFM | E-AFM | C-AFM | A-AFM | FM | |
|---|---|---|---|---|---|---|---|
| Mn1–Q2 | 0.308 | PBEsol | 0.321 | 0.272 | 0.260 | 0.290 | 0.202 |
| 0.322 | PBE | 0.424 | 0.401 | 0.384 | 0.420 | 0.385 | |
| Mn2–Q2 | 0.591 | PBEsol | 0.591 | 0.488 | 0.521 | 0.477 | 0.382 |
| 0.571 | PBE | 0.779 | 0.738 | 0.741 | 0.729 | 0.679 | |
| Mn1–Q3 | −0.101 | PBEsol | −0.097 | −0.105 | −0.082 | −0.107 | −0.107 |
| −0.098 | PBE | −0.142 | −0.136 | −0.132 | −0.135 | −0.137 | |
| Mn2–Q3 | −0.296 | PBEsol | −0.394 | −0.366 | −0.231 | −0.185 | −0.127 |
| −0.270 | PBE | −0.261 | −0.187 | −0.369 | −0.376 | −0.329 |
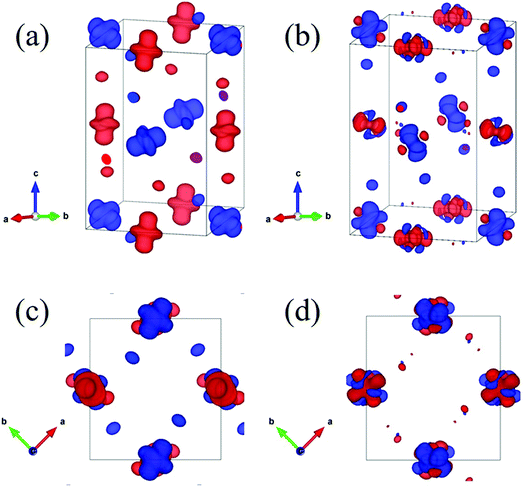
Now let us discuss how the distortion of the MnO6 octahedra affects the electronic structure of PSMO. From the Mn–O bond lengths listed in Table 2, one can clearly see that the Mn–O bond in the MnO6 octahedron is elongated in one direction, while being compressed in another direction. It is well known that such a distortion will make the double degenerate eg orbital in an ideal cubic perovskite split into two nondegenerate energy levels: one is the 3z2 − r2 orbital and the other is the x2 − y2 orbital. The famous example is the distortion of MnO6 octahedra in LaMnO3, in which the MnO6 octahedra are alternately elongated in the xy plane. Therefore, a 3x2 − r2/3y2 − r2 orbital ordering has been reported in LaMnO3.18 We wondered whether such an ordering will appear in PSMO. After systematically analyzing the Mn–O listed in Table 2, we find that in layer 1 the MnO6 octahedron at the Mn1 site is elongated along the z axis, while the MnO6 octahedron at the Mn2 site is elongated along the y axis. Thus, the orbital ordering for such a distortion can be expressed as 3z2 − r2/3y2 − r2 in layer 1. In layer 2, the MnO6 octahedra at the Mn2 sites are elongated along the x axis, while the MnO6 octahedra at the Mn1 sites are elongated along the y axis. Thus, in such a frame, the orbital ordering can be expressed as 3x2 − r2/3z2 − r2 in layer 2. Additionally, along the z axis they form 3z2 − r2/3x2 − r2-alternating and 3y2 − r2/3z2 − r2-alternating orbital orderings in a chain-like manner in the two adjacent chains. In order to characterize the orbital orderings more clearly, the spin charge density of the eg orbital is calculated within the PBEsol method. Fig. 3a and c show the eg spin charge density integrated from −1.5 eV to the Fermi level; Fig. 3b and d plot the eg spin charge density integrated from the Fermi level to 1.5 eV. It can clearly be seen that the spin charge density of the Mn1 site has a predominantly 3z2 − r2 orbital character, while at the Mn2 site the charge density has predominantly 3y2 − r2 and 3x2 − r2 orbital characters for layer 1 and layer 2, respectively. Therefore, such an alternating arrangement of orbital ordering in PSMO is three-dimensional and it is quite different from the in-plane two-dimensional orbital ordering (3x2 − r2/3y2 − r2 orbital ordering) in other RMnO3 (R = La–Lu, Y).9,14,16–18,23 It should also be emphasized that this three-dimensional orbital ordering is different from other three-dimensional orbital ordering, such as in strained LaMnO3 (where the behavior of the orbital ordering is expressed as 3z2 − r2/x2 − y2)18,39 and in bulk YVO3 (the VO6 octahedra are alternately elongated along the x and y axes in the xy plane in the first layer and along the y and x axes in the xy plane in the second layer; the behavior of the orbital ordering is expressed as xz/yz in the first layer and yz/xz in the second layer) (see Fig. S2†).40 Therefore, we reveal that PSMO possesses an unreported three-dimensional competitive orbital ordering. This result enriches research on orbital ordering in the family of rare-earth manganites.
Having systematically discussed the orbital ordering, now let us study how the three-dimensional cooperative orbital ordering affects the magnetic coupling between the NN Mn3+ ions. In PSMO, the spin–spin coupling consists of antiferromagnetic interactions (JA, from the t2g–O–t2g and t2g–O–eg orbitals) and ferromagnetic e–O–e interactions (JF, from the eg orbital), respectively. According to the Goodenough–Kanamori rules,41,42 the magnetic interactions between NN Mn3+ ions in monoclinic ScMnO3 should be FM, as shown in the ab plane of LaMnO3 in which the absolute value of JF (JF < 0) is stronger than that of JA (JA > 0).17 However, our calculated results predict an AFM interaction between NN Mn–Mn ions. This seems to be in contradiction with the Goodenough–Kanamori rule. This discrepancy is because the <Mn–O–Mn bond angle φ is much smaller than 180° in perovskite monoclinic ScMnO3. As shown by a previous model and DFT studies, the bond angle φ plays an important role in determining the magnetic interaction, through altering the relative magnitude of JA and JF interactions.15,16,43,44 It is well known that the hopping integral between Mn–eg states depends both on the bond angle φ and on the bond length. The tdp (the overlap integral between Mn-d and O-p states) is roughly described by 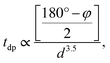 where d is the Mn–O bond length.16,45 According to the picture outlined by Zhou and Goodenough, the JF interactions decrease with φ while the JA interactions are nearly constant.16 The continuous reduction of JF in J = JF + JA as φ decreases could induce J to change from negative to positive. Based on the Heisenberg Hamiltonian, Yamauchi et al. calculate the magnetic interactions in orthorhombic RMnO3 (R = La–Lu, Y). They find that as R changes from La to Lu, the J monotonously increases from −12.9 to 0.2 meV.43 According to previous theoretical and experimental reports, the magnetic couplings between the NN Mn atoms are antiferromagnetic when the bond angles are less than 143.00°.15
where d is the Mn–O bond length.16,45 According to the picture outlined by Zhou and Goodenough, the JF interactions decrease with φ while the JA interactions are nearly constant.16 The continuous reduction of JF in J = JF + JA as φ decreases could induce J to change from negative to positive. Based on the Heisenberg Hamiltonian, Yamauchi et al. calculate the magnetic interactions in orthorhombic RMnO3 (R = La–Lu, Y). They find that as R changes from La to Lu, the J monotonously increases from −12.9 to 0.2 meV.43 According to previous theoretical and experimental reports, the magnetic couplings between the NN Mn atoms are antiferromagnetic when the bond angles are less than 143.00°.15
Herein, as a reference, we calculate the bond angles of perovskite HoMnO3 and LuMnO3 within the PBEsol method, because in these compounds, the in-plane magnetic couplings are both ferromagnetic and antiferromagnetic (see Fig. 2a). In HoMnO3, the calculated bond angles are 142.09° and 145.89° for φap and φp, respectively. In E-AFM LuMnO3, the calculated bond angles are 140.84° and 144.60° for φap and φp, respectively. Due to the three-dimensional orbital ordering, the bond angles considered in PSMO not only include the in-plane angles (φm–m and φl–s, see Fig. 2b), but also include the out-of-plane angles (φout, see Fig. 2c). In order to study the effect of the orbital ordering on the magnetic properties of this system, we calculated bond angles in PSMO. Within the PBEsol method, the calculated in-plane bond angles are 132.10° and 141.58° for φm–m and φl–s, respectively. Obviously, the in-plane bond angles are both less than 143°; thus the in-plane magnetic interactions between the NN Mn3+ ions are antiferromagnetic along both the x and y axes. Additionally, the calculated out-of-plane bond angle is 132.10° (still less than 143°). Therefore, the magnetic interaction along the z axis is also antiferromagnetic. To understand the microscopic origins of the G-AFM ground state PSMO, the exchange interactions are extracted from the calculated total energy of all considered magnetic orderings. Based on the Heisenberg Hamiltonian with a normalized spin moment used in a previous report,43 we can estimate the superexchange interaction energies Ji (i = x, y, z). The calculated results are 6.0, 2.8, and 3.3 meV for Jx, Jy, and Jz, respectively. The positive values indicate that the magnetic interactions are all antiferromagnetic.
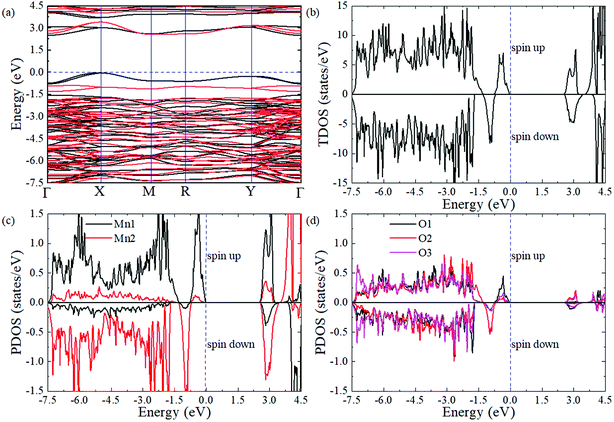
To obtain a comprehensive understanding of PSMO, we study its electric properties with a hybrid Heyd–Scuseria–Ernzerhof function (HSE06, the standard exact-exchange mixing parameter α of 0.25 is used).46 As shown in Fig. 4a, the valence band maximum (VBM) locates at the X point while the conduction band minimum (CBM) locates at the Γ point, suggesting that the PSMO is an indirect band gap semiconductor with a band gap of 2.50 eV (the spin-down band gap is 2.57 eV and the spin-up band gap is 2.50 eV). Interestingly, it is can be seen from the band structure (Fig. 4a) and the total density of states (DOS, Fig. 4b) that the spin-down bands and spin-up bands are not symmetrically occupied. Based on the above discussion, we can conclude that PSMO is a bipolar antiferromagnetic semiconductor,47 which can provide completely spin-polarized currents with tunable spin polarization simply by applying a gate voltage. In PSMO, when the Fermi energy is tuned in the range −0.78–0 eV, the conducting channel is opened for spin-up electrons; when the Fermi energy is tuned in the range −1.30 ∼ −0.78 eV, the conducting channel is opened for spin-down electrons. Such controllability of the spin polarization of current opens up new avenues for future spintronic devices. We also plot the partial density of states projected onto the Mn-d and O-p orbitals to investigate the component in the conduction and valence band edges, as shown in Fig. 4c and d. The valence and conduction band edges are mainly contributed by the Mn-d orbital. It can be seen that the split energies (the energy difference between the 3z2 − r2 and x2 − y2 orbitals) induced by the octahedral distortions are 2.50 and 3.28 eV for the Mn1 and Mn2 ions, respectively. Below the Fermi level the [−2.1 eV, 0 eV] energy window is mainly occupied by the 3z2 − r2 orbital of Mn ions, whereas above the Fermi level the [2.50 eV, 3.45 eV] energy window is mainly composed by the x2 − y2 orbital of Mn ions. Moreover, in the [−7.50 eV, 3.16 eV] energy window, the d orbital of Mn ions is strongly hybridized with the p orbital of O ions.
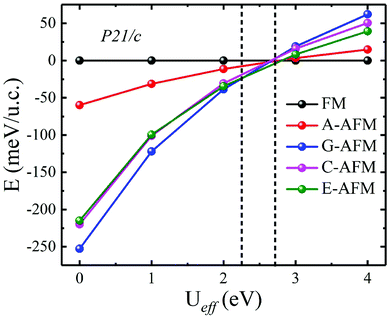
In the above calculations, we do not consider the electronic correlation of the d-electron of Mn3+ ions. It is generally accepted that the correlation has a notable effect on the magnetic ground state in rare-earth manganites.43,44,48–51 For instance, previous reports have pointed out that the small U (∼2.5 eV) is found to stabilize A-AFM with respect to E-AFM in distorted manganites such as HoMnO3 and LuMnO3 at variance with experiments, which show E-AFM as the ground state. Moreover, previous studies also showed that as the U parameter increases, the magnetic ordering will be FM. Additionally, with the constrained random-phase-approximation method, Solovyev obtained Ueff = U − J = 1.30 eV (U = 2.15 eV and J = 0.85 eV), Ueff = U − J = 1.38 eV (U = 2.24 eV and J = 0.86 eV), and Ueff = U − J = 1.31 eV (U = 2.16 eV and J = 0.85 eV) for the d orbitals of Mn3+ ions of orthorhombic LaMnO3, TbMnO3, and HoMnO3, respectively.52 This indicated that the magnetic ordering of ground state distorted manganites is rather strongly affected by the U parameter, which is, unfortunately, experimentally not known for ScMnO3. Nevertheless, we also carried out DFT + U calculations to investigate the influence of electronic correlation on the stability of the magnetic ground states. We recalculated the total energy of all spin orders using the GGA + U method with Ueff values changing over the range Ueff = 0–4 eV. The calculated results are displayed in Fig. 5. It can clearly be seen that the G-AFM state is the ground state when Ueff is less than 2.30 eV; then the E-AFM state is the ground state when Ueff is between 2.30 and 2.70 eV; and the FM state is the ground state when Ueff is larger than 2.70 eV. Obviously, we find a similar tendency in previous reports on the magnetic ordering being affected by the U parameter.44,50,51 This result can be attributed to the significant reduction in antiferromagnetic exchange interaction (JA), since the + U treatment enhances the localization of t2g states. While the eg states are not directly affected by + U treatment due to the strong hybridization between the eg and O-p states (JF). Thus, it is suggested that the smaller electronic correlation can give the correct magnetic ground state in calculating the magnetic properties of rare-earth manganites. According to the Ueff used in previous studies (Ueff < 2 eV),43,44,50,51 the magnetic ground state of PSMO is G-AFM. In order to overcome the problems related to the arbitrary choice of the Hubbard U parameter, we also carry out total energy calculations within the HSE06 function for PSMO with different magnetic orderings.46 The calculated results also show that the G-AFM state has the lowest energy (see Table 1).
4. Conclusion
In conclusion, the lattice, electric, and magnetic properties of highly distorted monoclinic PSMO have been systematically investigated with first-principles calculations. We find that the magnetic ground state of PSMO is the G-AFM state. It is also found that the G-AFM state can give correct structural information in describing the displacements of Mn3+ ions. Moreover, an unreported three-dimensional alternating cooperative orbital ordering is also reported in this study. Because of the smaller bond angle of <Mn–O–Mn induced by the high JT distortion, the nearest-neighbor Mn3+ ions exhibit an AFM magnetic interaction, although PSMO has a three-dimensional cooperative orbital ordering. Moreover, it is found that the PSMO is a bipolar antiferromagnetic semiconductor in which completely spin-polarized currents with reversible spin polarization can be tuned simply by applying a gate voltage. This controllability of the spin polarization of the current opens up new avenues for future spintronic devices. Our calculated results not only suggest that the ground magnetic ordering of PSMO is the G-AFM state, but also enrich the study of orbital ordering in rare-earth manganites. It is expected that more meticulous experiments detecting the magnetic structure of PSMO will validate our theoretical study and complete the magnetic phase diagram of rare-earth manganites.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work has been supported by the National Natural Science Foundation of China though Grant No. 11604113. We are grateful to the High Performance Computing Center (HPCC) of Nanjing University for doing the numerical calculations in this paper on its blade cluster system.References
- E. Dagotto, T. Hotta and A. Moreo, Phys. Rep., 2001, 344, 1–153 CrossRef CAS.
- B. Lorenz, Y.-Q. Wang and C.-W. Chu, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 104405 CrossRef.
- D. Lee, A. Yoon, S. Y. Jang, J. G. Yoon, J. S. Chung, M. Kim, J. F. Scott and T. W. Noh, Phys. Rev. Lett., 2011, 107, 057602 CrossRef CAS PubMed.
- Y. S. Chai, Y. S. Oh, L. J. Wang, N. Manivannan, S. M. Feng, Y. S. Yang, L. Q. Yan, C. Q. Jin and K. H. Kim, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184406 CrossRef.
- S. Mukherjee, A. Dönni, T. Nakajima, S. Mitsuda, M. Tachibana, H. Kitazawa, V. Pomjakushin, L. Keller, C. Niedermayer, A. Scaramucci and M. Kenzelmann, Phys. Rev. B: Condens. Matter Mater. Phys., 2017, 95, 104412 CrossRef.
- H. Y. Hwang, S. W. Cheong, P. G. Radaelli, M. Marezio and B. Batlogg, Phys. Rev. Lett., 1995, 75, 914–917 CrossRef CAS PubMed.
- D. A. Mota, A. Almeida, V. H. Rodrigues, M. M. R. Costa, P. Tavares, P. Bouvier, M. Guennou, J. Kreisel and J. A. Moreira, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 054104 CrossRef.
- T. Goto, T. Kimura, G. Lawes, A. P. Ramirez and Y. Tokura, Phys. Rev. Lett., 2004, 92, 257201 CrossRef CAS PubMed.
- B. Dabrowski, S. Kolesnik, A. Baszczuk, O. Chmaissem, T. Maxwell and J. Mais, J. Solid State Chem., 2005, 178, 629–637 CrossRef CAS.
- A. Oleaga, A. Salazar, D. Prabhakaran, J. G. Cheng and J. S. Zhou, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 184425 CrossRef.
- J. S. Zhou, J. B. Goodenough, J. M. Gallardo-Amores, E. Morán, M. A. Alario-Franco and R. Caudillo, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 014422 CrossRef.
- R. Basistyy, T. N. Stanislavchuk, A. A. Sirenko, A. P. Litvinchuk, M. Kotelyanskii, G. L. Carr, N. Lee, X. Wang and S. W. Cheong, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 024307 CrossRef.
- T. Katsufuji, M. Masaki, A. Machida, M. Moritomo, K. Kato, E. Nishibori, M. Takata, M. Sakata, K. Ohoyama, K. Kitazawa and H. Takagi, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 134434 CrossRef.
- M. Tachibana, T. Shimoyama, H. Kawaji, T. Atake and E. Takayama-Muromachi, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 144425 CrossRef.
- T. Kimura, S. Ishihara, H. Shintani, T. Arima, K. T. Takahashi, K. Ishizaka and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68, 060403 CrossRef.
- J. S. Zhou and J. B. Goodenough, Phys. Rev. Lett., 2006, 96, 247202 CrossRef PubMed.
- I. Solovyev, N. Hamada and K. Terakura, Phys. Rev. Lett., 1996, 76, 4825–4828 CrossRef CAS PubMed.
- Y. Murakami, J. P. Hill, D. Gibbs, M. Blume, I. Koyama, M. Tanaka, H. Kawata, T. Arima, Y. Tokura, K. Hirota and Y. Endoh, Phys. Rev. Lett., 1998, 81, 582–585 CrossRef CAS.
- P. Mandal and S. Das, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 15073–15080 CrossRef CAS.
- J. Hemberger, M. Brando, R. Wehn, V. Y. Ivanov, A. A. Mukhin, A. M. Balbashov and A. Loidl, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 064418 CrossRef.
- T. Kimura, T. Goto, H. Shintani, K. Ishizaka, T. Arima and Y. Tokura, Nature, 2003, 426, 55–58 CrossRef CAS PubMed.
- M. Kenzelmann, A. B. Harris, S. Jonas, C. Broholm, J. Schefer, S. B. Kim, C. L. Zhang, S. W. Cheong, O. P. Vajk and J. W. Lynn, Phys. Rev. Lett., 2005, 95, 087206 CrossRef CAS PubMed.
- T. Kimura, G. Lawes, T. Goto, Y. Tokura and A. P. Ramirez, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 224425 CrossRef.
- O. Prokhnenko, R. Feyerherm, E. Dudzik, S. Landsgesell, N. Aliouane, L. C. Chapon and D. N. Argyriou, Phys. Rev. Lett., 2007, 98, 057206 CrossRef CAS PubMed.
- A. Munoz, M. T. Casais, J. A. Alonso, M. J. Martinez-Lope, J. L. Martinez and M. T. Fernandez-Diaz, Inorg. Chem., 2001, 40, 1020–1028 CrossRef CAS.
- H. Chen, T. Yu, P. Gao, J. Bai, J. Tao, T. A. Tyson, L. Wang and R. Lalancette, Inorg. Chem., 2013, 52, 9692–9697 CrossRef CAS PubMed.
- T. Yu, T. A. Tyson, H. Y. Chen, A. M. M. Abeykoon, Y. S. Chen and K. H. Ahn, J. Phys.: Condens. Matter, 2014, 26, 495402 CrossRef CAS PubMed.
- V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS.
- J.-W. G. Bos, B. B. van Aken and T. T. M. Palstra, Chem. Mater., 2001, 13, 4804–4807 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 23, 5048–5079 CrossRef CAS.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- J. Kanamori, J. Appl. Phys., 1960, 31, S14–S23 CrossRef.
- C. P. Adams, J. W. Lynn, Y. M. Mukovskii, A. A. Arsenov and D. A. Shulyatev, Phys. Rev. Lett., 2000, 85, 3954–3957 CrossRef CAS PubMed.
- Y. S. Hou, H. J. Xiang and X. G. Gong, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 064415 CrossRef.
- G. R. Blake, T. T. M. Palstra, Y. Ren, A. A. Nugroho and A. A. Menovsky, Phys. Rev. Lett., 2001, 87, 245501 CrossRef CAS PubMed.
- J. B. Goodenough, Phys. Rev., 1955, 100, 564–573 CrossRef CAS.
- J. Kanamori, J. Phys. Chem. Solids, 1959, 10, 87–98 CrossRef CAS.
- K. Yamauchi, F. Freimuth, S. Blügel and S. Picozzi, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 014403 CrossRef.
- S. Picozzi, K. Yamauchi, G. Bihlmayer and S. Blügel, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 094402 CrossRef.
- J. C. Slater and G. F. Koster, Phys. Rev., 1954, 94, 1498–1524 CrossRef CAS.
- J. Heyd, J. E. Peralta, G. E. Scuseria and R. L. Martin, J. Chem. Phys., 2005, 123, 174101 CrossRef PubMed.
- X. Li, X. Wu, Z. Li, J. Yang and J. G. Hou, Nanoscale, 2012, 4, 5680–5685 RSC.
- I. Solovyev, N. Hamada and K. Terakura, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 7158–7170 CrossRef CAS.
- I. A. Vladimir, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9, 767 CrossRef.
- G. Li, X. Huang, J. Hu, G. Song and W. Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 085140 CrossRef.
- J. T. Zhang, C. Ji, J. L. Wang, W. S. Xia, X. M. Lu and J. S. Zhu, Phys. Rev. B: Condens. Matter Mater. Phys., 2018, 97, 085124 CrossRef.
- I. Solovyev, J. Phys. Soc. Jpn., 2009, 78, 054710 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra08507b |
| This journal is © The Royal Society of Chemistry 2019 |