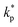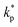DOI:
10.1039/C8RA08987F
(Paper)
RSC Adv., 2019,
9, 2516-2524
Thermal conductivity and molecular heat transport of nanofluids
Received
30th October 2018
, Accepted 9th January 2019
First published on 21st January 2019
Abstract
Fluid media such as water and ethylene glycol are usually quite poor conductors of heat. Nanoparticles can improve the thermal properties of fluids in a remarkable manner. Despite a plethora of experimental and theoretical studies, the underlying physics of heat transport in nanofluids is not yet well understood. Furthermore, the link between nanoscale energy transport and bulk properties of nanofluids is not fully established. This paper presents a thermal conductivity model, encapsulating solid–liquid interfacial thermal resistance, particle shape factor and the variation of thermal conductivity across a physisorbed fluidic layer on a nanoparticle surface. The developed model for thermal conductivity integrates the interfacial Kapitza resistance, the characteristics of a nanolayer, convective diffusion and surface energy with capillary condensation. In addition, the thickness of the nanolayer is predicted using the Brunauer–Emmett–Teller (BET) isotherms and micro/nano-menisci generated pressures of condensation. Such a comprehensive model for thermal conductivity of nanoparticles and systematic study has not hitherto been reported in the literature. The thermal conductivity model is evaluated using experimental data available in open literature.
1. Introduction
Nanoparticles have received growing attention for medical, environmental and electronic applications in the past decade.1–5 Nanofluids are a propitious choice for industrial cooling systems and powerplant heat exchangers owing to their improved thermal performance as efficient cooling agents.6,7 Improved fuel economy is also envisaged through the application of nanoparticles as lubricant additives in, for example, automotive powertrains.8
At the current state of the art, nanoparticles are dispersed in physically known fluid carriers such as ethylene glycol (EG), mineral oil (M-oil), poly-alpha-olefin (PAO) and water (H2O).8–10 Metallic and non-metallic nanoparticles have thermal conductivities of several orders of magnitude greater than the base fluid. Even a relatively small volumetric fraction of solid nanoparticles (<2%) dispersed in a fluid carrier can noticeably improve its bulk thermal conductivity.11 Maxwell12 studied the effective thermal conductivity of nanofluids using the thermal diffusion model for two-phase solid–liquid dilute dispersions. Various semi-empirical and theoretical models have been developed since the work of Maxwell to account for particle size, shape, volumetric concentration, clustering, monolayer surface adsorption, temperature, pH and zeta potential.13–17 Zeta potential determines the surface electric charge of particles and it can be adjusted using pH properties. Zeta potential is utilised to evaluate the electrostatic forces in nanofluids. The interplay between van der Waals and electrostatic forces is responsible for the stability of nanofluid and agglomeration of the particles. The thermal conductivity enhancement of the nanofluid depends on these forces.18–21 The Derjaguin–Landau–Verwey–Overbeek (DLVO) theory is widely utilised for stability studies. The thermal conductivity models attempt to relate the bulk properties of the two phases and predict the effective thermal conductivity of a nanofluid for a known range of materials. Only a few studies have targeted the underlying physics of the heat transport at molecular scale in nanofluids. Wang et al.22 utilised Langmuir's monolayer adsorption theory23 to predict the diameter of fluid molecules adsorbed to the surface of nanoparticles. They considered the nanoparticle size and clustering using a fractal model. Their model excludes the adsorption of additional molecular layers. Brunauer et al.24 showed that extra molecular layers would form on solid surfaces, based upon Arrhenius adsorption theory.25 Jang and Choi26 pioneered consideration of energy transport modes at molecular scale. They studied four transport modes, encapsulating fluid intermolecular collisions, thermal diffusion of nanoparticles, direct collision of nanoparticles (Brownian motion) and fluid–nanoparticle interactions. They showed analytically that their model conformed to the experimental data for three layers of molecules adsorbed to the surface of nanoparticles regardless of the progressive adsorption–desorption phenomenon. Their model included the thermal resistance of solid–liquid interface, whilst neglecting the variation of thermal conductivity across the adsorbed nanolayer. Although their model accounted for convective thermal diffusion through fluid flow past nanoparticles, they utilised an empirical coefficient to compensate for the deviations of their theoretical model from the measured experimental data. The adsorption mechanism and empirical parameters should be explained through fundamental physics for a better understanding of the underlying heat transfer of nanofluids.
The underlying physics of molecular heat transport phenomena is fundamental to the better understanding of the bulk thermal properties of nanofluids. This paper makes use of energy transport formulation of Jang and Choi,26 integrating the effective thermal conductivity of nanofluids to the physical chemistry of adsorption at the molecular scale. A multilayer adsorption model is established, based upon the Brunauer–Emmett–Teller (BET) theory. The activation energy of adsorption is predicted using micro/nano-menisci forces. The proposed model incorporates the variation of thermal conductivity across the adsorbed nanolayer, associating the empirical coefficient of convective diffusion to the shape factor of nanoparticles. This modified thermal conductivity model is verified using experimental data from open literature. A parametric study is also carried out to investigate the influences of interfacial thermal resistance, convective diffusion and surface energy upon the bulk thermal conductivity of nanofluids.
2. Methodology
In nanofluid dynamics, particles are subjected to various intermolecular forces (Fig. 1), some of which are regarded as negligible due to the minute size of the particles.27 The dominant forces are due to molecular interactions between molecules of the fluid and the nanoparticles, and the inertia of the adsorbed fluid layer. The direct interaction of nanoparticles, known as Brownian motion, is considered as negligible in dilute nanofluids.12,26 The molecular momenta of fluid–nanoparticle collisions affect the energy transport and thermal diffusion at nanoscale and thermal conductivity at microscale.
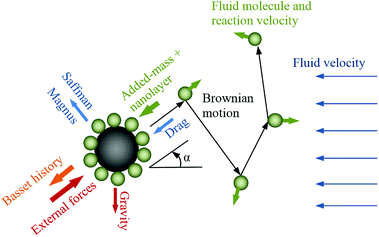 |
| | Fig. 1 Schematic of nanoparticle motion and applied forces. | |
2.1. Effective thermal conductivity of nanofluid
Jang and Choi's heat transport theory26 is adopted to describe the effective thermal conductivity of nanofluids, keff. Jang and Choi assumed that the Reynolds number, Re, for nanoparticles is greater than unity and the Prandtl number, Pr, is approximately 10. Therefore, the Nusselt number for the flow past spheres can be simplified to: Nu ∼ Re2Pr2. Nanoparticles can experience a Reynolds number of noticeably smaller than unity due to their diminutive size. Whitaker's formulation28 for the Nusselt number accurately predicts the coefficient of convective heat, h, for Re ≤ 50 as:| |
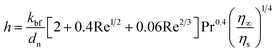 | (1) |
where, kbf is the thermal conductivity of the base fluid. dn, η∞ and ηs are diameters of the nanoparticle including the thickness of any adsorbed nanolayer, dynamic viscosity of the bulk fluid and that of the fluid in the vicinity of nanoparticle surface. Whitaker28 suggested that the dynamic viscosity ratio, η∞/ηs, is between 1.0 and 3.2 for the flow past a single sphere. Substituting eqn (1) into Jang and Choi's heat transport model,26 the effective thermal conductivity becomes:| |
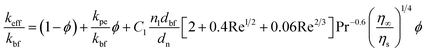 | (2) |
where, kpe is the effective thermal conductivity of nanoparticles. ϕ, nl and dbf are the volumetric concentration of nanoparticles, number of adsorbed molecular layers on the surface of the particles and the average diameter of the base fluid molecules respectively. The constant C1 was determined arbitrarily by Jang and Choi26 in order to compensate for any deviations of their theoretical predictions from the measured thermal conductivity. However, coefficient C1 is correlated to the nanoparticle's shape factor in this paper in Section 2.4. Reynolds, Re, and Prandtl, Pr, numbers are described as:| |
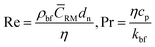 | (3) |
respectively, where, ρbf, η and cp are density, dynamic viscosity and the specific heat of the base fluid at constant pressure. The random average velocity of nanoparticles, ![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) RM is determined by Einstein's diffusion coefficient, Do29 and the mean free path of the base fluid's molecules, λbf as:
RM is determined by Einstein's diffusion coefficient, Do29 and the mean free path of the base fluid's molecules, λbf as:| |
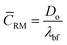 | (4) |
where, Do = kBT/3πηdn and 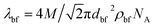 . In these relationships, kB and T are the Boltzmann constant and the absolute temperature of the base fluid. Parameters M and NA are the molar mass of base fluid molecules and Avogadro constant. The adsorption phenomenon leading to the formation of nanolayers, where nl is the number of layers, the equivalent thermal conductivity of nanoparticle after dispersion, kpe, and the shape factor, C1, are described in Sections 2.2 to 2.4.
. In these relationships, kB and T are the Boltzmann constant and the absolute temperature of the base fluid. Parameters M and NA are the molar mass of base fluid molecules and Avogadro constant. The adsorption phenomenon leading to the formation of nanolayers, where nl is the number of layers, the equivalent thermal conductivity of nanoparticle after dispersion, kpe, and the shape factor, C1, are described in Sections 2.2 to 2.4.
2.2. Adsorption process of fluid nanolayer
Jang and Choi26 assumed that three layers of molecules are always present (i.e. nl = 3 in eqn (2)) and the thermal conductivity of the adsorbed layers is the same as that of the nanoparticle itself. The number of molecular stacks in the nanolayer is physically imposed by the adsorption process. Fig. 2 shows how the molecular coverage might differ from Jang and Choi's model26 due to the progressive adsorption–desorption process. This is a contribution of the current analysis. The thermal conductivity across the nanolayer varies with the bonding strength between the neighbouring layers (Fig. 3).
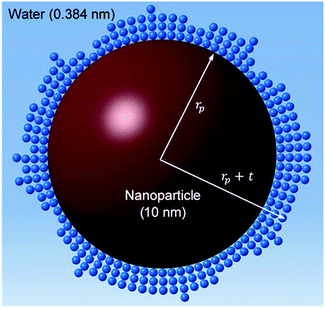 |
| | Fig. 2 Multi-layer molecular stacking due to adsorption of fluid molecules on the nanoparticle surface. | |
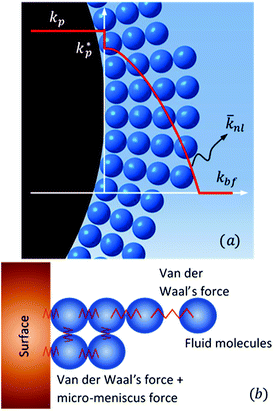 |
| | Fig. 3 (a) Variation of thermal conductivity at the interface and across the nanolayer thickness, and (b) diminution of surface energy and intermolecular bonding with distance. | |
Fluid molecules collide with the nanoparticle surface at high frequency due to long range van der Waals forces despite their weak interaction energy (i.e. ∼0.01–0.1 eV). Some of these molecules bounce off, whilst the remaining oscillate and shift their positions prior to reaching equilibrium (i.e. physisorption). The enthalpy of chemisorption is a few orders of magnitude greater than physisorption (i.e. ∼1–10 eV).30 The energy barrier between physisorption and chemisorption is large for stable crystalline nanoparticles (e.g. Al2O3 and CuO), and particles are assumed to be chemically inert during the formation of nanolayers.30,31 Arrhenius theory determines the rate of molecular collisions, kr, leading to adsorption25 as:
| |
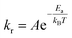 | (5) |
where coefficient
A is the total number of collisions with the nanoparticle surface and
Ea is the activation energy of adsorption. The enthalpy of adsorption varies with surface coverage due to the interaction of neighbouring adsorbate molecules and the growth of the nanolayer. Brunauer–Emmett–Teller
24 adopted Langmuir's theory
23 and considered the initial monolayer as the substrate for the adsorption of more molecular layers. The growth of nanolayer continues until the surface energy becomes comparable to that of the Lifshitz theory for free fluid molecules, and adsorption–desorption process progressively continues. The molecular volume of nanolayer,
v, can be interpreted as the average thickness of the nanolayer,
t, provided that the molecular volume of the base monolayer,
vm, is known, based on the BET (Brunauer–Emmett–Teller) theory
24 as:
| |
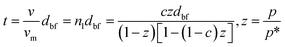 | (6) |
where, pressures
p and
p* indicate the equilibrium pressure of adsorbates at the adsorption temperature and the pressure of the bulk liquid above the last layer of adsorbate respectively. The latter is also known as the saturation pressure of adsorbate at the temperature of adsorption. Parameter
c is the reaction rate ratio of adsorption to desorption for the last monolayer and is quantified through use of the reaction enthalpy, Δ
HΘ31 as:
| |
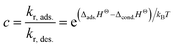 | (7) |
The constant c is well in excess of unity.24 The thickness of nanolayer depends on pressure, surface energy, and temperature of adsorption. The diameter of fluid molecules is considered to be about two orders of magnitude smaller than that of the nanoparticles. The surface of a single nanoparticle and particle clusters consist of smooth, shallow cavities suitable for capillary condensation.30 For hydrophilic (or oleophilic) surfaces, the physisorbed fluid molecules form a coherent layer of fluid. The solid surface interacts with the molecular layers of fluid through three forms of forces: (i) van der Waal's forces (physisorption), (ii) electrostatic double layer forces, and (iii) solvation forces.32–34 These forces vary in the range of a few pN at nanometre separation distances.34,35 Solvation forces are present in narrow conjunctions between solid ultra-smooth barriers. The effect of electrostatic double layer forces is negligible in nonpolar fluids. In polar fluids, this repulsive force and van der Waals attractive force interplay. Thus, capillary condensation initiates through physisorption and a coherent nanolayer of fluid forms due to surface free energy (micro/nano-menisci forces). Al-Samieh and Rahnejat32 showed that forces of menisci are dominant at the scale of a few molecular layers of fluid contiguous to contacting surfaces. The BET isotherm pressure can be evaluated using Kelvin's equation for capillary condensation:34,36,37
| |
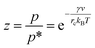 | (8) |
where,
γ is the surface energy of liquid and
v is the volume of liquid layer. The mean radius of curvature of meniscus,
rc, is a geometrical property of cavity and is given by:
| |
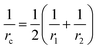 | (9) |
where,
r1 =
r2 =
rc for a hemispherical geometry.
2.3. Equivalent thermal conductivity of dispersed nanoparticles
The equivalent thermal conductivity of nanoparticle dispersion is the combined thermal conductivity of nanoparticles and their contiguous nanolayers. A sudden jump in thermal conductivity is expected at the solid–fluid interface due to the Kapitza thermal resistance.38–40 Khalatnikov39 showed the dependence of Kapitza resistance, Rk on temperature, pressure, structural stiffness and surface properties. This theory incorporates the reflection and transmission of phonons through lattice vibrations in crystalline structures. Transmission of phonons depends on three lattice waves: longitudinal, transverse and surface Rayleigh waves. The Kapitza resistance is:38–40| |
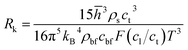 | (10) |
where, ![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) , ρs, cl, ct and cbf are the reduced Planck constant, density of solid, longitudinal speed of sound in solid, transverse speed of sound in solid, and speed of sound in the base fluid respectively. Function, F, usually varies between 1.5 and 2.0. Kapitza thermal resistance, Rk, varies between 10−8 and 10−2 (m2 K W−1) for various interfaces and it ranges from 0.2 × 10−8 to 5.0 × 10−8 (m2 K W−1) for hydrophilic solid–water interfaces.41,42 The thermal conductivity of nanoparticles after dispersion in fluid,
, ρs, cl, ct and cbf are the reduced Planck constant, density of solid, longitudinal speed of sound in solid, transverse speed of sound in solid, and speed of sound in the base fluid respectively. Function, F, usually varies between 1.5 and 2.0. Kapitza thermal resistance, Rk, varies between 10−8 and 10−2 (m2 K W−1) for various interfaces and it ranges from 0.2 × 10−8 to 5.0 × 10−8 (m2 K W−1) for hydrophilic solid–water interfaces.41,42 The thermal conductivity of nanoparticles after dispersion in fluid, 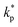 , is evaluated using the Kapitza resistance, Rk, thermal conductivity before dispersion, kp, and the equivalent radius of nanoparticle, rp. Eqn (11) describes the abrupt jump in the thermal conductivity associated with interfacial thermal resistance (as shown in Fig. 3a).
, is evaluated using the Kapitza resistance, Rk, thermal conductivity before dispersion, kp, and the equivalent radius of nanoparticle, rp. Eqn (11) describes the abrupt jump in the thermal conductivity associated with interfacial thermal resistance (as shown in Fig. 3a).| |
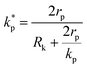 | (11) |
The surface area, S, and volume, V, of a nanoparticle can be associated with the radius, rp, of an equivalent sphere with volume, Veq, and surface area, Seq through geometrical relationship: rp = 3 V S−1. The thickness of the nanolayer, t, can be determined using the BET isotherms (eqn (6)). Considering knl as the thermal conductivity of the nanolayer with a thickness ratio βr = t/rp, then it can be established that the nanolayer thermal conductivity ratio becomes: 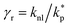 . The equivalent thermal conductivity of the dispersed nanoparticles, kpe is determined as:43
. The equivalent thermal conductivity of the dispersed nanoparticles, kpe is determined as:43
| |
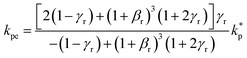 | (12) |
Jang and Choi26 assumed the same thermal conductivity for the nanolayer and nanoparticle. Thermal diffusion is related to the molecular momenta of the fluid. The internal bonding forces decay exponentially to those described by the Lifshitz theory for van der Waals' interaction variations with distance as the number of nanolayers increases.24 Therefore, the intermolecular spacing increases, resulting in the transition from short-wavelength high-frequency phonons to long-wavelength low-frequency phonons. Short-wavelength high-frequency phonons are responsible for the thermal behaviour of nanolayers. Therefore, it can be inferred that the thermal conductivity decreases exponentially across the nanolayer thickness:44,45
| |
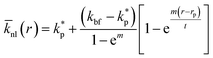 | (13) |
where,
m is a real positive value, usually with value of 2 (
ref. 45) and
r is the radial distance from the surface of the nanoparticle;
rp, to the outer boundary of the adsorbed nanolayer;
rp +
t. In addition, the average thermal conductivity of the nanolayer can be determined as:
44,45| |
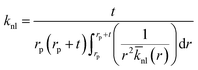 | (14) |
The distribution of thermal conductivity across the nanolayer, ![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) nl, equals
nl, equals 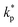 at its interface with the nanoparticle and equals kbf at its interface with the bulk base fluid.
at its interface with the nanoparticle and equals kbf at its interface with the bulk base fluid.
2.4. Shape factor
A larger surface area facilitates heat flow to the nanoparticle. Therefore, the surface-to-volume ratio is an important shape factor in the heat transfer mechanisms. If the apparent surface area and volume of nanoparticle are Sa and Va, then the surface area of an equivalent sphere with the same volume is Seq. The sphericity, Ψ, is then determined by Ψ and C1 as the shape factor:46| |
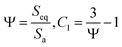 | (15) |
3. Results and discussion
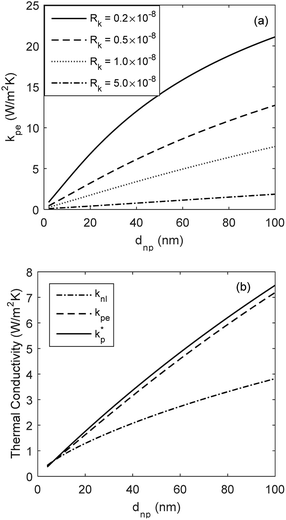
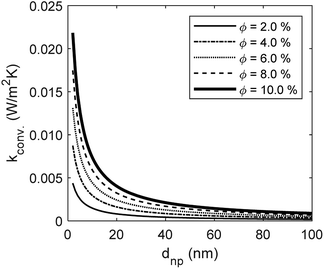
The developed model is used to better understand the underlying physics of heat transport in nanofluids, incorporating the effects of interfacial Kapitza resistance, thermal conductivity of the nanolayer, convective diffusion, surface energy and capillary condensation. A sensitivity analysis was carried out on the newly developed thermal conductivity model. The physical properties of alumina–water (Al2O3:H2O) nanofluid was utilised for this study (Table 1). Fig. 4a shows the sensitivity of thermal conductivity to Kapitza resistance. The results indicate that thermal conductivity of alumina nanoparticle reduces from 40 to below 25 (W m−2 K−1) when dispersed in water. The results in Fig. 4a show that equivalent thermal conductivity, kpe, is less sensitive to Kapitza resistance, Rk, for smaller nanoparticles. However, thermal conductivity of physisorbed nanolayer, knl, is greater than that of the base fluid and smaller than that of the dispersed nanoparticle as shown in Fig. 4b. Thermal conductivity of nanofluid is predicted to converge to that of base fluid for minute size particles (dnp < 10 nm). Following Jang and Choi's heat transport model,26 thermal conductivity is partially dependent on forced convective diffusion due to fluid molecule–nanoparticle interactions. The analytical results indicate that the effect of convective diffusion increases inversely proportional to the nanoparticle size and proportionally with the volumetric concentration as shown in Fig. 5. For a known volumetric concentration, a smaller particle size would result in a greater number of particles. Hence, the total surface area of nanoparticles, St increases with the number of particles, nt, as the simple geometrical relation 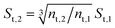 (nt,2 > nt,1) holds for spherical geometries. The predicted results in Fig. 5 also show that convective diffusion affects the thermal conductivity of alumina–water nanofluid by as much as 4% in theory.
(nt,2 > nt,1) holds for spherical geometries. The predicted results in Fig. 5 also show that convective diffusion affects the thermal conductivity of alumina–water nanofluid by as much as 4% in theory.
Table 1 Material properties for nanoparticles and base fluids at 300 K47–50
| Property |
Thermal conductivity |
Density |
Dynamic viscosity |
Equivalent diameter |
| Unit |
W m−2 K−1 |
m3 kg−1 |
Pa s |
nm |
| H2O (water) |
0.613 |
997 |
0.855 × 10−3 |
0.384 |
| Ethylene glycol |
0.253 |
1114 |
1.57 × 10−2 |
0.561 |
| Al2O3 (alumina) |
40 |
3880 |
— |
24.4 |
| CuO |
18 |
6510 |
— |
18.6 |
 |
| | Fig. 4 Equivalent thermal conductivity kpe of Al2O3 nanoparticles dispersed in H2O: (a) variations with particle size dnp and Kapitza resistance Rk, and (b) variations of equivalent thermal conductivity kpe with particle size dnp and with respect to those of the solid–liquid interface 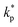 and the physisorbed nanolayer knl. and the physisorbed nanolayer knl. | |
 |
| | Fig. 5 The effect of Brownian motion through convective diffusion on thermal conductivity of Al2O3:H2O nanofluid. | |
The physisorption of a nanolayer is correlated to surface energy and molecular volume as shown in eqn (8). Surface energy differs for various solid–liquid combinations. In the molecular scale, surface energy also varies with atomic plane of reaction. For instance, H2O molecules can adsorb to Al2O3 surface either through Al planes or Ox planes.30 The surface free energy between fluid molecules vary between 20 and 80 (mJ m−2) for known fluids such as water and ethylene glycol.51,52 The formation of a coherent fluid film on the surface of nanoparticle is affected by the free surface energy of the fluid molecules.31,32 The current model shows that thermal conductivity is insensitive to surface energy, γ, above a critical limit (Fig. 6). This critical limit is affected by the volume of cavities on the surface of nanoparticles. The geometry of cavities for capillary condensation is assumed to be hemispherical. This geometrical feature can be interpreted as surface roughness in an analytical model. A greater cavity volume indicates fewer number of cavity sites with larger radii of curvature, representing greater surface roughness. Fig. 6 shows that the critical surface energy limit increases for smoother surfaces. The thermal conductivity variations with surface free energy are negligible in comparison with the effects of interface resistance, nanolayer's thermal conductivity and particle size. However, free surface energy affects the physisorption rate and its role in the formation of nanolayers cannot be neglected.
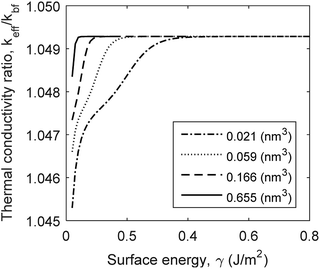 |
| | Fig. 6 Variation of thermal conductivity with surface energy and surface roughness (cavity volume) for Al2O3:H2O nanofluid. | |
The proposed thermal conductivity model is evaluated for four nanofluids as shown in Fig. 7. The physical properties of particles and base fluids are presented in Table 1. Values of Kapitza resistances, Rk, were empirically determined using the results of Lee et al.53 (Table 2). The predicted resistances are in the same order as those suggested for hydrophilic (or oleophilic) solid–liquid interfaces (10−8 m2 K W−1).42,43 The calculated thickness of nanolayer is larger in water than ethylene glycol. Fig. 7 shows the measured thermal conductivity for nanofluids with various particle sizes and volumetric concentrations. The regular lines indicate the prediction for the results by Lee et al.53 In Fig. 7a, experimental data for alumina–water nanofluid with dnp = 46 nm lies below the values for dnp = 24.4 nm and 28 nm. The discrepancy in the experimental results can be attributed to the difference in the experimental measurements conducted in different laboratories. The generic trend in the experimental results shows a rise in thermal conductivity with the nanoparticle size and volumetric concentration. The developed model closely replicates the observed trends. Similar trends are present in Fig. 7a–d. Overall, the theoretical predictions are in good agreement with the thermal conductivity ratios obtained experimentally.
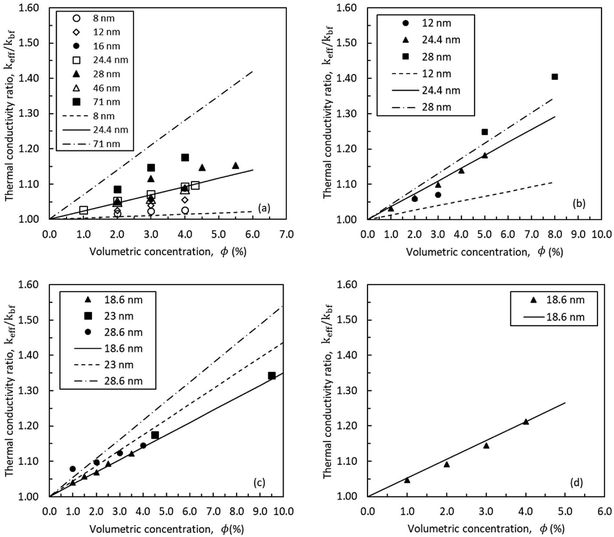 |
| | Fig. 7 Experimental results and predicted thermal conductivity using eqn (2): (a) alumina–water,53–55 (b) alumina–ethylene glycol,53–55 (c) copper oxide–water,53,55,56 and (d) copper oxide–ethylene glycol.53 | |
Table 2 Predicted interfacial Kapitza resistance and the number of adsorbed fluid molecular layers
| Nanofluid |
Rk (m2 K W−1) |
nl = v/vm (−) |
| Al2O3:H2O |
1.09 × 10−8 |
2.7 |
| Al2O3:EG |
1.86 × 10−8 |
1.6 |
| CuO:H2O |
0.51 × 10−8 |
2.7 |
| CuO:EG |
0.93 × 10−8 |
1.6 |
4. Concluding remarks
Although various thermal conductivity models with reasonable degree of accuracy have been proposed in the literature, the heat transport at molecular scale and its relationship with the bulk properties of nanofluids were not hitherto fully understood. Therefore, a new thermal conductivity model is proposed for the molecular heat transport of nanofluids using physisorption of fluid molecules onto nanoparticle surfaces through van der Waal's interactions and forces of fluidic menisci. The proposed model incorporates the effects of particle size, shape, volumetric concentration, forced convection due to fluid molecule–nanoparticle interactions, surface energy and particles' surface roughness. It is concluded that the effect of convective diffusion on thermal conductivity diminishes as the nanoparticle size increases. It was shown that the thermal conductivity of a nanolayer can increase by an order of magnitude in comparison with the bulk fluid. It was also found that the thermal conductivity of nanoparticles reduces by more than 50% due to thermal resistance at solid–liquid interface. Thermal conductivity is also predicted to be more sensitive to surface energy for smoother surfaces with shallower inter-asperity cavities. Theoretical predictions are in good agreement with the experimentally measured thermal conductivities. Therefore, the expounded thermal conductivity model provides a combined study of surface energy, physisorption and bonding energy across the nanolayer, an approach not hitherto reported in literature.
Conflicts of interest
There are no conflicts to declare.
Roman letters
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) RM RM | Nanoparticle random velocity in Brownian motion |
| C1 | Shape factor |
| c | Reaction rate ratio of adsorption to desorption |
| cbf | Speed of wave propagation in the base fluid |
| cl | Longitudinal speed of wave propagation in the solid |
| cp | Specific heat of base fluid |
| ct | Transverse speed of wave propagation in the solid |
| Do | Einstein's diffusion coefficient |
| dbf | Equivalent molecular diameter of the base fluid |
| dn | Diameter of nanoparticle including the nanolayer thickness |
| dnp | Diameter of nanoparticle prior to dispersion |
| Ea | Activation energy of adsorption |
| HΘ | Enthalpy of reaction |
| h | Coefficient of heat convection |
![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) | Reduced Planck constant |
| kB | Boltzmann constant |
| kbf | Thermal conductivity of the base fluid |
| keff | Effective thermal conductivity of the nanofluid |
| knl | Average thermal conductivity of the nanolayer |
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) nl nl | Thermal conductivity distribution across the nanolayer |
| kp | Thermal conductivity of nanoparticle prior to dispersion |
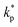 | Thermal conductivity of nanoparticle after dispersion |
| kpe | Equivalent thermal conductivity of nanoparticle including the nanolayer |
| kr | Reaction rate due to molecular collisions |
| M | Molar mass of base fluid |
| NA | Avogadro constant |
| Nu | Nusselt number |
| nl | Number of molecular layers in the nanolayer |
| nt | Total number of nanoparticles |
| Pr | Prandtl number |
| Re | Reynolds number |
| Rk | Interfacial Kapitza resistance |
| r | Radial distance from the centre of nanoparticle |
| rc | Mean radius of curvature of surface cavities/roughness |
| rp | Equivalent radius of nanoparticle excluding the nanolayer |
| S | Surface area of the nanoparticle |
| St | Total surface area of nanoparticles |
| T | Absolute temperature in degrees kelvin |
| t | Nanolayer thickness |
| V | Volume of nanoparticle |
| v | Total volume of nanolayer |
| z | Intermediate variable for pressure ratio |
Greek letters
| βr | Thickness ratio of nanolayer to nanoparticle radius |
| γ | Surface energy |
| γr | Thermal conductivity ratio of nanolayer to dispersed nanoparticle |
| Δ | Variation/difference |
| η | Dynamic viscosity |
| ηs | Dynamic viscosity of fluid in the vicinity of solid surface |
| η∞ | Bulk dynamic viscosity of fluid |
| λbf | Mean free path of base fluid molecules |
| ρbf | Density of base fluid |
| ρs | Density of solid nanoparticle |
| ϕ | Volumetric concentration of nanoparticles |
| Ψ | Shape factor of nanoparticle |
Abbreviations
| ads. | Adsorption |
| cond. | Condensation |
| des. | Desorption |
| vap. | Vaporisation |
References
- A. Krueger, Chem.–Eur. J., 2008, 14, 1382 CrossRef CAS PubMed.
- K. Kalantar-Zadeh, Nat. Nanotechnol., 2018, 13(9), 770 CrossRef CAS PubMed.
- V. N. Mochalin, O. Shenderova, D. Ho and Y. Gogotsi, Nat. Nanotechnol., 2011, 7(1), 11 CrossRef PubMed.
- A. M. Schrand, S. A. Ciftan Hens and O. Shenderova, Crit. Rev. Solid State Mater. Sci., 2009, 34, 18 CrossRef CAS.
- S. A. Angayarkanni and J. Philip, Adv. Colloid Interface Sci., 2015, 225, 146 CrossRef CAS PubMed.
- D. K. Devendiran and V. A. Amirtham, Renewable Sustainable Energy Rev., 2016, 60, 21 CrossRef CAS.
- L. S. Sundar, K. V. Sharma, M. K. Singh and A. C. M. Sousa, Renewable Sustainable Energy Rev., 2017, 68, 185 CrossRef CAS.
- M. Ivanoc and O. Shenderova, Curr. Opin. Solid State Mater. Sci., 2017, 21, 17 CrossRef.
- X. Q. Wang and A. S. Mujumdar, Int. J. Therm. Sci., 2007, 46, 1 CrossRef.
- W. Yu, H. Xie, Y. Li, L. Chen and Q. Wang, Colloids Surf., A, 2011, 380, 1 CrossRef CAS.
- S. U. S. Choi, in: The Proceedings of the 1995 ASME International Mechanical Engineering Congress and Exposition, San Francisco, USA, ASME, FED 231/MD, 1995, vol. 66, p. 99 Search PubMed.
- J. C. Maxwell, A Treatise of Electricity and Magnetism, Oxford University Press, London, 3rd edn, 1892, Part II, ch. IX, vol. 1, p. 435 Search PubMed.
- W. J. Minkowycz, E. M. Sparrow and J. P. Abraham, Nanoparticle heat transfer and fluid flow, CRC Press, Taylor and Francis Group, 2013, vol. 4, ch. 2, p. 41, ISBN: 978-1-4398-6192-9 Search PubMed.
- S. Kakaç and A. Pramuanjaroenkij, Int. J. Heat Mass Transfer, 2009, 52, 3187 CrossRef.
- H. Ş. Aybar, M. Sharifpur, M. R. Azizian, M. Mehrabi and J. P. Meyer, Heat Transfer Eng., 2015, 36(13), 1085 CrossRef CAS.
- M. Liu, C. Ding and J. Wang, RSC Adv., 2016, 6, 3571 RSC.
- P. V. Trinh, N. N. Anh, B. H. Thang, L. D. Quang, N. T. Hong, N. M. Hong, P. H. Khoi, P. N. Minh and P. N. Hong, RSC Adv., 2017, 7, 318 RSC.
- D. Lee, J. W. Kim and B. G. Kim, J. Phys. Chem. B, 2006, 110, 4323 CrossRef CAS PubMed.
- X. F. Li, D. S. Zhu, X. J. Wang, N. Wang, J. W. Gao and H. Li, Thermochim. Acta, 2008, 469, 98 CrossRef CAS.
- D. Zhu, X. Li, N. Wang, X. Wang, J. Gao and H. Li, Curr. Appl. Phys., 2009, 9, 131 CrossRef.
- G. Xia, H. Jiang, R. Liu and Y. Zhai, Int. J. Therm. Sci., 2014, 84, 118 CrossRef CAS.
- B. X. Wang, L. P. Zhou and X. F. Peng, Int. J. Heat Mass Transfer, 2003, 46, 2665 CrossRef CAS.
- I. Langmuir, J. Am. Chem. Soc., 1916, 38(11), 2221 CrossRef CAS.
- S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60(2), 309 CrossRef CAS.
- S. A. Arrhenius, Z. Phys. Chem., 1889, 4, 226 Search PubMed.
- S. P. Jang and S. U. S. Choi, Appl. Phys. Lett., 2004, 84(21), 4316 CrossRef CAS.
- H. Shahmohammadi, R. Rahmani, H. Rahnejat, C. P. Garner and N. Balodimos, Tribol. Int., 2017, 113, 50 CrossRef.
- S. Whitaker, AIChE J., 1972, 18(2), 361 CrossRef CAS.
- A. Einstein, Ann. Phys., 1905, 322(8), 549 CrossRef.
- N. H. de Leeuw and S. C. Parker, J. Am. Ceram. Soc., 1999, 82(11), 3209 CrossRef CAS.
- P. Atkins, J. de Paula and J. Keeler, Physical Chemistry, Oxford University Press, UK, 10th edn, 2018 Search PubMed.
- M. F. Al-Samieh and H. Rahnejat, J. Phys. D: Appl. Phys., 2002, 35, 2311 CrossRef CAS.
- R. Gohar and H. Rahnejat, Fundamentals of Tribology, Imperial College Press, London, 2nd edn, 2008 Search PubMed.
- G. A. Pilkington and W. H. Briscoe, Adv. Colloid Interface Sci., 2012, 179–182, 68 CrossRef CAS PubMed.
- W. H. Briscoe and R. G. Horn, Langmuir, 2002, 18, 3945 CrossRef CAS.
- W. Thomson, Proc. Royal Soc., 1870, 7, 63 Search PubMed.
- S. Cai and B. Bhushan, Philos. Trans. R. Soc., A, 2008, 366, 1627 CrossRef PubMed.
- P. L. Kapitza, Phys. Rev., 1941, 60, 354 CrossRef.
- I. M. Khalatnikov, Zh. Eksp. Teor. Fiz., 1952, 22, 687 CAS.
- G. L. Pollack, Rev. Mod. Phys., 1969, 41(1), 48 CrossRef CAS.
- E. V. Timofeeva, A. N. Gavrilov, J. M. McCloskey and Y. V. Tolmachev, Phys. Rev. E, 2007, 76, 061203 CrossRef PubMed.
- A. S. Tascini, J. Armstrong, E. Chiavazzo, M. Fasano, P. Asinari and F. Bresme, Phys. Chem. Chem. Phys., 2017, 19, 3244 RSC.
- L. M. Schwartz, E. J. Garboczi and D. P. Bentz, J. Appl. Phys., 1995, 78(10), 5898 CrossRef CAS.
- A. Khodayari, M. Fasano, M. Bozorg Bigdeli, S. Mohammadnejad, E. Chiavazzo and P. Asinari, Case Studies in Thermal Engineering, 2018, 12, 454 CrossRef.
- R. Pasrija and S. Srivastava, Heat Transfer—Asian Research, 2014, 43(3), 288 CrossRef.
- R. L. Hamilton and O. K. Crosser, Ind. Eng. Chem. Fundam., 1962, 1(3), 187 CrossRef CAS.
- F. D. S. Marquis and L. P. F. Chibante, JOM, 2005, 57(12), 32 CrossRef CAS.
- S. U. S. Choi and J. A. Eastman, 1995 International mechanical engineering congress and exhibition, ASME-Publications-Fed, San Francisco, CA, United States, 12–17 Nov 1995, vol. 231, p. 99 Search PubMed.
- M. Sheikholeslami and D. D. Ganji, Comput. Methods Appl. Mech. Eng., 2015, 283, 651 CrossRef.
- S. K. Das, N. Putra, P. Thiesen and W. Roetzel, J. Heat Transfer, 2003, 125, 567 CrossRef CAS.
- L. Martinez, R. Nevshupa, L. Alvarez, Y. Huttel, J. Mendez, E. Roman, E. Mozas, J. R. Valdes, M. A. Jimenez, Y. Gachon, C. Heau and F. Faverjon, Tribol. Int., 2009, 42, 584 CrossRef CAS.
- J. N. Israelachvili, Intermolecular and Surface Forces, Academic Press, London, 2nd edn, 1992 Search PubMed.
- S. Lee, S. U. S. Choi, S. Li and J. A. Eastman, J. Heat Transfer, 1999, 121, 280 CrossRef CAS.
- M. P. Beck, Y. Yuan, P. Warrier and A. S. Teja, J. Nanopart. Res., 2009, 11, 1129 CrossRef CAS.
- X. Wang, X. Xu and S. U. S. Choi, J. Thermophys. Heat Transfer, 1999, 13(4), 474 CrossRef CAS.
- J. Cai, X. Hu, B. Xiao, Y. Zhou and W. Wei, Int. J. Heat Mass Transfer, 2017, 105, 623 CrossRef CAS.
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *,
Ramin Rahmani,
Homer Rahnejat and
Colin P. Garner
*,
Ramin Rahmani,
Homer Rahnejat and
Colin P. Garner
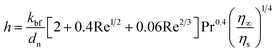
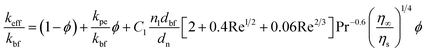
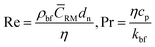
![[C with combining macron]](https://www.rsc.org/images/entities/i_char_0043_0304.gif) RM is determined by Einstein's diffusion coefficient, Do29 and the mean free path of the base fluid's molecules, λbf as:
RM is determined by Einstein's diffusion coefficient, Do29 and the mean free path of the base fluid's molecules, λbf as: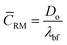
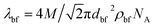 . In these relationships, kB and T are the Boltzmann constant and the absolute temperature of the base fluid. Parameters M and NA are the molar mass of base fluid molecules and Avogadro constant. The adsorption phenomenon leading to the formation of nanolayers, where nl is the number of layers, the equivalent thermal conductivity of nanoparticle after dispersion, kpe, and the shape factor, C1, are described in Sections 2.2 to 2.4.
. In these relationships, kB and T are the Boltzmann constant and the absolute temperature of the base fluid. Parameters M and NA are the molar mass of base fluid molecules and Avogadro constant. The adsorption phenomenon leading to the formation of nanolayers, where nl is the number of layers, the equivalent thermal conductivity of nanoparticle after dispersion, kpe, and the shape factor, C1, are described in Sections 2.2 to 2.4.


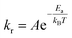
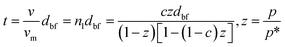
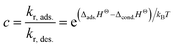
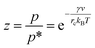
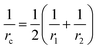
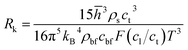
![[h with combining macron]](https://www.rsc.org/images/entities/i_char_0068_0304.gif) , ρs, cl, ct and cbf are the reduced Planck constant, density of solid, longitudinal speed of sound in solid, transverse speed of sound in solid, and speed of sound in the base fluid respectively. Function, F, usually varies between 1.5 and 2.0. Kapitza thermal resistance, Rk, varies between 10−8 and 10−2 (m2 K W−1) for various interfaces and it ranges from 0.2 × 10−8 to 5.0 × 10−8 (m2 K W−1) for hydrophilic solid–water interfaces.41,42 The thermal conductivity of nanoparticles after dispersion in fluid,
, ρs, cl, ct and cbf are the reduced Planck constant, density of solid, longitudinal speed of sound in solid, transverse speed of sound in solid, and speed of sound in the base fluid respectively. Function, F, usually varies between 1.5 and 2.0. Kapitza thermal resistance, Rk, varies between 10−8 and 10−2 (m2 K W−1) for various interfaces and it ranges from 0.2 × 10−8 to 5.0 × 10−8 (m2 K W−1) for hydrophilic solid–water interfaces.41,42 The thermal conductivity of nanoparticles after dispersion in fluid, 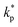 , is evaluated using the Kapitza resistance, Rk, thermal conductivity before dispersion, kp, and the equivalent radius of nanoparticle, rp. Eqn (11) describes the abrupt jump in the thermal conductivity associated with interfacial thermal resistance (as shown in Fig. 3a).
, is evaluated using the Kapitza resistance, Rk, thermal conductivity before dispersion, kp, and the equivalent radius of nanoparticle, rp. Eqn (11) describes the abrupt jump in the thermal conductivity associated with interfacial thermal resistance (as shown in Fig. 3a).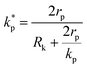
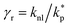 . The equivalent thermal conductivity of the dispersed nanoparticles, kpe is determined as:43
. The equivalent thermal conductivity of the dispersed nanoparticles, kpe is determined as:43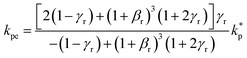
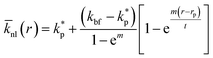
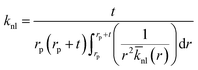
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif) nl, equals
nl, equals 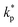 at its interface with the nanoparticle and equals kbf at its interface with the bulk base fluid.
at its interface with the nanoparticle and equals kbf at its interface with the bulk base fluid.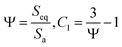
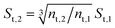 (nt,2 > nt,1) holds for spherical geometries. The predicted results in Fig. 5 also show that convective diffusion affects the thermal conductivity of alumina–water nanofluid by as much as 4% in theory.
(nt,2 > nt,1) holds for spherical geometries. The predicted results in Fig. 5 also show that convective diffusion affects the thermal conductivity of alumina–water nanofluid by as much as 4% in theory.