Open Access Article
Open Access ArticleComposition and distribution of internal resistance in an enzymatic fuel cell and its dependence on cell design and operating conditions
Ranran Wu a,
Chunling Maa,
Yang-Chun Yong
a,
Chunling Maa,
Yang-Chun Yong ab,
Yi-Heng P. Job Zhang
ab,
Yi-Heng P. Job Zhang a and
Zhiguang Zhu
a and
Zhiguang Zhu *a
*a
aTianjin Institute of Industrial Biotechnology, Chinese Academy of Sciences, 32 West 7th Avenue, Tianjin Airport Economic Area, Tianjin 300308, China. E-mail: zhu_zg@tib.cas.cn; Fax: +86-022-8486-1926; Tel: +86-022-2482-8797
bBiofuels Institute, School of the Environment, Jiangsu University, 301 Xuefu Road, Zhenjiang 212013, Jiangsu Province, China
First published on 5th March 2019
Abstract
A variety of sugar-based enzymatic fuel cells (EFCs) are able to completely oxidize fuels catalyzed by enzyme cascades, achieving high energy densities. However, the poor power output of EFCs limits their potential applications. In the present study, the composition of internal resistance throughout the EFCs affected by various factors, including the separator, enzyme loading, electron acceptor, applied voltage and operation time, was characterized by electrochemical impedance spectroscopy (EIS). Total resistance is divided into solution-separator resistance, charge transfer resistance, and diffusion resistance, respectively. The Nafion 212 membrane was found to yield a small solution-separator resistance and a high power density. Increased enzyme loading led to reduced internal resistance and improved cell performance, generating a maximum power density of 0.17 mW cm−2. Using potassium ferricyanide to replace oxygen as the electron acceptor could improve cathode performance significantly and resulted in a 4-fold increase in the power density. EIS was also performed for EFCs operated continuously for 16 h. Power output decreased distinctly over time, while the internal resistance, primarily the diffusion resistance, increased. Additionally, altering operation voltages had an impact on diffusion resistances. These results can be summarized that diffusion plays a rather important role in deciding the power and future efforts should be made towards increasing the mass transfer in EFCs.
1. Introduction
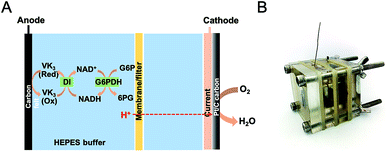
Enzymatic fuel cells (EFCs) have emerged as a promising technology to transform chemical energy to electric power using enzymes as biocatalysts. They are able to completely oxidize various fuels, such as sugar,1–3 alcohol,4 and glycerol,5 to achieve high energy densities catalyzed by enzyme cascades. Recently, our group has constructed several in vitro pathways to completely utilize a variety of inexpensive and widely-available pentose and hexose fuels, including maltodextrin,6 glucose,3 fructose,2 sucrose,2 and xylose,1 achieving very high Faraday efficiencies. However, the practical application of these sugar-based EFCs is still challenging. Their poor power output is still far from being applicable to powering portable or wearable electronic devices. Significant power loss over time can be observed because of multiple causes such as enzyme degradation, electrode fouling, and decreased mass transfer efficiency.7 Among our in vitro pathways, sugars are transformed to glucose-6-phosphate (G6P) under the catalysis of different enzymes. The oxidation of G6P catalyzed by glucose-6-phosphate dehydrogenase (G6PDH), as a key reaction, contributes to the electricity generation. Meanwhile, nicotinamide adenine dinucleotide (NAD+) is simultaneously reduced to NADH, which is subsequently re-oxidized by diaphorase (DI), producing two electrons per NADH. The electrons are further transferred to the anode by mediators. Therefore, the investigation of G6P-based EFC allows us to better understand the power limiting factors and enhance the performance of such sugar-based EFCs with high energy densities.Developing quantitative models based on the principles of fuel cells and biocatalysts and predicting the conditions that allow EFCs work at peak performance are of crucial importance to understand the fundamentals of EFCs and implement their applications. Various electrochemical tools such as cyclic voltammetry, differential pulse voltammetry, polarization curve, and chronoamperometry, have been employed to study the effects of cell configuration, electrode materials and operating conditions on the performance of many types of fuel cells. Among them, electrochemical impedance spectroscopy (EIS) has been demonstrated as a powerful technique to evaluate fuel cell properties and parameters.8,9 Different from other electrochemical techniques, EIS is considered as non-intrusive (i.e., it can be performed without disturbing the cell), and is of appreciable significance in diagnosing highly heterogeneous and complex systems.10 For example, several studies have been focused on the identification of the contribution of different internal resistances to the overall impedance of microbial fuel cells (MFCs), in order to find out the rate-limiting factor and draw the optimum power output.11–13 Generally, the overall internal resistance in MFCs can be determined by many aspects such as electrode, electrolyte, charge transfer, as well as mass transfer. Yet, the quantitative composition and distribution of the resistances and their dynamics under operation conditions remain unclear.
Since EFCs are very similar in principle and in configuration to MFCs, the same equivalent circuit model used for EIS studies of MFCs may also be suitable to analyze the impedance spectra of EFCs.14 To our limited knowledge, although EIS has been employed in a few studies to investigate immobilized enzyme electrodes15,16 or EFCs at limited operating conditions17 recently, more systematic work is desired to provide a better understanding for the distribution and dynamics of the resistances in EFCs.
Among various components of internal resistance, the one caused by separators is the most straightforward as they physically separate anodic and cathodic chambers and largely block the mass transfer in electrolyte, and it has been studied and optimized in MFCs since a decade ago.18,19 More recently, several membraneless EFCs have been constructed to totally remove the separator resistance and achieve the high power output, because of effective enzyme immobilization and high enzyme specificity.20–22 Besides separators, operating conditions also significantly influence the EFC performance. For example, Aaron et al. have demonstrated that in a hybrid EFC catalyzed by Pt on the anode and laccase on the cathode, increased enzyme loading results in improved power output and reduced internal resistance; EFCs operated continuously for 2 days lead to increases for all internal resistances; varying air-humidification temperatures have little effect on internal resistance.17 Wu et al. have investigated the electron transfer resistance of laccase-immobilized glassy carbon cathodes and concluded their electrochemical process as diffusion-limited.23 Campell et al. have also used EIS to examine the surface characteristics of the gold/carbon nanotube fiber anodes with various adsorbed materials and revealed a dramatically decreased electron transfer resistance by the modification of glucose oxidase with ferrocenyl acrylamide.24
Hereby, to systematically investigate the impact of separators and operating conditions on aforementioned sugar-based EFC performance, such as enzyme concentration, operation voltage, as well as operating time, a model EFC based on G6P oxidation was built and a detailed internal resistance analysis was conducted. The total internal resistance was divided into solution-separator, charge transfer, and diffusion resistances, to identify exactly which part of the internal resistance contributes to the changes in the performance under different operating conditions. This study can be used to guide the future design of EFCs with minimum internal resistance and enhanced performance.
2. Experimental
2.1 Materials
NAD+ and G6P purchased from Sigma-Aldrich (St. Louis, MO, USA) were reagent-grade. 1-Ethyl-3-[3-dimethylaminopropyl] carbodiimide hydrochloride (EDC) and poly-L-lysine (PLL) were purchased from Solarbio (Beijing, China). Multi-wall carbon nanotubes modified with carboxyl groups (Cheap Tubes Inc, Cambridgeport, VT, USA) were well dispersed in a 50% ethanol solution with a concentration of 5 mg mL−1. All other chemicals were analytical reagent grade and purchased from Sinopharm Chemical Reagent Co., Ltd (Shanghai, China). E. coli Top10 was used for DNA manipulation, and BL21 (DE3) containing a protein expression plasmid was used to produce the recombinant enzymes. E. coli cell growth and recombinant protein expression were performed in Luria–Bertani medium containing either 50 mg L−1 kanamycin or 100 mg L−1 ampicillin at 37 °C. Glucose-6-phosphate dehydrogenase (G6PDH) and diaphorase (DI) were purified using heat precipitation as described elsewhere.12.2 Preparation of bioanodes
Carbon felts (CF, Fuel Cell Earth, Stoneham, MA, USA) were cut into 1 × 1.5 cm2 and utilized to fabricate the bioanodes. Before being used, CFs were first treated with acetone (24 h) and 0.1 M HCl (24 h) successively and washed up with Milli-Q water. Then, 200 μL of 25 mM EDC solution, 100 μL of a PLL aqueous solution (2% (w/v)), 600 μL multi-walled carbon nanotube solution (5 mg mL−1 in 50% ethanol), 24 mg G6PDH, 12 mg DI, and 120 μL of a vitamin K3 (VK3) solution (0.29 M in acetone) were added onto the CF in the order mentioned. Drying at 40 °C for 20 min followed after each addition step. The enzyme-modified electrodes were rinsed in distilled water for 2 h to wash out non-immobilized enzymes before electrochemical measurements.2.3 EFC reactors and operation
Two-chambered, cubic-shaped EFCs with separate anodic and cathodic chambers were used in this study. Each chamber was 1 cm thick with an open internal area of 2 × 2 cm2. Enzymatic reaction occurred at the bioanode to generate the electrons while the terminal electron acceptor at the cathode was either oxygen or ferricyanide. The anolyte contained 4 mM NAD+, 100 mM G6P in a HEPES buffer (100 mM, pH 7.30) solution comprising of 100 mM NaCl, 5 mM MgCl2 and 0.5 mM MnCl2. For oxygen-based EFCs, HEPES (100 mM, pH 7.30) buffer served as the electrolyte in both chambers and Nafion 212, cellophane or glass fiber filter were used as the separator. Cathodes were made from wet proofing carbon cloth (CC, HCP330, Shanghai Chu Xi Industrial Co., LTD), with the water side coated by the Pt/C catalyst (0.5 mg cm−2 Pt) via 5% Nafion and isopropanol as the binder. In the tests using potassium ferricyanide as the electron acceptor, 100 mM NaCl served as catholyte and carbon clothes were used as cathode supporters. The projected area of the carbon cloth was 2 × 2 cm2. In the ferricyanide-based EFC, the cathodic and anodic chambers were separated by Nafion 212. The anode current collector was made of titanium wire, while the cathode current collector was a stainless steel mesh in contact with the cathode electrode. All experiments were operated in a batch mode at the room temperature in this study. A schematic of the EFC is shown in Fig. 1.2.4 Electrochemical measurements
Electrochemical measurements were performed with a Princeton PARSTAT 3000A potentiostat. EIS techniques were conducted using two-electrode measurements for the identification of total internal resistance of the whole cell, while the inclusion of a Ag/AgCl reference electrode was necessary for the measurement of individual electrode resistances. EIS spectra were obtained at open circuit potential over an AC frequency range of 100 kHz to 10 mHz, with a sinusoidal perturbation of 5 mV. The frequency range resulted in a scan time of approximately 30 min. In the test of applying varying voltages, anode was employed as the counter and reference electrode while five potentials were applied to the cathodes (0.7 V, 0.5 V, 0.3 V, 0.1 V and 0 V), and EIS was recorded when steady state was reached (30 min for each voltage). Polarization curve was conducted to evaluate the performance of EFCs. Open circuit potential was measured to determine the maximum voltage and linear sweep voltammetry was carried out at a scan rate of 1 mV s−1. The current density was calculated on the basis of the projected surface area of the bioanode and the power density was calculated by the product of the current density and potential recorded.2.5 Analysis
Because EFC is quite similar in construction to MFC, the equivalent circuit models often used for EIS of MFC studies can also be used for analyzing the EFC spectra.17 Commercial software (ZView version 3.1c, Scribner Associates, Inc.) was employed for equivalent circuit model fittings. The equivalent circuit for the whole cell is consisted of two parallel resistor–capacitor (R–Q) elements that are in series along with an extra resistor (Fig. 2). R is defined as the charge transfer resistance (Rct) and Q is the constant phase element (CPE). Each R–Q combination represents an electrode while the extra resistor represents a hybrid resistance that contains the anode solution, separator, and cathode solution. CPE represents a non-ideal capacitance occurring at the electrode–electrolyte interface, and it has an exponential factor n with a value between 0 and 1, where 1 corresponds to an ideal capacitor with a 2D surface and 0 represents a completely non-ideal behavior with some frequency dispersion caused by 3D surfaces of the electrode with high roughness. In this study, CPEs were used because the electrical double layers that form at the electrode interface were not ideal capacitors. A Warburg element (W) representing the impedance of semi-infinite linear diffusion was also considered in the equivalent electrical circuit, and such diffusion was appreciable mostly at the low AC frequency.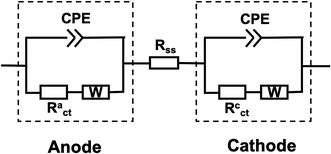 | ||
| Fig. 2 Equivalent electrical circuit model representing the EFC. R: Resister; CPE: constant phase element; W: Warburg diffusion element. | ||
In order to obtain the total resistance (Rt) of the full cell, linear sweep voltammetry was performed to get the voltage–current (U–I) curve between anode and cathode. A second-order polynomial regression equation was used to fit the measured U–I curve with current as the variate. The first derivative of the voltage–current curves (dU/dI) can be calculated according to the fitted equation and the total resistance of the cell was determined when current was 0 A.25,26 The total resistance consists of the solution and separator resistance (Rss), charge transfer resistance (Rct), and diffusion resistance (Rd). EIS was used to obtain solution-separator resistance and charge transfer resistance using equivalent circuits, with the diffusion resistance calculated as the difference between the total resistance and these two values mentioned above.27 When a single electrode was investigated, voltage–current curves between anode and Ag/AgCl, cathode and Ag/AgCl were obtained, respectively, to calculate total resistances of anode (Rat) and cathode (Rct). EIS was performed between the anode and Ag/AgCl, cathode and Ag/AgCl, respectively, to obtain solution-separator resistance (Rass, Rcss) and charge transfer resistance (Ract, Rcct) as well. The anode and cathode diffusion resistance Rad and Rcd were calculated as follow: Rad = Rat − Rass − Ract and Rcd = Rct − Rcss − Rcct.
2.6 Operating conditions explored via EIS
EIS measurements were performed to investigate the effects of various operating conditions on the internal resistances and power output of EFCs. The variables include separators, enzyme loadings, aeration, electron acceptors at the cathode and operating time. Separators included proton exchange membrane, cellulose membrane and glass fiber filter; enzyme loading were adjusted from 18 U cm−2 to 72 U cm−2; electron acceptors were oxygen and potassium ferricyanide; operating time varied from 0 h to 16 h; and the applied voltage to the EFC ranged from 0 to 0.7 V. Optimization of the conditions was expected to result in the improvement of power density for EFCs.3. Results and discussion
In general, membrane, enzyme loading, enzyme immobilization approach, salt concentration, electron mediator participation, external resistance, running time, and so on, were all expected to contribute to the resistance of EFCs. Because of the enzyme and mediator instability over time, as well as the substrate consumption, each experiment was performed with freshly immobilized enzyme electrode and fresh EFC materials for three times to ensure good reproducibility.3.1 Membrane resistances
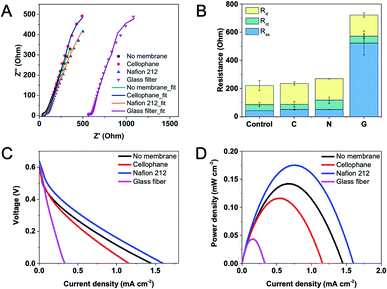
Three types of membranes including Nafion 212, cellophane and glass fiber were used in this study, and their properties are shown in Table 1. The impedance across the testing membrane was measured by EIS in a two-electrode mode with an anode served as the working electrode, and a cathode as the reference and counter electrode. The resistance corresponded to the minimum x-intercept of each experimental spectrum (closest to the origin) represented the combined solution and separator resistance (separator resistance + solution resistance). To obtain the separator resistance only, the combined resistance was deducted by the solution resistance, which was obtained from a blank experiment without a separator under the same testing condition. Fig. 3A shows Nyquist plots and fitted curves according to the equivalent circuit for EFCs equipped with different separators. Distribution of internal resistance was analyzed by using an equivalent circuit and presented in Fig. 3B. The results demonstrate that Nafion 212 and cellophane exhibit similar and pretty low membrane resistances (ca. 8 Ω) while glass fiber has the largest resistance (ca. 480 Ω), possibly due to the highest thickness of the glass fiber. Moreover, the diffusion resistance does not change much regardless of using a separator or not. In addition, we compared the resistances of EFCs using two different Nafion membranes, i.e. Nafion 117 and Nafion 212, but no evident difference was observed (data not shown).| Thickness (μm) | Exchange capacity (meq. g−1) | Density(g m−2) | Conductivity (S cm−1) | Pore size (μm) | |
|---|---|---|---|---|---|
| Nafion 212 | 50.8 | 0.95–1.01 | 100 | 0.083 | NA |
| Glass fiber | 200 | NA | NA | NA | 0.7 |
| Cellophane | 50 | NA | NA | NA | NA |
Open circuit voltage, power density and maximum current were also tested on EFCs with different membranes. It can be found that in the presence or absence of a membrane, all these EFCs can reach to an open circuit voltage of ca. 0.6 V (Fig. 3C). However, the maximum current and power density data varied greatly. Without a membrane, the maximum power density of the EFC was 0.14 mW cm−2 and the maximum current density was 1.45 mA cm−2. When using Nafion 212, the maximum power density and current density were even higher, possibly due to its high selectivity on protons. The maximum power and current density decreased slightly with the EFC using cellophane as a separator. The glass fiber showed the worst performance, possibly due to its large thickness and high resistance as mentioned above. The results of polarization curve coincide with the analysis of component internal resistances. Hence, Nafion 212 was adopted as the separator in following experiments.
3.2 Effects of enzyme loading on anode
The effect of enzyme loading was investigated using a series of immobilized enzyme electrodes with different enzyme quantities. According to our experience, the optimal weight ratio of G6PDH and DI was 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
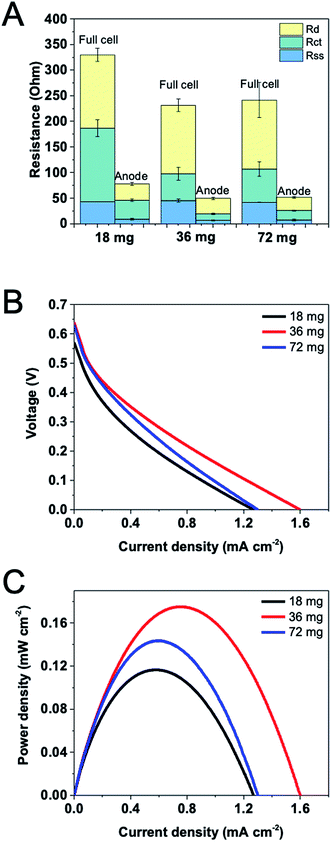
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and a 1 × 1.5 cm2 CF electrode immobilized with 16 mg cm−2 G6PDH and 8 mg cm−2 DI showed an excellent performance in a 4 mL three-electrode system (data not shown). Therefore, the enzyme loadings used for an optimization herein were 12 mg G6PDH/6 mg DI, 24 mg G6PDH/12 mg DI, and 48 mg G6PDH/24 mg DI, which in total were 18 mg, 36 mg and 72 mg enzymes immobilized, respectively. It is expected that the catalyst amount should have a strong influence on both the internal resistance and the power density of the cell.17 EIS was performed using a two-electrode mode for measuring the full cell resistance and using a three-electrode mode for obtaining anodic resistance with a Ag/AgCl as the reference electrode. In Fig. 4A, the distribution of internal resistance both for the full cell and the anode are presented with such three enzyme loadings. The total resistance decreased as the enzyme loading was increased from 18 mg to 36 mg. However, when enzyme loading was further increased, the total resistance remained unchanged. Comparing component internal resistances, separator-solution resistance showed a relatively stable value when changing enzyme loadings due to the uniform electrolyte and substrate concentration used in this study. Reduced charge transfer resistance for the full cell and the anode can be observed as the enzyme loading was increased from 18 mg to 36 mg. Nonetheless, charge transfer resistance was slightly increased if we further increased the enzyme amount. This may be because too many immobilized enzymes would over-occupy the surface of the electrode, impeding the charge transfer between the mediator and the accessible electrode. Notably, there is also no significant difference in the diffusion resistance when varying enzyme loadings. Fig. 4B shows that an insufficient enzyme loading significantly influence catalytic reaction rate on the anode, resulting in a lower voltage and current. The maximum current and power density tested on EFCs with different enzyme loadings confirmed that the optimal overall enzyme loading was 36 mg, which generated the output of 1.60 mA cm−2 and 0.17 mW cm−2 (Fig. 4C).
1, and a 1 × 1.5 cm2 CF electrode immobilized with 16 mg cm−2 G6PDH and 8 mg cm−2 DI showed an excellent performance in a 4 mL three-electrode system (data not shown). Therefore, the enzyme loadings used for an optimization herein were 12 mg G6PDH/6 mg DI, 24 mg G6PDH/12 mg DI, and 48 mg G6PDH/24 mg DI, which in total were 18 mg, 36 mg and 72 mg enzymes immobilized, respectively. It is expected that the catalyst amount should have a strong influence on both the internal resistance and the power density of the cell.17 EIS was performed using a two-electrode mode for measuring the full cell resistance and using a three-electrode mode for obtaining anodic resistance with a Ag/AgCl as the reference electrode. In Fig. 4A, the distribution of internal resistance both for the full cell and the anode are presented with such three enzyme loadings. The total resistance decreased as the enzyme loading was increased from 18 mg to 36 mg. However, when enzyme loading was further increased, the total resistance remained unchanged. Comparing component internal resistances, separator-solution resistance showed a relatively stable value when changing enzyme loadings due to the uniform electrolyte and substrate concentration used in this study. Reduced charge transfer resistance for the full cell and the anode can be observed as the enzyme loading was increased from 18 mg to 36 mg. Nonetheless, charge transfer resistance was slightly increased if we further increased the enzyme amount. This may be because too many immobilized enzymes would over-occupy the surface of the electrode, impeding the charge transfer between the mediator and the accessible electrode. Notably, there is also no significant difference in the diffusion resistance when varying enzyme loadings. Fig. 4B shows that an insufficient enzyme loading significantly influence catalytic reaction rate on the anode, resulting in a lower voltage and current. The maximum current and power density tested on EFCs with different enzyme loadings confirmed that the optimal overall enzyme loading was 36 mg, which generated the output of 1.60 mA cm−2 and 0.17 mW cm−2 (Fig. 4C).
3.3 Effects of electron acceptor on cathode
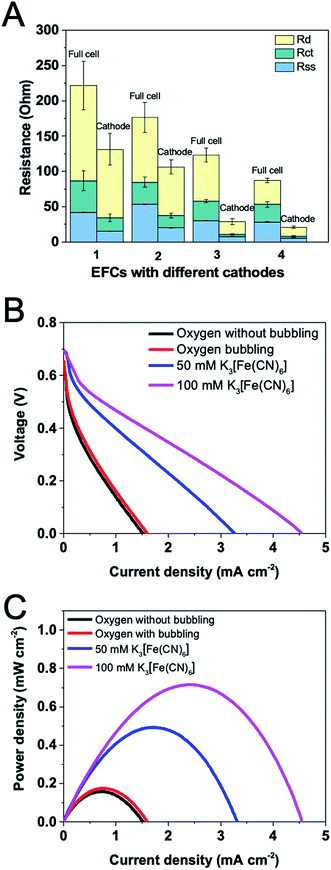
EIS measurements for the oxygen- or ferricyanide-based EFCs were conducted under open circuit conditions. Component internal resistances for both full cell and the cathode were shown in Fig. 5A. It is obviously shown that using ferricyanide as the electron acceptor greatly reduced the total resistance, especially the cathode resistance. This was in accordance with the impedance study of MFCs, in which ferricyanide-based one showed a much smaller charge transfer resistance in Nyquist plot than the oxygen-based one and the impedance did not extend into the low frequency region.28 External aeration was expected to lead to more dissolved oxygen available at the cathode, reducing the diffusion resistance and improving the catalytic rate for the oxygen reduction reaction. However, although charge transfer and diffusion resistances decreased under aeration, solution-separator resistance unexpectedly increased, which is possibly due to that the disturbance in the catholyte by aeration would impede the proton transfer in solution. When the ferricyanide concentration was increased from 50 mM to 100 mM, the total resistance for the full cell and the cathode further diminished, primarily arising from the decrease in diffusion resistance. Since ferricyanide reduction is a faster process, the minimum charge transfer resistance of cathode was found. In contrast, the oxygen-based cathode showed a higher charge transfer resistance. Because the ferricyanide has a lower redox potential (0.36 V vs. SHE) than oxygen (0.401 V vs. SHE), it possesses a stronger ability to receive electrons. Using ferricyanide instead of oxygen could also result in a smaller solution–separator resistance because of the alteration of catholyte.Polarization curves of the EFCs based on oxygen or ferricyanide were plotted (Fig. 5B and C). Although the total internal resistance was smaller under aeration when using oxygen as the terminal electron acceptor, the maximum current and power density showed no significant difference. This can be confirmed by another research which has demonstrated that the flow rate and oxygen concentration of the cathode gas stream had strong effects on stability but not on maximum current density.7 When ferricyanide (50 mM) was used, the maximum current and power density increased greatly, reaching to 3.31 mA m−2 and 0.49 mW m−2, respectively. When its concentration was further increased to 100 mM, in spite of the similar OCV generated, the maximum current and power density were improved to 4.55 mA m−2 and 0.72 mW m−2. A few studies have demonstrated that the maximum power can be increased by 50–80% by using ferricyanide instead of dissolved oxygen in MFCs.29,30 While in this study, we observed a 4-fold increase. The phenomenon demonstrates that the property of the cathode immensely influences the EFC performance.
3.4 EFC behavior over time
Fan et al.31 have demonstrated that the output of a fuel cell greatly influences EIS spectra. To study transport limitations near optimal operation, EIS measurements were conducted at the condition of yielding the maximum power density of the potassium ferricyanide-based EFC, which corresponded to applying ca. 50 Ω external resistance. The anode had 24 mg and 12 mg loadings of G6PDH and DI, respectively. During the operation, the solution (substrate, coenzyme, mediator, buffer etc.) was not refreshed. EIS and polarization curve measurements were performed on EFCs over time spans of 2 h, 4 h and 16 h.Fig. 6A shows the trend in each individual resistance, as well as in full cell resistance of the EFC over 16 h operation. The average total resistance increased by 13 folds from 88 Ω to 1143 Ω after 16 h. With time, the solution–separator resistance and charge transfer resistance were relatively unchanged while the diffusion resistance increased substantially. This observation was different from what Hudak et al. found that the solution resistance in EFCs increased over time because of water loss.7 Taking into account of that Nafion membrane is well known to persistently retain water, the consistent solution-separator resistance is reasonable. Due to the good stability of immobilized G6PDH, DI and VK3, the degradation of enzymes and mediator can be neglected, resulting in a constant charge transfer resistance. We speculated that the increasing diffusion resistance can be attributed to the substrate consumption on both electrodes, which was further confirmed by refilling experiments. After 16 h operation, 100 mM G6P was added into the anolyte. Component internal resistances reveal that the diffusion resistance dramatically decreased after the refilling. When the used catholyte was replaced with fresh potassium ferricyanide (100 mM) solution, the diffusion resistance further decreased. These results suggest that the consumption of substrate G6P and electron acceptor potassium ferricyanide were the primary causes of the increase in the total internal resistance of the EFC over time.
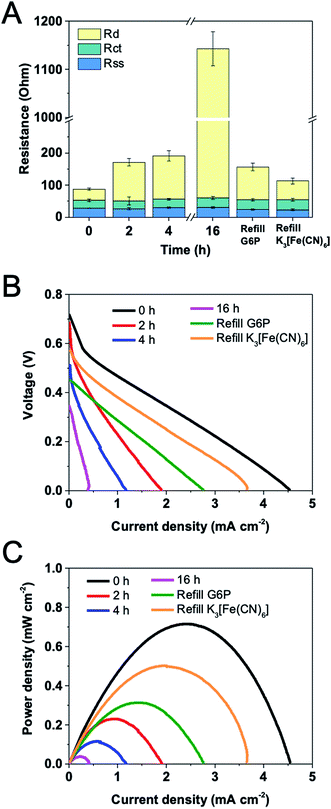 | ||
| Fig. 6 Variations of (A) internal resistances, (B) open circuit voltages and (C) power densities versus current density for a EFC operated for 16 h at a constant load of 50 Ω. | ||
Fig. 6B and C show the changes in OCV, current and power density over time for the EFC. OCV gradually decreased from 0.72 V to 0.35 V during the operation. It is apparent that the power density decreased significantly over the first hour to approximately 60% of the initial power output, from 0.72 mW m−2 to 0.27 mW m−2. Although enzyme/mediator degradation and water loss could also have contributed to this occurrence, this is considered unlikely because the power density decreased sharply during the experiment performed within a 1 h period. This can be further confirmed by the constant solution–separator and charge transfer resistances during the experiment. After 16 h, the power density was only 0.04 mW m−2, and the total resistance increased to 1143 Ω. It was found that the impedance and power output had a negative correlation, but not in an inversely proportional fashion. This happened because the resistance measured here do not include all internal impedances, such as capacitances and inductances. Besides, the enzymes and mediator may also slightly degrade over time.17 With the refilling of G6P after 16 h operation, OCV rose up to 0.45 V while maximum current and power density reached to 2.77 mA m−2 and 0.31 mW m−2, respectively. When fresh potassium ferricyanide solution was used, these values further increased. OCV, maximum current and power density were 0.58 V, 3.65 mA m−2 and 0.50 mW m−2, respectively. Combining with the results of the component internal resistances, it suggests that EIS can be used as a useful tool to detect the mechanism behind the loss of the cell performance.
3.5 Effects of operation voltage
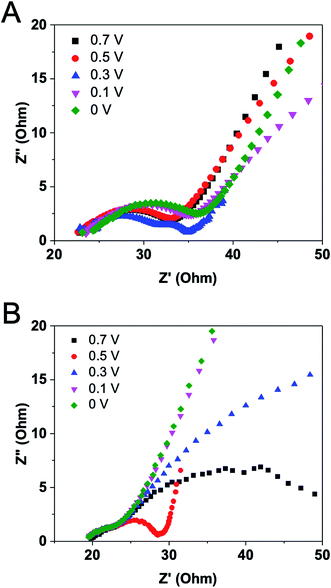
The behavior described in the previous studies indicates the necessity of acquiring EIS data for EFCs under diversified operating conditions.26 Varying operating conditions for an EFC will certainly change its internal resistance and power output. The effects of operation voltage on EFC internal resistance were therefore measured. The time allowed before measurements after a change in operation voltage was 30 min. It was found that Nyquist plot under 0.3 V exhibited a different pattern from plots under other voltages (Fig. 7A). It has two arcs in the range of low and medium frequencies, representing a two-time constants pattern involved. An insulating layer may occur under the voltage of 0.3 V. By analyzing component internal resistances, we noticed that the operation voltage had dominant effects on charge transfer and diffusion resistances. The second intercept on X-axis had a slight positive shift along with the decrease of operation voltage, demonstrating the increase of charge transfer resistance. In comparison with charge transfer resistance, the diffusion resistance varied greatly. The voltage of 0.3 V generated the smallest diffusion resistance value, possibly due to that the maximum power density can be produced under this voltage. This finding was also demonstrated by others that a minimum internal resistance was achieved at the maximum power density, rather than at the highest current.17Logan' group has revealed that diffusion resistance was usually the largest component internal resistance under high buffer cathode had effects on internal resistances.26 Cathode EIS spectra revealed that both the charge transfer and diffusion resistances were larger at 0.3 V than at 0.1 V at high buffer concentrations.26 Unlike in MFCs where operation voltages have effects on the growth of microorganisms and their extracellular electron transfer and hence cause the variations in charge transfer resistances, enzyme reaction in vitro is much more stable than microbial metabolism and thus the reaction rate in EFCs should not be affected by the external voltage. Therefore, the charge transfer resistance of the EFC maintained at a relatively steady value as noticed. Our result clearly indicates that the external voltage has an impact on substrate diffusion to the electrode or on product diffusion away from the electrode. The minimum internal resistance could be the result of minimized diffusion resistances at optimized voltage, as well as the reduction of other losses throughout the EFC.
To further confirm this, magnetic stirring was applied in the anodic chamber and EIS measurements were conducted under the same operation voltages. Fig. 7B shows quite similar results comparing with the experiment without stirring. The Nyquist plot suggests a two-time constants pattern and the lowest diffusion resistance under 0.5 V operation. However, the exact reason why diffusion resistance plays such an important role under different operation voltages has not been elucidated. More efforts should be focused on increasing the diffusion and mass transfer in EFCs using a flow-through mode.
4. Conclusions
Various aspects of EFC construction and operation conditions were investigated via EIS and the component internal resistances were obtained. Using different separators distinctly changed the performance of a EFC and Nafion 212 exhibited a small solution-separator resistance and a high power density of the EFC. Among operating conditions, enzyme loading, electrode acceptor at the cathode, operation voltage, and stability over time were of interests. Enzyme loading was demonstrated to have a very strong influence on both power density and internal resistances. As enzyme loading increased, the G6P oxidation reaction proceeded at a more rapid rate, contributing to a significant reduction in the charge transfer resistance. Using potassium ferricyanide as the terminal electron acceptor at the cathode instead of oxygen improved the cell performance meanwhile decreased the resistance of the cathode. Significant power loss and increased diffusion resistance of the EFC occurred over 16 h of operation, although the internal resistance and power density did not change in a correlative way. Additionally, the operation voltage also had an impact on the diffusion resistance of the EFCs.EIS technique has great potential in analyzing and studying component internal resistances of EFCs. However, it still has some limitations and knowledge of impedance alone is not sufficient. The equivalent circuit can hardly be modeled or accurately describe the real status of an EFC. Most EIS measurements in this study were conducted under OCP conditions, which may result in situations that differ from those occurring under practical working conditions. The performance and mechanism of a EFC could be fully understood by further combining EIS measurements with other electrochemical and biochemical methodologies.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Tianjin Institute of Industrial Biotechnology, Chinese Academy of Sciences (ZDRW-ZS-2016-3S), the National Natural Science Foundation of China (21706273) and the CAS Pioneer Hundred Talent Program (Type C, reference # 2016-081).Notes and references
- R. Wu, C. Ma, Y. H. P. Zhang and Z. Zhu, ChemCatChem, 2018, 10, 1–7 CrossRef.
- Z. G. Zhu, C. L. Ma and Y. H. P. Zhang, Electrochim. Acta, 2018, 263, 184–191 CrossRef CAS.
- Z. Zhu and Y. P. Zhang, Metab. Eng., 2017, 39, 110–116 CrossRef CAS PubMed.
- Y. H. Kim, E. Campbell, J. Yu, S. D. Minteer and S. Banta, Angew. Chem., Int. Ed. Engl., 2013, 52, 1437–1440 CrossRef CAS PubMed.
- D. P. Hickey, M. S. McCammant, F. Giroud, M. S. Sigman and S. D. Minteer, J. Am. Chem. Soc., 2014, 136, 15917–15920 CrossRef CAS PubMed.
- Z. Zhu, T. Kin Tam, F. Sun, C. You and Y. H. Percival Zhang, Nat. Commun., 2014, 5, 3026 CrossRef PubMed.
- N. S. Hudak, J. W. Gallaway and S. C. Barton, J. Electrochem. Soc., 2009, 156, B9–B15 CrossRef CAS.
- D. Kashyap, P. K. Dwivedi, J. K. Pandey, Y. H. Kim, G. M. Kim, A. Sharma and S. Goel, Int. J. Hydrogen Energy, 2014, 39, 20159–20170 CrossRef CAS.
- X. Dominguez-Benetton, S. Sevda, K. Vanbroekhoven and D. Pant, Chem. Soc. Rev., 2012, 41, 7228–7246 RSC.
- N. Sekar and R. P. Ramasamy, J. Microb. Biochem. Technol., 2013, S6, 004 Search PubMed.
- S. Sevda, K. Chayambuka, T. R. Sreekrishnan, D. Pant and X. Dominguez-Benetton, Bioelectrochemistry, 2015, 106(part A), 159–166 CrossRef CAS PubMed.
- Z. He and F. Mansfeld, Energy Environ. Sci., 2009, 2, 215–219 RSC.
- A. K. Manohar, O. Bretschger, K. H. Nealson and F. Mansfeld, Bioelectrochemistry, 2008, 72, 149–154 CrossRef CAS PubMed.
- S. Y. D. Aaron and C. Tsouris, Sep. Sci. Technol., 2008, 43, 2307–2320 CrossRef.
- R. Rahmanian, S. A. Mozaffari, H. S. Amoli and M. Abedi, Sens. Actuators, B, 2018, 256, 760–774 CrossRef CAS.
- G. Figueroa-Miranda, L. Y. Feng, S. C. C. Shiu, R. M. Dirkzwager, Y. W. Cheung, J. A. Tanner, M. J. Schoning, A. Offenhausser and D. Mayer, Sens. Actuators, B, 2018, 255, 235–243 CrossRef CAS.
- D. Aaron, A. P. Borole, S. Yiacoumi and C. Tsouris, J. Power Sources, 2012, 201, 59–65 CrossRef CAS.
- X. Zhang, S. Cheng, X. Wang, X. Huang and B. E. Logan, Environ. Sci. Technol., 2009, 43, 8456–8461 CrossRef CAS PubMed.
- G. Chen, B. Wei, Y. Luo, B. E. Logan and M. A. Hickner, ACS Appl. Mater. Interfaces, 2012, 4, 6454–6457 CrossRef CAS PubMed.
- S. A. Neto, R. D. Milton, D. P. Hickey, A. R. De Andrade and S. D. Minteer, J. Power Sources, 2016, 324, 208–214 CrossRef.
- N. Lalaoui, A. de Poulpiquet, R. Haddad, A. Le Goff, M. Holzinger, S. Gounel, M. Mermoux, P. Infossi, N. Mano, E. Lojou and S. Cosnier, Chem. Commun., 2015, 51, 7447–7450 RSC.
- M. J. Gonzalez-Guerrero, J. P. Esquivel, D. Sanchez-Molas, P. Godignon, F. X. Munoz, F. J. del Campo, F. Giroud, S. D. Minteer and N. Sabate, Lab Chip, 2013, 13, 2972–2979 RSC.
- G. Z. Wu, Y. Gao, D. Zhao, P. H. Ling and F. Gao, ACS Appl. Mater. Interfaces, 2017, 9, 40978–40986 CrossRef CAS PubMed.
- A. S. Campbell, H. Murata, S. Carmali, K. Matyjaszewski, M. F. Islam and A. J. Russell, Biosens. Bioelectron., 2016, 86, 446–453 CrossRef CAS PubMed.
- N. Wagner, J. Appl. Electrochem., 2002, 32, 859–863 CrossRef CAS.
- B. Wei, J. C. Tokash, F. Zhang, Y. Kim and B. E. Logan, Electrochim. Acta, 2013, 89, 45–51 CrossRef CAS.
- A. J. Hutchinson, J. C. Tokash and B. E. Logan, J. Power Sources, 2011, 196, 9213–9219 CrossRef CAS.
- R. P. Ramasamy, V. Gadhamshetty, L. J. Nadeau and G. R. Johnson, Biotechnol. Bioeng., 2009, 104, 882–891 CrossRef CAS PubMed.
- S. Oh, B. Min and B. E. Logan, Environ. Sci. Technol., 2004, 38, 4900–4904 CrossRef CAS PubMed.
- E. S. Yanzhen Fan and H. Liu, Environ. Sci. Technol., 2008, 42, 8101–8107 CrossRef.
- Y. Z. Fan, H. Q. Hu and H. Liu, J. Power Sources, 2007, 171, 348–354 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |