Open Access Article
Open Access ArticleInvestigation on the role of interfacial water on the tribology between graphite and metals
Yeonsoo Lim,
Haiwoong Park and
Arnaud Caron *
*
KoreaTech – Korea University of Technology and Education, Cheonan, 31253 Republic of Korea. E-mail: arnaud.caron@koreatech.ac.kr; Tel: +82-41-560-1363
First published on 4th March 2019
Abstract
We investigated the role of interfacial water on the atomic-scale tribology of graphite by contact atomic force microscopy. Upon the approach of Au and Pt tips toward graphite in water, the hydration layers on the respective surfaces interact with each other. This results in a discontinuous motion of the metallic tips towards the graphite surface. Snap-in forces measured with Au and Pt tips scale with their respective water adsorption energies. Moreover, we observed significant differences for the atomic-scale friction between the Au and Pt tips and graphite in water. The atomic-scale sliding friction between an Au tip and graphite is characterized by low friction forces (Ff < 1 nN in the range of normal force values Fn = 1–10 nN) and by a periodic stick-slip that corresponds to the honeycomb structure of graphite. With a Pt tip, the sliding friction on graphite in water is characterized by high friction forces (Ff ≈ 5 nN in the range of normal force values Fn = 1–10 nN) and by an atomic-scale stick-slip whose characteristic lengths may correspond to an ordered water adsorption layer between platinum and graphite.
A Introduction
The lubricating effect of graphite arises on the one hand from its weakly bonded basal planes that exhibit low resistance to shearing. Moreover, the lubrication of graphite has early been reported to depend on adsorbed layers that decrease the cohesion of graphite surfaces.1–3 In vacuum, graphite wears by dusting with a correspondingly high friction coefficient. For graphite rods or brushes sliding on copper, a friction coefficient of μ = 0.8 has been measured in vacuum. For the same tribological couple exposed to water vapor, wear was found to vanish with a corresponding decrease in the friction coefficient to μ = 0.18.1 Savage discussed these results based on the condensation of water vapor on graphite. Byrant et al. made similar observations on the effect of water vapor on the lubrication of graphite.2 In these studies, the authors discussed that in the presence of water vapor, the interlayer binding energy of graphite is significantly decreased when compared to that in the ultra-high vacuum conditions. Buckley and Brainard investigated the friction and wear of metals sliding on the prismatic and basal graphitic planes in different environments (high vacuum, HBr, O2, H2O vapor, and C2H2).4 For all of the tested metals (Au, Fe, and Ta), the friction was lower for the basal than the prismatic orientation of graphite. Coincidently, the tested metals were all observed to transfer onto the prismatic surface of graphite but not on its basal surface. Material transfer was however completely inhibited by the presence of physically adsorbed oxygen, water vapor, and acetylene. These results highlight the effect of metal/graphite adhesion on friction and how it can be inhibited by interfacial adsorbate layers.Recently, the friction of graphite has been experimentally revisited by means of atomic force microscopy. Such experiments allow the sliding of a single nm-scale asperity to be monitored as a function of both normal force and sliding velocity. The first of these experiments were conducted by Mate et al. with a tungsten tip.5 The authors observed a non-monotonous variation in the friction forces during sliding on the basal plane of graphite. The periodicity of these variations was found to correspond to the honeycomb structure of the graphitic surface. Jinesh and Frenken investigated the effect of humidity on the friction of graphite with a tungsten tip.6 At low relative humidity (up to 1%), the authors observed a stick-slip of motion with a periodicity corresponding to the honeycomb structure of graphite, as well. At larger relative humidity values (from 5% to 33%), an average stick-slip distance of 0.38 nm was derived and attributed to the crystalline structure of ice water. At a low scanning velocity, the presence of a crystalline water-adsorbed film gave rise to larger friction force values than those at low relative humidity. However, in immersed conditions, Vilhena et al. used Si3N4 tips to measure the atomic stick-slip on graphitic surfaces with a periodicity of their honeycomb structure.7
In this study, we investigated the role of interfacial water on the tribology of graphite in water with two different metallic tips, gold- and platinum-coated AFM tips. The structure of interfacial water and its effect on the snap-in, adhesion and friction forces between the tips and a graphite surface were probed by force spectroscopy, friction force microscopy, and spectral analysis. We discussed our results based on the reported structure and energetics of the adsorbed water on graphitic and metallic surfaces.
B Experimental
A graphitic surface was prepared by exfoliating the top layers of a highly oriented pyrolytic graphite (HOPG) sample with adhesive tape, followed by immersion in deionized water at T = 295 K. The as-prepared sample surface was then analyzed by atomic force spectroscopy and friction force microscopy using a XE-100 AFM, manufactured by Park Instruments, Republic of Korea. Both types of measurements were performed with an Au-coated cantilever (type contsc-Au, manufactured by NanoSensors, Switzerland) and a Pt-coated cantilever (type contsc-Pt, manufactured by NanoSensors, Switzerland). After measurements, the AFM tips were imaged by scanning electron microscopy and compared with pristine AFM tips of the same types (see Fig. 1). The measurements were also repeated with two different AFM cantilevers of each type to ensure the reproducibility of our results. In this study, only results obtained with single AFM tips of each of the aforementioned types are presented. In Fig. 1, a circle with a radius of 25 nm is overlaid on the apex of each tip. We observed that these circles matched well with the tip dimension, except for the unused Pt tip, which has a tip radius slightly less than 25 nm.Before the measurements were performed in water, the sensitivity of the photodiode was calibrated by recording a force–distance curve with each cantilever on a nanocrystalline thin film sample in air. Subsequently, the thermal vibration noise of the cantilevers was recorded in air and analysed accordingly to calculate the normal stiffness Cn of the cantilevers.8 After immersion in the water, the sensitivity of the photodiode was recalibrated by recording a force–distance curve with each cantilever on HOPG. The cantilevers' lateral stiffnesses Cl were then calculated according to the following formula:
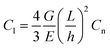 | (1) |
Force spectroscopy measurements were performed at various approach/retraction velocities in the range of dZ/dt = 50–2000 nm s−1 and over a Z-range of 30 nm, corresponding to a maximal normal force Fn,max ≈ 20 nN. For each approach/retraction velocity, 16 force–distance Fn(Z) curves were recorded. The analysis of the Fn(Z) curves consisted of extracting the snap-in force and the adhesion force values as a function of the approach/retraction velocity. Force-penetration Fn(δ) curves were also calculated by subtracting the cantilever deflection from the cantilever position, i.e.,
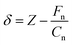 | (2) |
Friction measurements were performed over a scan area of 10 × 10 nm2 with a scanning velocity of 200 nm s−1 over a range of normal force values Fn = 1–10 nN. The friction measurements were repeated twice at each normal force value. Friction force maps were calculated according to the following formula
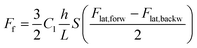 | (3) |
C Results and discussion
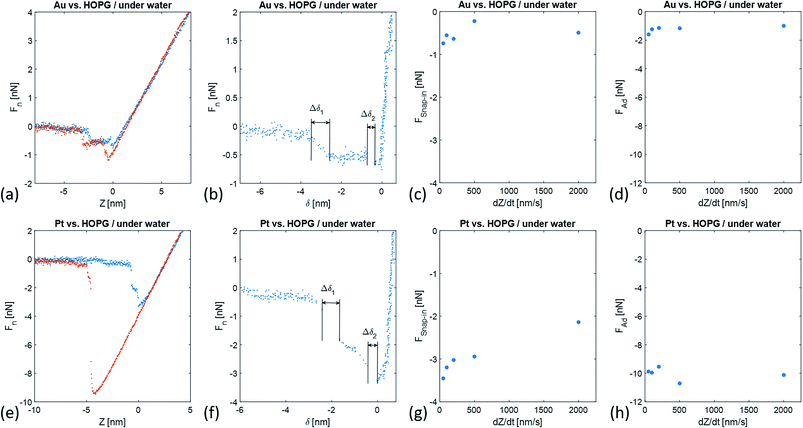
Fig. 2 compares typical Fn(Z) and Fn(δ) curves recorded under water on HOPG with Au-coated and Pt-coated tips. Upon both the approach and retraction of the tip towards/from the immersed HOPG surface, we observed distinct snap-in and detachment events in the force–distance curves that correspond to the sudden jumps of magnitude Δδ1,2 toward the immersed HOPG surface. In Fig. 2, the zero position of the Z-scanner was arbitrarily set to correspond to the minimum normal force value of the approach toward the immersed HOPG surface. For both Au- and Pt-coated tips, the magnitudes of these jumps are listed in Table 1.| Δδ1 | Δδ2 | k1 | k2 | k3 | k4 | |
|---|---|---|---|---|---|---|
| [pm] | [rad nm−1] | |||||
| Au | 616 | 359 | 25.76 | 49.01 | — | — |
| Pt | 770 | 433 | 11.62 | 16.96 | 22.62 | 28.9 |
The magnitudes of the jumps observed with a Pt-coated tip are ∼1.2 larger than those with an Au-coated tip. The maximum snap-in force FSnap-in values also significantly differed with the tip chemistry and only showed weak associations with the approaching velocity. In the case of the Au-coated tip, we found FSnap-in = −0.52 ± 0.09 nN, while for the Pt-coated tip we found FSnap-in = −2.95 ± 0.24 nN. The difference in the adhesion force Fad values between the immersed HOPG and the Au-coated and Pt-coated tips were significantly larger. For both tips, the Fad values also showed weak variations with the retraction velocity. In the case of the Au-coated tip, we found Fad = −1.23 ± 0.11 nN, while for a Pt-coated tip we found Fad = −9.95 ± 0.21 nN.
The geometries and energetics of the adsorbed water on Pt(111) were calculated by an ab initio molecular dynamics simulation.10 For a bilayer forming a 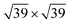 super-cell on Pt(111), a water bilayer was found to have thickness between 210 pm and 440 pm and a corresponding adsorption energy Eads = −0.615 eV. In the case of the Au(111) surface, the thickness of the different types of adsorbed water layers was found to vary between 361 pm and 399 pm with corresponding adsorption energies in the range of Eads = −0.15 eV and Eads = −0.11 eV.11 In the case of graphene, the thickness of the adsorbed water layer was computed to be ∼300 pm,12 while the adsorption energy was measured on the carbon nanotubes to be ∼−0.25 eV.13 It is noteworthy that the ratio of the snap-in forces for the Pt tip and the Au tip,
super-cell on Pt(111), a water bilayer was found to have thickness between 210 pm and 440 pm and a corresponding adsorption energy Eads = −0.615 eV. In the case of the Au(111) surface, the thickness of the different types of adsorbed water layers was found to vary between 361 pm and 399 pm with corresponding adsorption energies in the range of Eads = −0.15 eV and Eads = −0.11 eV.11 In the case of graphene, the thickness of the adsorbed water layer was computed to be ∼300 pm,12 while the adsorption energy was measured on the carbon nanotubes to be ∼−0.25 eV.13 It is noteworthy that the ratio of the snap-in forces for the Pt tip and the Au tip, 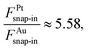 was close to the ratio of the water adsorption energies on the same metals, i.e.,
was close to the ratio of the water adsorption energies on the same metals, i.e., 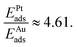
During force spectroscopy measurements in air or ultra-high vacuum, the snap-in of the AFM tip onto a surface is a fast process. In Fig. 2, the approach of metal tips toward an immersed HOPG surface consists of two types of processes: fast and slow. At large distance of metal tips from the HOPG surface the approach velocity follows the programmed value. In the case of an Au tip approaching towards immersed HOPG, we first observed an increase in the approach velocity, 3.345 nm away from the minimal snap-in force value and within the range of δ values Δδ1 = 616 pm. During this first attraction process, a force decrease of ΔF1 = −0.54 nN was measured. Subsequently, the Au tip further approached towards the HOPG surface with the pre-set velocity and under the same attraction force to a distance of 715 pm away from the surface, at which point a new and fast snap-in was observed. This snap-in event was characterized by Δδ2 = 359 pm and ΔF2 = −0.13 nN. In the case of a Pt tip approaching an immersed HOPG surface, a similar scenario was observed. At a tip-surface distance of 2.5 nm, we observed a first snap-in event characterized by Δδ1 = 770 pm and ΔF1 = −1.18 nN. However, further approaching toward the immersed HOPG surface, the force sensed by the cantilever further decreased at a roughly constant rate down to −2.72 nN, corresponding to a tip-sample distance of 573 pm. At this tip-sample distance, we observed a second snap-in event characterized by Δδ2 = 433 pm and ΔF2 = −0.51 nN.
The observed jumps in the Fn(δ) curves were expected to immediately follow the penetration of the metallic tips through the hydration layers between the metal tips and HOPG surface. Cheng et al. measured the density distribution of the interfacial water oxygen atoms by X-ray reflectometry as a function of the distance z from a mica surface.14 The density distribution ρ(z) plot showed a first maximum at a distance z = 132 pm, corresponding to the adsorbed layer of water onto mica. At larger distances of z = 252 pm, 373 pm, and ∼880 pm, broader maxima were observed and attributed to the hydration layers. Ho and Striolo compared different water models to simulate the structural properties of water at the interface with graphene by molecular dynamics.12 The calculated density distribution function for the oxygen atoms showed a first maximum at a distance from graphene of z = 320 pm, corresponding to the adsorbed water layer. At larger distances of z = 625 pm and z = 1 nm, broader maxima could be observed that correspond to the hydration layers. From these results, it is apparent that the spacings between the adsorbed water and the hydration layers depended on the hydrophobicity of the wetted surface, i.e. these spacings increased with the hydrophobicity of the surface. Trudeau et al. calculated the density distribution functions of water as a function of the distance from six surfaces with different hydrophobicity using a molecular dynamics simulation.15 In this study, the hydrophobicity of the simulated surfaces was characterized by their wetting angle that varied from 84° to 156°. Moreover, all of the six simulated surfaces had a rather hydrophobic character, an increase in the wetting angle resulted in a shift in the first maximum in the density distribution function to larger distances from the water/solid interfaces and its broadening. Further maxima corresponding to the hydration layers were found to shift to larger distances and to broaden with the increase in wetting angles. In the latter case, the shifting and broadening effects were more significant than in the case of the adsorbed water layer. Limmer et al. also used a molecular dynamics simulation to investigate the structure and hydration of Pt-like metal–water interfaces for two different metal surface orientations: (111) and (100).16 For both of these metallic surfaces, the authors observed a first maximum in the density distribution functions at a distance of z = 250 pm from the metal surface. At larger distances of z = 650 pm and z = 1 nm, broader maxima corresponding to the hydration layers were observed.
In our experiments, water adsorption and hydration needed to be considered for both the metallic tips and graphite surface. Upon the approach of an AFM tip towards a graphite surface in water, we expected the hydration and adsorbed layers on both the tip and sample surface to overlap and interact with each other. We attributed the snap-in events observed with an Au or Pt tip to the successive overlaps of the hydration layers on the graphite and metallic tips.
The overlap of the water layers could be expected to give rise to repulsive forces. As we observes in Fig. 2, while approaching toward immersed HOPG surface, the Au and Pt AFM tips underwent sudden jumps that were characterized by ΔF1,2 < 0. The jumps were however too fast to understand their mechanism by quasi-static methods, such as those applied in this study. Recently, Yang et al. investigated the hydration structures on mica and graphene by frequency modulation NC-AFM with a hydrophilic tip (Si/SiOx).17 In this study, the authors recorded the frequency shift Δf of the cantilever oscillation (with a natural frequency on the order of MHz) while approaching the AFM tip towards immersed mica and graphene surfaces. The measured Δf(Z) plots were found to exhibit oscillations for both the immersed mica and graphene, whose periods were attributed to the thickness of their hydration layers. For vibration amplitudes smaller than the tip-sample distance, a Δf(Z) plot relates to a force–distance curve according to the following formula:
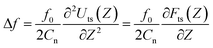 | (4) |
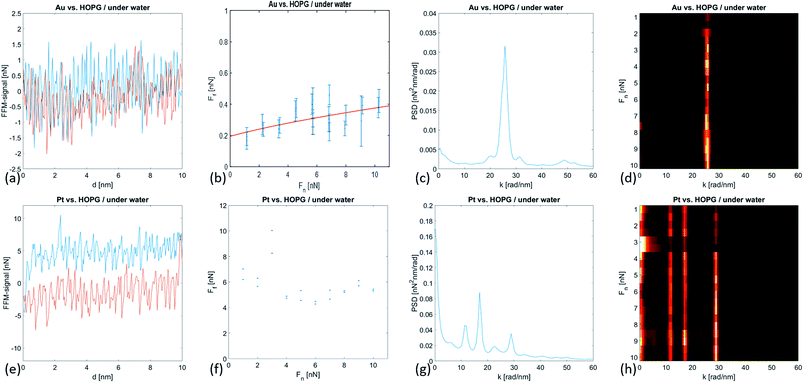
Fig. 3 shows the forward and backward FFM traces on the immersed HOPG with both types of tips. With the gold tip, the recorded signal was very weak, and the traces almost overlapped. Correspondingly, the friction force Ff values were small and showed weak variations while increasing the normal force Fn. In the case of the Pt-coated tip, the recorded FFM signals were significantly higher and corresponded to Ff values almost six times higher than those of the Au-coated tip. In the case of the Au tip, the friction force values displayed a weak dependence on the normal force values that can be fitted with the JKR model according to the following formula:19–21
| Ff = τAc | (5) |
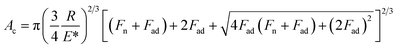 | (6) |
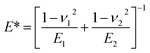 | (7) |
The friction force 〈Ff〉 value averaged over the whole range of normal force values was found to be high for larger adhesion forces Fad, i.e. 〈Ff〉Au = 0.62 ± 0.07 nN and Fad,Au = −1.23 ± 0.11 nN and 〈Ff〉Pt = 5.73 ± 1.19 nN and Fad,Pt = −9.57 ± 0.21 nN. It is interesting to note that for both tips, 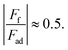
In both cases, the sliding motion of the tips exhibited an atomic scale stick-slip. We determined the periodicity of the stick-slip by calculating the PSD function of the FFM image. In the case of an Au-coated tip, we observed a clear peak at k1 = 25.76 rad nm−1 corresponding to a characteristic wavelength λ1 = 0.244 nm. We attributed this wavelength to the Cα–Cα interatomic distance aαα = 0.246 nm. At higher k-values, we observed a second and wider peak at k2 = 49.01 rad nm−1 that corresponded to the characteristic wavelength λ2 = 0.128 nm (see Table 2). This value somewhat agrees with the Cα–Cβ interatomic distance aαβ = 0.142 nm. In the case of the platinum tip, the one-dimensional PSD function of the FFM signal revealed four peaks at positions k1 = 11.94 rad nm−1, k2 = 16.96 rad nm−1, k3 = 22.62 rad nm−1, and k4 = 28.9 rad nm−1, corresponding to the characteristic wavelengths λ1 = 0.526 nm, λ2 = 0.370 nm, λ3 = 0.277 nm, and λ4 = 0.217 nm, respectively (see Table 2). It is interesting to compare these values with the structural lengths in ice water; the distance between the two O atoms in hexagonal ice was 276 pm (first coordination radius), the interlayer spacing was 367 pm and the third coordination radius was 526 pm.22 The wavelength λ4 = 0.217 nm might correspond to the Pt–O bond length.23
| λ1 | λ2 | λ3 | λ4 | |
|---|---|---|---|---|
| [pm] | ||||
| Au | 244 | 128 | — | — |
| Pt | 526 | 370 | 277 | 217 |
First atomic scale friction results on HOPG were presented.5 There, the authors monitored the lateral deflection of a bent W wire with a tip at its end during sliding on a cleaved HOPG surface to determine the friction force. In this study, the tip radius was in the range of 150 nm to 300 nm and the normal contact force values varied from 1.5 μN to 20 μN. The lateral deflection signal of the wire indicated that the tip did not continuously slide over the surface but exhibited a corrugation with a typical periodicity of 0.25 nm, corresponding to the periodicity of the honeycomb structure of graphite (0.246 nm). The stick-slip motion of a sharp tip sled on HOPG was only observed at particular scanning angles of the tip with respect to the sample surface.24 In line with previous observations that scanning tips can pick up a flat flake of graphite that is parallel to the basal plane of HOPG, the authors attributed the scanning angle dependence of the friction and atomic stick-slip to the commensurability of the contacting surfaces. The incommensurability of the HOPG surface and flake lattices led to ultra-low friction and continuous sliding motion commensurate with the stick-slip motion and higher friction. More recently, Vilhena et al. used a sharp silicon nitride tip with a radius of ∼2 nm (according to the manufacturer's data) to resolve the lattice parameters of graphite and graphene grown onto Ni and Cu in water.7 In this study, the range of the applied normal force values was 5 nN to 50 nN. For the experimental results obtained by Vilhena et al., the contact pressure could be computed by 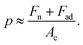 Using EHOPG = 30 GPa and νHOPG = 0.24, and ESi3N4 = 310 GPa and νSi3N4 = 0.27, and Fad = 0 nN (the adhesion force value was not reported by Vilhena et al.), we obtain that, in their study,7 the contact pressure varied between 4 GPa and 13 GPa. In our work, the AFM tip radii were measured to be ∼25 nm (see Fig. 1), and the normal load varied between 1 nN and 10 nN. Using EAu = 75 GPa, νAu = 0.44, and Fad,Au = −1.4 nN, and EPt = 168 GPa, νPt = 0.38 and Fad,Pt = −9.5 nN, we calculated that in this study the contact pressure varied over a range of p = 0.2–0.5 GPa with an Au tip and p = 0.3–0.5 GPa with a Pt tip. These values are significantly lower than the calculated values for the experimental data presented by Vilhena et al.7 We thus suggest that the high contact pressure values in their work were sufficiently high to penetrate through the adsorbed water layer.
Using EHOPG = 30 GPa and νHOPG = 0.24, and ESi3N4 = 310 GPa and νSi3N4 = 0.27, and Fad = 0 nN (the adhesion force value was not reported by Vilhena et al.), we obtain that, in their study,7 the contact pressure varied between 4 GPa and 13 GPa. In our work, the AFM tip radii were measured to be ∼25 nm (see Fig. 1), and the normal load varied between 1 nN and 10 nN. Using EAu = 75 GPa, νAu = 0.44, and Fad,Au = −1.4 nN, and EPt = 168 GPa, νPt = 0.38 and Fad,Pt = −9.5 nN, we calculated that in this study the contact pressure varied over a range of p = 0.2–0.5 GPa with an Au tip and p = 0.3–0.5 GPa with a Pt tip. These values are significantly lower than the calculated values for the experimental data presented by Vilhena et al.7 We thus suggest that the high contact pressure values in their work were sufficiently high to penetrate through the adsorbed water layer.
We believe that our force spectroscopy measurements describe the structure of the hydration layers and their interpenetration during the approach of an AFM tip to immersed HOPG. Moreover, the friction measurements appear to be sensitive to the adsorbed water layer between an AFM tip and HOPG. Interestingly, the periodicity of the atomic-scale stick-slip with an Au tip matches the periodicity of HOPG, while the evaluated wavelengths of the stick-slip with a Pt tip indicate the presence of an ice-like water layer. As reported in the literature, water weakly got adsorbed on Au and HOPG, while the adsorption of water on Pt was significantly stronger.10,11,13 We thus conclude that in our friction measurements, the weakly adsorbed water between Au and HOPG was swept away, while the strongly adsorbed water between Pt and HOPG acted as a glue between the solid bodies.
D Conclusions
We found that the tribological behaviour of graphite in water strongly depends on the adsorption strength of the interfacial water layer. For water on a gold tip with a weak adsorption strength, we observed an atomic-scale stick slip with a characteristic length corresponding to the honeycomb structure of graphite. In this case, both the adhesion and friction force values were low. In contrast, the strong adsorption strength of water on a platinum tip gave rise to significantly larger adhesion and friction force values (almost ten times larger than those with a gold tip of similar size). These results provide new insights into the effect of adsorbed water layers on friction.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by KOREATECH's Education and Research Promotion Program in 2018.References
- R. H. Savage, Graphite lubrication, J. Appl. Phys., 1948, 19, 1–10 CrossRef CAS.
- P. J. Bryant, P. L. Gutshall and L. H. Taylor, A study of mechanisms of graphite friction and wear, Wear, 1964, 7, 118–126 CrossRef.
- F. P. Bowden and J. E. Young, Friction of diamond, graphite and carbon and the influence of surface films, Proc. R. Soc. London, Ser. A, 1951, 208, 444–455 CAS.
- D. H. Buckley and W. A. Brainard, Friction and wear of metals in contact with pyrolytic graphite, Carbon, 1975, 13, 501–508 CrossRef CAS.
- C. M. Mate, G. M. McClelland, R. Erlandsson and S. Chiang, Atomic-scale friction of a tungsten tip on a graphite surface, Phys. Rev. Lett., 1987, 59, 1942–1945 CrossRef CAS PubMed.
- K. B. Jinesh and J. W. M. Frenken, Experimental evidence for ice formation at room temperature, Phys. Rev. Lett., 2008, 101, 036101 CrossRef CAS PubMed.
- J. G. Vilhena, C. Pimentel, P. Pedraz, F. Luo, P. A. Serena, C. M. Pina, E. Gnecco and R. Perez, Atomic-scale sliding friction on graphene in water, ACS Nano, 2016, 10, 4288–4293 CrossRef CAS PubMed.
- H.-J. Butt and M. Jaschke, Calculation of thermal noise in atomic force microscopy, Nanotechnology, 1985, 6, 1–7 CrossRef.
- H. E. Ko, S. G. Kwan, H. W. Park and A. Caron, Chemical effects on the sliding friction of Ag and Au(111), Friction, 2018, 6, 84–97 CrossRef CAS.
- S. Meng, E. G. Wang and S. Gao, Water adsorption on metal surfaces: A general picture from density functional theory studies, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 195404 CrossRef.
- A. Huzayyin, J. H. Chang, K. Lian and F. Dawson, Interaction of water molecule with Au(111) and Au(110) surfaces under the influence of an external electric field, J. Phys. Chem. C, 2014, 118, 3459–3470 CrossRef CAS.
- T. A. Ho and A. Striolo, Molecular dynamics simulation of the water-graphene interface: comparing water models, Mol. Simul., 2014, 40, 1190–1200 CrossRef CAS.
- T. Kokabu, S. Inoue and Y. Matsumara, Estimation of adsorption energy for water molecules on a multi-walled carbon nanotube thin film by measuring electric resistance, AIP Adv., 2016, 6, 115212 CrossRef.
- L. Cheng, P. Fenter, K. L. Nagy, M. L. Schlegel and N. C. Sturchio, Molecular-scale density oscillations in water adjacent to a mica surface, Phys. Rev. Lett., 2001, 87, 156103 CrossRef CAS PubMed.
- T. G. Trudeau, K. C. Jena and D. K. Hore, Water structure at solid surfaces of varying hydrophobicity, J. Phys. Chem. C, 2009, 113, 20002–20008 CrossRef CAS.
- D. T. Limmer, A. P. Willard, P. Madden and D. Chandler, Hydration of metal surfaces can be dynamically heterogeneous and hydrophobic, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 4200–4205 CrossRef CAS.
- C.-W. Yang, K. Miyasawa, T. Fukuma, K. Mitaya and I.-S. Hwang, Direct comparison between subnanometer hydration structures on hydrophilic and hydrophobic surfaces with three-dimensional scanning force microscopy, Phys. Chem. Chem. Phys., 2018, 20, 23522–23527 RSC.
- F. J. Giessibl, Forces and frequency shifts in atomic-resolution dynamic force microscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 16010–16015 CrossRef CAS.
- F. P. Bowden and D. Tabor, The friction and lubrication of solids, Oxford University Press, 1950 Search PubMed.
- K. L. Johnson, Contact mechanics, Cambridge University Press, 1985 Search PubMed.
- K. L. Johnson, K. Kendall, A. D. Roberts and D. Tabor, Surface energy and the contact of elastic solids, Proc. R. Soc. London, Ser. A, 1971, 324, 301–313 CrossRef CAS.
- J. Fraxedas, Water at interfaces: A molecular approach, CRC Press, 2014 Search PubMed.
- A. P. Seitsonen, Y. Zhu, K. Beduerftig and H. Over, Bonding mechanisms and atomic geometry of an hydroxyl overlayer on Pt(111), J. Am. Chem. Soc., 2001, 123, 7347–7351 CrossRef CAS PubMed.
- M. Dienwiebel, G. S. Verhoeven, N. Pradeep, J. W. M. Frenken, J. A. Heimberg and H. W. Zandbergen, Superlubricity of graphite, Phys. Rev. Lett., 2004, 92, 126101 CrossRef PubMed.
| This journal is © The Royal Society of Chemistry 2019 |