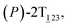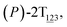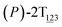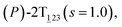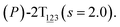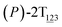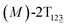Open Access Article
Open Access ArticleUnveiling the helicity switching mechanism of a rigid two-tiered stacked architecture†
Peng Liu *,
Yafei Duan,
Xihui Bian
*,
Yafei Duan,
Xihui Bian and
Xiaoyao Tan
and
Xiaoyao Tan
School of Chemistry and Chemical Engineering, State Key Laboratory of Separation Membranes and Membrane Processes, Tianjin, 300387, People's Republic of China. E-mail: liupeng012@tjpu.edu.cn
First published on 11th January 2019
Abstract
Conformational inversion of foldamers has been shown to transmit signals across the lipid membrane. Helicity switching is critical to fulfilling this function. Despite the importance of the conformational inversion, the mechanism that underlies the helicity switching process remains unclear. In the present contribution, a rigid two-tiered stacked architecture (2T) has been investigated at the atomic level using molecular simulations. The architecture consists of two conjugated cores and three flexible side chains. Two- and three-dimensional free-energy landscapes characterizing the isomerization of 2T reveal a four-stage helicity switching process. Four stages involve the flipping of three peripheral aromatic rings in the top tier and rotating of the bottom tier relative to the top one. The highest barrier hampering the transition between right-handed and left-handed helices emerges as the second benzene ring flips. Structural analysis shows that the ring flipping stretches the side chain, which leads to the deformation of conjugated cores, twist of dihedral angles within side chains, and the reorientation of amine moieties attached to chains. By deciphering the intricate mechanism whereby the rigid stacked architecture isomerizes, our understanding of the helicity switching is expected to be improved, helping in turn the construction of novel functional helices.
Introduction
Helicity is a property of asymmetry in molecules. Within helical structures, a set of substituents is held about an axis in a spiral arrangement that cannot be superimposed with its mirror image. Spiral arrangements widely exist in biological macromolecules, such as DNA. The elaborate biological helices are key structural motifs to store genetic information. Inspired by their sophisticated design, chemists have synthesized a series of artificial helical oligomers,1 polymers,2 and supramolecules3 in the right-handed (P) or left-handed (M) state as optical materials,4 chiral sensors5 and asymmetrical catalysts.6The property of helical architectures can be regulated by inducing a conformational inversion triggered by external stimuli, viz., high temperature,7 salt enrichment,8 and light irradiation.9 Inverting the helical direction can play an important role to transmit information across the lipid membrane.10 To mimic the function of G-protein-coupled receptors, Clayden and co-workers designed and fabricated helical foldamers.11 Binding of a chiral ligand with one terminal site inverts (P)- or/and (M)-helix. The helicity inversion propagates along the full length of foldamers and carries information to a reporter located at another terminus.12 Further experiments show that the helicity switching is critical for the communication between compartments in artificial tissues.13 However, the mechanism that underlies helicity switching is still an open question.
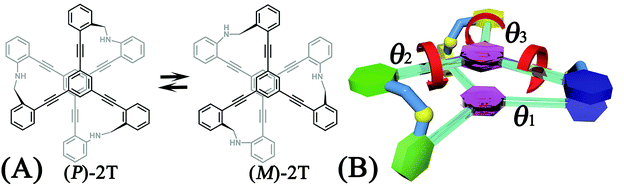
A two-tiered stacked architecture (2T) designed and fabricated by Hartley and co-workers14 can be considered as a paradigm for helical structures. This architecture was constructed by assembling discotic cores functionalized with three arms through imine formation. Based on 1H NMR spectra and DFT calculations, rotations of threes arms result in the helicity switching process (see Scheme 1A) occured in toluene. The free-energy barrier of activation, ΔG‡, was estimated as ca. +7.0 kcal mol−1, assuming a negligible ΔS‡. The primary thrust of the present contribution is identifying the switching pathway and understanding the underlying mechanism.
To the best of our knowledge, characterizing the helicity switching process within multi-tiered architecture at the molecular level is absent. To explore the unknown area, the three-dimensional free-energy landscape characterizing the rotational processes of three arms was determined. Intermediated states were identified and classified. All possible switching pathways share a four-stage pattern. These stages were characterized by drawing additional two- and three-dimensional free-energy landscapes in further. Analysis of structural features together with the reconstruction of least free-energy path help us to understand the helicity switching process of 2T.
Simulation details
Molecular models
The structure of 2T presented in Scheme 1A was constructed and immersed in a box of toluene. The initial size of the box was 70.0 × 70.0 × 69.3 Å3 with 1728 toluene molecules. To improve the convergence of free-energy calculations, the top tier of 2T was restrained to coplanar with the xy plane by means of a harmonic potential with a force constant of 5.0 kcal mol−1 Å−1. In the subsequent molecular dynamics (MD) simulations, the spinning of the top tier around the z axis was constrained. For the system, a 200 ns equilibrium MD simulation was preformed prior to the free-energy calculations.Molecular dynamics simulations
All the MD simulations reported here were conducted employing the NAMD 2.12 program,15 with the CHARMM general force field.16,17 The temperature and pressure were maintained at 300.0 K and 1 bar, respectively, employing Langevin dynamics and the Langevin piston method.18 The length of the covalent bonds involving a hydrogen atom was frozen to its equilibrium value by means of the Shake/Rattle and Settle algorithms.19 The r-RESPA multiple-time-stepping algorithm was applied to integrate the equations of motion with a time step of 2 and 4 fs for short- and long-range interactions, respectively. Short-range van der Waals and electrostatic interactions were truncated smoothly by means of a 12 Å spherical cutoff with a switching function applied beyond 10 Å. The particle-mesh Ewald20 algorithm was used to compute the long-range electrostatic interactions with a mesh spacing of <1.0 Å. Visualization and analysis of the MD trajectories were performed with VMD 1.9.3.21Free-energy calculations
The free-energy landscapes in this contribution were generated using the extended adaptive biasing force (eABF) algorithm22–26 implemented within the COLVAR module27 of NAMD.28 Informed by MD simulations, the transition coordinate, either two- or three-dimensional, was formed by reaction coordinates θ1, θ2, and θ3, chosen as the spin angle of the first (blue), second (green), and third (yellow) aromatic unit in the top tier around the alkyne moieties, respectively (see Scheme 1B). Instantaneous values of the force were accrued in mesh grids. The variation of the free energy, ΔG, was determined by integrating the average force acting on the transition coordinate.In order to have a full view of the free-energy landscape characterizing the helicity switching process, a coarse grid was applied in the calculation of ΔG (θ1, θ2, θ3). For each spin angle, the full range of rotation (−90° to 270°) was explored with a bin width of 6.0°. Further analysis reveals that 12 possible pathways of the helicity switching process share a common four-stage pattern containing three different kinds of stages, viz., stage I, stage II, and stage III. The first two stages were investigated by drawing the two-dimensional free-energy map along θ1 and θ2. These spin angles were explored in the range of rotation of −90° to 270° with a bin width of 2.0°. The spin angle θ3 was confined in the range of −90° to 30° by a harmonic wall restraint with a force constant of 5.0 kcal mol−1 deg−1. The free-energy landscape describing stage III was determined by applying eABF method on the three transition coordinates θ1, θ2, and θ3. The transition pathway being explored spanned 60° ≤ θ1 ≤ 220°, 60° ≤ θ2 ≤ 220°, and −60° ≤ θ3 ≤ 120°. A bin width of 2.0° was used for each transition coordinate. Total simulation time amounted to 1.0, 1.0, and 1.0 μs for the helicity switching process, the first two and the third stages, respectively, representing an aggregate time of 3.0 μs. The least free-energy pathways connecting minima of the two- and three-dimensional free-energy landscapes were identified using the LFEP29 and NMFEP30 algorithm. The concept of committor31,32 was utilized to prove that the model reaction coordinates formed by collective variable θ1, θ2 and θ3 correspond to an appropriate choice.
Results and discussion
Free-energy landscape
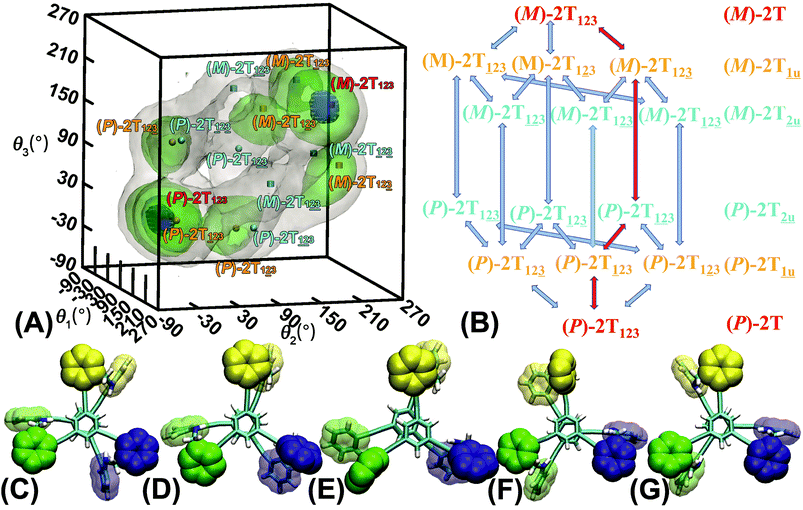
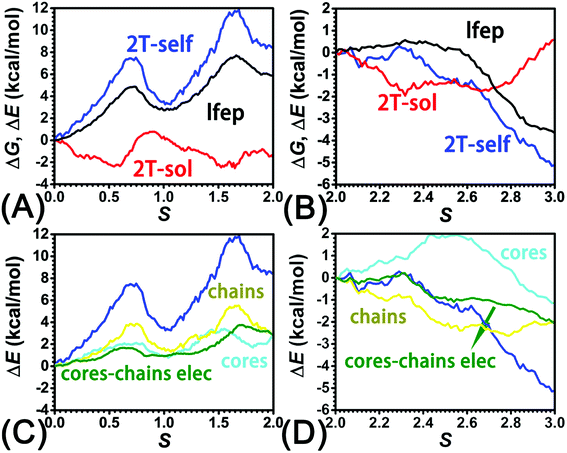
The three-dimensional free-energy landscape characterizing the helicity switching process of 2T in toluene is depicted in Fig. 1A. 14 minima presented in the complete reaction coordinate space can be classified into six categories, viz., representing the (P)- and (M)-conformations with 0, 1, and 2 aromatic unit(s) flipped, respectively. These minima are connected by 24 least free-energy pathways. Based on these pathways, 12 possible helicity switching pathways can be proposed. Enumeration of every possible pathway can be found in the ESI (see Table S1†). Every switching pathway contains four stages, viz.,
representing the (P)- and (M)-conformations with 0, 1, and 2 aromatic unit(s) flipped, respectively. These minima are connected by 24 least free-energy pathways. Based on these pathways, 12 possible helicity switching pathways can be proposed. Enumeration of every possible pathway can be found in the ESI (see Table S1†). Every switching pathway contains four stages, viz.,  The first and fourth stages are symmetrical. Hence, each helicity switching pathway contains three different stages. In the following section, our attention was focused on the first three stage of the switching pathway
The first and fourth stages are symmetrical. Hence, each helicity switching pathway contains three different stages. In the following section, our attention was focused on the first three stage of the switching pathway 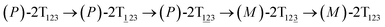 (marked by the red arrow in Fig. 1B). Involved conformers can be found in Fig. 1C–G. To prove that the sampling in the 1.0 μs eABF calculations is ergodic, the distribution of the spin angle of the bottom tier relative to the top tier within 200 ns, 400 ns, 600 ns, 800 ns, and 1.0 μs have been calculated, respectively (see Fig. S1†). Two peaks around ca. −25° and 25° correspond to (P)- and (M)-configurations. Increasing the sampling time only enhances the sampling density. The two-peak pattern shared by five curves remains unchanged. There results prove that the sampling is ergodic.
(marked by the red arrow in Fig. 1B). Involved conformers can be found in Fig. 1C–G. To prove that the sampling in the 1.0 μs eABF calculations is ergodic, the distribution of the spin angle of the bottom tier relative to the top tier within 200 ns, 400 ns, 600 ns, 800 ns, and 1.0 μs have been calculated, respectively (see Fig. S1†). Two peaks around ca. −25° and 25° correspond to (P)- and (M)-configurations. Increasing the sampling time only enhances the sampling density. The two-peak pattern shared by five curves remains unchanged. There results prove that the sampling is ergodic.
Free-energy pathways
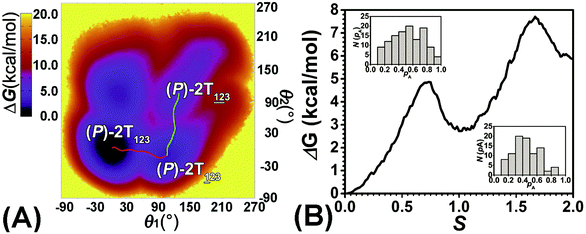
To examine the first two stages of the helicity switching process in detail, a two-dimensional free-energy surface was generated along θ1 and θ2 with confined θ3 (see Fig. 2A). This map features four basins corresponding to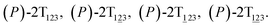 These basins are separated by four ridges. One gap is found on each ridge. The least free-energy pathways for
These basins are separated by four ridges. One gap is found on each ridge. The least free-energy pathways for 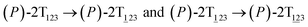 were determined using the LFEP algorithm.
were determined using the LFEP algorithm.
To prove that the confinement on θ3 does not bias calculated results, the free-energy landscapes spanned by θ1 and θ2 of two- and three-dimensional eABF calculations were compared. For the three-dimensional case, the landscape spanned by θ1 and θ2 is calculated by integration over θ3 (−90° ≤ θ3 ≤ 30°).33 Relevant results were gathered in Fig. S2.† Two landscapes are very similar. Least free-energy pathways within two landscapes were compared either. Two curves match well. These results prove that the constraint imposed on θ3 does not bias free-energy landscapes and least free-energy pathways.
The transition coordinates, θ1 and θ2, used herein, were checked by undertaking the committor analysis. Distributions of the committor, pA, at the position near the free-energy maxima, defined by (θ1, θ2) near the saddle points, i.e., (θ1 = 61°, θ2 = 3°) and (θ1 = 121°, θ2 = 55°), were determined (see Fig. 2B). The distributions are Gaussian-like and peaked at the probability of 0.5. The transition coordinate, θ1 and θ2, represents a reasonable combination of the collective variables to describe the first two stages of the helicity switching process.
As the helicity switches, the first ring in the top tier rotates from a stable conformation (−20° ≤ θ ≤ 20°) to a quasistable one (100° ≤ θ ≤ 120°) in the first stage (S0→1). Subsequent rotation of the second ring from the stable conformation to a quasistable one constitutes the second stage (S1→2). Successively rotations of two peripheral rings in the top tier were detected (see Fig. S3A†). Meanwhile, no obvious rotation of the bottom tier relative to the top tier was observed (see Fig. S3B†). The free-energy profile for stage I and II as a function of the position (s) is reported in Fig. 2B. s is the order parameter of the pathway. The detailed definition can be found in the work of Branduardi et al.33 s = 0.0, s = 1.0 and s = 2.0 correspond to the global minimum (P)-2T123 (θ1 = 5°, θ2 = 3°, ΔGs=0.0 = 0.0 kcal mol−1) and two local minima 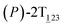 (θ1 = 107°, θ2 = −11°, ΔGs=1.0 = 2.7 kcal mol−1) and
(θ1 = 107°, θ2 = −11°, ΔGs=1.0 = 2.7 kcal mol−1) and 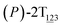 (θ1 = 129°, θ2 = 103°, ΔGs=2.0 = 5.9 kcal mol−1). Two peaks can be located in the free-energy profile. The height of the peaks relative to the global minimum, ΔG‡, is estimated to be 4.9 kcal mol−1 in the stage S0→1 and 7.4 kcal mol−1 in the stages S0→2.
(θ1 = 129°, θ2 = 103°, ΔGs=2.0 = 5.9 kcal mol−1). Two peaks can be located in the free-energy profile. The height of the peaks relative to the global minimum, ΔG‡, is estimated to be 4.9 kcal mol−1 in the stage S0→1 and 7.4 kcal mol−1 in the stages S0→2.
To examine stage III accurately, a three-dimensional free-energy landscape was generated along θ1, θ2, and θ3 within shorter ranges and fine grids (see Fig. 3A). This landscape features an asymmetrical dumbbell. Two minima were located at terminal spheres. The least free-energy path from one minimum 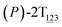 (θ1 = 127°, θ2 = 101°, θ3 = −15°) to another
(θ1 = 127°, θ2 = 101°, θ3 = −15°) to another 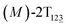 (θ1 = 171°, θ2 = 205°, θ3 = 85°) was determined. Concomitant rotations of three peripheral rings in the top tier were detected (see Fig. S3C†). The third peripheral ring in the top tier rotates from a stable conformation to the quasistable state. The first and second rings in the top tier transform from the quasistable state to another stable conformation (160° ≤ θ ≤ 200°). Meanwhile, an obvious rotation of the bottom tier relative to the top tier around the z axis indicates an adjustment of the framework for 2T (see Fig. S3D†).
(θ1 = 171°, θ2 = 205°, θ3 = 85°) was determined. Concomitant rotations of three peripheral rings in the top tier were detected (see Fig. S3C†). The third peripheral ring in the top tier rotates from a stable conformation to the quasistable state. The first and second rings in the top tier transform from the quasistable state to another stable conformation (160° ≤ θ ≤ 200°). Meanwhile, an obvious rotation of the bottom tier relative to the top tier around the z axis indicates an adjustment of the framework for 2T (see Fig. S3D†).
To check the transition coordinate, θ1, θ2, and θ3, used herein, a committor analysis was undertaken. Distribution of the committor, pA, at the position near the free-energy maximum (around θ1 = 131°, θ2 = 113°, and θ3 = 17°) was determined (see Fig. 3B). This distribution is Gaussian-like with a peak around pA = 0.5. It suggests that the combination of collective variables, θ1, θ2, and θ3, is a reasonable transition coordinate to describe the third stage of the helicity switching pathway.
The free-energy profile for the third stage of the switching pathway as a function of s is reported in Fig. 3B. s = 3.0 corresponds to the minimum 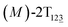 (ΔGs=3.0 = ΔGs=2.0 −3.7 kcal mol−1 = 2.2 kcal mol−1). This profile features a gentle slope with a week barrier emerges around the point (ca. s = 2.3). The height of the barrier, ΔG‡, is estimated to be 0.6 kcal mol−1 in the stage S2→3 and 6.5 kcal mol−1 (ΔGs=2.0 + 0.6 kcal mol−1) in the stages S0→3.
(ΔGs=3.0 = ΔGs=2.0 −3.7 kcal mol−1 = 2.2 kcal mol−1). This profile features a gentle slope with a week barrier emerges around the point (ca. s = 2.3). The height of the barrier, ΔG‡, is estimated to be 0.6 kcal mol−1 in the stage S2→3 and 6.5 kcal mol−1 (ΔGs=2.0 + 0.6 kcal mol−1) in the stages S0→3.
Based on the observation in this section, a deeper understanding of the four-stage (helicity switching) process emerges. Helicity switching of 2T involves rotations of three peripheral rings in the top tier from one stable conformation (−20° ≤ θ ≤ 20°) to a quasistable state (100° ≤ θ ≤ 120°), and then to another stable conformation (160° ≤ θ ≤ 200°). There is a peak in each stage. The highest peak appears in the second stage. The height of the peak relative to the global minimum, ΔG‡, equal to 7.4 kcal mol−1, matches well with the experimental measurement.14
Interactions responsible for the helicity switching
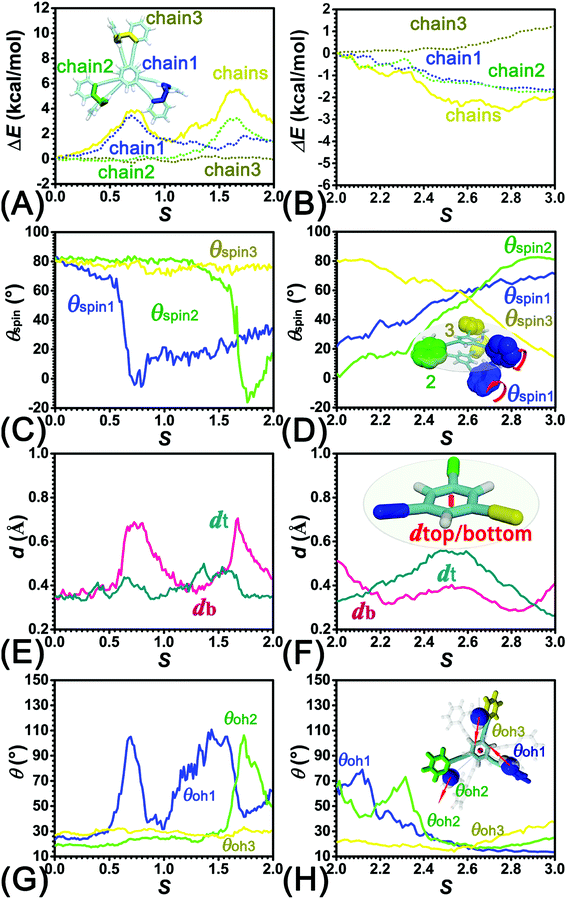
To identify the interaction components that contribute to the free-energy barrier, variation of constituent interactions of different nature was examined. 2T intramolecular (2T-self) interaction and 2T-solvent interaction were monitored along the least free-energy pathway. The resulting interaction components are gathered in Fig. 4A and B.To delve deeper into this analysis, the spin angles of aromatic rings within the bottom tier around the connected alkyne units were measured. The evolution of the average spin angles along s is shown in Fig. 5C and D. In stage I, the aromatic ring (in the bottom tier) in chain1 rotates from the perpendicular conformation (ca. 80°) to a horizontal conformation (around 0°). Rings in chain1 are pushed away from each other (see Fig. S4E and F†). The twist of dihedral angles within chain1 (see Fig. S5†) causes a barrier in chain1 and chains term. No rotation of rings in other chains was observed. In stage II, rotation of the benzene ring (within the bottom tier) in chain2 from ca. 80° to 0° results in the barrier in chain2 term. Rings (in the bottom tier) in chain1 and chain3 maintain the horizontal and perpendicular conformations, respectively. In stage III, switching back to the perpendicular conformations for rings (in the bottom tier) in chain1 and chain2 releases dihedral distortions. Although the ring (in the bottom tier) in chain3 rotating to the horizontal conformation causes novel twist, the dihedral distortions within 2T are partially released, thus rationalizing that chains term is favorable in stage III.
Conclusion
In this contribution, the helicity switching process within a two-tiered stacked architecture designed by Hartley and coworkers was investigated. Three-dimensional free-energy landscape characterizing the helicity switching was determined. The helical inversion process is constituted by four stages containing three different kinds. The four stages correspond to the spinning of three peripheral benzene rings in the top tier and the rotation of bottom tier relative the top one around the z axis. The height of the highest free-energy barrier located in the second stage was estimated as high as 7.4 kcal mol−1 matching with experimental observations. Based on the geometrical analysis and calculation of interactions, a switching mechanism was proposed. Spinning peripheral rings in the top tier causes the concomitant rotation of connected rings within the bottom tier leading to the separation of rings in the same side chain. The separation induces the geometrical deformation of the connected conjugated cores section and twist of dihedral angles within side chains. The twist reorientates polarized amine moieties attached to side chains. These factors collectively shape the least free-energy pathway in each stage.The present results provide a complete understanding of the helicity switching process, which is crucial for the rational design of novel functional helices. The effects of structural modifications on the function of helices can be evaluated in silico. Attention of synthesis should be focused on the candidates screened from a series of lead structures constructed from fragment libraries. The invested effort and cost can be dramatically decreased. Combination of experimental and computational efforts is expected along this line.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study is supported by National Natural Science Foundation of China (No. 21603160, 91745116, 21875184, and 51678409).References
- Y. Ferrand and I. Huc, Acc. Chem. Res., 2018, 51, 970–977 CrossRef CAS.
- E. Yashima, K. Maeda, H. Iida, Y. Furusho and K. Nagai, Chem. Rev., 2009, 109, 6102–6211 CrossRef CAS PubMed.
- M. Liu, L. Zhang and T. Wang, Chem. Rev., 2015, 115, 7304–7397 CrossRef CAS PubMed.
- H. Lu and N. Kobayashi, Chem. Rev., 2016, 116, 6184–6261 CrossRef CAS PubMed.
- D. J. van Dijken, J. M. Beierle, M. C. A. Stuart, W. Szymański, W. R. Browne and B. L. Feringa, Angew. Chem., Int. Ed., 2014, 53, 5073–5077 CAS.
- D. Taura, S. Hioki, J. Tanabe, N. Ousaka and E. Yashima, ACS Catal., 2016, 6, 4685–4689 CrossRef CAS.
- M. Peterca, M. R. Imam, C.-H. Ahn, V. S. K. Balagurusamy, D. A. Wilson, B. M. Rosen and V. Percec, J. Am. Chem. Soc., 2011, 133, 2311–2328 CrossRef CAS PubMed.
- R. Liu, H. Liu, X. Chen, M. Kirby, P. O. Brown and K. Zhao, Cell, 2001, 106, 309–318 CrossRef CAS.
- M. Mathews, R. S. Zola, S. Hurley, D.-K. Yang, T. J. White, T. J. Bunning and Q. Li, J. Am. Chem. Soc., 2010, 132, 18361–18366 CrossRef CAS PubMed.
- R. A. Brown, V. Diemer, S. J. Webb and J. Clayden, Nat. Chem., 2013, 5, 853–860 CrossRef CAS PubMed.
- M. De Poli, W. Zawodny, O. Quinonero, M. Lorch, S. J. Webb and J. Clayden, Science, 2016, 352, 575–580 CrossRef CAS PubMed.
- J. Solà, S. P. Fletcher, A. Castellanos and J. Clayden, Angew. Chem., Int. Ed., 2010, 49, 6836–6839 CrossRef PubMed.
- F. G. A. Lister, B. A. F. Le Bailly, S. J. Webb and J. Clayden, Nat. Chem., 2017, 9, 420–425 CrossRef CAS.
- F. Ren, K. J. Day and C. S. Hartley, Angew. Chem., Int. Ed., 2016, 55, 8620–8623 CrossRef CAS PubMed.
- J. C. Phillips, R. Braun, W. Wang, J. Gumbart, E. Tajkhorshid, E. Villa, C. Chipot, R. D. Skeel, L. Kalé and K. Schulten, J. Comput. Chem., 2005, 26, 1781–1802 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell, J. Comput. Chem., 2009, 31, 671–690 Search PubMed.
- W. Yu, X. He, K. Vanommeslaeghe and A. D. MacKerell, J. Comput. Chem., 2012, 33, 2451–2468 CrossRef CAS PubMed.
- S. E. Feller, Y. Zhang, R. W. Pastor and B. R. Brooks, J. Chem. Phys., 1995, 103, 4613–4621 CrossRef CAS.
- J.-P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comput. Phys., 1977, 23, 327–341 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- H. Fu, X. Shao, C. Chipot and W. Cai, J. Chem. Theory Comput., 2016, 12, 3506–3513 CrossRef CAS PubMed.
- A. Lesage, T. Lelièvre, G. Stoltz and J. Hénin, J. Phys. Chem. B, 2017, 121, 3676–3685 CrossRef CAS PubMed.
- E. Darve, M. A. Wilson and A. Pohorille, Mol. Simul., 2002, 28, 113–144 CrossRef CAS.
- J. Hénin and C. Chipot, J. Chem. Phys., 2004, 121, 2904–2914 CrossRef PubMed.
- H. Fu, X. Shao, C. Chipot and W. Cai, J. Chem. Theory Comput., 2017, 13, 1566–1576 CrossRef PubMed.
- G. Fiorin, M. L. Klein and J. Hénin, Mol. Phys., 2013, 111, 3345–3362 CrossRef CAS.
- B. Ensing, A. Laio, M. Parrinello and M. L. Klein, J. Phys. Chem. B, 2005, 109, 6676–6687 CrossRef CAS PubMed.
- M. Moradi, G. Enkavi and E. Tajkhorshid, Nat. Commun., 2015, 6, 8393 CrossRef CAS PubMed.
- A. C. Pan, D. Sezer and B. Roux, J. Phys. Chem. B, 2008, 112, 3432–3440 CrossRef CAS PubMed.
- P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Annu. Rev. Phys. Chem., 2002, 53, 291–318 CrossRef CAS PubMed.
- J. Comer, F. Dehez, W. Cai and C. Chipot, J. Phys. Chem. C, 2013, 117, 26797–26803 CrossRef CAS.
- D. Branduardi, F. L. Gervasio and M. Parrinello, J. Chem. Phys., 2007, 126, 054103 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Enumeration of 12 possible switching pathways in the helicity inversion of 2T. Distribution of the spin angle of the bottom tier relative to the top tier in the 200 ns, 400 ns, 600 ns, 800 ns, and 1.0 μs trajectories of eABF calculations. Free-energy landscape spanned by θ1 and θ2 comparing the results of two- and three-dimensional eABF calculations. Comparing of least free-energy pathways extracted from results of two- and three-dimensional eABF calculations. Variation of collective variables and the spin angle of the bottom tier relative to the top tier around the z axis along the least free-energy pathway. Average solvent accessible surface area of 2T and its cores section in the helicity switching process. Variation of distances between the center of mass of peripheral rings within the same side chain and three dihedral angles about chemical bonds of the methylene amine moiety with respect to s. See DOI: 10.1039/c8ra09226e |
| This journal is © The Royal Society of Chemistry 2019 |