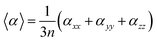Open Access Article
Open Access ArticleComputational investigations into the structural and electronic properties of CdnTen (n = 1–17) quantum dots†
Muhammad Imran a,
Muhammad Jawwad Saif
a,
Muhammad Jawwad Saif *a,
Aleksey E. Kuznetsov
*a,
Aleksey E. Kuznetsov b,
Nazeran Idrees
b,
Nazeran Idrees c,
Javed Iqbal
c,
Javed Iqbal d and
Asif Ali Tahir
d and
Asif Ali Tahir e
e
aDepartment of Applied Chemistry, Government College University Faisalabad, Pakistan. E-mail: jawwadsaif@gmail.com
bDepartamento de Química, Universidad Técnica Federico Santa María, Av. Santa María 6400, Vitacura, Santiago, Chile
cDepartment of Mathematics, Government College University Faisalabad, Pakistan
dDepartment of Chemistry, University of Agriculture, Faisalabad, Pakistan
eEnvironment and Sustainability Institute, University of Exeter, Penryn Campus, TR10 9FE, UK
First published on 11th February 2019
Abstract
Size-tunability of the electronic and optical properties of semiconductor quantum dots and nanoclusters is due to the quantum size effect, which causes variations in the electronic excitations as the particle boundaries are changed. Recently, CdSe and CdTe quantum dots have been used in energy harvesting devices. Despite these promising practical applications, a complete understanding of the electronic transitions associated with the surfaces of the nanoparticles is currently lacking and is difficult to achieve experimentally. Computational methods could provide valuable insights and allow us to understand the electronic and optical properties of quantum dots and nanoclusters. Hollow cage and endohedral or core–shell cage structures for CdnTen clusters have been reported before. We have performed systematic density functional theory (DFT) studies on the structure and electronic properties of the CdnTen (n = 1–17) clusters. As the number of atoms increases in the CdnTen clusters, the predicted geometries change from simple planar structures to more complicated 3D-structures. Two classes of the most stable structures were elucidated for clusters with n = 10–17: (i) hollow cage structures with an empty center; and (ii) endohedral or core–shell cage structures with one or more atoms inside the cage. Noticeably higher highest occupied molecular orbital (HOMO)-lowest unoccupied molecular orbital (LUMO) gaps were observed for the hollow cage isomers as compared to the core–shell structures. The highest occupied molecular orbitals of all of the clusters studied were shown to be localized on the surface of the cage for the hollow cage structures, while in the case of the core–shell structures, the HOMO electron densities were found to be distributed both on surface and the interior of the structures. Most of the small size clusters CdnTen (n = 2–9) showed minimal values for the dipole moments (close to zero) owing to the highly ordered and symmetric configurations of these structures. For isomers of the larger clusters (n = 10–17), it was observed that the core–shell structures have higher values for the dipole moments than the hollow cage species because of the highly symmetric structures of the hollow cages. Core–shell cage structures exhibited lower polarizability than the respective hollow cage structures.
1 Introduction
Semiconductor quantum dots have attracted significant interest owing to their tunable electronic and optical properties as a result of variations in the size, shape and surface chemistry of the particles.1 These semiconductor nanomaterials are becoming increasingly important owing to their potential applications in electronic and optoelectronic devices such as solar cells, electro-optical modulators, photodetectors, light emitting diodes and sensors.1–13 Size-tunability of the electronic and optical properties of semiconductor quantum dots and nanoclusters is due to the quantum size effect, which causes variations in the electronic excitations as the particle boundaries are changed.14 Recently, CdSe and CdTe quantum dots have been used in energy harvesting devices, for example, quantum dot-sensitized solar cells.6–10 Despite the promising practical applications of semiconductor quantum dots and nanoclusters, a complete understanding of the electronic transitions associated with the surface of nanoparticles is currently lacking and is difficult to achieve experimentally. However, computational methods could provide valuable insights to allow researchers to understand the electronic and optical properties of quantum dots and nanoclusters.15 This understanding of the electronic structure and a knowledge of how to manipulate it has great importance as far as practical applications are concerned. Numerous theoretical studies have been conducted to understand the electronic properties of CdSe and CdTe nanoclusters. Hybrid nanostructures have been developed combining graphene with CdTe quantum dots to tune the band gap of the system.16 A similar study was conducted with a hybrid nanostructure composed of a CdTe nanotube and fullerene to engineer the electronic structure and band gap of the nanocomposite.17 In one of the earliest computational studies on CdTe nanoclusters, Bhattacharya and Kshirsagar conducted a density functional theory (DFT) calculations for CdTe nanoclusters to determine their structural and electronic properties.18 The search for geometrical structures of CdnTen clusters remains the focus of many researchers and various structures containing a small number of CdTe units have been investigated for lowest energy geometry and stability.19–22 As the number of atoms increases in CdnTen clusters, the predicted structures change from simple planar structures to more complicated three-dimensional structures and multiple structures can be predicted for clusters with the same number of CdTe units. Hollow cages and endohedral or core–shell cage structures for a single CdnTen cluster have been reported.23 Magic size quantum dots such as Cd33Se33 and Cd33Te33 have been simulated to evaluate their structural and electronic properties both in the bare form and when capped with ligands.24 The structural and electronic properties of small-sized nanoparticles (n = 6, 9) of CdSe and CdTe have also been computed for both the bare and capped forms.25 A comparative study (DFT) of seven telluride compounds, such as XTe (X = Bi, Cd, Pb, Zn), X2Te3 (X = Bi, Sb) and X2YxTe3_x (X = Bi, Y = Se, x = 0 to 0.3) revealed CdTe to be the best compound for conductivity as compared to other compounds.26 A theoretical investigation of CdTe multi-cage nanochains demonstrated their increased stability and factors such as the assembly mode and the number of cages were shown to affect the energy gap, density of states and charge density distribution.27The aim of the present study is to explore possible structures for CdnTen with optimized geometries and the lowest energy for each cluster. We performed DFT calculations to systematically optimize the most stable geometries and explore the electronic properties of CdnTen (n = 1–17) clusters. Band gap analysis of these clusters has also been performed and is discussed in detail.
2 Computational methods
Initial structural geometries were obtained from the published literature, an unbiased search on the potential energy surface was performed using a stepwise simulated annealing technique incorporating first-principles molecular dynamics.19–21,23 Furthermore, we employed the particle swarm optimization (PSO)28,29 technique as implemented in CALYPSO30,31 using PWSCF code32 as the DFT engine to expand the canvas of candidate structures. For the CALYPSO structural search, we set different parameters for the population size and the number of generations for the PSO algorithm. The population size and the number of generations was fixed to 10 for CdnTen (n = 1–5), 20 for CdnTen (n = 6–9) and 30 for CdnTen (n = 10–17). Many candidate geometries were also constructed manually considering the hexagonal and wurtzite crystal motifs for CdnTen clusters. Some of the initial structures were adopted from published studies on semiconductor clusters such as GaAs, GaN, BN, and ZnO. After initial screening, the most probable candidate geometries with the lowest energies were first optimized using hybrid functional B3LYP33 with basis sets of Los Alamos double-ζ effective core potential (Lanl2dz)34–36 and were then optimized again using a PBE0 (ref. 37) hybrid functional with basis sets of Los Alamos double-ζ effective core potential (Lanl2dz). The PBE0 functional has been previously found to provide a good description of the semiconductor clusters.38,39 In order to accommodate the dispersions, empirical dispersion parameters (PBE0-D3) were implemented as proposed by Grimme et al.40 All of the calculations for the candidate structures and final structures were carried out using both the B3LYP/Lanl2dz and PBE0-D3/Lanl2dz approaches and implemented in the Gaussian 09W software package.41 Only the lowest energy structure of each CdnTen cluster (n = 1–9) was considered suitable to study the electronic properties. Two types of isomeric structures (i.e., hollow cages and endohedral or core–shell cages structures) were constructed for the larger clusters CdnTen (n = 10–17). All of the calculations were performed in the gas phase. Frequency analysis was performed at the same DFT theory levels to insure that the optimized structures were the true minima and not transition states (confirmed by the absence of an imaginary frequency). Single point second-order Møller–Plesset perturbation theory (MP2)42–44 energy calculations were performed using a larger basis set Def2-TZVP45 to evaluate the energy values of the final lowest energy structure and were found to be in better agreement with the PBE0-D3/Lanl2dz calculations than with the B3LYP/Lanl2dz calculations. Therefore, the results of the PBE0-D3/Lanl2dz calculations are discussed throughout this paper unless mentioned otherwise, and the results of the B3LYP/Lanl2dz and MP2/Def2-TZVP approaches are given in Tables S1 and S2 (ESI†), respectively.The binding energies, highest occupied molecular orbital (HOMO)/lowest unoccupied molecular orbital (LUMO) band gaps, dipole moments and static dipole polarizabilities were also calculated. The calculated structures and molecular orbitals of the CdnTen clusters were visualized using GaussView software.
3 Results and discussion
Before discussing the results of the present study, two previous reports published by Bhattacharya20 and Zhao21 are worth mentioning. Both reports describe the theoretical investigation of CdnTen clusters. These previously published reports are based on plane-wave DFT methods. The plane-wave DFT method expands the Kohn–Sham orbitals in terms of the plane waves, up to a certain maximum kinetic energy and assumes the system to be fully periodic. However, the present work is based on the localized-orbital (Gaussian) DFT approach. Therefore, comparison of the results must be performed while keeping the different nature of the DFT approaches in mind. The optimized geometries of the CdnTen clusters are presented in Fig. 1 and 2. Fig. 1 shows the gas phase optimized hollow cage type structures of CdnTen, in which n = 1–9. Fig. 2 shows the structures of the two types; hollow cage and core–shell cage geometries. Zhao et al. reported that the core–shell cage structures were more stable than the hollow cages for n ≥ 12.21 However, our calculations revealed that the core–shell cage structures become more stable than the hollow cages for n ≥ 9.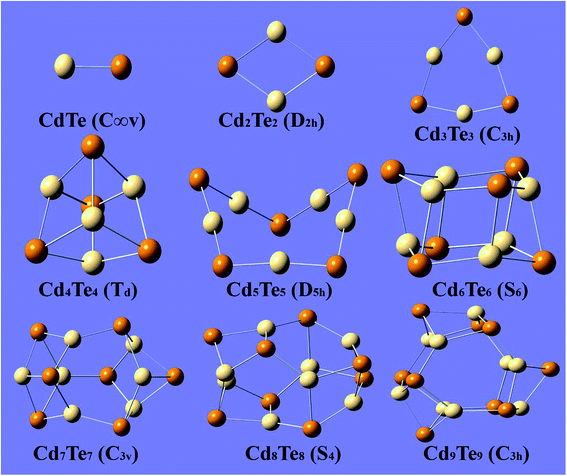 | ||
| Fig. 1 The lowest-energy optimized structures of CdnTen (n = 1–9) with the point group symmetry. Te is indicated with dark colored spheres and Cd with light colored spheres. | ||
The calculated binding energies of all of the optimized configurations studied in this work are given in Table 1. The binding energy (Eb) per Cd–Te unit was calculated for the optimized geometries using the following expression:
| Eb = {n[E(Cd) + E(Te)] − E(CdnTen)}/n |
| Cluster | Eb (eV per unit) | HOMO/LUMO (eV) | μ (debye) | 〈α〉 (bohr3 per unit) |
|---|---|---|---|---|
| Cd1Te1 | 2.01 | −5.7/−4.07 | 5.8233 | 78.59 |
| Cd2Te2 | 3.76 | −5.83/−3.21 | 0 | 71.49 |
| Cd3Te3 | 4.45 | −6.31/−2.67 | 0.0001 | 72.71 |
| Cd4Te4 | 4.68 | −6.44/−2.98 | 0.0003 | 70.01 |
| Cd5Te5 | 4.56 | −6.15/−2.86 | 0.6762 | 78.88 |
| Cd6Te6 | 5 | −6.38/−2.81 | 0.0001 | 70.62 |
| Cd7Te7 | 5.01 | −6.41/−2.76 | 1.2246 | 71.4 |
| Cd8Te8 | 5.11 | −6.41/−2.76 | 0.0001 | 71.43 |
| Cd9Te9 | 5.16 | −6.53/−2.78 | 0.0022 | 71.14 |
| Core–shell cages | Hollow cages | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ee (eV) | Eb (eV per unit) | HOMO/LUMO (eV) | μ (debye) | 〈α〉 (bohr3 per unit) | Ee (eV) | Eb (eV per unit) | HOMO/LUMO (eV) | μ (debye) | 〈α〉 (bohr3 per unit) | |
| Cd10Te10 | 0.00 | 5.2 | −6.19/−2.81 | 3.198 | 71.05 | 1.92 | 4.97 | −6.4/−2.83 | 1.4702 | 71.81 |
| Cd11Te11 | 0.00 | 5.2 | −6.32/−2.95 | 4.2208 | 71.11 | 0.37 | 5.21 | −6.46/−2.8 | 1.2824 | 71.95 |
| Cd12Te12 | 0.00 | 5.3 | −6.36/−2.92 | 1.5299 | 69.84 | 0.43 | 5.25 | −6.76/−2.76 | 0.0018 | 71.77 |
| Cd13Te13 | 0.00 | 5.4 | −6.47/−2.79 | 3.4536 | 70.1 | 1.66 | 5.25 | −6.44/−2.87 | 1.9381 | 73.53 |
| Cd14Te14 | 0.00 | 5.3 | −6.04/−3.02 | 2.3672 | 71.89 | 1.18 | 5.25 | −6.52/−2.87 | 0.8573 | 72.78 |
| Cd15Te15 | 0.00 | 5.4 | −6.37/−3.2 | 5.4224 | 72.03 | 1.35 | 5.27 | −6.66/−2.86 | 0.0007 | 72.7 |
| Cd16Te16 | 0.00 | 5.3 | −5.81/−2.97 | 5.683 | 72.63 | 1.14 | 5.27 | −6.61/−2.91 | 0.4124 | 72.79 |
| Cd17Te17 | 0.00 | 5.4 | −6.27/−2.99 | 10.788 | 71.71 | 0.97 | 5.31 | −6.51/−2.95 | 3.4917 | 73.62 |
CdTe is optimized as a dimer and a bond length of 2.61 Å and 2.65 Å at the PBE0-D3/Lanl2dz and B3LYP/Lanl2dz levels of theories was observed, respectively. Previous calculations by Zhao and co-workers21 predicted a bond length of 2.61 Å and Bhattacharya and Kshirsagar18 predicted a bond length of 2.57 Å.
For the CdnTen clusters in which 2 ≤ n ≤ 8, Cd and Te atoms adapt to alternate positions with a planar geometry and a coordination number of two. The optimized structure of Cd2Te2 is a rhombus (D2h), and for Cd3Te3 is planar (C3h) with Cd–Te bond lengths of 2.79 Å and 2.73 Å at the PBE0-D3/Lanl2dz level of theory, respectively, which agrees with the bond length predicted by Zhao and co-workers,21 while Cd2Te2 and Cd3Te3 showed bond lengths of 2.83 Å and 2.77 Å at the B3LYP/Lanl2dz levels of theory, respectively. This comparison of bond lengths revealed a difference of 0.04 Å when the clusters are optimized with the PBE0-D3/Lanl2dz and B3LYP/Lanl2dz levels of theories. Two different geometries (Td and D4h) for Cd4Te4 were found. These two geometries were found to be very close in terms of energy with an energy difference of 0.49 eV making the tetrahedral (Td) geometry a little more stable as compared to the square planar (D4h) structure. This finding is different from that found in the study published by Zhao and co-workers who reported that the square planar geometry had the minimum energy. The Cd–Te bond lengths for the tetrahedral Cd4Te4 and square Cd4Te4 were calculated to be 2.95 Å and 2.75 Å, respectively. Cd5Te5 adapts a non-symmetric 3D distorted envelop structure and has a Cd–Te bond length of 2.71 Å, unlike the planar pentagon structure reported by Bhattacharya and Zhao. A planar to 3D shift starts to occur at n = 5 as we observe a distortion from the planar geometry.
The lowest-energy structures of CdnTen with n = 6–9 are closed polyhedral cages, which is in agreement with the previous reports. These structures are mainly composed of 4-membered and 6-membered rings with an alternate Cd and Te atomic arrangement. For these polyhedral cages, the coordination number increases from two to three. For n = 6, the minimum energy structure has a S6 point group. The optimized structure is composed of two six-membered rings. For Cd7Te7, the optimized structure consists of three six-membered rings and six four-membered rings that have C3v symmetry. This optimized geometry agrees with the previously reported structure for Cd7Te7. The optimized geometry of Cd8Te8 consists of four distorted 6-membered rings and six 4-member rings and has a S4 point group. The lowest-energy structure of Cd9Te9 consists of five distorted 6-membered rings and six 4-membered rings with a C3h point group.
Two classes of the most stable structures were elucidated for the clusters with n = 10–17. These structures are categorized into the hollow cage structures with an empty center and the endohedral or core–shell cage structures with one or more atoms inside the cage. The structures for lowest energy of clusters n = 10–17 of both classes are shown in Fig. 2. All of the core–shell structures contain at least one atom at the center of the cage, whereas the hollow cage structures have an empty center. The lowest-energy hollow cage structure for Cd10Te10 has a C3 point group symmetry and is composed of six six-membered rings and six four-membered rings, while the core–shell structure for the Cd10Te10 cluster has a point group of C1 and has a 1.92 eV lower energy than the hollow cage structure, and is hence more stable than the hollow cage structure (as shown in Fig. 2). The idea of the core–shell structure comes from the previously published work by Zhao et al.21 in which they employed first-principles molecular dynamics algorithms to search for the possible geometries. Herein, the favorable presence of the core–shell CdnTen (n ≥ 10) clusters was predicted using the localized-orbitals DFT approach.
Similarly, the core–shell structures of the clusters Cd11Te11 and Cd12Te12 both have C1 point group symmetry as compared to the hollow cage structures that have Cs and Ci point group symmetries, respectively. Both of the core–shell structures were found to be more stable than their counterpart hollow cage structures by 0.37 and 0.43 eV, respectively. The cluster Cd13Te13 was an exception and its core–shell structure is more stable than all of the others studied structures with a binding energy of 5.38 eV per unit. The most stable hollow cage structure for the Cd13Te13 cluster contains nine six-membered rings and six four-membered rings in its cage with a C3 point group symmetry, while the core–shell structure has a C1 point group and has 1.66 eV lower energy than the hollow cage structure. The most stable hollow cage structure for the Cd14Te14 cluster is composed of ten six-membered rings, and six four-membered rings with point group Cs symmetry, whereas the core–shell structure of the Cd14Te14 cluster has a C1 point group and has a 1.18 eV lower energy than the hollow cage structure, and is hence more stable. The hollow cage structure of Cd15Te15 is made of six four-membered rings and eleven six-membered rings with a C3h point group symmetry and is less stable than the core–shell structure of Cd15Te15 (C1 point group symmetry) by 1.35 eV. The core–shell structure Cd16Te16 contains two (one Cd and one Te atom) atoms inside the cage with a C1 point group and is found to be more stable than a hollow cage of the Cd16Te16 cluster, which is composed of six-four membered rings and twelve six-membered rings (C1 point group symmetry), by 1.14 eV. The hollow cage of the Cd17Te17 cluster has thirteen six-membered rings and six four-membered rings with a C1 point group symmetry, while the core–shell structure of this cluster (C3 point group) is more stable than its hollow cage counterpart by 0.97 eV. From the above discussion, it can be generalized that out of these two configurations the core–shell cage configurations are the most stable as compared to the hollow cage configurations for all of the cluster sizes.
The binding energies of the clusters calculated using the PBE0-D3/Lanl2dz level of theory (as shown in Table 1) are somewhat different from the calculations with the B3LYP/Lanl2dz level of theory (see Table S1, ESI†). The inclusion of dispersion interactions in the theoretical simulations is considered advantageous to achieving chemical accuracy.40,46
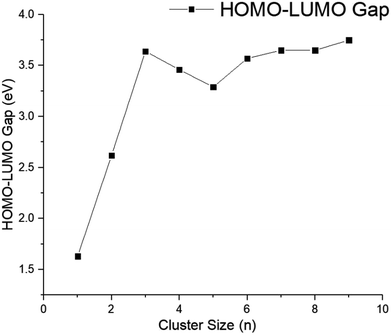
In order to understand the electronic properties of the CdnTen clusters, the HOMO–LUMO energy gaps were calculated (see Fig. 3 and 4). We understand that the HOMO–LUMO energy gap values should be used with caution, but we have used them to show how the electronic properties of the clusters studied change along with the cluster size and geometries. The HOMO–LUMO gap analysis did not reveal a regular trend based on the size and geometries of the CdnTen clusters, except that noticeably higher HOMO–LUMO gaps were observed for the hollow cage isomers as compared to the core–shell structures (see Fig. 4). The CdTe dimer had the smallest HOMO–LUMO gap of 1.63 eV. The HOMO–LUMO gaps of all of the other clusters varied between 2.62 eV (HOMO–LUMO gap of Cd2Te2 structure) and 4.00 eV (HOMO–LUMO gap of Cd12Te12 hollow cage structure) and no systematic change in the gap energy was observed in these nanoclusters. The Cd12Te12 hollow cage structure demonstrated the highest HOMO–LUMO gap (4.00 eV) amongst all of the clusters. Interestingly, the Cd9Te9 cluster has a HOMO–LUMO gap of 3.75 eV, which is the largest HOMO–LUMO gap amongst the small CdnTen clusters (n = 1–9, Fig. 3).
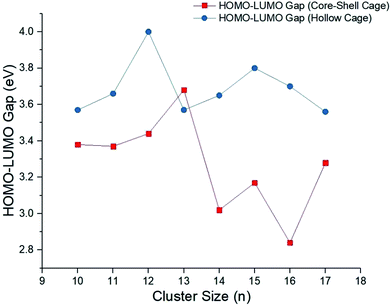 | ||
| Fig. 4 HOMO–LUMO gaps for the CdnTen nanoclusters of both the isomeric structure core–shell cages and the hollow cages (n = 10–17). | ||
The dipole moments for the lowest-energy structures of all of the types of clusters were computed to understand the symmetries of the structures (dipole moments for all of the structures are presented in Table 1). Most of the small size clusters CdnTen (n = 2–9) show minimal values for the dipole moments (close to zero) owing to the highly ordered and symmetric configurations of these structures. As the CdTe dimer is a linear structure, it possesses a very high dipole moment (5.8233 debye). Another exception is observed for the Cd5Te5 cluster with a C1 symmetry and the Cd7Te7 cluster with a C3v symmetry which have a relatively high dipole moment (0.6762 and 1.2246 debye, respectively) as compared to the other small size clusters (n = 2–9). For the isomers of the larger clusters (n = 10–17), it was observed that the core–shell structures have higher values for the dipole moments than the hollow cage structures because of the highly symmetric structures of the hollow cages of CdnTen (n = 10–17) with the symmetries: C3, Cs, Ci, and C3h. The hollow cage structures have a symmetric charge distribution around the geometric centers, and hence small dipole moments, while the core–shell structures are nonsymmetrical and therefore have high values for the dipole moments.
The mean polarizability per CdTe unit is presented in Table 1 and Fig. 5. The isotropic polarizability is an average of the polarizability in all orientations taken as a function of the cluster size. Therefore, the mean polarizability per CdTe unit can be defined as:
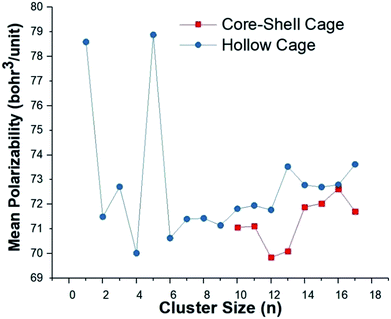
Fig. 5 shows a trend for the polarizability in relation to the size and geometry of the CdnTen clusters. Cd5Te5 showed the highest value for the mean polarizability 〈α〉 owing to its distorted out of plane envelop geometry. It is evident that all the core–shell cage structures exhibited lower polarizabilities than the respective hollow cage structures. The core–shell Cd12Te12 has the lowest value of mean polarizability 〈α〉 (69.84 bohr3 per unit) compared to all of the other clusters. These results revealed that the geometries of the clusters greatly influence the polarizability, and changes in the geometries from planer to three dimensional and open geometries to more compact geometries lower the value of polarizability.47
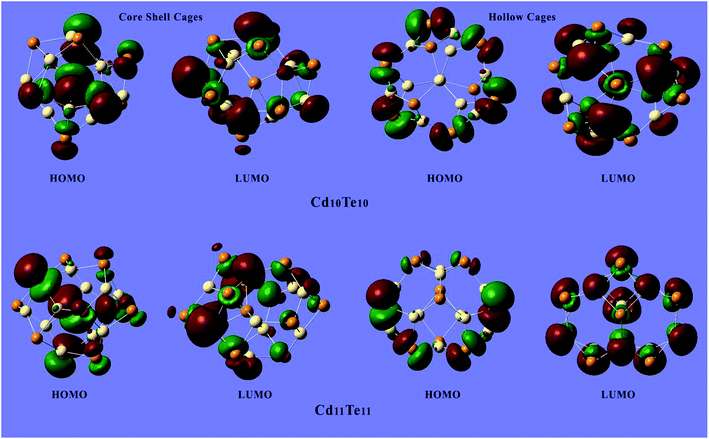
Fig. 6 shows the plots of the HOMO and LUMO of the representative clusters and plots of the HOMO and LUMO of all of the studied clusters are presented in the ESI (Fig. S1 and S2†). The electron densities of the HOMOs lie on the surface of the cage for the hollow cage structures while in the case of the core–shell structures the electrons densities of the HOMO are distributed both on the surface and the interior of the structures. This HOMO and LUMO analysis also revealed a trend for the electron densities localization in the HOMO of the clusters, while a clear delocalization of electron densities is demonstrated by the LUMO of the clusters. This electron density delocalization is also quite pronounced for the LUMO+1, and LUMO+2 of the clusters studied (see ESI†).
4 Conclusions
As the number of atoms increases in the CdnTen clusters, the predicted structures change from simple planar structures to more complicated 3D-structures. Multiple structures can be predicted for clusters with the same number of CdTe units. The hollow cage and the endohedral or core–shell cage structures for the same CdnTen clusters have been reported previously. We have performed systematic DFT and MP2 studies to evaluate the structures and electronic properties of the CdnTen (n = 1–17) clusters. The study results can be summarized as follows:(i) For the CdnTen clusters with 2 ≤ n ≤ 8, the Cd and Te atoms adapt alternate positions with a planar geometry and a coordination number of two. Two different geometries (Td and D4h) were found for Cd4Te4. These geometries were found to be very close in energy, with an energy difference of only 0.12 eV, making the tetrahedral structure a little more stable. The Cd5Te5 cluster was shown to adopt a non-symmetric 3D distorted envelop structure, unlike the planar pentagon structure reported by Bhattacharya and Zhao. Thus, a planar-to-3D shift starts to occur at n = 5 as we observe distortion from the planar geometry.
(ii) The lowest-energy structures for CdnTen with n = 6–9 were found to be closed polyhedral cages, in agreement with the previous reports. These structures are mainly composed of 4-membered and 6-membered rings with an alternate Cd and Te atomic arrangement. For these polyhedral cages, the coordination number increases from two to three.
(iii) Two classes of the most stable structures were elucidated for the clusters with n = 10–17. These structures were categorized into the hollow cage structure with an empty center and the endohedral or core–shell cage structure with one or more atoms inside the cage. All the core–shell structures were shown to contain at least one atom at the center of the cage. The idea of the core–shell structure comes from the previously published work by Zhao et al.21 in which the researchers employed first-principles MD algorithms to search for the possible geometries. In our study, the favorable presence of the core–shell CdnTen (n ≥ 9) clusters was predicted using the localized-orbitals DFT approach.
(iv) The most stable species, according to their binding energy values, eV per unit, were calculated to be the Cd12Te12 (core–shell cage) 5.29 eV per unit, Cd13Te13 (core–shell cage) 5.38 eV per unit, Cd14Te14 (core–shell cage) 5.33 eV per unit, Cd15Te15 (core–shell cage) 5.36 eV per unit, Cd16Te16 (core–shell cage) 5.34 eV per unit, Cd17Te17 (core–shell cage) 5.37 eV per unit, and the Cd17Te17 (hollow cage) 5.31 eV per unit. The binding energies were found to increase significantly up to n = 9 and then varied within a 0.19 eV range (see Table 1).
(v) The HOMO–LUMO gap analysis revealed no regular trend based on the size and geometries of the CdnTen clusters, except that noticeably higher HOMO–LUMO gaps were observed for the hollow cage isomers as compared to the core–shell structures. The CdTe dimer has the smallest HOMO–LUMO gap of 1.63 eV. The HOMO–LUMO gaps of all of the other clusters vary between 2.62 eV (HOMO–LUMO gap of Cd2Te2) and 4.0 eV (HOMO–LUMO gap of the Cd12Te12 hollow cage structure). The Cd12Te12 hollow cage structure demonstrated the highest HOMO–LUMO gap (4.0 eV) amongst all of the clusters.
(vi) For the larger clusters with n = 10–12 the HOMO–LUMO gap values increase gradually and Cd12Te12 (hollow cage) showed the highest value, with a HOMO–LUMO gap of 4.00 eV. For clusters with n = 13–17 the HOMO–LUMO gap values vary randomly with a sudden increase and sharp decrease, the Cd16Te16 (core–shell cage) has a HOMO–LUMO gap value of 2.84 eV which is the lowest amongst the larger clusters. The Cd15Te15 (hollow cage), cluster has the second largest HOMO–LUMO gap, 3.80 eV amongst the investigated clusters. Among the small CdnTen clusters (n = 1–9) the largest HOMO–LUMO gap 3.75 eV was shown by the Cd9Te9 cluster. In general, for the hollow cage isomers, the HOMO–LUMO gap changes are much less pronounced than for the core–shell structures.
(vii) The core–shell cage structures exhibited lower polarizabilities than the respective hollow cage structure. The core–shell Cd12Te12 has the lowest value for the mean polarizability 〈α〉 (69.84 bohr3 per unit) than all of the other clusters. These results revealed that the geometries of the clusters greatly influence the polarizability, and that changes in the geometries from planar to three dimensional and open to more compact geometries lower the value of the polarizability.
We propose that our findings contribute a more profound and detailed understanding of the trends in the changes in the structural and electronic properties of the CdnTen nanoclusters and will be helpful in both computational and experimental studies of larger CdTe NP-containing systems.
Conflicts of interest
There are no conflicts to declare.References
- S. V. Kershaw, L. Jing, X. Huang, M. Gao and A. L. Rogach, Mater. Horiz., 2017, 4, 155–205 RSC.
- H. Zou, M. Liu, D. Zhou, X. Zhang, Y. Liu, B. Yang and H. Zhang, J. Phys. Chem. C, 2017, 121, 5313–5323 CrossRef CAS.
- M. Amelia, C. Lincheneau, S. Silvi and A. Credi, Chem. Soc. Rev., 2012, 41, 5728–5743 RSC.
- C. C. Tu and L. Y. Lin, Appl. Phys. Lett., 2008, 93, 6–9 Search PubMed.
- D. A. R. Barkhouse, A. G. Pattantyus-Abraham, L. Levina and E. H. Sargent, ACS Nano, 2008, 2, 2356–2362 CrossRef CAS PubMed.
- N. Yaacobi-Gross, N. Garphunkin, O. Solomeshch, A. Vaneski, A. S. Susha, A. L. Rogach and N. Tessler, ACS Nano, 2012, 6, 3128–3133 CrossRef CAS PubMed.
- J. W. Xiao, S. Ma, S. Yu, C. Zhou, P. Liu, Y. Chen, H. Zhou and Y. Li, Nano Energy, 2018, 46, 45–53 CrossRef CAS.
- J. Huang, B. Xu, C. Yuan, H. Chen, J. Sun, L. Sun and H. Agren, ACS Appl. Mater. Interfaces, 2014, 6, 18808–18815 CrossRef CAS PubMed.
- G. H. Carey, A. L. Abdelhady, Z. Ning, S. M. Thon, O. M. Bakr and E. H. Sargent, Chem. Rev., 2015, 115, 12732–12763 CrossRef CAS PubMed.
- A. Bosio, G. Rosa and N. Romeo, Sol. Energy, 2018, 175, 31–43 CrossRef CAS.
- P. O. Anikeena, J. E. Halpert, M. G. Bawendi and V. Bulovic, Nano Lett., 2009, 9, 2532–2536 CrossRef PubMed.
- S. Kanagasubbulakshmi, R. Kathiresan and K. Kadirvelu, Colloids Surf., A, 2018, 549, 155–163 CrossRef CAS.
- H. Liang, D. Song and J. Gong, Biosens. Bioelectron., 2014, 53, 363–369 CrossRef CAS PubMed.
- V. I. Klimov, Nanocrystal quantum dots, 2010 Search PubMed.
- S. V. Kilina, P. K. Tamukong and D. S. Kilin, Acc. Chem. Res., 2016, 49, 2127–2135 CrossRef CAS PubMed.
- B. Rajbanshi, S. Sarkar and P. Sarkar, J. Mater. Chem. C, 2014, 2, 8967–8975 RSC.
- S. Sarkar, S. Saha, S. Pal and P. Sarkar, RSC Adv., 2014, 4, 14673–14683 RSC.
- S. K. Bhattacharya and A. Kshirsagar, Eur. Phys. J. D, 2008, 48, 355–364 CrossRef CAS.
- P. Seal, S. Sen and S. Chakrabarti, Chem. Phys., 2010, 367, 152–159 CrossRef CAS.
- S. K. Bhattacharya and A. Kshirsagar, Phys. Rev. B, 2007, 75, 035402 CrossRef.
- J. Wang, L. Ma, J. Zhao and K. A. Jackson, J. Chem. Phys., 2009, 130, 214307 CrossRef PubMed.
- P. Karamanis and C. Pouchan, Chem. Phys. Lett., 2009, 474, 162–167 CrossRef CAS.
- L. Ma, J. Wang and G. Wang, Chem. Phys. Lett., 2012, 552, 73–77 CrossRef CAS.
- A. E. Kuznetsov and D. N. Beratan, J. Phys. Chem. C, 2014, 118, 7094–7109 CrossRef CAS.
- E. Lim, A. E. Kuznetsov and D. N. Beratan, Chem. Phys., 2012, 407, 97–109 CrossRef CAS.
- E. V. Shah and D. R. Roy, Comput. Mater. Sci., 2014, 88, 156–162 CrossRef CAS.
- Z. Wu, Y. Zhang, S. Huang and S. Zhang, Comput. Mater. Sci., 2013, 68, 238–244 CrossRef CAS.
- R. C. Eberhart and Y. Shi, Proc. Congress on Evolutionary Computation, 2001 Search PubMed.
- R. C. Eberhart and J. Kennedy, Proceedings of the Sixth International Symposium on Micro Machine and Human Science, 1995, pp. 39–43 Search PubMed.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Phys. Rev. B, 2010, 82, 094116 CrossRef.
- Y. Wang, J. Lv, L. Zhu and Y. Ma, Comput. Phys. Commun., 2012, 183, 2063–2070 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo and A. Dal Corso, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 270–283 CrossRef CAS.
- W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298 CrossRef CAS.
- P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- K. A. Nguyen, R. Pachter, P. N. Day and H. Su, J. Chem. Phys., 2015, 142, 234305 CrossRef PubMed.
- K. A. Nguyen, R. Pachter, J. Jiang and P. N. Day, J. Phys. Chem. A, 2018, 122, 6704–6712 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Revision A.1, Gaussian, Inc., Wallingford CT, 2009 Search PubMed.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 275–280 CrossRef CAS.
- M. J. Frisch, M. Head-Gordon and J. A. Pople, Chem. Phys. Lett., 1990, 166, 281–289 CrossRef CAS.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, Chem. Phys. Lett., 1988, 153, 503–506 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228 CAS.
- I. Vasiliev, S. Öğüt and J. R. Chelikowsky, Phys. Rev. Lett., 1997, 78, 4805 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Supporting information contains Fig. S1. HOMO and LUMO of the most stable lowest-energy clusters CdnTen (n = 1–9); Fig. S2. HOMO and LUMO of the lowest-energy core–shell cage and hollow cage structures CdnTen (n = 10–17); Fig. S3. Plots of the LUMO+1 for clusters CdnTen (n = 1–17); Fig. S4. Plots of the LUMO+2 for clusters CdnTen (n = 1–17); Table S1. The binding energy (Eb) in eV per CdTe unit, point groups, HOMO values, LUMO values and HOMO–LUMO gaps calculated using the B3LYP/Lanl2dz level of theory for the lowest energy optimized structures of CdnTen (n = 1–17), the hollow cage and endohedral (core–shell) cage structures (n = 10–17) and Table S2. The binding energy (Eb) in eV per CdTe unit, point groups calculated using the MP2/Def2-TZVP level of theory for the lowest energy optimized structures of CdnTen (n = 1–17), the hollow cage and endohedral (core–shell) cage structures (n = 10–17). See DOI: 10.1039/c8ra09465a |
| This journal is © The Royal Society of Chemistry 2019 |