Open Access Article
Open Access ArticleThe structure and photoluminescence of a ZnO phosphor synthesized by the sol gel method under praseodymium doping†
F. I. H. Rhouma *ab,
F. Belkhiriaa,
E. Bouzaieneb,
M. Daoudic,
K. Taibid,
J. Dhahrib and
R. Chtouroua
*ab,
F. Belkhiriaa,
E. Bouzaieneb,
M. Daoudic,
K. Taibid,
J. Dhahrib and
R. Chtouroua
aUniversité Tunis el Manar, Laboratoire de Nanomatériaux et des Systèmes pour les Énergies Renouvelables (LANSER), Centre de Recherches et des Technologies de l’Energie, BP.95 Hammam Lif 2050, Tunisia. E-mail: rhouma.feten@yahoo.fr; Fax: +21679325934; Tel: +21650913492
bLaboratoire de la Matière Condensée et des Nanosciences, Département de Physique, Faculté des Sciences de Monastir, 5019, Tunisia
cLaboratoire de Recherche Energie et Matière pour les Développements des Sciences Nucléaire, Centre National des Sciences et Technologie Nucléaires, 2020 Sidi-Thabet, Tunisia
dLaboratoire de Sciences et Génie des Matériaux, Faculté de Génie Mécanique et Génie des Procédés, Université des Sciences et de la Technologie Houari Boumediene, BP 32, Bab Ezzouar 16111, Alger, Algeria
First published on 18th February 2019
Abstract
This work outlines some interesting results regarding the effects of Pr3+ substitution on the structural and optical properties of 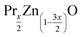 (x = 0 and 0.02) samples. Our samples were synthesized using the Pechini sol–gel method. The structural study using Rietveld refinement of XRD patterns showed a hexagonal structure with the P63mc space group for all the samples and also the existence of a secondary phase attributed to the praseodymium oxide (Pr6O11) for 2% wt Pr-doped ZnO. The refinement results revealed that both the lattice parameter and the unit cell volume increase with the increase of Pr content. X-ray peak broadening analysis was used to evaluate the crystallite size and lattice strain by the Williamson–Hall (W–H) method and size–strain plot method (SSPM). The physical parameters such as strain, stress and energy density values were also calculated using the W–H method with different models, namely uniform deformation model (UDM), uniform stress deformation model (USDM) and uniform deformation energy model (UDEDM). The obtained results showed that the mean particle size of the ZnO and Pr0.01Zn0.97O estimated from W–H analysis and the SSPM method are highly intercorrelated. Shifting of the absorption edge to lower wavelength and blue shift of the band gap are observed in the UV-visible spectra of Pr-doped ZnO samples. Particular emphasis was put on the PL measurements of such composites. A noticeable decrease of the maximum intensity of PL response was found after adding Pr3+ to ZnO. This finding is discussed in terms of the photo excited limitation of electron–hole pairs in such nanocomposites.
(x = 0 and 0.02) samples. Our samples were synthesized using the Pechini sol–gel method. The structural study using Rietveld refinement of XRD patterns showed a hexagonal structure with the P63mc space group for all the samples and also the existence of a secondary phase attributed to the praseodymium oxide (Pr6O11) for 2% wt Pr-doped ZnO. The refinement results revealed that both the lattice parameter and the unit cell volume increase with the increase of Pr content. X-ray peak broadening analysis was used to evaluate the crystallite size and lattice strain by the Williamson–Hall (W–H) method and size–strain plot method (SSPM). The physical parameters such as strain, stress and energy density values were also calculated using the W–H method with different models, namely uniform deformation model (UDM), uniform stress deformation model (USDM) and uniform deformation energy model (UDEDM). The obtained results showed that the mean particle size of the ZnO and Pr0.01Zn0.97O estimated from W–H analysis and the SSPM method are highly intercorrelated. Shifting of the absorption edge to lower wavelength and blue shift of the band gap are observed in the UV-visible spectra of Pr-doped ZnO samples. Particular emphasis was put on the PL measurements of such composites. A noticeable decrease of the maximum intensity of PL response was found after adding Pr3+ to ZnO. This finding is discussed in terms of the photo excited limitation of electron–hole pairs in such nanocomposites.
1 Introduction
Recently, nanostructured ZnO materials have drawn much attention thanks to their potential applications in electronics, optics and photonics.1–5 In particular, ZnO synthesized under nano-size forms have found wide applications in ultraviolet (UV) lasers, solar cells, capacitors, varistors, gas sensors, transparent UV resistance coatings, photo printing, electrophotography, electrochemical and electromechanical nanodevices, sunscreen lotion (cream), cosmetic and medical creams, etc.6–9 Some of the future applications include catalysts for organic reactions and delivering drugs to infected areas of the body.10 The optical properties of ZnO depend mainly on the microstructures of the materials, including crystallite size, orientation, morphology, defects and lattice strain. It is necessary to study the size-dependent properties of ZnO particles and to explore their applications in various areas of nanotechnology. Moreover, it is important to look for simple and cost-effective approaches to synthesize ZnO in the ultra-small size range where the quantum confinement effect and surface effects may be prominent and to study their structure-dependent properties. While a majority of the studies have focused on the optical properties of ZnO nanostructures, to date, very few studies have been carried out to understand the microstructure of ZnO material. Numerous methods such as the physical vapor deposition (PVD) and the chemical vapor deposition (CVD) have been devoted to prepare ZnO particles with exciting structures. However, these methods usually require high temperature, multiple steps and expensive equipment.11 On the contrary, wet chemical processes seem more attractive for many reasons: their low cost, better safety, and thus ease scaling up; compatibilities with flexible organic substrates and the growth process may occur at relatively low a temperature, which reduces the need for metal catalysts. Besides, there are a variety of parameters that allow to effectively control the morphologies and properties of the final products.12 Wet chemical processes such as spray pyrolysis13 hydrothermal process14 sol–gel processing,15 precipitation16 and co-precipitation17 are cost effective and scalable and have been used in the synthesis of a wide variety of ZnO nanostructures.11 Among these methods, sol–gel is a promising method that is known as a facile, reproducible, convenient, cost effective synthesis procedure and provides an effective way for the preparation of uniform nanostructured materials.18 Moreover, the sol gel method offers various advantages for the doping process, such as (i) the lower temperature of the process allows the avoidance of any undesired dopant phase, and (ii) a low (trace) concentration can be used, which is more easily introduced into the structure of the oxide.19 Generally, the electrical and optical properties of the semiconducting material systems are improved through doping some foreign trace elements. Doping ZnO nanoparticles by rare-Earth (RE) ions has received great attention due to the exclusive optical properties originating from the 4f transitions.20,21 Besides, there are reports on the results of Europium doping.22 Moreover, the structural, optical and electrical properties of the RE cations depend on the host structure and dopant composition.23 Considering the unique optical properties, along with the tunable emission wavelengths ranging from blue to infrared region, Pr3+ ions, a well-known activator dopant is used in the current study.24 The sharp and intense emissions of this rare earth metal in its trivalent form could support the fore mentioned application aspect.25 The luminescence study of Pr3+ ion is more interesting when compared with that of the other lanthanide ions, such as Er3+, Nd3+, and Yb3+ ions, because Pr3+ ion gives emission lines originating from three different levels (3P0, 1D2, and 1G4). The energies of the excited states of Pr3+ are potentially well suited for down-conversion (DC) in silicon solar cells. Well Pr-doped crystals have already been widely investigated26–29 and found their main application in lasers, to the authors' knowledge, only a few reports exist on Pr-doped ZnO.30,31 For this reason, we intend to study the effects of Pr-dopant on the structural; morphological and optical properties of ZnO nanoparticles. In addition, it has been reported that Pr doping is effective in improving the optoelectrical performance of ZnO films.32–34 Furthermore, a ZnO:Pr varistor doped with Co and K has a reliability, high quality, good and hardly varied varistor characteristics such as a varistor voltage and an insulation resistance. One or more rare earth cations including Pr were doped to ZnO and some other metal oxides to fabricate an electroluminescent solid state device. Mataranglo et al. reported that a Pr-doped ZnO photocatalyst showed the better photo catalytic performance for dislocating and mineralizing Eriochrome Black T in aqueous solution both under UV and visible-light illumination than Ce- or Eu doped ZnO photo catalysts.35Therefore, we have carried out a systematic study on the synthesis of pure ZnO and rare earth element Pr-doped ZnO by the sol gel method. In addition, a comparative evaluation of the mean particle size of pure and doped ZnO obtained from powder XRD procedures is reported. The strain associated with the ZnO and Pr0.01Zn0.97O sample due to lattice deformation was estimated by a modified form of W–H, namely uniform deformation method (UDM). The other modified models, such as uniform stress deformation model (USDM), uniform deformation energy density model (UDEDM) and the size strain plot method (SSPM) allow to understand the stress–strain relation and the strain ε as a function of energy density (u). Furthermore, we investigated the structure and the photoluminescence (PL) properties of the resulting samples in detail.
2 Experimental
2.1 Preparation of 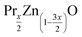
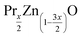 (x = 0 and 0.02) nanostructures were synthesized under identical conditions via the sol–gel based Pechini method, starting from zinc acetate dehydrate (C4H6O4Zn·2H2O) and Praseodymium oxide (Pr6O11) and citric acid. All reagents were provided by Sigma-Aldrich. The reagents were weighed according to their stoichiometric amounts. In this process, stoichiometric amounts of the precursors were first dissolved in distilled water to obtain a mixed solution. Subsequently, when these precursors completely dissolved in the solution, controlled amounts of citric acid were incorporated and dissolved while stirring. The mole ratio was fixed as 1
(x = 0 and 0.02) nanostructures were synthesized under identical conditions via the sol–gel based Pechini method, starting from zinc acetate dehydrate (C4H6O4Zn·2H2O) and Praseodymium oxide (Pr6O11) and citric acid. All reagents were provided by Sigma-Aldrich. The reagents were weighed according to their stoichiometric amounts. In this process, stoichiometric amounts of the precursors were first dissolved in distilled water to obtain a mixed solution. Subsequently, when these precursors completely dissolved in the solution, controlled amounts of citric acid were incorporated and dissolved while stirring. The mole ratio was fixed as 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of precursors to citric acid. A small amount of ammonia was added to the solution to adjust the pH value at about 7. The solution was heated on a hot plate under regular stirring to 363 K. Then, ethylene glycol was added as a polymerization agent. Heating and stirring continued for about 4 h until obtaining a gel. The obtained gel was dried at 473 K to attain dry foam which was ground in a mortar, then dried at 400 °C for 12 h in air. The powder was obtained after subsequent treatments. Finally, the obtained powder was pressed into pellets and sintered at 600 °C (12 h), 600 °C (12 h) and 600 °C (6 h) in order to obtain the corresponding phase. Various reports available for the synthesis of ZnO and Pr doped ZnO using the same temperature.36–39
1 of precursors to citric acid. A small amount of ammonia was added to the solution to adjust the pH value at about 7. The solution was heated on a hot plate under regular stirring to 363 K. Then, ethylene glycol was added as a polymerization agent. Heating and stirring continued for about 4 h until obtaining a gel. The obtained gel was dried at 473 K to attain dry foam which was ground in a mortar, then dried at 400 °C for 12 h in air. The powder was obtained after subsequent treatments. Finally, the obtained powder was pressed into pellets and sintered at 600 °C (12 h), 600 °C (12 h) and 600 °C (6 h) in order to obtain the corresponding phase. Various reports available for the synthesis of ZnO and Pr doped ZnO using the same temperature.36–39
2.2 Instrumentation
Solid phases were identified by powder X-ray diffraction (PXRD) “PANalyticalX’Pert Pro” diffract meter with filtered (Ni filter) Cu radiation from 2θ = 5° to 90° at a count rate of 23.6 s per step of 0.017° at room temperature. The PXRD was refined by the Rietveld method40 using the Full proof program (version 1.9 C-May 2016-LLB-JRC). Background, scale factors, zero-point positions, cell parameters, atomic positions, and profile coefficients for the Pseudo-Voight/FCJ asymmetric peak-shape function were refined until achieving convergence. The microstructure studies were performed using scanning electron microscopy (SEM) along with EDX. The pictures were taken at room temperature on a Phillips XL30 equipped with a field emission gun at 20 KV. The UV-Vis DRS spectra in a wavelength of 300–1800 nm were recorded through a UV-Vis spectrophotometer (SHIMADZU UV 3100S) with an integrated sphere for determining the band gap.The photoluminescence measurements of the prepared samples were performed under variable temperatures (10–300 K) using closed cryostat. The PL was excited with a 266 nm line of a laser lamp. The signal was detected through a 250 mm Jobin-Yvon monochromator and by a GaAs photomultiplier associated with a standard lock-in apparatus.
3 Results and discussion
3.1 X-ray diffraction analysis
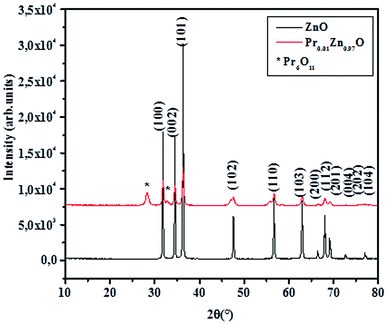
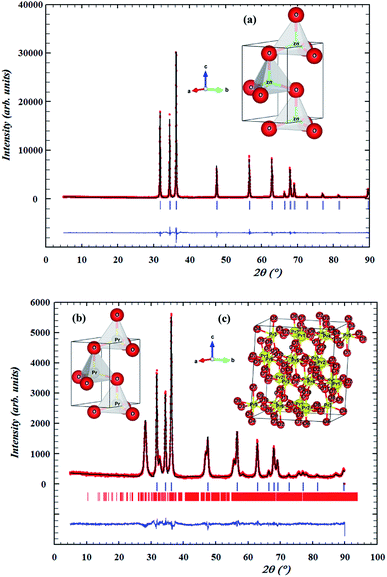
The structural properties of the samples were analyzed by powder X-ray diffraction. A typical XRD pattern of the final product is shown in Fig. 1. The investigated samples showed sharp and intense peaks of hexagonal Wurtzite structure of ZnO.41 For Pr0.01Zn0.97O, a peak located at 2θ = 28.10° emerged, as shown in Fig. 1 (marked with *), which is assigned to Pr6O11 phase.42 It is well known that, for high concentration of Pr, ZnO undergoes a significant phase segregation and/or phase separation.43 This can be attributed to the different of dimensions of the two atoms, coherently with the highest ionic radius of Pr with respect to Zn. According to Shannon,44 the ionic radii of Zn and Pr are, respectively, rZn2+ = 0.66 Å and rPr3+ = 1.13 Å. Moreover, Pr has a +3 charge and Zn2+ charge, so a different content (major) of oxygen is necessary to ensure the stoichiometry of the resulting mixed oxide. Then because of the high mismatch that the substitution of Pr causes, only a small quantity of this dopant could be tolerated by the ZnO structure and consequently the excess of dopant is found as a secondary phase. Although, Pr atoms incorporation preserves the hexagonal wurtzite structure. The crystallite size is affected by Pr. The incorporation of Pr atoms in the particles matrix may alter the nucleation step during particles, which consequently reduces the size of crystallite. The same conclusion was reported by Kumar et al.45 in doped ZnO thin films, Srinivasan et al.46 in Mn-doped ZnO, Paul et al.47 in Zr-doped ZnO thin films, Nunes et al.48 in Al-doped ZnO thin films and Nahm49 in V2O5-doped ZnO ceramics. The XRD data of the samples were subjected to Rietveld refinement using Full proof program, based on the low values of the residuals for the weighted pattern Rwp, the pattern Rp, the structure factor Rf and the goodness of fit χ2, as listed in table. Fig. 2 displays the Rietveld refinement of the samples. An excellent agreement was found between the experimental spectra and the calculated values. XRD patterns can be indexed in the hexagonal system with P63mc space group for all the synthesized samples. This result is consistent with the literature for the undoped sample prepared by Muneer M. Ba-Abbad et al.,50 where the Zn atoms were located at 2a (1/3, 2/3, 0) position and oxygen vacancy at a 2b (1/3, 2/3, z) position. The doped sample Pr0.01Zn0.97O has peaks that do not refine in P63mc hexagonal structure. These peaks are related to the presence of a minor (Pr6O11) phase, which crystallizes in a monoclinic structure with P21/c space group (no. 14). Their refinement results are given in Table 1. We can see from Table 1 that the presence of Pr leads to an increase of the cell parameters as well as the cell volume of the ZnO. A similar increase in the lattice parameters was reported for (PrZnO) by various researchers.51,52 This behavior can be related to the larger ionic radius of Pr ion. It is also confirmed by the evaluation of the (Pr, Zn)–O bond length distance using Rietveld refinement, which also increased with Pr content (Table 1). The calculated angles confirm the hexagonal structure of all the samples. The insets (a), (b) and (c) illustrate the hexagonal structure of ZnO, Pr0.01Zn0.97O and the monoclinic structure of the impurity (Pr6O11) on the basis of the parameters obtained from the Rietveld refinement of such samples.| Samples | ZnO | Pr0.01Zn0.97O | Pr6O11 |
|---|---|---|---|
| Space group | P63mc | P63mc | P21/c |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Cell parameters | |||
| a (Å) | 3.25088 | 3.25089 | 6.64145 |
| b (Å) | 3.25088 | 3.25089 | 11.61907 |
| c (Å) | 5.2059 | 5.20735 | 12.88155 |
| V (Å)3 | 47.6466 | 47.660 | 978.493 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Atoms | |||
| (Zn) Biso (Å2) | 0.802 | 0.400 | |
| (Pr) Biso (Å2) | — | 0.400 | |
| (O) Biso (Å2) | 0.969 | 1.000 | |
| z (O) | 0.38321 | 0.38979 | |
| d(Pr,Zn)–O (Å) | 1.995 | 2.030 | |
| θ(O–Pr,Zn–O) (°) | 107.94 | 107.00 | |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||
| Discrepancy factors | |||
| Rp (%) | 11.2 | 12.3 | |
| Rwp (%) | 12.4 | 12.2 | |
| RF (%) | 4.52 | 3.09 | |
| χ2 (%) | 5.80 | 1.74 | |
3.2 Particle size and strain
By dividing Kα-doublet of all observed peaks, we found that the peaks would be implicitly described by the Cauchy function. Therefore, while determining the physical broadening; the hardware broadening is subtracted from the integral width of the experimental peaks. Considering that the forms of mathematical functions that describe different types of physical broadening are unknown, different methods were proposed to determine microstructural parameters (crystallite size and micro strain). The analysis of the crystallite size was carried out using the broadening of XRD peaks. Generally, peak broadening results from both finite crystallite size and strain effect within the crystal lattice. The crystallite size (D) was calculated using Scherrer's method (SM), Williamson–Hall method (WHM), and size strain plot method (SSPM).
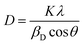 | (1) |
| SM | UDM | USDM | UDEDM | SSPM | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D (nm) | D (nm) | ε | D (nm) | σ (MPa) | ε | D (nm) | U | ε | σ (MPa) | D (nm) | ε | |
| ZnO | 46 | 39 (1) | −4.07 × 10−4 (1) | 39 (1) | −48.15 (4) | −4.07 × 10−4 (2) | 39 (1) | −9.95 (3) | 1.29 × 10−5 (3) | 1.52 (3) | 136 (1) | −3.38 × 10−4 (2) |
| Pr0.01Zn0.97O | 23 | 20 (1) | −7.97 × 10−4 (1) | 20 (1) | −94.24 (4) | −7.97 × 10−4 (2) | 20 (1) | −13.92 (4) | 1.53 × 10−5 (3) | 1.80 (3) | 70 (1) | −6.60 × 10−4 (3) |
3.2.2.1 Uniform deformation model (UDM). Ignoring the strain-induced broadening due to crystal imperfection might leads to an underestimation of the crystallite size. According to Stokes and Wilson, there is a relationship between the strain, ε and the breath, β from the Scherer lines, where the maximum strain can be obtained using eqn (2).56
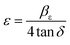 | (2) |
Afterwards, Williamson and Hall considered size-induced broadening, βD and strain-induced broadening, βε, and proposed a method as stated in eqn (3) to separate size and strain related broadening in XRD pattern, where the breadth of the Bragg peak, βhkl is the sum of these contributions.56
| βhkl = βD + βε | (3) |
The size and strain induced broadening obtained from eqn (1) and (2), respectively, can be substituted into eqn (3), then rearranged to give an equation as follows:
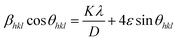 | (4) |
Eqn (4) is called Williamson–Hall equation. It assumes that the strain is uniform in all crystallographic directions and known as uniform deformation model (UDM). In this model the crystal is considered as isotropic in nature and it is assumed that the properties of a material are independent of the direction along which it is measured. A plot of βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl against 4
θhkl against 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
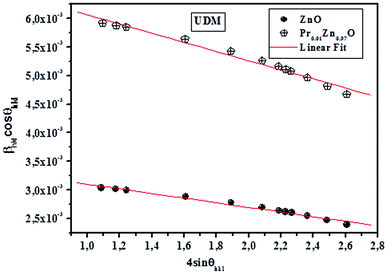
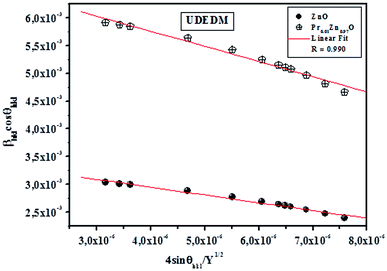
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl is shown in Fig. 3. Accordingly, the slope and y-intersect of the fitted line represent strain and particle size, respectively. The plots showed a negative strain for the samples. This strain may be due to the lattice shrinkage observed in the calculation of lattice parameters. The results of the UDM analysis for the samples are summarized in Table 2.
θhkl is shown in Fig. 3. Accordingly, the slope and y-intersect of the fitted line represent strain and particle size, respectively. The plots showed a negative strain for the samples. This strain may be due to the lattice shrinkage observed in the calculation of lattice parameters. The results of the UDM analysis for the samples are summarized in Table 2.
3.2.2.2 Uniform stress deformation model (USDM). In the uniform stress deformation model there is a proportionality between stress and strain given by σ = Yε which is known as Hook's law within the elastic limit. In this relation, σ is the stress and Y is Young's modulus. This equation is merely an approximation that is valid for a significantly small strain. Assuming that small strain is present in the pure ZnO and doped ZnO particles, Hook's law can be applied to estimate the lattice deformation stress. Beyond the elastic limit or with a further increase in strain, the stress in the particles deviates from this linear proportionality. Hence, by assuming that the lattice deformation stress remains uniform in all crystallographic directions, the strain factor of eqn (4) is replaced by
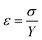 and the model equation is given by:
and the model equation is given by:
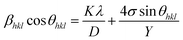 | (5) |
For a hexagonal crystal, Young's modulus is given by the following relation57
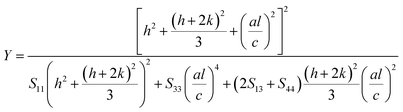 | (6) |
Here S11, S13, S33 and S44 are the elastic compliances of ZnO with the values of (7.858 × 10−12) (−2.206 × 10−12), (6.94 × 10−12) and (23.57 × 10−12) m2 N−1, respectively.58. Morever, a graph is drawn between 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl and βhkl
θhkl and βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
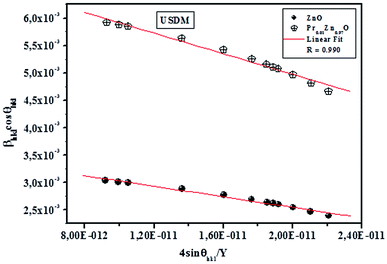
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl and fitted as straight line. The uniform deformation stress and crystallite size are estimated from the slope and y-intercept of the graph respectively. Thus, the lattice strain extracted from the crystal is measured by using the Y value. From Fig. 3, it can be seen that athoughthere is a small scattering of experimental data points closer to the linear fit, it allows the uniformity of the stress to a reasonable approximation. Herein, the scatter of data points from the linear fit is due to the introduction of anisotropic Young's modulus in eqn (5).
θhkl and fitted as straight line. The uniform deformation stress and crystallite size are estimated from the slope and y-intercept of the graph respectively. Thus, the lattice strain extracted from the crystal is measured by using the Y value. From Fig. 3, it can be seen that athoughthere is a small scattering of experimental data points closer to the linear fit, it allows the uniformity of the stress to a reasonable approximation. Herein, the scatter of data points from the linear fit is due to the introduction of anisotropic Young's modulus in eqn (5).
3.2.2.3 Uniform energy density model (UDEDM). As already described, the lattice strain and density of deformation energy are assumed as anisotropic, unlike the deformation stress which was isotropic. This homogeneity and isotropy of nano crystalline materials are no longer consistent; here the anisotropic nature of the lattice deformation stress is also taken into account. The deformation energy (energy per unit volume) as a function of strain is given by Hook's law as:
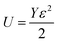 . Hence, the W–H eqn (5) is modified to uniform density model (UDEDM) as given in eqn (7).
. Hence, the W–H eqn (5) is modified to uniform density model (UDEDM) as given in eqn (7).
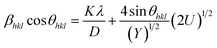 | (7) |
Here the deformation stress and deformation energy density are related by: 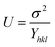 . The crystallite size and uniform energy density (U) are estimated from the y-intercept and slope of the straight line plot of βhkl
. The crystallite size and uniform energy density (U) are estimated from the y-intercept and slope of the straight line plot of βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl as a function of 4
θhkl as a function of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl/Y1/2. Then, the deformation stress and the lattice strain were extracted from the deformation energy density value by knowing Y values. The UDEDM results are shown in Table 2.
θhkl/Y1/2. Then, the deformation stress and the lattice strain were extracted from the deformation energy density value by knowing Y values. The UDEDM results are shown in Table 2.
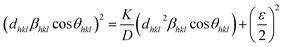 | (8) |
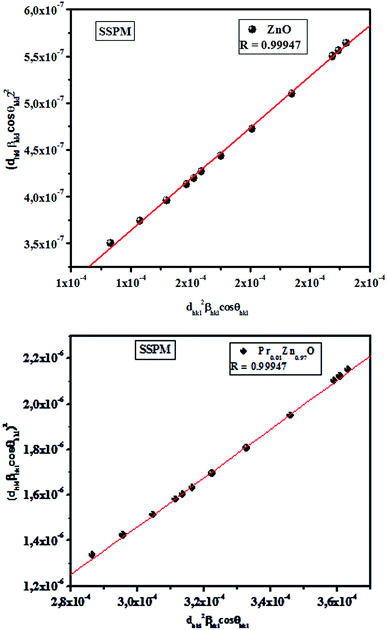
Fig. 6 shows the plots of (dhklβhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl)2 and (dhkl2βhkl
θhkl)2 and (dhkl2βhkl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θhkl) on y and x axes, respectively. In this case, the particle size is calculated from the slope of the linearly fitted data and the root of y-intercept gives the strain. As can be seen from Fig. 6, all the experimental points match well with the straight line. The results obtained from the Scherrer's method (SM), W–H models (UDM, USDM and UDEDM) and (SSPM) methods are shown in Fig. 3–6 and Table 2. The values of the average crystallite size of ZnO and Pr0.01Zn0.97O ceramics obtained from the different models are more or less similar, implying that the inclusion of strain in various forms has a very small effect on the average crystallite size. By exploring the plots, it appears that the result of the (SSPM) model is found to be more accurate than the UDM, USDM and UDEDM models, as the data were fitted more accurately in this model, with all high-intensity points touching the linear fit.
θhkl) on y and x axes, respectively. In this case, the particle size is calculated from the slope of the linearly fitted data and the root of y-intercept gives the strain. As can be seen from Fig. 6, all the experimental points match well with the straight line. The results obtained from the Scherrer's method (SM), W–H models (UDM, USDM and UDEDM) and (SSPM) methods are shown in Fig. 3–6 and Table 2. The values of the average crystallite size of ZnO and Pr0.01Zn0.97O ceramics obtained from the different models are more or less similar, implying that the inclusion of strain in various forms has a very small effect on the average crystallite size. By exploring the plots, it appears that the result of the (SSPM) model is found to be more accurate than the UDM, USDM and UDEDM models, as the data were fitted more accurately in this model, with all high-intensity points touching the linear fit.
3.3 Morphological studies
In order to check the existence of all the elements in the ZnO and Pr doped ZnO compounds energy dispersive X-ray analysis was performed. EDX plot of the samples is shown in Fig. 7 and the resulted cations proportions are indicated in Table 3. EDX plots show the presence of all chemical species in the ZnO and Pr0.01Zn0.97O. EDX analysis shows that chemical composition of samples is close to the nominal one within the experimental uncertainties. The inset of Fig. 7 shows the scanning electron microscopy (SEM) photograph for the two samples. The micrographs indicate that the grains are uniformly distributed over the entire surface of the samples.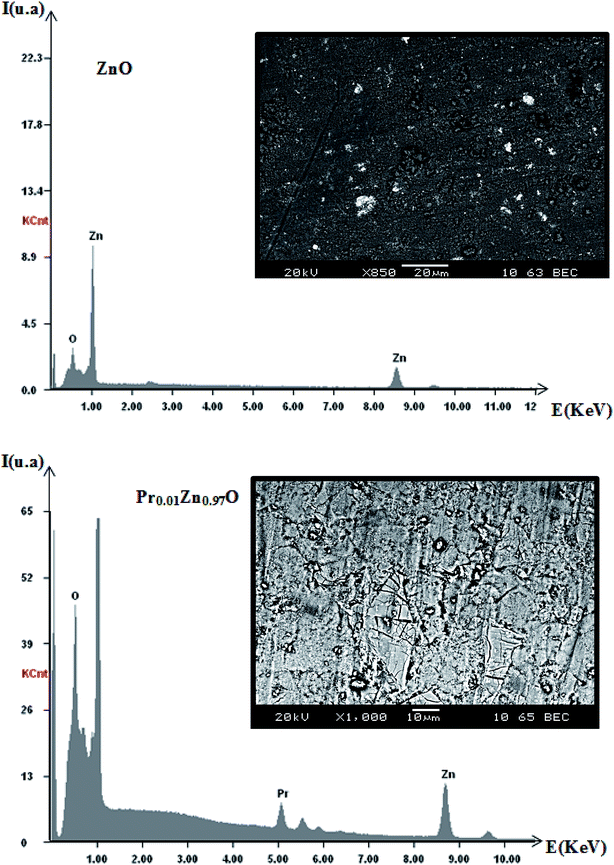 | ||
| Fig. 7 Plot of EDX analysis of chemical species of ZnO and Pr0.01Zn0.97O. Inset shows their corresponding SEM graph. | ||
| x | Chemical species | Nominal composition | |
|---|---|---|---|
| Zn | Pr | ||
| 0 | 0.8066 | — | ZnO |
| 0.2 | 0.7797 | 0.1158 | Pr0.01Zn0.97O |
3.4 Optical properties
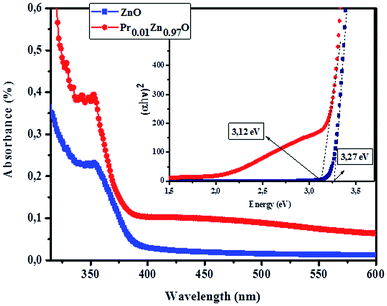
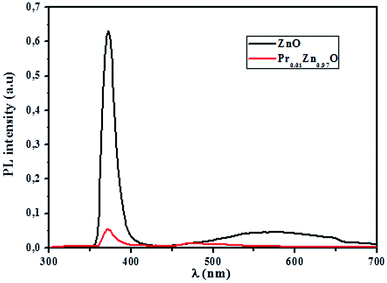
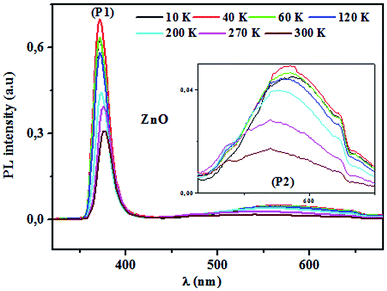
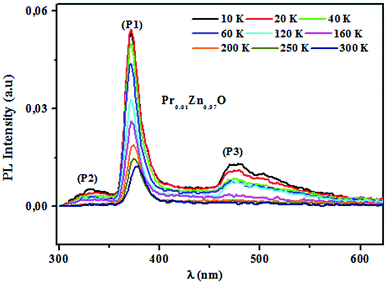
3.4.2.1 Identification of transitions. The photoluminescence (PL) spectroscopy provides important insights into the purity and quality of materials. Fig. 9 shows PL spectra of undoped ZnO and Pr-doped ZnO nanoparticles at 10 K. At a first glance, undoped ZnO and Pr-doped ZnO spectra seem to have the same behavior. The spectrum of ZnO consists of a sharp emission peak (P1) situated at 372 nm which is a near band-edge emission52 that usually considered a characteristic emission of ZnO and is attributed to band-edge emission or donor-band excitation,63 this is justified in absorption spectrum. Another broad green emission band (P2) shown in the PL spectrum of ZnO situated at 575 nm was usually attributed to oxygen vacancies, zinc vacancies and surface defects.64,65 A blue shift in the visible emission of ZnO nanoparticles was observed to take place towards lower wavelength region from 575 nm to 473 nm on the introduction of Pr ions into ZnO lattice and a significant quenching of the maximum UV/VIS emission. Such a PL quenching in the UV/VIS emission may be due to change in the defect chemistry of ZnO:Pr samples and it is consistent with successful substitution of Pr ions in ZnO lattice reported in ref. 66.
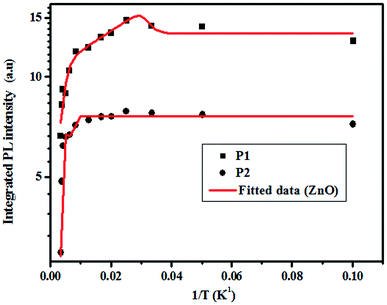
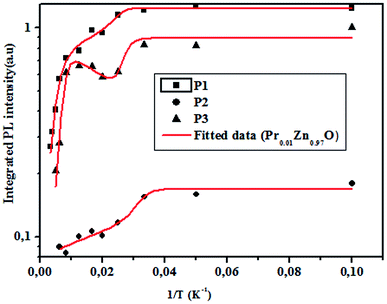
3.4.2.2 Photoluminescence study at room temperature. Fig. 10 and 11 depict PL spectra of pure ZnO and Pr-doped ZnO nanocomposites obtained at different temperatures from 10 K to 300 K, for an excitation wavelength of λ = 2660 Å. The PL intensity of the two samples fell remarkably until 300 K with increasing temperature. This fall is attributed to the phonon density in the system that rises with the temperature, and therefore, non-radiative relaxation of the excited electron–hole pairs becomes predominant.66 To investigate the mechanism governing the behavior of PL responses of the two samples, the inverse temperature dependence of integrated PL intensity of each band were performed. The activation energy was calculated by fitting the spectra using Origin Pro8 us software and the model determined by G. Saint-Girons et al.67
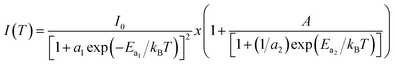 | (9) |
| ZnO | Pr0.01Zn0.97O | ||||
|---|---|---|---|---|---|
| P1 | P2 | P1 | P2 | P3 | |
| Ea1 (meV) | 57.17 | 307.29 | 52.39 | 38.07 | 62.74 |
| Ea2 (meV) | 56.01 | 307.90 | 50.62 | 36.91 | 64.63 |
| R2 | 0.96 | 0.98 | 0.99 | 0.96 | 0.95 |
4 Conclusion
In summary, pure and Pr-doped ZnO nanoparticles have been synthesized by sol–gel method and characterized by X-ray diffraction and PL technique. The Rietveld refinement from the X-ray diffraction patterns, showed a hexagonal structure wurtzite for the investigated samples and the appearance of minor impurity phase identified as praseodymium oxide (Pr6O11) belonging to a Monoclinic structure for Pr doped ZnO. An increase in the lattice parameters of the hexagonal unit cell has been observed with increasing Pr content. This possibly occurs due to the difference in ionic radii of Zn2+ and Pr3+ ions. Furthermore, the line profile of the scanned XRD patterns was analyzed by Scherrer formula, modified forms of Williamson Hall analysis and size strain plot method. In Scherrer equation, the physical origin of peak broadening is due to the crystallite size alone, which the evaluated crystallite size could be underestimated. However, in Williamson Hall analysis and SSPM method, the peak broadening is contributed by crystallite size and lattice strain. According to the results, SSPM method obtains the best fitting line to the data points among other techniques, with leads to high precision of estimated values for these types of materials. Blue shift in band gap attributed to Burstein–Moss effect may be a consequence of the incorporation of Pr2+ in ZnO lattice. The PL results suggest that the ZnO sample could sensitize the rare-earth activator and lead to an energy transfer, resulting a blue emission bands. The latest property seems so interesting for possible optoelectronic application since a cost effective process has been used to prepare composite material. Further studies are in progress to test these products as structures having oxygen vacancy in some sensitivity applications such as photo catalysis, gas and biosensors.Conflicts of interest
There are no conflicts to declare.References
- Ü. Özgür, Y. I. Alivov, C. Liu, A. Teke, M. A. Reshchikov, S. Doğan, V. Avrutin, S. Cho and H. Morkoç, A comprehensive review of ZnO materials and devices, J. Appl. Phys., 2005, 98, 4130, DOI:10.1063/1.1992666.
- Z. Fan and J. G. Lu, Zinc Oxide Nanostructures: Zinc oxide nanostructures: Synthesis and Properties, J. Nanosci. Nanotechnol., 2005, 5, 1562–1573, DOI:10.1166/jnn.2005.182.
- Z. L. Wang, Zinc oxide nanostructures: growth, properties and applications, J. Phys.: Condens. Matter, 2004, 16, 829, DOI:10.1088/0953-8984/16/25/R01.
- Y. W. Heo, D. P. Norton, L. C. Tien, Y. Kwon, B. S. Kang, F. Ren and S. J. Pearton, ZnO nanowire growth and devices, J. Mater. Sci. Eng., 2004, 47, 1–47, DOI:10.1016/j.mser.2004.09.001.
- G. Yi, C. Wang and W. Il Park, ZnO nanorods: synthesis, characterization and applications, Semicond. Sci. Technol., 2005, 20, 22–34, DOI:10.1088/0268-1242/20/4/003.
- H. T. Wang, B. S. Kang, F. Ren, L. C. Tien, P. W. Sadik, D. P. Norton, S. J. Pearton, J. Lin, H. T. Wang, B. S. Kang, F. Ren and J. Lin, Hydrogen-selective sensing at room temperature with ZnO nanorods, Appl. Phys. Lett., 2005, 86, 243503, DOI:10.1063/1.1949707.
- J. Wu, G. Chen, H. Yang, C. Ku and J. Lai, Effects of dye adsorption on the electron transport properties in ZnO-nanowire dye-sensitized solar cells, Appl. Phys. Lett., 2007, 90, 213109, DOI:10.1063/1.2742639.
- S. F. Yu, C. Yuen, S. P. Lau, W. I. Park, G. Yi, S. F. Yu, C. Yuen and S. P. Lau, Random laser action in ZnO nanorod arrays embedded in ZnO epilayers, Appl. Phys. Lett., 2004, 84, 3241, DOI:10.1063/1.1734681.
- N. Serpone, D. Dondi and A. Albini, Inorganic and organic UV filters: Their role and efficacy in sunscreens and suncare products, Inorganica Chim. Acta, 2007, 360, 794–802, DOI:10.1016/j.ica.2005.12.057.
- W. Huang, G. Fang and C. Wang, A nanometer-ZnO catalyst to enhance the ozonation of 2, 4, 6-trichlorophenol in water, Colloids Surf., A, 2005, 260, 45–51, DOI:10.1016/j.colsurfa.2005.01.031.
- S. Sepulveda-guzman, B. Reeja-jayan, E. De Rosa and A. Torres-castro, Synthesis of assembled ZnO structures by precipitation method in aqueous media, Mater. Chem. Phys., 2009, 115, 172–178, DOI:10.1016/j.matchemphys.2008.11.030.
- S. Xu and Z. L. Wang, One-Dimensional ZnO Nanostructures: Solution Growth and Functional Properties, J. Nano Res., 2011, 4, 1013–1098, DOI:10.1007/s12274-011-0160-7.
- T.-Q. Liu, O. Sakurai, N. Mizutani and M. Kato, Preparation of spherical fine ZnO particles by the spray pyrolysis method using ultrasonic atomization techniques, J. Mater. Sci., 1986, 21, 3698–3702, DOI:10.1007/BF02403024.
- U. Pal, Synthesis and optical properties of ZnO nanostructures with different morphologies, Opt. Mater., 2006, 29, 65–69, DOI:10.1016/j.optmat.2006.03.015.
- P. Ferrão, K. Al and S. Awad, Synthesis of ZnO Nanopowders By Using Sol-gel and Studying their Structural and Electrical Properties at Different Temperature, Energy Procedia, 2017, 119, 565–570, DOI:10.1016/j.egypro.2017.07.080.
- V. Sesha Sai Kumar and K. Venkateswara Rao, X-ray peak broadening analysis and optical studies of ZnO nanoparticles derived by surfactant assisted combustion synthesis, J. Nano- Electron. Phys., 2013, 5, 1–6 Search PubMed.
- A. Katiyar, N. Kumar and A. Srivastava, Optical properties of ZnO nanoparticles synthesized by co-precipitation method using LiOH, Mater. Today: Proc., 2018, 5, 9144–9147, DOI:10.1016/j.matpr.2017.10.034.
- D. Raoufi and T. Raoufi, The effect of heat treatment on the physical properties of sol – gel derived ZnO thin films, Appl. Surf. Sci., 2009, 255, 5812–5817, DOI:10.1016/j.apsusc.2009.01.010.
- T. Hernández, S. De Parra, J. Ibarra and B. Kharisov, Sol–gel based Pechini method synthesis and characterization of Sm1−xCaxFeO3 perovskite 0.1≤ x ≤0.5, J. Powder Technol., 2012, 229, 290–293, DOI:10.1016/j.powtec.2012.06.057.
- M. Zhong, G. Shan, Y. Li, G. Wang and Y. Liu, Synthesis and luminescence properties of Eu3+-doped ZnO nanocrystals by a hydrothermal process, Mater. Chem. Phys., 2007, 106, 305–309, DOI:10.1016/j.matchemphys.2007.06.007.
- C. Yang, S. Cheng, H. Lee and S. Chen, Effects of phase transformation on photoluminescence behavior of ZnO:Eu prepared in different solvents, Ceram. Int., 2006, 32, 37–41, DOI:10.1016/j.ceramint.2004.11.016.
- A. Ishizumi and Y. Kanemitsu, Structural and luminescence properties of Eu-doped ZnO nanorods fabricated by a microemulsion method, Appl. Phys. Lett., 2005, 86, 253106, DOI:10.1063/1.1952576.
- P. Mohanty and S. Ram, Enhanced photoemission in dispersed Eu2O3 nanoparticles in amorphous Al2O3, J. Mater. Chem., 2003, 13, 3021–3025, 10.1039/b307028j.
- T. Suyama, K. Okamoto and Y. Hamakawa, New type of thin film electroluminescent device having a multilayer structure, Appl. Phys. Lett., 2001, 462, 1980–1983, DOI:10.1063/1.93532.
- S. S. Ashtaputre, A. Nojima, S. K. Marathe, D. Matsumura, T. Ohta, R. Tiwari, G. K. Dey and S. K. Kulkarni, Investigations of white light emitting europium doped zinc oxide nanoparticles, J. Phys. D: Appl. Phys., 2008, 41, 015301, DOI:10.1088/0022-3727/41/1/015301.
- Z. Nie, J. Zhang, X. Zhang, X. Ren, G. Zhang and X.-j. Wang, Evidence for Visible Quantum Cutting via Energy Transfer in SrAl12O19:Pr,Cr, Opt. Lett., 2007, 32, 991–993, DOI:10.1364/OL.32.000991.
- R. T. Wegh, H. Donker, E. V. D. van Loef, K. D. Oskam and A. Meijerink, Quanttum Cutting Through Down Conversion in Rare-earth Compounds, J. Lumin., 2000, 87–89, 1017–1019, DOI:10.1016/S0022-2313(99)00514-1.
- N. Chanthima, K. Boonin, P. Limsuwan and J. Kaewkhao, Visible Luminescence of Pr3+ in Bismuth Borate Glasses, Adv. Mater. Res., 2013, 770, 59–63, DOI:10.4028/www.scientific.net/AMR.
- Y. An, C. Labbe, L. Khomenkova, M. Morales, X. Portier and F. Gourbilleau, Microstructure and optical properties of Pr3+-doped hafnium silicate films, Adv. Mater. Res., 2013, 8(1), 8–43, DOI:10.1186/1556-276X-8-43.
- Y. Sato, J. P. Buban, T. Mizoguchi, N. Shibata, M. Yodogawa, T. Yamamoto and Y. Ikuhara, Role of Pr Segregation in Acceptor-State Formation at ZnO Grain boundaries, Phys. Rev. Lett., 2006, 97, 106802, DOI:10.1103/PhysRevLett.97.106802.
- H. Li, K. Luo, M. Xia and P. W. Wang, Synthesis and Optical Properties of Pr3+ Doped Quantum Dots, J. Non-Cryst. Solids, 2014, 383, 176–180, DOI:10.1016/j.jnoncrysol.2013.04.028.
- H. Li, J. Meng, Y. Liu, B. Zhang and G. Cheng, Effect of Pr Doping on the Photoelectric Properties of ZnO Transparent Conducting Thin films, Mater. Rev., 2015, 29(4b), 11–15 CAS.
- D. Xu, K. He, R. H. Yu, Y. Tong, J. P. Qi, X. J. Sun, Y. T. Yang, H. X. Xu, H. M. Yuan and J. Ma, Microstructure and electrical properties of praseodymium oxide doped Bi2O3 based ZnO varistor films Materials Technology, Adv. Funct. Mater., 2015, 30, A24–A28, DOI:10.1179/1753555714Y.0000000242.
- A. A. Dakhel, Nanocrystalline Pr-doped ZnO insulator for metal–insulator–Si Schottky diodes, J. Cryst. Growth, 2009, 311, 4183–4187 CrossRef CAS.
- V. Vaiano, M. Matarangolo, O. Sacco and D. Sannino, Photocatalytic Removal of Eriochrome Black T Dye over ZnO Nanoparticles Doped with Pr, Ce or Eu, Chem. Eng. Trans., 2017, 57, 625–630, DOI:10.3303/CET1757105.
- P. Kumbhakar, S. Biswas and P. Kumbhakar, Observation of high photocatalytic activity by tuning of defects in chemically synthesized ethylene glycol capped ZnO nanorods, Optik, 2018, 154, 303–314, DOI:10.1016/j.ijleo.2017.10.039.
- D. Verma, A. K. Kole and P. Kumbhakar, Red shift of the band-edge photoluminescence emission and effects of annealing and capping agent on structural and optical properties of ZnO nanoparticles, J. Alloys Compd., 2015, 625, 122–130, DOI:10.1016/j.jallcom.2014.11.102.
- S. Klubnuan, S. Suwanboon and P. Amornpitoksuk, Effects of optical band gap energy, band tail energy and particle shape on photocatalytic activities of different ZnO nanostructures prepared by a hydrothermal method, Opt. Mater., 2016, 53, 134–141, DOI:10.1016/j.optmat.2016.01.045.
- M. Chattopadhyay, P. Kumbhakar, C. S. Tiwary, A. K. Mitra, U. Chatterjee and T. Kobayashi, Three-photon-induced four-photon absorption and nonlinear refraction in ZnO quantum dots, Opt. Lett., 2009, 34(23), 3644–3646 CrossRef CAS PubMed.
- N. Assoudi, I. Walha, E. Dhahri, S. Alleg and E. K. Hlil, Structural, magnetic and on magnetocaloric properties near the paramagnetic to ferromagnetic phase transition in La0.5 0.1Ca0.4MnO3 Oxide, Solid State Commun., 2018, 277, 13–18, DOI:10.1016/j.ssc.2018.04.003.
- D. A. A. Santos, A. D. P. Rocha and M. A. Macêdo, Rietveld refinement of transition metal doped ZnO, Powder Diffr., 2008, 23(2), 36–41, DOI:10.1154/1.2903739.
- A. M. Dehkordi, S. Bhattacharya, T. Darroudi, H. N. Alshareef and T. M. Tritt, New insights on the synthesis and electronic transport in bulk polycrystalline Pr-doped SrTiO3, J. Appl. Phys., 2015, 117(5), 055102, DOI:10.1063/1.4905417.
- A. Gulino, F. Castelli, P. Dapporto, P. Rossi, I. Fragala, S. Chimiche and A. Doria, Synthesis and Characterization of Thin Films of Cadmium Oxide, Chem. Mater., 2002, 474, 704–709 CrossRef.
- R. D. Shannon and C. T. Prewitt, Effective Ionic Radii in Oxides and Fluorides, Acta Crystallogr., 1969, 25(5), 925–946, DOI:10.1107/S0567740869003220.
- P. M. R. Kumar, C. S. Kartha, K. P. Vijayakumar, F. Singh and D. K. Avasthi, Modifications of ZnO thin films under dense electronic excitation, J. Appl. Phys., 2005, 97, 013509, DOI:10.1063/1.1823574.
- G. Srinivasan and J. Kumar, Effect of Mn doping on the microstructures and optical properties of sol–gel derived ZnO thin films, J. Cryst. Growth, 2008, 310, 1841–1846, DOI:10.1016/j.jcrysgro.2007.10.056.
- G. K. Paul, S. Bandyopadhyay, S. K. Sen and S. Sen, Structural, optical and electrical studies on sol – gel deposited Zr doped ZnO films, Mater. Chem. Phys., 2003, 79, 71–75 CrossRef CAS.
- P. Nunes, E. Fortunato, P. Tonello, F. B. Fernandes and P. Vilarinho, Effect of different dopant elements on the properties of ZnO thin films, Vaccum, 2002, 64, 281–285 CrossRef CAS.
- C. Nahm, Microstructure and electrical characteristics of MnTa-doped ZnO–V2O5-ceramics with sintering, J. Alloy. Comp., 2010, 505, 657–660, DOI:10.1016/j.jallcom.2010.06.102.
- M. M. Ba-abbad, M. S. Takriff and A. A. H. Kadhum, Solar photocatalytic degradation of 2-chlorophenol with ZnO nanoparticles: optimisation with D-optimal design and study of intermediate mechanisms, Environ. Sci. Pollut. Res., 2016, 24(3), 2804–2819, DOI:10.1007/s11356-016-8033-y.
- M. M. Ba-abbad, M. S. Takriff, A. Benamor and A. Wahab, Synthesis and characterisation of Co2+-incorporated ZnO nanoparticles prepared through a sol-gel method, Adv. Powder Technol., 2016, 27(6), 1–9, DOI:10.1016/j.apt.2016.08.009.
- M. Wang, Synthesis of Pr-doped ZnO nanoparticles by sol-gel method and varistor properties study, J. Alloy. Comp., 2014, 621, 220–224, DOI:10.1016/j.jallcom.2014.09.208.
- V. Biju, N. Sugathan, V. Vrinda and S. L. Salini, Estimation of lattice strain in nanocrystalline silver from X-ray diffraction line broadening, J. Mater. Sci., 2008, 43, 1175–1179, DOI:10.1007/s10853-007-2300-8.
- J. S. Lee and R. J. De Angelis, X-ray diffraction patterns from nanocrystalline binary alloys, Nanostruct. Mater., 1996, 7, 805–812, DOI:10.1016/S0965-9773(96)00045-1.
- P. Kaur, S. Kumar, C. Liang and C. Y. Hsu, Investigations on structural, magnetic and electronic structure of Gd-doped ZnO nanostructures synthesized using sol–gel technique, Appl. Phys. A: Mater. Sci. Process., 2016, 122(3) DOI:10.1007/s00339-016-9707-5.
- A. Ben Hassen, F. I. H. Rhouma, J. Dhahri and N. Abdelmoula, Effect of the substitution of titanuim by chrome on the structural, dielectric and optical properties in Ca0.67La0.22Ti1-xCrxO3 perovskites, J. Alloy. Comp., 2015, 663, 436–443, DOI:10.1016/j.jallcom.2015.09.087.
- B. R. Kumar and B. Hymavathi, X-ray peak profile analysis of solid-state sintered alumina doped zinc oxide ceramics by Williamson–Hall and size-strain plot methods, Journal of Asian Ceramic Societies, 2017, 5, 94–103, DOI:10.1016/j.jascer.2017.02.0.
- M. A. Tagliente and M. Massaro, Strain-driven (0 0 2) preferred orientation of ZnO nanoparticles in ion-implanted silica, Nucl. Instrum. Methods Phys. Res. B, 2008, 266, 1055–1061, DOI:10.1016/j.nimb.2008.02.036.
- A. K. Zak, A. M. Hashim and M. Darroudi, Optical properties of ZnO/BaCO3 nanocomposites in UV and visible regions, Nanoscale Res. Lett., 2014, 9(1), 399, DOI:10.1186/1556-276X-9-399.
- B. E. Semelius, K. F. Berggren, Z. C. Jin, I. Hamberg and C. G. Graqvist, Band-gap tailoring of ZnO by means of heavy Al doping, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37(17), 10244–10248, DOI:10.1103/physrevb.37.10244.
- A. Chanda, S. Guptab, M. Vasundhara, S. R. Joshid, G. R. Muttae and J. Singh, Study of structural, optical and magnetic properties of cobalt doped ZnO nanorods, RSC Adv., 2017, 7, 50527–50536, 10.1039/C7RA08458G.
- A. Khataee, A. Karimi, S. Arefi-Oskoui, R. D. C. Soltani, Y. Hanifehpour, B. Soltani and S. W. Joo, Sonochemical synthesis of Pr-doped ZnO nanoparticles for sonocatalytic degradation of Acid Red 17, Ultrason. Sonochem., 2014, 22, 371–381, DOI:10.1016/j.ultsonch.2014.05.023.
- S. K. S. Parashar, B. S. Murty, S. Repp, S. Weber and E. Erdem, Investigation of intrinsic defects in core-shell structured ZnO nanocrystals, J. Appl. Phys., 2012, 111, 113712, DOI:10.1063/1.4725478.
- H. Kaftelen, K. Ocakoglu, R. Thomann, S. Tu, S. Weber and E. Erdem, EPR and photoluminescence spectroscopy studies on the defect structure of ZnO nanocrystals, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 014113, DOI:10.1103/PhysRevB.86.014113.
- E. Erdem, Microwave power, temperature, atmospheric and light dependence of intrinsic defects in ZnO nanoparticles: A study of electron paramagnetic resonance (EPR) spectroscopy, J. Alloys Compd., 2014, 605, 34–44, DOI:10.1016/j.jallcom.2014.03.157.
- N. Mohamed, J. Hassan, K. A. Matori, R. Syahidah, Z. A. Wahab, Z. Maisarah, M. Ismail, N. Fadilah, S. Syuhaida and A. Rashid, Influence of Pr doping on the thermal, structural and optical properties of novel SLS-ZnO glasses for red phosphor, Results Phys., 2017, 7, 1202–1206, DOI:10.1016/j.rinp.2017.03.018.
- G. Saint-Girons and I. Sagnes, Photoluminesence quenching of a low-pressure metal-organic vapor-phase-epitaxy grown quantum dots array with bimodal inhomogeneous broadening, J. Appl. Phys., 2002, 91, 10115, DOI:10.1063/1.1481968.
- F. Belkhiria, F. I. H. Rhouma, S. Hcini, M. Daoudi, H. Gammoudi and M. Amlouk, Full length article process along with temperature dependent photoluminescence, J. Lumin., 2017, 181, 1–7, DOI:10.1016/j.jlumin.2016.08.045.
- H. Gammoudi, F. Belkhiria, K. Sahlaoui, W. Zaghdoudi, M. Daoudi, S. Helali, F. Morote, H. Saadaoui, M. Amlouk, G. Jonusauskas, T. Cohen-Bouhacina and R. Chtourou, Enhancement of the photoluminescence property of hybrid structures using single-walled carbon nanotubes/pyramidal porous silicon surface, J. Alloy. Comp., 2018, 731, 978–984, DOI:10.1016/j.jallcom.2017.10.040.
- D. Venkatesan, D. Deepan, M. Velavan, R. Sankar, R. Jayavel and R. Dhanasekaran, Preparation and Characterization of Rare Earth (Pr, Nd) Doped ZnO nanoparticles, International Conference on Nanoscience and Nanotechnology, 2010, pp. 343–347 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra09939a |
| This journal is © The Royal Society of Chemistry 2019 |