Open Access Article
Open Access ArticleNew high-pressure phases of Fe7N3 and Fe7C3 stable at Earth's core conditions: evidences for carbon–nitrogen isomorphism in Fe-compounds†
Nursultan Sagatov *ab,
Pavel N. Gavryushkin
*ab,
Pavel N. Gavryushkin ab,
Talgat M. Inerbaevac and
Konstantin D. Litasovab
ab,
Talgat M. Inerbaevac and
Konstantin D. Litasovab
aSobolev Institute of Geology and Mineralogy, Siberian Branch of the Russian Academy of Sciences, Novosibirsk, 630090 Russia. E-mail: sagatinho23@gmail.com
bNovosibirsk State University, Novosibirsk, 630090 Russia
cL. N. Gumilyov Eurasian National University, Astana, 010008 Kazakhstan
First published on 25th January 2019
Abstract
We carried out ab initio calculations on the crystal structure prediction and determination of P–T diagrams within the quasi-harmonic approximation for Fe7N3 and Fe7C3. Two new isostructural phases Fe7N3-C2/m and Fe7C3-C2/m which are dynamically and thermodynamically stable under the Earth's core conditions were predicted. The Fe7C3-C2/m phase stabilizes preferentially to the known h-Fe7C3 at 253–344 GPa in the temperature range of 0–5000 K, and the Fe7N3-C2/m stabilizes preferentially relative to the β-Fe7N3 – at ∼305 GPa over the entire temperature range. This indicate that carbon and nitrogen can mutually coexist and replace each other in the Earth's and other planetary cores similarly to low pressure phases of the same compounds.
1. Introduction
Iron carbides' and nitrides' behaviour at high pressures is important due to the close correspondence of the density and elastic properties of these compounds to those of the Earth's core.2 Carbides are classical candidates for the list of the Earth's core potential phases,3,4 while nitrides are newcomers in this list. The uprising interest to iron nitrides is due to their recent findings in meteorites and deep mantle rocks.6–9Fe7C3 and Fe7N3 stoichiometries are considered as potential inner core constituents among known Fe–C and Fe–N compounds. In the case of Fe7C3, this assumption is based on the experimental results, showing that this compound crystallizes first from the iron melt at pressures of 130 GPa, and also on the close correspondence of its density to that of the Earth's core.10–12 In the case of Fe7N3, the assumption is based on the greater stability of Fe7N3 compared to the other nitrides under the inner core conditions.13,14
Fe7C3 iron carbide presents in the form of two modifications: low-pressure orthorhombic o-Fe7C3 (Pbca) and high-pressure hexagonal h-Fe7C3 (P63mc). o-Fe7C3 was synthesized in the pressure range of 7–15 GPa with heating to about 2000 K, and was traced up to pressures of ∼205 GPa and temperatures above 3700 K.15 Based on the results, the authors assumed the stability of o-Fe7C3 under the conditions of the Earth's inner core. In contrast, the calculations within the density functional theory (DFT) show that at 0 K transition from o- to h-phase takes place at ∼100 GPa.16,17 The equation of state of the h-phase was experimentally determined up to 71 GPa and 1973 K,11 and theoretically – up to 364 GPa at 0 K.18 In the same work, the disappearance of the magnetic moment was predicted at pressures near 67 GPa. The close correspondence of the h-phase elastic properties and those of PREM (preliminary reference Earth model)5 at 350 GPa and 6500 K was shown with molecular dynamic simulations.19 However, the obtained density is significantly lower than that of PREM. With evolutionary crystal structure prediction method, which we also applied here, it was shown that the h-Fe7C3 phase is the most energetically favourable modification in the pressure range of 100–400 GPa at 0 K.20
Fe7N3 was synthesized in the form of the low-pressure ε- and high-pressure β-phases.14,21,22 The ε-phase transforms into the β-phase at 41 GPa and 1000 K, which remains stable at least up to 132 GPa.14 Crystal structure of β-phase has not been determined experimentally. However, based on the similarity of its powder diffraction pattern to that of h-Fe7C3, the conclusion about similarity of their structures has been inferred. With DFT calculations we have confirmed this conclusion, shown that β-Fe7N3 (isostructural to h-Fe7C3) became more favourable than ε-phase at pressures above 67 GPa at 0 K.23 In the same work we also found the new phase Fe7N3-Amm2, which is energetically more favourable than the β-phase in the pressure range of 43–128 GPa at 0 K. The apparent difference between the experimental and theoretical stability fields of the β- and Amm2-phases was explained by the kinetic effects, preventing transformation of high-temperature β-phase to the low-temperature Amm2-phase.
In the present study, we show the results of ab initio determination of Fe7N3 and Fe7C3 phase diagrams at pressures up to the Earth's inner core conditions, i.e. 350 GPa and 6000 K, illustrating crystallochemical similarity of these compounds and described new crystal structure, which are potentially applicable for the phases stable in the Earth's inner core.
2. Computational details
The calculations were performed using two structure prediction codes based on fundamentally different approaches: USPEX24–27 based on evolutionary algorithms and AIRSS28,29 based on a random sampling method. Both methods show their effectiveness in predicting crystal structures of inorganic compounds,30–33 including carbides and nitrides.20,23,34The calculations of the electronic structure were carried out within the DFT using the VASP 5.3 package.35–37 The exchange–correlation interaction was taken into account in the generalized gradient approximation (GGA) in the form of the Perdew–Burke–Ernzerhof (PAW) functional.38 Since the recent theoretical16,18,23 and experimental12,15 results showed that for iron carbides and nitrides, the disappearance of the magnetic moment occurs at pressures below 100 GPa, we performed non spin-polarized calculations above this pressure.
The crystal structure prediction calculations (by both USPEX and AIRSS) were performed for Fe7N3 and Fe7C3 stoichiometries. For each compound, we performed calculations for two formula units and 150, 200, 300 and 400 GPa. The size of the first generation in the calculations with USPEX code was equal to 30 structures. 60% of the structures with the lowest enthalpy were selected after the optimization and then used for producing the next generation (40% – by heredity, 20% – by atomic mutation, 10% – by lattice permutation, and 30% – randomly). Using AIRSS 900–1100 structures were randomly generated and optimized and those with the lowest enthalpy were selected. The atomic positions were optimized within the DFT for the structures obtained with both prediction methods. The computation parameters were as follows: energy cut-off – 450 eV; the density of the grid of Monkhorst–Pack k-point mesh39 – 0.5 Å−1; electronic smearing – with Methfessel-Paxton scheme;40 parameter σ = 0.05 eV. The most promising predicted structures were then optimized with higher accuracy at various pressures. In these calculations, the cut-off energy was 600 eV, the density of k-points was 0.2 Å−1, and parameter σ = 0.01 eV.
To take into account the temperature effect and predict the phase diagrams, we used the method of lattice dynamics within the quasi-harmonic approximation (QHA). For this task, the phonon frequencies were calculated with the PHONOPY code.41 The energy cut-off in this case has been increased to 800 eV (for the details of the method see the ESI†).
3. Results and dicussion
3.1 Iron nitride Fe7N3
The comparison of crystal structure predictions by USPEX and AIRSS methods are summarized in Table S1 in the ESI,† whereas structural data of the new phases – in Table 1. At 150, 200 and 300 GPa, both methods revealed preferential stability of the experimentally synthesized phase β-Fe7N3 (P63mc) and a new structure Cmc21. However, at 400 GPa the results of predictions are different. USPEX found the new C2/m structure as the most favourable, while AIRSS found Cmc21. Thus, in case of Fe7N3 compound USPEX algorithms show higher efficiency in revealing of energetically favourable structures. The same was observed for iron carbides.20| Phase | Pressure (GPa) | Space group | Lattice parameters (Å, degree) | Atomic coordinates | |||||
|---|---|---|---|---|---|---|---|---|---|
| Atom | x | y | z | ||||||
| β-Fe7N3 | 150 | P63mc (#186) | a = 6.1895 | b = 6.1895 | c = 4.0302 | Fe1 | 0.87626 | 0.12374 | 0.09945 |
| Fe2 | 0.54300 | 0.45700 | 0.77221 | ||||||
| α = 90.00 | β = 90.00 | γ = 120.00 | Fe3 | 0.33333 | 0.66667 | 0.75557 | |||
| N1 | 0.18882 | 0.81117 | 0.00704 | ||||||
| Fe7N3-Cmc21 | 300 | Cmc21 (#36) | a = 14.1246 | b = 4.0580 | c = 4.1031 | Fe1 | 0.13011 | 0.43015 | 0.09662 |
| Fe2 | 0.07758 | 0.07317 | 0.46654 | ||||||
| Fe3 | 0.22858 | 0.15317 | 0.38888 | ||||||
| α = 90.00 | β = 90.00 | γ = 90.00 | Fe4 | 0.00000 | 0.38436 | 0.79986 | |||
| N1 | 0.16249 | 0.18579 | 0.76342 | ||||||
| N2 | 0.00000 | 0.78323 | 0.67610 | ||||||
| Fe7N3-C2/m | 400 | C2/m (#12) | a = 7.4226 | b = 2.1497 | c = 7.1380 | Fe1 | 0.80328 | 0.00000 | 0.89918 |
| Fe2 | 0.04345 | 0.00000 | 0.80958 | ||||||
| Fe3 | 0.31221 | 0.00000 | 0.63162 | ||||||
| α = 90.00 | β = 106.0204 | γ = 90.00 | Fe4 | 0.00000 | 0.00000 | 0.50000 | |||
| N1 | 0.64161 | 0.00000 | 0.67115 | ||||||
| N2 | 0.00000 | 0.50000 | 0.00000 | ||||||
| Fe7C3-C2/m | 400 | C2/m (#12) | a = 7.3888 | b = 2.1581 | c = 7.0895 | Fe1 | 0.80215 | 0.00000 | 0.89823 |
| Fe2 | 0.04461 | 0.00000 | 0.81018 | ||||||
| Fe3 | 0.31877 | 0.00000 | 0.63295 | ||||||
| α = 90.00 | β = 104.9195 | γ = 90.00 | Fe4 | 0.00000 | 0.00000 | 0.50000 | |||
| C1 | 0.64452 | 0.00000 | 0.66454 | ||||||
| C2 | 0.00000 | 0.50000 | 0.00000 | ||||||
At 300 GPa the density of Fe7N3-C2/m is ∼1% higher than the density of Cmc21 phase. The density difference can be explained by differences in coordination numbers. In the structure of the C2/m phase carbon is in the seven- and eightfold coordinations by iron with one-cap trigonal prism and cube as coordination polyhedrons. In the less dense Cmc21 phase – in the six- and sevenfold coordinations, with trigonal prism and the one-cap trigonal prism as coordination polyhedrons (Fig. 1).
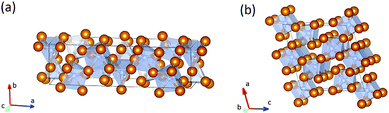 | ||
| Fig. 1 Structural models of Fe7N3-Cmc21 (a) and -C2/m (b). The brown balls correspond to iron atoms, blue balls – to nitrogen atoms. | ||
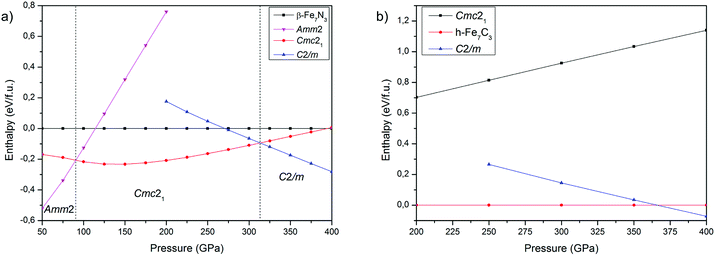
The calculated dependencies of enthalpy on pressure at 0 K (Fig. 2a) show that Amm2 phase is energetically favorable in the low-pressure region. At 90 GPa Amm2 phase transforms to the Cmc21, which in turn transforms to the C2/m at 313 GPa. The β-phase is metastable over the entire pressure range. As noted above, β-phase was synthesized at 41 GPa and 1000 K and remains stable up to 132 GPa and 2500 K. To resolve this inconsistency between computations and experimental results we constructed phonon spectra and performed the Gibbs free energy calculations. The phonon spectra confirmed the dynamic stability of all predicted phases, with the exception of the β-Fe7N3 phase, which phonon spectrum is characterized by small negative frequencies in the region of the Γ-point (Fig. S1 in the ESI†).
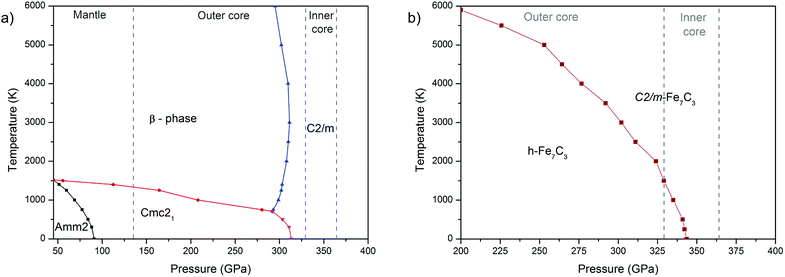
The calculated P–T phase diagram (Fig. 3a) explains synthesis of β-phase in the experiment. According to the diagram Amm2 and Cmc21 are low-temperature phases, which on heating above 1000–1500 K transform into the β-phase. Due to a significant structural difference between the Amm2 and β-phases, in the experiment the β-phase remained stable during rapid quenching in the diamond anvil cell, which hinder synthesis of Amm2 and Cmc21-phases.
The calculated phase diagram also shows stability of C2/m-phase over the entire pressure-temperature range of the inner core, which highlight importance of this phase for the chemistry of the Earth's core.
3.2 Iron carbide Fe7C3
Both structure prediction methods revealed the well-known h-Fe7C3 as the most favorable phase in the range of 100–400 GPa. A similar result using the USPEX method was obtained by Bazhanova et al.20 With AIRSS method, the h-phase was not found and the most favorable among predicted structures was Cmc21.34 A comparison of Cmc21-structures of Fe7C3 and Fe7N3 shows their isostructural character, confirming crystallochemical similarity of carbon and nitrogen compounds at high pressures. Accordingly, we made the assumption about existence of Fe7C3-C2/m isostructural to Fe7N3-C2/m. The calculations of the enthalpies for Fe7C3-C2/m, indeed, confirmed both dynamic (Fig. S2 in the ESI†) and thermodynamic stability of this phase (Fig. 2b). According to these calculations h-Fe7C3 will transform into Fe7C3-C2/m at 366 GPa at 0 K. The calculation of Gibbs free energies indicate expanded stability of C2/m at the high-temperatures (Fig. 3b), and at 366 GPa Fe7C3-C2/m appears to be the most stable in the entire temperature range. At the pressures of the inner core boundary, 329 GPa, Fe7C3-C2/m becomes more favorable than h-Fe7C3 at temperature of ∼1500 K.3.3 Carbon–nitrogen content in the inner core
We calculated the density of the predicted Fe7N3-C2/m and Fe7C3-C2/m phases in the pressure range of 250–360 GPa and compared them with those of the Earth's inner core (Fig. 4). The density of the Fe7N3-C2/m and Fe7C3-C2/m is about 11% and 9% lower than those of hcp-Fe, respectively. If we assume that the core density deficit is compensated by the Fe7N3-C2/m phase, then its amount in the inner core is 30.9–42.7 wt% at 5000–6000 K. The same values for Fe7C3-C2/m are 28.3–38.9 wt%. The nitrogen and carbon content at such concentrations of nitride and carbide in the inner core will be 2.8–4.1 wt% and 2.2–3.3 wt%, respectively (Table 2).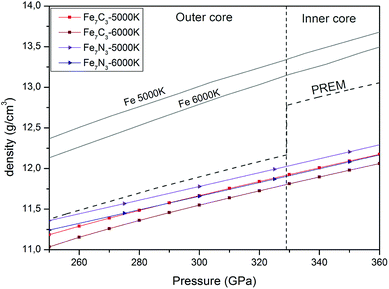 | ||
| Fig. 4 Pressure and density profiles of Fe7N3-C2/m, Fe7C3-C2/m and hcp-Fe1 in comparison with PREM model5 under the Earth's core conditions. | ||
| Phase | Temperature, K | ρ329 GPa, g cm−3 | ρ364 GPa, g cm−3 | (C, N), wt% |
|---|---|---|---|---|
| PREM | 12.76 | 13.09 | ||
| Fe7N3-C2/m | 5000 | 12.025 | 12.33 | 4.0–4.1 |
| 6000 | 11.903 | 12.202 | 2.8–3.0 | |
| Fe7C3-C2/m | 5000 | 11.917 | 12.21 | 3.2–3.3 |
| 6000 | 11.803 | 12.095 | 2.2–2.4 | |
| hcp-Fe | 5000 | 13.34 | 13.72 | |
| 6000 | 13.14 | 13.53 |
4. Conclusions
As the result of the first-principle study of Fe7N3 and Fe7C3, we revealed new phases to be stable at Earth's core pressures. Fe7N3-Cmc21 is relatively low temperature phase and cannot be observed within the Earth's interiors, while the Fe7N3-C2/m is the only stable phase of this composition above 300 GPa through the entire temperature range. Isostructural phase of the carbide Fe7C3-C2/m has similar stability field with Fe7N3-C2/m in the pressure-temperature range of the inner core. This gives the base for the consideration of C2/m-phases of Fe7C3 and Fe7N3 as the possible hosts of carbon and nitrogen within Earth's core. The found similarity of the carbide and nitride P–T diagrams confirms crystallochemical similarity of carbon and nitrogen compounds and possible isomorphism between them.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Prof Chris Pickard for his help with AIRSS code. We are grateful to the Supercomputer Center, Novosibirsk State University, for access to the resources of the cluster. This work was supported by the Russian Science Foundation (project no. 17-17-01177).Notes and references
- T. Sakai, S. Takahashi, N. Nishitani, I. Mashino, E. Ohtani and N. Hirao, Phys. Earth Planet. Inter., 2014, 228, 114–126 CrossRef CAS.
- K. Litasov and A. Shatskiy, Russ. Geol. Geophys., 2016, 57, 22–46 CrossRef.
- K. D. Litasov, I. S. Sharygin, P. I. Dorogokupets, A. Shatskiy, P. N. Gavryushkin, T. S. Sokolova, E. Ohtani, J. Li and K. Funakoshi, J. Geophys. Res.: Solid Earth, 2013, 118, 5274–5284 CrossRef CAS.
- B. J. Wood, Earth Planet. Sci. Lett., 1993, 117, 593–607 CrossRef CAS.
- A. M. Dziewonski and D. L. Anderson, Phys. Earth Planet. Inter., 1981, 25, 297–356 CrossRef.
- V. Busigny and G. E. Bebout, Elements, 2013, 9, 353–358 CrossRef CAS.
- M. M. Grady and I. P. Wright, Space Sci. Rev., 2003, 106, 231–248 CrossRef CAS.
- N. Sugiura, Meteorit. Planet. Sci., 1998, 33, 393–409 CrossRef CAS.
- F. Kaminsky and R. Wirth, Am. Mineral., 2017, 102, 1667–1676 CrossRef.
- B. Chen, L. Gao, B. Lavina, P. Dera, E. E. Alp, J. Zhao and J. Li, Geophys. Res. Lett., 2012, 39, L18301 CrossRef.
- Y. Nakajima, E. Takahashi, N. Sata, Y. Nishihara, K. Hirose, K.-i. Funakoshi and Y. Ohishi, Am. Mineral., 2011, 96, 1158–1165 CrossRef CAS.
- B. Chen, Z. Li, D. Zhang, J. Liu, M. Y. Hu, J. Zhao, W. Bi, E. E. Alp, Y. Xiao and P. Chow, Proc. Natl. Acad. Sci. U.S.A., 2014, 111, 17755–17758 CrossRef CAS PubMed.
- J. F. Adler and Q. Williams, J. Geophys. Res.: Solid Earth, 2005, 110, B01203 Search PubMed.
- S. Minobe, Y. Nakajima, K. Hirose and Y. Ohishi, Geophys. Res. Lett., 2015, 42, 5206–5211 CrossRef CAS.
- C. Prescher, L. Dubrovinsky, E. Bykova, I. Kupenko, K. Glazyrin, A. Kantor, C. McCammon, M. Mookherjee, Y. Nakajima and N. Miyajima, Nat. Geosci., 2015, 8, 220 CrossRef CAS.
- Z. Raza, N. Shulumba, N. M. Caffrey, L. Dubrovinsky and I. A. Abrikosov, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 214112 CrossRef.
- T. Das, S. Chatterjee, S. Ghosh and T. Saha-Dasgupta, Geophys. Res. Lett., 2017, 44, 8776–8784 CrossRef CAS.
- M. Mookherjee, Y. Nakajima, G. Steinle-Neumann, K. Glazyrin, X. Wu, L. Dubrovinsky, C. McCammon and A. Chumakov, J. Geophys. Res.: Solid Earth, 2011, 116, B04201 Search PubMed.
- Y. Li, L. Vočadlo, J. Brodholt and I. Wood, J. Geophys. Res.: Solid Earth, 2016, 121, 5828–5837 CrossRef CAS.
- Z. G. Bazhanova, A. R. Oganov and O. Gianola, Phys.-Usp., 2012, 55, 489–497 CrossRef CAS.
- K. Litasov, A. Shatskiy, S. Ovchinnikov, Z. Popov, D. Ponomarev and E. Ohtani, JETP Lett., 2014, 98, 805–808 CrossRef CAS.
- K. Litasov, A. Shatskiy, D. Ponomarev and P. Gavryushkin, J. Geophys. Res.: Solid Earth, 2017, 122, 3574–3584 CrossRef CAS.
- P. Gavryushkin, N. Sagatov, Z. Popov, A. Bekhtenova, T. Inerbaev and K. Litasov, JETP Lett., 2018, 107, 379–383 CrossRef CAS.
- C. W. Glass, A. R. Oganov and N. Hansen, Comput. Phys. Commun., 2006, 175, 713–720 CrossRef CAS.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- A. O. Lyakhov, A. R. Oganov and M. Valle, Comput. Phys. Commun., 2010, 181, 1623–1632 CrossRef CAS.
- A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172–1182 CrossRef CAS.
- C. J. Pickard and R. Needs, Phys. Rev. Lett., 2006, 97, 045504 CrossRef PubMed.
- C. J. Pickard and R. Needs, J. Phys.: Condens. Matter, 2011, 23, 053201 CrossRef PubMed.
- C. J. Pickard and R. J. Needs, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 104101 CrossRef.
- P. N. Gavryushkin, N. S. Martirosyan, T. M. Inerbaev, Z. I. Popov, S. V. Rashchenko, A. Y. Likhacheva, S. S. Lobanov, A. F. Goncharov, V. B. Prakapenka and K. D. Litasov, Cryst. Growth Des., 2017, 17, 6291–6296 CrossRef CAS.
- D. Smith, K. V. Lawler, M. Martinez-Canales, A. W. Daykin, Z. Fussell, G. A. Smith, C. Childs, J. S. Smith, C. J. Pickard and A. Salamat, Phys. Rev. Mater., 2018, 2, 013605 CrossRef.
- A. R. Oganov, C. W. Glass and S. Ono, Earth Planet. Sci. Lett., 2006, 241, 95–103 CrossRef CAS.
- G. L. Weerasinghe, R. Needs and C. J. Pickard, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 174110 CrossRef.
- G. Kresse, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- M. Methfessel and A. Paxton, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 40, 3616 CrossRef CAS.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Method of quasi-harmonic approximation, phonon dispersion curves, structures predicted by USPEX and AIRSS method. See DOI: 10.1039/c8ra09942a |
| This journal is © The Royal Society of Chemistry 2019 |