Open Access Article
Open Access ArticleIn silico design of mimosine containing peptides as new efficient chelators of aluminum†
J. I. Mujika a,
G. Dalla Torre
a,
G. Dalla Torre ab,
J. I. Lachowicz
ab,
J. I. Lachowicz c and
X. Lopez
c and
X. Lopez *a
*a
aKimika Fakultatea, Euskal Herriko Unibertsitatea UPV/EHU, Donostia International Physics Center (DIPC), P.K. 1072, 20080 Donostia, Euskadi, Spain. E-mail: xabier.lopez@ehu.es
bUCBIO/REQUIMTE, Departamento de Química e Bioquímica, Faculdade de Ciências, Universidade do Porto, Porto, Portugal
cUniversity of Cagliari, Department of Chemical and Geological Sciences, Cittadella Universitaria, Monserrato, Italy
First published on 7th March 2019
Abstract
The design of new and efficient chelators that can remove aluminium(III), a metal with increasing recognition as a potential toxic agent, from biological systems is an area of high therapeutic relevance. In the present paper, we present an extensive computational study of a new promising type of these chelators based on mimosine containing peptides. The reason to choose mimosine is that the sidechain of this residue is similar to deferiprone, a ligand known to tightly interact with highly-valent metals, and in particular with Al(III). In this article we analyze systematically, using a combination of methods that include QM/MM MD simulations, how the size and sequence of the polypeptides can alter the fundamental binding patterns to aluminum, in comparison with the binding to deferiprone. Particular attention is given towards the identification of the smallest peptide that interacts efficiently with aluminum, since polypeptide size is a fundamental factor to allow a given polypeptide to efficiently cross the cell membrane. The results indicate that the longest peptides, with 8 or 9 amino acids, show no difficulties interacting with Al(III) in an optimum arrangement. By contrast, when the peptide contains five or six amino acids Al(III) is pentacoordinated, reducing the stability of the resultant complex. In summary, our study demonstrates that the mimosine containing peptides can efficiently coordinate highly valent metals such as Al(III), with a subtle dependence of the binding on the specific chain-lengths of the polypeptide. We believe that the present study sheds light on the adequacy of this new type of chelator towards aluminum binding.
Introduction
Aluminium is the most abundant metal (about 8.3% by mass) in the Earth's crust,1 found in more than 270 different minerals in the insoluble form of hydroxy-aluminosilicates. It remained inaccessible to living matter for billions of years, until acid rain started the massive export of aluminum from the crust of the earth to surface waters, putting vegetables, animals and humans in contact with absorbable cationic aluminium species, probably for the first time in their history.2In the 1970s, aluminum was recognized as a neurotoxin and since then, numerous scientific reports have linked aluminum to neurological disorders and bone and brain pathologies.3 A role of aluminium in human pathology has been clearly established in at least three diseases: dialysis dementia,4 osteomalacia5 and microcytic anaemia without iron deficiency.6,7 The principal symptoms of its toxicity are: diminished intellectual function, forgetfulness, inability to concentrate; speech and language impairment; personality changes, altered mood, depression; dementia; visual and/or auditory hallucinations; osteomalacia with fracturing; motor disturbances; weakness, fatigue, mainly related to microcytic anaemia; epileptic seizures.
In the case of aluminum intoxication, Al(III) chelation is performed to reduce Al(III) organ levels (especially in bone) and reduce toxicity of Al(III). This may benefit patients with end-stage renal disease or with neurodegenerative disorders as well as patients suffering from neurobehavioral toxicity due to prolonged occupational Al(III) exposure.8 In chronic hemodialysis patients chelation therapy is indicated at serum Al(III) concentration higher than 80 μg L−1.9 Previously, the only available chelator for treating Al(III) overloaded patients was deferoxamine (DFO) originally developed for decorporation of iron in transfusional iron overload in thalassemia and sickle cell anemia patients. The hydrophilic chelator DFO is poorly absorbed in the gastrointestinal tract and must be administered parenterally, either subcutaneously, intramuscularly, or intravenously. DFO is not an ideal chelating agent due to the high frequency of side effects, the need for parenteral administration restricting off-clinic self-administration, and high price. However, despite the advent of alternative chelators for Al(III) chelation, DFO still has an important role in treatment of Al(III) intoxication.10 An extensive body of evidence from in vitro and experimental animal studies demonstrates the potential of hydroxypyridinone derivatives from both series to reduce Al(III) toxicity and promote Al(III) decorporation. The most promising compound among the hydroxypyridinones for iron chelation after extensive animal experimentation, 1,2-dimethyl-3-hydroxy-4-pyridone (deferiprone, DFP, see Scheme 1) went into clinical trial initially for iron decorporation and is licenced in USA and Europe for treatment of iron overload in thalassemia major. Even if less efficient in aluminum coordination respect to DFO, DFP is orally administrated, somewhat less toxic, and much cheaper than DFO.11 DFP was extensively studied during past years by Hider12–14 and Santos,15–17 who prepared its oligodentate derivatives mostly as Fe(III) chelators, which ultimately found new application as Ga68 complexes for PET immagining.14,18,19 Recently, Abbate et al. reported novel targeting peptides incorporating DFP as the iron(III) chelating units.20
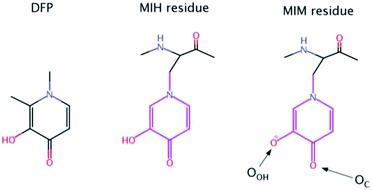 | ||
| Scheme 1 Chemical structures of Deferiprone (DFP) and mimosine residue in its neutral (MIH) and ionic (MIM) form. The labels of the two O atoms of mimosine residue are also illustrated. | ||
Nevertheless, there is an urgent need for other, more efficient, less toxic and cheaper aluminum chelators. In this paper, we proposed for the first time that mimosine containing peptides could be a promising candidate as efficient chelators of aluminum. Mimosine [β-[N-(3-hydroxy-4-oxypyridyl)]-α-aminopropionic acid] (see Scheme 1) is a non-protein amino acid found in the members of Mimosoideae family. It has been found to have various biological activities such as antibacterial, anti-cancer, antiinflammation, anti-fibrosis, anti-influenza, anti-virus, herbicidal and insecticidal activities.21 In the 90's mimosine was studied as an inducer of G1/S phase arrest22 and over the past years of active research, mimosine evolved as promising agent for the treatment of cancer disease. Mimosine dipeptides and tetrapeptides were synthesised as neuraminidase,23 tyrosinase23,24 and cyclooxygenase24 inhibitors.
The presence of the carbonyl and alcohol groups in the side chain of mimosine makes this residue an effective ligand for binding metal ions, and thus mimosine can bind divalent, trivalent and tetravalent transition metal ions.25–27 Due to its structural similarity to DFP it is expected a high affinity towards Al(III) as well. Moreover, joining three mimosine residues in the same peptide could enhance significantly aluminum complex stability, and obtain new class of chelating agents based on non-proteinogenic amino acids. However, the size of the peptide might be critical for its successful absorption into the organism.
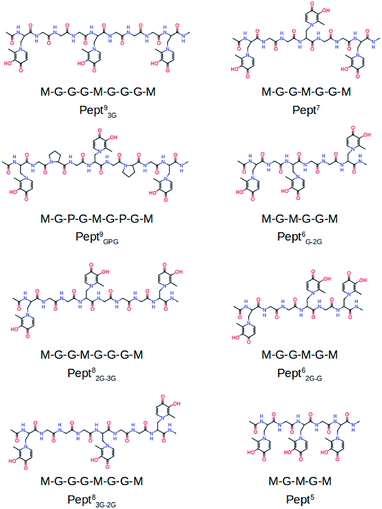
To the best of our knowledge the activity of mimosine containing peptides as chelator of Al(III) has not been investigated yet. The present study aims to find the smallest mimosine containing peptide that interacts tightly with Al(III). To do that, we employed state-of-the-art computational methods to characterize systematically the complexation of Al(III) to several peptides of different lengths that contain three mimosine residues (shown in Fig. 1). The geometric and energetic stabilities of all the Al·Pept complexes were analyzed, paying special attention on the interactions between the cation and the peptide. We also compare all these data with the complex formed by DFP. All this information allows us to propose for the first time the shortest mimosine-based peptide with the highest coordination stability toward Al(III) ions. This will certainly open the field to a new type of chelators, not only for Al(III), but for highly valent metals showing similar coordination features as Al(III), e.g. lanthanides with their peculiar magnetic properties used in PET imagining.
Methodology
Systems set-up
The complexation of Al(III) to eight mimosine containing peptides of different length has been investigated following the protocol shown in Scheme 2. All peptides contain three mimosine residues (sequences presented in Fig. 1) and they differ in the two linkers connecting the mimosine residues: the two longest peptides contain nine amino acids so that their two linkers are made of three amino acids: in Pept93G the linker includes three glycine residues, whereas in Pept9GPG a proline was inserted into the peptide in order to support turn formation upon metal complexation. Next, two eight residues-long peptides were built, what implies two different linkers: GG and GGG in Pept82G–3G and the reverse in Pept83G–2G. Next, Pept7 includes two symmetric linkers made of two glycine residue each. The six amino acid long peptides involve two asymmetric linkers, namely G and GG in Pept6G–2G and the opposite in Pept62G–G. Finally, Pept5 is the shortest peptide, with just a glycine residue at each of the two linkers. In all peptides, the N- and C-terminals were neutralized by adding methyl groups. | ||
| Scheme 2 Theoretical protocol used throughout this study (described in Methodology section) for each of the structures shown in Fig. 1. | ||
The Al·Pept93G system was the first one to be built, for what the Fe(III)–N-derivatized 3-hydroxy-4-pyridiones complex28 was used as initial template. Once the complex was set up and equilibrated by molecular dynamics simulation, its structure was used as template to build the initial structure for the complexes formed by Pept9GPG, Pept82G–3G and Pept83G–2G. In a similar manner, previously equilibrated Al·Pept structures were used to build the initial structures for the complexes of the remaining shorter peptides.
Molecular dynamics simulations
Each of the eight systems listed about was sampled by QM/MM molecular dynamics simulation using the Amber14 suit of programs.29 The choice of running QM/MM MD simulations was based on two main reasons: (a) lack of reliable MM parameters for the non-standard mimosine amino acid, and (b) description of the metal binding site by a quantum methods allows polarization, what it is expected to be relevant with a highly charged cation such as Al(III). The PM6 semiempirical method30 was chosen to treat the Al(III) binding site, since it provides a good compromise between calculation speed and accuracy.The LEaP program was used to build the topology of each system, for which Amber ff14SB all-atom force field parameters31 were chosen for standard amino acids. The parameters for MIM needed to build the system (but not used during the QM/MM MD simulations) were obtained with Antechamber. Periodic boundary conditions were applied in all directions using an octahedron cell, with a minimal distance between the peptide and the wall of the cell set to 10 Å. The structures were solvated by a box of TIP3P-type water molecules.32
First a MM minimization was carried out to relax the solvent, in which the Al·Pept complex was restrained. Then, in order to keep the initial rearrangement, a second minimization was performed restraining only the three mimosine residues and Al(III). Next, the system was heated to 300 K by a 1 ns-long equilibration defining a canonical thermodynamic ensemble (NVT), and using the Langevin thermostat to couple the temperature of the system (collision frequency of 1.0 ps−1). Again, the Al·Pept solute was restrained. All this calculations were carried out at MM level.
The QM part was treated with the PM6 semi-empirical method and includes the side chains of the three unprotonated MIM residues (pink region depicted in Scheme 1) and Al(III), so that the total charge of the QM part was always neutral. The Amber ff14SB force field was employed to describe the remaining part of the system.
Once the system was heated, the QM/MM MD simulations were carried out without applying any restraint and keeping the condition at the heating stage, that is, NVT ensemble and the Langevin thermostat to couple the temperature of the system (collision frequency of 1.0 ps−1). All bonds involving hydrogens were constrained with the SHAKE algorithm,33 allowing for an integration time step of 2 fs. Long-range electrostatics were calculated using the smooth particle mesh Ewald (PME) method,34,35 and a cutoff of 8 Å was defined for all nonbonded interactions. The first 1 ns of the QM/MM MD simulation were leave to equilibrate the system, whereas the remaining 20 ns of simulations were employed for the analysis. From each QM/MM MD simulation, representative structures were extracted by cluster analysis using the cpptraj utility in Amber14.36
Relative binding energies
From the QM/MM MD simulations, relative binding energies of the eight peptides towards Al(III) were computed according to the next reaction:| Al·[Peptx·(MIM)3] + Pepty·(MIH)3 ↔ Al·[Pepty·(MIM)3] + Peptx·(MIH)3 | (1) |
| ΔΔHBindingx–y = 〈E〉Al·[Pepty·(MIM)3] + 〈E〉Peptx·(MIH)3 − 〈E〉Al·[Peptx·(MIM)3] – 〈E〉Pepty·(MIH)3 | (2) |
Nevertheless, the computation of the ΔΔHBindingx–y values is not straightforward since the number of explicit water molecules differs at each MD simulation (and therefore with unbalance number of interactions), making unrealistic a direct comparison between them. In order to overcome this problem, the potential energies were determined replacing the explicit water molecules by a Generalized Born implicit solvent37 as implemented in Amber 14. The structures saved every 5 ps of each simulation were used to calculate the 〈E〉 average potential energies with implicit solvent.
The estimation of the relative binding energies (eqn (2)) requires the energies of the apoform of the peptides as well. 20 ns long QM/MM MD simulations were also performed for the eight apoform of the peptides using an implicit solvent. The computed RMSDs (shown in Fig. S4†) indicate that the structures were equilibrated at the end of the simulations. Note that unlike when the mimosine residues interact with Al(III), we assume the mimosine residues protonated in solution. This assumption relies on the pKa values estimated by cyclic voltammetry38 for the two oxygen atoms of deferiprone: 3.5 and 10.2. Based on these values, it is clear that the two oxygen atoms should be as a keto and hydroxide group, respectively, and therefore, the later protonated. However, when they interact with Al(III), it is expected a significant drop of their pKa values, as computed for some oxygen-containing standard amino acids interacting with Al(III).39 Consequently, it is reasonable to assume that the hydroxide group is deprotonated when complexated to Al(III), but protonated in the apoform.
DFT binding energies
Optimizations were carried out in solution with Gaussian16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 at B3LYP-D3(BJ)/6-31+G(d) and using the IEFPCM solvation model.41 In addition, the DFT energies were refined with single point calculations at the B3LYP-D3(BJ)/6-311++G(3df,2p) level of theory. Representative structure of each system (shown in Fig. 2), determined by cluster analysis on the MD trajectories (using the cpptraj facility36 in Amber14), were used as initial structures for the optimizations. To confirm that optimized structures were real minima on the potential energy surfaces, frequency calculations were carried out at the same level of theory. All structures showed positive force constants for all normal modes of vibration. The frequencies were then used to evaluate the zero-point vibrational energy (ZPVE) and thermal (T = 298 K) vibrational corrections to the Gibbs free energies within the harmonic oscillator approximation. To calculate the entropy, the different contributions to the partition function were evaluated using the standard statistical mechanics expressions in the canonical ensemble and the harmonic oscillator and rigid rotor approximation.
40 at B3LYP-D3(BJ)/6-31+G(d) and using the IEFPCM solvation model.41 In addition, the DFT energies were refined with single point calculations at the B3LYP-D3(BJ)/6-311++G(3df,2p) level of theory. Representative structure of each system (shown in Fig. 2), determined by cluster analysis on the MD trajectories (using the cpptraj facility36 in Amber14), were used as initial structures for the optimizations. To confirm that optimized structures were real minima on the potential energy surfaces, frequency calculations were carried out at the same level of theory. All structures showed positive force constants for all normal modes of vibration. The frequencies were then used to evaluate the zero-point vibrational energy (ZPVE) and thermal (T = 298 K) vibrational corrections to the Gibbs free energies within the harmonic oscillator approximation. To calculate the entropy, the different contributions to the partition function were evaluated using the standard statistical mechanics expressions in the canonical ensemble and the harmonic oscillator and rigid rotor approximation.
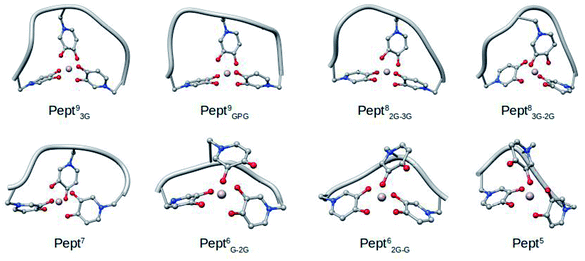 | ||
| Fig. 2 Representative snapshots of the MD simulations of the eight Al·Pept complexes determined by cluster analysis. | ||
The next reaction was defined to evaluate the formation energies of the eight Al·Pept complexes and Al·DFP3:
| [Al(H2O)6]3+(aq, 1 M) + Pept0(aq, 1 M) ↔ [Al·(Pept3−)]0(aq, 1 M) + 3H2O(aq, 1 M) + 3H3O+(aq, 1 M) | (3) |
| [Al(H2O)6]3+(aq, 1 M) + 3DFP0(aq, 1 M) ↔ [Al·(DFP−)3]0(aq, 1 M) + 3H2O(aq, 1 M) + 3H3O+(aq, 1 M) | (4) |
Notice that the peptides (and DFP) are neutral (protonated) in solution but deprotonated in the complexes, so three hydronium molecules are included as products in order to balance the reaction. The enthalpy in solution corresponding to the binding of the ligand to Al(III) is therefore calculated as:
ΔHaq = Haq(Al·Ligdeprot) + 3Haq(H2O) + 3Haq(H3O) − Haq(Al(H2O)6) − Haq(Ligprot) + ΔnRT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(24.46) ln(24.46)
| (5) |
ΔGaq = Gaq(Al·Ligdeprot) + 3Gaq(H2O) + 3Gaq(H3O) − Gaq(Al(H2O)6) − Gaq(Ligprot) + ΔnRT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(24.46) + 3RT ln(24.46) + 3RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(55.34) ln(55.34)
| (6) |
Prediction of solvation energies of small charged ions such as H3O+ using a continuum solvation models implies a significant deviation from the real value. In order to alleviate this problem, the Gibbs free energy of the hydronium ion was calculated as:
| Gaq(H3O) = Ggas + ΔGsolv(exp) | (7) |
Moreover, a correction term in the free energies is introduced to account for the hydronium concentration, which depends on the pH:
GpH = m(−pH)RT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(10) ln(10)
| (8) |
In order to validate PM6, all this procedure was repeated with this semiempirical method and the results between DFT and PM6 compared (PM6 results included in ESI†). In overall, the geometries and energies computed with both level of theories are comparable, so we believe PM6 provides meaningful results.
Results
The sequences of the eight peptides studied herein are shown in Fig. 1. The name of each peptide is composed by a superscript indicating the length of the peptide, and a subscript referring to the linker sequences (one for symmetric peptides, and two for the asymmetric ones). For instance, the Pept9GPG system is nine residues long and contains three mimosine residues, which are spaced with GPG sequence linkers. The two oxygen atoms of mimosine residue are denoted as OC and OOH, and correspond to the carbonyl and hydroxyl oxygen atoms, respectively (Scheme 1). Along the body text, the atom names include a subscript to specify the atom type and a superscript to refer to the residue number.The RMSD computed on the QM/MM molecular dynamic simulations for the eight Al·Pept complexes (shown in Fig. S3†) demonstrate that all systems are equilibrated after the 20 ns run of production. Representative snapshots of each simulation are shown in Fig. 2. First, the structural data of each complex is analyzed, with special attention on the metal coordination shell. Next, the binding energy values of each Al·Pept complex are discussed, and finally, these complexes compared with Al·DFP3.
Structural stability of the first Al(III) coordination shell
The optimum coordination shell of Al(III) is the one presented in Al·DFP3 (see Fig. S1†),43 with the cation octahedral and the three MIM residues bidentate through the OC and OOH atoms. In order to investigate if this arrangement is maintained by all the peptides studied, some geometrical parameters are analyzed: (i) distances between Al(III) and the six O atoms of the three MIM residues (Table 1 and Fig. 3), (ii) all possible O–Al–O angles formed by the six oxygen atoms (Fig. 4 and Table S3†). The complexes are presented from the longest to the shortest peptides.| MIMA | MIMB | MIMC | ||||
|---|---|---|---|---|---|---|
| Al–OC | Al–OOH | Al–OC | Al–OOH | Al–OC | Al–OOH | |
| a Since the indexes of the three mimosine residues differ on the systems, they are referred to as A, B and C for the first, central and last mimosine in the corresponding sequence shown in Fig. 1. | ||||||
| Pept93G | 1.961 (0.075) | 1.922 (0.066) | 1.969 (0.079) | 1.935 (0.068) | 1.957 (0.075) | 1.931 (0.068) |
| Pept9GPG | 1.969 (0.086) | 1.921 (0.065) | 1.982 (0.140) | 1.936 (0.069) | 1.950 (0.087) | 1.931 (0.060) |
| Pept82G–3G | 1.970 (0.077) | 1.923 (0.066) | 1.972 (0.093) | 1.939 (0.069) | 1.955 (0.079) | 1.931 (0.070) |
| Pept83G–2G | 1.961 (0.099) | 1.931 (0.069) | 1.967 (0.078) | 1.934 (0.068) | 1.962 (0.073) | 1.927 (0.067) |
| Pept7 | 1.934 (0.070) | 1.934 (0.070) | 2.514 (0.944) | 1.917 (0.085) | 1.938 (0.072) | 1.932 (0.070) |
| Pept6G–2G | 1.932 (0.069) | 1.891 (0.059) | 4.347 (0.197) | 1.842 (0.057) | 1.892 (0.062) | 1.926 (0.066) |
| Pept62G–G | 1.903 (0.065) | 1.913 (0.064) | 4.252 (0.235) | 1.836 (0.057) | 1.935 (0.070) | 1.896 (0.062) |
| Pept5 | 1.917 (0.068) | 1.911 (0.065) | 4.112 (0.634) | 1.839 (0.063) | 2.090 (0.586) | 1.889 (0.062) |
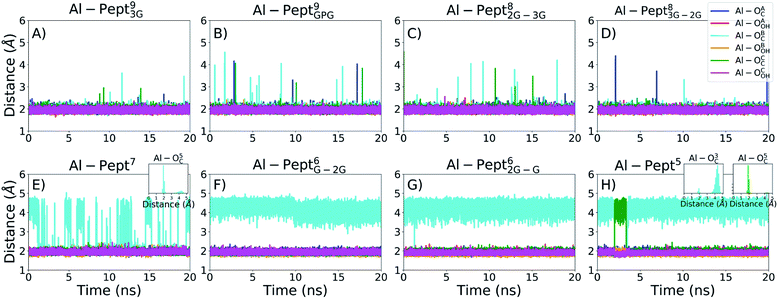 | ||
| Fig. 3 Evolution of the distances between Al(III) and the two OC and OOH atoms of the mimosine residues during the QM/MM MD simulations. From left to right, upper line: (A) Pept93G, (B) Pept9GPG, (C) Pept82G–3G, (D) Pept83G–2G; bottom line: (E) Pept7, (F) Pept6G–2G, (G) Pept62G–G, (H) Pept5. The colour scheme is shown in the upper-right panel. Since the indexes of the three mimosine residues differ on the systems, they are referred to as A, B and C for the first, central and last mimosine in the corresponding sequence shown in Fig. 1. | ||
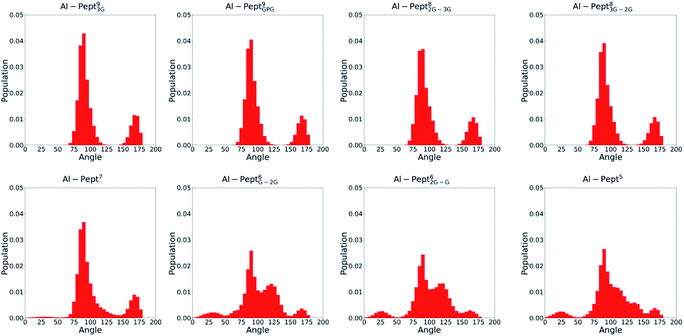 | ||
| Fig. 4 Distribution of all OMim–Al–OMim angles computed along the QM/MM MD simulations trajectories of the eight Al·Pept complexes (sequences shown in Fig. 1). From left to right, upper line: Pept93G, Pept9GPG, Pept82G–3G and Pept83G–2G; bottom line: Pept7, Pept6G–2G, Pept62G–G and Pept5. | ||
The OMim–Al–OMim angles computed for the two Al·Pept9 complexes confirm that Al(III) adopts a nearly octahedral arrangement. We can observe in Fig. 4 that OMim–Al–OMim angles are divided in two sets: a prevalent one centered on 90 degrees and a second one centered on 160 degrees, which correspond to equatorial and axial angles, respectively, in a typical octahedral arrangement. A deeper analysis of the angles (Table S3†) shows that during the simulation of the Al·Pept93G complex, 11 out of the 15 angles are in the 86–92 degree range (the range is slightly wider for Al·Pept9GPG: 82–94 degrees), very close to the ideal value of 90 degrees for equatorial angles. OOH1–Al–OOH9 is the only angle out of these ranges, with average values of 101 degrees on both complexes. On the other hand, the values of the remaining three angles, namely the OC1–Al–OC9, OOH1–Al–OOH5 and OC5–Al–OOH9, are in the 164–168 degree range, thus near to the optimum value for axial angles. Hence, both Pept9 peptides are long enough to allow the mimosine side chains to adopt a near-octahedral arrangement (see Fig. 2).
The distribution of the O–Al–O angles reflects such multiple conformations. Even if two clear peaks are located at 90 and 160 degrees, the angles population between these two peaks has increased, and it is not any more nearly zero (as in the simulations with larger peptides). Moreover, the peak of the axial angles has shifted to smaller values. At this point, the simulation suggests that Pept7 presents less stable octahedral arrangement, even if still this coordination mode is the most prevalent one (see below).
The angles distribution computed on the MD simulations of the shortest three peptides are very similar and confirm that the octahedral arrangement of Al(III) is not possible due to the shortness of the peptides. The peak ascribed to the axial angles has lowered, and even if the peak located at around 90 degrees is still predominant, the angle distribution is significantly broader than with longer peptides.
Al(III) coordination mode
The analysis of the geometries has shown that the peptide length clearly influences the interaction of the peptide with Al(III). In order to quantify this trend, we calculated the coordination number (C.N.) of Al(III) along each MD simulation, which can be either 5 or 6. In order to do that, two alternative geometrical criteria were defined to consider a frame from a trajectory octahedral: (i) six Al–O distances shorter than 2.5 Å, and (ii) if three axial O–Al–O angles are present (larger than 150 degrees). The results presented in Table 2 show the same trend for both criteria, although the percentages of C.N. = 6 are slightly lower with the angle criteria.| % Oct (dist) | % Oct (angle) | ΔΔHBindingx–y | ||
|---|---|---|---|---|
| Pept93G | 100.0 | 98.0 | 0.0 | |
| Pept9GPG | 99.6 | 96.5 | 1.8 | |
| Pept82G–3G | 99.8 | 94.2 | 2.5 | |
| Pept83G–2G | 99.9 | 93.1 | 1.7 | |
| Pept7 | 74.9 | 72.1 | 11.4 | 9.4 (C.N. = 6) |
| 17.3 (C.N. = 5) | ||||
| Pept6G–2G | 0.0 | 0.0 | 12.9 | |
| Pept62G–G | 0.0 | 0.1 | 13.9 | |
| Pept5 | 0.1 | 2.2 | 20.0 | |
During the corresponding QM/MM MD simulations, Pept9 and Pept8 bind an octahedral Al(III). According to the distance criterion, during almost all their simulations the C.N. is six. The percentage is slightly lower according to the angle criterion, ca. 97% for the two Pept9 peptides and 94% for the two Pept8 peptides. The three shortest peptides, with five and six residues, do not form octahedral complexes with Al(III) ions (the percentage of frames with C.N. = 6 is almost zero).
By contrast, the Al·Pept7 complex is the border line system, in which both C.N. = 5 and C.N. = 6 are highly sampled. However, C.N. = 6 prevails during the MD simulation, with 72–75% of the structures with hexa coordination mode, whereas in the remaining 25–28% of snapshots the metal ion is pentacoordinated.
Relative stability of the Al·Pept complexes
The Pept93G peptide was taken as reference to estimate the relative binding energies (ΔΔHBinding) of the eight peptides, which were computed from the QM/MM MD simulations of the apoform and holoforms of free peptides (see Methodology section). The results are presented in Table 2.The ΔΔHBinding values indicate that there is a direct relationship between the length of the peptide, the stability of their Al·Pept complexes, and the coordination mode of Al(III): the complexes formed by the four longest peptides present similar energies and in all of them Al(III) is octahedral. The Al·Pept93G complex is the most stable one, followed by Pept83G–2G (ΔΔHBinding = +1.7 kcal mol−1), Pept9GPG (ΔΔHBinding = +1.8 kcal mol−1) and Pept82G–3G (ΔΔHBindingx–y = +2.5 kcal mol−1).
The remaining four complexes are clearly less stable. Among them, Al·Pept7 is the most stable one, with ΔΔHBinding = +11.4 kcal mol−1. It must be pointed out that this is the relative energy computed with consideration of all snapshots extracted from the MD simulation. As described above, in the Al·Pept7 complex Al(III) is as either hexacoordinated (ca. 72% of the structures) or pentacoordinated (ca. 28%). When the relative energies are analysed separately, for each of the coordination mode, the ΔΔHBinding value of hexacoordinated structures reduces to +9.4 kcal mol−1, whereas the ΔΔHBinding value of Al(III)–pentacoordinated complex increases to +17.3 kcal mol−1.
The complexes formed by the two Pept6 peptides present similar energies, with ΔΔHBinding values of +12.9 (Al·Pept6G–2G) and +13.9 (Al·Pept62G–G) kcal mol−1. The Al·Pept5 is the less stable complex, with a ΔΔHBinding value of 20.0 kcal mol−1.
The ΔΔHBinding values not only depend on the stability of the Al·Pept complexes, but also on the stability of the peptide in solution (see reaction (1)). The stability of the free peptides is difficult to quantify precisely, but it is reasonable to assume that the formation of hydrogen bonds may contribute to their stability, and therefore, the larger the number of hydrogen bonds formed by a peptide, the higher its stability. The list of all individual backbone hydrogen bond interactions during the QM/MM MD simulations of the peptides in solution and their lifetimes are shown in ESI.† The data collected reveals the total number of hydrogen bonds is low, not surprising for such a small peptides, even that a clear trend is observed: the longest peptides form more hydrogen bond interactions than the shortest ones. Among them, the only peptide with a significant number of interactions is Pept9GPG peptide, due to the presence of the proline residues. On the other hand, in none of the Al·Pept complexes hydrogen bond interactions were detected. Thus, we can conclude that the computed relative binding energies rely mainly on the stability of the Al·Pept complexes.
Comparison with deferiprone
As pointed out in the Introduction, deferiprone (DFP) is a widely used Al(III) chelator, and therefore it is a good reference to determine whether the mimosine peptides can also play this role efficiently. With this aim, we compare the binding energies and metal binding site geometries between Al·DFP3 and the eight Al·Pept studied herein. The structures were optimized by means of a high level DFT method, for which representative structures extracted from each QM/MM MD simulation were chosen as initial structure for the geometry optimizations. The ΔHaq and ΔGaq values associated to the Al·Pept complex formations were calculated according to reaction (3) and (4), and are shown in Table 3. Moreover, as in Table 2, the relative ΔΔHaq and ΔΔGaq values, taking the Al·Pept93G complex as reference, are also presented.| ΔHaq | ΔGaq | ΔΔHaq | ΔΔGaq | |
|---|---|---|---|---|
| a The relative ΔΔHaq and ΔΔGaq values, taking Pept93G as reference, are also shown. All energies in kcal mol−1. | ||||
| Al·Pept93G | −25.9 | −97.0 | 0.0 | 0.0 |
| Al·Pept9GPG | 6.5 | −70.3 | 32.4 | 26.6 |
| Al·Pept82G–3G | −8.8 | −80.2 | 17.1 | 16.7 |
| Al·Pept83G–2G | −21.7 | −90.3 | 4.2 | 6.6 |
| Al·Pept7 (C.N. = 6) | −3.0 | −72.6 | 23.0 | 24.4 |
| Al·Pept7 (C.N. = 5) | −1.0 | −73.2 | 25.0 | 23.7 |
| Al·Pept6G–2G | 14.9 | −59.6 | 40.8 | 37.4 |
| Al·Pept62G–G | 1.8 | −70.2 | 27.7 | 26.8 |
| Al·Pept5 | −8.2 | −73.8 | 17.8 | 23.2 |
| Al·DFP3 | −28.8 | −84.0 | −2.9 | 13.0 |
The calculations of both ΔHaq and ΔGaq allow us to estimate as well the entropy associated to the complex formation. As it can be seen in Table 3, there are not significant deviations in the ΔΔHaq and ΔΔGaq values, indicating that the change in entropy is similar for each of the eight complexes. However, a large difference is observed between the ΔHaq and ΔGaq values, what points to a large entropic contribution in the formation of each compound. However, it should bear in mind that in reaction (3) there are more product species than reactants (Δn = 5), and that they are considered infinitively separated, leading to an overestimation of the entropy contribution. Hence, for absolute values the ΔHaq values are more trustable, although we remark that the relative ΔΔGaq values are also useful to confirm similar entropic effects for all complexes.
Hence, we focus on the ΔΔHaq values. In overall, the trend in the relative energies computed with DFT is similar to the one obtained from the QM/MM MD simulations, albeit the values are larger with DFT, i.e., Al·Pept93G is more stable with DFT. The results confirm that the complexes formed by the longest peptides are more stable than the ones formed by the shortest peptides, even though there are some exceptions (see below). The three most stable complexes correspond to the longest peptides: Al·Pept93G (ΔΔHaq = 0.0 kcal mol−1), Al·Pept83G–2G (ΔΔHaq = 4.2 kcal mol−1) and Al·Pept82G–3G (ΔΔHaq = 17.1 kcal mol−1). On the other hand, Al·Pept6G–2G is the less stable complex (ΔΔHaq = 40.8 kcal mol−1), whereas the ΔΔHaq values of the remaining five complexes are in the 23.0/32.4 kcal mol−1 range.
However, there are some remarkable differences between the stability trends obtained from DFT and MD calculations. The Al·Pept9GPG complex is significantly less stable with DFT (ΔΔHaq = 32.4 kcal mol−1) than the value computed from MD simulation (ΔΔHaq = 1.8 kcal mol−1). Al·Pept6G–2G is also much less stable with DFT (40.8 vs. 12.9 kcal mol−1), whereas Al·Pept5 is more stable (17.8 vs. 20.0 kcal mol−1). It must point out that the two set of energies were obtained by different approaches. The DFT energies, which are computationally more demanding, are based on a unique structure. Alternatively, the QM/MM ΔΔHaq values were averaged over all the frames stored in the trajectories, what provides a better sampling of the system, particularly important with the more flexible aporforms of the peptides. Nevertheless, the high level DFT energies are useful for two main reasons. Firstly, the data collected by this method, which is conceptually more robust than the PM6 semiempirical method, support the energy trends obtained with PM6 (see Table S14†). Secondly, we can compare directly the stability of the Al·Pept complexes and Al·DFP3. As it can be seen in Table 3, the ΔHaq of Al·DFP3 is −28.8 kcal mol−1, 2.9 kcal mol−1 more stable than Al·Pept93G. Note that the entropic penalty is larger with Al·DFP3, but this is expected due to the complexation of three infinitively separated DFP molecules, whereas with the peptides the three mimosine residues belong to the same molecule. All in all, these results suggest that Pept93G can compete with DFP as efficient chelator of Al(III).
We also analyze the metal binding sites of Al·DFP3 and Al·Pept93G by comparing the distances and angles of three structures (shown in Fig. S1 and S2,† data in Table S1†): (i) experimental structure of the Al·DFP3 complex crystallized in water,43 (ii) the Al·DFP3 complex optimized by a DFT high level quantum method,† and (iii) a DFT optimized structure of Al·Pept93G. Regarding the Al·DFP3 complex, the DFT structure is equivalent to the experimental one, although the six Al–O distances computed on the DFT optimized structures are systematically 0.02 Å longer than in the X-ray structure. The computed angles are also very similar, with differences less than 1 degree between the experimental and theoretical Al·DFP3 structures. On the other hand, the distances computed on the Al·DFP3 and Al·Pept93G structures optimized with DFT, are also very similar. The electron delocalization indices, which describe the electronic arrangement of the metal first coordination shell, were also computed on the two DFT structures (see Table S15†), showing equivalent values. All in all, all these evidences support the fact that the interactions between Al(III) and Pept93G mimics the ones at the Al·DFP3 complex, and that the peptide backbone does not influence substantially the position of the three pyrodine rings.
Conclusions
In the present study we explore the adequacy of a new family of high-valent metal chelators, based on mimosine containing polypeptides, as efficient chelator of Al(III). We analyze the structural and energetic stability of the complexes formed by Al(III) with several mimosine containing peptides of different lengths and sequences, going from the shortest polypeptide of five amino acids to the largest ones with nine residues.The results reveal that the longest four peptides, made of 8 and 9 residues, show no difficulties for a hexadentate interaction with Al(III). A comparative analysis of the geometrical and electronic features characterized for these complexes reveals Al–O interactions very similar to the ones found in Al·DFP3. The geometrical analysis indicates that the ligands of the cation are posed in a near-optimum octahedral arrangement, very similar to the disposition adopted by the aromatic rings in the Al·DFP3 complex. In addition, thermodynamically the Al·Pept93G complex is almost as stable as Al·DFP3. On the other hand, the shortest three peptides, with only five or six residues, are too short to place the side chains of the three mimosine residues in the right position to form six stable interactions with the cation. Consequently, the central mimosine is a monodentate ligand so that only five mimosine oxygen atoms interact with Al(III). Finally, the Pept7 peptide is in the borderline, as during the QM/MM MD simulation of its complex both coordination modes are sampled, that is, with Al(III)–penta- or hexacoordinated. During the simulation the octahedral arrangement is predominant, but the stability of the complex formed by this peptide is lower than the ones formed by the longest peptides.
The results presented herein point to a direct correlation between peptide length, metal coordination number and complex stability. Thus, the four complexes with Al(III) octahedral are clearly the most stable ones. The relative energies of all these complexes (see Table 2) are in 2.5 kcal mol−1 range, Pept93G being the most stable one. On the other hand, with the remaining peptides, the shorter the peptide, the less stable the complex, so that the stability trend is: Pept7 > Pept6 > Pept5. Among them, Pept7 is the most stable one, 11.4 kcal mol−1 less stable than Pept93G. This trend suggests that a larger peptide would certainly increase its affinity towards Al(III). Nevertheless, we remark that a good chelator requires an optimum balance between the affinity towards the metal and its size, which must be as small as possible to allow an efficient crossing of the molecule across the membrane. Based on these prerequisites, we believe the longest peptides considered in this work, and more in particular Pept93G, emerges as the best potential mimosine containing chelator of Al(III), since this peptide are relatively small and provides an optimum interaction mode with the cation.
In summary, the computational study presented herein provides a deep description of the interaction between Al(III) and mimosine containing peptides, and provide notable atomistic details about the interaction between the peptide and the cation. The present results can encourage further experimental characterization of these polypeptides which we predict has promising properties to chelate not only aluminum, but also highly-charged metals such as Fe(III) that show octahedral coordination and that for which Deferiprone is a good chelator.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research has been funded by the Spanish MINECO/FEDER Projects CTQ2015-67608-P (X. L.) and the Basque Country Consolidated Group Project No. IT588-13. The authors would like to thank the technical and human support provided by the SGI/IZO (SGIker) of the UPV/EHU. Financial support comes as well from the European Commission, Horizon 2020 Research and Innovation Programme (grant agreement N 642294-TCCM).Notes and references
- J. W. Richards, Aluminium; its history, occurrence, properties, metallurgy and applications, including its alloys, H. C. Baird & Co., Philadelphia, 1896 Search PubMed.
- J. Kopáček, J. Hejzlar, J. Kaňa, S. A. Norton, P. Porcal and J. Turek, J. Inorg. Biochem., 2009, 103, 1439–1448 CrossRef PubMed.
- G. Crisponi, D. Fanni, C. Gerosa, S. Nemolato, V. M. Nurchi, M. Crespo-Alonso, J. I. Lachowicz and G. Faa, Biomol. Concepts, 2013, 4, 77–87 CAS.
- A. C. Alfrey, G. R. LeGendre and W. D. Kaehny, N. Engl. J. Med., 1976, 294, 184–188 CrossRef CAS PubMed.
- D. A. Bushinsky, S. M. Sprague, P. Hallegot, C. Girod, J. M. Chabala and R. Levi-Setti, J. Bone Miner. Res., 2009, 10, 1988–1997 CrossRef PubMed.
- M. Touam, F. Martinez, B. Lacour, R. Bourdon, J. Zingraff, S. Di Giulio and T. Drüeke, Clin. Nephrol., 1983, 19, 295–298 CAS.
- A. Campbell and S. C. Bondy, Cell. Mol. Biol., 2000, 46, 721–730 CAS.
- J. Aaseth, G. Crisponi and O. Anderson, Chelation Therapy in the Treatment of Metal Intoxication, 1st edn, 2016 Search PubMed.
- M. A. Canteros-Piccotto, J. L. Fernandez-Martin, M. J. Cannata-Ortiz and J. B. Cannata-Andia, Nephrol., Dial., Transplant., 1996, 11, 1488–1489 CrossRef CAS.
- W. C. Kan, C. C. Chien, C. C. Wu, S. B. Su, J. C. Hwang and H. Y. Wang, Nephrol., Dial., Transplant., 2010, 25, 1604–1608 CrossRef CAS PubMed.
- R. A. Yokel, Coord. Chem. Rev., 2002, 228, 97–113 CrossRef CAS.
- T. Zhou, Y. Ma, X. Kong and R. C. Hider, Dalton Trans., 2012, 41, 6371–6389 RSC.
- Y. Ma, T. Zhou, X. Kong and R. C. Hider, Curr. Med. Chem., 2012, 19, 2816–2827 CrossRef CAS PubMed.
- A. Cilibrizzi, V. Abbate, Y.-L. Chen, Y. Ma, T. Zhou and R. C. Hider, Chem. Rev., 2018, 118, 7657–7701 CrossRef CAS PubMed.
- S. Chaves, S. M. Marques, A. M. Matos, A. Nunes, L. Gano, T. Tuccinardi, A. Martinelli and M. A. Santos, Chem.–Eur. J., 2010, 16, 10535–10545 CrossRef CAS PubMed.
- R. Grazina, L. Gano, J. Šebestík and M. Amelia Santos, J. Inorg. Biochem., 2009, 103, 262–273 CrossRef CAS PubMed.
- R. Cappai, K. Chand, J. I. Lachowicz, S. Chaves, L. Gano, G. Crisponi, V. M. Nurchi, M. Peana, M. A. Zoroddu and M. A. Santos, New J. Chem., 2018, 42, 8050–8061 RSC.
- R. Cusnir, C. Imberti, R. Hider, P. Blower, M. Ma, R. Cusnir, C. Imberti, R. C. Hider, P. J. Blower and M. T. Ma, Int. J. Mol. Sci., 2017, 18, 116 CrossRef PubMed.
- D. J. Berry, Y. Ma, J. R. Ballinger, R. Tavaré, A. Koers, K. Sunassee, T. Zhou, S. Nawaz, G. E. D. Mullen, R. C. Hider and P. J. Blower, Chem. Commun., 2011, 47, 7068–7070 RSC.
- V. Abbate, O. Reelfs, X. Kong, C. Pourzand and R. C. Hider, Chem. Commun., 2015, 52, 784–787 RSC.
- B. C. Q. Nguyen and S. Tawata, Phytother. Res., 2016, 30, 1230–1242 CrossRef CAS PubMed.
- M. Lalande, Exp. Cell Res., 1990, 186, 332–339 CrossRef CAS PubMed.
- A. Upadhyay, J. Chompoo, N. Taira, M. Fukuta, S. Gima and S. Tawata, J. Agric. Food Chem., 2011, 59, 12858–12863 CrossRef CAS PubMed.
- B. C. Q. Nguyen and S. Tawata, Molecules, 2016, 30, 1230–1242 CAS.
- B. Z. Mascaliovas, F. R. G. Bergamini, A. Cuin and P. P. Corbi, Powder Diffr., 2015, 30, 357–361 CrossRef CAS.
- E. Chruscinska, J. Inorg. Biochem., 1999, 75, 225–232 CrossRef CAS.
- R. C. Scarrow, P. E. Riley, K. Abu-Dari, D. L. White and K. N. Raymond, Inorg. Chem., 1985, 24, 954–967 CrossRef CAS.
- M. a Telpoukhovskaia, C. Rodríguez-Rodríguez, L. E. Scott, B. D. G. Page, B. O. Patrick and C. Orvig, J. Inorg. Biochem., 2014, 132, 59–66 CrossRef PubMed.
- D. A. Case, V. Babin, J. T. Berryman, R. M. Betz, Q. Cai, D. S. Cerutti, T. E. Cheatham III, T. A. Darden, R. E. Duke, H. Gohlke, A. W. Goetz, S. Gusarov, N. Homeyer, P. Janowski, J. Kaus, I. Kolossváry, A. Kovalenko, T. S. Lee, S. LeGrand, T. Luchko, R. Luo, B. Madej, K. M. Merz, F. Paesani, D. R. Roe, A. Roitberg, C. Sagui, R. Salomon-Ferrer, G. Seabra, C. L. Simmerling, W. Smith, J. Swails, R. C. Walker, J. Wang, R. M. Wolf, X. Wu and P. A. Kollman, AMBER 14, University of California, San Francisco, 2014 Search PubMed.
- J. J. P. Stewart, J. Mol. Model., 2007, 13, 1173–1213 CrossRef CAS PubMed.
- J. A. Maier, C. Martinez, K. Kasavajhala, L. Wickstrom, K. E. Hauser and C. Simmerling, J. Chem. Theory Comput., 2015, 11, 3696–3713 CrossRef CAS PubMed.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- J. P. Ryckaert, G. Ciccotti and H. J. C. Berendsen, J. Comp. Physiol., 1977, 23, 327–341 CrossRef CAS.
- T. Darden, D. York and L. Pedersen, J. Chem. Phys., 1993, 98, 10089–10092 CrossRef CAS.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8592 CrossRef CAS.
- D. R. Roe and T. E. Cheatham, J. Chem. Theory Comput., 2013, 9, 3084–3095 CrossRef CAS PubMed.
- D. Bashford and D. A. Case, Annu. Rev. Phys. Chem., 2000, 51, 129–152 CrossRef CAS PubMed.
- H. Yadegari, A. Jabbari, H. Heli, A. A. Moosavi-Movahedi and S. Majdi, J. Braz. Chem. Soc., 2008, 19, 1017–1022 CrossRef CAS.
- J. I. Mujika, J. M. Ugalde and X. Lopez, Theor. Chem. Acc., 2010, 128, 477–484 Search PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian16 Revision A.03 Search PubMed.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 2999–3093 CrossRef CAS PubMed.
- M. W. Palascak and G. C. Shields, J. Phys. Chem. A, 2004, 108, 3692–3694 CrossRef CAS.
- W. O. Nelson, S. J. Rettig and C. Orvig, J. Am. Chem. Soc., 1987, 109, 4121–4123 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Additional structural details of Al·DFP3 and Al·Pept93G, RMSD of MD, radius of gyration, individual hydrogen bond interactions, PM6 and DFT comparison. See DOI: 10.1039/c8ra10139f |
| This journal is © The Royal Society of Chemistry 2019 |