Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Superconductivity of boron-doped graphane under high pressure†
Ya Cheng ab,
Xianlong Wang*ab,
Jie Zhanga,
Kaishuai Yang
ab,
Xianlong Wang*ab,
Jie Zhanga,
Kaishuai Yang ab,
Caoping Niuab and
Zhi Zeng*ab
ab,
Caoping Niuab and
Zhi Zeng*ab
aKey Laboratory of Materials Physics, Institute of Solid State Physics, Chinese Academy of Sciences, Hefei 230031, China. E-mail: xlwang@theory.issp.ac.cn; zzeng@theory.issp.ac.cn
bUniversity of Science and Technology of China, Hefei 230026, China
First published on 8th March 2019
Abstract
Based on first-principles calculations, the properties of B-doped graphane under high pressure up to 380 GPa are investigated. We find that B-doped graphane undergoes a phase transition from phase-α to phase-β at 6 GPa. Different from pristine graphane (X. Wen, L. Hand, V. Labet, T. Yang, R. Hoffmann, N. W. Ashcroft, A. R. Oganov and A. O. Lyakhov, Graphane sheets and crystals under pressure, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6833–6837), phase-γ of B-doped graphane is kinetically unstable. The calculated superconducting transition temperature of B-doped graphane at ambient pressure is 45 K, and pressurization can increase the transition temperature notably, e.g., 77 K at 100 GPa. Both the electronic states at the Fermi level and the electron–phonon coupling are mainly contributed by B–C characteristics, indicating that the B-doping plays a key role in the superconductivity.
Introduction
Finding high critical temperature superconductors (Tc) is one of central topics of condensed matter physics and materials science. In the last several years, important progress was achieved in hydrogen-rich compounds. In 2015, under high pressure, H2S and H3S was identified as high-temperature superconductors with a Tc of 80 K and 203 K.1–4 Recently, Tc as high as 215–260 K was reported in the La-Hx system.5,6 These hydrogen-rich compounds are conventional superconductors similar to MgB2,7 in which the superconductivity can be explained by Bardeen–Cooper–Schrieffer (BCS) theory.8 In the conventional superconductors, higher vibrational frequency generally gives higher Tc. Since hydrogen is the lightest element, hydrogen in the solid metallic phase will have a high Debye frequency leading to above 3000 K Debye temperature.9,10 In addition to hydrogen, carbon in the solid phase can have a Debye temperature of as high as 2230 K,11 and it usually forms networks of covalent bonds, such as graphene and diamond. Therefore, high Tc can also be expected in metallized carbon.Since boron (B) has one electron less than carbon, B dopant is an effective way to realize the metallization of carbon networks with hole-doping.12–16 Boron dopant is also widely used to extend the applications of carbon materials, for example, B doped graphene has important applications in the fields of lithium storage17,18 and catalysts19 Furthermore, since the electronic states of the B–C sigma bonds will cross the Fermi level. For example, B dopant can turn diamond into superconductor with the Tc of ∼4 K,12 where sigma bond plays an important role.20 The p-type doping in organic materials can induce superconductivity, such as diamond-like crystalline hydrocarbon,21 hydrogenated carbon nanostructures,22 and polyethylene,23 and they all have noticeable superconducting transition temperatures. Actually, in the carbon based low-dimensional materials, such as graphene and carbon nanotubes,15,24,25 much stronger electron–phonon coupling (EPC) has been proved. Theoretical results show that B-doped graphene will have high Tc ranging from 49 K to 72 K.25 Furthermore, based on the uniform hole-doping model by removing electrons from the system, maximum value of Tc = 96 K was reported in hole-doped graphane at ambient pressure.16
In spite of doping, pressure is another important and effective route to achieve higher Tc in the conventional superconductors, for example, pressure-induced high Tc in HxS systems.1,2,4,26,27 This is partially because that pressure can increase the phonon frequencies and induce some new phases. However, the effects of pressure on the superconductivity behaviors of carbon based two-dimensional materials have not been clarified yet. Does the pressure can also increase the Tc of carbon based two-dimensional materials notably?
In this work, we investigate the superconductivity of B-doped graphane under high pressure. The phase transition of B-doped graphane under high pressure is examined at first. Then, the properties of superconductivity are analyzed, which shows that the Tc of B-doped graphane can be notably increased from 45 K to 77 K by pressure. The discrepancies between chemical doping (B dopant) and ideal uniform hole-doping (remove electrons from the system)16 has been clarified, where localized hole distribution exists in the case of B dopant but even (homogeneous) hole distribution occurs in the ideal uniform hole-doping model.
Methods
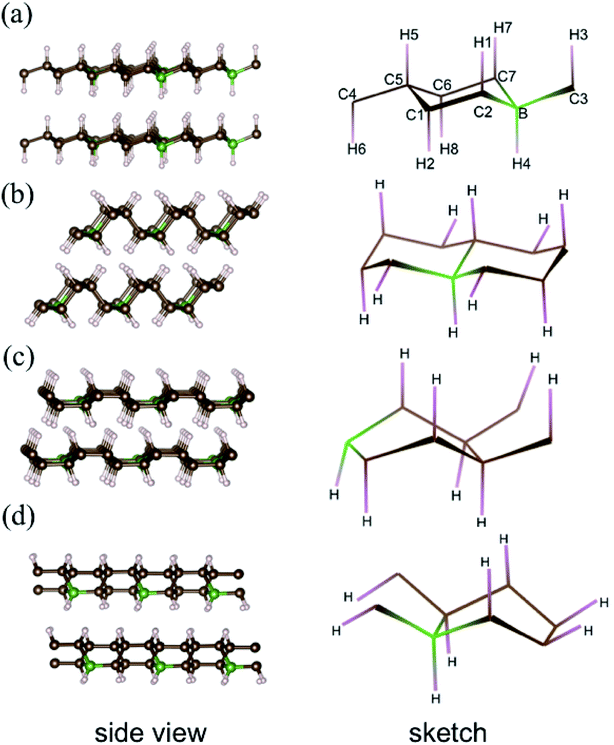
Previous simulations pointed out that for graphane, there are four stable phases with different carbon ring configurations (chair-like or boat-like) and C–H bond orientations.28 These graphane phases are more stable than benzene from ambient pressure to high pressure (300 GPa),29 and the enthalpies of several CH phases are shown Fig. S1† as a function of pressure. We introduce 12.5 mol% B dopants in these four stable phases, which are shown in the Fig. 1 as phase-α, phase-β, phase-γ, and phase-δ, respectively. Phase-α and phase-β are chair-like configurations. Seeing from the right panel of Fig. 1(a), neighboring C–H bonds locate at opposite side in phase-α. However, in phase-β (Fig. 1(b)), three adjacent C–H bonds orientate to the same direction, and the other three C–H bonds orientate in opposite directions. The other two phases are boat like, orientations of C–H bonds or B–H bonds are displayed in the sketches of each phase in the right part of Fig. 1.Structural optimization, enthalpies, and electronic structures were calculated using the Vienna ab initio simulation (VASP) code30–32 with projector-augmented plane-wave (PAW) potentials. We employed 1s1, 2s22p2, 2s22p1 valence states for H, C, and B potential, respectively. The energy cutoff was set to 800 eV in all calculations, and 2 × 2 × 2 supercells of graphane were used. The k-point grid was generated by Monkhorst–Pack scheme and ensured that the energies converged to within 1 meV per atom. The forces were converged to less than 0.001 eV Å−1. EPC were calculated using Quantum Espresso (QE) code33 with density-functional perturbation theory (DFPT).34 The cutoff energies for wave functions and charge densities were set to 40 Ry and 240 Ry, respectively. We used 2 × 2 × 2 q-point meshes for EPC parameter λ, and denser k-point meshes 8 × 8 × 8 for electron–phonon interaction matrix element calculation.
Results and discussion
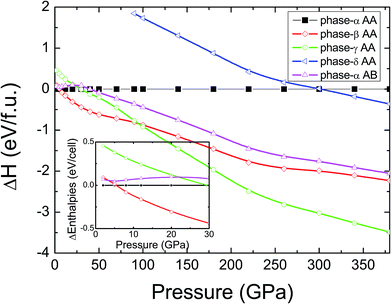
In pristine bulked graphane, AA-stacking features were proved to be more stable than AB-stacking cases.28 To check the stability of AA-stacking or AB-stacking in B-doped graphane, we calculated enthalpies of phase-α in AA-stacking and in AB-stacking. The calculated enthalpies are shown in Fig. 2. The inset of Fig. 2 zooms in low pressure range, and it shows that the enthalpy of phase-α in AA-stacking is smaller than that of phase-α in AB-stacking, indicating that similar to pristine graphane, B-doped graphane in AB-stacking is metastable below 40 GPa. Therefore, we will only consider the stability of phase-α, phase-β, phase-γ, and phase-δ in AA-stacking profiles, and the calculated enthalpies of these phases are shown in Fig. 2 as function of pressure.We can find from Fig. 2 that the most stable phase in the pressure range 0–6 GPa is the phase-α in AA-stacking, which has a symmetry of P3m1. Above 6 GPa, phase-β becomes more stable than phase-α, and phase-β keeps the stability up to 95 GPa. Upon further compression, phase-γ has the lowest enthalpy at the pressure higher than 95 GPa. Phase-δ is not competitive in enthalpy with other configurations in the whole pressure range from 0 to 380 GPa. Moreover, imaginary frequencies are observed in the phonon dispersions of phase-γ, indicating that it is kinetically unstable. Therefore, for B-doped graphane, phase-α (0–6 GPa) and phase-β (6–380 GPa) are two stable phases under pressure. The phase transition of B-doped graphane is different from that of pristine, which undergoes phase transition from phase-α to phase-β at 15 GPa then to phase-γ at 240 GPa.28 For comparison, we calculated the phase transition of 6.125 mol% B dopants in these three phases (see in Fig. S2†), we can find that the phase transition sequence of 6.125 mol% B-doped graphane is constant with the case of 12.5 mol%-doped case. The critical pressure of 6.125 mol% B-doped graphane from phase-α to phase-β is 11 GPa, then transform to phase-γ at 123 GPa. The critical pressure points fall in between pristine and 12.5 mol% B dopants graphane.
With pressure increasing, distance between atoms will change, and the results are summarized in Table S1,† will change. The B–H bond length (dB–H) in B-doped graphane keeps decreasing from 1.208 Å (phase-α at ambient pressure) to 1.150 Å (phase-β at 100 GPa). On the other hand, C–H bond length (dC–H) is slightly shorter (0.1 Å) than dB–H under pressure. From Bader charge analysis of phase-α (see Fig. 3(c)), we can see that the electrons of B atom transform to neighbor atoms (H and C), since the electronegativity of B is weaker than C and H. The length of C–C bond next to B atom is shorter than that of C–C bond far from B atom, because of the charge transformation of B to C. Furthermore, over the whole investigated pressure range, B-doped graphane crystal keeps layer stacking and the layer distance represented as dH–H in Table S1† decreases with pressure increasing.
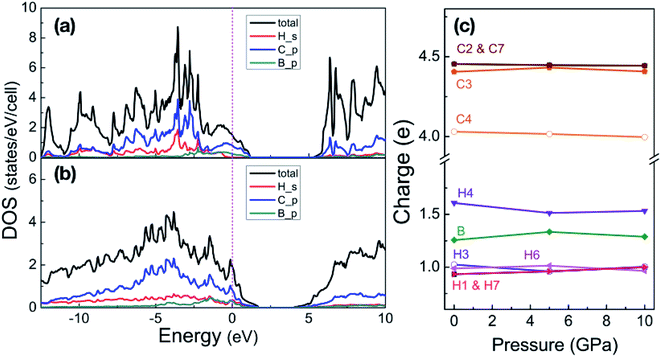 | ||
| Fig. 3 Partial density of states of phase-α at 5 GPa (a) and phase-β at 100 GPa (b). Energy is respected to the Fermi level. (c) Shows the Bader charges of atoms in the phase-α are shown as a function of pressure, the numbers match the sketch of phase-α in Fig. 1. | ||
We now inspect the electronic structure of the most stable phases – phase-α and phase-β. The partial density of states (PDOS) of phase-α at 5 GPa and phase-β at 100 GPa shown in Fig. 3(a) and (b) illustrate that B-doped graphane in both phase-α and phase-β are metal. The electrons of C p-orbitals and B p-orbitals make the most contribution to the density of states but not those of H s-orbitals indicating that the metallization origins from the C–B rings. Moreover, the H s-orbitals electrons contribute to the superconductivity of phase-β, since H s-orbitals cross the Fermi level. As shown in Table 1, density of states at the Fermi level increases slightly with pressure increasing in phase-β, e.g., the electronic states increase from 8.50 states per cell at 20 GPa to 10.96 states per cell at 100 GPa.
| Phases | Pressure (GPa) | λ | NEF (states per cell) | ωlog (K) | Tc (K) | |
|---|---|---|---|---|---|---|
| μ* = 0.10 | μ* = 0.13 | |||||
| Phase-α | 0 | 1.62 | 9.66 | 369 | 45 | 41 |
| 5 | 1.52 | 9.75 | 588 | 68 | 62 | |
| 10 | 1.26 | 9.53 | 730 | 69 | 62 | |
| Phase-β | 20 | 0.92 | 8.25 | 644 | 39 | 33 |
| 50 | 1.00 | 10.16 | 718 | 50 | 43 | |
| 100 | 1.72 | 10.96 | 602 | 77 | 71 | |
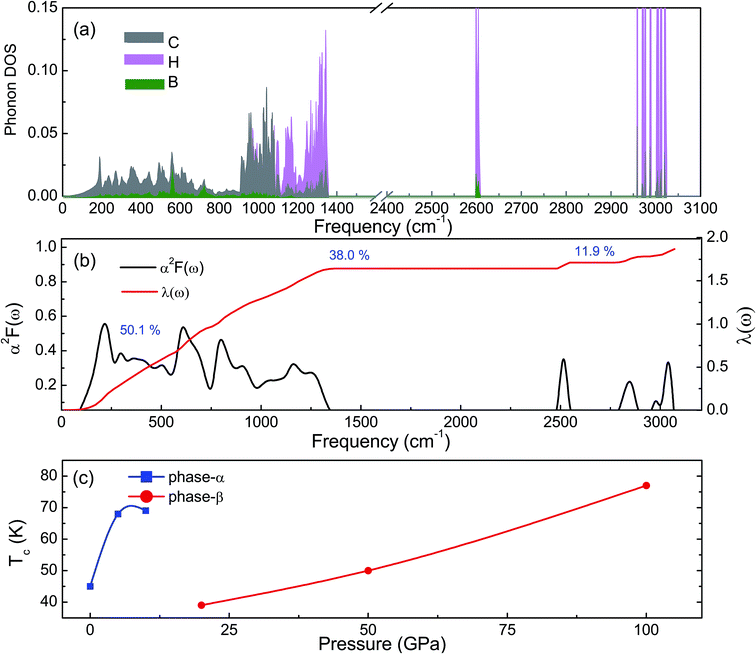
The phonon dispersion curves of phase-α (see Fig. S2†) and phase-β (see Fig. 4) under pressure were calculated to explore the lattice dynamics of B-doped graphane. The absence of imaginary frequencies implies the kinetically stability of phase-β under high pressure. The whole phonon density of states of phase- α at 10 GPa can be divided into three parts, which is shown in Fig. 5(a). The low-frequency vibration below 750 cm−1 mainly comes from the C–C or C–B stretching vibrations, C–H and B–H bonds shear motions contribute to the middle-frequency vibration (750–1500 cm−1).16 After a large gap, C–H and B–H bonds stretching mainly contribute to the highest frequency area above 2500 cm−1. Among this area, B–H stretching vibration appears around 2600 cm−1, while C–H stretching mode sites around 3000 cm−1. Phase-α and phase-β at all calculated pressure points have similar profiles in phonon dispersion, all of them can be divided into three parts in frequency.
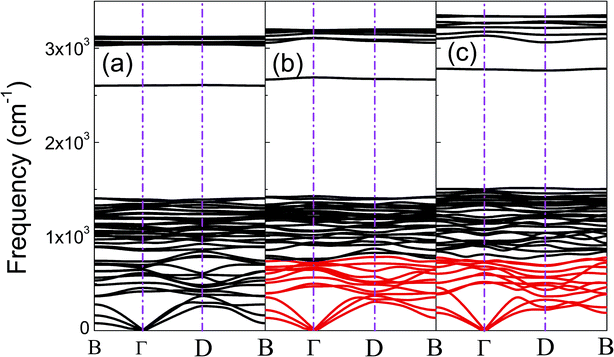 | ||
| Fig. 4 (a), (b), and (c) show the phonon dispersions of phase-β at 20 GPa, 50 GPa, and 100 GPa, respectively. The softened phonon branches at D point are shown in red at (b) and (c). | ||
Taking phase-β at 100 GPa for example, from the Eliashberg phonon spectral function α2F(ω) and integrated EPC parameter (λ) as shown in Fig. 5(b), the low-frequency (blow 750 cm−1) and (750–1500 cm−1) middle-frequency vibration contributes as much as 50.1% and 38.0% of total electron–phonon coupling constant, respectively. The remaining λ comes from high-frequency C–H and B–H stretching motions. This result indicates the significant role of low-frequency and middle-frequency vibrational modes. However, C–H and B–H stretching motions contribute less to electron–phonon interaction. Namely, B–C rings play an important role in the superconductivity of B-doped graphane.
Based on the λ and logarithm of average frequency (ωlog), we employed the modified McMillan equation by Allen and Dynes to calculate the Tc.
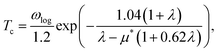 | (1) |
To clarify the pressure effects on the superconductivity of B-doped graphane, we calculated the critical temperature of superconductivity of both phases. The Tc of B-doped graphane at the pressure ranging from ambient pressure to 100 GPa was calculated, and the results are presented in Fig. 5(c). At ambient pressure, the Tc of phase-α is 45 K, while it increases to 68 K at the pressure of 5 GPa. The Tc at 10 GPa (69 K) is comparable with that of 5 GPa, and the reason is that from 5 GPa to 10 GPa, the decrease of λ counteracts the increase of ωlog as shown in Table 1. It is noticeable that the Tc of phase-α we simulated at ambient pressure is 45 K, much lower than that (96 K) predicted by Savini et al.16 The reason lead to this large divergence mainly comes from the charge distribution difference between chemical doping and ideal uniform electronic doping. In the ideal uniformed electronic doping model by removing electrons from the investigated system, due to the nesting of the Fermi surface, large medium frequency phonon soften appears at gamma point.16 As shown in Fig. S4,† we obtain similar phonon soften in the graphane by removing 12.5% electrons. However, in the case of chemical doping, the charge is localized around B atom but not uniformly distributed in real chemical doping mode of phase-α. It can be found in Fig. 3(c) that charges of B atom transform to atoms nearby (C and H). That is the reason that we did not find the medium frequency phonon soften at gamma point as shown in Fig. 4. In phase-β, the ωlog of phase-α at 20 GPa and 50 GPa is 644 K and 718 K, respectively. However, it decreases to 602 K at the pressure of 100 GPa. The decrease of ωlog from 50 GPa to 100 GPa origins from the soften of phonon at the D point (Fig. 4 (b) and (c)) induced by pressure. The pressure-induced phonon softening is a common behavior of superconductors at high pressure,35–37 and it plays a crucial role in enhancing the electron–phonon coupling.1,38,39 Therefore, the λ of phase-β increases with the pressure increasing, which counteracts the decrease of ωlog. We can find that, over the pressure range from 20 GPa to 100 GPa, the Tc of phase-β almost monotonously increases from 39 K to 77 K. Our results show that the Tc of each B-doped graphane phase will notably increase with pressure increasing. The B–C bonds make the most contribution to Tc in both phase-α and phase-β, and upon further compression, H s-orbitals electrons in the phase-β will contribute more to the metallization and superconductivity of B-doped graphane. For the lower doping concentration, e.g., 6.125 mol% B-doped graphane, the electronic states at the Fermi level will become smaller. Therefore, similar to the concentration effect of hole-doped graphane,16 lower B concentration may lead to lower superconducting critical temperature.
Conclusions
We have investigated the phase transition, metallization, and superconductivity of B-doped graphane in the framework of density functional theory. We found that at low pressure (0–6 GPa), B-doped graphane in phase-α with AA-stacking is the most stable phase, and AB-stacking are metastable configuration. Phase-β is the most stable case within the pressure ranging from 6 to 380 GPa. All B-doped graphane phases are metal, and B–C and C–C vibrations dominantly contribute to the electron–phonon coupling. At ambient pressure, because of the Fermi surface nesting induced phonon softening, the ideal uniform hole-doping model by removing electrons from graphane gives higher Tc than that of the B-doped case. Moreover, pressure-induced phonon softening in B-doped graphane is observed, and pressure can significantly increase the Tc of B-doped graphane in both phase-α and phase-β.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the NSFC under Grant of 11674329, Science Challenge Project No. TZ2016001, the National Science Foundation for Young Scientists of China (Grant No. 11504381), and the Major/Innovative Program of Development Foundation of Hefei Center for Physical Science and Technology. The calculations were partly performed in Center for Computational Science of CASHIPS, the ScGrid of Supercomputing Center and Computer Network Information Center of Chinese Academy of Sciences.References
- Y. Li, J. Hao, H. Liu, Y. Li and Y. Ma, The metallization and superconductivity of dense hydrogen sulfide, J. Chem. Phys., 2014, 140, 174712 CrossRef PubMed.
- D. Duan, X. Huang, F. Tian, D. Li, H. Yu, Y. Liu, Y. Ma, B. Liu and T. Cui, Pressure-induced decomposition of solid hydrogen sulfide, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 180502 CrossRef.
- D. Duan, Y. Liu, F. Tian, D. Li, X. Huang, Z. Zhao, H. Yu, B. Liu, W. Tian and T. Cui, Pressure-induced metallization of dense (H2S)2H2 with high-Tc superconductivity, Sci. Rep., 2014, 4, 6968 CrossRef CAS PubMed.
- A. P. Drozdov, M. I. Eremets, I. A. Troyan, V. Ksenofontov and S. I. Shylin, Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system, Nature, 2015, 525, 73–76 CrossRef CAS PubMed.
- A. P. Drozdov, V. S. Minkov, S. P. Besedin, P. P. Kong, M. A. Kuzovnikov, D. A. Knyazev and M. I. Eremets, Superconductivity at 215 K in lanthanum hydride at high pressures, 2018, arXiv: 1808.07039.
- M. Somayazulu, M. Ahart, A. K. Mishra, Z. M. Geballe, M. Baldini, Y. Meng, V. V Struzhkin and R. J. Hemley, Evidence for superconductivity above 260 K in lanthanum superhydride at megabar pressures, 2018, arXiv: 1808.07695.
- J. Nagamatsu, N. Nakagawa, T. Maranaka, Y. Zenitani and J. Akimitsu, Superconductivity at 39 K in copper doping magnesium diboride, Nature, 2001, 410, 63–64 CrossRef CAS PubMed.
- J. Bardeen, L. N. Cooper and J. R. Schrieffer, Theory of superconductivity, Phys. Rev., 1957, 108, 1175–1204 CrossRef CAS.
- N. W. Ashcroft, Metallic hydrogen: a high-temperature superconductor?, Phys. Rev. Lett., 1968, 21, 1748–1749 CrossRef CAS.
- V. L. Ginzburg, The Physics of a Lifetime: Reflections on the Problems and Personalities of 20th Century Physics, Springer, 2001 Search PubMed.
- C. Kittel, Introduction to Solid State Physics, John Wiley & Sons, 8 edn, 2004 Search PubMed.
- E. A. Ekimov, V. a Sidorov, E. D. Bauer, N. N. Mel’nik, N. J. Curro, J. D. Thompson and S. M. Stishov, Superconductivity in diamond, Nature, 2004, 428, 542–545 CrossRef CAS PubMed.
- E. A. Ekimov, V. A. Sidorov, A. Zoteev, Y. Lebed, J. D. Thompson, E. D. Bauer and S. M. Stishov, Superconductivity in diamond induced by boron doping at high pressure, Phys. Status Solidi B, 2009, 246, 667–672 CrossRef CAS.
- H. Fukuyama, Y. Ohta, T. Shirakawa and S. Horiuchi, Superconductivity in B-doped diamonds, J. Phys. Chem. Solids, 2008, 69, 3265–3268 CrossRef CAS.
- A. Y. Kasumov, M. Kociak, M. Ferrier, Y. A. Kasumov, S. Gueron, B. Reulet, I. I. Khodos, Y. B. Gorbatov, V. T. Volkov, L. Vaccarini and H. Bouchiat, Superconductivity in ropes of single-walled carbon nanotubes, Phys. Rev. Lett., 2001, 86, 2416–2419 CrossRef PubMed.
- G. Savini, A. C. Ferrari and F. Giustino, First-principles prediction of doped graphane as a high-temperature electron-phonon superconductor, Phys. Rev. Lett., 2010, 105, 037002 CrossRef CAS PubMed.
- D. Das, R. P. Hardikar, S. S. Han, K. R. Lee and A. K. Singh, Monolayer BC2: an ultrahigh capacity anode material for Li ion batteries, Phys. Chem. Chem. Phys., 2017, 19, 24230–24239 RSC.
- X. Wang, Z. Zeng, H. Ahn and G. Wang, First-principles study on the enhancement of lithium storage capacity in boron doped graphene, Appl. Phys. Lett., 2009, 95, 183103 CrossRef.
- J. Y. Damte, S. L. Lyu, E. G. Leggesse and J. C. Jiang, Methanol decomposition reactions over a boron-doped graphene supported Ru-Pt catalyst, Phys. Chem. Chem. Phys., 2018, 20, 9355–9363 RSC.
- J. M. An and W. E. Pickett, Superconductivity of MgB2: covalent bonds driven metallic, Phys. Rev. Lett., 2001, 86, 4366–4369 CrossRef CAS PubMed.
- C. Lian, J. Wang, W. Duan and C. Chen, superconductivity in hole- doped diamond-like crystalline hydrocarbon, Sci. Rep., 2017, 7, 1–6 CrossRef CAS PubMed.
- A. Sanna, A. Davydov, J. K. Dewhurst and S. Sharma, Superconductivity in hydrogenated carbon nanostructures, Eur. Phys. J. B, 2018, 91, 177 CrossRef.
- A. F. José, M. Graužinytė, Li. Boeri, G. Profeta and A. Sanna, Superconductivity in doped polyethylene at high pressure, Eur. Phys. J. B, 2018, 91, 176 CrossRef.
- F. Mazzola, J. W. Wells, R. Yakimova, S. Ulstrup, J. A. Miwa, R. Balog, M. Bianchi, M. Leandersson, J. Adell, P. Hofmann and T. Balasubramanian, Kinks in the σ band of graphene induced by electron-phonon coupling, Phys. Rev. Lett., 2013, 111, 216806 CrossRef PubMed.
- F. Mazzola, T. Frederiksen, T. Balasubramanian, P. Hofmann, B. Hellsing and J. W. Wells, Strong electron-phonon coupling in the σ band of graphene, Phys. Rev. B, 2017, 95, 075430 CrossRef.
- A. F. Goncharov, S. S. Lobanov, I. Kruglov, X. Zhao, X. Chen, A. R. Oganov, Z. Konôpková and V. B. Prakapenka, Hydrogen sulfide at high pressure: change in stoichiometry, Phys. Rev. B, 2016, 93, 174105 CrossRef.
- T. Ishikawa, A. Nakanishi, K. Shimizu, H. Katayama-Yoshida, T. Oda and N. Suzuki, Superconducting H5S2 phase in sulfur-hydrogen system under high-pressure, Sci. Rep., 2016, 6, 23160 CrossRef CAS PubMed.
- X. Wen, L. Hand, V. Labet, T. Yang, R. Hoffmann, N. W. Ashcroft, A. R. Oganov and A. O. Lyakhov, Graphane sheets and crystals under pressure, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 6833–6837 CrossRef CAS.
- X. Wen and N. W. Ashcroft, Benzene under high pressure: a story of molecular crystals transforming to saturated networks, with a possible intermediate metallic phase, J. Am. Chem. Soc., 2011, 133, 9023–9035 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Efficiency of ab initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- S. Baroni, S. de Gironcoli, A. D. Corso and P. Giannozzi, Phonons and related crystal properties from density-functional perturbation theory, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- Y. Cheng, C. Zhang, T. Wang, G. Zhong, C. Yang, X. Chen and H. Q. Lin, Pressure-induced superconductivity in H2-containing hydride PbH4(H2)2, Sci. Rep., 2015, 5, 16475 CrossRef CAS PubMed.
- G. Zhong, C. Yang, X. Chen and H. Lin, Superconductivity in solid benzene molecular crystal, J. Phys.: Condens. Matter, 2018, 30, 245703 CrossRef PubMed.
- M. L. Cohen, Electronphonon induced pairing and its limits for superconducting systems, Phys. E, 2011, 43, 657–660 CrossRef CAS.
- P. B. Allen and R. C. Dynes, Transition temperature of strong-couple superconductors reanalyzed, Phys. Rev. B: Condens. Matter Mater. Phys., 1975, 12, 905–922 CrossRef CAS.
- N. Bernstein, C. S. Hellberg, M. D. Johannes, I. I. Mazin and M. J. Mehl, What superconducts in sulfur hydrides under pressure and why, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 060511 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra10241d |
| This journal is © The Royal Society of Chemistry 2019 |