Molecular design principles towards exo-exclusive Diels–Alder reactions

Abstract

The exo selective Diels–Alder reactions, reported as special cases, usually involve catalytic reaction conditions and specific cyclic structural motifs on the diene and/or the dienophile. Here we report a systematic computational investigation on the substituent effect for simple, linear dienes and dienophiles towards exo control in Diels–Alder reactions under thermal conditions. Through detailed characterization of reaction pathways for Diels–Alder cycloadditions between linear dienes and dienophiles with various substituents, we summarize a set of design principles aiming for an optimal and nearly-exclusive exo selectivity. These results shall lead to valuable guidelines and more versatile strategies in organic synthesis that are in accordance with the principles of green chemistry.

---

Introduction

The Diels–Alder cycloaddition reaction ranks among one of the most classical organic reactions with new aspects continuing to emerge.¹ Typically, in a normal electronic demand inter-molecular Diels–Alder reaction, an electron-rich diene and an electron-deficient dienophile are reacted to form an ortho or para cycloadduct with exo or endo possibilities. Traditionally, the exo adduct is believed to be thermodynamically more stable due to less steric repulsion, but the endo product, usually the major product found in most reactions, is kinetically favored as predicted by the empirical Alder-endo rule.² Over the past few decades, the endo rule has mainly been explained by the well-known and controversial “secondary orbital interaction”,^3–5 although different factors including charge transfer effects, CH⋯π interactions, dipole effects, steric interactions, electrostatic forces, and etc., have also been proposed.^4–10 The less frequently seen exo selectivity may also be achieved under certain reaction conditions, e.g. in the catalytic environment involving specific structural motifs on diene or dienophile,^11–22 or in the presence of complex and bulky Lewis acids.^23–31 Although the steric effect was usually regarded as the key for exo-controlling in Diels–Alder reactions, other factors are believed to also contribute to the observed exo selectivity, e.g., the orbital, the electrostatic, and the dispersive interactions between the strained reactants at the transition states, or the non-covalent interactions between the catalyst and the diene.^31–33

On the other hand, the exo selectivity under non-catalytic thermal Diels–Alder reaction conditions has only been observed in few scenarios, reported as special cases,^34–37 and has not been investigated in detail. Recently, Ho et al. found that the exo-selectivity may occur between simple, linear dienes and dienophiles under thermal conditions, an essential and an optimal condition in order to increase the flexibility and usefulness of the Diels–Alder reactions in constructing diverse molecular scaffolds. This newly-found anomalous, yet in the meanwhile systematic, exo-selectivity implies that certain steric or electronic interactions critical to exo-control may have been overlooked for a long time.

In the previously reported cycloaddition between the 2-silylated dienes and various dienophiles, qualitative to quantitative agreements on the stereoselectivity have been observed in most cases between computation and experiments.³⁸ Theoretical analysis indicated that the stereoselectivity may be primarily derived from the competition between different interaction forces in two pathways, specifically, the steric repulsion between R_β at the C_β position of the dienophile and the silyl group at the C₂ position of the diene in the exo pathway, and the steric repulsion between the electron withdrawing group (EWG) of the dienophile and the R at C₄ of the diene in the endo pathway. Most remarkably, the overall observed exo selectivity trend in terms of EWGs in the sequence of ester > nitrile > aldehyde > ketone, are faithfully reproduced by ab initio calculations, regardless of the substitutions or choice of the functional (Fig. S1†). This has been rationalized by the combination of the size effect and the electron-withdrawing power of the EWG groups.³⁸

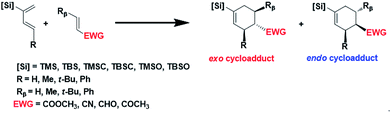
Here we report a systematic computational investigation on the substituent effect aiming for an ultimate exo-control in Diels–Alder reactions between simple, acyclic reactants under thermal conditions. We focus on the para cycloadduct formed between a C₂-silyl substituted diene and an α,β-unsaturated carbonyl dienophile (Scheme 1). Combinations of different substitutions at three positions are simulated and discussed: the silyl group at the C₂ position, and the alkyl group at the C₄ position of the diene, represented by [Si] and R, respectively, and the alkyl group at the C_β position of the dienophile, represented by R_β. Here the silyl group, abbreviated as [Si], represents the general form of trialkylsilyl, trialkylsilyloxy, or trialkylsilylmethyl groups. Six silyl groups ranging from TMS, TBS, TMSCH₂, TBSCH₂, TMSO and TBSO groups are considered as shown in Scheme 1, where TMS refers to trimethylsilyl group, TBS refers to tert-butyldimethylsilyl group, TBSO refers to tert-butyldimethylsilyloxy group, and etc. Based on the simple steric model, one shall expect increasing exo or endo selectivity with increasing substituent size in R and R_β, respectively. Therefore, a series of reactions with the increasing substituent size from hydrogen, methyl, to t-butyl or phenyl are designed and calculated for R and R_β.

Scheme 1 Structures of dienes and dienophiles investigated in this study.

Computational details

Ground state and transition state (TS) optimizations are performed utilizing density functional theory (DFT) using the program Gaussian 09 in the scheme of M06-2X hybrid functionals with the 6-311++G(d,p) basis set. Product distributions at room temperature are calculated using the Arrhenius rate expression derived from standard transition state theory.^39–43 Solvation corrections are included using the polarizable continuum model (PCM) method.⁴⁴ The activation strain model (ASM) are utilized to differentiate and quantize the relative contributions to the activation barrier. More specifically, the activation barrier (ΔE^‡) are decomposed into a distortion energy (ΔE^‡_d) and an interaction energy (ΔE^‡_i), i.e. ΔE^‡ = ΔE^‡_d + ΔE^‡_i.^10,45–47 The distortion energy is the energy difference between the energies of the reactants in the optimized geometries (e.g. E[A] + E[B]) and the same molecules in the transition state (TS) conformations, but without interactions in between (e.g. (E[A^‡] + E[B^‡]), where A^‡ and B^‡ are taken from the TS complex (AB) ^‡ = A^‡ − B^‡). The interaction energy is the energy difference between the energies of the reactants in the TS conformations, summed separately (e.g. E[A^‡] + E[B^‡]), and the energy of the entire TS complex (e.g. E[A^‡ − B^‡]).

Results and discussions

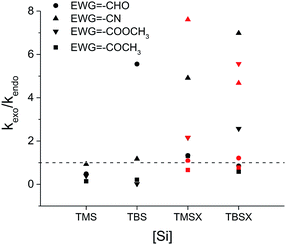
While most of the previous studies utilize a smaller silyl group, either TMS or TMSO in the Danishefsky's diene,²² a much bulkier TBSO group was used in the recent study.³⁸ We suspect the substantial size difference of the silyl group may lead to the systematic exo-selective behaviors in Diels–Alder reactions. Fig. 1 shows the calculated product ratio based on relative reaction rate constants estimated by the Arrhenius equation. Our results indicate that all combinations of reactants result in an endo major product as the C₂ of diene is substituted with the smallest TMS group, but uniformly and gradually shift to exo-selectivity as the size of the silyl group increases, regardless of the choice of EWG. For most cases, the activation energy of the endo transition state (TS_endo) surpasses that of the exo pathway when the silyl group exceeds a certain size.

Fig. 1 The calculated product ratio k_exo/k_endo of the Diels–Alder reaction pathways. For TMSX and TBSX, the red and black data points represent those for X=O and X=CH₂, respectively. Here R = Ph for all dienes and R_β = Me for all dienophiles.

Evidently, a slight modification from TMS to TMSX, or from TBS to TBSX (X=O or CH₂) could result in a reversed stereoselectivity. In addition, in most cases, higher exo-selectivity is predicted for X=O than for X=CH₂. A recent study by Song et al. reported high exo selectivity in Diels–Alder reactions involving dienes functionalized by a large bis(silyl) group at the C₂ position.⁴⁸ The two bulky silyl groups result in a strong steric hindrance at both the top and the bottom sides of the diene to the EWG group when the dienophile approaches in the endo orientation. On the contrary, our results indicate that, the effect of bis-silyl group substitution may as well be achieved by a single silyl group when a bridging methylene group or oxygen atom is inserted between the C₂ of diene and the Si atom as in TMSX or TBSX, (X=CH₂ or O) for the Diels–Alder reaction with a trans substituted dienophile. In this case, the silyl group is rotated away from the R_β of the dienophile at TS_exo, significantly alleviating the steric repulsion between the [Si] of the diene and the R_β of the dienophile, as shown in Fig. 2.

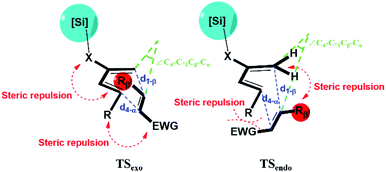Fig. 2 Illustration for the geometry and major interactions for exo and endo transition states. X represents the bridging O or CH₂ group inserted between C₂ of diene and the Si atom.

The critical geometric parameters of the transition states are analyzed as shown in Fig. S2.† Between the two newly formed C–C bonds, d_1-β (bond distance between C₁ of diene and C_β of dienophile, ∼1.9–2.0 Å) is significantly longer than d_4-α (bond distance between C₄ of diene and C_α of dienophile, ∼2.7–2.9 Å), indicating the typical concerted asynchronous behavior in most asymmetric Diels–Alder reactions.¹⁵ As the bridging group X is inserted, the bond length difference between the shorter d_1-β and the longer d_4-α further increases, indicating an increased asynchronicity. Also note that the d_4-α is increased much more when X=O than when X=CH₂, which may result from the electrostatic repulsion between the bridging O atom in the TBSO and the EWG.^22,34,38

Many of the previous studies attributed the most destabilizing interaction in the endo pathway to the steric repulsion between the EWG of the dienophile and the C₄-phenyl group of the diene.²² Surprisingly, we find that a much worse exo-selectivity is presented with the most bulky t-butyl group with respect to methyl substitution or even unsubstituted R, as shown in Table 1. As the size of R increases, both the exo and the endo pathways become more sterically destabilized. In the case when R = t-Bu, the distortion energy of the exo pathway even exceeds that of the endo (Fig. 3), possibly due to enhanced steric repulsion between the R_β and the silyloxyl group as the EWG is twisted away along the C₄–C₁-C_β–C_α dihedral angle. In the contrary, a substituent with a small to moderate size, e.g. the methyl group, in combination with a strongly exo-inducting EWGat the dienophile, e.g. the ester group, could allow for an exo/endo ratio as high as 32 (Table 1).

Table 1 The calculated product ratio k_exo/k_endo of the Diels–Alder reaction pathways with different R group in the diene

EWG	H	Me	t-Bu	Ph
COOCH3	6.12	32.06	0.68	5.57
CN	5.17	6.38	3.23	4.68
CHO	0.84	1.13	0.65	1.21
COCH3	1.02	0.78	0.08	0.08

---

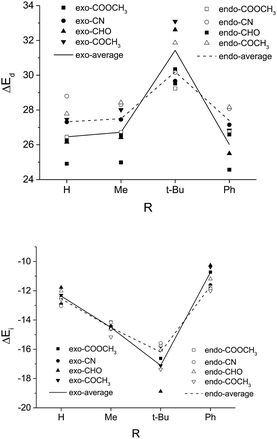Fig. 3 The distortion energy (ΔE_d) and the interaction energy (ΔE_i) of TS_exo and TS_endo for Diels–Alder reactions with different R and EWG groups (systems in Table 1). Here R_β = Me for all dienophiles.

On the other hand, based on a simple spatial arrangement of the transition state geometries, one may crudely assume that the substituent on C_β of the dienophile exerts a stronger steric repulsion with the C₂-silyl group of the diene in the exo than in the endo pathway. Similarly, we computed and compared the stereoselectivities of a series of reactions by changing R_β from hydrogen, methyl, to t-butyl and phenyl, as shown in Table 2. Surprisingly, the much bulkier phenyl and the t-butyl group exhibits the best exo selectivity among all cases and is against our original assumption. A careful geometry analysis reveals that, as the d_1-β of the TS naturally increases with increasing size of R_β, the d_4-α decreases, indicating an overall decrease of asynchronicity (Fig. S4†). However, the TS_exo remains more asynchronous than TS_endo, especially for the exo-dominating pathways when R_β = t-butyl or phenyl. Also note that the C₄–C₁–C_β–C_α twist angle for the endo TS significantly increases with increasing size of the R_β, as shown in Fig. S3,† which in turn results in an elevated distortion energy (Fig. 4) and a more destabilized reaction pathway with respect to the exo TS.

Table 2 The calculated product ratio k_exo/k_endo of the Diels–Alder reaction pathways with different R_β group in the dienophile

EWG	H	Me	t-Butyl	Phenyl
COOCH3	0.19	4.15	6.02	35.55
CN	0.53	2.29	7.26	32.98
CHO	0.22	1.21	10.73	12.72
COCH3	0.13	0.78	1.14	5.05

---

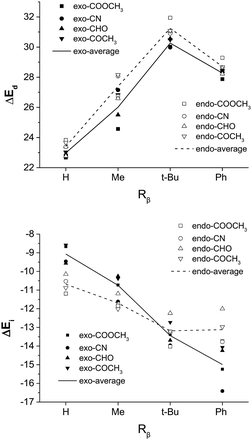Fig. 4 The distortion energy (ΔE_d) and the interaction energy (ΔE_i) of TS_exo and TS_endo for Diels–Alder reactions with different R_β and EWG groups (systems in Table 2). Here R = Ph for all dienes.

The energy decomposition analysis in Fig. 4 also reveals a much more stabilizing interaction energy for phenyl substitution at the C_β position. In the exo orientation, as the EWG points away from the diene fragment, the substituent at the trans-C_β position would point towards the diene fragment. Therefore, with a good overlap between the π* orbital of the diene fragment and the π orbital of the trans-C_β substituent, what is defined as the exo configuration with respect to the EWG group is endo with respect to the trans-C_β substituent, and may be stabilized by the secondary orbital stabilization. In other words, for a dienophile with a π-bearing EWG as well as a π-bearing trans-C_β substituent, both endo and exo pathways involve a secondary orbital interaction between the diene fragment and different parts of the dienophile. In this sense, neither endo nor exo is predominantly stabilized by an electronic factor, and the major product is determined by the magnitude of distortion. In this case, the endo dominance may be tilted without much effort. We designed and examined the hypothetical Diels–Alder reaction involving the trans-C_β ethenyl substituted dienophiles and confirmed a much better exo selectivity than the similar-sized methyl group regardless of the EWG substitution, as shown in Table S1 and Fig. S5.† In particular, the ethenyl substituent needs to be in the s-cis conformation in order to form good orbital overlap with the diene fragment, as shown in Fig. S6.†

Conclusion

Based on our investigation on the substituent effect at three different positions of the dienes and dienophiles, some design principles for exo-exclusive Diels–Alder reaction may be summarized as the following:

(1) A bulkier and more electronegative trialkylsilyloxy group at the C₂ of diene provides a higher exo-selectivity.

(2) C₄ substitution of diene with a moderate size provides a higher exo-selectivity.

(3) A substitutional group involving π-conjugation at the trans-C_β of dienophile provides a higher exo-selectivity.

(4) For the choice of EWG, the exo-selectivity follows the general trend: ester > nitrile > aldehyde > ketone.

The combination of the substitutional groups at different positions may lead to an accumulative effect. For example, a combination of [Si] = TBSO, R=Me, R_β = Ph and EWG = COOMe is computationally expected to reach an exo/endo product ratio as high as about 200 (Table S2†), implying an almost exo-exclusive product distribution. Overall, we find that there is a high potential in achieving exo stereoselectivity for simple, terminal-substituted dienes and dienophiles in thermal conditions through a delicate control of substituent identities. We believe this extensive theoretical investigation could offer effective guidelines to achieve an accurate maneuver of the stereochemistry of Diels–Alder reactions.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the Ministry of Science and Technology (MOST) in Taiwan (MOST 105-2113-M-003-008 and MOST 106-2113-M-003-010-MY3). We thank National Center for High-performance Computing (NCHC) of Taiwan for the help on computational resources.

Notes and references

1. O. Diels and K. Alder, Justus Liebigs Ann. Chem., 2006, 460, 98–122.
2. K. Alder and G. Stein, Angew. Chem., 1937, 50, 510–519.
3. R. Hoffmann and R. B. Woodward, J. Am. Chem. Soc., 1965, 87, 4388–4389.
4. C. S. Wannere, A. Paul, R. Herges, K. N. Houk, H. F. Schaefer III and P. v R. Schleyer, J. Comput. Chem., 2007, 28, 344–361.
5. J. I. Garcia, J. A. Mayoral and L. Salvatella, Acc. Chem. Res., 2000, 33, 658–664.
6. R. B. Woodward and H. Baer, J. Am. Chem. Soc., 1944, 66, 645.
7. A. L. Ringer, M. S. Figgs, M. O. Sinnokrot and C. D. Sherrill, J. Phys. Chem. A, 2006, 110, 10822–10828.
8. S. Maity, R. Sedlak, P. Hobza and G. N. Patwari, Phys. Chem. Chem. Phys., 2009, 11, 9738–9743.
9. W. R. Roush and B. B. Brown, J. Org. Chem., 1992, 57, 3380–3387.
10. D. H. Ess and K. N. Houk, J. Am. Chem. Soc., 2007, 129, 10646.
11. M. Ge, B. M. Stoltz and E. J. Corey, Org. Lett., 2000, 2, 1927–1929.
12. G. M. Sammis, E. M. Flamme, H. Xie, D. M. Ho and E. J. Sorensen, J. Am. Chem. Soc., 2005, 127, 8612–8613.
13. T. A. Cernak and J. L. Gleason, J. Org. Chem., 2008, 73, 102–110.
14. J. Qi and W. R. Roush, Org. Lett., 2006, 8, 2795–2798.
15. K. Takeda, I. Imaoka and E. Yoshii, Tetrahedron, 1994, 50, 10839–10848.
16. S. G. Pyne, J. Safaei-G, D. C. R. Hockless, B. W. Skelton, A. N. Sobolev and A. H. White, Tetrahedron, 1994, 50, 941–956.
17. E. J. Corey and T. P. Loh, J. Am. Chem. Soc., 1991, 113, 8966–8967.
18. T. Yoon, J. Danishefsky Samuel and S. de Gala, Angew. Chem., Int. Ed. Engl., 2003, 33, 853–855.
19. M. Kawamura and K. Kudo, Chirality, 2002, 14, 727–730.
20. T. S. Powers, W. Jiang, J. Su, W. D. Wulff, B. E. Waltermire and A. L. Rheingold, J. Am. Chem. Soc., 1997, 119, 6438–6439.
21. Y. Sudo, D. Shirasaki, S. Harada and A. Nishida, J. Am. Chem. Soc., 2008, 130, 12588–12589.
22. Y.-h. Lam, P. H.-Y. Cheong, J. M. Blasco Mata, S. J. Stanway, V. Gouverneur and K. N. Houk, J. Am. Chem. Soc., 2009, 131, 1947–1957.
23. K. Maruoka, H. Imoto and H. Yamamoto, J. Am. Chem. Soc., 1994, 116, 12115–12116.
24. C. E. Cannizzaro, J. A. Ashley, K. D. Janda and K. N. Houk, J. Am. Chem. Soc., 2003, 125, 2489–2506.
25. A. Heine, E. A. Stura, J. T. Yli-Kauhaluoma, C. Gao, Q. Deng, B. R. Beno, K. N. Houk, K. D. Janda and I. A. Wilson, Science, 1998, 279, 1934.
26. K. A. Ahrendt, C. J. Borths and D. W. C. MacMillan, J. Am. Chem. Soc., 2000, 122, 4243–4244.
27. K. Ishihara and K. Nakano, J. Am. Chem. Soc., 2005, 127, 10504–10505.
28. T. Kano, Y. Tanaka and K. Maruoka, Org. Lett., 2006, 8, 2687–2689.
29. H. Gotoh and Y. Hayashi, Org. Lett., 2007, 9, 2859–2862.
30. J.-L. Li, T.-Y. Liu and Y.-C. Chen, Acc. Chem. Res., 2012, 45, 1491–1500.
31. D. Yepes, P. Perez, P. Jaque and I. Fernández, Org. Chem. Front., 2017, 4, 1390–1399.
32. B. J. Levandowski and K. N. Houk, J. Am. Chem. Soc., 2016, 138, 16731–16736.
33. B. J. Levandowski, T. A. Hamlin, R. C. Helgeson, F. M. Bickelhaupt and K. N. Houk, J. Org. Chem., 2018, 83, 3164–3170.
34. M. Node, K. Nishide, H. Imazato, R. Kurosaki, T. Inoue and T. Ikariya, Chem. Commun., 1996, 2559–2560.
35. S. A. Kozmin and V. H. Rawal, J. Org. Chem., 1997, 62, 5252–5253.
36. M. E. Jung and N. Nishimura, J. Am. Chem. Soc., 1999, 121, 3529–3530.
37. B. Boren, J. S. Hirschi, J. H. Reibenspies, M. D. Tallant, D. A. Singleton and G. A. Sulikowski, J. Org. Chem., 2003, 68, 8991–8995.
38. G. M. Ho, C. J. Huang, E. Y. Li, S. K. Hsu, T. Wu, M. M. Zulueta, K. B. Wu and S. C. Hung, Sci. Rep., 2016, 6, 35147.
39. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. Robb, J. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. Izmaylov, J. Bloino, G. Zheng, J. Sonnenberg, M. Hada,M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda,O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, revision C.01, Gaussian, Inc., Wallingford, CT, 2009.
40. Y. Zhao and D. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
41. W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257.
42. P. C. Hariharan and J. A. Pople, Theor. Chem. Acc., 1973, 28, 213.
43. J. W. Moore and R. G. Pearson, Kinetics and Mechanism, John Wiley & Sons Inc., New York, 3rd edn, 1981, Ch. 7.
44. J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027.
45. Y.-H. Lam, et al., J. Am. Chem. Soc., 2009, 131, 1947–1957.
46. F. Liu, R. S. Paton, S. Kim, Y. Liang and K. N. Houk, J. Am. Chem. Soc., 2013, 135, 15642.
47. I. Fernández, Phys. Chem. Chem. Phys., 2014, 16, 7662.
48. Z. Liu, X. Lin, N. Yang, Z. Su, C. Hu, P. Xiao, Y. He and Z. Song, J. Am. Chem. Soc., 2016, 138, 1877–1883.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8ra10438g

---