The effect of oxidation on the electronic properties of penta-graphene: first-principles calculation

Abstract

Herein, using first-principles calculations, we systematically studied the effect of oxidation on the structural and electronic properties of penta-graphene. We have found that the oxygen atom prefers to adsorb at the center of the C=C bond, and the interaction between the oxygen atom and penta-graphene is a strong chemical bond. When the oxygen coverage increases, the band gap of penta-graphene gradually widens due to the rigid up-shift of the conduction band. More importantly, we found that the oxygen molecule on the penta-graphene surface could self-decompose into oxygen atoms without any metal catalyst. Our calculated results show that penta-graphene would be chemically unstable when it is exposed to air. Therefore, from the application point of view, penta-graphene-based devices must be encapsulated or functionalized before exposure to air. Oxidized penta-graphene exhibits a large band gap, which can facilitate its application as dielectric layers in electronic devices.

---

1. Introduction

Recently, significant efforts have been devoted towards two-dimensional materials due to their novel structural and electronic properties. As is well-known, pristine graphene is a gapless semiconductor, which has limited applications in electronic devices. Various efforts have been made to design graphene-based devices by tuning its band gap. In this regard, substitution doping is a straightforward way to achieve graphene with a controllable band gap. Rafique et al.¹ found that nitrogen doping could open the band gap of graphene. The band gap could be increased if additional hydrogen atoms were adsorbed on N-doped graphene. By loading 3d metal trioxide or tetraoxide clusters onto pristine graphene or vacancy-defect graphene, Shuai's group^2,3 systematically studied the structural, electronic and magnetic properties of graphene. They found that the metal oxide clusters not only changed the electronic structures of graphene, but also introduced local magnetic moments into two-dimensional graphene. More interestingly, some metal oxide clusters could also open up the band gap; this could facilitate the practical applications of graphene in nanoelectronics, spintronics and magnetic storage devices.

Unlike graphene, penta-graphene, a new carbon allotrope, which can be obtained by exfoliation from bulk T12 carbon,⁴ has an intrinsic band gap.⁵ It has been reported that penta-graphene also exhibits interesting mechanical properties,⁵ i.e., ultrahigh ideal strength, relatively higher stability, and unusual negative Poisson's ratio. These unique properties make penta-graphene promising for potential applications in optoelectronics, photovoltaics, and electronics. Ever since penta-graphene has been proposed by Zhang et al.,⁵ there has been a rapid growth in theoretical studies, including ab initio calculations^6–9 and multiscale simulations,^10,11 to acquire an atomic-level understanding of the electronic,^6–8 magnetic,^12–14 mechanical,^15–17 and thermal^18–20 properties of penta-graphene.

In addition to penta-graphene that exhibits intrinsic properties, the derivatives of penta-graphene, such as penta-graphene nanoribbons^12,13,21 and nanotubes,^22,23 exhibit fascinating electronic properties. Rajbanshi et al.²¹ found that penta-graphene nanoribbons are direct wide-band gap semiconductors, and the variation of the band gap with the ribbon width is significantly smaller for wider ribbons. However, the band gap of penta-graphene nanoribbons decreases under uniaxial strain. It has been^12,13 shown that penta-graphene nanoribbons possess intrinsic ferromagnetism under the cooperative effect of bending strain and electric field that is useful in digital memory devices. Wang et al.²² predicted that moderate strains could drive the structural transition of the β-phase penta-graphene to the γ-phase penta-graphene. They have also reported that the band gap of penta-graphene is not sensitive to chirality; this makes penta-graphene an appealing material for applications in flexible nano-optoelectronics.

Surface modification or doping is another effective way to tune the electronic, magnetic and mechanical properties of penta-graphene. Hydrogenation and fluorination have been shown to significantly widen the band gap of penta-graphene, resulting in the transformation of penta-graphene from a semiconductor to an insulator.^24–27 More importantly, after surface functionalization, penta-graphene can withstand temperatures as high as 1000 K.²⁴ The hydrogenated penta-graphene shows a notable and unexpectedly large improvement in thermal conductivity.²⁷ In contrast, substitutional doping can reduce the band gap of penta-graphene. For example, the band gap of penta-graphene can be tuned by Si-, B-, and N-atom substitution for sp²-hybridized carbon atoms.²⁸ The strongest reduction in the band gap is observed for transition-metal substitution for either sp²- or sp³-hybridized carbon atoms, which facilitates the transformation of penta-graphene from a wide-band gap semiconductor to a narrow-band gap semiconductor.²⁹

Chemical functionalization of penta-graphene can also provide opportunities to broaden its potential applications. Guo et al.³⁰ have found that the hydrogen spillover reaction can occur at appropriate temperatures for onboard hydrogen storage systems employed in light-duty vehicles by loading Pd₄ and Ni₄ clusters onto penta-graphene. Enriquez et al.²⁹ showed that the adsorption energy of H₂ on Ti- and V-doped penta-graphene, especially for doping in sp²-hybridized C atoms, is appropriate (i.e., between −0.207 and 0.415 eV);³¹ this indicates that penta-graphene can be a promising candidate material for onboard, reversible solid-state hydrogen molecule storage. Penta-graphene has been theoretically predicted to be a promising anode material for Li-ion and Na-ion batteries with high storage capacities and fast charge/discharge rates.³² Guo et al.³³ have indicated that penta-graphene is a high-performance channel material since the intrinsic properties of penta-graphene are preserved in all-carbon vdW heterojunctions composed of penta-graphene and graphene. Moreover, owing to its novel structural characteristics, penta-graphene will likely render the process of CO oxidation autocatalytic without any metal catalyst. Krishnan et al.³⁴ have studied CO oxidation on the penta-graphene surface and found that penta-graphene is a potential, metal-free, and low-cost catalyst for low-temperature CO oxidations.

It has been reported that penta-graphene exhibited highly dynamic, thermal, and mechanical stability. Generally speaking, devices based on penta-graphene in practical applications would be exposed to air. Then, the following question arises: how does oxidation affects the electronic properties of penta-graphene? Moreover, studies on the oxidation process and the effects of oxidation on the properties of penta-graphene are still missing. Following this line of thought, we performed density functional theory calculations to study the effect of oxidation on the electronic properties of penta-graphene with different oxygen coverages. We found that the oxygen atom or molecule preferred to adsorb at the middle of the C=C bonds to form epoxides or carboxides, and the interaction between the oxygen atom or oxygen molecule and penta-graphene was strong. The calculation results showed that the band gap of penta-graphene increased with an increase in the oxygen coverage. This increase in the band gap can be attributed to the up-shift of the conduction band minimum during the oxidation of penta-graphene. These results suggest that the oxidized penta-graphene with large band gaps can be synthesized by experiment and used as dielectric layers in electronic devices. More interestingly, we showed that the oxygen molecule on the penta-graphene surface could self-decompose without any metal catalyst. On the other hand, this result indicates that penta-graphene would be chemically unstable when exposed to air. Therefore, from an application point of view, penta-graphene-based devices must be encapsulated or functionalized before being exposed to air.

2. Calculation method

First-principles calculations were performed based on the density functional theory (DFT) with generalized gradient approximation (GGA) in the form of Perdew–Burke–Ernzerhof (PBE)^35,36 for the exchange–correlation energy functionals, as implemented in the VASP code.^37–39 The interaction between the valence electrons and the nuclei as well as the effect of the core electrons were treated by the projector-augmented wave (PAW) approach.^40,41 The wave functions were expanded in a plane-wave basis set at the energy cut-off of 400 eV. Gaussian smearing with a width of σ = 0.05 eV was used in the calculations. All the atoms in the supercell were allowed to relax until the forces on each atom were smaller than 0.01 eV Å⁻¹. The supercell dimensions were kept fixed during relaxation.

To model the oxidation effect of penta-graphene, a 4 × 4 supercell was used to accommodate different geometries for the adsorptions of oxygen atoms on penta-graphene. For single-atom adsorption, some possible adsorption sites are shown in Fig. 1(a). After careful structural relaxations, structures with oxygen atom adsorption at the C=C sites were found to be energetically favorable. There are 32 C=C bonds in the 4 × 4 supercell of penta-graphene; therefore, the ratio of the oxygen atoms over the C=C bond is 1 : 32. The adsorption of different oxygen species was also studied to examine the oxidation effects when penta-graphene was exposed to air. In addition, the adsorption of oxygen molecule on penta-graphene was investigated. In the calculations, k-point sampling of the 9 × 9 × 1 Monkhorst–Pack grids in the first Brillouin zone was used.

Fig. 1 (a) The supercell and primitive cell (indicated by the shaded square) of penta-graphene. Some possible adsorption sites for oxygen atom and molecule are indicated by A, B, C and D. (b) The electronic band structure and density of states (DOS) of the primitive cell of penta-graphene obtained by the PBE (b) and HSE06 (c) calculations.

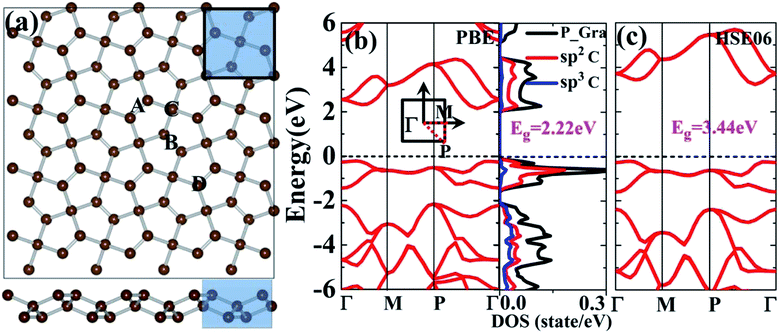
The space group of a primitive cell of tetragonal penta-graphene is P4̄2₁m. The optimized lattice constant a obtained from our calculation is 3.66 Å, which agrees well with the previous theoretical value of 3.64 Å.⁵ Fig. 1(a) shows the primitive cell (indicated by the shaded tetragon) of penta-graphene, which has two sp³- and four sp²-hybridized carbon atoms. Alternating long and short bonds are observed in penta-graphene. The calculated electronic band structure and density of states of penta-graphene are shown in Fig. 1(b). From the band structure, it is evident that the top of the valence band is located at Γ–P, and the bottom of the conduction band is located at Γ–P; this indicates the formation of a quasi-direct-band gap semiconductor. The calculated quasi-direct band gap is 2.22 eV at the GGA/PBE level, which is consistent with the previously reported GGA/PBE studies indicating a band gap of 2.29 eV.²⁸ Both the valence and the conduction bands are dominated by the sp²-hybridized carbon atoms, as observed in Fig. 1(b). Furthermore, we calculated the electronic band structure of penta-graphene using the HSE06 hybrid functional. The results are shown in Fig. 1(c). The band gap obtained by the hybrid functional HSE06 calculation is 3.44 eV, which is consistent with the previously reported hybrid functional calculations (i.e., 3.25 eV).⁵ Note that the electronic band structure of penta-graphene obtained by the PBE calculation is similar to the band structures obtained by the HSE06 calculations, except for an almost rigid shift in the conduction band. Furthermore, it has been shown that when different exchange–correlation functionals are used, the trend of the band gap change remains unaffected.²⁸ Therefore, the trend of the band gap change obtained via the current GGA-PBE calculations should be similar to those obtained via the hybrid functionals. The results and discussions provided hereinafter are based on the results obtained via the GGA-PBE calculations.

Although a hybrid functional may provide more accurate adsorption energies, for the oxygen adsorption system studied herein, which contains about ∼100 atoms in the supercell, the hybrid functional HSE calculation is still very time-consuming. We have found that the PBE calculation overestimates the adsorption energies. But the trend of the adsorption energy is not dependent on the choice of the exchange–correlation functional. Therefore, the PBE calculations can provide a reasonable trend of the adsorption energies.

3. Results and discussion

3.1 Adsorption of oxygen atoms

For single oxygen atom adsorption, only two stable adsorption structures (i.e., A and B sites) are obtained since other possible adsorption sites are relaxed into the A and B sites after optimization. These two structures are referred to as O/P_Gra_A and O/P_Gra_B. The adsorption energies for the oxygen atom adsorption are defined as

E_ads = E_{O/P_Gra} − E_O − E_{P_Gra}

where E_{O/P_Gra} and E_{P_Gra} are the total energies with and without oxygen atom adsorption, and E_O is the energy per oxygen atom in a molecule of oxygen. The adsorption energies of the oxygen atom at the A and B sites have been calculated to be −1.83 and 2.17 eV, respectively, which indicate that the oxygen atom adsorption is exothermic for adsorption at the A site, and the A site is the energetically favorable site. In contrast, adsorption at the B site is not energetically favorable due to the positive adsorption energy. The calculated bond lengths of C=C and C–C in the structures of O/P_Gra_A and O/P_Gra_B are 1.46 Å and 1.58 Å and 1.40 Å and 1.52 Å, respectively, which are relatively larger than those obtained in pristine penta-graphene (i.e., 1.34 Å (C=C) and 1.55 Å (C–C)). These calculated results show that the adsorption of the oxygen atom elongates the original carbon–carbon bond and weakens the interaction between carbon–carbon bonds in penta-graphene. We also examined the bond lengths of the C–O bonds and found that the bond length of the C–O bond in O/P_Gra_A was shorter than that in O/P_Gra_B, as shown in Table 1. This indicates that the interaction between the oxygen atom and penta-graphene is stronger in O/P_Gra_A than that in O/P_Gra_B. This finding is consistent with the abovementioned energy analysis, which shows that the oxygen atom prefers to adsorb at the A site of penta-graphene.

Table 1 Adsorption energy (eV), dipole moment (debye), magnetic moment (μ_B), charge transfer (electron), band gap (eV), and distance (Å) for the C–O, C=C, and C–C bonds

	Eads (eV)	p (debye)	M (μB)	Δq (e)	Eg (eV)	dC–O (Å)	dC=C (Å)	dC–C (Å)
P_Gra	—	—	—	—	2.22	—	1.34	1.55
O/P_Gra_A	−1.83	0.42	0.00	0.83	2.21	1.43	1.46	1.58
O/P_Gra_B	2.17	0.80	0.00	0.66	2.04	1.54	1.40	1.52
O2/P_Gra_D1	−2.28	2.13	0.00	1.01	2.08	1.20	2.56	1.64
O2/P_Gra_D2	−1.82	0.83	0.00	0.85	2.20	1.43	1.46	1.58
O2/P_Gra_M1	−0.79	0.98	0.00	0.49	2.21	1.45	1.50	1.61
O2/P_Gra_M2	−0.01	0.02	2.00	0.04	1.86	4.33	1.34	1.55

---

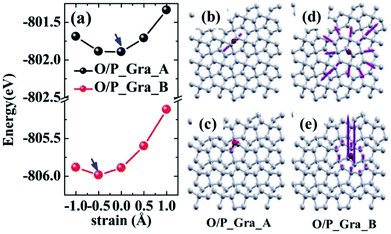
Moreover, the biaxial strains and lattice distortions of penta-graphene induced by the adsorption of oxygen atoms were investigated. The calculated results show that the lattice parameters of penta-graphene remain unchanged for the adsorption of the oxygen atom at the A site (i.e., O/P_Gra_A). However, the lattice parameters of penta-graphene become smaller for the oxygen atom adsorption at the B site (i.e., O/P_Gra_B), as can be observed in Fig. 2(a). In the case of O/P_Gra_A, the total energy exhibits the minimum at zero biaxial strain. Therefore, the lattice parameters of penta-graphene remain almost unchanged after oxygen adsorption. However, for the O/P_Gra_B configuration, the total energy minimum was changed from the zero biaxial strain to a 0.5% compressive strain, as can be observed in Fig. 2(a) (indicated by the blue arrow). This calculation result indicates that the adsorption of the oxygen atom would change the lattice parameters of penta-graphene; however, these changes are negligible. To observe the lattice distortion of penta-graphene, we also plotted the in-plane and out-of-plane lattice distortions of the penta-graphene layer upon the adsorption of the oxygen atom. These maximum in-plane distortions are about 0.4% and 0.6% of the bond length of C=C bonds in penta-graphene for O/P_Gra_A and O/P_Gra_B, respectively. To more clearly see the distortions, the displacements indicated by the purple arrows in the plots have been enlarged by a factor of 300 for the in-plane and by a factor of 35 for the out-of-plane distortion for better visualization. The distortion patterns (or strain field) in the penta-graphene layer caused by the adsorption of the oxygen atom at the A and B sites are very similar and are mainly localized at the carbon atoms surrounding the oxygen atom. However, the distortion in O/P_Gra_B is larger than that in O/P_Gra_A, as observed in Fig. 2(b)–(e), especially for the out-of-plane lattice distortions. The larger deformations of penta-graphene for O/P_Gra_B would require more energy, leading to lower stability. The deformation analysis agrees well with the abovementioned adsorption energy. Again, these results indicate that the O/P_Gra_A configuration is more energetically favorable than the O/P_Gra_B configuration.

Fig. 2 (a) The biaxial strains of O/P_Gra_A and O/P_Gra_B as a function of the total energy. (b)–(e) In-plane and out-of-plane lattice distortions of the penta-graphene layer due to the adsorption of the oxygen atom. The arrow lengths represent the amplitudes of distortion, and the arrow directions represent the direction of distortion. The displacements have been enlarged by a factor of 300 for the in-plane and 35 for the out-of-plane distortion for clear visualization.

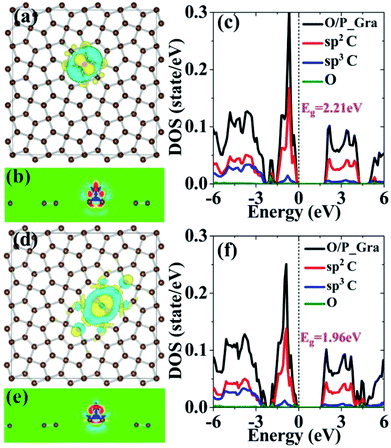
Charge transfer is an important parameter to investigate the interaction between the adsorbates and the substrate. Therefore, we have also calculated charge transfer for the adsorption of oxygen on penta-graphene by the Bader analysis.⁴² The Bader charge analysis revealed that there were 0.83 and 0.66 electrons for charge transfer from penta-graphene to the oxygen atom, as listed in Table 1, for the structures of O/P_Gra_A and O/P_Gra_B, respectively; this analysis result was consistent with the abovementioned results of the energy and structural analysis; the stronger interaction between the oxygen atom and penta-graphene could be attributed to the more charge transfer from penta-graphene to the oxygen atom. The interaction as well as charge transfer can also be qualitatively observed from the interaction charge density difference, as shown in Fig. 3(a) and (d). The interaction charge density difference Δρ(r) is defined as the difference between the charge density of the adsorption system and the charge densities of pristine penta-graphene and an isolated oxygen atom, i.e., Δρ(r) = ρ(r) − ρ_{P_Gra}(r) − ρ_O(r), calculated using the same supercell and setups. This charge density difference accounts for charge redistribution due to the interaction between different atoms. The golden color in the plot indicates an increase in the electron density, and the blue color indicates a loss in the electron density loss. It can be clearly seen that the oxygen atom gains more electrons from penta-graphene. According to the 3D charge density difference contour shown in Fig. 3(a) and (d), the interaction charge densities are mainly located at the oxygen atom and its nearest carbon atoms. Compared to the interaction charge density of O/P_Gra_B, the interaction charge density of O/P_Gra_A is relatively localized. As evident from Fig. 3(b), there are noticeable bonding charge distributions between the oxygen atom and its nearest carbon atoms; this suggests that there is a significant covalent bonding between the oxygen and carbon atoms that leads to larger adsorption energies for O/P_Gra_A. In comparison, the bonding charge and the degree of covalent bonding between the oxygen atom and its nearest carbon atoms are much weaker in O/P_Gra_A, as can be observed in Fig. 3(e).

Fig. 3 (a) and (d) 3D interaction charge densities with isosurface in the range from −0.008 electron per ų (cyan) to 0.008 electron per ų (golden). (b) and (e) 2D interaction charge density (color scale is in the range from −0.08 (blue) to 0.08 (red) electrons per ų), cutting through the O atoms. (c) and (f) are the electronic density of states (only the spin-up states are shown) for the adsorption of a single oxygen atom at the A and B sites of penta-graphene. Note that the electronic densities of states are normalized.

The quantitative charge transfer from penta-graphene to oxygen leads to surface dipole moment, as can be observed in Table 1. We computed the electric dipole moment p in the z direction for the unit cell of the O/P_Gra system as p = ∫(r − R_c)ρ_i+e(r)d³r, where R_c is the position of the net charge distribution in the supercell, and ρ_i+e is the charge density of the ions and valence electrons. The electronic dipole moments obtained from our calculations are listed in Table 1 and shown in Fig. 3. Evidently, the more the charge transfer from penta-graphene to the oxygen atom, the larger the electronic dipole moment obtained. The dipole moments of the O/P_Gra_A and O/P_Gra_B systems are 0.42 and 0.80 debye, respectively. Note that although the charge transfer in O/P_Gra_A is larger than that in O/P_Gra_B, the dipole moment in O/P_Gra_A is smaller than that in O/P_Gra_B. This is because charge redistribution in O/P_Gra_B is relatively delocalized; this results in a large surface dipole moment. Finally, we determined that there was no intrinsic magnetic moment in the oxygen adsorption on penta-graphene systems since the magnetic moment was zero in both the O/P_Gra_A and the O/P_Gra_B systems, as shown in Table 1.

To gain more insights into the effect of oxidation on the electronic properties of penta-graphene, we also investigated the electronic density of states of penta-graphene upon oxygen atom adsorption, as shown in Fig. 3(c) and (f). Note that only the spin-up electronic densities of states are shown due to the degeneracy of spin-up and spin-down states. For the O/P_Gra_A structure, the valence and conduction bands are also dominated by sp²-hybridized carbons; however, the p states of the oxygen atom are mainly located from −2.0 to −1.5 eV, and they do not affect the valence and conduction bands; this leads to an almost unchanged band gap. However, when the oxygen atom adsorption occurs at the B site, the p states of the oxygen atom are mainly located from −2.0 to −1.5 eV, −0.5 to 0.0 eV, and 4.0 to 5.0 eV. Especially, for the p states within the energy window from −0.5 to 0.0 eV, the width of the valences band broadens, and the band gap narrows down to 2.04 eV. These calculation results show that the adsorption of the oxygen atom on penta-graphene may change penta-graphene from a wide-band gap semiconductor to a narrow-band gap semiconductor for physisorption.

3.2 The effects of the oxygen adsorption concentration

To examine the effect of oxidation on the electronic properties of penta-graphene with different oxidation coverages, we also studied the relationship between the oxygen atom coverage and the electronic properties of penta-graphene. As abovementioned, the adsorption of the oxygen atom at the A site (i.e., C=C bond center) is stable. Therefore, based on the most stable structure for the adsorption of a single oxygen atom on penta-graphene, we placed different numbers of oxygen atoms at the A site to model different oxygen coverages. There are 32 C=C bonds in the 4 × 4 supercell of penta-graphene; therefore, we have defined the ratio of one oxygen atom over the C=C bonds, i.e., 1 : 32, as the coverage of one oxygen on penta-graphene. For the coverages of 8 : 32 and 16 : 32, the oxygen atoms are located on the same side of penta-graphene, whereas for the coverages of 24 : 32 and 32 : 32, the oxygen atoms are placed on both sides of penta-graphene. Furthermore, 2, 4, or 6 oxygen atoms are removed from the 32 : 32 structures for obtaining the coverages of 30 : 32, 28 : 32 and 26 : 32, respectively. Therefore, the oxygen coverages of 25%, 50%, 75%, 81.25%, 87.5%, 93.75%, and 100% could be obtained.

At first, we examined the adsorption energy as a function of oxygen coverage, as shown in Fig. 4(a). It is found that the adsorption energy per oxygen atom becomes smaller as the oxygen coverage increases; this indicates that the interaction between charged oxygen atoms is repulsive, and thus, a partial amount of the adsorption energy is consumed. The Bader analysis shows that each oxygen atom gains 0.82 electrons from penta-graphene for different coverages of oxygen atom adsorption on penta-graphene; this leads to negatively charged oxygen atoms. As abovementioned, the charge transfer from penta-graphene to oxygen atoms causes surface dipole moments. As a result, when the oxygen coverage expands, the dipole moments of the systems would enlarge. We found that the dipole moments of oxygen on the penta-graphene surface firstly increased and achieved maximum at 50% coverage; then, they gradually decreased and finally reached zero, as shown in Fig. 4(b). This is because the oxygen atoms can absorb on both sides of penta-graphene, and each site possesses 16 C=C bonds. When these 16 adsorption sites are saturated, the oxygen atom would absorb at the other sites of penta-graphene. Therefore, the surface dipole moment of one side of penta-graphene would be compensated by that of the other side of penta-graphene; this would lead to a net zero dipole moment in the system when all the C=C bonds are occupied by the O atoms.

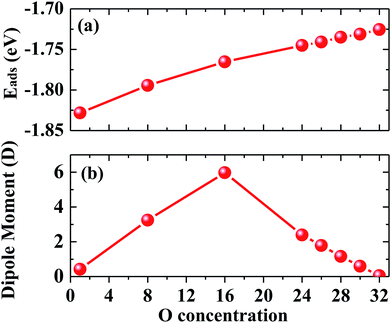Fig. 4 (a) Adsorption energy and (b) dipole moments for the adsorption of oxygen atoms on penta-graphene as a function of oxygen atom coverage.

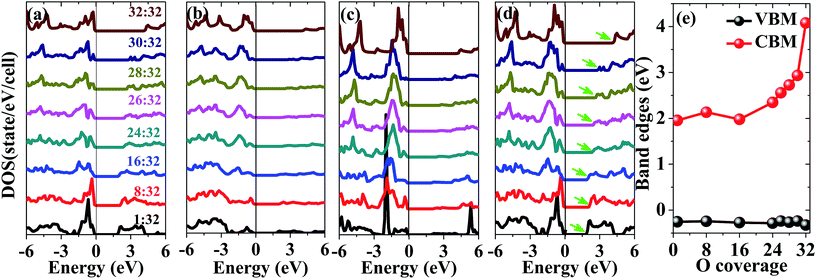
The electronic density of states as a function of oxygen coverage is studied to gain more insights into the effect of oxidation on the electronic properties of penta-graphene. The partial electronic density of states of sp²- and sp³-hybridized carbon atoms and oxygen atoms as well as the total electronic density of states of the entire system are shown in Fig. 5(a)–(d). Different coloured lines represent different oxygen coverages, and the oxygen coverage is gradually increased from the bottom to the top in the plot. In Fig. 5(a), it is evident that the p states of the sp²-hybridized carbon atoms are mainly located at 1.7 eV below the Fermi level, and the peak of the p states of the sp²-hybridized carbon atom is sharp; this indicates that the intensity of the p states is strong for the adsorption of a single oxygen atom on the penta-graphene surface. When the oxygen coverage increases, it is found that the peak of the p states of sp²-hybridized carbon splits into two peaks, and the intensities of the peaks weaken. Furthermore, note that the center of the p states of the sp²-hybridized carbon atoms is closer to the Fermi level. More detailed information is shown in Fig. 5(a). The p states of the sp³-hybridized carbon atoms are mainly below the Fermi level, and the intensity increases when the oxygen coverage increases since numerous sp²-hybridized carbon atoms are gradually destroyed; this can clearly observed in Fig. 5(b). Note that the trend of the peaks of the p states of oxygen atoms is similar to that of the peak of the p states of sp²-hybridized carbon atoms. The peak of the p states of the oxygen atoms becomes broader, and the center of the p states of the oxygen atoms is closer to the Fermi level, as shown in Fig. 5(c); this indicates strong hybridizations between the oxygen atoms and sp²-hybridized carbon atoms.

Fig. 5 (a)–(d) Density of states (DOS) for different oxygen atom coverages on penta-graphene. (a) The p states of sp²-hybridized carbon atoms. (b) The p states of sp³-hybridized carbon atoms. (c) The p states of the oxygen atoms. (d) Total density of states of the entire system. Note that all the densities of states are normalized. (e) The band edges as a function of oxygen coverage.

Fig. 5(d) shows the total density of states of the entire system as a function of the increase in the oxygen coverage. We found that the top of the valence band was below the Fermi level and remained almost unchanged with an increase in the oxygen coverage; on the other hand, the bottom of the conduction band shifted upward; this led to a large band gap. The underlying reason for this increase in the band gap of the entire system is attributed to the rigid upward shift of the p anti-bonding orbital of the sp²-hybridized carbon atoms, as shown in Fig. 5(a). If the band edges are plotted as a function of oxygen coverage, it can be clearly seen that the maximum of the valence band remains almost unchanged, whereas the minimum of the conduction band gradually shifts to higher energy with an increase in the oxygen coverage, as shown in Fig. 5(e). This finding suggests that the increase in the band gap makes the oxidized penta-graphene become an insulator. This feature can be exploited for the potential uses of the oxidized penta-graphene as dielectric layers in electronic devices.

Note that the effects of oxidation and oxidation process can be observed in the experiments for a wide range of oxygen coverages. On the other hand, from the practical application point of view, devices based on penta-graphene would be supported by substrates; therefore, it may be difficult to adsorb oxygen atoms on both sides of penta-graphene. However, it has been shown that the interaction between penta-graphene and its substrate is weak and has vdW interaction character in the electronic devices based on penta-graphene.³³ Therefore, the oxygen molecule or atom can diffuse into both sides of penta-graphene. Although the interactions between penta-graphene and its substrate are stronger, the oxygen molecule or atoms can also adsorb on and diffuse into the bare surface of penta-graphene in the devices. Therefore, the oxygen coverage studied herein can be realized in experiments.

As abovementioned, penta-graphene would be chemically unstable upon exposure to air. To obtain air-stable penta-graphene devices, penta-graphene should be fully encapsulated. Encapsulation layers, such as graphene, transition metal dichalcogenides, hexagonal boron nitride (h-BN), etc., with novel electronic properties are candidate materials for device design: for example, an electronic device with an all-carbon heterojunction composed of graphene and penta-graphene,³³ where penta-graphene is fully encapsulated by inert graphene. From an experimental point of view, penta-graphene can be dried on some substrates, stored in a low-temperature environment, or a liquid-phase method can be used to disperse the prepared penta-graphene in some liquids to avoid oxygen contact.

3.3 Adsorption of the oxygen molecules

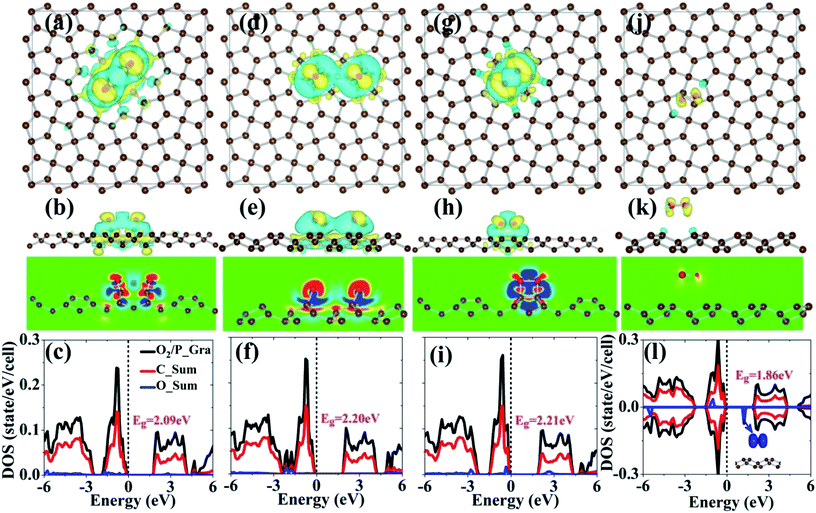
We finally examined the adsorption structure of one oxygen molecule on the surface of penta-graphene. All the possible adsorption sites are schematically shown in Fig. 1(a). For the adsorption of oxygen molecules on penta-graphene, two types of motifs were considered: dissociated adsorption mode and molecular adsorption mode, as shown in Fig. 6. For the dissociated adsorption mode, the oxygen molecule dissociates into oxygen atoms to form the carboxide and epoxide groups, which are referred to as O₂/P_Gra_D1 and O₂/P_Gra_D2, respectively. Herein, D represents the dissociated adsorption mode. In the case of the molecular adsorption mode, the oxygen molecule is horizontally adsorbed on the convex and concave C=C bonds. The shape of the oxygen molecule is still maintained after structural relaxation. We referred them as O₂/P_Gra_M1 and O₂/P_Gra_M2, where M represents the molecular adsorption mode.

Fig. 6 ((a) and (b), (d) and (e), (g) and (h), and (j) and (k)) 3D interaction charge density with isosurface in the range from −0.008 electron per ų (cyan) to 0.008 electron per ų (golden); ((b), (e), (h), and (k)) 2D interaction charge density (color scale is from −0.04 (blue) to 0.04 (red) electrons per ų), cutting through O atoms; and ((c), (f), and (i)) electronic density of states (only the spin-up state is shown) of the oxygen molecule adsorption on the penta-graphene surface. (l) Spin-polarized electronic density of states of the oxygen molecule on the penta-graphene surface. Inset shows the spin-polarized charge density of the oxygen molecule on penta-graphene. Note that the electronic densities of states are normalized.

The calculated adsorption energies of O₂/P_Gra_D1, O₂/P_Gra_D2, O₂/P_Gra_M1, and O₂/P_Gra_M2 are −2.28, −1.82, −0.79, and −0.01 eV, respectively. Accordingly, the C=C bond center is the most stable adsorption site for the adsorption of the oxygen molecule on the penta-graphene surface. Note that the oxygen molecule on penta-graphene prefers to dissociate into oxygen atoms after structural relaxation since the adsorption energy of the dissociated oxygen is much lower than that of molecular oxygen by 1.0–1.5 eV, as listed in Table 1. These results show that the oxygen molecule can self-decompose on penta-graphene without a metal catalyst. The dissociated oxygen atoms obtained from the molecule chemically adsorb on the surface of penta-graphene with the adsorption energy of −2.28 eV. Therefore, it is difficult to desorb the dissociated oxygen atoms. From this point of view, penta-graphene is not a metal-free catalyst for the decomposition of an oxygen molecule; however, it is good for the decomposition of the oxygen molecule because the process of oxygen molecule dissociation is barrier-less. These results show that the oxygen molecule can self-decompose on penta-graphene without any catalysts. Although the oxygen molecule is decomposed into two oxygen atoms in the structures of O₂/P_Gra_D1 and O₂/P_Gra_D2, two carboxide and epoxide groups are formed between the oxygen atoms and carbon atoms, respectively, as shown in Fig. 6(a) and (d). Note that the structure with the oxygen molecule on top of the C=C bond proposed by Krishnan et al.³⁴ (Fig. 6(g)) is not energetically favorable as compared to that of the dissociated oxygen molecule. However, for the structure proposed by them, the adsorption energy of O₂ based on our calculations is −1.58 eV, which is consistent with the adsorption energy reported by them. The bond lengths of O–O are 1.51 and 1.24 Å for the O₂/P_Gra_M1 and O₂/P_Gra_M2 structures, respectively, suggesting that the interaction between the oxygen and the carbon atoms weakens the strength of the O–O bond in O₂/P_Gra_M1. However, as shown in Fig. 6(j), the oxygen molecule on penta-graphene would undergo physisorption since the adsorption energy is extremely small.

The larger adsorption energy can be explained by the structural parameters of various bonds, i.e., C–O, C=C, and C–C bonds, as shown in Table 1. The bond lengths of C–O are 1.20, 1.43, 1.45, and 4.33 Å in the geometries of O₂/P_Gra_D1, O₂/P_Gra_D2, O₂/P_Gra_M1, and O₂/P_Gra_M2, respectively, showing that the interaction between the oxygen and carbon atoms gradually becomes weak. The stronger interaction between the oxygen and the carbon atoms induces much larger distortion in the C–C and C=C bonds in penta-graphene, whereas a weak interaction leads to perfect single and double bonds in penta-graphene, especially in the O₂/P_Gra_M2 structure, as listed in Table 1. There are some relationships between the adsorption energy and the charge transfer. The larger adsorption energy can be attributed to the larger amount of charge transfer from penta-graphene to the oxygen atoms. The quantitative Bader analysis reveals that each oxygen atom gains 1.01, 0.85, 0.49, and 0.04 electrons from penta-graphene, again indicating that O₂/P_Gra_D1 is the most stable structure, whereas the O₂/P_Gra_M2 structure exhibits physisorption characteristics. The larger amount of charge transfer results in large dipole moments in the system. The electronic dipole moments in the O₂/P_Gra_D1, O₂/P_Gra_D2, O₂/P_Gra_M1, and O₂/P_Gra_M2 structures are 2.13, 0.83, 0.98, and 0.02 debye, respectively, as listed in Table 1.

The interaction between the oxygen molecule and penta-graphene is also evident from the interaction charge density, as shown in Fig. 6. The interaction charge densities for all the systems are localized and mainly located at the oxygen atoms and their nearest carbon atoms, except for the structure of O₂/P_Gra_M2 that exhibits weaker interactions and physisorption characteristics. For clearer visualization, we plotted the 2D interaction charge density distribution cutting through the C–O bonds or O–O bonds, as shown in Fig. 6(b), (e), (h) and (k). From the plot, it is evident that there are significant charge densities between the oxygen and carbon atoms, as shown in Fig. 6(b), (e) and (h), whereas there is almost no net charge density distribution between the oxygen molecule and penta-graphene, as shown in Fig. 6(k); this indicates weaker interactions in O₂/P_Gra_M2; this is consistent with the abovementioned analysis.

Note that except for the physisorption of the oxygen molecule, there is no net magnetic moment. Therefore, for the electronic properties of penta-graphene, only the spin-up states are shown hereinafter. Finally, we also studied the electronic structures of penta-graphene when the oxygen molecule was adsorbed on the penta-graphene surface. The calculated electronic density of states are shown in Fig. 6(c), (f), (i) and (l). For the O₂/P_Gra_D1 structure, the p states of the oxygen atoms and the p states of the carbon atoms are strongly hybridized in the energy window from −2.0 to 0.0 eV. The p states of the oxygen atom occupy the top of the valence band; this leads to a relatively smaller band gap as compared to that of pristine penta-graphene. In the case of O₂/P_Gra_D2, the p states of the oxygen atoms are located at the bottom of the valence band below the Fermi level, i.e., from −1.5 to −2.0 eV, and they do not affect the band edges. Therefore, the band gap remains almost unchanged in the O₂/P_Gra_D2 structure. The p states of the oxygen atoms are below the Fermi level and at −0.5 eV, and the band edges of penta-graphene are not affected by the adsorption of the oxygen molecule. For oxygen molecule physisorption, the net magnetic moment originates from the oxygen molecule, and the net spin-polarized charge density is mainly located at the oxygen molecule, as shown in the inset in Fig. 6(l). The p states of the oxygen molecule are located from −5.7 to −5.3 eV, −1.3 to −0.88 eV, and 1.1 to 1.3 eV. The states in the energy window of 1.1–1.3 eV are above the Fermi level and located at the band gap of penta-graphene. The presence of the oxygen molecule gap states reduces the band gap of penta-graphene to 1.86 eV; this converts penta-graphene from a wide-band gap semiconductor to a small-band gap semiconductor. By careful experimental techniques, physisorption of the oxygen molecule can be achieved to meet the band gap requirements for various device applications.

4. Conclusions

In summary, we performed the density functional theory calculations to study the effect of oxidation on the structural and electronic properties of penta-graphene. Our results demonstrate that the C=C bond center is the most stable adsorption site, and the oxygen atom prefers to form an epoxide group on the penta-graphene surface. When the oxygen coverage increases, the band gap of penta-graphene increases. This opens up a possible way for researchers to synthesize oxidized penta-graphene with large band gaps for use as dielectric layers in electronic devices. We have also found that the process of oxygen molecule dissociation is barrier-less; this indicates that the oxygen molecule can self-decompose on penta-graphene without any catalysts. More importantly, penta-graphene would be chemically unstable when exposed to air; this would lead to the formation of oxidized penta-graphene. In penta-graphene-based devices, penta-graphene must be encapsulated by an inert layer, such as graphene, h-BN, etc. We believe that our theoretical studies will inspire experimental studies on the oxidation of penta-graphene or the encapsulation of penta-graphene, which can then be used as a potential candidate for future generation nanoelectronics and optical devices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the support provided by the National Natural Science Foundation of China under Grant No. 11574044, and the Fundamental Research Funds for the Central Universities. The calculations were also performed on TianHe-1(A) at the National Supercomputer Center in Tianjin.

References

1. R. Muhammad, Y. Shuai and H.-P. Tan, Phys. E, 2017, 88, 115–124.
2. R. Muhammad, Y. Shuai, H.-P. Tan and H. Muhammad, Appl. Surf. Sci., 2017, 399, 20–31.
3. R. Muhammad, Y. Shuai, H.-P. Tan and H. Muhammad, Appl. Surf. Sci., 2017, 408, 21–33.
4. Z. Zhao, F. Tian, X. Dong, Q. Li, Q. Wang, H. Wang, X. Zhong, B. Xu, D. Yu, J. He, H. Wang, Y. Ma and Y. Tian, J. Am. Chem. Soc., 2012, 134, 12362–12365.
5. S. Zhang, J. Zhou, Q. Wang, X. Chen, Y. Kawazoe and P. Jena, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2372–2377.
6. Z. Wang, F. Don, B. Shen, R. Zhang, Y. Zheng, L. Chen, S. Wang, C. Wang, K. Ho, Y. Fan, B. Jin and W. Su, Carbon, 2016, 101, 77–85.
7. G. R. Berdiyorov and M. E. Madjet, RSC Adv., 2016, 6, 50867.
8. H. Einollahzadeh, R. S. Dariani and S. M. Fazeli, Solid State Commun., 2016, 229, 1–4.
9. F. Wang, J. Yu, Q. Wang, Y. Kawazoe and P. Jena, Carbon, 2016, 105, 424–429.
10. S. Winczewski, M. Y. Shaheen and J. Rybicki, Carbon, 2018, 126, 165–175.
11. M. Chen, H. Zhan, Y. Zhu, H. Wu and Y. Gu, J. Phys. Chem. C, 2017, 121, 9642–9647.
12. C. He, X. F. Wang and W. X. Zhang, Phys. Chem. Chem. Phys., 2017, 19, 18426–18433.
13. P. F. Yuan, Z. H. Zhang, Z. Q. Fan and M. Qiu, Phys. Chem. Chem. Phys., 2017, 19, 9528–9536.
14. Y. Aierken, O. Leenaerts and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2016, 94, 155410.
15. H. Sun, S. Mukherjee and C. V. Singh, Phys. Chem. Chem. Phys., 2016, 18, 26736–26742.
16. Y. Zhang, Q. Pei, Z. Sha, Y. Zhang and H. Gao, Nano Res., 2017, 10, 3865–3874.
17. S. W. Cranford, Carbon, 2016, 96, 421–428.
18. F. Wang, J. Liu, X. Li, Q. Wang and Y. Kawazoe, Appl. Phys. Lett., 2017, 111, 192102.
19. X. Wu, V. Varshney, J. Lee, T. Zhang, J. L. Wohlwend, A. K. Roy and T. Luo, Nano Lett., 2016, 16, 3925–3935.
20. Y. Zhang, Q. Pei, Y. Cheng, Y. Zhang and X. Zhang, Comput. Mater. Sci., 2017, 137, 195–200.
21. B. Rajbanshi, S. Sarkar, B. Mandal and P. Sarkar, Carbon, 2016, 100, 118–125.
22. Z. Wang, X. Cao, C. Qiao, R. J. Zhang, Y. X. Zheng, L. Y. Chen, S. Y. Wang, C. Z. Wang, K. M. Ho, Y. Fan, B. Jin and W. Su, Nanoscale, 2017, 9, 19310.
23. J. J. Quijano-Briones, H. N. Fernández-Escamilla and A. Tlahuice-Flores, Comput. Theor. Chem., 2017, 108, 70–75.
24. X. Li, S. Zhang, F. Q. Wang, Y. Guo, J. Liu and Q. Wang, Phys. Chem. Chem. Phys., 2016, 18, 14191.
25. J. J. Quijano-Briones, H. N. Fernandez-Escamilla and A. Tlahuice-Flores, Phys. Chem. Chem. Phys., 2016, 18, 15505.
26. L. Liu, Y. Wang, C. Chen, H. Yu, L. Zhao and X. Wang, RSC Adv., 2017, 7, 40200.
27. X. Wu, V. Varshney, J. Lee, T. Zhang, J. L. Wohlwend, A. K. Roy and T. Luo, Nano Lett., 2016, 16, 3925–3935.
28. G. R. Berdiyorov, G. Dixit and M. E. Madjet, J. Phys.: Condens. Matter, 2016, 28, 475001.
29. J. I. G. Enriquez and A. R. C. Villagracia, Int. J. Hydrogen Energy, 2016, 41, 12157–12166.
30. J. Guo, D. Liu, X. Li, H. Liu and G. Chen, Int. J. Hydrogen Energy, 2018, 43, 2247–2255.
31. R. C. Lochan and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 1357–1370.
32. B. Xiao, Y. Li, X. Yu and J. Cheng, ACS Appl. Mater. Interfaces, 2016, 8, 35342.
33. Y. Guo, F. Q. Wang and Q. Wang, Appl. Phys. Lett., 2017, 111, 073503.
34. R. Krishnan, W. Su and H. Chen, Carbon, 2017, 114, 465–472.
35. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
36. G. Makov and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014–4022.
37. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
38. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
39. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
40. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
41. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
42. G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360.

---

Footnote

† These authors contributed equally.

---