Binding thiourea derivatives with dimethyl methylphosphonate for sensing nerve agents

Abstract

In an effort to develop efficient substrates to sense organophosphonate nerve agents, we used the density-functional theory calculations to determine binding energies and geometries of 1 : 1 complexes formed between dimethyl methylphosphonate (DMMP) and 13 thiourea derivatives (TUn), including four newly-synthesized ones (n = 10–13). The four new thiourea derivatives have a 3,5-bis-(trifluoromethyl)phenyl group as one N-substituent and an alkylphenyl group with zero to three methylene linkages as the other N-substituent. The calculated geometries show that intermolecular double H-bonding is the most important factor influencing the formation of stable complexes at the molecular level. When the calculated binding energies were compared with the receptor efficiencies of the corresponding TUn substrates in a quartz crystal microbalance (QCM), a high degree of correlation was found. However, deviations from the correlation trend were found for a few TUn. We explained the deviations with a series of real time diffuse reflectance IR spectra as well as the calculated geometries. The most efficient receptor, determined from the QCM analysis and the IR spectroscopy, was TU13, in which three methylene linkages may provide an extra flexibility in the side chain. However, the calculated binding energy of the TU13 complex was small as a folded geometry of the bare TU13 hindered the double H-bonding. In contrast, the TU13 molecules in the QCM and the IR analyses may exist in unfolded geometries that are ready to form the double H-bonding.

---

1 Introduction

Chemical warfare agents (CWAs)^1–3 may cause mass casualties when they are sprayed in terrorist or war situations. Therefore, sensing them rapidly is of critical importance for military defense, as well as for civilian safety. For the CWA sensors to be effective, substrates that can strongly bind target CWAs must be developed, but the task is not easy since handling CWAs for any test is hazardous. Therefore, a simulant which has a similar structure to a target CWA is often used to characterize the CWA sensor.

Among CWAs, tabun [GA, (CH₃)₂NPO(CN)OCH₂CH₃], sarin [GB, CH₃POFOCH(CH₃)₂], soman [GD, CH₃POFOCHCH₃C(CH₃)₃], and VX [{(CH₃)₂CH}₂NCH₂CH₂SPOCH₃OC₂H₅] are classified as the nerve agents⁴ which disrupt message transfer mechanism in living creatures. They belong to the organophosphonate group of chemicals and have a moiety (–P(O)–O–) that can work as a good hydrogen bond acceptor. Therefore, Brönsted acid type molecules have been considered as the effective binder to sense nerve agents or their simulants.^5,6

A popular simulant for the nerve agents is dimethyl methylphosphonate [DMMP, CH₃PO(OCH₃)₂]. This molecule is classified as a schedule 2 chemical, since it may be used in the production of CWAs. DMMP is relatively nontoxic^7,8 and is used for numerous industrial applications, such as a flame retardation. Since the structure of DMMP includes the phosphonate moiety, strong binders for DMMP are likely to work effectively for sensing the nerve agents.

Thiourea (H₂NCSNH₂) or its derivatives can generally bind the organophosphonates well through a H-bonding between thioureic hydrogens and phosphonate oxygen.^9–11 To enhance the H-donating property, Hammond et al.¹² synthesized N-3,5-bis-(trifluoromethyl)phenyl substituted thiourea and used it as a major receptor for sensing DMMP in multilayered carbon nanotube substrates. Hiscock et al.¹³ used the ¹H NMR titration method to investigate the binding ability of thiourea derivatives in which thiourea (TU) was structurally modified with various negatively charged N-aryl group.

More recently, some of us synthesized a different list of thiourea derivatives and tested their coated films for sensing DMMP.¹⁴ The synthesized thiourea derivatives in the previous work, namely TUn (n = 1–9) series, are shown in Scheme 1. The test results employing quartz crystal microbalance (QCM) and ¹H-NMR spectroscopy can be summarized as follows: (1) N-benzyl substitution (as in TU4) induced the higher sensing efficiency than N-phenyl (TU1), N-n-butyl (TU2), or N-cyclohexyl substitutions (TU3); (2) introducing electron-withdrawing fluoro group (as in TU5) or electron-donating methoxy group (as in TU6) to para position of the N-benzyl group did not change the sensing efficiency significantly; and (3) the symmetric thiourea derivative with N-benzyl substitutions at both branches (as in TU7) reduced the sensing efficiency probably because of increased self-aggregation.

Scheme 1 DMMP and thiourea derivatives in this study.

Perhaps, strength of binding between each thiourea derivative and DMMP is a major factor for the trend in the experimental observations, while other properties such as self-aggregation should not be neglected. In this respect, a computational approach to find structures, energies, and other features of the binding complexes would be useful. The computational method we adopted for this purpose was the density functional theory (DFT), the method considered to be the most efficient and practical for the size of molecular system in this study. Although they may not be as accurate in determination of energies as higher level calculations based on wave function, the DFT calculations usually give correct structures. For the structures of weakly bound complexes as in this study, the weakness of the DFT calculation in describing long-ranged correlation effect can be complimented by additional dispersion interaction terms.¹⁵

The computation provides a variety of molecular level information in the isolated state, while the sensing experiments use substrates in various forms. Therefore, the results from the computation may miss some binding properties in real state of sensors. Yet, it would be interesting to know whether the sensing efficiency is closely related to the molecular level interaction provided by the computation. If so, the computation would be useful to design receptor molecules for sensing inaccessible nerve gases.

In this work, we first compared the binding energies of TUn (n = 1–9) calculated from the DFT method with the sensing efficiencies obtained from the previous work.¹⁴ The results from the DFT calculation and the QCM experiment matched excellently, as shown in a later section. This motivated us to test new thiourea derivatives, TUn (n = 10–13, shown in Scheme 1), both computationally and experimentally. The new series have a 3,5-bis-(trifluoromethyl)phenyl (abbreviated as in TFMP) group at one of the N-branches, while the other N-branch is an alkyl phenyl group [(CH₂)_m-phenyl, where m = 0, 1, 2, 3 for TU10, TU11, TU12, TU13, respectively]. In this series, CF₃ functionalized-phenyl group was expected to render stronger hydrogen donor ability than phenyl or benzyl groups, and the different number of methylene linkages was expected to provide variable structural flexibility. The TFMP substituted thiourea has been used as effective organic catalysts,¹⁶ possibly because of involvement of highly polar ortho-CH bond in the complexation.¹⁷

2 Methods

2.1 Sample preparation and QCM test

All chemicals were purchased from Sigma-Aldrich or Tokyo Chemical, and used without further purification. TU10, 11, 12 and 13 were synthesized following procedures in ref. 18–20. As shown in the previous reports,¹⁴ the QCM test can detect a trace amount of mass change by frequency shift of the crystal oscillator upon adsorption and desorption of a target molecule (i.e., DMMP). Prior to the QCM measurements, a drop (4 μL) of TUn (n = 10–13) solution in DMF (2 mg mL⁻¹) was casted for coating on the surface of a quartz crystal (8 MHz, AT cut). The TUn-coated quartz crystal was dried for an hour under vacuum and then in an oven at 80 °C for another hour to obtain a stable film. The frequency shifts were monitored in situ under nitrogen and DMMP gas flow. The concentration of the DMMP in the flow was controlled using a mass flow controller (MFC) and it was calculated according to ref. 21. As DMMP was adsorbed on the TUn-coated quartz, the resonance frequency shifted to a lower value proportional to the adsorption mass. The adsorbed DMMP molecules could be removed by purging with pure nitrogen.

2.2 Diffuse reflectance IR spectroscopy

In order to obtain information on structures of the binding complexes in real substrate, a series of IR spectra were recorded in situ as gaseous DMMP was adsorbed to a selected TUn sample. The apparatus to perform this measurement consisted of two compartments, a gas introduction compartment and an IR spectroscopy compartment. In the gas introduction compartment, a small bottle of liquid DMMP was maintained at 40 °C and bubbled with dry air (99.999%). The DMMP bubble flowed through a polytetrafluoroethylene line and was mixed with dry air from a separate line. The flow rates of the two gases were controlled individually by MFCs. (The flow rates were 20 mL min⁻¹ for the bubbled gas and 30 mL min⁻¹ for the balancing dry air.) While a major part of the gas mixture was directed into the IR spectroscopy compartment, a small fraction of it was diverted into a gas chromatography analyzer, from which the DMMP concentration was determined.

The major instrument of the IR spectroscopy compartment was an FT-IR spectrometer (Nicolet iS10, Thermo-Fisher Scientific) operating in a diffuse reflectance mode using a set of commercial accessories (Praying Mantis, Harrick). The sample compartment of the spectrometer was connected directly with the gas introduction line and was covered to prevent the sample from being exposed to ambient air. A selected TUn sample, mixed with KBr powder at a weight ratio of 1 : 19, was contained in a vessel and was pre-annealed at 110 °C for 12 h to remove moisture. Then, dry air was flowed into the sample compartment for 60 min with the rate of 50 mL min⁻¹, followed by introduction of the gas mixture for dosing DMMP. The sample in the vessel was illuminated with an IR beam at a 60° incident angle. The diffused reflection off the sample surface was collected by 6× off-axis ellipsoid mirror to enter an interferometer for Fourier transform (FT) detection. Each FT-IR spectrum was obtained in the region between 4000 and 650 cm⁻¹, with the background signal obtained from clean KBr powder.

2.3 Computation

Geometries and energies of low energy conformers of each TUn-DMMP complex or its constituent bare molecules were obtained from the following steps. In the first step, molecular dynamics (MD) calculations were performed to search for low energy geometries at the level of density-functional-tight-binding (DFTB) theory²² using a DFTB + code,²³ and at the semiempirical level using a CP2K program.²⁴

In the second step, the low energy geometries obtained from the MD calculations were used as starting geometries for final optimization at the level of DFT-D3, where D3 represents Grimme's dispersion correction.²⁵ We chose BLYP for the DFT functional since the BLYP-D3 gave minimal mean absolute deviation (MAD)²² when tested for the S22 benchmark dataset of DNA base pairs, amino acid pairs and small model complexes. As 6-31+G(d) was used for the basis set, we will refer this method to as BLYP-D3/6-31+G*.

Several low energy conformers whose energies from the DFT calculations were within 3 kcal mol⁻¹ of those of the global minimum were further analyzed. The frequencies were obtained to check if the optimized geometry was indeed at a local minimum, and they provided zero-point energy (ZPE) correction for electronic part of energy (E_e). Binding energy of complex AB is then defined as:

BE = −ΔE = E(A) – E(B) + E(AB) (1)

where E represents E_e or E₀ (=E_e + ZPE).

We also carried out the natural bond order analysis^26,27 to investigate further details of the intermolecular interaction. The results from the additional analyses are shown in the ESI,† while only core results that are directly comparable to the experimental ones are shown in the main text. A Gaussian²⁸ program was the main computational tool.

3 Results & discussion

3.1 QCM results for TUn (n = 10–13)

We first show the QCM result for the newly-synthesized TUn (n = 10–13) series for improving structural effects. As shown in Fig. 1, the frequency shift (ΔF) for TU10 was very small (−5 Hz) while that for TU13 was very large (−3200 Hz). However, caution should have been taken when preparing TU13 sample; extra drying time was needed to obtain a stable QCM oscillation.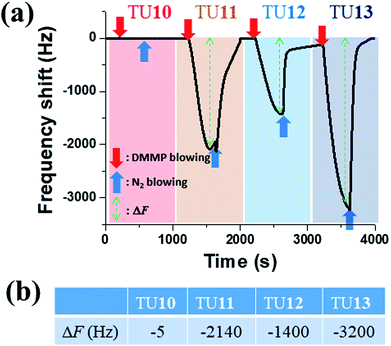

Fig. 1 The QCM response curves for TUn (n = 10–13) receptors (a) and the table for the corresponding ΔF values (b). The DMMP concentration was 60 ppm.

For comparison, the ΔF value for TU4, which was the most efficient receptor in the previous report,¹⁴ was −830 Hz. Therefore, TU13 is newly the best receptor among TUn (n = 1–13) series, followed by TU11, then TU12. It is interesting that the odd number of methylenes in the alkyphenyl substituent appeared more efficient for sensing DMMP, which suggests that not only the H-bonding strength, but also other secondary interactions in which the methylene linkage is involved play roles in the TUn-DMMP interaction.

3.2 IR spectra for TUn (n = 10–13)

Diffuse reflectance IR spectra for TUn (n = 10–13) during the DMMP adsorption are displayed in Fig. 2. Only the high wavenumber region between 2500 and 3500 cm⁻¹ is shown because any vibrations in this region are stretching modes of either C–H or N–H bonds. Each spectral window consists of a sequence of 37 spectra recorded with 5 min interval starting from 30 s after dosing DMMP. The bottom spectrum in each spectral window is the first spectrum taken at 30 s after dosing DMMP, while the top one is the last spectrum taken at 3 hours later.

Fig. 2 Diffuse reflectance IR spectra of TUn (n = 10–13) during the DMMP adsorption process. Each spectral window consists of a sequence of 37 spectra recorded with 5 min interval starting from 30 s after dosing DMMP. The values denoted with ΔAbs are the differences in the integrated intensities between the last spectrum and the first spectrum.

Obviously, the integrated intensities of each spectrum series grew with time. They grew at the lowest rate for TU10 and at the fastest rate for TU13, followed by TU11, then TU12. The differences in the integrated (over the 2500 and 3500 cm⁻¹ region) intensities between the last spectrum and the first spectrum are 102, 197, 142, 212 for TU10, TU11, TU12, TU13, respectively. This order is in a good consistency with the order of ΔF in Fig. 1(b). Therefore, we conclude that TU13 is the most efficient binder for DMMP among this series while TU10 is the opposite.

The spectra in Fig. 2 consist of many unassignable sharp or broad peaks. It suggests that many conformers or isomers with numerous intermolecular interactions contributed to a single spectrum. Nevertheless, a few vibrational features can be explained with the aid of vibrational analysis using the BLYP-D3/6-31+G* method (shown in ESI†). The broad peaks at higher than 3200 cm⁻¹ must be NH stretching modes. Upon increasing the DMMP dosing, the peak positions of these modes shifted toward higher wavenumbers. The broad peaks at between 3000 and 3100 cm⁻¹ are assignable to CH stretching modes in aromatic ring of TUn. Changes in these peaks upon the DMMP dosing were small. The sharp peaks at 2855 and 2956 cm⁻¹, marked with A and B in Fig. 2, may be assigned to CH stretching modes in methyl and methoxy moieties of DMMP, respectively. The intensities of these peaks were enhanced upon binding DMMP.

The shifts of the NH stretching peaks upon dosing DMMP should be discussed. According to the vibrational analysis shown in ESI,† intensities of the NH stretching peaks in the TUn-DMMP spectra must be enhanced by an order of magnitude and their positions must be shifted toward lower wavenumbers from those of the bare TUn spectra. In contrast, the shifts in Fig. 2 show the opposite trend. An explanation for this result is that the initial states of TUn were not isolated molecules but amorphous film in which TUn molecules interacted with neighboring ones through H-bonding. The intensities of the NH stretching peaks did not show extra enhancement due to forming new H-bonding because the peak intensities at the initial state were already high due to H-bonding with neighboring TUn. Therefore, we believe that the spectral change in the NH stretching region was induced by transformation of the H-bonding with neighbors to the H-bonding with DMMP.

The spectral changes upon dosing DMMP onto the substrates of TU10 and TU13 appeared small, while those on the substrates of TU11 and TU12 appeared large. This must be related to the structural transformation of the TUn receptors during formation of double H-bonded complexes. This point will be addressed again after the computational results are presented.

3.3 Energies and geometries of TUn (n = 1–9)

First of all, we discuss geometries of bare DMMP and thiourea derivatives reported to date. The geometries of DMMP and thiourea (TU) were reported by Suenram et al.²⁹ and by Puzzarini,³⁰ respectively, and they are consistent with our calculations shown in ESI.† For thiourea derivatives with singly substituted side groups (R₁ = H and R₂ = substituent in Scheme 1), Bryantsev and Hay³¹ calculated energies of the trans- and cis-isomers using the MP2/aug-cc-pVDZ method. Here, the cis/trans term was defined as the position of the N-substituent with respect to the C=S bond. They found that when the N-substituent was one of the alkyl groups (methyl, ethyl, isopropyl, t-butyl) the cis isomer was more stable than the trans isomer by 0.70–1.04 kcal mol⁻¹. However, when the N-substituent was phenyl, the trans isomer was more stable by 2.65 kcal mol⁻¹. They also calculated the energies of the transition states from which barriers for the cis ↔ trans isomerization can be deduced; the barriers ranged between 9.1 and 10.2 kcal mol⁻¹. The magnitudes of the rotational barrier for singly substituted thiourea derivatives were larger by 5–10% than that for urea derivatives³² but were considerably lower than those for amides (16–20 kcal mol⁻¹) or sulfoamides.³³

The thiourea derivatives in this work have four cis/trans isomeric forms in the orientation of the two N-substituents R₁ and R₂ to the C=S bond. In naming the isomers, we state the prefix for R₂ first, followed by the prefix for R₁. We investigated the geometry and energy of the lowest energy conformer from each cis/trans isomeric form of TUn (n = 1–9) and the results are shown in ESI (Fig. S2 through S10 and Table S1†). Here, we summarize the results as follows. The aromatic substituents (phenyl, benzyl, fluorobenzyl, methoxybenzyl) preferred the trans position with respect to the C=S bond, while the alkyl substituents (ethyl, n-propyl, cyclohexyl) preferred the cis position, as are consistent with the report³¹ of Bryantsev and Hay. Thereby, the lowest energy conformers for TUn (n = 1, 4–7) took on the trans–cis form and that for TU9 took on the cis–trans form. TU2 and TU3 have two alkyl substituents and thereby took on the cis–cis form. Although TU8 has the two aromatic substituents, the lowest energy conformer took on the trans–cis form (BLYP-D3 result) or the cis–trans form (MP2 result) as the trans–trans isomer was not stable due to high steric hindrances.

During the MD simulation to search for the conformers, we observed frequent trans ↔ cis interconversions at 300 K, implying that barriers for the interconversion were not high. To confirm this observation, we carried out the Nuclear Overhauser Effect Spectroscopy (NOESY) for several TUn molecules in solution. In most of the NOESY data, the coupling peaks between the two thioureic hydrogens were unresolved, probably because the investigated TUn's were present in multiple isomeric forms. This is consistent with the NMR results on urea and thiourea reported by Haushalter et al.³⁴

We also carried out the NBO analysis to find bond orders and bond ionicities (or polarities) of several selected bonds around the thioureic moiety (shown in ESI, Table S2†). Specifically, we were interested in the relative acidities of two N–H bonds. Compared to those of TU, the bond orders of the two N–H bonds in any isomeric forms of TUn (n = 1–9) decreased, while their bond ionicities increased except in a few cases of cis–cis isomeric forms. Therefore, any N-substituent in this work enhanced the acidity of the N–H bond. The acidity increase, judged from the bond order and ionicity, were greater for the hydrogen in the cis orientation (i.e. the corresponding substituent in the trans orientation), and also greater with the aromatic substituent than with the alkyl substituents. The π-electron delocalization provided by the aromatic substituent must work effectively to increase the acidity, and this effect was greater with more effective substituent in the trans position.

3.4 Energies and geometries of TUn (n = 10–13)

The newly synthesized TUn (n = 10–13) series for this work consist of TFMP as one fixed N-substituent and alkylphenyl as the other variable N-substituent. TFMP was expected to enhance the acidity of N–H bond, while the variable length of the methylene linkage in alkylphenyl was expected to control the effectiveness for the acidity enhancement and the flexibility for additional intermolecular interaction with DMMP. For this series, the geometries, energies, and NBO bond characteristics of the lowest energy conformers for all isomeric forms were calculated (shown in ESI, Fig. S11 through S14, Tables S1 through S2†). Here, the geometries of the global minimum conformers for TUn (n = 10–12) and the four lowest energy conformers for the four isomeric form of TU13 are shown in Fig. 3.

Fig. 3 Geometries of global minimum conformers of TUn (n = 10–12) and four lowest energy conformers for the four isomers of TU13. For the four isomers of TU13, the relative values of E_e and E₀ in kcal mol⁻¹ are shown in parentheses and square brackets, respectively.

Interestingly, in all the global minimum conformers of TUn (n = 10–13), the TFMP substituent was at the trans position with respect to the C=S bond. From the studies for TUn (n = 1–9), the phenyl and the benzyl substituents also preferred the trans position, with a higher priority given to benzyl. Since the alkylphenyl substituents in the global minimum conformers of TUn (n = 11–13) were oriented at the cis position, TFMP can be thought of a more effective substituent than the other alkylphenyl substituents in TUn (n = 10–13).

We also found that cis–cis conformers for the four TUn were not stable; E₀ energies of the cis–cis conformers of TUn (n = 10–13) were calculated to be higher by 4.94, 3.04, 3.47, 6.71 kcal mol⁻¹, respectively, than those of the global minimum conformers in Fig. 3 (This is shown in ESI†). This is consistent with that all the substituents in Fig. 3 preferred the trans position to enhance the acidity of NH bond.

During the MD simulations at 300 K, unlike the cases of TUn (n = 1–9) the substituents at the trans position of any global minimum conformers in Fig. 3 rarely interconverted to the cis position. In other words, the phenyl substituent in TU10, the TFMP substituent in TUn (n = 10–13), and the thioureic moieties involving theses substituents must be rigid. In contrast, the methylene linkages in the alkylphenyl substituents in TUn (n = 11–13) may provide a structural flexibility, which helped the benzene ring of the alkylphenyl substituents to approach the TFMP for additional interaction. As the result, TU13 was folded to maximize π–π interaction between two benzene rings.

3.5 Energies and geometries of TUn-DMMP complexes

Geometries of the global minimum conformers of TUn-DMMP (n = 1–13) complexes are shown in Fig. 4. Other low energy conformers are shown in ESI (Fig. S15 through S26†). Note that all the complexes were formed by at least one H-bonding between the thioureic hydrogen of TUn and the sulfonic oxygen of DMMP, suggesting that the H-bonding is a major intermolecular interaction. TUn molecules underwent geometry changes to ease the H-bonding and to enhance other intermolecular interactions such as the H–π interaction. Although the cis–cis forms were not the most stable geometries for most bare TUn molecules, they turned out to be the most stable geometries for most TUn-DMMP complexes. The exceptions were TUn-DMMP (n = 1, 3, 10).

Fig. 4 Geometries of the lowest energy conformers of TUn-DMMP (n = 1–13) complexes optimized at the BLYP-D3/6-31+G(d) level of theory. The electronic part of the binding energy (−ΔE_e) and the ZPE corrected binding energy (−ΔE₀) are shown inside parentheses and square brackets, respectively. NH⋯O hydrogen bonds are denoted with broken green lines.

In all the cis–cis conformers, the two thioureic hydrogens formed double H-bonding with the sulfonic oxygen of DMMP. To form such geometry, the cis–trans or trans–cis form of the bare TUn must undergo a rather big geometry change. We hypothesize that the initial H-bonding must be made to one thioureic hydrogen in the cis–trans or trans–cis form of TUn molecule, followed by internal rotations for the trans ↔ cis interconversion. Then, the subsequent H-bonding must be made in the cis–cis form of the intermediate. Such a scenario of double H-bonding may be plausible in the gas phase. However, whether the scenario also holds for the substrate states of TUn needs further discussion.

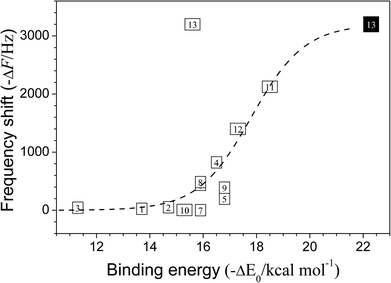
3.6 Correlation between the binding energies and the QCM frequency shifts

In Fig. 5, the calculated binding energies (−ΔE₀) of TUn-DMMP (n = 1–13) are plotted versus the frequency shifts (ΔF) in the QCM measurement. The dashed curve is drawn to provide a visual guideline of the plotted points. Except for TU13-DMMP, the plotted points did not deviate much from the guideline curve. The frequency shifts for TUn-DMMP (n = 1, 3) were measured to be very low and the binding energies were calculated to be low as well, because they did not form the double H-bonded geometries. The frequency shift and the binding energy for TU2-DMMP were also low because the two substituents did not enhance the acidities of the thioureic moieties. The frequency shifts and the binding energies for TUn-DMMP (n = 4–6, 8, 9) were higher than those for TUn-DMMP (n = 1–3) because the benzyl substituents enhanced the acidities to produce effective double H-bonds. On the other hand, the frequency shift for TU7-DMMP was not as much as expected from the calculated binding energy probably because TU7 formed a crystalline substrate in the QCM.¹⁴

Fig. 5 The correlation between the binding energies (−ΔE₀) of TUn-DMMP complexes calculated with the BLYP-D3/6-31+G* method and the QCM frequency shifts (ΔF) of the corresponding receptors upon DMMP dosing. The number in each plotting symbol represents n. The plotting points for TU6 and TU8 are almost overlapped. The dashed curve is drawn as a visual guideline. In addition to 13 hollow square symbols, one filled square symbol is added for n = 13. The binding energy of this symbol was obtained between the global minimum conformer of TU13-DMMP and the unfolded cis–cis conformer of TU13.

For TUn-DMMP (n = 10–12), the frequency shift and the binding energy for TU10-DMMP were much lower than those of TU11-DMMMP or TU12-DMMP. As it has the two rigid substituents in trans–trans isomeric form, TU10 must overcome a larger rotational barrier to form the cis–cis geometry than the others. In contrast, owing to the flexibility provided by the methylene linkage in TU11 and TU12, the interconversion to the cis–cis geometry to make double H-bonds may be easier.

The excellent correlation between the two sets of data excluding that of TU13-DMMP suggests that the geometries of TUn in the QCM substrates and their DMMP complexes must be close to those in the gas phase. This is plausible since most TUn substrates were prepared in amorphous film, in which internal rotations of substituents to make double H-bonding would be plausible. On the contrary, if a prepared substrate was in a good crystalline state like TU7, the QCM frequency shift would not be so much as expected from the calculated binding energy because a greater intermolecular interaction in higher degree of crystalline state would enhance barrier height for the internal rotation.

The largest deviation from the visual guideline was found for TU13-DMMP, whose frequency shift was the highest among all TUn-DMMP in this work while the calculated binding energy was significantly low. The low binding energy must be due to the folded geometry of bare TU13, which was excessively stabilized through intramolecular π–π interaction. Such a folded geometry must interfere an approach of DMMP and as the result the H-bonded TU13-DMMP must have been strained.

While the cis–trans, trans–cis, trans–trans isomers of TU13 showed folded geometries, the cis–cis isomer was unfolded (Fig. 3). The E₀ energy of the unfolded cis–cis isomer was higher by 6.7 kcal mol⁻¹ than that of the global minimum conformer. Therefore, the unfolded cis–cis isomer could not exist in gas phase. However, in the substrate states of the QCM and the IR spectroscopy, interaction with the neighboring TU13's may have unfolded the geometry. We wish to emphasize that extra time was needed to prepare TU13 substrates for stable QCM oscillations. During the extra time, the structural transformation to the unfolded cis–cis TU13 may have occurred in the substrate. Then, the unfolded cis–cis geometry was ready to accept DMMP without much structural transformation such as a cis/trans interconversion. Therefore, if the correlation plot of Fig. 5 was made with the binding energy of TU13-DMMP between the cis–cis TU13 and the global minimum conformer of TU13-DMMP, a substantial improvement of correlation was obtained.

The above proposal on the structural transformation of TUn (n = 10–13) is also consistent with the trend in the IR spectra shown in Fig. 2. TU10 was rigid, so the structural transformation was restricted. Accordingly, it only made a single H-bonding as shown in Fig. 4. As a result, the changes in the spectral shapes were small. Unlike the isolated TU13, TU13 in the substrate state consisted of numerous conformers with unfolded cis–cis geometries. Therefore, the IR spectra exhibited broad features which did not change much upon dosing DMMP since significant structural transformation to make double H-bonding was not necessary.

4 Conclusion

We computed the geometries and energies of thiourea derivatives (TUn) as well as their 1 : 1 complexes with the nerve agent simulant DMMP at the DFT level. The computed binding energies of the most complexes were well-correlated with the QCM frequency shifts upon dosing DMMP to the corresponding TUn receptors. This implies that the binding features at the molecular level still worked as major factors for binding in substrate states of the thiourea derivatives. The computed geometries of most complexes showed double H-bonding, in which an internal rotation of an N-substituent was required. For those receptors that form highly crystalline substrates, the binding efficiencies were less than expected from the calculated binding energy.

The thiourea derivative that showed the greatest frequency shift in the QCM experiment was TU13 which has 3,5-bis-(trifluoromethyl)phenyl as one N-substituent and (CH₂)₃-phenyl as the other N-substituent. However, the computed binding energy of TU13-DMMP was rather small. This is because the methylene linkage of the bare TU13 produced a folded geometry, which made it difficult to invite DMMP for the double H-bonding. The structure of TU13 in the substrate for the QCM must be very different from the calculated geometry. Unlike other thiourea derivatives, extra time was required to prepare the TU13 substrate that induced a stable QCM oscillation. During the extra time the TU13 structure may have been transformed from the folded to the unfolded. The unfolded TU13 must be in the cis–cis isomeric form, so that forming double H-bonded complex with DMMP was easier with little structural transformation. This scenario for the complex geometry and the structural transformation upon dosing DMMP was also supported by a series of diffuse reflectance IR spectra for TUn (n = 10–13). Changes in integrated spectral intensities were ordered as TU10 < TU12 < TU11 < TU13, the same order in the QCM frequency shifts. The changes in the spectral shape during the DMMP dosing were small for TU10 because the molecule was rigid and formed a single H–bonded complex, while the changes were larger for TU11 or TU12, since the internal rotation of substituent was necessary to form the double H-bonded complex. The spectral shape change was very small for TU13 since not much structural transformation was needed to form the double H-boned complex.

Even with the excellent agreement between the calculated results, the QCM data, and the IR spectra, few discrepancies or ambiguities are inevitable because of the complex nature of the receptor substrate. Yet, predicting the binding efficiency with a proper choice of computational method would be useful especially when the target is a hazardous chemical such as CWAs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the Agency for Defense Development through the Chemical and Biological Defense Research Center. YKC was supported by the Program for Returners into R&D (KW-2015-PPD-0175) of Center for Women in Science, Engineering and Technology.

References

1. D. Hank Ellison, Handbook of Chemical and Biological Warfare Agents, CRC Press, 2nd edn, 2007.
2. E. Croddy, Chemical and Biological Warfare: A Comprehensive Survey for the Concerned Citizen, Copernicus Books, New York, 2002.
3. K. Kim, O. G. Tsay, D. A. Atwood and D. G. Churchill, Chem. Rev., 2011, 111, 5345.
4. C. H. Gunderson, C. R. Lehmann, F. R. Sidell and B. Jabbari, Neurology, 1992, 42, 946.
5. F. Wang, H. Gu and T. M. Swager, J. Am. Chem. Soc., 2008, 130, 5392.
6. F. Wang and T. M. Swager, J. Am. Chem. Soc., 2011, 133, 11181.
7. J. K. Dunnick, B. N. Gupta, M. W. Harris and J. C. Lamb 4th, Toxicol. Appl. Pharmacol., 1984, 72, 379.
8. K. Blumbach, A. Pähler, H. M. Deger and W. Dekant, Toxicol. Sci., 2000, 53, 24.
9. T. Gunnlaugsson, M. Glynn, G. M. Tocci, P. E. Kruger and F. M. Pfeffer, Coord. Chem. Rev., 2006, 250, 3094.
10. V. Kumar and E. V. Anslyn, J. Am. Chem. Soc., 2013, 135, 6338.
11. V. Kumar and M. P. Kaushik, Analyst, 2011, 136, 5151.
12. K. Saetia, J. M. Schnorr, M. M. Mannarino, S. Y. Kim, G. C. Rutledge, T. M. Swager and P. T. Hammond, Adv. Funct. Mater., 2014, 24, 492.
13. J. R. Hiscock, N. J. Wells, J. A. Ede, P. A. Gale and M. R. Sambrook, Org. Biomol. Chem., 2016, 14, 9560.
14. S. Ha, M. Lee, H. O. Seo, S. G. Song, K. Kim, C. H. Park, I. H. Kim, Y. D. Kim and C. Song, ACS Sens., 2017, 2, 1146.
15. S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211.
16. Z. Zhang, K. M. Lippert, H. Hausmann, M. Kotke and P. R. Schreiner, J. Org. Chem., 2011, 76, 9764.
17. K. M. Lippert, K. Hof, D. Gerbig, D. Ley, H. Hausmann, S. Guenther and P. R. Schreiner, Eur. J. Org. Chem., 2012, 5919.
18. A. Serra-Pont, I. Alfonso, J. Solà and C. Jimeno, Org. Biomol. Chem., 2017, 15, 6584.
19. M. Formica, V. Fusi, L. Giorgi, G. Piersanti, M. Retini and G. Zappia, Tetrahedron, 2016, 72, 7039.
20. L. Caruana, F. Kniep, T. K. Johansen, P. H. Poulsen and K. A. Jørgensen, J. Am. Chem. Soc., 2014, 136, 15929.
21. A. B. Butrow, J. H. Buchanan and D. E. Tevault, J. Chem. Eng. Data, 2009, 54, 1876.
22. M. Elstner, D. Porezag, G. Jungnickel, J. Elsner, M. Haugk, Th. Frauenheim, S. Suhai and G. Seifert, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 7260.
23. B. Aradi, B. Hourahine and Th. Frauenheim, J. Phys. Chem. A, 2007, 111, 5678.
24. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15.
25. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
26. A. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735.
27. F. Weinhold and C. R. Landis, Discovering Chemistry with Natural Bond Orbitals, Wiley, Hoboken, 2012.
28. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, T. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 09, Revision B.01, Gaussian, Inc., Wallingford, 2010.
29. R. D. Suenram, F. J. Lovas, D. F. Plusquellic, A. Lesarri, Y. Kawashima, J. O. Jensen and A. C. Samuels, J. Mol. Spectrosc., 2002, 211, 110.
30. C. Puzzarini, J. Phys. Chem. A, 2012, 116, 4381.
31. V. S. Bryantsev and B. P. Hay, J. Phys. Chem. A, 2006, 110, 4678.
32. V. S. Bryantsev, T. K. Firman and B. P. Hay, J. Phys. Chem. A, 2005, 109, 832.
33. K. B. Wiberg, in The Amide Linkage: Structural Significance in Chemistry, Biochemistry, and Materials Science, ed. A. Greenberg, C. M. Breneman and J. F. Liebman, John Wiley & Sons, Inc., New Jersey, 2000.
34. K. A. Haushalter, J. Lau and J. D. Roberts, J. Am. Chem. Soc., 1996, 118, 8891.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra00314b

‡ These authors contributed equally to this work.

§ Changsik Song and Seong Kyu Kim are co-corresponding authors.

---