Theoretical studies on the structures and properties of doped graphenes with and without an external electrical field

Abstract

To expand the applications of graphene in optoelectronic devices, B, Al, Si, Ge, As, and Sb doped graphenes (marked as B-G, Al-G, Si-G, Ge-G, As-G, and Sb-G, respectively) were synthesised. The geometric structures, population analyses, and also electronic and optical properties of these doped graphene materials were investigated employing the density functional theory (DFT) method. It was shown that the band gaps of doped graphenes were opened and their absorption spectra were red-shifted by the addition of doping atoms, and their dielectric functions and refractive indexes of low frequency were decreased compared with those of pure graphene. Moreover, the electronic and optical properties of doped graphenes under an external electrical field ranging from −0.4 to 1.2 eV Å⁻¹ have been explored. It was found that the band gaps of As-G and Sb-G were increased to 0.864 and 1.841 eV under a 1.2 eV Å⁻¹ external electrical field, respectively. On the contrary, the band gaps of B-G, Al-G, Si-G, and Ge-G were decreased with the increase of the external electrical field intensity. Additionally, the absorption peaks of B-G, Al-G, Si-G, and Ge-G were red-shifted upon applying the external electrical field. Correspondingly, their dielectric functions and refractive indexes of low frequency were increased. Surprisingly, the absorption spectra, dielectric functions, and refractive indexes of As-G and Sb-G have no significant changes.

---

1. Introduction

Graphene is a carbon material with a two-dimensional network structure of atomic thickness. Many scholars have been interested in studying graphene since its successful preparation.^1,2 Graphene demonstrates incredible electronic performance,^3–5 outstanding optical properties,⁶ interesting thermal performance,⁷ larger specific surface area,^8,9 excellent elastic modules etc.¹⁰ Especially, the incredible electronic performance makes graphene a potential candidate in electronic devices.^11–13 However, the zero band gap of graphene needs to be opened to expand its range of applications in photonics, integrated circuits, solar cells etc. So far, many chemical and physical methods have been used to open the band gap of graphene. Most chemical methods were achieved mainly through hybridization, for example mono and double doped graphenes were experimentally fabricated and theoretically predicted to show a change in electronic properties. The single dopant graphenes mainly comprise a main group element or subgroup element. The main group elements include B,¹⁴ N,¹⁵ Al,^16,17 P,^17,18 S,^17–21 Si,^22–24 Se^25,26 etc. The subgroup elements include Mg, Co, Ni,²⁷ Fe,^28–30 U, Th³¹ etc. Double doped graphenes include P–N,^32,33 S–N,^34,35 Si–N,^35,36 Be–B,³⁷ Be–N,³⁸ Be–S,³⁹ N–Al,⁴⁰ N–B^41,42 etc. Some physical methods were also applied to open the band gap of graphene. For example, two-dimensional graphenes were clipped into one-dimensional nanoribbons;^43,44 a tensile or shear strain was applied on the graphene sheet;^45,46 graphene nano-mesh was obtained by adding topological nano-holes into graphene sheet,⁴⁷ an electric field was applied for the graphene-base system⁴⁸ etc. On the other hand, the optical properties of doped graphenes were reported scarcely although the electronic properties were studied.^21,30

Some studies have shown that the electrical and optical properties of graphene are affected not only by the impurity atoms but also by the content of the impurity atoms. Shuai et al. reported that the band gap of Si doped graphene was increased with increasing Si concentration in graphene sheet. The refractive index and absorption spectra of the graphene were also changed after Si doping.²⁴ Jindal et al. introduced that the electronic properties and absorption spectra of graphene were not affected after single B and N doping except that the absorption spectra of graphene occurred red-shift after B/N codoping at high contents.⁴⁸ Nourbakhsh et al. reported higher refractive index of Fe doped graphene and Co doped graphene sheets.³⁰ However, these studies are only limited to the studies on the electronic and optical properties of metal or non-metal doped graphenes. A very little amount of studies are done to explore the influences of metallic and metalloid-based dopants on the structural, electronic and optical properties of graphene under external electrical field.

In this study, the metallic and metalloid-based dopants (i.e. boron (B), silicon (Si), aluminum (Al), germanium (Ge), arsenic (As), stibonium (Sb)) doped graphenes (marked as B-G, Si-G, Al-G, Ge-G, As-G, and Sb-G, respectively) model are built to investigate the effect of various dopants on the electronic and optical properties of graphene sheet by employing DFT method. Meanwhile, the electronic and optical properties of doped graphenes under external electrical field ranging from −0.4 to 1.2 eV Å⁻¹ have also been explored. Considering the fact that the content of dopant atoms is proportional to the properties of doped graphenes,²⁴ four dopant atoms are introduced into graphene sheets, and the structures of doped graphenes are detailedly analyzed.

2. Models and methods

In this study, the structures, electronic and optical properties of the doped graphenes mentioned above are investigated employing the CASTEP module.^21,40 According to the literature, the generalized gradient approximation (GGA) with Perdew–Burke–Ernzerhof (PBE) has been used for exchange–correlation functional to simulate the properties of the doped graphenes. Moreover, the Grimme method for DFT-D correction and the spin unrestriction are selected to calculate the van der Waals (vdW) interactions and the different orbital spins, respectively.^21,30,40 Ultrasoft pseudo-potential is selected to perform the core treatment.

4 × 4 × 1 supercell was built to model the original graphene (OG) sheet. For doped graphenes, four dopant atoms are introduced into graphene sheet. The vacuum space of 20 Å is set in the direction perpendicular to the sheet to avoid the interactions between periodic structures. The energy cutoff is set to 400 eV. A 17 × 17 × 1 and 36 × 36 × 1 mesh of k-point is used for geometry optimization and electronic structure calculations of OG and doped graphenes, respectively. All atoms are allowed to relax and convergence in energy, force, and displacement are 2 × 10⁻⁵ eV, 0.004 Ha Å⁻¹, and 0.005 Å, respectively. Moreover, the set of 36 × 36 × 1 k-mesh and 50 empty bands were used for the calculation of optical properties.

3. Results and discussion

3.1 Structure analysis

In order to verify the reliability of the established model and data, the electronic and geometric structures of graphene are calculated and shown in Fig. 1. As shown in Fig. 1(a), the length of C–C bond of OG is 1.420 Å, which is consistent with the literature data.^37,39 Fig. 1(b) shows the band gap and total density of states (DOS) of OG. Obviously, the band gap of OG is zero at Dirac point, which is consistent with the result of the experimental study and theoretical simulation.⁴¹ So, the reliability of the established model and simulation methods should be confirmed. Under the same simulation condition, the optimized doped graphenes are shown in Fig. 2. Because the covalent radii of B (85 pm), Al (126 pm), Si (116 pm), Ge (124 pm), As (121 pm), and Sb (140 pm) atoms are different from that of C (75 pm) atom, the different degrees of structural deformation for doped graphenes will occur. In view of the position of B, Al, and Si atoms in the periodic table and the purpose of obtaining the maximum band gap of graphene, B, Al, and Si atoms replace carbon atom of OG in situ. However, due to the large radii of As and Sb atoms, their positions in the doped graphenes are set outwards from the surface of graphene. For Ge atom, preliminary analysis indicates that the band gap of in situ replaced graphene was larger than that of protruded from the surface of graphene. As presented in Table 1, the calculated bond lengths of B–C (1.503 Å), Al–C (1.764 Å), Si–C (1.684 Å), and Ge–C (1.740 Å) are consistent with previous studies.^24,30,37,40 As for the As–C and Sb–C bonds, they are 1.875 and 2.109 Å, respectively. Moreover, the C–C bonds around the dopant atoms are also changed by the introduction of these dopant atoms with large covalent radii. The ortho, meta, and para C atoms around the dopant atoms are marked as C₁, C₂, and C₃, respectively. Analyses of the neighboring (C₁–C₂) and next-adjacent (C₂–C₃) C–C bonds around the dopant atoms for all the structures suggest that the bond lengths of C₁–C₂ (from 1.420 to 1.435 Å) are close to that of C–C (1.420 Å) of OG. While the bond lengths of C₂–C₃ (from 1.478 to 1.546 Å) are longer than that of C–C of OG. These phenomena may be attributed to the stronger interaction between the dopant atom and ortho C atom compared with that of the meta and para C atoms, which is consistent with the conclusions of Shuai²⁴ and Zhao et al.⁴⁰ Expectedly, the structural changes of doped graphenes and the properties of dopant atoms will also influence the electronic structures and optical properties of system.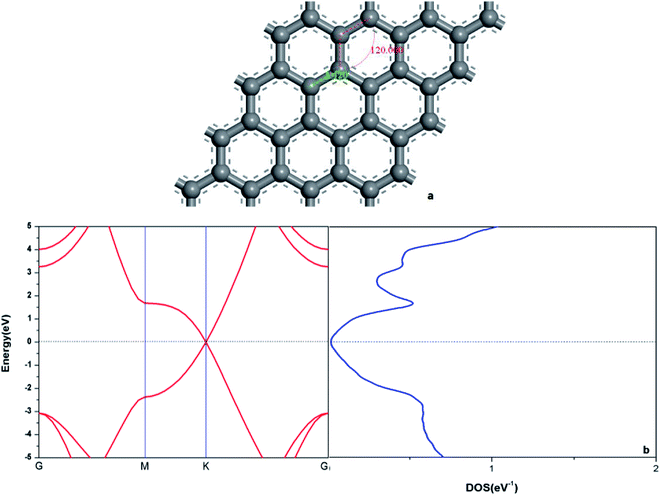

Fig. 1 The geometric structure (a), band structure (b: left), and electron density of state (b: right) of graphene.

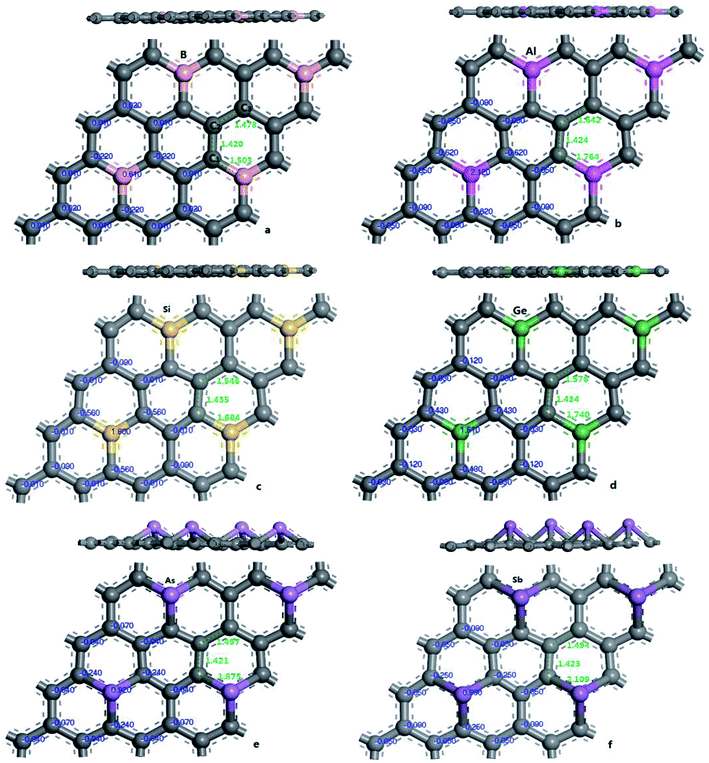Fig. 2 The geometric structures and Mulliken charges of doped graphenes: B-G (a), Al-G (b), Si-G (c), Ge-G (d), As-G (e), and Sb-G (f).

Table 1 The charge of X (X = B, Al, Si, Ge, As, and Sb) and C atoms, length of C–X and C–C bond in the original graphene and doped graphenes

Systems	Charge (eV)				Band length (nm)
	X	C1	C2	C3	X–C1	C1–C2	C2–C3
OG		0	0	0		1.420	1.420
B-G	0.610	−0.220	0.010	0.020	1.503	1.420	1.478
Al-G	2.120	−0.620	−0.050	−0.090	1.764	1.424	1.642
Si-G	1.800	−0.560	−0.010	−0.090	1.684	1.435	1.546
Ge-G	1.510	−0.430	−0.030	−0.120	1.740	1.434	1.576
As-G	0.920	−0.240	−0.040	−0.070	1.875	1.421	1.497
Sb-G	0.990	−0.250	−0.050	−0.090	2.109	1.423	1.494

---

3.2 Population analysis

To explore the effects of geometric structures on the electronic and optical properties, the Mulliken charge analysis is performed first on the basis of the optimized structures. As shown in Fig. 2(a), B atom carries 0.610e charge and the charge of the ortho, meta, and para C atoms around B atom is −0.220e, 0.010e, and 0.020e, respectively, suggesting that the meta and para C atoms lose a few electrons and the ortho C atom gains a lot of electrons. It should be due to the fact that both the electronegativity and covalent radius of B (2.04 and 85 pm) atom is close to that of C (2.55 and 75 pm) atom, resulting in more charge transfers between B and ortho C atom compared to the meta and para C atoms. For Al-G, the charge of Al atom is 2.120e and Al transfers −0.620, −0.050, and −0.090e charges to its ortho, meta, and para C atoms (Fig. 2(b)), suggesting that Al and C atoms are electron donors and acceptors, respectively. Moreover, the meta and para C atoms get less electrons than ortho C atom. Similarly, this phenomenon also occurs in the Si, Ge, As, and Sb doped graphenes, illustrating that Si, Ge, As, and Sb atoms are also electron donors. As a result, the orders of the lost charges for the dopant atoms are as follows: Al (2.120) > Si (1.800) > Ge (1.020) > Sb (0.990) > As (0.920) > B (0.610), suggesting that Al and Si atoms lose more electrons than B, As, Ge, and Sb atoms. This difference can be attributed to the smaller electronegativity of Al (1.61) and Si (1.90) atoms than that of C atom, and the other atoms have similar electronegativity with C atom. Furthermore, the position of the dopant atoms in the graphene may also play an important role, which will be explored in future studies.

The electron density difference can visually exhibit the ability of atomic charge transfer.^42,50 As shown in Fig. 3, red and blue regions indicate the electron enrichment and electron scarcity, respectively. For OG, the electrons are uniformly distributed around the bonds of graphene's six-membered ring. After B, Al, Si, As, Ge, and Sb doping, the area of electron coverage is larger than that of pure graphene, indicating that electron transfer occurs between dopant atoms and C atoms. For B-G, the electron density around B atoms is slightly decreased compared with OG. Similarly, the same is also true for the electron density around meta and para C atoms. On the contrary, the electron density around ortho C atom near B atom is significantly increased, suggesting that most of electrons transfer to the ortho C atom from B atom compared with that of the meta and para C atoms. For the other doped graphenes, the electron density around dopant atoms is drastically reduced. Moreover, the electron densities around ortho C are much more than those around meta and para C atoms, indicating that the dopant atoms transfer more electrons to ortho C atoms.

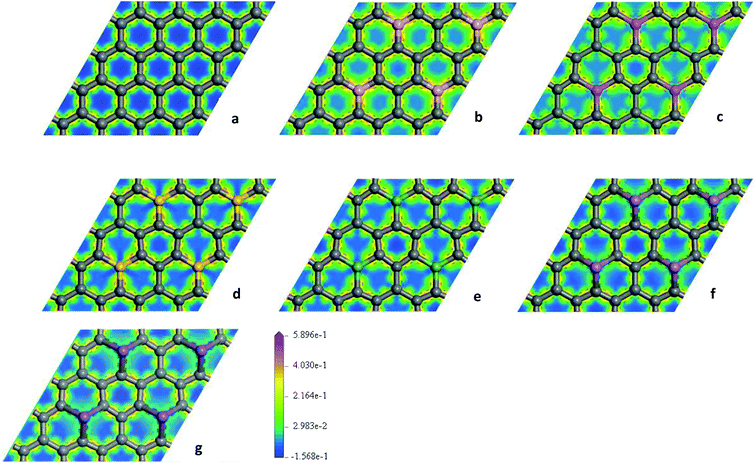Fig. 3 The electron density difference maps for OG (a), B-G (b), Al-G (c), Si-G (d), Ge-G (e), As-G (f), and Sb-G (g), respectively.

3.3 Electronic properties

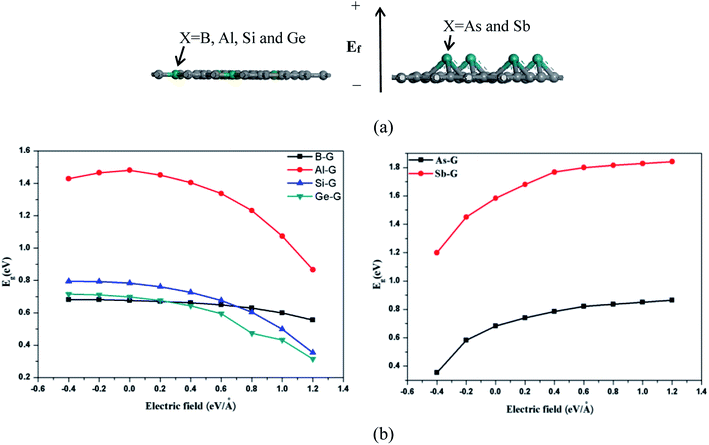
The band structure analyses of B-G (a), Al-G (b), Si-G (c), Ge-G (d), As-G (e), and Sb-G (f) are shown in Fig. S1 (left).† It is found that the introduction of dopant atoms open the band gap of graphene. Compared with OG, B, Al, and Sb doping makes the energy level curves move to the high energy, resulting in the Fermi level (E = 0) to pass through the valence band (Fig. S1(a, b, and f)†). On the contrary, for Si-G, As-G, and Ge-G, the highest energy level curves of the valence band nearly approach the Fermi level. Meanwhile, the energy level curves of the conduction band move up to higher Fermi energy (E_F) (Fig. S1(c, d, and e)†). This phenomenon can also be proved by the analyses of the density of states (DOS) as shown in Fig. S1 (right).† For B-G (Fig. S1(a)†), the band gap is 0.663 eV, which is consistent with the result obtained by Nath et al.⁴¹ Fig. S1(b)† shows that the band gap of Al doped graphene is 1.480 eV, which is larger than that of the Al-doped graphene with 3.13% atomic concentration (0.40 eV).⁴⁰ In our study, the atomic concentration of Al is 12.5%, indicating that the band gaps of doped graphenes are affected by the dopant concentration. Fig. S1(c)† shows that the band gap of Si-G is 0.783 eV, which is close to the previous studies.^23,24 As shown in Fig. S1(d),† the band gap of Ge-G is 0.698 eV, where the band gap of Ge-doped graphene with 3.13% atomic concentration is 0.20 eV.³⁰ As for As-G and Sb-G (Fig. S1(e and f)†), the band gaps of them are 0.682 and 1.583 eV, respectively, suggesting that the addition of sufficient numbers of dopant atoms can effectively open the band gap of graphene. Note that Sb-G has the largest band gap among all the doped graphenes although Sb atom do not lose more electrons than Al, Si, and Ge atoms. As a result, the orders of the band gaps for the doped graphenes are as follows: Sb-G (1.583) > Al-G (1.480 eV) > Si-G (0.783 eV) > Ge-G (0.698 eV) > As-G (0.682 eV) > B-G (0.663 eV).

Subsequently, the influences of the external electric field (E_f) on the electronic properties of doped graphenes have been discussed, where the electric field is perpendicular to the doped graphenes surface. As shown in Fig. 4, the band gaps of B-G, Si-G, and Ge-G decrease with the changes of E_f from −0.4 to 1.2 eV Å⁻¹. As for the band gap of Al-G, it increases first and then decreases. On the contrary, the band gaps of As-G and Sb-G increase with the changes of E_f from −0.4 to 1.2 eV Å⁻¹. In details, the band gaps of the doped graphenes under the external electric fields from −0.4 to 1.2 eV Å⁻¹ have been summarized in Table 2.

Fig. 4 The sketch map of doped graphenes under the external electric field (E_f) (a), and the band gap (E_g) of doped graphene as a function of the electric fields (b), where E_f is introduced along z direction and the upward E_f is defined as positive labeled with symbol “+”.

Table 2 The band gap (E_g) of doped graphenes under applied electrical field (in eV Å⁻¹)

System	Eg (eV)
	−0.4	−0.2	0	0.2	0.4	0.6	0.8	1.0	1.2
B-G	0.681	0.681	0.676	0.670	0.662	0.649	0.629	0.600	0.556
Al-G	1.428	1.465	1.481	1.451	1.405	1.337	1.232	1.074	0.866
Si-G	0.795	0.793	0.783	0.761	0.727	0.677	0.604	0.499	0.354
Ge-G	0.715	0.711	0.698	0.676	0.643	0.595	0.473	0.433	0.314
As-G	0.354	0.582	0.682	0.741	0.786	0.821	0.835	0.850	0.864
Sb-G	1.20	1.450	1.583	1.680	1.768	1.80	1.815	1.828	1.841

---

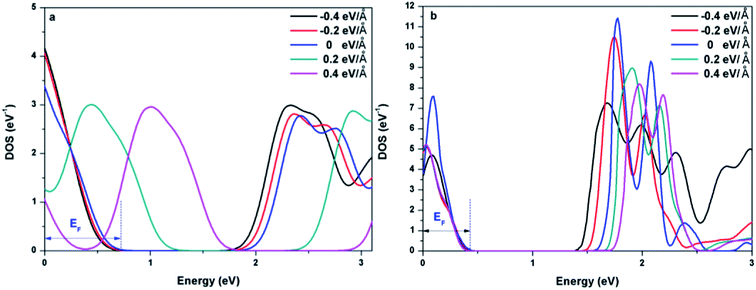
To further explore the effect of E_f on the electronic properties of the doped graphenes, the representative DOS of Al-G and Sb-G has been explored. As shown in Fig. 5, the DOS of the doped graphenes has been influenced irrespective of the positive or negative electric fields. For Al-G, the Fermi energy measured from the top of the valence bands and bottom of the conduction bands slightly moves downward to the Fermi level under the E_f from 0 to −0.4 eV Å⁻¹. Moreover, the migration of the conduction bands is faster than that of the valence bands, resulting in the decrease of the band gap of Al-G with the increase of E_f. On the contrary, under the E_f from 0 to 0.4 eV Å⁻¹, the energy of the valence bands and conduction bands moves upward to higher energy level and shift away from the Fermi level. Moreover, the migration of the valence bands is faster than that of the conduction bands, leading to the decrease of the band gap with the increase of E_f. Therefore, the external electric field will reduce the band gap of Al-G. As shown in Fig. 5(b), for Sb-G under the E_f from 0 to −0.4 eV Å⁻¹, the energy of the valence bands has no obvious changes and the energy of the conduction bands moves downward to the Fermi level, resulting in the decrease of the band gap with the increase of E_f. However, the band gap of Sb-G is increased with the increase of E_f from 0 to 0.4 eV Å⁻¹, which may be due to the fact that the energy of the conduction bands moves upward to higher energy level. Therefore, the band gap of Sb-G increases and decreases with the increase of the intensity of positive and negative electric fields, respectively. Probably, these phenomena may be related to the charge distributions on the doped graphenes. To clarify this point, the electron density difference maps for Al-G and Sb-G have been constructed. As shown in Fig. 6, the charge distribution is obviously affected by the electric field. For Al-G (Fig. 6(a)), despite the fact that the whole system has more uniformly distributed electrons under the electric field, the difference of charge between Al and C atoms is not obvious, indicating that the electric fields induce a weak dipole moment. So the band gap of Al-G is decreased under the external electric field. For Sb-G (Fig. 6(b)), under negative electric fields, the amounts of charge transfer between Sb and C atoms are less than that of zero field case. But under positive electric fields, more electron charges are transferred to C atoms around Sb atoms. These phenomena show that the positive electric fields have certain contributions to open the band gap of Sb-G.

Fig. 5 DOS of Al-G (a) and Sb-G (b) under different external electric fields.

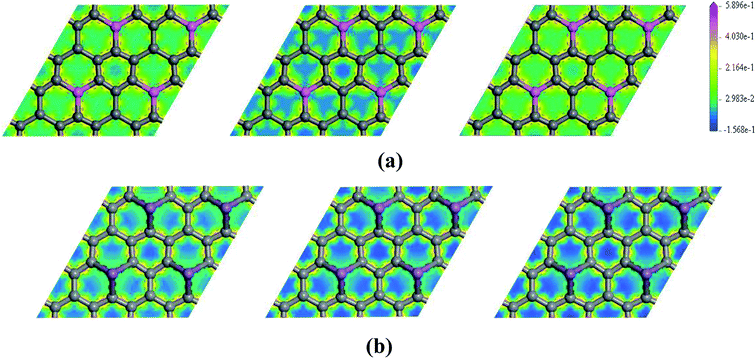Fig. 6 The electron density difference maps for Al-G (a) and Sb-G (b), where the map from left to right is plotted for E_f = −0.4, 0, 0.4 eV Å⁻¹.

3.4 Optical properties

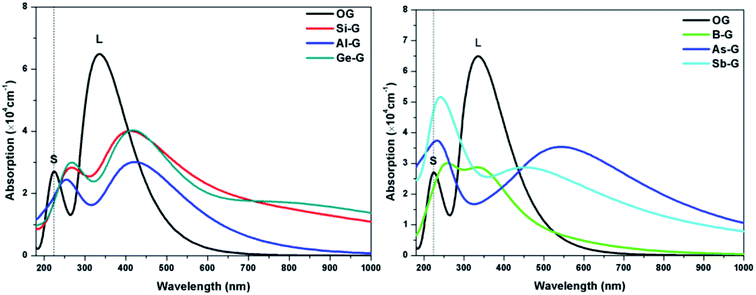
To explore the influences of the geometric structure on the optical properties, the absorption spectra, complex dielectric function, complex refractive index, and loss function (smearing = 0.2 eV) of OG and doped graphenes have been analyzed, where parallel electromagnetic wave polarization to sheet are taken into account. According to the optical selection rules, only π → π* (long wavelength or low frequency region) and σ → σ* (short wavelength or high frequency region) transitions are allowed. As a result, the curves of optical properties of OG and doped graphenes are similar with the results of previous studies. Here, the minor differences should be attributed to the different sizes of supercell, concentration of doped atom, k-point mesh, and smearing values employed in the calculations.

3.4.1 Absorption spectra. On the basis of the standard DFT Kohn–Sham orbitals, the absorption spectra of OG and doped graphenes have been calculated. As shown in Fig. 7, two absorption peaks of OG are located at 230(2.9 × 10⁴) and 340(6.8 × 10⁴ cm⁻¹) nm, respectively, where the data in parentheses refer to the corresponding intensity if not noted otherwise. Here, the positions of these two peaks are in agreement with previous studies,^40,49 where two peaks are marked as S and L below for simplicity, respectively. Note that the S and L peaks are ascribed to σ → σ* and π → π* transitions, respectively.

Fig. 7 The absorption spectra of OG, B-G, Al-G, Si-G, Ge-G, As-G, and Sb-G.

For B-G, the intensity of S peak is stronger compared with that of OG and its maximum value appears at 255 nm, suggesting that S peak shifts toward the long wavelength. However, L peak of B-G lies at 347(2.87 × 10⁴ cm⁻¹) nm, implying that there was no significant changes except for the decrease in peak strength, which is line with the result of Nath et al.⁴¹ For Al-G, S and L peaks appear at 257(2.42 × 10⁴) and 404(3.04 × 10⁴ cm⁻¹) nm, respectively, implying that the Al dopant can result in red shift for absorption peaks of graphene. These values are close to the values reported by Zhao et al.⁴⁰ Moreover, the intensity of L peak is stronger than that of S peak, implying that π → π* transitions is stronger than σ → σ* transitions during the orbital transition of Al-G system. Especially, the same is also true for the peaks of Si-G and Ge-G, where S/L peaks of them are located at 267(2.83 × 10⁴)/412(4.01 × 10⁴) and 227(5.65 × 10⁴)/531(3.96 × 10⁴ cm⁻¹) nm, respectively, which are close to Rafique and Kheyri's results.^24,30 For As-G, S and L peaks are located at 227(5.65 × 10⁴) and 541(3.96 × 10⁴) nm, respectively, suggesting that S and L peaks occur red shift and the intensity of S peak is stronger than that of graphene. Interestingly, S peak becomes a sharp peak compared with L peak, suggesting that σ → σ* transitions is stronger than π → π* transitions during the orbital transition of As-G. Similarly, this phenomenon can also be observed for Sb-G. Here, S and L peaks are located at 246(5.01 × 10⁴) and 454(2.87 × 10⁴ cm⁻¹) nm, respectively. As a result, the absorption peaks of doped graphenes shift toward the long wavelength and their intensities are weaker than that of pure graphene. Comparatively speaking, the S peak intensities of Al-G, Si-G, and Ge-G are weaker than those of L peak. However, the opposite is true for the B-G, As-G, and Sb-G.

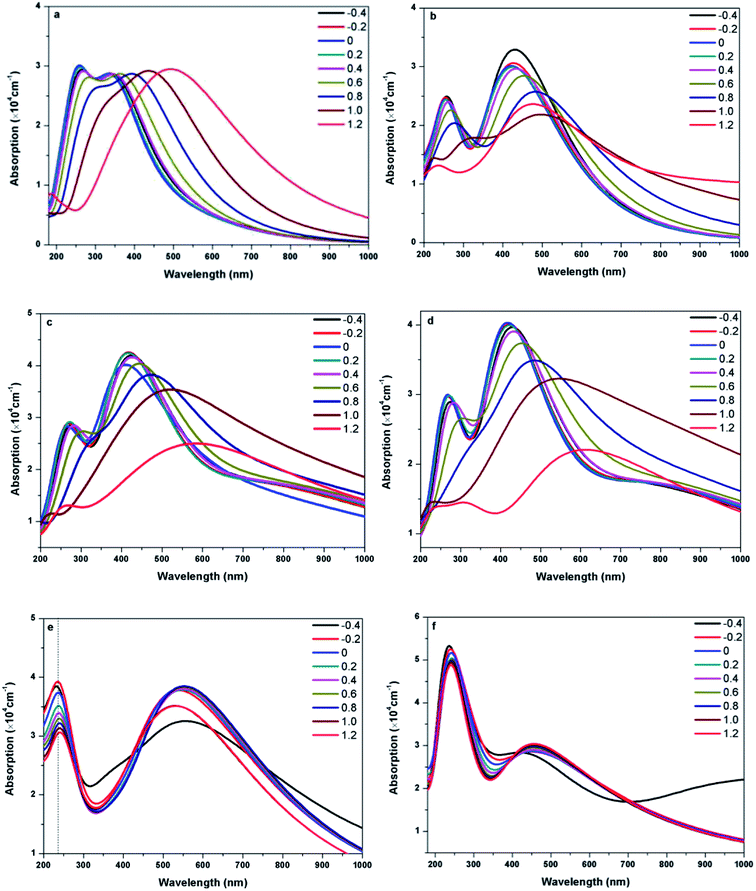
Fig. 8 presents the absorption spectra of doped graphenes under E_f ranging from −0.4 to 1.2 eV Å⁻¹. Obviously, the external electric fields have significant influences on the optical properties of B-G, Al-G, Si-G, and Ge-G. The higher the E_f, the more obvious the red shift of L peaks of B-G, Al-G, Si-G, and Ge-G. Moreover, the S peaks gradually disappear. Therefore, the external electric field may contribute to π → π* transitions especially under the higher E_f. For example, as shown in Fig. 8(a), the intensity of L peak for B-G has no significant changes after applying E_f, but L peak appears at 345, 338, 332, 338, 350, 367, 395, 440, and 492 nm under −0.4, −0.2, 0.0, 0.2, 0.4, 0.6, 0.8, 1.0, and 1.2 eV Å⁻¹, respectively. It implies that L peaks are red-shifted obviously with the increase of E_f independent of the direction of the electric field. Similarly, this phenomenon can also be observed for Al-G. As shown in Fig. 8(b), the L peaks of Al-G are shifted from 420(0.0), then 435(−0.4), 430(−0.2), 424(0.2), 435(0.4), 457(0.6), 482(0.8), and 500(1.0) to 482 nm (1.2 eV Å⁻¹), implying that the absorption spectra of Al-G are transferred from the purple region to blue region by the applied external electric field. Furthermore, the intensity of L peaks has been strengthened under the negative electric field direction. For Si-G system, as shown in Fig. 8(c), its L peaks are located at 429(4.19 × 10⁴), 419(4.25 × 10⁴), 417(4.24 × 10⁴), 424(4.16 × 10⁴), and 443(4.04 × 10⁴ cm⁻¹) nm under −0.4, −0.2, 0.2, 0.4, and 0.6 eV Å⁻¹, respectively. Therefore, the intensities of L peak are stronger than that of the zero electric field irrespective of the direction of the electric field, suggesting that the lower electric field may enhance the ability of π → π* transitions. On the other hand, L peaks are shifted from 470(3.82 × 10⁴) to 600(2.50 × 10⁴ cm⁻¹) nm when E_f ranges from 0.8 to 1.2 eV Å⁻¹, suggesting that the higher electric field makes the spectra of Si-G into the yellow region. For Ge-G, as shown in Fig. 8(d), the external electric field makes the L peak intensity decrease independent of the direction of the electric field. Meanwhile, L peaks are red-shifted from 417(0.0), then 431(−0.4), 422(−0.2), 420(0.2), 431(0.4), 457(0.6), 49(0.8), and 551(1.0) to 620 nm (1.2 eV Å⁻¹), implying that the absorption spectra of Ge-G have been transferred from the purple region to the orange region by applying the external electric field. Surprisingly, the absorption spectra of As-G and Sb-G exhibit the opposite phenomena. As shown in Fig. 8(e), the position of S peak of As-G has no obvious changes except the intensity of peak. L peaks fluctuate around 541 nm with the same intensity independent of the variation of the positive E_f. Under the negative E_f, the intensity of L peak decreases significantly. Similarly, as shown in Fig. 8(f), external electric field has only a slight effect on the intensity of the absorption peak of Sb-G. Probably, this point can be due to the fact that the degree of the migration for the valence band and conduction band under the external electric field is relatively small as shown in Fig. 5(b).

Fig. 8 The absorption spectra of B-G (a), Al-G (b), Si-G (c), Ge-G (d), As-G (e), and Sb-G (f) under different E_f ranging from −0.4 to 1.2 eV Å⁻¹.

3.4.2 Dielectric function and refractive index. The dielectric functions and refractive indexes of OG and doped graphenes have been shown in Fig. 9. As shown in Fig. 9(a), the real part of dielectric function (ε₁(0)) of OG at zero frequency is 7.20 eV. The imaginary part of the dielectric function (ε₂(ω)) of OG shows two peaks at 3.02 and 5.08 eV, respectively. As shown in Fig. 9(b), the refractive index n₀ (at zero frequency) is 2.68 eV for OG. Two peaks of the refractive index k(ω) of OG are located at 3.50 and 5.50 eV, respectively, which corresponds to the peaks of ε₂(ω). These results for OG are in good agreement with the experimental and other theoretical studies.^30,40,41 For the doped graphenes, the ε₁(0) of B-G, Al-G, Si-G, Ge-G, As-G, and Sb-G is 1.65, 1.90, 3.65, 3.80, 3.32, and 3.41 eV, respectively. Therefore, the doped graphenes have low ε₁(0) due to wider band gaps compared with OG. Compared with the other theoretical studies, ε₁(0) of B-G and Al-G are smaller than Nath⁴¹ and Zhao's⁴⁰ results due to the different k-point meshes used. ε₁(0) of Si-G and Ge-G is smaller than Kheyri and Rafique's results^24,30 due to the different concentrations of doped atom. As for As-G and Sb-G, no experimental and theoretical results are available at present. Moreover, the real part of dielectric function of OG does not show remarkable peaks in the range of 0–4 eV, while some peaks can be observed for B-G (1.87 eV), Al-G (2.14 eV), Si-G (0.86 and 2.22 eV), Ge-G (0.79 and 2.21 eV), As-G (2.29 eV), and Sb-G (0.53 eV). Similarly, the same is also true for the imaginary part of dielectric function. In the rang of 0–4 eV, there are very obvious peaks for Al-G (2.67 eV), Si-G (1.25 and 2.60 eV), Ge-G (1.20 and 2.57 eV), and As-G (1.83 eV) in the imaginary part. At the same time, there are weak peaks for B-G (2.67 eV) and Sb-G (1.84 eV) in this range. Therefore, the imaginary dielectric functions for doped graphenes move toward the low frequency compared with that of OG due to π → π* transitions, which is consistent with the changes of absorption spectra mentioned above. Moreover, this trend can be further confirmed by the analyses below.

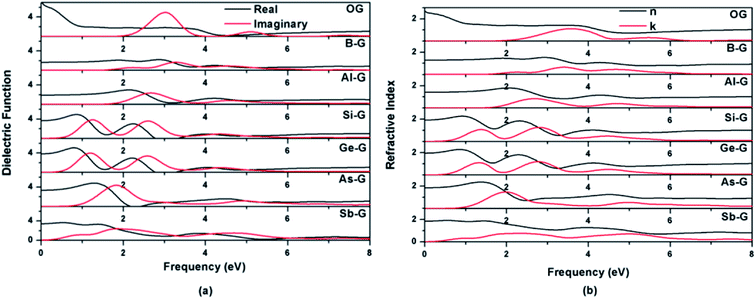Fig. 9 Dielectric functions (a) and refractive indexes (b) of OG, B-G, Al-G, Si-G, Ge-G, As-G, and Sb-G.

As shown in Fig. 9(b), the features of the refractive index of the doped graphenes are similar with that of dielectric function. The n₀ values of B-G, Al-G, Si-G, Ge-G, As-G, and Sb-G are 1.28, 1.40, 1.91, 1.95, 1.84, and 1.85 eV, respectively, indicating that the n₀ values of doped graphenes are smaller than that of OG. Meanwhile, doped graphenes also show obvious peaks of k(ω), corresponding to the peaks of ε₂(ω). In the 0–4 eV, the gentle peaks of B-G and Sb-G are located at 2.25 and 2.36 eV, respectively. The strong peaks occur at 2.68 eV for Al-G, 1.38 and 2.80 eV for Si-G, 1.33 and 2.78 eV for Ge-G, and 2.0 eV for As-G, respectively.

Fig. S2† shows the dielectric functions of doped graphenes under E_f ranging from −0.4 to 1.2 eV Å⁻¹. The real part of dielectric function (ε₁(0)) of doped graphenes at zero frequency are given in Table 3. Obviously, the ε₁(0) values of B-G, Al-G, Si-G, and Ge-G increase with the increase of E_f independent of the direction of the electric field. Moreover, as shown in Fig. S2,† the peak positions of the imaginary part of dielectric function for B-G, Al-G, Si-G, and Ge-G move toward low frequency under the same E_f. For As-G and Sb-G, the ε₁(0) values slowly increase and then decrease from −0.4 to 1.2 eV Å⁻¹, where a maximum value appears at 1.0 eV Å⁻¹. As for the imaginary part of dielectric function, it is similar to that of the real part. Overall, these results indicate that the applied electric field may contribute to the increase of the dielectric constant of B-G, Al-G, Si-G, and Ge-G except for As-G and Sb-G, which can be attributed to the fact that the applied electric field facilitates π → π* transitions of B-G, Al-G, Si-G, and Ge-G compared with As-G and Sb-G. Moreover, this phenomenon has also been reflected from the analyses of refractive index and loss function of doped graphenes under the external electric field.

Table 3 The real part of dielectric function (ε₁(0)) and refractive index (n(0)) of doped graphenes at zero frequency under different external electric fields

System		External electric field (eV Å^−1)
		−0.4	−0.2	0	0.2	0.4	0.6	0.8	1.0	1.2
B-G	ε1(0)	1.68	1.66	1.65	1.67	1.70	1.76	1.85	2.02	2.34
	n(0)	1.29	1.29	1.29	1.29	1.30	1.33	1.36	1.42	1.53
Al-G	ε1(0)	3.33	2.49	1.90	1.99	2.02	2.07	2.22	2.70	5.06
	n(0)	1.83	1.58	1.41	1.41	1.42	1.44	1.48	1.64	2.25
Si-G	ε1(0)	3.69	3.65	3.65	3.73	3.86	4.12	4.54	5.44	5.78
	n(0)	1.92	1.91	1.91	1.93	1.97	2.03	2.13	2.33	2.41
Ge-G	ε1(0)	3.84	3.79	3.81	3.88	4.03	4.32	4.82	6.53	4.42
	n(0)	1.96	1.95	1.95	1.97	2.01	2.08	2.20	2.55	2.10
As-G	ε1(0)	3.11	3.35	3.40	3.47	3.51	3.53	3.35	3.29	3.28
	n(0)	1.76	1.83	1.84	1.86	1.87	1.88	1.83	1.81	1.81
Sb-G	ε1(0)	3.40	3.41	3.42	3.48	3.50	3.50	3.51	3.52	3.28
	n(0)	1.20	1.85	1.85	1.87	1.768	1.87	1.87	1.88	1.88

---

Fig. S3† shows the refractive indexes of doped graphenes under the applied electric field. Compared with the results without electric field, some changes of their peak positions and peak intensities occur. Namely, the curves of them tend to lower frequency with stronger intensity.

3.4.3 Loss function. The loss functions of OG and doped graphenes are shown in Fig. S4.† It is clear that two main peaks of the loss function for OG appear at 4.27 and 5.76 eV because of the π and σ plasmon electrons excitation, respectively, which is consistent with the reported results.^30,40,41 Moreover, the first peak of the loss function of doped graphenes shifts toward low frequency with a weak intensity. For Al-G, Si-G, Ge-G, and As-G, the shift degrees of peak position are larger than those of B-G and Sb-G in the range of 0–4 eV. These phenomena are well consistent with the above results of 3.4.1 and 3.4.2 Sections. In conclusion, the values of the absorption spectra, dielectric function, refractive index, and loss function of the doped graphenes are shifted toward low frequency, resulting from interband transitions.

As show in Fig. S5,† the peaks of B-G and Al-G shift toward low frequency with decreasing intensity from −0.4 to 1.2 eV Å⁻¹. For Si-G and Ge-G, their peaks move toward low frequency with decreasing intensity from −0.4 to 0.8 eV Å⁻¹ and there is only a gentle peak in the range of 1.0–1.2 eV Å⁻¹. For As-G and Sb-G, there are no noticeable changes for their peak positions and intensities.

4. Conclusions

In this study, the electronic and optical properties of B, Al, Si, Ge, As, and Sb doped graphenes have been detailedly investigated by using DFT method in the absence and presence of the external electric field. The results illustrate that the band gap of B-G, Al-G, Si-G, Ge-G, As-G, and Sb-G is 0.676, 1.481, 0.783, 0.698, 0.682, and 1.583 eV, respectively. After applying the external electric field, the band gaps of B-G, Al-G, Si-G, and Ge-G are decreased with the increase of the external electric field intensity. On the contrary, for As-G and Sb-G, the band gaps of them have been increased and reached 0.864 and 1.841 eV under 1.2 eV Å⁻¹, respectively.

As for the absorption spectra, red shifts occur for B-G (347 nm), Al-G (404 nm), Si-G (412 nm), Ge-G (513 nm), As-G (531 nm), and Sb-G (454 nm) compared with that of graphene without the external electric field. Moreover, the peak positions of dielectric function, refractive index, and loss function of doped graphenes are moved toward low frequency region. The real part of dielectric function (ε₁(0)) and refractive index (n₀) of doped graphenes at zero frequency are smaller than that of pure graphene. After applying the external electric field, the absorption spectra of B-G, Al-G, Si-G, and Ge-G are shifted to longer wavelengths of visible light with the increase of the electric field intensity. Meanwhile, the peak positions of dielectric function, refractive index, and loss function of doped graphenes are moved toward lower frequency region. For As-G and Sb-G, the external electric field can not almost change the peak positions of the absorption spectra, dielectric function, refractive index, and loss function. It is expected that the present results of the properties of these doped graphenes will be beneficial to their applications in the field of optoelectronics.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by National Natural Science Foundation of China (21577076), Natural Science Foundation of Shandong Province (No. ZR2018MB020), the Project of Shandong Province Higher Educational Science and Technology Program (SK201504), and High Performance Computing Center of Qufu Normal University.

References

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric field effect in atomically thin carbon films, Science, 2004, 306, 666–669.
2. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, Two-dimensional gas of massless Dirac fermions in graphene, Nature, 2005, 438, 197–200.
3. C. W. J. Beenakker, Colloquium: Andreev reflection and Klein tunneling in graphene, Rev. Mod. Phys., 2008, 80, 1337–1354.
4. A. H. Castro Neto, F. Guinea, N. M. R. Peres, K. S. Novoselov and A. K. Geim, The electronic properties of graphene, Rev. Mod. Phys., 2009, 81, 109–162.
5. S. D. Sarma, S. Adam, E. H. Hwang and E. Rossi, Electronic transport in two dimensional graphene, Rev. Mod. Phys., 2011, 83, 407–470.
6. R. R. Nair, P. Blake, A. N. Grigorenko, K. S. Novoselov, T. J. Booth, T. Stauber, N. M. R. Peres and A. K. Geim, Fine structure constant defines visual transparency of graphene, Science, 2008, 320, 1308.
7. A. A. Balandin, S. Ghosh, W. Bao, I. Calizo, D. Teweldebrhan, F. Miao and C. N. Lau, Superior thermal conductivity of single-layer graphene, Nano Lett., 2008, 8, 902–907.
8. B. Luo, B. Wang, X. L. Li, Y. Y. Jia, M. H. Liang and L. J. Zhi, Graphene-confined Sn nanosheets with enhanced lithium storage capability, Adv. Mater., 2012, 24, 3538–3543.
9. C. H. Xu, B. H. Xu, Y. Gu, Z. G. Xiong, J. Sun and X. S. Zhao, Graphene-based electrodes for electrochemical energy storage, Energy Environ. Sci., 2013, 6, 1388–1414.
10. C. Lee, X. D. Wei, J. W. Kysar and J. Hone, Measurement of the elastic properties and intrinsic strength of monolayer graphene, Science, 2008, 321, 385–388.
11. G. Eda and M. Chhowalla, Chemically derived graphene oxide: towards large-area thin-film electronics and optoelectronics, Adv. Mater., 2010, 22, 2392–2415.
12. X. Huang, Z. Zeng, Z. Fan, J. Liu and H. Zhang, Graphene-based electrodes, Adv. Mater., 2012, 24, 5979–6004.
13. Q. Hu, X. Wu, Z. Yin and H. Zhang, Graphene-based electronic sensors, Chem. Sci., 2012, 3, 1764–1772.
14. L. Wang, Z. Sofer, P. Simek, I. Tomandl and M. Pumera, Boron-doped graphene: scalable and tunable p-type carrier concentration doping, J. Phys. Chem. C, 2013, 117, 23251–23257.
15. R. Lv, Q. Li, A. R. Botello-Mendez, T. Hayashi, B. Wang, A. Berkdemir and Q. Hao, Nitrogen-doped graphene: beyond single substitution and enhanced molecular sensing, Sci. Rep., 2012, 2, 586.
16. A. Fukushima, A. Sawairi, K. Doi, M. Senami, L. Chen, H. Cheng and A. Tachibana, Role of an aluminum atom on graphene for hydrogen adsorption, J. Phys. Soc. Jpn., 2011, 80, 074705.
17. P. A. Denis, Band gap opening of monolayer and bilayer graphene doped with aluminium, silicon, phosphorus, and sulfur, Chem. Phys. Lett., 2010, 492, 251–257.
18. D. Gonzalez Larrude, Y. Garcia-Basabe, F. Lazaro Freire Jr and M. L. M. Rocco, Electronic structure and ultrafast charge transfer dynamics of phosphorous doped graphene layers on a copper substrate: a combined spectroscopic study, RSC Adv., 2015, 5, 74189–74197.
19. S. Yang, L. Zhi, K. Tang, X. Feng, J. Maier and K. Müllen, Efficient synthesis of heteroatom (N or S)-doped graphene based on ultrathin graphene oxideporous silica sheets for oxygen reduction reactions, Adv. Funct. Mater., 2012, 22, 3634–3640.
20. Z. Wang, P. Li, Y. Chen, J. He, W. Zhang, O. G. Schmidt and Y. Li, Thiophene–sulfur doped reduced graphene oxide: synthesis, structure, and electrical properties, Nanoscale, 2014, 6, 7281–7287.
21. L. Wei, G. L. Liu, D. Zh. Fan and G. Y. Zhang, Density functional theory study on the electronic structure and optical properties of S absorbed graphene, Phys. B, 2018, 545, 99–106.
22. Y. Zou, F. Li, Z. H. Zhu, M. W. Zhao, X. G. Xu and X. Y. Su, An ab initio study on gas sensing properties of graphene and Si-doped graphene, Eur. Phys. J. B, 2011, 81, 475–479.
23. M. Houmad, H. Zaari, A. Benyoussef, A. E. Kenz and H. Ez-Zahraouy, Optical conductivity enhancement and band gap opening with silicon doped graphene, Carbon, 2015, 94, 1021–1027.
24. M. Rafique, Y. Shuai and N. Hussain, First-principles study on silicon atom doped monolayer graphene, Phys. E, 2018, 95, 94–101.
25. Z. Jin, H. Nie, Z. Yang, J. Zhang, Z. Liu, X. Xu and S. Huang, Metal-free selenium doped carbon nanotube/graphene networks as a synergistically improved cathode catalyst for oxygen reduction reaction, Nanoscale, 2012, 4, 6455–6460.
26. P. A. Denis, Chemical reactivity and band-gap opening of graphene doped with gallium, germanium, arsenic, and selenium atoms, ChemPhysChem, 2014, 15, 3994–4000.
27. R. J. Toh, H. L. Poh, Z. Sofer and M. Pumera, Transition metal (Mn, Fe Co, Ni)-doped graphene hybrids for electrocatalysis, Chem.–Asian J., 2013, 8, 1295–1300.
28. J. Zhao, Q. Deng, A. Bachmatiuk, G. Sandeep, A. Popov, J. Eckert and M. H. Rümmeli, Free-standing single-atom-thick iron membranes suspended in graphene pores, Science, 2014, 343, 1228–1232.
29. A. W. Robertson, B. Montanari, K. He, J. Kim, C. S. Allen, Y. A. Wu, J. Olivier, J. Neethling, N. Harrison, A. I. Kirkland and J. H. Warner, Dynamics of single Fe atoms in graphene vacancies, Nano Lett., 2013, 13, 1468–1475.
30. A. Kheyri, Z. Nourbakhsh and E. Darabi, Effect of Fe, Co, Si and Ge impurities on optical properties of graphene sheet, Thin Solid Films, 2016, 612, 214–224.
31. Z. Sofer, O. Jankovsky, P. Simek, K. Klimova, A. Mackova and M. Pumera, Uraniumand thorium-doped graphene for efficient oxygen and hydrogen peroxide reduction, ACS Nano, 2014, 8, 7106–7114.
32. E. Cruz-Silva, F. López-Urías, E. Muñoz-Sandoval, B. G. Sumpter, H. Terrones, J. C. Charlier, V. Meunier and M. Terrones, Electronic transport and mechanical properties of phosphorus- and phosphorus–nitrogen-doped carbon nanotubes, ACS Nano, 2009, 3, 1913–1921.
33. X. Ma, G. Ning, C. Xu and J. Gao, Phosphorus and nitrogen dual-doped few-layered porous graphene: a high performance anode material for lithium ion batteries, ACS Appl. Mater. Interfaces, 2014, 6, 14415–14422.
34. B. Feng, J. Xie, C. Dong, S. Zhang, G. Cao and X. Zhao, Graphite oxide to nitrogen and sulfur Co-doped few-layered graphene by a green reduction route via Chinese medicinal herbs, RSC Adv., 2014, 4, 17902–17907.
35. P. A. Denis and C. Pereyra Huelmo, Structural characterization and chemical reactivity of dual doped graphene, Carbon, 2015, 87, 106–115.
36. M. M. Ervasti, Z. Fan, A. Uppstu, A. Krasheninnikov and A. Harju, Silicon and silicon-nitrogen impurities in graphene: structure, energetics and effects on electronic transport, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 235412.
37. S. Ullah, A. Hussain, W. Syed, M. A. Saqlain, I. Ahmad, O. Leenaerts and A. Karim, Band-gap tuning of graphene by Be doping and Be, B co-doping: a DFT study, RSC Adv., 2015, 5, 55762–55773.
38. A. Hussain, S. Ullah and A. Farhan, Fine tuning the band-gap of graphene by atomic and molecular doping: a density functional theory study, RSC Adv., 2016, 6, 55990–56003.
39. O. Olaniyan, E. Mapasha, D. Momodu, J. Madito, A. A. Khaleed, F. U. Ugbo, A. Bello, F. Barzegar, K. Oyedotun and N. Manyala, Exploring the stability and electronic structure of beryllium and sulphur Co-doped graphene: first principles study, RSC Adv., 2016, 6, 88392–88402.
40. X. Zhou, C. H. Zhao, G. F. Wu, J. H. Chen and Y. Q. Li, DFT study on the electronic structure and optical properties of N, Al, and N-Al doped graphene, Appl. Surf. Sci., 2018, 459, 354–362.
41. P. Nath, S. Chowdhury, D. Sanyal and D. Jana, Ab-initio calculation of electronic and optical properties of nitrogen and boron doped graphene nanosheet, Carbon, 2014, 73, 275–282.
42. G. C. Loh and R. Pandey, A graphene-boron nitride lateral heterostructure – a first-principles study of its growth, electronic properties, and chemical topology, J. Mater. Chem. C, 2015, 3, 5918–5932.
43. M. Y. Han, B. Ozyilmaz, Y. B. Zhang and P. Kim, Energy band-gap engineering of graphene nanoribbons, Phys. Rev. Lett., 2007, 98, 206805.
44. Y. W. Son, M. L. Cohen and S. G. Louie, Half-metallic graphene nanoribbons, Nature, 2006, 44, 347–349.
45. Y. Lu and J. Guo, Band gap of strained graphene nanoribbons, Nano Res., 2010, 3, 189–199.
46. G. Cocco, E. Cadelano and L. Colombo, Gap opening in graphene by shear strain, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 241412.
47. V. Hung Nguyen, et al., Disorder effects on electronic bandgap and transport in graphene-nanomesh-based structures, J. Appl. Phys., 2013, 113, 013702.
48. P. Rani, G. S. Dubey and V. K. Jindal, DFT study of optical properties of pure and doped graphene, Phys. E, 2014, 62, 28–35.
49. R. Muhammad, Y. Shuai and H. P. Tan, First-principles study on hydrogen adsorption on nitrogen doped graphene, Phys. E, 2017, 88, 115–124.
50. X. Lu, X. Gao, J. Ren, C. Li, X. Guo, X. Yan and P. La, Effects of diverse metal adsorptions on the electronic and optical properties of the β-Si3N4 (2 0 0) surface: a first-principles study, Comput. Mater. Sci., 2018, 151, 296–306.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra00326f

---