Open Access Article
Open Access ArticleImpacts of 5d electron binding energy and electron–phonon coupling on luminescence of Ce3+ in Li6Y(BO3)3
Yiyi Ou a,
Weijie Zhou
a,
Weijie Zhou a,
Dejian Houb,
Mikhail G. Brikcde,
Pieter Dorenbos
a,
Dejian Houb,
Mikhail G. Brikcde,
Pieter Dorenbos f,
Yan Huangg and
Hongbin Liang
f,
Yan Huangg and
Hongbin Liang *a
*a
aMOE Key Laboratory of Bioinorganic and Synthetic Chemistry, KLGHEI of Environment and Energy Chemistry, School of Chemistry, Sun Yat-sen University, Guangzhou 510275, China. E-mail: cesbin@mail.sysu.edu.cn
bSchool of Materials Science and Engineering, Hanshan Normal University, Chaozhou, 521041, China
cCollege of Sciences, Chongqing University of Posts and Telecommunications, Chongqing 400065, China
dInstitute of Physics, University of Tartu, Tartu 50411, Estonia
eInstitute of Physics, Jan Długosz University, PL-42200 Częstochowa, Poland
fFaculty of Applied Sciences, Delft University of Technology, Mekelweg 15, 2629 JB Delft, The Netherlands
gBeijing Synchrotron Radiation Facility, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100039, China
First published on 11th March 2019
Abstract
In this work, the crystal structure and electronic structure as well as the synchrotron radiation vacuum ultraviolet-ultraviolet-visible (VUV-UV-vis) luminescence properties of Li6Y(BO3)3 (LYBO):Ce3+ phosphors were investigated in detail. The Rietveld refinement and DFT calculation reveal the P21/c monoclinic crystal phase and the direct band gap of the LYBO compound, respectively. Only one kind of Ce3+ 4f–5d transition is resolved in terms of the low temperature VUV-UV excitation, UV-vis emission spectra and luminescence decay curves. Furthermore, by constructing the vacuum referred binding energy (VRBE) scheme and applying the frequency-degenerate vibrational model, the impacts of 5d electron binding energy and electron–phonon coupling on luminescence of Ce3+ in LYBO are analysed. The results show that the Ce3+ emission in LYBO possesses a moderate intrinsic thermal stability. With the increase in concentration, the thermal stability of the emission gets worse due to the possible thermally-activated concentration quenching. In addition, the simulation of Ce3+ emission profile at low temperature reveals that the 4f–5d electronic transitions of Ce3+ ions can be treated to couple with one frequency-degenerate vibrational mode having the effective phonon energy of ∼257 cm−1 with the corresponding Huang–Rhys parameter of ∼6, which indicates a strong electron–phonon interaction of Ce3+ luminescence in the Li6Y(BO3)3 host. Finally, the X-ray excited luminescence spectrum of the LYBO:5%Ce3+ phosphor is measured to check the potential scintillator applications.
1. Introduction
Due to the large absorption cross section, high efficiency, tuneable emission wavelength and fast decay of the spin- and parity-allowed 4f–5d transitions, the Ce3+ activated inorganic compounds have been extensively studied for their application in solid-state lighting, ionizing radiation detection, and so on.1,2 For instance, Ce3+ activated Y3Al5O12 with high quantum efficiency and good thermal stability is a commercial yellow phosphor for the white light-emitting diodes driven by a blue chip.3 The Ce3+ activated LaBr3 with large light output, excellent energy resolution, and fast decay time is a good scintillator for gamma-ray discrimination.4 In addition, Ce3+ can also serve as an efficient sensitizer for other lanthanide luminescence.5,6In essence, two factors impose great influence on the luminescence of Ce3+ in a dielectric inorganic compound. Firstly, the crystal field strength and nephelauxetic effect together determine the 5d energy (including the crystal field splitting and the centroid shift) of Ce3+ in a given host compound.7 From a viewpoint of electron binding energy, the Ce3+ 5d electron binding energy, rather than that of 4f electron, mainly decides the absorption energy of Ce3+ activated phosphors.8 Furthermore, due to the thermal ionization mechanism for Ce3+ emission thermal quenching, the gap of Ce3+ 5d electron binding energy to the bottom of host conduction band (CB) also impacts the thermal stability of Ce3+ luminescence.9,10 Secondly, the electron–phonon coupling significantly influences the Ce3+ luminescence. The resulting Stokes shift along with the absorption wavelength of Ce3+ determines the emission colour of phosphors.11 Moreover, the width of emission bands that are attributed to the vibronic transitions progressing up to several harmonics of the vibrational frequencies further affects the phosphor colour purity.12 Consequently, it is critical to understand the influences of 5d electron binding energy and electron–phonon coupling on luminescence to develop the superior Ce3+ activated phosphors with desired properties.
In this work, the crystal structure and electronic structure of the host compound Li6Y(BO3)3 (LYBO) and Ce3+ doped samples prepared via a high-temperature solid-state reaction method were investigated. The VUV-UV excitation spectra, the UV-vis emission spectra and the decay curves of doping samples at different concentrations and temperatures were studied in detail. The construction of the vacuum referred binding energy scheme13 and the simulation with the frequency-degenerate model14 were performed to get insight into the impacts of 5d electron binding energy and electron–phonon coupling on luminescence of Ce3+ in Li6Y(BO3)3, including the intrinsic thermal stability and spectral profile of Ce3+ emissions. These analyses could also be applied to other Ce3+ doped systems and help to develop the novel phosphors with desired properties.
2. Experimental section
The Ce3+ doped powder samples Li6Y1−xCex(BO3)3 (x = 0.05, 0.08, 0.10, 0.15) were synthesized via a conventional high-temperature solid-state reaction method. Stoichiometric amounts of starting materials Li2CO3 (Analytical Reagent, AR), H3BO3 (AR), Y2O3 (99.99%), and CeO2 (99.99%) were weighted and ground finely in an agate mortar. The homogeneous mixture was calcined in an alumina crucible at 700 °C for 6 hours in thermal carbon reductive atmosphere and cooled down to room temperature (RT). Finally, the obtained products were ground into powder for further measurements. The phase purity of powder samples was checked by a Rigaku D-MAX 2200 VPC X-ray diffractometer with Cu Kα radiation (λ = 1.5418 Å) at 40 kV and 26 mA. High-quality XRD data over a 2θ range of 5° to 100° at an interval of 0.02° for Rietveld refinement was collected by a Bruker D8 advanced X-ray diffractometer with Cu Kα radiation (λ = 1.5418 Å) at 40 kV and 40 mA. The Rietveld refinement was performed by using the TOPAS-Academic program.15 The UV-vis luminescence spectra and decay curves were recorded on an Edinburgh Instrument FLS920 combined fluorescence lifetime and steady-state spectrometer. The vacuum ultraviolet-ultraviolet (VUV-UV) excitation spectra were recorded on the beamline 4B8 of the Beijing Synchrotron Radiation Facility (BSRF).16 The X-ray excited luminescence spectrum was recorded by using a Philips PW2253/20 X-ray tube and a Cu anode operating at 40 kV and 25 mA at Delft University of Technology, the Netherlands.The atomic structures of the LYBO host unit cell were fully relaxed by using periodic density functional theory (DFT) calculations with the PBE functional17 as well as the PBE0 hybrid functional,18 as implemented in the VASP code.19,20 The electrons of Li(1s22s1), Y(4s24p64d15s2), B(2s22p1), and O(2s22p4) were treated as valence electrons, and their interactions with the respective cores were described by the projected augmented wave (PAW) method.21 The convergence criteria for total energies and atomic forces were set to 10−6 eV and 0.01 eV Å−1, respectively. A 3 × 2 × 3 k-point grid in the Monkhorst–Pack scheme was used to sample the Brillouin zone, with a cutoff energy of 530 eV for the plane wave basis.
3. Results and discussion
3.1 Crystal structure and electronic structure of LYBO
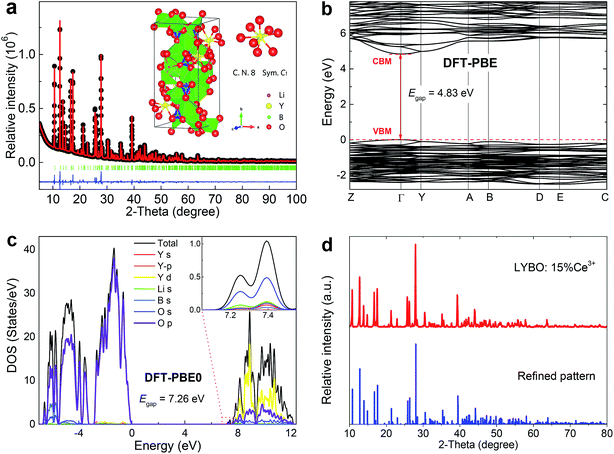
Rietveld refinement of high-quality XRD data of synthesized LYBO compound was conducted by using P21/c (monoclinic) structure as an initial model (Fig. 1a).22 The reliability factors Rwp (∼4.983%), Rp (∼3.319%) and RB (∼2.876%) all imply a good fitting quality. No other impurity was found, indicating the single pure phase of the synthesized sample. The refined structural parameters are listed in Table 1. The compound LYBO has a monoclinic structure with space group P21/c and the lattice parameters are a = 7.180 (1) Å, b = 16.43 (2) Å, c = 6.634 (1) Å, β = 105.3 (1) deg, V = 754.9 Å3 and Z = 4. All the constituent ions sit on the 4e Wyckoff positions. There are six kinds of lithium ions: four of them coordinate to five oxygens to construct the distorted Li–O trigonal bipyramids, and two remaining link to four oxygens to form the Li–O tetrahedron. Three kinds of boron ions all coordinate to three oxygens to form the planar triangles. There is only one type of Y3+ ion and it is surrounded by eight oxygens with C1 point symmetry, which forms a Y–O distorted tetragonal prism. The average Y–O bond length is ∼2.376 Å. The distance between the nearest Y3+ ions is ∼3.879 Å. As shown in the inset of Fig. 1a, these Li–O, Y–O polyhedral and B–O planar triangles share their apexes or edges to construct the structural framework of LYBO compound.| Atom | Site | x | y | z | occ. | beq |
|---|---|---|---|---|---|---|
| Y1 | 4e | 0.0801 (3) | 0.3112 (1) | 0.1542 (3) | 1 | 1.12 |
| Li1 | 4e | 0.0713 (2) | 0.5040 (2) | 0.1735 (5) | 1 | 1.28 |
| Li2 | 4e | 0.550 (1) | 0.4696 (9) | 0.675 (2) | 1 | 1.28 |
| Li3 | 4e | 0.712 (2) | 0.2050 (8) | 0.867 (2) | 1 | 1.28 |
| Li4 | 4e | 0.306 (2) | 0.4639 (9) | 0.941 (2) | 1 | 1.28 |
| Li5 | 4e | 0.438 (2) | 0.2945 (9) | 0.952 (2) | 1 | 1.28 |
| Li6 | 4e | 0.862 (2) | 0.0519 (8) | 0.917 (2) | 1 | 1.28 |
| B1 | 4e | 0.440 (1) | 0.3852 (6) | 0.312 (1) | 1 | 1.15 |
| B2 | 4e | 0.715 (1) | 0.1201 (5) | 0.497 (1) | 1 | 1.15 |
| B3 | 4e | 0.083 (1) | 0.1356 (5) | 0.161 (1) | 1 | 1.15 |
| O1 | 4e | 0.6078 (8) | 0.4211 (3) | 0.4242 (8) | 1 | 1.39 |
| O2 | 4e | 0.4206 (8) | 0.3022 (3) | 0.2738 (8) | 1 | 1.39 |
| O3 | 4e | 0.2782 (8) | 0.0685 (3) | 0.7298 (8) | 1 | 1.39 |
| O4 | 4e | 0.5361 (8) | 0.0887 (3) | 0.4133 (8) | 1 | 1.39 |
| O5 | 4e | 0.7400 (8) | 0.2970 (3) | 0.0556 (8) | 1 | 1.39 |
| O6 | 4e | 0.8773 (8) | 0.0745 (3) | 0.5400 (8) | 1 | 1.39 |
| O7 | 4e | 0.0873 (8) | 0.0528 (3) | 0.1769 (8) | 1 | 1.39 |
| O8 | 4e | 0.1472 (8) | 0.1847 (3) | 0.3338 (7) | 1 | 1.39 |
| O9 | 4e | 0.0087 (8) | 0.3263 (3) | 0.4735 (8) | 1 | 1.39 |
The atomic structures of LYBO unit cell were optimized, and the calculated parameters with the PBE (PBE0) functional are a = 7.237 (7.176) Å, b = 16.501 (16.332) Å, c = 6.711 (6.641) Å, β = 105.488 (105.428) deg, in good agreement with experimental data. The band structure of LYBO calculated with the PBE functional is displayed in Fig. 1b, showing a direct band gap of 4.83 eV with the valence band maximum (VBM) and the conduction band minimum (CBM) both located at the k-point Γ. It is well known that the band gaps of inorganic compounds are usually underestimated by DFT-PBE calculations, and can be obtained quite accurately by hybrid DFT calculations. Fig. 1c gives the calculated total and orbital projected densities of states (DOS) for LYBO with the PBE0 functional. The band gap is predicted to be 7.26 eV, close to the experimentally estimated value of 7.44 eV as discussed below. The top of the valence band is dominated by O 2p states, and the bottom of the conduction band is mainly composed of Y 4d states with small contributions from O 2s, 2p states. The conduction band edge is constituted by a small peak at 7.26 eV above the VBM, which is mainly derived from s-character states of O atoms. It is noted that, with the PBE functional, the calculated orbital characters for the valence and conduction bands are basically the same, although with a much smaller band gap.
For the Ce3+ doped samples, their structures were studied via XRD technique. Fig. 1d shows the representative result. The pattern of concentrated sample Li6Y0.85Ce0.15(BO3)3 (LYBO:15%Ce3+) agrees well with the refined result, which implies a single LYBO phase. Due to the comparable effective ionic radii [r(Y3+) = 101.9 pm, r(Ce3+) = 114.3 pm]23 and the same valence state (3+), the doped Ce3+ ions are thought to enter Y3+ sites in LYBO.
3.2 Photoluminescence and VRBE scheme of Ce3+ in LYBO
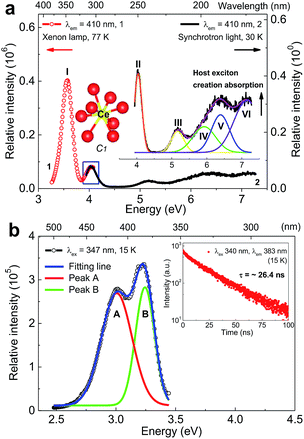
Fig. 2a shows the VUV-UV excitation (λem = 410 nm) spectra of sample Li6Y0.95Ce0.05(BO3)3 (LYBO:5%Ce3+) recorded by using the xenon lamp (curve 1) and synchrotron light (curve 2) at 77 and 30 K, respectively. These two curves display a good consistence in their energetic overlapping range of 3.93–4.07 eV, viz., 304–315 nm. The excitation band at ∼7.04 eV can be assigned as the host exciton creation absorption of LYBO.24 Thus, the corresponding exciton creation energy (Eex) is ∼7.04 eV. By adopting a value of 0.008 × (Eex)2 for the exciton binding energy,25 the bottom of CB is estimated to be about 7.04 + 0.40 = 7.44 eV higher than the top of VB. This mobility band gap value is near that of LiCaBO3 (∼7.78 eV),26 Ca3La3(BO3)5 (∼7.65 eV),27 and Ba2Ca(BO3)2 (∼7.61 eV).28 In addition, the other low-lying excitation bands in Fig. 2a can be aligned to the 5d excitation bands of Ce3+ in LYBO. Since the Ce3+ ion enters the eight-fold coordinated Y3+ sites with C1 point symmetry, the 5d1 configuration of Ce3+ should be split into five levels by crystal field. In the related literature,24 due to the severe overlapping of Ce3+ 5d excitation bands in LYBO, only four bands at ∼345 nm (∼3.59 eV), ∼305 nm (∼4.06 eV), ∼240 nm (∼5.16 eV), and ∼217 nm (∼5.71 eV) are well resolved at RT and one high-lying excitation band remains vague. In our case, the band I at ∼3.57 eV (∼347 nm) in curve 1 can be assigned to the lowest 5d excitation (4f–5d1) band. To further determine the energies of higher 5d excitation bands of Ce3+ and host absorption, we fitted the curve 2 by using a sum of five Gaussian functions. As shown in the inset of Fig. 2a, the band VI at ∼7.04 eV corresponds to the host exciton creation absorption of LYBO as discussed above; the bands II (∼4.04 eV), III (∼5.16 eV) and IV (∼5.91 eV) are in good accordance with the above-cited reference; the band V at ∼6.39 eV is then tentatively assigned to the highest 5d excitation band of Ce3+. With these assignments, the centroid energy of Ce3+ 5d states in LYBO, i.e. the arithmetic mean value of five Ce3+ 5d excitation energies, is calculated to be ∼5.01 eV. Compared to the free Ce3+ ion case (∼6.35 eV), the centroid shift energy (εc) is ∼1.34 eV for our case, which is similar to other borates such as LuBO3 (∼1.39 eV),29 Sr2Mg(BO3)2 (∼1.36 eV)30 and Ba2Mg(BO3)2 (∼1.34 eV).31 This indicates that these host compounds have similar covalence, spectroscopic polarizability and nephelauxetic effect.29 In addition, the crystal field splitting energy (Ecfs) of Ce3+ 5d states in LYBO, i.e. the energy difference between the highest and lowest 5d excitation bands of Ce3+, is estimated to be ∼2.82 eV. Compared to the Ecfs values of other Ce3+ ions occupying the sites with similar coordination number (8) and point symmetry (C1) in borates like YBO3 (∼2.72 eV),32 Ca3(BO3)2 (∼2.34 eV)24 and SrB2O4 (∼2.16 eV),33 the Ecfs value of our case is a bit larger, implying its greater distortion of coordination polyhedron and smaller site size.34Fig. 2b shows the emission (λex = 347 nm) spectrum of sample LYBO:5%Ce3+ at 15 K. A sum of two Gaussian functions was applied to fit this curve. Two fitting emission bands (A and B) are at ∼3.01 eV (∼412 nm) and ∼3.24 eV (∼383 nm), respectively. They pertain to the transitions from the lowest 5d excited state (5d1) to the 4f ground states 2F7/2 and 2F5/2 of Ce3+, respectively. Their energy difference is about 0.23 eV, which is near the common value (0.25 eV).35 The Stokes shift of Ce3+ in LYBO is calculated to be ∼0.33 eV by using the peak energies of 4f–5d1 excitation band I and emission band B. It is quite normal for Ce3+ luminescence.36 The luminescence decay curve (λex = 340 nm, λem = 383 nm) at 15 K in the inset of Fig. 2b slightly deviates from the single exponential behaviour, which indicates a small concentration quenching of Ce3+ emission. Then, the lifetime of Ce3+ emission is fitted to be ∼26.4 ns, which is close to the average result (∼29 ns) of Li6(Y,Lu)(BO3)3 mixed crystals in reference.37
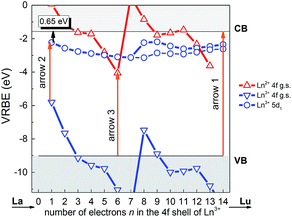
As a useful tool to evaluate the binding energies of lanthanides, especially the Ce3+ ions, in host compounds and study their impacts on the lanthanide luminescence, the vacuum referred binding energy (VRBE) scheme of lanthanide 4f and 5d states in LYBO is then constructed in Fig. 3. The required experimental data include the mobility host band gap EBG (∼7.44 eV, see arrow 1 in Fig. 3) of LYBO, the lowest 5d excitation energy (E5d1) of Ce3+ (∼3.57 eV, see arrow 2) in LYBO, the centroid shift energy (εc) of Ce3+ 5d states (∼1.34 eV), and the O2− → Eu3+ charge transfer energy ECT (∼4.96 eV, see arrow 3).38 The related semi-empirical models and construction process39 are briefly introduced below.
Firstly, due to their similar fashion affected by the chemical environment, the Coulomb repulsion energy U(6, LYBO) representing the difference between the 4f ground state binding energies of Eu2+ and Eu3+ in LYBO, is estimated to be ∼6.98 eV by using the εc of Ce3+ 5d states as shown in eqn (1).32 This obtained value falls in a common range of 6–7.6 eV for U(6, A) in inorganic host A.32 Then, based on the chemical shift model which employs a simple Coulomb repulsion interaction between 4f electrons and a hypothetic environment screening charge to describe the rises of Eu2+/Eu3+ 4f electron binding energies,8 the VRBE of Eu2+ 4f ground state (g. s.) E4f(Eu2+) is calculated to be about −4.06 eV with eqn (2). Consequently, the binding energy of Eu3+ 4f ground state E4f(Eu3+) = E4f(Eu2+) − U(6, LYBO) = −4.06 − 6.98 = −11.04 eV relative to the vacuum level. With these two 4f ground state VRBEs of Eu2+/Eu3+ ions as the pinpoints, the 4f ground state VRBEs of other divalent and trivalent lanthanide ions (Ln2+/Ln3+) can be derived in LYBO by using the corresponding universal shapes of zigzag curves for Ln2+/Ln3+.32 Therefore, the VRBE of Ce3+ 4f ground state E4f(Ce3+) is calculated to be about −5.80 eV. By adding the Ce3+ lowest 5d excitation energy (E5d1, ∼3.57 eV), the VRBE of Ce3+ lowest 5d excited state is around −2.23 eV.
| U(6, LYBO) = 5.44 + 2.834e−εc/2.2 (eV) | (1) |
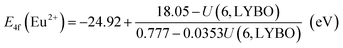 | (2) |
In addition, the charge transfer model40 demonstrates that the O2− → Eu3+ charge transfer energy provides the 4f ground state binding energy of Eu2+ relative to the top of valence band that is comprised by O 2p orbitals. Thus, the VRBE of electrons in the top of valence band is E4f(Eu2+) − ECT = −4.06 − 4.96 = −9.02 eV and that of electrons in the bottom of conduction band is −9.02 + EBG = −1.58 eV.
Generally, the intrinsic thermal quenching of Ce3+ f–d emission is thought to be mainly caused by the thermal ionization of electrons from the lowest 5d excited state to the bottom of CB in the isolated Ce3+ scenario where not taking the effect of concentration quenching into account.41 Therefore, when the binding energy of Ce3+ lowest 5d state is known, its energy gap to the bottom of conduction band can be a clue that evaluates the thermal stability of Ce3+ f–d emission. From the constructed VRBE scheme of lanthanide ions in LYBO (Fig. 3), one can immediately obtain this energy gap is about 0.65 eV, which is smaller when compared to those of Ce3+ in other hosts, such as LiCaBO3 (∼0.74 eV),26 KSrPO4 (∼1.27 eV),42 and so on. This implies that the Ce3+ emission in LYBO host may possess a moderate thermal stability. When the doping concentration increases, the thermal stability of Ce3+ f–d emission is further influenced by the thermally-activated concentration quenching.43 We will discuss it later.
The influence of doping concentration on Ce3+ emission is investigated as follows. Fig. 4 displays the highest-height-normalized emission (λex = 347 nm) spectra of samples LYBO:xCe3+ (x = 0.05–0.15) at RT. Their spectral profiles and energetic positions almost keep unchanged. Only the relative intensity of emission band at high-energetic side (375–400 nm) slightly decreases with the doping concentration increasing, which is caused by the enhanced self-absorption of Ce3+ emissions. The inset of Fig. 4 shows that the integrated emission intensity of Ce3+ firstly increases in the concentration range of 0.05–0.10, and then it drops at x = 0.15. Consequently, the concentration quenching occurs in this concentration range, viz., the excitation energy is more possibly transferred to the traps or quenching sites via energy migration between Ce3+ ions rather than emitted radiatively.35
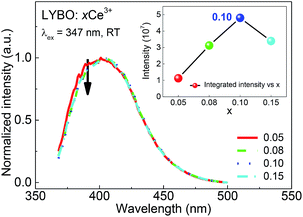 | ||
| Fig. 4 Highest-height-normalized emission (λex = 347 nm) spectra of sample LYBO:xCe3+ (x = 0.05–0.15) at RT. The inset shows the integrated emission intensity as a function of doping concentration. | ||
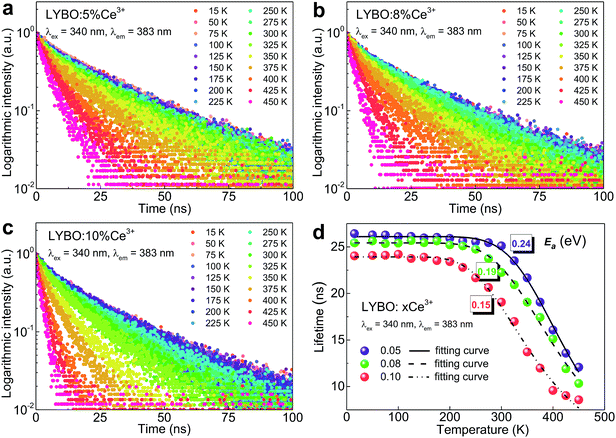
In addition, the thermal stability of Ce3+ emission is studied. It is believed that the temperature-dependent luminescence decay curves of Ce3+ emissions give the more precise information on their thermal quenching properties compared to the intensity measurements.43 Consequently, the luminescence decay curves (λex = 340 nm, λem = 383 nm) of samples LYBO:xCe3+ (x = 0.05–0.10) in the temperature range of 15–450 K are collected as shown in Fig. 5a–c. With the increase of temperature, the Ce3+ luminescence decay turns faster, which indicates that the thermal quenching of Ce3+ emission happens. More clearly, we further extracted the lifetime values of Ce3+ emissions in Fig. 5d via the average lifetime equation.44 For the results of sample LYBO:5%Ce3+, there are two stages separated by about 300 K: (i) when the temperature is lower than 300 K, the lifetime values seem unchanged (∼26.1 ns) and the platform implies no thermal quenching in this temperature range; (ii) when the temperature exceeds 300 K, the lifetime values gradually decrease due to the thermal quenching of Ce3+ emission. As for other concentrated samples, the temperature points corresponding to the beginning of the thermal quenching are about 250 and 200 K for samples LYBO:8%Ce3+ and LYBO:10%Ce3+, respectively, which indicate that the Ce3+ emissions turn to thermally quench more easily when the doping concentration increases. We then used the Arrhenius equation45 to fit the lifetime data in Fig. 5d and the obtained activation energy (Ea) values are ∼0.24, ∼0.19, and ∼0.15 eV for these three samples, which further confirm the worse thermal stability of Ce3+ emissions in the concentrated samples. In fact, these phenomena are because of the thermally-activated concentration quenching of Ce3+ emissions at high-doping level.43 From the decreasing lifetime values (∼26.1, ∼25.4, and ∼23.9 ns) corresponding to the thermally-stable platforms of samples LYBO:xCe3+ (x = 0.05–0.10) in Fig. 5d, it is evident that the Ce3+ emissions experience the concentration quenching in this investigated range, which is consistent with the results in Fig. 4. Consequently, when the temperature increases, the energy transfer between Ce3+ ions may be thermally enhanced and finally leads to the result that the excitation energy is more possibly transferred to the traps or quenching sites, i.e. the more severe concentration quenching. As for the difference between the VRBE-scheme-derived energy gap and the Arrhenius-equation-fitted activation energies that both describe the thermal quenching properties of Ce3+ emission, it can be related to the lattice relaxation process.45
3.3 Electron–phonon coupling of Ce3+ in LYBO
To further study the impact of electron–phonon coupling on Ce3+ luminescence in LYBO host, we select the emission (λex = 347 nm) spectrum of sample LYBO:5%Ce3+ at 15 K as shown in Fig. 6 as a presentation. Generally, at low temperature, the vibronic emission transitions of Ce3+ ions are thought to occur from the zero-phonon level (N = 0) of the initial state (5d1 state). The probability (pN) for a transition from the zero-phonon level of 5d1 state to the Nth vibrational level (Nℏω) of the final state, such as 4f1 2F5/2 or 2F5/2 state, can be expressed in the framework of Franck–Condon principle as follows:46
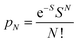 | (3) |
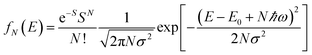 | (4) |
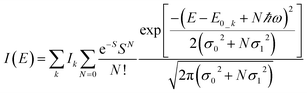 | (5) |
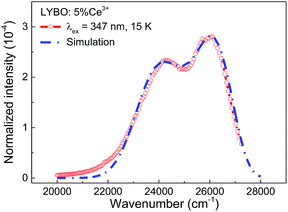 | ||
| Fig. 6 Normalized emission (λex = 347 nm) spectrum of sample LYBO:5%Ce3+ at 15 K and the simulated curve via the frequency-degenerate model. | ||
| k | Ik/I1 | E0_k (cm−1) | ℏω (cm−1) | S | σ0, σ1 (cm−1) |
|---|---|---|---|---|---|
| 1 | 1 | 27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 500 |
257 | 6 | 100, 220 |
| 2 | 0.85 | 26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 600 |
3.4 X-ray excited luminescence of Ce3+ in LYBO
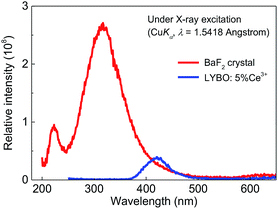
Finally, the X-ray excited luminescence measurement is carried out to check the potential scintillator application of sample LYBO:5%Ce3+. The X-ray with a wavelength of 1.5418 Å is used as the excitation source. Fig. 7 displays the X-ray excited luminescence spectra of sample LYBO:5%Ce3+ at RT. Its spectral profile and energetic position are similar to that under UV excitation in Fig. 4. To further estimate its scintillation light yield, the BaF2 crystal is also measured at the same condition as shown in Fig. 7. By calculating the ratio of the integrated intensity of sample LYBO:5%Ce3+ with that of BaF2 (∼8880 ph MeV−1) crystal, its scintillation light yield is then estimated to be ∼864 ph MeV−1, which indicates that the sample LYBO:5%Ce3+ is not suitable for X-ray detection scintillators.4. Conclusions
In summary, we have systematically studied the crystal structure, the electronic structure and the synchrotron radiation VUV-UV excitation, the UV-vis emission spectra and the luminescence decay dynamics of LYBO:Ce3+ phosphors at different concentrations and temperatures. The pure P21/c monoclinic single phase of synthesized samples is confirmed by the Rietveld refinement. The DFT calculations reveal that the LYBO host has a direct band gap. The top of VB mainly comprises of the 2p orbitals of O atoms, while the bottom of CB is mostly made up of the 4d orbitals of Y atoms. The calculated band gap of LYBO is ∼7.26 eV, which is close to the experimental result (∼7.44 eV). The low temperature VUV-UV excitation spectrum of sample LYBO:5%Ce3+ gives the energies of five crystal-field-splitting 5d states of Ce3+ ions at only one kind of Y3+ sites as ∼3.57, ∼4.04, ∼5.16, ∼5.91, ∼6.39 eV, respectively. Consequently, the centroid energy of Ce3+ 5d states in LYBO is ∼5.01 eV and the corresponding crystal field splitting energy is ∼2.82 eV. Furthermore, by constructing the VRBE scheme of lanthanides in LYBO host, the binding energy of Ce3+ lowest 5d electron is evaluated to be ∼−2.23 eV and this value shows an energy gap (∼0.65 eV) to the bottom of the host CB, which indicates that the Ce3+ emission in LYBO may possess a moderate intrinsic thermal stability. However, the more concentrated samples are found to have worse thermal stability due to the possible thermally-activated concentration quenching. In addition, to study the impact of electron–phonon coupling on Ce3+ luminescence in LYBO host, the low temperature emission spectrum of sample LYBO:5%Ce3+ is simulated by using one frequency-degenerate vibrational mode. The results show that the zero-phonon lines of the 5d1 → 2F5/2, 2F7/2 transitions are located at ∼27![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 and ∼26
500 and ∼26![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 600 cm−1, respectively. The degenerate mode has an effective phonon energy of ∼257 cm−1. The obtained Huang–Rhys parameter is ∼6, which indicates a strong electron–phonon interaction of Ce3+ luminescence in Li6Y(BO3)3. The X-ray excited luminescence spectrum shows that sample LYBO:5%Ce3+ is not suitable to serve as X-ray detection scintillators. These results provide an understanding of the impacts of 5d electron binding energy and electron–phonon coupling on luminescence of Ce3+ in LYBO, which can be also applied to other Ce3+ doped systems and help to develop the novel phosphors with desired properties.
600 cm−1, respectively. The degenerate mode has an effective phonon energy of ∼257 cm−1. The obtained Huang–Rhys parameter is ∼6, which indicates a strong electron–phonon interaction of Ce3+ luminescence in Li6Y(BO3)3. The X-ray excited luminescence spectrum shows that sample LYBO:5%Ce3+ is not suitable to serve as X-ray detection scintillators. These results provide an understanding of the impacts of 5d electron binding energy and electron–phonon coupling on luminescence of Ce3+ in LYBO, which can be also applied to other Ce3+ doped systems and help to develop the novel phosphors with desired properties.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to Prof. Lixin Ning in Anhui Normal University for his professional assistances in the DFT calculation. The work is financially supported by the National Natural Science Foundation of China (Grants U1632101 and 21671201). M. G. B. thanks supports from the Program for the Foreign Experts (Contract No. W2017011) and Wenfeng High-end Talents Project (Grant No. W2016-01) offered by Chongqing University of Posts and Telecommunications, China–Poland Intergovernmental Science and Technology Cooperation Program (Grant No. 2015[170]/36-13), Ministry of Education and Research of Estonia, Project PUT430 European Regional Development Fund (project TK141), and Guest Professorship at Kyoto University (Prof. S. Tanabe laboratory).References
- Z. G. Xia and A. Meijerink, Chem. Soc. Rev., 2017, 46, 275–299 RSC.
- P. A. Tanner, L. Zhou, C. K. Duan and K.-L. Wong, Chem. Soc. Rev., 2018, 47, 5234–5265 RSC.
- L. X. Ning, X. W. Ji, Y. Y. Dong, W. Jin, Y. C. Huang, Z. F. Pan and P. A. Tanner, J. Mater. Chem. C, 2016, 4, 5214–5221 RSC.
- E. V. D. van Loef, P. Dorenbos and C. W. E. van Eijk, Appl. Phys. Lett., 2001, 79, 1573–1575 CrossRef CAS.
- J. S. Huo, L. P. Dong, W. Lü, B. P. Shao and H. P. You, Phys. Chem. Chem. Phys., 2017, 19, 17314–17323 RSC.
- C. Y. Xu, H. X. Guan, Y. H. Song, Z. C. An, X. T. Zhang, X. Q. Zhou, Z. Shi, Y. Sheng and H. F. Zou, Phys. Chem. Chem. Phys., 2018, 20, 1591–1607 RSC.
- L. X. Ning, L. H. Lin, L. L. Li, C. B. Wu, C.-K. Duan, Y. F. Zhang and L. Seijo, J. Mater. Chem., 2012, 22, 13723–13731 RSC.
- P. Dorenbos, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 165107 CrossRef.
- D. J. Hou, W. J. Zhou, C. Wu, P. Dorenbos, H. B. Liang, T.-K. Sham, B. B. Zhang, Y. Huang and Y. Tao, Phys. Chem. Chem. Phys., 2015, 17, 22035–22041 RSC.
- Y. Y. Ou, W. J. Zhou, C. M. Liu, L. T. Lin, M. G. Brik, P. Dorenbos, Y. Tao and H. B. Liang, J. Phys. Chem. C, 2018, 122, 2959–2967 CrossRef CAS.
- Q. Peng, C. M. Liu, D. J. Hou, W. J. Zhou, C.-G. Ma, G. K. Liu, M. G. Brik, Y. Tao and H. B. Liang, J. Phys. Chem. C, 2016, 120, 569–580 CrossRef CAS.
- D. Y. Zhai, L. X. Ning, Y. C. Huang and G. K. Liu, J. Phys. Chem. C, 2014, 118, 16051–16059 CrossRef CAS.
- H. D. Luo, A. J. J. Bos, A. Dobrowolska and P. Dorenbos, Phys. Chem. Chem. Phys., 2015, 17, 15419–15427 RSC.
- G. K. Liu, J. Lumin., 2014, 152, 7–10 CrossRef CAS.
- A. A. Coelho, Coelho Software, Version 4, Topas Academic, Brisbane, Australia, 2005 Search PubMed.
- Y. Tao, Y. Huang, Z. H. Gao, H. Zhuang, A. Y. Zhou, Y. L. Tan, D. W. Li and S. S. Sun, J. Synchrotron Radiat., 2009, 16, 857–863 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- C.-Y. Tu, A.-D. Jiang and Z.-D. Luo, J. Struct. Chem., 1989, 8, 215–219 CAS.
- R. D. Shannon, Acta Crystallogr., 1976, A32, 751–767 CrossRef CAS.
- M. J. Knitel, P. Dorenbos, C. W. E. van Eijk, B. Viana, A. Kahn-Harari and D. Vivien, Nucl. Instrum. Methods Phys. Res., Sect. A, 2000, 443, 364–374 CrossRef CAS.
- P. Dorenbos, Opt. Mater., 2017, 69, 8–22 CrossRef CAS.
- W. J. Zhou, D. J. Hou, F. J. Pan, B. B. Zhang, P. Dorenbos, Y. Huang, Y. Tao and H. B. Liang, J. Mater. Chem. C, 2015, 3, 9161–9169 RSC.
- C. M. Liu, H. B. Liang, X. J. Kuang, J. P. Zhong, S. S. Sun and Y. Tao, Inorg. Chem., 2012, 51, 8802–8809 CrossRef CAS PubMed.
- H. H. Lin, H. B. Liang, B. Han, J. P. Zhong and Q. Su, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 76, 035117 CrossRef.
- P. Dorenbos, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 125117 CrossRef.
- H. B. Liang, H. H. Lin, G. B. Zhang, P. Dorenbos and Q. Su, J. Lumin., 2011, 131, 194–198 CrossRef CAS.
- H. H. Lin, H. B. Liang, Z. F. Tian, Q. Su, H. Y. Xie and J. F. Ding, J. Mater. Res., 2006, 21, 864–869 CrossRef CAS.
- P. Dorenbos, J. Lumin., 2013, 135, 93–104 CrossRef CAS.
- Y. Fujimoto, T. Yanagia, Y. Yokota, N. Kawaguchi, K. Fukuda, D. Totsuka, K. Watanabe, A. Yamazaki and A. Yoshikawa, Opt. Mater., 2011, 34, 444–447 CrossRef CAS.
- P. Dorenbos, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 15640–15649 CrossRef CAS.
- G. Blasse and B. C. Grabmaier, Luminescent Materials, Springer Verlag, Berlin, 1994 Search PubMed.
- P. Dorenbos, J. Lumin., 2000, 91, 155–176 CrossRef CAS.
- S. K. Pan, W. Liu, G. H. Ren, J. Y. Zhang, J. G. Pan, N. Li, Z. Wu and Y. K. Heng, J. Alloys Compd., 2018, 767, 976–981 CrossRef CAS.
- V. Jubera, J. P. Chaminade, A. Garcia, F. Guillen and C. Fouassier, J. Lumin., 2003, 101, 1–10 CrossRef CAS.
- P. Dorenbos, ECS J. Solid State Sci. Technol., 2013, 2, R3001–R3011 CrossRef CAS.
- P. Dorenbos, J. Phys.: Condens. Matter, 2003, 15, 8417–8434 CrossRef CAS.
- P. Dorenbos, J. Phys.: Condens. Matter, 2005, 17, 8103–8111 CrossRef CAS.
- R. F. Zhou, L. T. Lin, C. M. Liu, P. Dorenbos, Y. Tao, Y. Huang and H. B. Liang, Dalton Trans., 2018, 47, 306–313 RSC.
- V. Bachmann, C. Ronda and A. Meijerink, Chem. Mater., 2009, 21, 2077–2084 CrossRef CAS.
- W. J. Zhou, F. J. Pan, L. Zhou, D. J. Hou, Y. Huang, Y. Tao and H. B. Liang, Inorg. Chem., 2016, 55, 10415–10424 CrossRef CAS PubMed.
- J. Ueda, P. Dorenbos, A. J. J. Bos, A. Meijerink and S. Tanabe, J. Phys. Chem. C, 2015, 119, 25003–25008 CrossRef CAS.
- M. Wagner, J. Chem. Phys., 1964, 41, 3939–3943 CrossRef CAS.
- M. G. Brik, C.-G. Ma, H. B. Liang, H. Y. Ni and G. K. Liu, J. Lumin., 2014, 152, 203–205 CrossRef CAS.
- É. Tichy-Rács, Á. Péter, V. Horváth, K. Polgár, K. Lengyel and L. Kovács, Mater. Sci. Forum, 2013, 729, 493–496 Search PubMed.
| This journal is © The Royal Society of Chemistry 2019 |