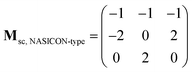Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Computational investigation of the Mg-ion conductivity and phase stability of MgZr4(PO4)6†
Koki Nakano a,
Yusuke Nodab,
Naoto Tanibataac,
Masanobu Nakayama
a,
Yusuke Nodab,
Naoto Tanibataac,
Masanobu Nakayama *abcde,
Koichi Kajihara
*abcde,
Koichi Kajihara f and
Kiyoshi Kanamuraf
f and
Kiyoshi Kanamuraf
aDepartment of Advanced Ceramics, Nagoya Institute of Technology, Gokiso, Showa, Nagoya, Aichi 466-8555, Japan. E-mail: masanobu@nitech.ac.jp
bCenter for Materials Research by Information Integration (CMI2), Research and Services Division of Materials Data and Integrated System (MaDIS), National Institute for Materials Science (NIMS), 1-2-1 Sengen, Tsukuba, Ibaraki 305-0047, Japan
cElements Strategy Initiative for Catalysts and Batteries (ESICB), Kyoto University, 1-30 Goryo-Ohara, Nishikyo, Kyoto 615-8245, Japan
dFrontier Research Institute for Materials Science (FRIMS), Nagoya Institute of Technology, Gokiso, Showa, Nagoya, Aichi 466-8555, Japan
eGlobal Research Center for Environment and Energy based on Nanomaterials Science (GREEN), National Institute for Materials Science (NIMS), 1-1 Namiki, Tsukuba, Ibaraki 305-0047, Japan
fDepartment of Applied Chemistry for Environment, Graduate School of Urban Environmental Sciences, Tokyo Metropolitan University, 1-1 Minami-Osawa, Hachioji, Tokyo 192-0397, Japan
First published on 23rd April 2019
Abstract
Solid electrolyte materials exhibiting high Mg-ion conductivity are required to develop Mg-ion batteries. In this study, we focused on a Mg-ion-conducting solid phosphate based electrolyte, MgZr4(PO4)6 (MZP), and evaluated the ionic conductivity of NASICON-type and β-iron sulfate-type MgZr4(PO4)6 structures via density functional theory calculations. The calculations suggest that the migration energy of Mg is 0.63 eV for the NASICON-type structure and 0.71 eV for the β-iron sulfate-type one, and the NASICON-type structure has higher ion conductivity. Although the NASICON-type MZP structure has not been experimentally realised, there is only an energy difference of 14 meV per atom with respect to that of the β-iron sulfate-type structure. Therefore, in order to develop a synthesis method for the NASICON-type structure, we investigated pressure- and temperature-dependent variations in the free energy of formation using density functional perturbation theory calculations. The results suggest that the formation of the NASICON-type structure is disfavoured under the 0–2000 K and 0–20 GPa conditions.
Introduction
Lithium ion batteries (LIBs) are widely used in portable electronic devices, such as mobile phones and laptop computers, owing to their high energy density and long cycle life. In recent years, the use of (hybrid) electric vehicles (EVs) has gradually increased to address the environmental and energy issues.1 Therefore, LIBs are also attracting attention as secondary batteries for on-vehicle use. However, the following two major technical drawbacks of current LIBs need to be overcome: (i) insufficient driving range of the vehicle compared to the conventional petro-powered vehicle due to the small energy density and (ii) safety concerns arising from inflammable organic electrolytes. In this respect, developing all solid-state Mg-ion batteries (MIBs) is believed to be one of the ultimate solutions to resolve the above two issues.2 The Mg ion is divalent and can carry two electrons, so that the energy density is expected to double. All solid-state battery technology also contributes to the fabrication of a bipolar-type battery, thus enabling increased energy density, and replacement of organic electrolyte by an inflammable solid electrolyte can solve the safety concerns.However, the generally poor Mg diffusivity in the solid state prevents the realisation of MIB-based devices, since divalent Mg ions strongly interact with counter anions. Therefore, it is necessary to understand the factors affecting the Mg-ion conductivity and find fast Mg-ion conductors to develop future all solid-state MIBs.
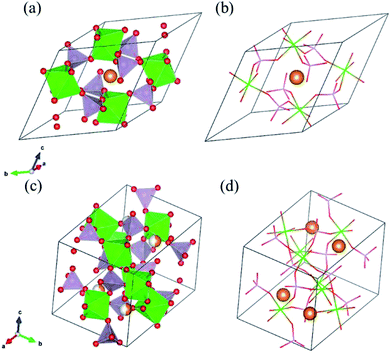
As solid electrolyte materials, oxide-based Na super ionic conductor (NASICON)-type structures are attractive for LIBs because NASICON-type ion conductors show high ion conductivity in both Na3–9 and Li10–17 systems. So far, one of the best Mg-ion conductors is rhombohedral NASICON-type (Mg0.1Hf0.9)4/3.8Nb(PO4)3 (Fig. 1(a and b)), in which the ionic conductivity of Mg2+ is 2.1 × 10−6 S cm−1 at 573 K and its activation energy is 0.68 eV.18 This compound consists of (Nb,Hf)O6 octahedra and PO4 tetrahedra alternately bridged at the two-coordinated edge O atoms, and Mg ions migrate through the interstitial sites of the corner-shared network. This local bonding rule leads to another type of structure with a different network topology, known as the monoclinic β-iron sulfate-type structure, and MgZr4(PO4)6 belonging to this structure type (Fig. 1(c and d)) also exhibits relatively high Mg-ion conductivity.19,20 An example of a material with this type of structure is Mg0.7(Zr0.85Nb0.15)4(PO4)6. The ionic conductivity of this compound is 1.1 × 10−7 S cm−1 at 573 K and the activation energy is 0.92 eV,21 and Mg-ion conduction of this compound at 350 °C has been recently confirmed using non-blocking Mg metal electrodes.22 Interestingly, both the NASICON-type and β-iron sulfate-type structural frameworks have a polymorphic relationship represented by AxB4(XO4)6 frameworks. In case of Na ion migration, the NASICON-type structure has been reported to show higher conductivity than that of the β-iron sulfate-type one for the composition of Na3Zr2Si2PO12.4 The lower activation energy for the Mg ion conduction in the NASICON-type (Mg0.1Hf0.9)4/3.8Nb(PO4)3 structure than in the β-iron sulfate-type Mg0.7(Zr0.85Nb0.15)4P6O24 structure has been attributed to the higher structural symmetry of the former structure.15 NASICON-type MgZr4(PO4)6 has not been synthesised primarily because the stability of the NASICON-type structure is lower for small interstitial cations like Mg2+ ions.19
However, the relationship between the structure and ionic conductivity is not yet clear for the case of Mg ions, because there are no experimental ionic conductivity data of both structures with the same composition. In this study, we evaluate the ionic conductivity for both the NASICON-type and β-iron sulfate-type structures with the stoichiometric composition of MgZr4(PO4)6 (MZP) using first-principles molecular dynamics (FPMD) study based on density functional theory (DFT). So far, MZP has been experimentally prepared only in the β-iron sulfate-type structure, and no report on the synthesis of the NASICON-type structure is known. We also investigated the phase stability of NASICON-type and β-iron sulfate-type structures under various temperature and pressure conditions.
Experimental section
Computational details
Structure relaxation parameters including the lattice parameters and internal coordinates were calculated by first-principles DFT calculations. In detail, a Vienna ab initio simulation package (VASP)23–26 based on DFT27 with a projector augmented-wave (PAW)28,29 method and a plane-wave basis set was used. Further, we used a generalized gradient approximation (GGA)-type exchange–correlation functional developed by Perdew, Burke, and Ernzernhof and later modified for solid materials (PBEsol).30 The cutoff energy for the plane-wave basis was set to 500 eV and k-point resolution was set to ∼1000 (i.e., Nx, Ny, and Nz, the number of grids in kx-, ky-, and kz-directions of the reciprocal space were set to satisfy Nx × Ny × Nz × Natom ≈ 1000, where Natom is the number of atoms in each unit cell).The NASICON-type structure was constructed by replacing Li ions in the structure of LiZr2(PO4)3 taken from the inorganic crystal structure database (ICSD) (ID: 92250, original data reported by Catti et al.)31 with Mg ions and vacancies, because there are no reports of the experimental synthesis. The crystal structure input for β-iron sulfate-type MZP was extracted from the ICSD (ID: 250452, original data reported by Gobechiya et al.).32
Table 1 lists DFT-derived relaxed lattice parameters, cell volume, and calculated total electron energies for (a) NASICON-type and (b) β-iron sulfate-type MZP. In the NASICON-type structure, three Mg ions and vacancies reside at the 6b and/or 36f Wyckoff position (36f sites are split around the 6b site). The most stable Mg/vacancy arrangement was determined using a genetic algorithm (GA), as described in our previous paper.33–35 Mg-ion occupation at 6b sites is the most stable after GA optimisation, and the energy difference among the GA-derived structures (2400 samples) is within 60 meV per atom.
| a/Å | b/Å | c/Å | α/° | β/° | γ/° | Cell volume per atom/Å3 per atom | Electron energy per atom/eV per atom | |
|---|---|---|---|---|---|---|---|---|
| (a) | 8.91 | 8.98 | 22.4 | 89.80 | 89.99 | 119.99 | 14.8 | −8.041 |
| (b) | 12.52 | 8.97 | 8.95 | 90.00 | 90.49 | 90.00 | 14.4 | −8.055 |
In contrast, Mg ions and vacancies occupied the 4e sites of the Wyckoff position at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio in the β-iron sulfate-type MZP. Three configurations of Mg/vacancy arrangements were calculated for the unit cell of Mg2Zr8P12O48, and the most stable one was chosen for following calculations. The volumetric and energetic differences among the three configurations are 0.19 Å3 per atom and 12 meV per atom, respectively, indicating a small dependence on the Mg arrangement.
1 molar ratio in the β-iron sulfate-type MZP. Three configurations of Mg/vacancy arrangements were calculated for the unit cell of Mg2Zr8P12O48, and the most stable one was chosen for following calculations. The volumetric and energetic differences among the three configurations are 0.19 Å3 per atom and 12 meV per atom, respectively, indicating a small dependence on the Mg arrangement.
The obtained Mg/vacancy configurations for NASICON-type and β-iron sulfate-type MZP structures and their lattice parameters were thereafter used as structural inputs for following calculations, unless specified otherwise.
As listed in Table 1, the β-iron sulfate-type MZP is slightly more stable than the NASICON-type one by only 14 meV per atom, and the cell volume per atom difference between β-iron sulfate-type MZP (14.4 Å3 per atom) and NASICON-type (14.8 Å3 per atom) is small. Therefore, both structures are reasonably stable and are expected to be good candidates for comparing the Mg-ion diffusivity.
FPMD calculations were performed to compare the Mg-ion conductivity of the NASICON-type and the β-iron sulfate-type MZP structures. Initially, all the Mg atoms were located in the 6b sites for the NASICON-type structure and 4e sites for the β-iron sulfate-type structure.
The supercell structure including eight MZP units (i.e., Mg8Zr32P48O192) was prepared to evaluate the Mg-ion conductivity via FPMD simulations. The lattice constants of the supercell of the NASICON-type and β-iron sulfate-type MZP are a = 12.54 Å, b = 17.62 Å, c = 17.64 Å, α = 89.99°, β = 90.01°, γ = 89.00° and a = 12.52 Å, b = 17.94 Å, c = 17.90 Å, α = 90.00°, β = 90.49°, and γ = 90.00°, respectively. The lattice vectors asc, bsc, and csc in the supercell are described by a linear combination of lattice vectors ap, bp, and cp in a primitive cell of the NASICON-type or β-iron sulfate-type structure, as shown below:
| (ascbsccsc) = (apbpcp)Msc |
FPMD simulations were performed for NASICON-type and β-iron sulfate-type structure in the temperature range of 1573 to 1973 K with increments of 50 K for 100 ps. The DFT calculation settings used were equivalent to those of the structure relaxation calculations except for the cutoff energy and k-point grids as follows: the cutoff energy for the plane-wave basis was set to 350 eV and 1 × 1 × 1 k-point grid (only Γ point) was employed to reduce the computational cost. For MD simulations, the time step was set to 1 fs, and the NVT canonical ensemble was adopted using a Nosé thermostat.36 The mean square displacements (MSD) of all elements were calculated, and then the diffusion coefficients of Mg-ion conduction and corresponding migration energies were determined. Above FPMD studies have been performed in our previous studies, showing reasonable accordance between the experimental and the computational results.10,11,37
We evaluated the thermodynamic stability of the MZP polymorphs by first principles DFT calculations. Temperature- and/or pressure-dependent phase stability was also evaluated using DFT-based phonon calculations or cell-volume constraint calculations, respectively. We used the same lattice as that used for FPMD simulations. Structural relaxation calculations were performed for a structure in which the lattice constant was varied from 95 to 103% under the condition of constant lattice volume. The energy–volume relationship is fitted with the Murnaghan equation of state:38,39
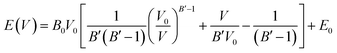 | (1) |
| B = −Vdp/dV | (2) |
Phonon frequencies and their contribution to free energy changes were calculated using the PHONOPY code.40 Density functional perturbation theory (DFPT),41,42 also implemented in VASP, was used to estimate the real-space force constants of the supercells. The other calculation conditions were the same as those used for the structure relaxation calculations.
From these calculations, the free energy was calculated by changing the temperature from 0 to 2000 K and the pressure was changed from 0 to 20 GPa.
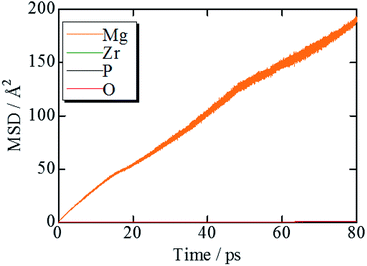
Results and discussion
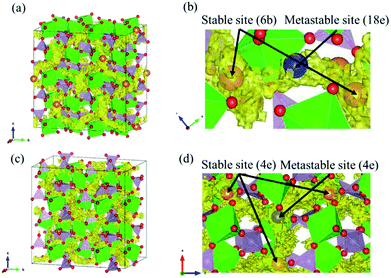
Fig. 2 shows the evolution of the time-averaged mean square displacement (MSD) for constituent ions in MZP with β-iron sulfate-type structure. The MSD of Mg ions increases linearly with the MD step (time), indicating that Mg2+ ions diffuse over the lattice. In contrast, the MSD profiles of the other ions remains constant (<1.1 Å2). Therefore, Zr, P, and O ions remain near their original sites during the MD run, and these MSD values represent the magnitude of thermal vibrations. Similar MSD profiles were obtained for the NASICON-type structure, in which only Mg ions are found to diffuse in the lattice.Diffusion path of Mg ions at 1573 K and 1973 K, i.e. both the lowest and the highest simulation temperatures, are visualised through isosurfaces of the Mg-ion probability density distribution from the FPMD simulation for (Fig. 3(a and b) and ESI Fig. S1(a)†) the NASICON-type and (Fig. 3(c and d) and ESI Fig. S1(b)†) β-iron sulfate-type structures. We confirmed the formation of a 3-dimensional pathway for both structures. Moreover, metastable Mg-ion sites are indicated in both (Fig. 3b) NASICON-type and (Fig. 3d) β-iron sulfate-type structures by varying the isosurface level (Li ion probability density). In Fig. 3b and d, the stable and metastable sites are marked with orange and blue circles, respectively. On one hand, the metastable Mg sites in β-iron sulfate-type structure are linked to three neighbouring 4e stable Mg/vacancy sites with a straight diffusion path. On the other hand, the metastable Mg sites (18e sites) are connected to two neighbouring 6b stable sites, which is consistent with the reported Li migration pathway in LiZr2(PO4)3 and its derivative.43
Diffusion coefficients were extracted through a simple linear fitting with the following expression:
| 〈x2〉 = 2nDt | (3) |
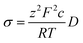 | (4) |
The Arrhenius plots for the NASICON-type and the β-iron sulfate-type structures is shown in Fig. 4, and the migration energies of Mg were evaluated by a simple linear fitting scheme. Higher Mg-ion conductivity and lower migration energy are derived for the NASICON-type structure compared to those of the β-iron sulfate-type structure.
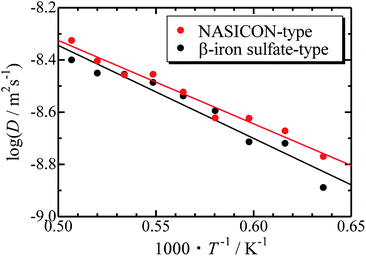 | ||
| Fig. 4 Arrhenius plots of the temperature-dependent Mg-ion diffusion coefficients fitted with a straight line. | ||
The migration energy of Mg in the β-iron sulfate-type structure obtained in this study (0.71 eV) is different from the experimental value (1.6 eV),21 which may owe to inclusion of grain boundary conduction for experimental results. The β-iron sulfate-type structure has a higher migration energy than the NASICON-type structure (0.63 eV) in present computations. This tendency agrees that the migration energy of β-iron sulfate-type Mg0.7(Zr0.85Nb0.15)4(PO4)6 (0.92 eV)21 is higher than that of NASICON-type (Mg0.1Hf0.9)4/3.8Nb(PO4)3 (0.68 eV).18 This result suggests that the NASICON-type structure has better ion conductivity than the β-iron sulfate-type one.
Since NASICON-type MZP has higher Mg-ion conductivity, the pressure- and temperature-dependence of the phase stability was investigated for NASICON-type and β-iron sulfate-type structures. Fig. 5 displays the difference between the phase stability of β-iron sulfate-type structure and NASICON-type one, ΔE, as functions of temperature and pressure. ΔE is described as follows:
| ΔE = E(β-iron sulfate-type) − E(NASICON-type) | (5) |
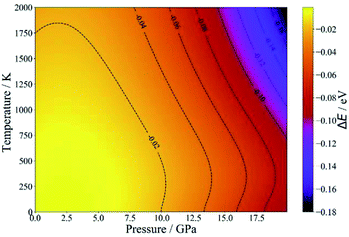 | ||
| Fig. 5 Temperature- and pressure-dependent free energies of β-iron sulfate-type and NASICON-type MZP. | ||
Conclusions
First-principles DFT calculations were performed to clarify the difference between the Mg-ion conductivity in β-iron sulfate-type and NASICON-type MZP. The results of the FPMD calculations suggest that the NASICON-type structure has higher Mg-ion conductivity than the β-iron sulfate-type one. However, evaluation of the pressure- and temperature-dependent free energies by DFT calculations indicated that the formation of NASICON-type MZP is disfavoured. Therefore, the composition should be appropriately optimised to stabilize the NASICON-type structure.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was partially supported by the ALCA-SPRING program from the Japan Science and Technology Agency (JST), a Grant-in-Aid for Scientific Research (18K19129) from the Japanese Ministry of Education Culture, Sports, Science and Technology (MEXT), and the MEXT program “Elements Strategy Initiative to Form Core Research Center” (since 2012). M. N. and Y. N. thank the support by the “Materials research by Information Integration” Initiative (MI2I) project of the “Support Program for Starting Up Innovation Hub” from the JST. Figures of crystal structures in this paper are drawn with VESTA.45References
- R. Van Noorden, Nature, 2014, 507, 26–28 CrossRef CAS PubMed.
- H. Srour, L. Chancelier, E. Bolimowska, T. Gutel, S. Mailley, H. Rouault and C. C. Santini, J. Appl. Electrochem., 2016, 46, 149–155 CrossRef CAS.
- Y. Deng, C. Eames, L. H. B. Nguyen, O. Pecher, K. J. Griffith, M. Courty, B. Fleutot, J.-N. Chotard, C. P. Grey, M. S. Islam and C. Masquelier, Chem. Mater., 2018, 30, 2618–2630 CrossRef CAS.
- J. B. Goodenough, H.-P. Hong and J. A. Kafalas, Mater. Res. Bull., 1976, 11, 203–220 CrossRef CAS.
- H.-P. Hong, Mater. Res. Bull., 1976, 11, 173–182 CrossRef CAS.
- W. Zhou, Y. Li, S. Xin and J. B. Goodenough, ACS Cent. Sci., 2017, 3, 52–57 CrossRef CAS PubMed.
- F. Lalère, J. B. Leriche, M. Courty, S. Boulineau, V. Viallet, C. Masquelier and V. Seznec, J. Power Sources, 2014, 247, 975–980 CrossRef.
- Y. Noguchi, E. Kobayashi, L. S. Plashnitsa, S. Okada and J. Yamaki, Electrochim. Acta, 2013, 101, 59–65 CrossRef CAS.
- A. G. Jolley, G. Cohn, G. T. Hitz and E. D. Wachsman, Ionics, 2015, 21, 3031–3038 CrossRef CAS.
- Y. Noda, K. Nakano, H. Takeda, M. Kotobuki, L. Lu and M. Nakayama, Chem. Mater., 2017, 29, 8983–8991 CrossRef CAS.
- Y. Noda, K. Nakano, M. Otake, R. Kobayashi, M. Kotobuki, L. Lu and M. Nakayama, APL Mater., 2018, 6, 060702 CrossRef.
- X. Zhao, Z. Zhang, X. Zhang, B. Tang, Z. Xie and Z. Zhou, J. Mater. Chem. A, 2018, 6, 2625–2631 RSC.
- P. Knauth, Solid State Ionics, 2009, 180, 911–916 CrossRef CAS.
- V. Thangadurai and W. Weppner, Ionics, 2006, 12, 81–92 CrossRef CAS.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- X. Yao, B. Huang, J. Yin, G. Peng, Z. Huang, C. Gao, D. Liu and X. Xu, Chin. Phys. B, 2016, 25, 018802 CrossRef.
- C. Cao, Z.-B. Li, X.-L. Wang, X.-B. Zhao and W.-Q. Han, Front. Energy Res., 2014, 2, 25 Search PubMed.
- S. Tamura, M. Yamane, Y. Hoshino and N. Imanaka, J. Solid State Chem., 2016, 235, 7–11 CrossRef CAS.
- K. Nomura, S. Ikeda, K. Ito and H. Einaga, Bull. Chem. Soc. Jpn., 1992, 65, 3221–3227 CrossRef CAS.
- S. Ikeda, M. Takahashi, J. Ishikawa and K. Ito, Solid State Ionics, 1987, 23, 125–129 CrossRef CAS.
- N. Imanaka, Y. Okazaki and G. Adachi, Electrochem. Solid-State Lett., 1999, 3, 327 CrossRef.
- K. Kajihara, H. Nagano, T. Tsujita, H. Munakata and K. Kanamura, J. Electrochem. Soc., 2017, 164, A2183–A2185 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- M. Catti and S. Stramare, Solid State Ionics, 2000, 136–137, 489–494 CrossRef CAS.
- E. R. Gobechiya, M. V. Sukhanov, V. I. Pet'kov and Y. K. Kabalov, Crystallogr. Rep., 2008, 53, 53–59 CrossRef CAS.
- G. Trimarchi and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 104113 CrossRef.
- N. L. Abraham and M. I. J. Probert, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 224104 CrossRef.
- S. M. Woodley, P. D. Battle, J. D. Gale and C. R. A. Catlow, Phys. Chem. Chem. Phys., 1999, 1, 2535–2542 RSC.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- R. Jalem, Y. Yamamoto, H. Shiiba, M. Nakayama, H. Munakata, T. Kasuga and K. Kanamura, Chem. Mater., 2013, 25, 425–430 CrossRef CAS.
- F. Birch, Phys. Rev., 1947, 71, 809–824 CrossRef CAS.
- F. Birch, J. Appl. Phys., 1938, 9, 279–288 CrossRef.
- Togo, Phonopy, https://atztogo.github.io/phonopy/, (accessed 5 December 2018) Search PubMed.
- K. Refson, P. R. Tulip and S. J. Clark, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 155114 CrossRef.
- S. Baroni, S. de Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515–562 CrossRef CAS.
- P. Padma kumar and S. Yashonath, J. Phys. Chem. B, 2001, 105(29), 6785–6791 CrossRef.
- H. Takahashi and H. Takamura, Mater. Trans., 2012, 53, 932–93545 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra00513g |
| This journal is © The Royal Society of Chemistry 2019 |