The nature of the chemical bond in oxyanionic crystals based on QTAIM topological analysis of electron densities

Abstract

The nature of the chemical bond in 31 oxyanionic crystals was analyzed using ab initio calculations and quantum theory of atoms in molecules (QTAIM). The QTAIM topological analysis of the calculated electron densities in oxyanionic crystals revealed that some of the metal–oxygen, metal⋯metal, metal–ligand and hydrogen bonds are partly covalent in nature. The covalency criteria for metal–oxygen and hydrogen bonds based on electron densities at the bond critical points were obtained. The densities at the bond critical points correlate with the corresponding overlap populations, electronegativities, H-bond lengths and energies. The distances between cationic nuclei and the bond critical points correlate with cationic radii. There are weak anion⋯anion interactions.

---

1. Introduction

Oxyanionic crystals such as nitrates, chlorates and perchlorates are used as energetic oxidizers in propellants and explosive and pyrotechnic systems, and as sources of oxygen in respiratory apparatus.^1–4 Lithium perchlorate is also applied as a component of electrolytes for solid-state lithium batteries,⁵ with sodium chlorate as a nonlinear optic material,⁶ and some nitrates are used in lasers.⁷ Besides, nitrates and perchlorates are promising candidates for being used as NLC (negative linear compressibility) materials in ultrasensitive pressure detectors, shock resistant materials, artificial muscles, body armor, and pressure switches.^8–10 It is interesting to note that perchlorates were detected on Mars and they can be useful for future studies.^11,12 At Martian surface conditions, the mono- and di-hydrate sodium perchlorates are the most relevant phases.¹³ The application of metal sulfates is extensive and various, such as road bases and airfield pavement construction, and they are a component of fire-resistant compounds and can be used in electrochemical industry for battery manufacturing,¹⁴ as a radiopaque and catalytic material,¹⁵ in pyrotechnics and ceramics,¹⁶ and as a solid lubricant in molds and engines.¹⁷ Gypsum is used in construction and in medicine, in the pulp and paper industry and as a refractory material. Sulfates were found in sulfate sediments on Mars and in meteorites.^18,19 Nitrates and sulfates are mineral components of coal.^20,21

Crystal structures of oxyanionic crystals were studied both experimentally and using first-principles calculations. The findings of ab initio structural studies compared to the existing X-ray and neutron diffraction data are presented in ref. 9 and 22–26. Volumes per formula units, metal–oxygen distances and intra-anionic bond lengths tend to increase with an increasing radius of metal cation, and in most cases almost linearly. The presence of nonequivalent oxygen and hydrogen atoms is typical for oxyanionic crystals. The results of theoretical studies of electron, elastic, vibrational and thermal properties (based on density functional theory) of oxyanionic crystals compared to the existing experimental data were reported in ref. 9, 10 and 22–28. Band gap decreases with increasing cation and central atom electronegativity. Cationic states notably affect the formation of density spectra of valence and unoccupied states of oxyanionic crystals with polyatomic cations and metal cations with high electronegativity. Substantial hybridization of anionic and cationic states can occur. There are bands of mixed (anion-water) nature in the density of states spectrum of oxyanionic hydrates. A characteristic feature of many oxyanionic crystals is compressibility anisotropy, and some crystals are even characterized by such a rare phenomenon as negative linear compressibility.^9,10 Compressibility of intra-ionic bonds is substantially smaller than that of interionic bonds. Elastic bulk modulus, shear modulus, Young modulus and hardness tend to increase with decreasing radius of metal cation. External lattice vibrations and high-frequency internal vibrations of molecular structural units both determine vibrational spectrum of oxyanionic crystals. Intramolecular modes have noticeably smaller values of the Grüneisen parameter, than most external vibrational modes. Combined (mixed) vibrations of anions and water molecules are possible.²⁶ Temperature dependency of heat capacity at T > 200 K is mainly determined by intramolecular vibrations and the Dulong–Petit law fails at room temperature.²⁷ Recently synthesized energetic 3,3′-diamino-4,4′-azo-1,2,4-triazole nitrate and perchlorate have good detonation properties.²⁹

The macroscopic behavior of the materials is eventually controlled by their microscopic properties, such as interatomic interactions.³⁰ The condition for formation of the chemical bond is the presence of bond critical point (BCP).^31,32 According to Bader's quantum theory of atoms in molecules (QTAIM),^31,32 the chemical bonds can be quantified in terms of features of the BCPs in electron density. The analysis of electron density properties at BCPs provides information on the nature of atomic interactions. Difference or deformation electron densities and also the Laplacian of electron density at BCP (Δρ_c), which describe concentration of electron density in the bonding region, are used to distinguish between non-covalent closed shell interaction (ionic, etc.) and covalent one.^33,34 However, these characteristics are insufficient to identify weak covalent bonds.^34,35 When such bonds are formed, the electron density flows out of the internuclear region, however, the residual density is sufficient for covalent bonding to form due to increase in the absolute value (magnitude) of the potential energy.^34,35 Therefore, apart from deformation density and the Laplacian Δρ_c, the energy density H_с is used.³⁴ H_с = G_c + V_c = 0.25Δρ_c – G_c, where G_c and V_c are the kinetic and potential energy densities at the BCP, respectively.³¹ Kinetic energy density G_c relates to electron density and the Laplacian at the BCP.^36,37 The condition H_c > 0 (ρ_c is destabilizing) corresponds to non-covalent closed shell interaction, while at H_c < 0 (ρ_c is stabilizing) the bond has a covalent component.^34,38 So, the bond with covalent component is characterized by predominance of local potential energy at the BCP. Therefore, both electrostatic (Hellmann–Feynman) and energetic description of chemical bond is needed.^34,35

The atomic interactions can be classified^38–40 as shared interactions (Δρ_c < 0, H_c ≪ 0), transit (intermediate) interactions (Δρ_c > 0, H_c < 0) and closed shell interactions (Δρ_c > 0, H_c > 0). Shared interactions are covalent and polar covalent bonds.^40,41 Intermediate interactions are partially covalent interactions which include coordination (dative) bonds, strong hydrogen bonds, metallic bond, etc.^39,41,42 Closed shell interactions include ionic bond and weak intermolecular interactions (weak and medium hydrogen bonds, van der Waals interactions, etc.).^39,41 It should be noted that Δρ_c > 0, H_c ≪ 0 (relatively high H_c) and relatively high ρ_c value correspond to polar covalent bond.^41,43 For the record, the strongest coordination and hydrogen bonds have the characteristics of covalent bonds.⁴¹ Additionally, atomic interactions can be classified by the bond degree parameter BD = H_c/ρ_c (the total energy per electron at BCP).^38,40 For non-covalent closed shell interactions the BD parameter is positive and indicates a softening degree (SD): the weaker and more closed shell in nature is the interaction, the greater is the SD magnitude. The BD parameter is negative and indicates the covalence degree (CD) of interactions for shared and intermediate (partially covalent) interactions: the stronger and more covalent the interactions are, the greater the CD magnitudes are.

The value of electron density at BCP is an important characteristic.^31,32 Electron density at bond critical points (ρ_c) for typical ionic crystals LiF, NaF, NaCl and MgO does not exceed 0.04 a.u.⁴⁴ On the other hand, partially covalent (intermediate) Mn–F bond in fluoride KMnF₃ is characterized by ρ_c ∼0.07 a.u.⁴⁵ Partial covalence for strong H-bonds (d_H⋯O < 1.65 Å) of some molecular crystals corresponds to 0.05 < ρ_c < 0.12 a.u.³⁹ The closed shell (electrostatic) H⋯O hydrogen bonds for amide dimers are characterized by ρ_c < 0.035 a.u., while partially covalent (H_c < 0) bonds comply with 0.035 < ρ_c < 0.11 a.u.⁴¹ The covalent interactions exhibit ρ_c > 0.14 a.u.³⁹

Experimental QTAIM studies of topological electron density properties were performed for oxyanionic crystals such as urea nitrate, sodium chlorate and potassium perchlorate.^46–48 However, experimental determination of charge density presents certain difficulty due to the experimental problem of deconvolution of thermal motion and electron density even at low temperature.^49,50 The abilities of multipole model to describe the experimental electron density Laplacian for the bonds having a covalent component are restricted.^39,51 So, the main origin of topological discrepancies between experimental and theoretical crystal charge densities is attributed to the nature of radial functions in the experimental multipole model.⁵² The theoretical total and difference electron density maps of oxyanionic crystals and chemical bond analysis were reported in ref. 10, 22, 23, 25 and 53–57. However, as it was mentioned above, QTAIM topological analysis is needed for adequate study of the nature of chemical bond. As we know, theoretical study of QTAIM topological properties of electron density at BCP has been performed only for potassium perchlorate.⁴⁸

Thus, the chemical bond of oxyanionic crystals has not been studied sufficiently. There is no systematic investigation of chemical bond in oxyanionic crystals based on QTAIM topological analysis. The purpose of this work is a systematic ab initio study of the nature of chemical bond in oxyanionic crystals on the basis of QTAIM topological analysis of electron densities.

2. Computational details

Density Functional Theory (DFT) is an effective tool for modelling and predicting of physical and chemical properties of a wide range of materials.⁵⁸ In most cases the results obtained via DFT calculations are in reasonable agreement with the experimental data. Due to theoretical calculation it is possible to predict physical and chemical properties of solids at the microscopic level. We used CRYSTAL software⁵⁹ and PBE functional⁶⁰ to perform calculations in the present work. We used dispersion correction scheme of Grimme (DFT-D2),⁶¹ integrated in the standard DFT description in order to include the long-range intermolecular interactions. The correction to DFT takes into account the dispersive interactions based on damped atomic pairwise potentials. Recently, DFT-D2 method was successfully applied to describe properties of various crystals.^{4,9,10,22–25,62–66}

The experimental determination of the exact atomic positions and bond lengths, especially for hydrogen-containing compounds, is a well-known problem.^67–70 Even neutron-diffraction measurements are not sufficient to receive reliable structural information because of the thermal libration effect (bond shortening).^71,72 A more detailed atomic structure can be obtained due to first-principles calculations.⁷³ We used optimized (by calculations) crystal structures and basis sets of atomic orbitals according to ref. 9 and 22–26. Energy convergence was better than at 10⁻⁸ a.u. Visualization of crystal structures was performed using CrystalExplorer software.⁷⁴

The topological analysis of the electron density, within the framework of the QTAIM, has become a powerful tool for chemical bond study.⁷⁵ The TOPOND code⁷⁶ integrated in the CRYSTAL program used for QTAIM topological analysis of the electron density. Energies of interatomic and intermolecular interactions (closed shell and intermediate), hydrogen bonds in particular, can be estimated as E_int = −0.5V_c.^77,78 This correlation between bond energy and potential energy density at BCP (V_c) is valid for medium and strong hydrogen bonds, coordinate bonds, weak intermolecular and interionic interactions.^77–81 It is proved by the good agreement between the sublimation enthalpy obtained by summation of all the E_int for crystals and thermochemical data.⁷⁸ We used this relation in our calculations of interaction energies. It should be noted that along with QTAIM analysis there are crystal orbital overlap population (COOP) and crystal orbital Hamiltonian population (COHP) ones as tools for studying chemical bonds in solids.^82,83 However, the COOP as well as COHP are basis set dependent quantities and therefore are not an absolute bonding indicators.⁸⁴ One of the advantages of Bader QTAIM approach is the possibility to detect even the weakest bonding interatomic interactions and estimate their energies.^80,81

3. Results and discussion

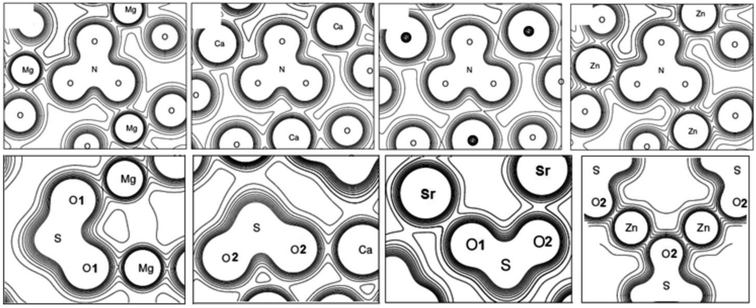
The crystals with metal cations are ones of the most well-known among oxyanionic crystals. Fig. 1 shows optimized structures of nitrates, chlorates, perchlorates and metal sulfates. The structures of ambient (II) and higher pressure (IV, at P ∼ 0.3 GPa) phases are given for KNO₃. Isosurfaces of electron density (ρ = 0.03 a.u.) for oxyanionic crystals are also shown in Fig. 1.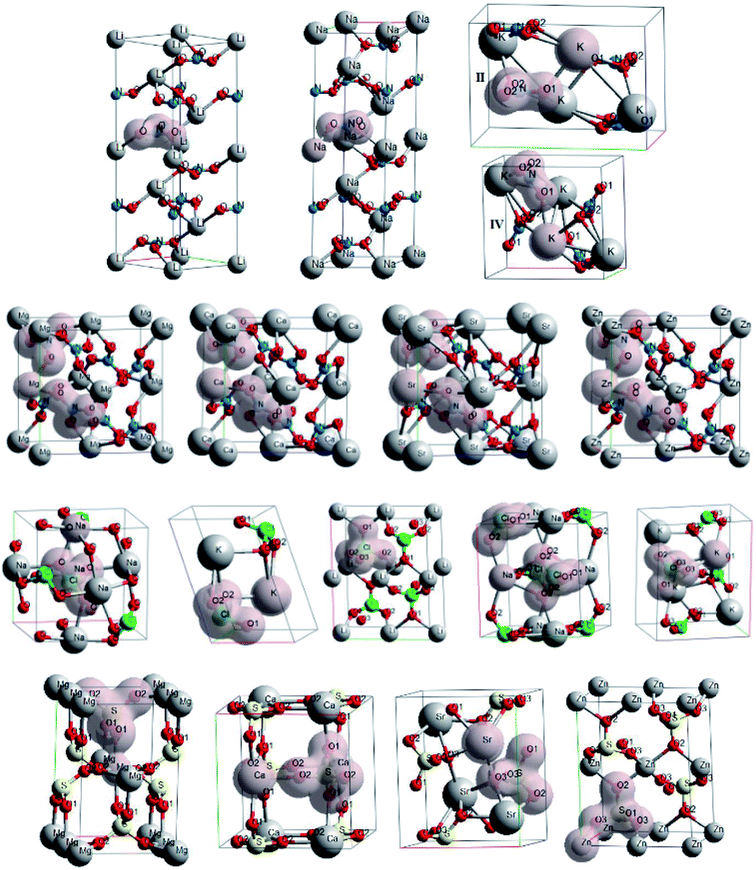

Fig. 1 Optimized structures and isosurfaces (ρ = 0.03 a.u.) of electron density for oxyanionic crystals with metal cations.

First of all we considered the chemical bond in oxyanionic crystals with alkali metal cations. Table 1 presents electron density ρ_c, the Laplacian of electron density Δρ_с and energy density H_c calculated at critical points for the shortest metal–oxygen and intraanionic bonds of oxyanionic crystals with alkali metal cations. Atomic numbering is in accordance with Fig. 1. The negative value of the Laplacian Δρ_с reveals concentration of electron density between the pair of interacting atoms. There is depletion of electron density for positive values of Δρ_с. Electron density at BCPs for M–O bonds does not exceed 0.02 a.u. (Table 1), Δρ_с > 0 and H_c > 0, that prove closed shell (ionic) character of interactions between alkali metals and oxygens. On the other hand, the ρ_c values for N–O and Cl–O bonds are significantly higher, the Laplacian and energy density are negative, which indicates the shared (covalent) nature of intra-anionic bonds. The calculated electron densities of perchlorates ρ_c are in good agreement with the experimental values, which are ∼0.36 and 0.01 a.u. for Cl–O and K–O bonds of potassium perchlorate, respectively.⁴⁸ Besides, our calculations are in reasonable agreement with experimental ρ_c (ref. 46) for Cl–O bonds (0.355 a.u.) and Na–O bonds (0.013 a.u.) of sodium chlorate. It should be noted that B3LYP hybrid functional leads to results which are similar to PBE ones. So, the differences between B3LYP and PBE values of ρ_с, Δρ_с and H_с are smaller than 10%.

Table 1 Topological properties of electron density calculated at BCPs for metal–oxygen and intra-anionic bonds

Crystal	Bonds	ρс (а.u.)	Δρс (а.u.)	Hс (a.u.)
LiNO3	N–O	0.435	−0.818	−0.785
	Li–O	0.015	0.103	0.0060
NaNO3	N–O	0.434	−0.803	−0.781
	Na–O	0.015	0.094	0.0052
KNO3	N–O1	0.429	−0.760	−0.764
	N–O2	0.429	−0.763	−0.764
	K–O1	0.011	0.052	0.0028
	K–O2	0.013	0.057	0.0027
NaClO3	Cl–O	0.287	−0.400	−0.392
	Na–O	0.014	0.082	0.0045
KClO3	Cl–O1	0.288	−0.404	−0.394
	Cl–O2	0.291	−0.418	−0.402
	K–O1	0.013	0.054	0.0024
	K–O2	0.012	0.053	0.0026
LiClO4	Cl–O1	0.311	−0.564	−0.457
	Cl–O2	0.327	−0.682	−0.503
	Cl–O3	0.318	−0.594	−0.475
	Li–O1	0.015	0.104	0.0060
	Li–O2	0.016	0.121	0.0072
	Li–O3	0.009	0.058	0.0037
NaClO4	Cl–O1	0.322	−0.632	−0.487
	Cl–O2	0.320	−0.605	−0.480
	Na–O1	0.012	0.073	0.0043
	Na–O2	0.011	0.065	0.0039
KClO4	Cl–O1	0.325	−0.650	−0.495
	Cl–O2	0.320	−0.604	−0.480
	Cl–O3	0.317	−0.584	−0.472
	K–O1	0.007	0.036	0.0023
	K–O2	0.010	0.045	0.0024
	K–O3	0.012	0.053	0.0026

---

Atomic charges for NaNO₃ (Q_Na = +0.912, Q_N = +0.747, Q_O = −0.553e), calculated in the present work by integration of electron density over topological atomic basins (Bader AIM charges), are in good agreement with the charges (Q_Na = +1.0, Q_N = +0.639, Q_O = −0.546e), used in empirical fitted potentials.⁸⁵ Obtained from theoretical and experimental (in parentheses, ref. 46) electron density AIM charges for sodium, chlorine and oxygen atoms in NaClO₃ are +0.899 (0.91), +1.536 (1.36), −0.812 (−0.76)e, respectively. As to KClO₄, calculated in the present work and reported in ref. 48 (in parentheses) AIM charges are Q_K = +0.95 (+1.0), Q_Cl = +2.037 (+2.3), 〈Q_O〉 = −0.749 (−0.8)e. Thus, the charges of the central atom (chlorine) for chlorate and perchlorate anions are considerably higher than the charge of the central atom (nitrogen) for nitrate anion. As the charges of the central atom (nitrogen, chlorine) and oxygen are opposite, intra-anionic bond is polar covalent. The cationic charges are near 0.9e that indicate ionic bond between alkali metals and anions.

It is interesting to note that there are weak bonding anion⋯anion interactions in oxyanionic crystals (Table 2). So, as for sodium chlorate, ClO₃⋯ClO₃ anionic interactions occur through weak interactions between chlorine and oxygen atoms with the opposite charge sign (Cl⋯O) and between oxygen atoms (O⋯O). Herewith, the electron density and its Laplacian at BCP for Cl⋯O interactions (ρ_с = 0.009, Δρ_с = 0.033 a.u.) calculated in our work are in good agreement with experimental values (ρ_с = 0.010, Δρ_с = 0.042 a.u.) reported in ref. 46. Smaller topological properties at BCP (ρ_с = 0.005, Δρ_с = 0.017 a.u.) correspond to O⋯O interactions. Positive Δρ_с indicate the closed shell (electrostatic and dispersion) character of bonding anion⋯anion interactions. The energies of O⋯O and Cl⋯O interactions are 2.96 and 6.54 kJ mol⁻¹, respectively.

Table 2 The topological properties at BCPs and interaction energies for weak anion⋯anion interactions

Crystal	Bonds A–B	ρс (а.u.)	Δρс (а.u.)	Hс (а.u.)	Eint (kJ mol^−1)
LiNO3	O⋯O	0.011	0.044	0.0021	8.91
NaNO3	O⋯O	0.006	0.023	0.0013	4.01
KNO3	N⋯N	0.005	0.025	0.0017	3.84
	O1⋯O1	0.003	0.010	0.0007	1.56
	O2⋯O2	0.004	0.016	0.0010	2.51
NaClO3	Cl⋯O	0.009	0.033	0.0016	6.54
	O⋯O	0.005	0.017	0.0010	2.96
KClO3	Cl⋯O1	0.006	0.020	0.0011	3.68
	Cl⋯O2	0.003	0.010	0.0007	1.56
	O1⋯O1	0.003	0.011	0.0007	1.67
	O2⋯O2	0.004	0.016	0.0010	2.51
	Cl⋯Cl	0.003	0.010	0.0007	1.56
LiClO4	O1⋯O2	0.011	0.042	0.0019	8.70
	O1⋯O3	0.012	0.047	0.0021	9.88
	O2⋯O2	0.010	0.041	0.0021	7.98
	O2⋯O3	0.008	0.029	0.0015	5.58
NaClO4	O1⋯O1	0.008	0.035	0.0020	6.24
	O1⋯O2	0.007	0.029	0.0017	5.10
KClO4	O1⋯O1	0.005	0.018	0.0011	3.07
	O1⋯O2	0.005	0.019	0.0012	3.18
	O2⋯O3	0.006	0.022	0.0013	3.90
	O3⋯O3	0.006	0.021	0.0012	3.79

---

Similarly to NaClO₃, there are Cl⋯O and O⋯O weak anion⋯anion interactions in potassium chlorate. Only O⋯O weak interactions can be detected in LiNO₃, NaNO₃ and alkali metal perchlorates. Weak O⋯O interactions have been also detected in other crystals.^80,81 It is interesting to note that interactions between central atoms of anions (N⋯N, Cl⋯Cl) occur in potassium nitrate and potassium chlorate. It can be seen that the energies of anion⋯anion interactions for oxyanionic salts with lithium and sodium cations are higher than those for potassium salts. The nature of anion–anion interactions was previously discussed in ref. 80. Bonding anion–anion interactions, most likely, have electrostatic (dipole–dipole) and dispersion nature. A certain role is played by the orbital overlap, as well as the polarization effects.⁸⁰ Cation–anion interactions also partially compensate for Coulomb repulsion between anions.⁸⁰

Moreover, we considered the chemical bond in oxyanionic crystals with divalent metal cations. Tables S1 and S2† present electron density ρ_c, the Laplacian of electron density Δρ_с and energy density H_c calculated at critical points for the shortest metal–oxygen and intraanionic bonds of oxyanionic crystals with divalent metal cations. Fig. 2 shows electron density distributions ρ for alkali-earth metal and zinc nitrates and sulfates. The intervals between isodensity curves are 0.01 a.u.

Fig. 2 Electron density distributions for oxyanionic crystals with divalent metal cations.

It is clearly seen that there is a substantial covalent bond inside nitrate and sulfate anions. Anion atoms have a large number of common contours, typical of covalent bonds. At the same time the our calculated electron densities ρ_с for critical points of N–O bonds in divalent metal nitrates are relatively high (∼0.44 a.u.), Δρ_с < 0 (∼−0.7 a.u.) and H_c ≪ 0 (∼−0.79 a.u.), which indicate covalent bond inside nitrate anions. As for sulfates S–O bonds, the electron densities ρ_с calculated in our work are relatively high (∼0.25 a.u.), H_c ≪ 0 (∼−0.22 a.u.). However, Δρ_с are positive (∼0.8 a.u.). Therefore, intra-anionic bonds are polar covalent in sulfates.

Five common contours for anions and cations are visible in zinc nitrate and zinc sulfate, therefore, electron densities at BCPs for Zn–O bonds are more than 0.05 a.u. As cation electronegativity decreases, the number of common contours decreases as well. Thus, there are three common contours for magnesium nitrate, while there are only two for calcium nitrate and strontium nitrate (Fig. 2). Nevertheless, electron density at Ca–O BCP in Ca(NO₃)₂ is considerably higher (1.6 times) than electron density at Na–O BCP in NaNO₃. There are almost four common contours for magnesium sulfate, three for calcium sulfate, and only two for strontium sulfate (Fig. 2). Therefore, ρ_с in magnesium, calcium and strontium nitrates and sulfates for M–O bonds does not exceed 0.04 a.u. (0.020–0.039 a.u.). At the same time Δρ_с > 0 (0.082–0.264 a.u.) and H_c > 0 (0.003–0.009 a.u.), which indicates the ionic character of anion–cation bond in these compounds. It is interesting to note that energy densities for M–O bonds of zinc and lead nitrates and sulfates at BCPs are negative (−0.005 < H_c < −0.0003 a.u.), which indicates partially covalent nature of Zn–O and Pb–O bonds. However, the energy density H_c for Pb–O bonds of lead nitrate and sulfate is negative even at relatively small ρ_с (0.026–0.035 a.u.). It is due to the fact that H_c relates not only to the electron density ρ_с, but also to the Laplacian Δρ_с,^31,36 quite small for these bonds (0.075–0.120 a.u.). It should be noted that calculations with B3LYP hybrid functional also reveal negative values of energy densities for M–O bonds of zinc and lead nitrates and sulfates. Thus, interionic bond in oxyanionic crystals with metal cations with high electronegativity is of both electrostatic and covalent nature (mixed electrostatic-covalent character).

As for oxyanionic crystals, we found out that the distances between cationic nuclei and the bond critical points (R_c) correlate with cationic radii R_M.⁸⁶ The computed parameters of the linear approximation R_c = a + bR_M are given in Table 3. The scatterplots for the linear correlations listed in Table 3 are presented in the ESI (Fig. S1†). There is a good correlation between R_с and R_M (R² > 0.99). Thus, R_с can be used to estimate cationic radii and vice versa. A good correlation between R_с and R_M agrees well with the fact that the anion-cationic bond for most of oxyanionic crystals has predominantly electrostatic character. Some difference between R_с and R_M can be due to the fact that cationic charges are smaller than cationic valence (ionicity degree is not 100%). On the other hand, distances between the nuclei of central atoms (nitrogen, chlorine, sulfur) and the bond critical points in anions for isoanionic series remain practically the same. As for metal nitrates, chlorates, perchlorates and sulfates, they are ∼0.62 (0.71), 0.76 (1.02), 0.72 (1.02) and 0.68 (1.05), respectively (covalent radii⁸⁷ of central atoms are given in parentheses). The differences between covalent radii and BCPs distances for central atoms indicate the polarity of intra-anionic bonds.

Table 3 The parameters of the cationic dependencies R_c = a + bR_M (with R² correlations) for oxyanionic crystals with metal cations

Crystals	a (Å)	b	R^2
Alkali metal nitrates	0.278	0.875	0.997
Divalent metal nitrates	0.328	0.943	0.991
Alkali metal chlorates	0.247	0.905	1.000
Alkali metal perchlorates	0.275	0.916	0.999
Divalent metal sulfates	0.364	0.877	0.995

---

It is appealing to summarize the results of the study of chemical bond nature and establish some criteria for covalence. The dependencies between bond degree (H_c/ρ_c), electron density ρ_c, overlap population P_M–O and cationic electronegativities χ_M for M–O bonds of oxyanionic crystals calculated in our work are presented in Fig. 3.

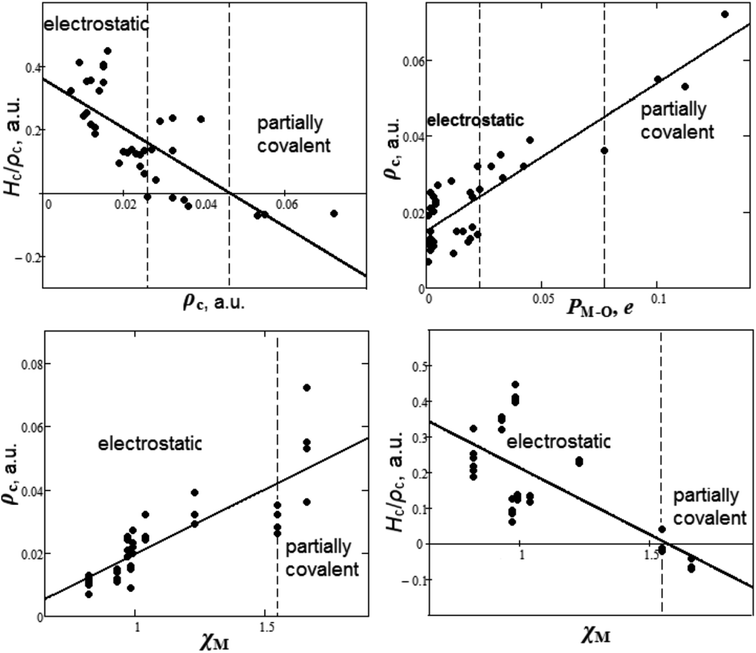Fig. 3 Dependencies between bond degree (H_c/ρ_c), electron density ρ_c, overlap population P_M–O and cationic electronegativities χ_M for metal–oxygen bonds of oxyanionic crystals.

It can be seen from Fig. 3 that there are two ranges of values of electron densities ρ_c for oxyanionic crystals with the corresponding M–O bonds different in nature. This is the range with positive values of bond degree and the range with H_c/ρ_c < 0. Herewith, closed shell (electrostatic) in nature M–O bonds exhibit ρ_c < 0.026 a.u., while partially covalent (H_c/ρ_c < 0) metal–oxygen interactions are characterized by ρ_c > 0.046 a.u. For example, in accordance with Tables 1 and S1,† Na–O bonds of NaNO₃ and Ca–O bonds of Ca(NO₃)₂ lie in electrostatic region. It is interesting to note that there is a transition region 0.026 < ρ_c < 0.046 a.u., where both electrostatic and partially covalent in nature M–O bonds are possible. As for oxyanionic crystals, it is interesting to find out how electron density at BCP is related to other characteristics, such as Mulliken overlap populations and electronegativities. It can be seen from Fig. 3 that as overlap population increases, electron density ρ_c for M–O bond increases as well as 0.015 + 0.389P_M–O (correlation is R² = 0.78). In these circumstances electrostatic in nature metal–oxygen bonds show P_M–O <0.023e, while partially covalent bonds agree with P_M–O > 0.077e. The transition region is characterized by 0.023 < P_M–O < 0.077e. As for cationic electronegativity χ_M,^88,89 electron density ρ_c have a tendency to increase (Fig. 3) along with increase of χ_M. In linear approximation ρ_c = −0.021 + 0.041χ_M (correlation is R² = 0.70). Bond degree (H_c/ρ_c) tends to decrease with increase of density ρ_c and electronegativity χ_M (Fig. 3). So, electrostatic M–O bonds (H_c/ρ_c > 0) correspond to comparatively low cationic electronegativities χ_M < 1.55, while partially covalent M–O bonds (H_c/ρ_c < 0) correspond to high χ_M > 1.55. It is interesting to note that for intra-anionic A–O bonds the covalence degree magnitude (|H_c/ρ_c|) increases with increase of central atom electronegativity χ_A^88,89 as well as −2.673 + 1.454χ_A (R² = 0.98). At the same time, ρ_c = −0.512 + 0.302χ_A (R² = 0.85) for intra-anionic bonds.

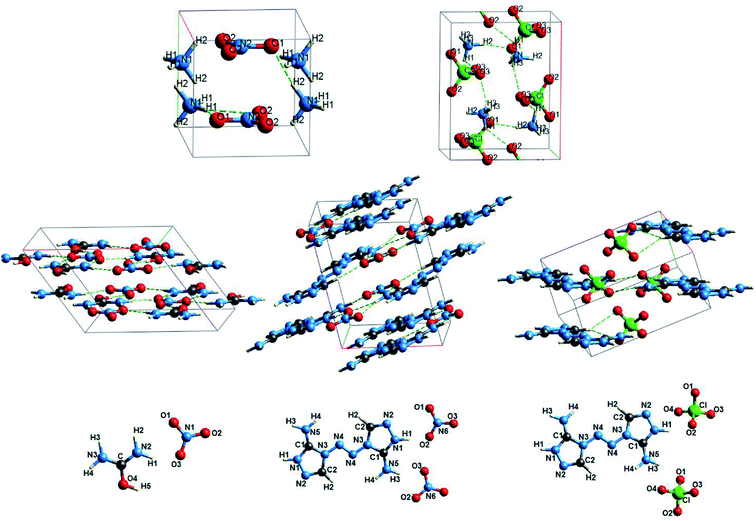
More complicated structures have oxyanionic crystals with polyatomic cations that contain nitrogen, hydrogen, and carbon (Fig. 4).

Fig. 4 Optimized structures for oxyanionic crystals with polyatomic inorganic and organic cations.

Nitrate and perchlorate with molecular inorganic ammonium cation are among such crystals (Fig. 4). Unlike oxyanionic crystals with metal cation, nitrate and perchlorate with polyatomic ammonium cation are characterized by the presence of H⋯O hydrogen bonds. The electron density ρ_c, the Laplacian of electron density Δρ_с and energy density H_c calculated at critical points for H⋯O hydrogen bonds of ammonium nitrate and perchlorate (AN and AP) are presented in Table 4. Atomic numbering is in accordance with Fig. 4. The electron density at BCPs for hydrogen bonds in ammonium nitrate and perchlorate does not exceed 0.03 a.u., Δρ_с > 0 and H_c > 0 (Table 4). B3LYP calculations also reveal positive H_c values. Thus, these H-bonds are closed shell (electrostatic) in nature.

Table 4 Topological properties of electron density calculated at BCPs for H⋯O hydrogen bonds in oxyanionic crystals with polyatomic inorganic and organic cations

Crystal	H-bonds	ρс	Δρс	Hс
AN	H2⋯O1	0.022	0.077	0.0015
	H1⋯O1	0.021	0.071	0.0013
	H1⋯O2	0.011	0.048	0.0024
AP	H2⋯O1	0.030	0.104	0.0004
	H3⋯O3	0.016	0.063	0.0023
	H1⋯O2	0.014	0.061	0.0027
	H1⋯O3	0.013	0.051	0.0022
UN	H5⋯O1	0.067	0.149	−0.0193
	H2⋯O3	0.032	0.091	−0.0017
	H1⋯O3	0.028	0.077	−0.0010
	H3⋯O2	0.026	0.071	−0.0006
	H4⋯O2	0.022	0.065	0.0005
DATN	H1⋯O2	0.051	0.140	−0.0085
	H4⋯O1	0.030	0.075	−0.0021
	H3⋯O3	0.028	0.070	−0.0016
	H2⋯O1	0.011	0.034	0.0013
DATP	H4⋯O1	0.031	0.086	−0.0016
	H1⋯O2	0.029	0.077	−0.0014
	H3⋯O2	0.022	0.059	0.0000
	H2⋯O1	0.012	0.036	0.0012

---

Other representatives of oxyanionic crystals with polyatomic cations include nitrates and perchlorates with polyatomic organic cations. Fig. 4 presents optimized structures of 3,3-diamino-4,4-azo-1,2,4-triazole nitrate and perchlorate (C₄H₈N₁₀(NO₃)₂, DATN and C₄H₈N₁₀(ClO₄)₂, DATP),²⁹ as well as urea nitrate ((NH₂)₂COH·NO₃, UN). An interesting peculiarity is that cationic hydrogen atoms are involved in hydrogen bonds with oxygen atoms of anions. The electron density ρ_c, the Laplacian of electron density Δρ_с and energy density H_c calculated at critical points for H⋯O hydrogen bonds of UN, DATN nitrates and DATP perchlorate are presented in Table 4. Atomic numbering is in accordance with Fig. 4. The highest electron densities at BCPs (0.067 and 0.051 a.u.) correspond to H5⋯O1 and H1⋯O2 hydrogen bonds in nitrates. The electron densities ρ_с for H⋯O bonds in UN (0.022–0.067 a.u.) calculated in our work are in reasonable agreement with the experimental ones (0.017–0.054 a.u., ref. 47). Also PBE results are in reasonable agreement with B3LYP ones (differences are smaller than 10%). Our calculations, as well as the experiment,⁴⁷ reveal that maximal ρ_с values for UN correspond to the H-bond which involved cationic hydroxyl group. In general, 0.03 a.u. < ρ_c < 0.07 a.u., Δρ_с > 0 and H_c < 0 (Table 4) are performed for H5⋯O1, H2⋯O3, H1⋯O2 (DATN), H4⋯O1 (DATP) hydrogen bonds of nitrates and perchlorates with polyatomic organic cations, which indicates the presence of a covalent component for these bonds. It is interesting to note that electron densities at BCPs for H1⋯O3, H3⋯O2 (UN), H4⋯O1 (DATN), H3⋯O3 and H1⋯O2 (DATP) hydrogen bonds have comparatively small values (0.026 a.u. < ρ_c < 0.03 a.u.), however, the energy densities H_c are negative and the nature of these bonds is partially covalent. It is due to the fact that the Laplacian Δρ_с for these bonds is quite small (H_c relates not only to electron density ρ_с, but also to the Laplacian Δρ_с^31,36). H4⋯O2, H2⋯O1, H3⋯O2 (DATP) hydrogen bonds are electrostatic in nature (ρ_c < 0.026 a.u., Δρ_с > 0 and H_c > 0).

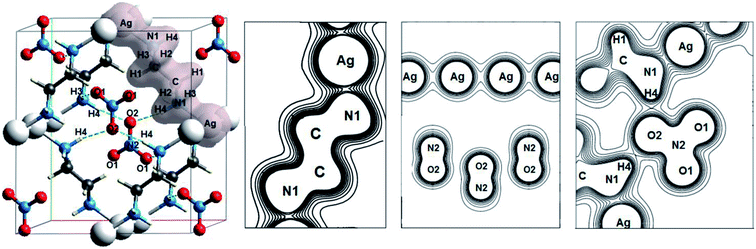
Another interesting class of oxyanionic crystals can be distinguished, that is metal–organic compounds containing organic ligands coordinated to metal cations. It is known that metal–organic nitrate [Ag(ethylenediamine)]NO₃ belongs to this group of crystals, where ethylenediamine molecules coordinated to silver cations via Ag–N bonds act as ligands.⁸ Fig. 5 presents optimized structure of this metal–organic nitrate (ethylenediamine-silver(I) nitrate), hereinafter referred as [Ag(en)]N.

Fig. 5 Optimized structure and electron density distributions for [Ag(ethylenediamine)]NO₃.

Such crystals have a framework structure and are coordination polymers (CPs), therefore they are called metal–organic frameworks (MOFs), or metal–organic coordination polymers.^90,91 It should be noted that the term metal–organic has been used to cover broadly those compounds with metal–carbon bonds (usually known as organometallic compounds), as well as metal–oxygen–carbon compounds (alkoxides or alcoholates), and coordination compounds of metals and organic molecules (ligands).^92,93

Fig. 5 shows electron density distributions for [Ag(en)]N. The interval between isodensity curves is 0.01 a.u. It is seen that chemical bond is substantially covalent inside organic ligands and nitrate anions. The atoms of ligands and anions have a large number of common contours, which is typical of covalent bond. [Ag(en)]N has an interesting feature, that is metal–ligand (Ag–N1) and metal⋯metal (Ag⋯Ag) bonds. Hydrogen bonds between anions and ligands are also of interest, where hydrogen atoms of ligands and oxygen atoms of nitrate anions are involved. More than five common contours are visible for silver cations and nitrogen atoms of ligands. Two contours that are common to the chain of silver cations also attract attention. Almost three common contours are visible for hydrogen bonds H4⋯O2 (Fig. 5).

Table 5 presents the electron density ρ_c, the Laplacian of electron density Δρ_с and energy density H_c at critical points for Ag–N1, Ag⋯Ag and H⋯O bonds of metal–organic nitrate [Ag(en)]N. Atomic numbering is in accordance with Fig. 5.

Table 5 Topological properties of electron density calculated at BCPs for the bonds in [Ag(en)]N

Bonds	ρс	Δρс	Hс
Ag–N1	0.085	0.329	−0.0198
Ag⋯Ag	0.023	0.051	−0.0011
H4⋯O2	0.030	0.078	−0.0018
H3⋯O1	0.019	0.056	0.0008

---

As can be seen from the Table, comparatively high density ρ_c > 0.08 a.u. takes place for metal–ligand (Ag–N1) bonds, which can be compared with ρ_c typical of covalent bonds (>0.14 a.u.³⁹). And H_c < 0, that indicates the presence of covalent component for metal–ligand bond. As for argentophilic bonds Ag⋯Ag, the electron density ρ_c is comparatively small and equals ∼0.02 a.u., however, the energy density is negative, therefore, there is covalent component of bond. Thus, there are argentophilic bonds Ag⋯Ag and coordination bonds Ag–N1 in [Ag(en)]N, which are partly covalent in nature. Electrostatic and covalent nature of metal–ligand bonds in metal–organic compounds has been earlier discussed in ref. 94–96. Ag–N coordination bond energy calculated in our work equals 159 kJ mol⁻¹, which is comparable with typical covalent bond energies. The energy of argentophilic bonds Ag⋯Ag is significantly smaller (∼20 kJ mol⁻¹). Associations of like-charged ions were previously discussed in ref. 80, where the possibility of bonding anion–anion and cation–cation interactions is confirmed. It has been noted that orbital overlap of gold atoms takes place in aurophilic interaction Au⋯Au.⁸⁰ According to ref. 97, the formation of cation–cation associates is stimulated and due to their stabilization through cation–anion interactions. It is quite interesting that our calculations for isolated dimers of silver cations revealed their stability (E_Ag⋯Ag = 60 kJ mol⁻¹), if the dimer charge equals +1 e (Ag^+0.5⋯Ag^+0.5). As for hydrogen bonds, one of them, namely H4⋯O2 (with higher ρ_c), has a partially covalent nature (H_c < 0), while the other, namely H3⋯O1, is caused only by electrostatic interaction (H_c > 0).

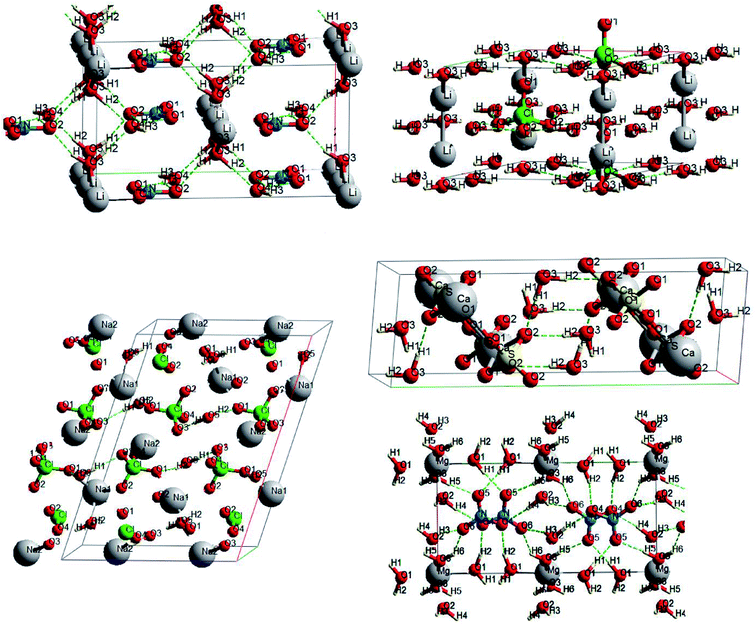
Oxyanionic compounds with crystal water molecules (crystalline hydrates) is another class of oxyanionic crystals. Fig. 6 presents optimized structures of lithium perchlorate trihydrate (LPH), sodium perchlorate monohydrate (SPH), calcium sulfate dihydrate (CSH), lithium nitrate trihydrate (LNH) and magnesium nitrate hexahydrate (MNH).

Fig. 6 Optimized structures for oxyanionic crystalline hydrates.

Anion-water and water–water interactions through H⋯O hydrogen bonds is an interesting peculiarity of oxyanionic crystalline hydrates. Table 6 presents the calculated electron density ρ_c, the Laplacian of electron density Δρ_с and energy density H_c at critical points for H⋯O hydrogen bonds in LNH, LPH, SPH, CSH and MNH. Atomic numbering is in accordance with Fig. 6.

Table 6 Topological properties of electron density calculated at BCPs for H⋯O hydrogen bonds in oxyanionic crystalline hydrates

Crystal	H-bonds	ρс	Δρс	Hс
LNH	H2⋯O4	0.039	0.113	−0.0035
	H1⋯O2	0.033	0.115	−0.0002
	H3⋯O1	0.026	0.081	0.0002
	H3⋯O2	0.014	0.067	0.0032
LPH	H⋯O2	0.023	0.079	0.0012
SPH	H2⋯O1	0.031	0.101	−0.0004
	H1⋯O3	0.019	0.070	0.0019
CSH	H1⋯O2	0.036	0.102	−0.0028
	H2⋯O2	0.030	0.087	−0.0011
MNH	H2⋯O4	0.038	0.115	−0.0027
	H5⋯O5	0.035	0.105	−0.0020
	H1⋯O5	0.032	0.096	−0.0013
	H4⋯O4	0.031	0.093	−0.0010
	H3⋯O6	0.025	0.076	0.0002
	H6⋯O6	0.020	0.062	0.0009

---

As can be seen from the Table 6, the hydrogen bonds of lithium perchlorate hydrate are electrostatic in nature (ρ_c ∼ 0.02 a.u., H_c > 0). Besides, comparatively small electron densities (0.019 a.u. < ρ_c < 0.026 a.u.) and H_c > 0 (Table 6) correspond to H3⋯O1(2), H1⋯O3, H3⋯O6, H6⋯O6 bonds of the hydrates under consideration, that indicates closed shell (electrostatic) nature of these bonds. The highest electron densities ρ_c (0.039 and 0.038 a.u.) correspond to H2⋯O4 hydrogen bonds in lithium and magnesium nitrate hydrates, for which H_c < 0 (Table 6), that proves the presence of a covalent component for these bonds. Hydrogen bonds of gypsum and H2⋯O1 bonds of sodium perchlorate hydrate are also characterized by partially covalent nature (H_c < 0). Thus, hydrogen bonds in oxyanionic crystalline hydrates may have both electrostatic and covalent contribution (mixed electrostatic-covalent character).

It is quite interesting to summarize the results of the study of the nature of hydrogen bond and establish some criteria of covalence. The dependencies between bond degree (H_c/ρ_c), electron density ρ_c, overlap population P_H⋯O, bond length d_H⋯O and energy E_HB for H⋯O hydrogen bonds in oxyanionic crystals calculated in our work are presented in Fig. 7.

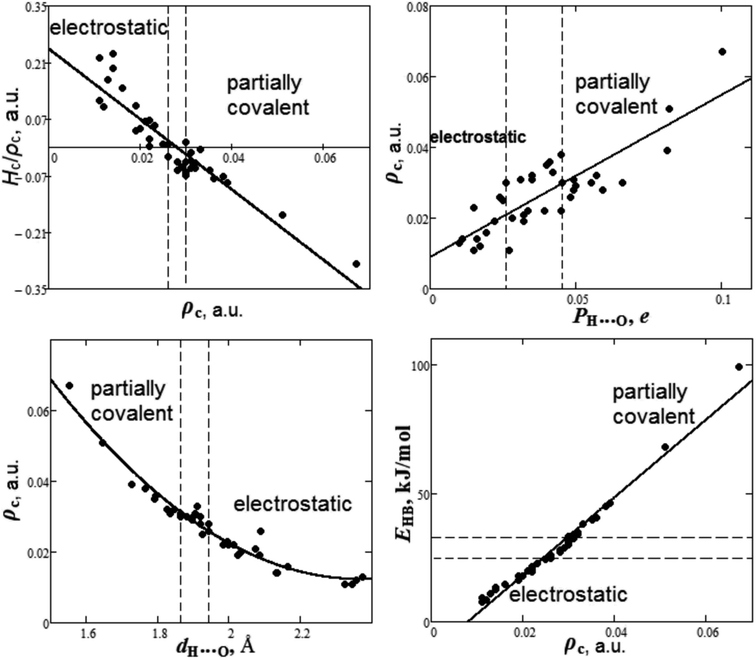Fig. 7 Dependencies between bond degree (H_c/ρ_c), electron density ρ_c, overlap population P_H⋯O, bond length d_H⋯O and energy E_HB for H⋯O hydrogen bonds in oxyanionic crystals.

As can be seen from Fig. 7, there are two ranges of values of electron densities ρ_c for oxyanionic crystals with the corresponding H⋯O bonds different in nature. This is the range with positive values of bond degree and the range with H_c/ρ_c < 0. Herewith, closed shell (electrostatic) in nature H⋯O hydrogen bonds exhibit ρ_c < 0.026 a.u., while partially covalent (H_c/ρ_c < 0) characterized by ρ_c > 0.030 a.u. It is interesting to note that there is transition region 0.026 < ρ_c < 0.030 a.u., where both electrostatic and partially covalent in nature H⋯O hydrogen bonds are possible.

It was shown that for the same acceptor (O) of H-bonds between DNA and actinomycin, a greater overlap population corresponds to a shorter H⋯O distance.⁹⁸ It is interesting to find out how electron density at BCP is related to other characteristics, such as Mulliken overlap populations, bond length and energy for H-bonds of oxyanionic crystals. As can be seen from Fig. 7, the electron density ρ_c, along with overlap population increase, grows as well as 0.009 + 0.459P_H⋯O (correlation is R² = 0.71). In these circumstances, electrostatic in nature H⋯O bonds show P_H⋯O < 0.026e, while partially covalent bonds satisfy the condition P_H⋯O > 0.045e. The transition region is characterized by 0.026 < P_H⋯O < 0.045e. As for H-bond geometric characteristic, such as bond length d_H⋯O, the electron density ρ_c tends to decrease (Fig. 7) as the bond length increases, as much as ρ_c = 0.433 − 0.356d_H⋯O + 0.075d_H⋯O² (correlation is R² = 0.95). Relatively short H-bonds (d_H⋯O < 1.87 Å) are partly covalent in nature, while the relatively long ones (d_H⋯O > 1.94 Å) have electrostatic character. The transition region corresponds to 1.87 < d_H⋯O < 1.94 Å. Moreover, we have considered the dependency between electron density ρ_c and energy E_HB for H⋯O hydrogen bonds in oxyanionic crystals (Fig. 7). Along with electron density ρ_c increase, our calculated the hydrogen bond energy E_HB increases as much as −12.22 + 1515ρ_c (correlation is R² = 0.97). Based on DFT calculations of electron densities and vibration frequencies, it was revealed that E_HB (in kJ mol⁻¹) = −12.94 + 1001ρ_c for intramolecular H⋯O hydrogen bonds in the DNA related molecules.⁹⁹ As it was pointed out in ref. 99, the discrepancies between real H-bond energies and energies calculated by means of the Espinosa–Molins–Lecomte equation⁷⁷ for molecules and molecular H-bonded complexes may originate from the fact that the latter has been parametrized using H-bonds data for the substance in crystalline state that effectively strengthens H-bonds. Our calculations show (Fig. 7) that electrostatic in nature H⋯O hydrogen bonds have energies lower than 25 kJ mol⁻¹, while partially covalent ones have the energies higher than 33 kJ mol⁻¹. The transition region is characterized by 25 < E_HB < 33 kJ mol⁻¹.

Pressure behavior of crystals is of certain interest.^100–104 In conclusion, we considered the pressure effect as exemplified by some oxyanionic crystals. It is quite interesting to find out how the electron densities and energies will change at critical points, hence the nature of the chemical bond under external pressure. Fig. 8 shows the pressure dependencies of the relative electron charge densities and energy at the BCPs for metal–oxygen bonds in lithium, sodium, and potassium nitrates. It is seen that electron density ρ_c increases by ∼10–20% as the pressure increases up to 3 GPa, however, the ionic character of M–O bond still remains (H_c > 0).

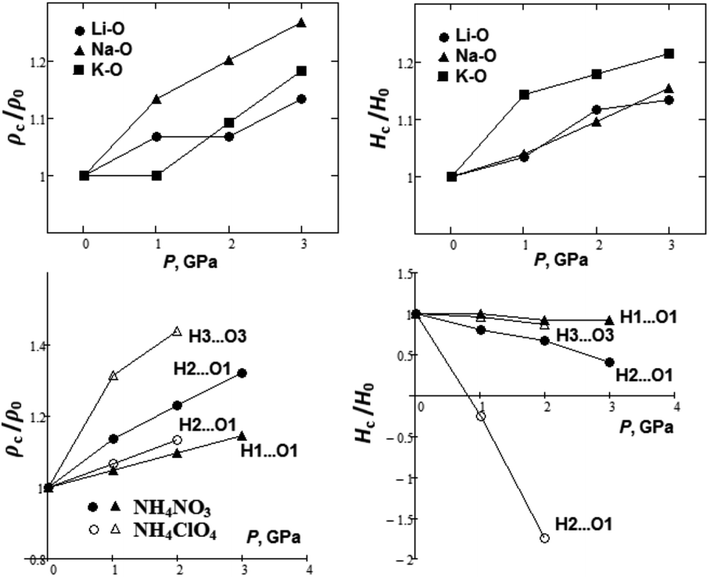Fig. 8 Pressure dependencies of charge density and energy at critical points for M–O and H⋯O bonds of oxyanionic crystals.

Besides, Fig. 8 shows pressure dependencies of relative electron charge densities and energy at the BCPs for H⋯O hydrogen bonds in ammonium nitrate and perchlorate. It is seen that the electron density ρ_c increases by ∼10–40% as pressure grows up to 2 GPa, especially for H2⋯O1 and H3⋯O3 bonds in in ammonium nitrate and perchlorate, respectively. At the same time energy density H_c decreases as the pressure increases, especially for H2⋯O1 bonds. We can see that H_c is negative for H2⋯O1 bonds in ammonium perchlorate even at ∼1 GPa. B3LYP calculations also confirm this. H_c should change the sign in ammoinium nitrate at ∼4 GPa. Thus, covalent component of H2⋯O1 hydrogen bonds appears as the pressure increases. Hydrogen bonds for compressed NH₄NO₃ and NH₄ClO₄ are partially covalent in nature. So, the pressure caused changes in the nature of hydrogen bonds in oxyanionic crystals. Moreover, we considered pressure behavior of the Ag–N coordination bond projections on a- and b-axes in [Ag(en)]N. The magnitude of a-projection (in Å) increases with pressure as 1.883 + 0.033P (R² = 0.92), whereas the magnitude of b-projection decreases with pressure as 1.274–0.065P (R² = 0.97). Such pressure dependencies correlate with negative and positive compressibility along a- and b-axes, respectively.^8,9

4. Conclusions

Systematic ab initio study of the nature of chemical bond in oxyanionic crystals has been performed on the basis of QTAIM topological analysis of calculated electron densities. Electron densities and their Laplacians at the bond critical points, energy densities at the BCPs, bond degrees and interaction energies have been calculated. The calculated electron densities at the BCPs are in reasonable agreement with the available experimental data.

The QTAIM topological analysis showed that intra-anionic bonds are polar covalent in nature. For intra-anionic bonds the covalence degree increases with growth of central atom electronegativity. The study revealed that there are weak bonding anion⋯anion interactions in oxyanionic crystals. The energies of anion⋯anion interactions for oxyanionic salts with lithium and sodium cations are higher than those for potassium salts. The distances between the cationic nucleus and the bond critical points correlate with cationic radius. There are different in nature (electrostatic and partially covalent) metal–oxygen and hydrogen bonds in oxyanionic crystals. The QTAIM topological analysis of the calculated electron densities in oxyanionic crystals revealed the covalency criteria for metal–oxygen and hydrogen bonds. There is the transition region of electron densities at BCPs where both electrostatic and partially covalent in nature metal–oxygen and hydrogen bonds are possible. It has been demonstrated that there are argentophilic bonds Ag⋯Ag and coordination bonds Ag–N in metal–organic nitrate [Ag(ethylenediamine)]NO₃, which are partly covalent in nature. The dependencies between electron density at the BCP, overlap population, electronegativities, H-bond length and energy were calculated. The study has also revealed that electron density at BCP increases along with the growth of overlap population for metal–oxygen and hydrogen bonds. As cationic electronegativity increases, electron densities at the BCPs for metal–oxygen bonds have a tendency to increase. Electron density at the BCP decreases with H-bond length increase and H-bond energy increases as electron density grows at the BCP. It has been demonstrated that the pressure caused changes in the nature of hydrogen bonds in oxyanionic crystals.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The work was supported by the Ministry of Education and Science of the Russian Federation (Project No 15.3487.2017/PP).

References

1. G. P. Sutton and O. Biblarz, Rocket Propulsion Elements, John Wiley Sons Inc., New Jersey, 2010.
2. G. Steinhauser and T. M. Klapotke, Angew. Chem., Int. Ed., 2008, 47, 3330.
3. E. C. Koch, Propellants, Explos., Pyrotech., 2004, 29, 67.
4. N. Yedukondalu and G. Vaitheeswaran, Mater. Chem. Phys., 2016, 181, 54.
5. S. U. Patil, S. S. Yawale and S. P. Yawale, Bull. Mater. Sci., 2014, 37, 1403.
6. D. F. Xue and S. Y. Zhang, Chem. Phys. Lett., 1998, 287, 503.
7. O. V. Buganov, A. S. Grabtchikov, Y. I. Malakhov, Y. M. Popov, V. A. Orlovich and S. A. Tikhomirov, Laser Phys. Lett., 2012, 9, 786.
8. W. Cai and A. Katrusiak, Nat. Commun., 2014, 5, 4337.
9. D. V. Korabel’nikov and Yu. N. Zhuravlev, Phys. Chem. Chem. Phys., 2016, 18, 33126.
10. D. V. Korabel’nikov and Yu. N. Zhuravlev, J. Phys. Chem. A, 2017, 121, 6481.
11. M. H. Hecht, S. P. Kounaves, R. C. Qurinn, S. J. West, S. M. Young, D. W. Ming, D. C. Catling, B. C. Clark, W. V. Boynton, J. Hoffman, L. P. DeFlores, K. Gospodinova, J. Kapit and P. H. Smith, Science, 2009, 325, 64.
12. M. Smith, M. Claire, D. Catling and K. Zahnle, Icarus, 2014, 231, 51.
13. V. F. Chevrier, J. Hanley and T. S. Altheide, Geophys. Res. Lett., 2009, 36, L10202.
14. Z. Yan and X. Hu, Mater. Chem. Phys., 2003, 77, 402.
15. J. Peng, X. Li, C. Tang and W. Bai, Green Chem., 2014, 16, 108.
16. M. N. I. Castro, J. M. A. Robles, D. A. C. Hernandez, J. C. E. Bocardo and J. T. Torres, Ceram. Int., 2010, 36, 1205.
17. T. Murakami, J. H. Ouyang, K. Umeda and S. Sasaki, Mater. Sci. Eng., A, 2006, 432, 52.
18. A. Wang, J. J. Freeman, B. L. Jolliff and I. Chou, Geochim. Cosmochim. Acta, 2006, 70, 6118.
19. A. E. Rubin, Meteorit. Planet. Sci., 1997, 32, 231.
20. A. Radenovic, Kem. Ind., 2006, 55, 65.
21. A. J. Nalwalk, R. A. Friedel and J. A. Queiser, Energy Sources, 1974, 1, 179.
22. D. V. Korabel’nikov and Yu. N. Zhuravlev, J. Phys. Chem. Solids, 2015, 87, 38.
23. D. V. Korabel’nikov and Yu. N. Zhuravlev, Phys. Solid State, 2017, 59, 254.
24. D. V. Korabel’nikov and Yu. N. Zhuravlev, J. Phys. Chem. Solids, 2018, 119, 114.
25. D. V. Korabel’nikov and Yu. N. Zhuravlev, J. Struct. Chem., 2016, 57, 446.
26. D. V. Korabel’nikov and Yu. N. Zhuravlev, Phys. Solid State, 2018, 60, 2058.
27. D. V. Korabel’nikov, Phys. Solid State, 2018, 60, 571.
28. D. V. Korabel’nikov and Yu. N. Zhuravlev, Phys. Solid State, 2016, 58, 1166.
29. W. Liu, S. Li, Y. Li, Y. Yang, Y. Yu and S. Pang, J. Mater. Chem. A, 2014, 2, 15978.
30. V. V. Boldyrev, Russ. Chem. Rev., 2006, 75, 177.
31. R. F. W. Bader, Atoms in Molecules - A Quantum Theory, Oxford University Press, Oxford, 1990.
32. R. F. W. Bader, Chem. Rev., 1991, 91, 893.
33. P. Coppens and E. D. Stevens, Adv. Quantum Chem., 1977, 10, 1.
34. D. Cremer and E. Kraka, Angew. Chem., Int. Ed., 1984, 23, 627.
35. D. Cremer and E. Kraka, Croat. Chem. Acta, 1984, 57, 1259.
36. Yu. A. Abramov, Acta Crystallogr., Sect. A: Found. Crystallogr., 1997, 53, 264.
37. D. A. Kirzhnits, J. Exp. Theor. Phys., 1957, 5, 64.
38. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529.
39. M. V. Vener, A. V. Manaev, A. N. Egorova and V. G. Tsirelson, J. Phys. Chem. A, 2007, 111, 1155.
40. C. Gatti, Z. Kristallogr., 2005, 220, 399.
41. S. J. Grabowski, Chem. Rev., 2011, 111, 2597.
42. G. Gervasio, R. Bianchi and D. Marabello, Chem. Phys. Lett., 2004, 387, 481.
43. R. F. W. Bader, in Encyclopedia of Computational Chemistry, John Wiley Sons Inc., La Jolla, 1998, https://www.wiley.com//legacy/wileychi/ecc/samples/sample02.pdf.
44. V. Tsirelson, Yu. Abramov, V. Zavodnik, A. Stash, E. Belokoneva, J. Stahn, U. Pietsch and D. Fell, Struct. Chem., 1998, 9, 249.
45. Yu. Ivanov, T. Nimura and K. Tanaka, Acta Crystallogr., Sect. B: Struct. Sci., 2004, 60, 359.
46. Yu. V. Nelyubina, K. A. Lyssenko, R. G. Kostyanovsky, D. A. Bakulin and M. Yu. Antipin, Mendeleev Commun., 2008, 18, 29.
47. Yu. V. Nelyubina, K. A. Lyssenko, D. G. Golovanov and M. Yu. Antipin, CrystEngComm, 2007, 9, 991.
48. D. Marabello, R. Bianchi, G. Gervasio and F. Cargnoni, Acta Crystallogr., Sect. A: Found. Crystallogr., 2004, 60, 494.
49. R. Herbst-Irmer, J. Henn, J. J. Holstein, C. B. Hübschle, B. Dittrich, D. Stern, D. Kratzert and D. Stalke, J. Phys. Chem. A, 2013, 117, 633.
50. A. A. Kovalenko, Yu. V. Nelyubina, A. A. Korlyukov, K. A. Lyssenko and I. V. Ananyev, Z. Kristallogr., 2018, 233, 317.
51. V. G. Tsirelson, in Recent Advances in Quantum Theory of Atoms in Molecules, Wiley-VCH, Weinheim, Germany, 2007.
52. A. Volkov, Yu. Abramov, P. Coppens and C. Gatti, Acta Crystallogr., Sect. A: Found. Crystallogr., 2000, 56, 332.
53. Yu. N. Zhuravlev and A. S. Poplavnoi, J. Struct. Chem., 2003, 44, 187.
54. Yu. N. Zhuravlev and A. S. Poplavnoi, J. Struct. Chem., 2001, 42, 882.
55. M. Catti, A. Pavese, R. Dovesi and V. R. Saunders, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 9189.
56. M. Aydinol, J. V. Mantese and S. P. Alpay, J. Phys.: Condens. Matter, 2007, 19, 496210.
57. A. J. Skinner, J. P. LaFemina and H. J. F. Jansen, Am. Mineral., 1994, 79, 205.
58. A. D. Becke, J. Chem. Phys., 2014, 140, 18A301.
59. R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre and P. D'Arco, Int. J. Quantum Chem., 2014, 114, 1287.
60. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
61. S. Grimme, J. Comput. Chem., 2006, 27, 1787.
62. I. A. Fedorov, Chem. Phys., 2019, 518, 8.
63. B. M. Abraham, J. P. Kumar and G. Vaitheeswaran, ACS Omega, 2018, 3, 9388.
64. I. A. Fedorov and Yu N. Zhuravlev, Chem. Phys., 2014, 436, 1.
65. K. Babu and G. Vaitheeswaran, Chem. Phys. Lett., 2014, 592, 132.
66. S. Appalakondaiah, G. Vaitheeswaran, S. Lebegue, N. E. Christensen and A. Svane, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 035105.
67. D. W. J. Cruickshank, Acta Crystallogr., 1956, 9, 757.
68. W. R. Busing and H. A. Levy, Acta Crystallogr., 1964, 17, 142.
69. K. Fucke and J. Steed, Water, 2010, 2, 333.
70. C. J. Pickard and R. J. Needs, Nat. Phys., 2007, 3, 473.
71. B. Berglund, R. Tellgren and J. O. Thomas, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1976, 32, 2444.
72. J. W. Steed and J. L. Atwood, Supramol. Chem., Wiley, Chichester, 2009.
73. I. Ortega, R. Escribano, D. Fernandez, V. Herrero, B. Mate, A. Medialdea and M. Moreno, Chem. Phys. Lett., 2003, 378, 218.
74. S. K. Wolff, D. J. Grimwood, J. J. McKinnon, M. J. Turner, D. Jayatilaka and M. A. Spackman, CrystalExplorer, University of Western Australia, Australia, 2012.
75. C. F. Matta and R. J. Boyd, The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design, Wiley-VCH Verlag GmbH & Co. KgaA, Weinheim, 2007.
76. C. Gatti and S. Casassa, TOPOND14 User's Manual. CNR-ISTM Milano, Milano, 2014.
77. E. Espinosa, E. Molins and C. Lecomte, Chem. Phys. Lett., 1998, 285, 170.
78. A. O. Borissova, A. A. Korlyukov, M. Y. Antipin and K. A. Lyssenko, J. Phys. Chem. A, 2008, 112, 11519.
79. K. A. Lyssenko and I. L. Eremenko, J. Organomet. Chem., 2018, 867, 284.
80. Yu. V. Nelyubina, M. Yu. Antipin and K. A. Lyssenko, Russ. Chem. Rev., 2010, 79, 167.
81. E. A. Zhurova, A. I. Stash, V. G. Tsirelson, V. V. Zhurov, E. V. Bartashevich, V. A. Potemkin and A. A. Pinkerton, J. Am. Chem. Soc., 2006, 128, 14728.
82. T. Hughbanks and R. Hoffman, J. Am. Chem. Soc., 1983, 105, 3528.
83. R. Dronskowski and P. E. Blochl, J. Phys. Chem., 1993, 97, 8617.
84. A. Grechnev, R. Ahuja and O. Eriksson, J. Phys.: Condens. Matter, 2003, 15, 7751.
85. R. A. Jackson and K. A. Mort, Comput. Mater. Sci., 2000, 17, 230.
86. L. Pauling, J. Am. Chem. Soc., 1927, 49, 765.
87. B. Cordero, V. Gomez, A. E. Platero-Prats, M. Reves, J. Echeverria, E. Cremades, F. Barragan and S. Alvarez, Dalton Trans., 2008, 0, 2832.
88. A. L. Allred and E. G. Rochow, J. Inorg. Nucl. Chem., 1958, 5, 264.
89. E. J. Little and M. M. Jones, J. Chem. Educ., 1960, 37, 231.
90. V. V. Butova, M. A. Soldatov, A. A. Guda, K. A. Lomachenko and C. Lamberti, Russ. Chem. Rev., 2016, 85, 280.
91. S. R. Batten, N. R. Champness, X.-M. Chen, J. Garcia-Martinez, S. Kitagawa, L. Ohrstrom, M. O'Keeffe, M. P. Suh and J. Reedijk, CrystEngComm, 2012, 14, 3001.
92. M. Sittig, Metal–Organic Compounds, in Advances in Chemistry, Am. Chem. Soc., Washington, 1959,  DOI:10.1021/ba-1959-0023.pr001.
93. H. Kooijman, S. Tanase, E. Bouwman, J. Reedijk and A. L. Spek, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2006, 62, m510.
94. B. Ivanova and M. Spiteller, Polyhedron, 2017, 137, 256.
95. A. O. Borissova and K. A. Lyssenko, Mendeleev Commun., 2011, 21, 160.
96. C. Lepetit, B. Vabre, Y. Canac, M. E. Alikhani and D. Zargarian, Theor. Chem. Acc., 2018, 137, 141.
97. M. A. Carvajal, S. Alvarez and J. J. Novoa, Theor. Chem. Acc., 2006, 116, 472.
98. C. Bendic, M. Enache and E. Volanschi, J. Mol. Graphics Modell., 2005, 24, 10.
99. T. Yu. Nikolaienko, L. A. Bulavin and D. M. Hovorun, Phys. Chem. Chem. Phys., 2012, 14, 7441.
100. E. Zurek and W. Grochala, Phys. Chem. Chem. Phys., 2015, 17, 2917.
101. B. A. Zakharov, Z. Galc, D. Cruickshank and E. V. Boldyreva, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2018, 74, 613.
102. E. V. Boldyreva, J. Mol. Struct., 2004, 700, 151.
103. B. A. Zakharov and E. V. Boldyreva, CrystEngComm, 2019, 21, 10.
104. B. A. Zakharov, P. A. Gribov, A. A. Matvienko and E. V. Boldyreva, Z. Kristallogr., 2017, 232, 751.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra01403a

---