Open Access Article
Open Access ArticleStrain vs. charge mediated magnetoelectric coupling across the magnetic oxide/ferroelectric interfaces
Binod Paudelad,
Igor Vasiliev a,
Mahmoud Hammourib,
Dmitry Karpovc,
Aiping Chen
a,
Mahmoud Hammourib,
Dmitry Karpovc,
Aiping Chen d,
Valeria Lautere and
Edwin Fohtung
d,
Valeria Lautere and
Edwin Fohtung *af
*af
aDepartment of Physics, New Mexico State University, Las Cruces, NM 88001, USA. E-mail: efohtung@nmsu.edu
bDepartment of Physics, California State University, Los Angeles, CA 90032, USA
cSwiss Light Source, Paul Scherrer Institute, Villigen, 5232, Switzerland
dCenter for Integrated Nanotechnologies (CINT), Los Alamos National Laboratory, Los Alamos, NM 87544, USA
eNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, TN 37831, USA
fLos Alamos National Laboratory, Los Alamos, NM 87544, USA
First published on 29th April 2019
Abstract
We utilize polarized neutron reflectometry (PNR) in consort with ab initio based density functional theory (DFT) calculations to study magnetoelectric coupling at the interface of a ferroelectric PbZr0.2Ti0.8O3 (PZT) and magnetic La0.67Sr0.33MnO3 (LSMO) heterostructure grown on a Nb-doped SrTiO3 (001) substrate. Functional device working conditions are mimicked by gating the heterostructure with a Pt top electrode to apply an external electric field, which alters the magnitude and switches the direction of the ferroelectric (FE) polarization, across the PZT layer. PNR results show that the gated PZT/LSMO exhibits interfacial magnetic phase modulation attributed to ferromagnetic (FM) to A-antiferromagnetic (A-AF) phase transitions resulting from hole accumulation. When the net FE polarization points towards the interface (positive), the interface doesn't undergo a magnetic phase transition and retains its global FM ordered state. In addition to changes in the interfacial magnetic ordering, the global magnetization of LSMO increases while switching the polarization from positive to negative and decreases vice versa. DFT calculations indicate that this enhanced magnetization also correlates with an out of plane tensile strain, whereas the suppressed magnetization for positive polarization is attributed to out of plane compressive strain. These calculations also show the coexistence of FM and A-AF phases at zero out of plane strain. Charge modulations throughout the LSMO layer appear to be unaffected by strain, suggesting that these charge mediated effects do not significantly change the global magnetization. Our PNR results and DFT calculations are in consort to verify that the interfacial magnetic modulations are due to co-action of strain and charge mediated effects with the strain and charge effects dominant at different length scale.
Introduction
Magnetoelectric multiferroics (MFs), having the simultaneous occurrence of two ferroic order parameters (i.e. ferroelectric (FE) and anti/ferromagnetic), exhibit novel and exotic functionalities due to coupling between these parameters and show promise for new device applications.1–3 The control of magnetism (electricity) via electric (magnetic) degrees of freedom finds application in magnetic random access memory, magnetic field sensors and spintronic devices and can be exploited for device miniaturization.4–6 However, single-phase multiferroics with large magnetoelectric (ME) coupling of the FM and FE order parameters that can operate well above room temperatures are rare. This is because of the mutually exclusive chemistry required for the existence of two order parameters.7–9 To circumvent this limitation, ME multiferroic composites comprised of magnetic and FE phases are constructed; where ME effects are realized via cross-coupling between piezoelectric and magnetostrictive properties of the FE and FM layers respectively.4,5,9 These heterostructures have an advantage over single phase multiferroics in that the ME coupling coefficient can be tuned by choosing FM layers with optimized magnetostrictive properties and enhanced Curie temperatures, and FE layers with excellent piezoelectric properties.10In this article, we report ME coupling at the interface of La0.67Sr0.33MnO3 (LSMO) and PbZr0.2Ti0.8O3 (PZT) layers grown on a Nb-doped STO (001) substrate and investigate interfacial magnetism modulations by switching the ferroelectric polarization orientations in the PZT layer. Hole doped lanthanum manganites such as La1−xAx MnO3 (A = Sr, Ca, Ba) well recognized for their colossal magnetoresistance property exhibit varied phases as a function of hole dopant concentration and temperature, as they carry strong interplay between charge, lattice, orbital and spin degrees of freedom.11–15 La1−xSrx MnO3 with x = 0.33 is the optimum doped manganite owing to the half-metallic behavior and optimized spin polarization with relatively high Curie temperature (TC = 360 K); which is manifested through dominant double-exchange mechanisms that delocalize eg electrons.16–18 PbZrxTi1−xO3 the solid solution of PbZrO3 and PbTiO3 with x = 0.2 was chosen in our experiments because of its high Curie temperature and large saturation polarization.19,20 For this reason, the LSMO/PZT heterostructure is considered as one of the best building blocks to fabricate ultra-low power spintronic devices that can be controlled with electric fields.
The methods of inducing and controlling magnetism across the interface of ferroelectric and magnetic layers in heterostructures have been profoundly studied in recent years since they are promising to replace energy consuming current controlled spin transfer torque (STT) memory devices.21–23 Recent studies have shown that the interface magnetoelectric coupling persists from a few unit cells to tenths of nanometers. However, understanding the mechanism of magnetoelectric coupling across such length scales under device working conditions requires a combination of theoretical and non-invasive experimental probes. These probes can access both the local distribution and changes in the magnetic polarization with atomic resolution across tens of unit cells. The electronic reconstructions at atomic scales via electric field induced strain coupled magnetism tuning in manganites, due to changes in electron hopping rates and associated changes in the atomic bond angles and lengths, have been widely studied.5,24–29 Electric field induced charge (electron–hole pairs) mediated coupling across FM/FE interfaces also alters the charge carrier concentrations at the FM oxide layers via an accumulation or depletion process depending on the direction of FE polarization.30 The interfacial magnetism and thus ME coupling can be manipulated through changing the magnetic moments due to the flipping of spin ordering or orbital reconstruction, changing the exchange interactions (resulting in competition between different magnetic phases), and by changing global magnetization (a result of changes in magnetic anisotropy).23 Charge mediated magnetism and ME coupling in LSMO/PZT multiferroic heterostructures has been extensively reported31–34 and some studies have ME coupling associated with the strain-mediated effects across the FE/FM interface. However, to understand the ME coupling that is persistent from Angstroms to tens of nm length-scales, we need probes that are capable of disentangling coupled charge and strain effects with local and atomic scale sensitivity. In this article, we combine PNR and DFT to elucidate the mechanisms of charge vs. strain mediated ME coupling across the PZT/LSMO interface and we explore contributions from an external electric field driven strain and charge mediated ME coupling.
Extensive experimental and theoretical work has been performed to understand magnetic modulations at LSMO/PZT interfaces.18,31,33–40 Vaz et al.31 studied ME coupling effects across the LSMO/PZT interface and attributed the observed ME coupling to interface charge mediations. Using X-ray absorption spectroscopy (XAS), they demonstrated that the modulation of Mn-ion valency is responsible for polarization induced magnetism changes at the LSMO interface region. They also argued that the observed suppression of magnetization at the interfacial layer associated with charge accumulation was attributed to strongly depopulated 3d z2 orbitals. This, in turn, favours the idea that super exchange interactions lead to the A-AF coupling at this interface.23 The authors concluded that the origin of the observed ME coupling was completely charge mediated i.e. not strain – driven. Spurgeon et al.34 studied the polarization surface charge screening, which induced magnetic phase gradients at LSMO/PZT interfaces. The authors utilized electron energy loss spectroscopy (EELS), PNR and DFT calculations to study the nature of magnetic phase transition across the interfaces.34,35 They also observed an asymmetrical magnetic phase gradient accompanied by a 30% difference in local FE polarization at the top and bottom interfaces. Interfacial spin state control of LSMO/PZT interfaces as a function of polarization orientations was studied by X. Ma et al.36 They observed that the spin states of a one-unit cell containing Mn ions changed from FM to A-AF due to an exchange interaction without a net change in the bulk magnetization. Zhou et al.37 studied the thickness dependence of LSMO/PZT heterostructures on interfacial ME coupling by measuring valence states of Mn atoms from XAS and observed an increase in Mn valency with increasing thickness of LSMO/PZT. Recently, Mayer et al. investigated the evolution of magnetic moments at the LSMO/PZT interfaces using PNR.38 The authors noticed that the surface and interface magnetization of LSMO was enhanced with the introduction of an FE capping layer. They observed enhanced interfacial magnetization for the polarization direction oriented towards interface and suppressed for the opposite direction. The thickness of the layer at the interface where the magnetization changed was found to be 2 nm, which agrees with the field screening.
Burton and Tsymbal39 studied the electric field induced magnetic reconstruction on La1−xAxMnO3 (LAMO)/BTO (A = Sr, Ca or Ba) interfaces for LAMO residing at FM and A-AF phase boundaries. This comprehensive study confirmed the occurrence of an A-AF phase at the interfaces for every phase boundary of all hole doped manganites. Chen and Ismail-Beigi18 studied ME coupling across LSMO/PTO interfaces using DFT. They found that the interfacial spin reconstruction of Mn atoms, resulted from carrier modulation due to polarization, are accounted for the changes in magnetization. Recently our group (M. Hammouri et al.)40 utilized DFT to study ME coupling across the LSMO/PZT interface. We observed the modulation of interfacial magnetization due to the presence of antiferromagnetic (A-AF) and FM phases at the LSMO/PZT interface. We also noticed that the balance of the magnetic (A-AF and FM) modulation could be altered by an electric field induced FE polarization.
However, all the charge mediated results reported above are not convergent and consistent with the bulk phase diagram of La1−xSrxMnO3.15 Vaz et al. and Meyer et al. found enhanced magnetization at LSMO (x = 0.2)/PZT interface even though hole accumulation brings LSMO towards the A-AF insulating phase and suppressed magnetization for hole accumulation that brings LSMO towards the FM metallic phase.31,38 Moreover, magnetic suppression at the LSMO/PZT interface is frequently encountered due to polar discontinuity and interface mixing.41,42 Spurgeon et al. found local polarization asymmetry at two LSMO interfaces with PZT and reported hole depletion for both interfaces instead of accumulation on bottom and depletion on top, which is not in agreement with the phase diagram of LSMO.34 Along with charge screening effects, many effects and phenomena that can contribute to magnetic modulations at the LSMO/PZT interfaces co-exist simultaneously. Issues that have not been addressed include (i) whether strain and charge mediation co-exist, (ii) and if so at what length scales do charge screening and the strain effect persists to contribute to the reported ME coupling?
To address these issues, we utilized PNR in consort with DFT calculations to understand the role of strain and charge mediated interfacial ME coupling in a heterostructure of LSMO/PZT. We utilized the Magnetism Reflectometer at the Spallation Neutron Source, Oak Ridge National Laboratory to provide polarized neutron beams to the LSMP/PZT sample.43 PNR is a probe that is particularly well suited for determining the nanostructures of magnetic thin films and multilayers.44,45
Experimental methods
Sample preparation and characterization
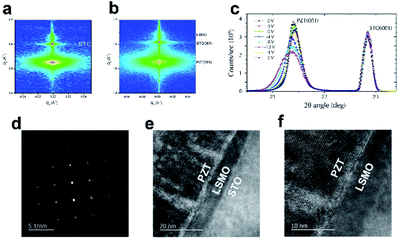
We utilized a substrate-induced self-poling technique to spontaneously pole the PZT layer during growth.35 Initially, a ∼5 nm La0.67Sr0.33MnO3 layer was deposited onto a bulk Nb-doped SrTiO3 (001) (STO) substrate using pulsed laser deposition. This approach prescribes the appropriate electrostatic boundary to spontaneously self-pole the PZT “towards” or “away” from the STO substrate35,46–49 next to ≃75 nm thick PbZr0.2Ti0.8O3. Finally, circular-shaped Pt contacts (gated as top electrodes) with a thickness of about 2–5 nm and area of 1.0 mm2 were dc-sputtered through a shadow mask. The choice for thin Pt electrode was motivated by earlier studies reporting better fatigue characteristics due to enhanced partial switching regions.50 The Nb-doped STO served as the bottom electrode to the system.Reciprocal space maps, obtained with the X-ray diffraction (XRD), of the system, show the films are epitaxial and of good quality. Fig. 1(a) shows the peaks corresponding to PZT, STO and LSMO layers in the absence of an external electric field, whereas Fig. 1(b) displays the reciprocal space map of LSMO/PZT heterostructure on STO for the applied field of +2 V, showing the layers are still epitaxial with change in shape of PZT peak, which shows the polarization in PZT layer. 2Θ–ω (001) peaks for PZT for different electric fields as shown in Fig. 1(c). Negative and remnant fields have increased the out of plane tensile strain while positive fields decreased it. Applied electric fields on PZT/LSMO heterostructures cause lattice distortion along [001] and [100] directions, which is verified by shifting of all peaks towards smaller Qz values and larger Qx values respectively.
Polarized neutron reflectometry (PNR)
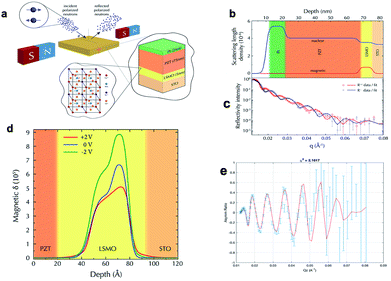
Bulk magnetometry probes are not sensitive to magnetic profiles within the sub-nanometre range or to the individual magnetization contribution of layers comprising the heterostructure.34,38 PNR is a non-destructive probe capable of detecting magnetization profiles along the directions of momentum transfer vectors Qz, for specular reflection51–53 and along Qx or Qy, for off-specular scattering.43–45,54,55 The neutrons encounter the nuclear and magnetic potentials U(z) = 2πħ2/m {Nj(bj)n} + {Nj(bj)m} of the samples where, Nj is the neutron number density of the sample and (bj)n, (bj)m are the neutrons' nuclear and magnetic scattering lengths. The first and second terms inside brackets are nuclear and magnetic scattering length densities (NSLD and MSLD) respectively. NSLD and MSLD respectively correspond to depth profiles of chemical and in-plane magnetization vector distributions. These can be obtained from a simultaneous fit of reflectivity data measured with neutron spin polarization parallel R++(Q) and antiparallel R−−(Q) to external guide field, where Q is the momentum transfer vector between incoming and reflected neutrons. The depth profiles of in-plane magnetization and the film structure can be obtained from a simultaneous fit of R++(Q) and R−−(Q). For our sample, we measured in-plane magnetization depth profiles of the LSMO layer across the LSMO/PZT interface and modulations arising due to polarization induced interfacial charge screening and lattice distortions. This can be done by measuring only non-spin flip reflectivity intensities (R++ and R−−), which gives net magnetic moments along the field directions. The calculated spin asymmetry ratio A = (R++ − R−−)/(R++ + R−−) is a measure of the normalized net magnetic moment along the field direction. However, a non-collinear magnetization vector distribution results in spin-flip scattering intensities (R+− and R−+), which measures the in-plane sample magnetization profiles perpendicular to the neutron polarization directions. The collection of these four reflectivity intensities provides the entire in-plane magnetization of all layers comprising the sample along with the nuclear depth profiles. The sample schematic used in this study with different layers, electrodes and the traditional set up for PNR is depicted in Fig. 2(a).Computational methods
We applied first-principles computational methods based on density functional theory (DFT)56,57 to study the magnetoelectric coupling in the interfacial region between LSMO and PZT. The calculations were carried out using the Quantum ESPRESSO (open-Source Package for Research in Electronic Structure, Simulation, and Optimization) electronic structure code.58 Within the Quantum ESPRESSO code, the electronic wave functions were expanded using a plane-wave basis set with periodic boundary conditions. We employed the Kleinman-Bylander form59 of norm-conserving ultra-soft Vanderbilt pseudopotentials60 in our calculations. The pseudopotentials were generated while considering the relativistic correction. The exchange–correlation energy functional was evaluated using the generalized gradient approximation (GGA) parameterized by Perdew, Burke, and Ernzerhof.61 The plane-wave kinetic energy cutoff was set to 30 Ry for the wave functions and 300 Ry for the charge density and potential. The Brillouin zone was sampled according to the Monkhorst–Pack scheme.62 Structural optimization was performed using the conjugate gradient algorithm. The optimization was carried out until all residual interatomic forces were smaller than 0.02 eV Å−1. The calculated total energies and equilibrium lattice parameters of all studied structures were tested for convergence with respect to the energy cutoff and the number of k points.The crystal structure of bulk La0.67Sr0.33MnO3 was modeled using a 1 × 1 × 6 tetragonal supercell containing 30 atoms. The Brillouin zone was sampled with an 8 × 8 × 3 k-point mesh. To improve the accuracy of the theoretical description of the magnetic properties of LSMO, we used the Hubbard-corrected GGA+U exchange–correlation functional63–65 for Mn atoms. The Hubbard parameters for the Coulomb and exchange interactions were selected to be U = 2 eV and J = 0 eV, respectively. These parameters have been used in previous DFT studies of the electronic and magnetic properties of LSMO.40 The crystal structure of bulk PbZr0.2Ti0.8O3 was modeled using a 1 × 1 × 5 tetragonal supercell containing 25 atoms. The Brillouin zone was sampled with a 5 × 5 × 4 k-point mesh. The La0.66Sr0.33MnO3/PbZr0.2Ti0.8O3 (001) interface was modeled using a tetragonal supercell containing 6 unit cells of LSMO and 5 unit cells of PZT. The supercell was constructed using the LSMO layer containing Sr atoms in the 2-nd and 4-th unit cells and the PZT layer containing a Zr atom in the middle cell. The termination of the interfacial layers of LSMO and PZT in our theoretical model was consistent with the experimental studies, in which PZT was connected to the predominantly La-terminated surface of LSMO. We selected left-right symmetric positions for the substitutional Sr atoms in the modeled layer of LSMO to allow a more meaningful comparison of the distribution of Mn magnetic moments at the left and right sides of the LSMO layer. The Brillouin zone was sampled with a 6 × 6 × 3 k-point mesh. The total thickness of the modeled LSMO/PZT interfacial region was approximately 40 Å.
The optimized structures of tetragonal supercells for bulk LSMO, bulk PZT, and the LSMO/PZT (001) interface were calculated by DFT.40 A positive and negative uniaxial strain was applied to the modeled structure by expanding and contracting the size of the supercell in the direction orthogonal to the LSMO/PZT interface by ±1.5% and ±3%. After that, the structure of the LSMO/PZT interface was optimized by simultaneously relaxing the positions of all atoms and the lattice parameters in the plane parallel to the interface, while keeping the lattice parameter in the direction orthogonal to the interface constant.
Results
PNR results
PNR was conducted on Magnetism Reflectometer at 298 K with an in-plane applied magnetic field of 1 T along [100] sample direction. The model fitted normalized reflectivity intensities, shown in Fig. 2(b), give the nuclear (NSLD) and magnetic (MSLD) scattering length density profiles, which are plotted in Fig. 2(a). For the entire sample, NSLD only changes at the interfaces between different layers showing different nuclear contents and such contents are uniform over each layer. The MSLD is only sensitive to the magnetic layer LSMO and does not distinguish the contrast between different non-magnetic layers, giving zero MSLDs for Pt, PZT, and STO. There is an enhanced MSLD throughout the LSMO nano-layer with discontinuities at PZT/LSMO and LSMO/PZT interfaces, which reveals that the LSMO layer has non-zero magnetic moments. The accuracy of NSLD and MSLD depend on the data quality determined by the quality of sample and experimental statistics of the data. The periods of oscillation give the thickness of the film and the slope of the curves give roughness. The layer thickness of LSMO given by the fit is close to the actual thickness of 5 nm and layer interfaces seem almost sharp.To understand the ferroelectric polarization induced magnetic modulations at the PZT/LSMO interface, PNR magnetic depth profiles of LSMO for different polarization states are shown in Fig. 2(d). Magnetic depth profiles in the figure are not uniform and a few unit cells of magnetic dead layers are distinctly visible at left interfaces, which is attributed to the polarization of the ferroelectric PZT layer. Such changes in magnetization profile at the interface due to electric polarization are caused by magnetoelectric coupling. Polarization surface charges are produced at both surfaces of PZT, with polarization pointing either towards or away from the interfaces. These PZT surface charges screen the charges of equal and opposite sign at the LSMO interface to modulate the carrier concentrations either by accumulation or depletion of holes. Carrier modulation is restricted to only a few unit cells because of Thomas-Fermi screening lengths.66 Our LSMO is optimum doped half metal with a concentration of 0.33, which has larger screening depths as compared to metallic conductors. Therefore, the electric field induced interfacial magnetic modulations on LSMO are strongly noticed as shown in Fig. 2(d). For positive polarization with a field of +2 V (i.e. polarization pointing towards the interface), the magnetic modulation is almost zero because the depletion of holes cannot switch FM into A-AF phase as the screening charges at the LSMO surface would not be enough to achieve that. The hole depletion drives the magnetic phase towards the left of ferromagnetic metal (FMM) phase (x < 0.33) that may bring LSMO interface towards the ferromagnetic insulator (FMI) phase, thereby stabilizing the ferromagnetic phase at the expense of Curie temperature.67 If the polarization is negative, i.e. it points away from the interface due to the field of −2 V, accumulation of holes takes place at the LSMO interface due to positive screening charges. Few unit cells of LSMO at the interface are modulated as it undergoes a phase transition from FMM to AFM close to x = 0.5, thereby suppressing the FM phase. This phase transition favors the super-exchange interactions flipping the magnetic moments of Mn atoms close to the interface and hence magnetic reconstruction may arise within a few unit cells (2 nm) of LSMO. The PZT layer will be in a self-polarized state at zero field with polarization pointing away from the interface and will still accumulate holes at the LSMO interface, modulating magnetization due to the presence of almost same AF layer that was for −2 V. This supports the strong interplay between charge and spin degrees of freedom in manganites. Such interfacial modulation is accompanied by an increase in bulk magnetization for two accumulation states (i.e. for −2 V and 0 V) as compared to depletion (i.e. for +2 V). Within the FM-metallic phase, the magnetization of the LSMO layer becomes proportional to doping concentration as a higher hole concentration provides strong double exchange interactions to hop more carriers between Mn3+ and Mn4+. This is consistent with the increase in bulk magnetization of LSMO while going from +2 V to −2 V through 0 V as a result of tensile and compressive strains along with charge modulations due to applied fields. The strain coupling on magnetostrictive LSMO from the PZT layer modulates the magnetism and such modulations vary from interface to the surface.35 Therefore, strain effects are mostly contributing to bulk magnetic modulations whereas charge effects are only limited to interfaces modulations as shown in PNR. Fig. 2(e) shows the spin asymmetry ratio as a function of Qz. This gives the orientation of magnetic moments perpendicular to the interface.68
DFT results
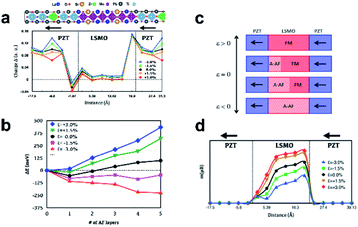
In order to give the quantitative contributions to magnetism modulations, observed in PNR, from charge and strain mediated effects due to applied fields, we simulated different values of uniaxial strains (tensile and compressive) by compressing and relaxing LSMO/PZT along [001] from DFT calculations. Electronic charge distributions across the interface as the influence of applied simulated uniaxial strains are shown in Fig. 3(a). The vertical axis displays the deviation of the Löwdin atomic charges for the Mn, Ti and Zr atoms at the LSMO/PZT interface from those in bulk LSMO and bulk PZT. Due to the use of periodic boundary conditions, a layer of LSMO in our theoretical model was sandwiched between two layers of PZT. The polarization of PZT was directed away from the surface of LSMO on the left side of the LSMO layer and towards the surface of LSMO on the right side of the LSMO layer. As expected, our calculations predicted a decrease of electronic charges at the left PZT/LSMO interface and an increase of electronic charges at the right interface. The observed charge variations could be explained by the electrostatic screening of ferroelectric PZT by half-metallic LSMO. The polarization of PZT produced a negative surface charge at the left PZT/LSMO interface and a positive surface charge at the right LSMO/PZT interface. The polarization surface charge of PZT was screened by charge carriers from LSMO, resulting in a lower electron density (higher hole density) at the left PZT/LSMO interface and a higher electron density (lower hole density) at the right LSMO/PZT interface. It is interesting to note, that the applied uniaxial strain did not significantly change the distribution of charge density across the LSMO layer. The only noticeable change of charge density distribution occurred near Zr atoms within the PZT layer. This result suggests that the applied strains/fields have no significant influence on the charge accumulation and depletion across the LSMO/PZT interface.To investigate the influence of PZT polarization and applied uniaxial strain on the magnetic properties of the LSMO/PZT interface, we calculated the total energies and magnetic moments of the LSMO/PZT interfacial region in different magnetic configurations. According to the phase diagram of tetragonal manganites reported by Fang et al.,69 bulk LSMO has ferromagnetic (FM) order of Mn magnetic moments at the Sr doping level of x = 0.33 and the lattice ratio c/a = 1. An A-type antiferromagnetic (A-AF) order is favored when the c/a lattice ratio is reduced to approximately 0.97. Other types of magnetic order, such as C-type AF and G-type AF, are expected to be significantly higher in energy if the c/a lattice ratio is close to 1.0. In agreement with the phase diagram of tetragonal manganites, our calculations predicted that the FM configuration was lower in energy than the A-AF configuration for bulk La0.66Sr0.33MnO3. In contrast, we found that the LSMO/PZT interfacial region generally favored a mixed magnetic configuration with FM layers on the right side where the polarization of PZT pointed towards the surface of LSMO and A-AF layers on the left side where the polarization of PZT was directed away from the surface of LSMO. The dependence of the total energy of the LSMO/PZT interfacial region on the magnetic configuration of LSMO for different values of applied uniaxial strain is shown in Fig. 3(b).
In the absence of applied strain, the magnetic configuration with a single A-AF layer on the left side of the LSMO slab had the lowest total energy.40 A positive strain stabilizes the FM magnetic configuration of LSMO and decreases the number of A-AF layers on the left side of the LSMO slab, whereas a negative strain stabilizes the A-AF magnetic configuration of LSMO and increases the number of A-AF layers on the left side of the LSMO slab. This result is consistent with the increase in bulk magnetization while switching from +2 V to −2 V in experiment. The lowest-energy magnetic state of the LSMO slab was found to be completely FM for ε ≥ 3%, and completely A-AF for ε ≤ −3%.
Fig. 3(c) presents a schematic illustration of the influence of applied uniaxial strain on the distribution of magnetization across the LSMO/PZT interfacial region. The number of A-AF layers on the left side of the LSMO slab in the lowest-energy magnetic configuration increased with a negative applied strain (compression) and decreased with a positive applied strain (expansion). A simulated magnetic profile of the LSMO layer for different values of applied strain is displayed in Fig. 3(b). The simulated profile was obtained as a statistical distribution of the FM, A-AF, and mixed FM/A-AF LSMO/PZT magnetic configurations at T = 300 K and B = 0.1 T. Our study demonstrated the possibility of the existence of a layer of A-AF LSMO at the left LSMO/PZT interface, where the polarization of PZT was directed away from the surface of LSMO. The presence of the A-AF phase of LSMO in the LSMO/PZT interfacial region could be responsible for the presence of a nonmagnetic layer near the LSMO/PZT interface shown in Fig. 2(c). We found that a positive strain increased, and a negative strain decreased the magnetization of LSMO. The results of our calculations demonstrated that the spatial distribution of magnetization inside the LSMO slab is strongly influenced by the direction of the PZT polarization and by the applied strain.
When an electric field is applied to the ferroelectric layers, the modulation of carriers at the interfaces and distortion of lattices in response to the direction of the field take place simultaneously. This implies that charge and strain mediated effects are contributing collectively to modulate magnetic properties across LSMO as shown from PNR and DFT. The lattice distortion results as the strain is transferred to the magnetic layers from the FE layers, thereby changing the magnetic properties of the interfacial region due to magnetostrictive effects. To explore the interplay between electric field induced strains and bulk magnetic moments, we simulated magnetic phases on LSMO for different values of applied strain because the magnetic properties of LSMO strongly depend on the lattice parameters. The number of A-AF layers at the left interface shown in Fig. 3(b) and (c) corresponds to the magnitudes of bulk magnetization/magnetic moments of LSMO but does not represent the length of interfacial ME coupling as charge effects are less noticeable, as explained by the DFT results. Fig. 3(c) shows that out of plane compressive strain decreases magnetization of LSMO and out of plane tensile strain increases magnetization of LSMO regardless of the polarization direction of PZT i.e. for both accumulation and depletion. This is because the coupling of strain and magnetism is directly related to the distortion of MnO6 octahedra,12 where altering Mn–O bond angles triggers the Jahn–Teller distortion that directly affects the double-exchange mechanism. Even at the zero strain the co-existence of FM and A-AF phases is exhibited. This is attributed to the competition between two phases as LSMO shifts towards the A-AF phase for the negative polarization. The hopping of eg electrons is influenced by the strain states as the out of plane compressive strain reduces the hopping probability by increasing the bond lengths and decreasing the kinetic energy of the hopped electrons.14 Therefore, the A-AF phase starts to dominate the FM phase for larger compressive strains. For tensile strains, the electron hopping probability is very high, as there is a reduction in the Mn–O bond lengths and 3-D hopping starts to work, which favors double exchange interactions and increases the FM phase for larger tensile strains as illustrated in Fig. 3(c). The phase evolution of LSMO can also be explained in terms of orbital reconstructions. Since the eg electron orbital is doubly degenerated, such degeneracy can be lifted by either compression or elongation of Mn–O octahedra called Jahn–Teller distortions; which implies either favoring d3Z2−r2 or dx2−y2, i.e. either imposing tensile or compressive strains.18,70 Ferromagnetic ordering is isotropic along x-, y- and z-direction, but A-type antiferromagnetic ordering is intralayer ferromagnetic and out of plane interlayer antiferromagnetic.18 Under a compressive strain, the d3Z2−r2 occupancy decreases resulting in a lowering of the fraction of the FM phase. In contrast, a tensile strain increases the d3Z2−r2 occupancy that increases the fraction of the FM phase thereby increasing hopping along the c-direction.
Discussion
Since the LSMO phase diagrams are studied as the function of dopant concentrations and tetragonal distortion (c/a),69 the compressed and relaxed LSMO/PZT structure in DFT calculations along the [001] direction gives different values of tetragonal distortion, which also brings LSMO into different strain states. The magnetic phase evolution at the interfaces and variation of magnetic moments throughout the LSMO layer as a function of tetragonal distortions are obtained from those calculations. In the experiment, several positive and negative voltages are applied along the [001] direction in a complete polarization hysteresis loop, but the only +2 V, −2 V and 0 V values have been measured in PNR. Measurements at 0 V (with residual tensile strain), +2 V and −2 V were performed while going from negative to positive voltages to complete the butterfly loop like strain versus electric fields curve. In this way, 0 V and +2 V have the tensile strains and −2 V has the compressive strain. In DFT calculations, the effect of the negative (positive) voltage was modeled by applying a tensile (compressive) out of plane strain to the modeled interface. PNR results show that there are magnetically dead layers of ∼2 nm for the −2 V and 0 V and the magnetization increases while going from 0 V to −2 V. In contrast, for the +2 V, the total magnetization decreases with the absence of dead layers.Since the applied electric field not only distorts the lattices but also polarizes the PZT layer, these results can be explained with the strain states simulated in DFT and the charge modulation on LSMO due to charge screening from PZT polarization. According to the phase diagram of tetragonal manganites reported by Fang et al.,69 the magnetic phase modulations at interface and bulk regions are jointly influenced by strain states from tetragonal distortion of LSMO and hole concentration.64 The entire region above the phase boundary line is FM and below is A-AF phase. For DFT calculations, the magnetic phases are only studied residing on the nominal hole doping (x = 0.33), shown by vertical red line in Fig. 4. The obtained results from both studies are tentatively consistent with the phase diagram from Fang et al. that LSMO shows the mixed phase of FM and A-AF phases at c/a = 0.97 and x = 0.33. When accumulation tends towards x > 0.33, LSMO undergoes transition to the A-AF phase, but the depletion brings towards x < 0.33 that leads to FM-phase as shown in Fig. 4. Moreover, for c/a ≥ 0.97 with hole depletion, LSMO shifts towards the FM phase and for c/a ≤ 0.97 with hole accumulation LSMO shifts towards the A-AF phase as shown in the phase diagram.71 A larger c/a ratio results in the FM phase, whereas a smaller c/a ratio results in the A-AF phase. Interfacial A-AF layers appear when the PZT polarization points away from the interface and the FM phase appears when the PZT polarization points towards the interface. Our DFT calculations demonstrate that coupling between the PZT and LSMO layers significantly enhances the sensitivity of the magnetic configuration of LSMO to the applied strain. The high sensitivity of the magnetic configuration of LSMO to the applied strain can be explained by the coexistence of FM and AFM phases in the PZT/LSMO interfacial region. The simultaneous presence of FM and AFM phases near the PZT/LSMO interface can explain the experimentally observed variations of the magnetic profiles within the LSMO layer. Experimental results can be compared with the phase diagram residing at three LSMO doping concentrations corresponding to −2 V, 0 V and +2 V. The interfacial magnetization is suppressed with the formation of a magnetically dead layer up to ∼2 nm accompanied by the increase in bulk magnetization for 0 V and −2 V. However, the width of the interfacial magnetically dead layer for a negative polarization decreases while going from 0 V to −2 V, i.e. increasing the out of plane tensile strains, which is consistent with the DFT predictions shown in Fig. 3(c). The bulk magnetization has increased while going from 0 V to −2 V, as more Mn3+ ions find their Mn4+ counterparts to have double exchange coupling due to the increase in hole concentration from x = 0.33. The LSMO layer has suppressed magnetization up to larger distances for +2 V, but still remains in the FM phase. This result can be explained by the depletion of holes which decrease the total magnetization. The bulk and interfacial magnetic modulations for the three applied voltages are consistent with the results of our calculations, as the magnetization is increasing with increasing the values of the c/a ratio while going from +2 V to −2 V with 0 V in between. However, the length of A-AF layer has not increased in PNR while applying −2 V from 0 V, this might be a reason that the presence of Pt capping layer generally reduces the nominal hole concentration.71 Therefore, a tensile strain increases the magnetization and introduces the interfacial A-AF layer, whereas a compressive strain reduces the magnetization and retains its ferromagnetic phase intact at the interface.
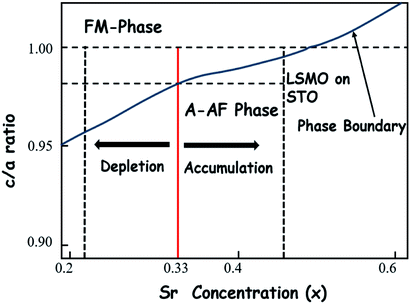 | ||
| Fig. 4 Phase diagram of LSMO as a function of Sr concentration (x) and tetragonality c/a.69 LSMO experiences a compressive strain when grown on STO. The phase transitions due to accumulation and depletion of holes in LSMO and varied tetragonal ratios of the sample are shown.69,71 | ||
Conclusions
In summary, this study was conducted to observe what magnetic properties at the interface can strain and charge mediated effects (separately or jointly) modulate and how? PNR results show the interface undergoes ferromagnetic to A-AF phase transition for the polarization pointing away from the interface due to hole accumulation and remains ferromagnetic for polarization pointing towards interface despite the hole depletion. As these modulations are only limited to the interfaces and giving same length scales (<2 nm) of coupling for different tensile strains (at 0 V and −2 V) and no coupling for compressive strain (at +2 V), these are of completely electrical origin or charge mediated. This implies that charge mediated effects are only polarization direction dependent. Moreover, DFT calculations show an increase in global magnetization of the LSMO layer has observed while going from compressive to tensile strains and from lower to higher tensile strain values. As this modulation of global magnetization is irrespective of interfacial charge modulations, it is completely strain mediated effect and dependent on strength of polarization and its direction. The results from PNR and DFT are consistent to prove these findings. From these, we can conclude that charge and strain effects act in tandem to modulate the magnetism at the interface even though the strain-mediated effect is dominant over charge effects. Furthermore, interfacial ME couplings are only depending on polarization direction, but global magnetization depends on both direction and magnitude of polarization.Conflicts of interest
The authors declare no conflict of interests.Acknowledgements
This research was supported by the DoD Air Force Office of Scientific Research (AFOSR) under award No FA9550-18-1-0196. Prof. E. Fohtung also acknowledges partial support for the LANSCE Professorship sponsored under Triad National Security, LLC through the New Mexico Consortium under subcontract No 350. The research conducted at the Spallation Neutron Source was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy. The work at Los Alamos National Laboratory was supported in part by the NNSA's Laboratory Directed Research and Development Program and was performed, in part, at the Center for Integrated Nanotechnologies, an Office of Science User Facility operated for the U.S. Department of Energy Office of Science. Los Alamos National Laboratory, an affirmative action equal opportunity employer, is managed by Triad National Security, LLC for the U.S. Department of Energy's NNSA, under contract 89233218CNA000001.References
- R. Ramesh and N. A. Spaldin, Nat. Mater., 2007, 6(1), 21 CrossRef CAS PubMed.
- S. W. Cheong and M. Mostovoy, Nat. Mater., 2007, 6(1), 13 CrossRef CAS PubMed.
- W. Eerenstein, N. D. Mathur and J. F. Scott, Nature, 2006, 442(7104), 759 CrossRef CAS PubMed.
- N. A. Spaldin and M. Fiebig, Science, 2005, 309(5733), 391–392 CrossRef CAS PubMed.
- W. Eerenstein, M. Wiora, J. L. Prieto, J. F. Scott and N. D. Mathur, Nat. Mater., 2007, 6(5), 348 CrossRef CAS PubMed.
- M. Fiebig, J. Phys. D: Appl. Phys., 2005, 38(8), R123 CrossRef CAS.
- N. A. Hill, J. Phys. Chem. B, 2000, 104(29), 6694–6709 CrossRef CAS.
- T. Zhao, A. Scholl, F. Zavaliche, K. Lee, M. Barry, A. Doran, M. P. Cruz, Y. H. Chu, C. Ederer, N. A. Spaldin and R. R. Das, Nat. Mater., 2006, 5(10), 823 CrossRef CAS PubMed.
- C. W. Nan, M. I. Bichurin, S. Dong, D. Viehland and G. Srinivasan, J. Appl. Phys., 2008, 103(3), 1 CrossRef.
- Y. Wang, J. Hu, Y. Lin and C. W. Nan, NPG Asia Mater., 2010, 2(2), 61 CrossRef.
- A. P. Ramirez, J. Phys.: Condens. Matter, 1997, 9(39), 8171 CrossRef CAS.
- Y. Tokura and Y. Tomioka, J. Magn. Magn. Mater., 1999, 200(1–3), 1–23 CrossRef CAS.
- D. Bhattacharya, A. Chakraborty and H. S. Maiti, J. Phys.: Condens. Matter, 1999, 11(30), 5845 CrossRef CAS.
- J. van den Brink, G. Khaliullin and D. Khomskii, Phys. Rev. Lett., 1999, 83(24), 5118 CrossRef CAS.
- A. Urushibara, Y. Moritomo, T. Arima, A. Asamitsu, G. Kido and Y. Tokura, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51(20), 14103 CrossRef CAS.
- C. Zener, Phys. Rev., 1951, 82(3), 403 CrossRef CAS.
- A. Moreo, S. Yunoki and E. Dagotto, Science, 1999, 283(5410), 2034–2040 CrossRef CAS PubMed.
- H. Chen and S. Ismail-Beigi, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86(2), 024433 CrossRef.
- B. Jaffe, R. S. Roth and S. Marzullo, J. Res. Natl. Bur. Stand., 1955, 55(5), 239–254 CrossRef CAS.
- C. A. F. Vaz, J. Hoffman, Y. Segal, M. S. J. Marshall, J. W. Reiner, Z. Zhang, R. D. Grober, F. J. Walker and C. H. Ahn, J. Appl. Phys., 2011, 109(7), 07D905 CrossRef.
- F. Matsukura, Y. Tokura and H. Ohno, Nat. Nanotechnol., 2015, 10(3), 209 CrossRef CAS PubMed.
- H. Ohno, D. Chiba, F. Matsukura, T. Omiya, E. Abe, T. Dietl, Y. Ohno and K. Ohtani, Nature, 2000, 408(6815), 944 CrossRef CAS PubMed.
- C. A. Vaz, J. Phys.: Condens. Matter, 2012, 24(33), 333201 CrossRef CAS PubMed.
- M. K. Lee, T. K. Nath, C. B. Eom, M. C. Smoak and F. Tsui, Appl. Phys. Lett., 2000, 77(22), 3547–3549 CrossRef CAS.
- D. Dale, A. Fleet, J. D. Brock and Y. Suzuki, Appl. Phys. Lett., 2003, 82(21), 3725–3727 CrossRef CAS.
- C. Thiele, K. Dörr, O. Bilani, J. Rödel and L. Schultz, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(5), 054408 CrossRef.
- W. Zhao, D. Zhang, D. Meng, W. Huang, L. Feng, C. Hou, Y. Lu, Y. Yin and X. Li, Appl. Phys. Lett., 2016, 109(26), 263502 CrossRef.
- D. Yi, J. Liu, S. Okamoto, S. Jagannatha, Y. C. Chen, P. Yu, Y. H. Chu, E. Arenholz and R. Ramesh, Phys. Rev. Lett., 2013, 111(12), 127601 CrossRef PubMed.
- C. Thiele, K. Dörr, L. Schultz, E. Beyreuther and W. M. Lin, Appl. Phys. Lett., 2005, 87(16), 162512 CrossRef.
- Z. G. Sheng, J. Gao and Y. P. Sun, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(17), 174437 CrossRef.
- C. A. F. Vaz, J. Hoffman, Y. Segal, J. W. Reiner, R. D. Grober, Z. Zhang, C. H. Ahn and F. J. Walker, Phys. Rev. Lett., 2010, 104(12), 127202 CrossRef CAS PubMed.
- C. A. Vaz, J. Hoffman, C. H. Ahn and R. Ramesh, Adv. Mater., 2010, 22(26-27), 2900–2918 CrossRef CAS PubMed.
- C. A. F. Vaz, Y. Segal, J. Hoffman, R. D. Grober, F. J. Walker and C. H. Ahn, Appl. Phys. Lett., 2010, 97(4), 042506 CrossRef.
- S. R. Spurgeon, P. V. Balachandran, D. M. Kepaptsoglou, A. R. Damodaran, J. Karthik, S. Nejati, L. Jones, H. Ambaye, V. Lauter, Q. M. Ramasse and K. K. Lau, Nat. Commun., 2015, 6, 6735 CrossRef CAS PubMed.
- S. R. Spurgeon, J. D. Sloppy, D. M. Kepaptsoglou, P. V. Balachandran, S. Nejati, J. Karthik, A. R. Damodaran, C. L. Johnson, H. Ambaye, R. Goyette and V. Lauter, ACS Nano, 2013, 8(1), 894–903 CrossRef PubMed.
- X. Ma, A. Kumar, S. Dussan, H. Zhai, F. Fang, H. B. Zhao, J. F. Scott, R. S. Katiyar and G. Lüpke, Appl. Phys. Lett., 2014, 104(13), 132905 CrossRef.
- J. Zhou, V. T. Tra, S. Dong, R. Trappen, M. A. Marcus, C. Jenkins, C. Frye, E. Wolfe, R. White, S. Polisetty and J. Y. Lin, Appl. Phys. Lett., 2015, 107(14), 141603 CrossRef.
- T. L. Meyer, A. Herklotz, V. Lauter, J. W. Freeland, J. Nichols, E. J. Guo, S. Lee, T. Z. Ward, N. Balke, S. V. Kalinin and M. R. Fitzsimmons, Phys. Rev. B, 2016, 94(17), 174432 CrossRef.
- J. D. Burton and E. Y. Tsymbal, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80(17), 174406 CrossRef.
- M. Hammouri, E. Fohtung and I. Vasiliev, J. Phys.: Condens. Matter, 2016, 28(39), 396004 CrossRef PubMed.
- H. Boschker, J. Verbeeck, R. Egoavil, S. Bals, G. van Tendeloo, M. Huijben, E. P. Houwman, G. Koster, D. H. Blank and G. Rijnders, Adv. Funct. Mater., 2012, 22(11), 2235–2240 CrossRef CAS.
- J. W. Freeland, J. J. Kavich, K. E. Gray, L. Ozyuzer, H. Zheng, J. F. Mitchell, M. P. Warusawithana, P. Ryan, X. Zhai, R. H. Kodama and J. N. Eckstein, J. Phys.: Condens. Matter, 2007, 19(31), 315210 CrossRef CAS PubMed.
- V. Lauter, H. Ambaye, R. Goyette, W. T. H. Lee and A. Parizzi, Phys. B, 2009, 404(17), 2543–2546 CrossRef CAS.
- V. Lauter-Pasyuk, Collect. SFN, 2007, 7, s221–s240 CrossRef.
- B. P. Toperverg, Phys. Met. Metallogr., 2015, 116(13), 1337–1375 CrossRef.
- C. L. Jia, V. Nagarajan, J. Q. He, L. Houben, T. Zhao, R. Ramesh, K. Urban and R. Waser, Nat. Mater., 2007, 6(1), 64 CrossRef CAS PubMed.
- V. P. Afanasjev, A. A. Petrov, I. P. Pronin, E. A. Tarakanov, E. J. Kaptelov and J. Graul, J. Phys.: Condens. Matter, 2001, 13(39), 8755 CrossRef CAS.
- P. Yu, W. Luo, D. Yi, J. X. Zhang, M. D. Rossell, C. H. Yang, L. You, G. Singh-Bhalla, S. Y. Yang, Q. He and Q. M. Ramasse, Proc. Natl. Acad. Sci. U. S. A., 2012, 109(25), 9710–9715 CrossRef CAS PubMed.
- J. Karthik, A. R. Damodaran and L. W. Martin, Adv. Mater., 2012, 24(12), 1610–1615 CrossRef CAS PubMed.
- E. G. Lee, J. G. Lee and S. J. Kim, J. Korean Phys. Soc., 2006, 48(5), 956 CAS.
- J. F. Ankner and G. P. Felcher, J. Magn. Magn. Mater., 1999, 200(1–3), 741–754 CrossRef CAS.
- C. F. Majkrzak, K. V. O'Donovan and N. F. Berk, Neutron Scattering from Magnetic Materials, Elsevier Science, 2006, pp. 397–471 Search PubMed.
- M. R. Fitzsimmons, S. D. Bader, J. A. Borchers, G. P. Felcher, J. K. Furdyna, A. Hoffmann, J. B. Kortright, I. K. Schuller, T. C. Schulthess, S. K. Sinha and M. F. Toney, J. Magn. Magn. Mater., 2004, 271(1), 103–146 CrossRef CAS.
- B. P. Toperverg and H. Zabel, Experimental Methods in the Physical Sciences, Academic Press, 2015, vol. 48, pp. 339–434 Search PubMed.
- V. Lauter, H. J. C. Lauter, A. Glavic and B. P. Toperverg, Reflectivity, Off-Specular Scattering, and GISANS Neutrons, Elsevier, 2016, ISBN: 978-0-12-803581-8 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140(4A), A1133 CrossRef.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni and I. Dabo, et al., J. Phys.: Condens. Matter, 2009, 21(39), 395502 CrossRef PubMed.
- L. Kleinman and D. M. Bylander, Phys. Rev. Lett., 1982, 48(20), 1425–1428 CrossRef CAS.
- D. Vanderbilt, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41(11), 7892–7895 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13(12), 5188 Search PubMed.
- V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44(3), 943–954 CrossRef CAS.
- V. I. Anisimov, F. Aryasetiawan and A. I. Lichtenstein, J. Phys.: Condens. Matter, 1997, 9(4), 7359–7367 CrossRef CAS.
- B. Himmetoglu, A. Floris, S. de Gironcoli and M. Cococcioni, Int. J. Quantum Chem., 2013, 114(1), 14–49 CrossRef.
- E. O. Kane, Phys. Rev., 1963, 131(1), 79 CrossRef.
- H. Lu, T. A. George, Y. Wang, I. Ketsman, J. D. Burton, C. W. Bark, S. Ryu, D. J. Kim, J. Wang, C. Binek and P. A. Dowben, Appl. Phys. Lett., 2012, 100(23), 232904 CrossRef.
- S. J. Blundell and J. A. C. Bland, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(6), 3391 CrossRef.
- Z. Fang, I. V. Solovyev and K. Terakura, Phys. Rev. Lett., 2000, 84(14), 3169–3172 CrossRef CAS PubMed.
- A. Sadoc, B. Mercey, C. Simon, D. Grebille, W. Prellier and M. B. Lepetit, Phys. Rev. Lett., 2010, 104(4), 046804 CrossRef PubMed.
- G. Radaelli, D. Gutiérrez, M. Qian, I. Fina, F. Sánchez, L. Baldrati, J. Heidler, C. Piamonteze, R. Bertacco and J. Fontcuberta, Adv. Electron. Mater., 2016, 2(12), 1600368 CrossRef.
| This journal is © The Royal Society of Chemistry 2019 |