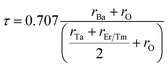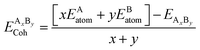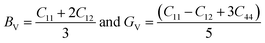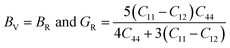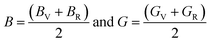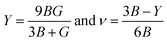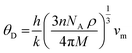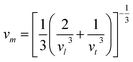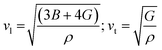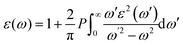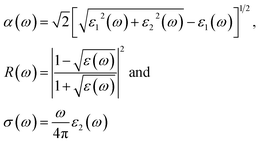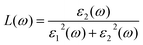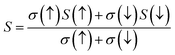Study of the magneto-electronic, optical, thermal and thermoelectric applications of double perovskites Ba₂MTaO₆ (M = Er, Tm)

Abstract

The structural, electronic, optical, thermodynamic and thermoelectric properties of double perovskites Ba₂MTaO₆ (M = Er, Tm) have been studied. These alloys stabilize in cubic structure with paramagnetic phases and structural parameters that are in good agreement with experimental results. The elastic parameters reveal both materials as being super hard and brittle in nature. The band profile displays the direct bandgap semiconducting behavior of both compounds in the spin-up channels. The optical coefficients, viz. optical conductivity, reflectivity and electron energy loss, are intended for a photon energy of up to 14 eV to perceive the optical response. The effects of temperature and pressure on the thermodynamic properties have also been evaluated via the quasi-harmonic Debye model. Post-DFT treatment was performed to explore the thermoelectric properties; both perovskites exhibit a colossal power factor of 90 × 10¹¹ W m⁻¹ K⁻² s⁻¹ and 5 × 85 × 10¹¹ W m⁻¹ K⁻² s⁻¹ for Ba₂TmTaO₆ and Ba₂ErTaO₆, respectively, at 800 K.

---

1 Introduction

Ceramics with layered structure represent the richest class of materials and are the subject of interest to material scientists and solid-state chemists, showing diverse physical, chemical and catalytic properties used for technological applications.^1–6 They show amazingly high adaptability due to their structural and chemical flexibility with the basic formula of ABX₃.⁷ The complex perovskites are created by ion replacements in the structure of simple perovskites. The chemical identity, coordination environment, deformation and tilting of the octahedral B-site cation define the physical and chemical behavior of these perovskites. The selection of B-site is influential for the vital interesting properties of these oxides. This site is occupied by ions of smaller radii with relatively low coordination numbers. Usually, transition/non-transition metal or rare-earth ion occupies position B.⁸ Generally, double perovskites have cubic Fm3̄m structure, possessing a regular arrangement of corner-sharing BO₆ and B′O₆ octahedral units, alternating along the three directions of the crystal. Due to the occupation of cation A and also cations B and B′ at different positions in the double perovskite, several structures with different space groups are possible. Due to high structural and chemical flexibility of perovskites, they possess many charming properties including high T_c superconductivity, giant magnetoresistance (CMR), ionic conductivity, catalytic properties, ferromagnetic properties, anti-ferromagnetic to ferri-magnetic ordering, and multiferroicity.^9–13 These oxide structures have also achieved tremendous attention in many technological aspects and spin-electronics (spintronics), as they possess mesmerizing and supreme magneto-electronic properties. Spintronics are thought-provoking, as they show dissimilar character in different spin channels.^14–16

A lot of work has been done on double perovskites, with position B occupied by rare-earth or transition metal elements (e.g., 3d, 4d or 5d) and the A site occupied by alkaline-earth elements (Sr and Ba),^17–20 and more work is yet to be performed. Various properties including the crystal structure of Ba₂LnNbO₆ (where Ln = lanthanide) have been investigated.¹⁷ The magnetic and structural properties of M₂LnTaO₆ (M = Ba, Sr) were also provided earlier.²¹ They observed that Sr-based compounds possess monoclinic structure, whereas Ba-based compounds possess cubic as well as monoclinic structures. Many barium-based double-perovskites like Ba₂LnNbO₆ were synthesized,²² and they reported that they mostly possessed cubic structures except for ‘La’ doped alloys, which possessed tetragonal distorted structure. Ba₂HoSbO₆ and Ba₂ErSbO₆, along with other rare-earth variants (Ba₂RNbO₆, R = Nd, Sm, Eu, Gd, Tb, Yb), were also previously characterized.^23–25 The Ho and Er variants were reported to have cubic structure with an Fm3̄m phase, with a = 8.417 Å for Ho and a = 8.397 Å for Er. The double perovskite A₂ErSbO₆ was studied for its various properties and uses.²⁶ Nair et al.²⁷ observed the dielectric properties of Ba₂TmSbO₆ and concluded that the compound had the lowest dielectric loss. Rare earth-based double perovskites have found a wide variety of applications. Double perovskites with lanthanides in the B-site have found a variety of microwave applications and can be used as dielectric resonators.^28,29 Tantalum-based oxides have found an ample array of applications including piezoelectric actuators, sensors, transducers, half-metallics and photocatalytic activity.³⁰ Ba₂ErTaO₆ (ref. 18 and 31) and Ba₂TmTaO₆ compounds have been synthesized experimentally, but no theoretical studies have been conducted so far. Thus, we investigated the structural, magnetic, thermodynamic, thermoelectric, and mechanical properties of these materials through DFT, which could possibly find scope for many applications.

2 Computational details

We used the full-potential linearized augmented plane wave method as embedded in Wien2k.^32,33 Exchange and correlation were treated by GGA and GGA + U approximation within the Perdew–Burke–Ernzerhof of parameterization. GGA + U was used for the consideration of on-site correlation in the d and f electrons of the transition metal atoms. The effective coulomb–exchange interaction U_eff (U–J) with J = 0.001 was U_eff = 0.28 Ry for f electrons and 0.18 Ry for d-electrons. We optimized the lattice constant at the lowest energy and found it to be close to the measured value. The cut-off parameter R_MTK_max, which determines the size of the basis set, was chosen to be 7.0 for energy convergence, where R_MT is the smallest muffin-tin sphere radii and K_max is the largest reciprocal lattice vector. The self-consistent calculations are considered to be converged when the integration of the absolute charge density difference between the input and output electron density is less than 0.0001e per f.u., where ‘e’ is the electron charge. We used 3000 K points in the first Brillouin zone (BZ) and performed harmonic expansion up to l_max = 10 in each atomic sphere. For thermodynamic calculation, the quasi-harmonic Debye model was used, as discussed elsewhere.³⁴ The transport properties are calculated in the framework of the semi-classical Boltzmann theory using BoltzTraP code under constant relaxation time approximation.³⁵ The elastic constants were also determined to check the mechanical stability of the materials.

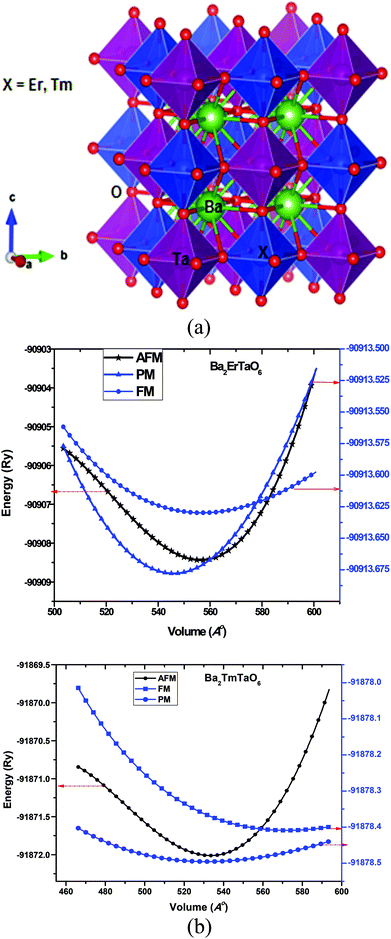
Double perovskites A₂BB′O₆ are driven from perovskites ABO₃ by replacing half of the B cations with different B′ cations at a 1 : 1 ratio. Here, the B and B′ cations are ordered in a rock salt manner, resulting in idealized Fm3̄m cubic structure with twice the length of the ABO₃ perovskite subcell. The Ba-atom is 12-coordinated to oxygen atoms, while (M = Er, Tm) lies within cages of 6-oxygen atoms. The structure of Ba₂MTaO₆ is an extension of octahedral ErO₆ and TaO₆ over three dimensions with Ba occupying the hollow void. The crystal structure of the present perovskites is represented in Fig. 1a.

Fig. 1 (a) Pictorial representation of double perovskites Ba₂ErTaO₆ and Ba₂TmTaO₆. (b) Energy as a function of volume in the paramagnetic (PM), ferromagnetic (FM) and antiferromagnetic (AFM) phases for Ba₂MTaO₆ (M = Er, Tm).

3 Results and discussions

The structural, electronic, magnetic, optical, thermal and thermoelectric properties of tantalum-based double perovskites Ba₂ErTaO₆ and Ba₂TmTaO₆ are discussed below.

3.1 Structural properties

The structure and geometry of Ba₂MTaO₆ (M = Er, Tm) compounds were calculated at equilibrium lattice parameters, which are obtained by optimizing the volume against the energy. In this process, the unit cell energy is varied with respect to volume, and the energy against volume for each unit cell was minimized by fitting the Birch–Murnaghan equation of state.³⁶ Both rare earth-based double perovskites were found to crystallize in cubic (Fm3̄m) structure, as reported experimentally as well as by calculating the tolerance factor.³¹ The tolerance factor is calculated as:
where r_Ba is the ionic radius of a barium atom, r_O is the ionic radius of an oxygen atom, r_Er is the ionic radius of an erbium atom and r_Tm is the ionic radius of a thulium atom. Materials with τ in the vicinity of 0.9–1.0 have perfect cubic structure, while τ in the range 0.71–0.9 forms rhombohedral or orthorhombic structure. The value of the tolerance factor computed for Ba₂MTaO₆ (M = Er, Tm) is equal to 1.0 and lies within the cubic range. The atoms occupy positions as: Ba (0.25,0.25,0.25); M (0,0,0); Ta (0.5,0.5,0.5); and O (0.25,0,0). The compounds have been searched for stability in paramagnetic, ferromagnetic and anti-ferromagnetic phases, and both were found to be stable in the paramagnetic state with optimized lattice constants equal to 8.45 Å and 8.43 Å for Ba₂ErTaO₆ and Ba₂MTaO₆, respectively, and are in decent agreement with the previous experimental results.^18,31,37,38 The optimization plots for both compounds are depicted in Fig. 1b. These plots show that they are stable in the paramagnetic state, as they owe minimum energy in this phase. The relaxed lattice constants, bulk modulus, derivatives of the bulk modulus and ground state energies are shown in Table 1.

Table 1 Optimized values of the lattice constant, unit cell volume, bulk modulus (B), bulk modulus derivate (B′), and the minimum energy of Ba₂MTaO₆, where M = Er, Tm

Properties	Ba2ErTaO6	Exp.	Ba2TmTaO6	Exp.
Lattice constant (Å)	8.45	8.424 (ref. 18)	8.43	8.406 (ref. 18)
		8.422 (ref. 31)		8.40 (ref. 37)
		8.423 (ref. 37)		8.41 (ref. 38)
		8.40 (ref. 38)
Volume (Å)^3	538.64	—	536.33	—
B (GPa)	146.23	—	148.87	—
B′	4.49	—	4.12	—
Minimum energy (Ry)	−90913.675	—	−91878.50	—

---

3.2 Densities of states and electronic properties

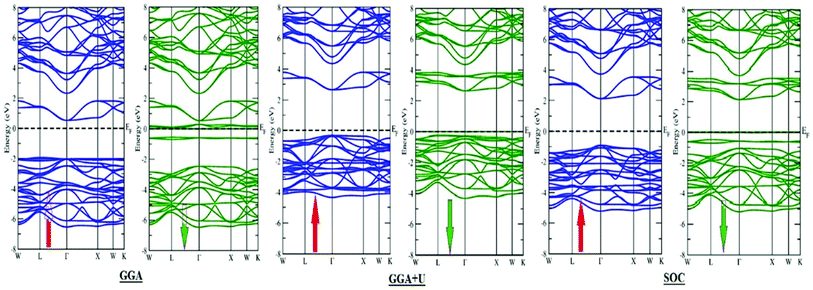
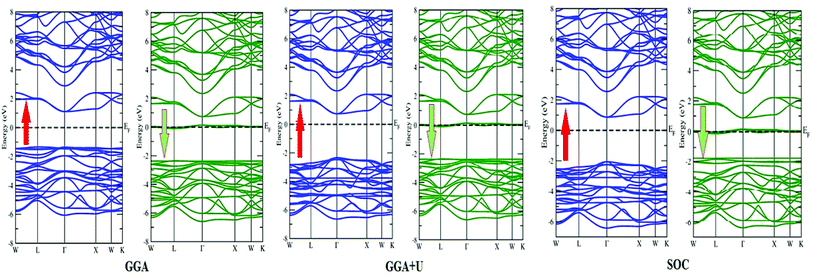
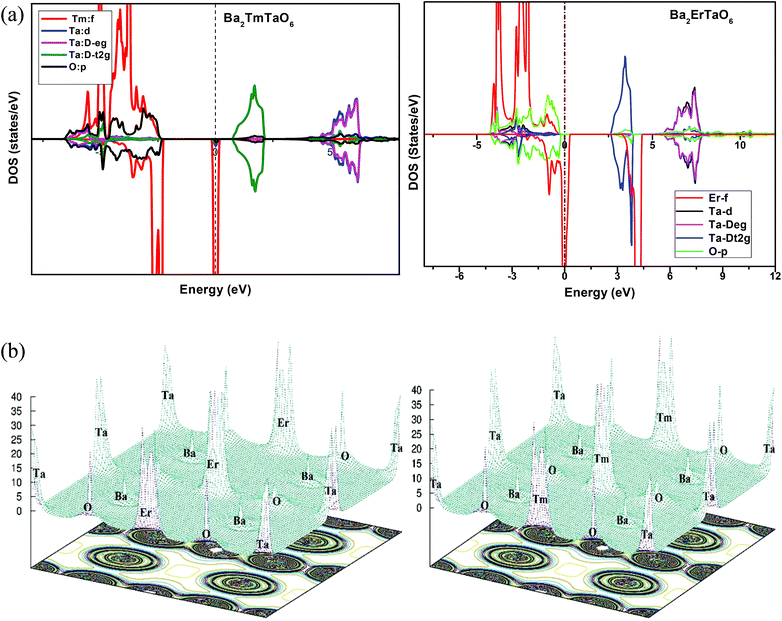
In search of smart devices for technological applications, the electronic properties of these materials were evaluated by employing GGA, SOC and GGA + U and are explained on the basis of band structure, the total density of states (DOS) and the partial density of states (PDOS). The spin-polarized band structure was calculated by GGA, SOC and GGA + U. However, GGA + U calculations were used, as it provides better treatment for correlated electrons, thus providing a better description of the band gap and magnetic properties.³⁷ The Hubbard interaction parameter U_eff (U–J) where J = 0.001 and U_eff was changed until we obtained the correct band structure profile, and the optimized value or U_eff for f-electrons and d-electrons was set to 0.28 Ry for Er and Tm and 0.18 Ry for Ta atoms in Ba₂ErTaO₆ and Ba₂TmTaO₆, as these values provide a correct band profile and magnetic properties. The GGA calculation designates the semiconducting behavior in the spin-up state with a direct band gap of 2.50 eV in Ba₂ErTaO₆ and 2.40 eV in Ba₂TmTaO₆, while both compounds in the spin down state showed metallic nature. Upon application of spin–orbit coupling (SOC), there was no significant effect though the energy bands are shifted towards the Fermi level in the valence band. By applying the on-site Hubbard potential, the ‘U’ energy levels shift towards the Fermi level in the valence band and drift away from the Fermi level in the conduction band resulting in larger band gaps in the spin-up channel, as compared to GGA and SOC. The band gap value varies from 2.50 eV to 2.75 eV after applying GGA + U in the case of Ba₂ErTaO₆, while for Ba₂TmTaO₆, the gap changes from 2.43 eV to 2.87 eV. In the case of the spin-up channel, the separation between the conduction band and the Fermi level are 0.71 eV and 0.18 eV, and the separation between the valence band and Fermi level are 2.1 eV and 2.57 eV in Ba₂ErTaO₆ and Ba₂TmTaO₆, respectively. This energy gap is responsible for 100% spin polarization at the Fermi level for Ba₂ErTaO₆ and Ba₂TmTaO₆. The spin-polarized band structures are displayed in Fig. 2 and 3. In addition to the band structure, the total DOS within GGA, SOC and GGA + U are presented in Fig. 4–6 for both compounds. Upon comparing the DOS calculated by the GGA, SOC and GGA + U approximations for both compounds, there are no considerable differences in the majority spin states, which confirms the metallic character, while in the minority state, the power of Coulomb interaction is clearly seen from Fig. 4. In the case of Ba₂MTaO₆ (M = Er, Tm), the maximum contribution to the DOS comes from the f-states of Er and Tm atoms, as observed in Fig. 5. In order to perceive the contribution of each atom to the electronic structure, the projected DOS of Ba, M (M = Er, Tm), Ta and O are also calculated by GGA + U approximation and shown in Fig. 6a.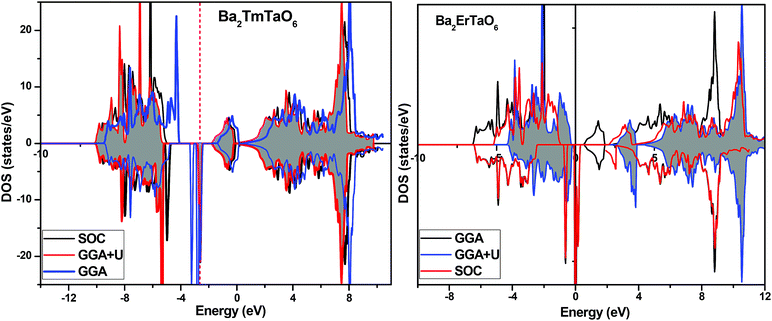

Fig. 2 Spin-polarized band structure of Ba₂ErTaO₆ calculated by GGA and GGA + U approximation.

Fig. 3 Spin-polarized band structure of Ba₂TmTaO₆ calculated by GGA and GGA + U approximation.

Fig. 4 Spin-polarized total density of states (DOS) of Ba₂MTaO₆ (where M = Er, Tm) at the equilibrium lattice constant calculated by GGA, SOC and GGA + U methods.

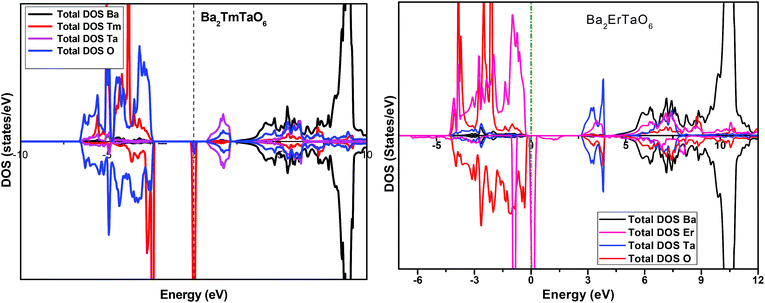Fig. 5 Spin-polarized total density of states (DOS) of individual atoms Ba₂MTaO₆ (M = Er,Tm) at the equilibrium lattice constant calculated by the GGA + U method.

Fig. 6 (a) Spin-polarized total density of states (DOS) of individual atoms Ba₂MTaO₆ (M = Er, Tm) at the equilibrium lattice constant calculated by GGA + U method. (b) 3-D electron charge density contour plots along the (111) crystallographic planes.

The basis of half-metallic nature can be well described with the help of the partial density of states plots given in Fig. 6a. The crystal field splitting removes the 5-fold degeneracy of the d-states of Ta⁵⁺ into two non-degenerate groups, triplet d-t_2g states and doublet d-e_g states and the f-states of the Tm³⁺ and Er³⁺ ions in the T_1u, T_2u, and A_2u schemes. In the spin-down channel, metallic behavior ascends due to the occupation of the f-state at the Fermi level by Er and Tm ions in Ba₂ErTaO₆ and Ba₂TmTaO₆, respectively. The Ta⁵⁺ ion has no valence electrons, so the d-t_2g (↑) and d-e_g (↑) states are empty and reside in the conduction bands for both spin states. On the other side, Tm³⁺ has twelve valence electrons, two single electrons and a pair of electrons in the antibonding T_1u orbital, while there are four pairs in the T_2u and A_2u bonding orbitals. The spin-up state is thus the majority spin channel as most valence electrons enter the channel. Only one electron enters the T_1u state in a spin down orientation, making it reside at the Fermi level, which gives rise to the metallic nature in the respective spin channel. The d-orbital of Er³⁺ in the majority spin channel is completely occupied and remains in the valence band. The p-states of oxygen gains electrons from all other ions and are the chief contributors to the valence band. The valence band in the spin-up states arises due to the strong hybridization between the f-states of Tm and Er, the d_t2g of Ta and the p-states of O. The semiconducting behavior is attributed to the nonappearance of energy states at the Fermi level in the spin-up channel.

3.3 Electron charge density

The electron charge density helps us to understand the bonding and charge sharing among the various ions. The electron charge densities calculated in the 3-D counter plots along the (111) crystallographic planes are displayed in Fig. 6b. The charge distribution around Ba is spherical, revealing the whole transfer of electrons from Ba to O, indicating the ionic character between Ba and O. Ionic bonding occurs because of the difference of the electronegativity (Pauling scale) between Ba and O atoms being 2.19. However, distribution transforms from spherical to an almost dumbbell shape along the chain of Ta–O–Tm and Ta–O–Er. Thus, this reveals the overlapping of states among Tm–O and Ta–O in Ba₂TmTaO₆ and Er–O and Ta–O in Ba₂ErTaO₆, which reflects the covalent nature of bonding between the atoms. Due to the increase in the electronegativity from Ba (0.89) to Tm (1.25), Ta (1.50), and Er (1.24) the nature of the bonding changes from ionic to covalent. From the overall charge distribution, it is evident that both the alloys have polar covalent (admixture of ionic and covalent) bonding.

3.4 Magnetic properties and magnetic susceptibility

The GGA approximation usually provides the quenched orbital moment for transition-metal oxides, which results in diffusive d-orbitals accompanied by stronger interactions. By GGA + U calculation, the on-site Coulomb energy “U” was considered, and the spin moments of all transition metal atoms were expected to be enhanced due to the localization and enhanced exchange integral. So, in general, the on-site ‘U’ slightly enhances the orbital moments of the transition-metal ions in double perovskites because of the stronger orbital polarization in the d-orbital. The polarization of the spin results in the creation of significant magnetic moment by Er and Tm via the GGA + U method atoms, while other atoms display feeble magnetic moments. The main source of magnetization in Ba₂MTaO₆ is due to the 4f orbital. As a result, the atoms with 4f electrons carry most of the magnetic moment with a little contribution of O atoms. In the presence of diffusive 6s valence configuration and the ionic behavior of the alkaline earth metal element, the magnetic moment of the Ba atoms is negligible. The spin magnetic moment of oxygen atoms is small because of the nearly closed 2p shell. The magnetic moment of the tantalum atom is also negligibly small in spite of the stronger spin–orbit interaction in the 5d orbital. This results from the larger size of 5d orbital and thus enhanced crystal field. Thus, half-metallicity along with spin-polarized character and high magnetic moments will facilitate their application in spintronic devices.

The magnetic susceptibility defines the magnetic behavior of the materials in the applied field. The magnetic susceptibility (χ) and inverse susceptibility (χ⁻¹) for both compounds are plotted in Fig. 7. From Fig. 7, we determined that the magnetic susceptibility (χ) shows a decreasing trend with increasing temperature. In the case of Ba₂ErTaO₆, χ shows a considerable decrease from 50–300 K, while the change is insignificant from 300 K to 800 K. In the case of Ba₂TmTaO₆, χ shows a decreasing trend of up to 500 K and then remains almost constant. The decrease in the magnetic susceptibility may be due to the deterioration in the alignment of the magnetic moment due to thermal agitation. The Curie Weiss law of paramagnetism is justified by the Weiss constant (θ) for Ba₂ErTaO₆ and Ba₂TmTaO₆ at 0 K. The magnitude of the magnetic susceptibility for both compounds at room temperature for Ba₂ErTaO₆ is 9 × 10⁻⁹ emu mol⁻¹ and is 8.23 × 10⁻⁹ emu mol⁻¹ for Ba₂TmTaO₆, respectively. So, inverse susceptibility curves also favor the paramagnetic phase in both Ba₂ErTaO₆ and Ba₂TmTaO₆.

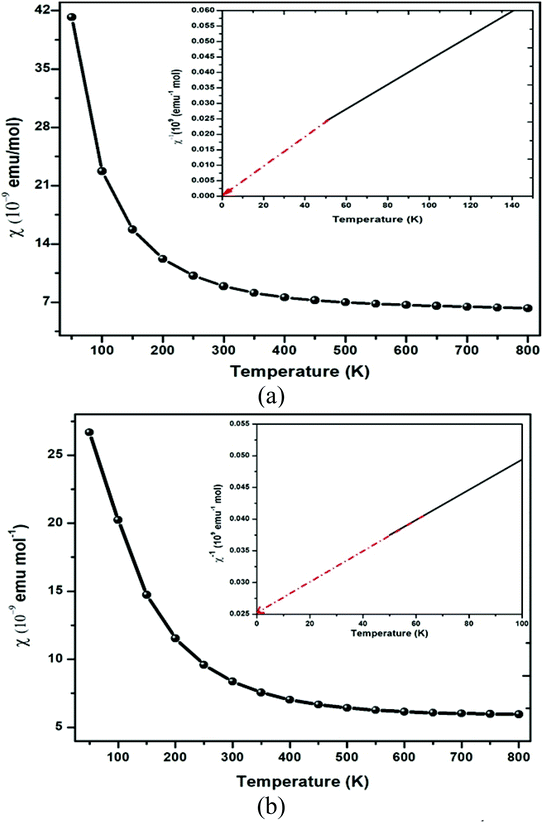Fig. 7 Magnetic susceptibility (χ) and inverse of magnetic susceptibility (χ⁻¹) plot versus temperature of (a) Ba₂ErTaO₆ and (b) Ba₂TmTaO₆.

3.5 Cohesive energy

Cohesive energy (E^coh) is the energy required to split a solid into its component atoms or into elementary structural blocks. This energy plays an important role in the stability of compounds. The larger the cohesive energy of a compound, the more robust will be its stability. This energy signifies how strongly atoms are held together in solid. The general equation for the cohesive energy per atom of an alloy A_xB_y with x and y denoting number of A and B atoms, respectively, is given by the relation:³⁹
E_AxBy is the equilibrium energy of an alloy obtained at optimization. In the case of double perovskites, the cohesive energy can be calculated as:

The calculated value per atom is 6.03 eV per atom for both compounds. The obtained values indicate that the atoms are strongly held to form the crystal.

3.6 Elastic properties

Elastic properties determine the response of the crystal to applied stress and the ability of the crystal to regain its shape upon the removal of the deforming force. Elastic properties also help to understand the mechanical stability of the compound including its strength, hardness, durability, reliability, binding forces and performance of the material. We determined the elastic constants (C_ij) and other interrelated properties. For cubic crystals, the necessary criteria for existence in the stable phase were determined on the basis of the mechanical stability condition satisfying the Born–Huang stability criteria:⁴⁰

C₁₁ > 0, C₄₄ > 0, C₁₁ − C₁₂ > 0, C₁₁ + 2C₁₂ > 0, and C₁₂ < B < C₁₁

From the computed values of C_ij, it was found that both materials followed the stability criteria and were mechanically stable. By using the above elastic constants, various properties of the materials were calculated as presented in Table 2. The bulk and shear moduli, which define the hardness of the material was given by the Voigt–Hill method. The Voigt bounds of the bulk modulus (B_V) and shear modulus (G_V) for the cubic systems are:⁴¹

Table 2 The calculated elastic constants (C_ij), Cauchy pressure (C_p), Bulk modulus (B), Shear modulus (G), Young's modulus (Y), Pugh's ratio (B/G) all in GPa, Poisson's ratio (ν), anisotropy constant (A), Debye temperature (θ_D) and melting temperature (T_m) for Ba₂MTaO₆

Parameter	Ba2ErTaO6	Ba2TmTaO6
C11	262.79	263.32
C12	33.00	32.25
C44	59.44	60.40
Cp	−26.44	−28.15
B	109.59	109.27
Y	201.17	202.49
GV	94.82	95.35
GR	73.66	74.65
G	84.24	85.00
ν	0.19	0.19
B/G	1.30	1.28
A	0.51	0.52
ρ	19.78	19.96
vt	2065	2065
vl	3348.13	3573.93
vm	5673.60	5809.10
θD	925.83	950.00
Tm	2106.35	2109.00

---

Also, the Reuss formula for the bulk and shear moduli are:

The Hill approximation is used to calculate bulk and shear (B, G) can be calculated as:⁴²

The Young's modulus (Y) and Poisson's ratio (ν) are calculated from Hill's bulk and shear (B, G) elastic moduli by the following equations:

The Young's modulus measures the stiffness of a material. The higher the value of Y, the more stiff the nature of the material. Ba₂MTaO₆ had a larger value of Y, indicating its stiff nature. Also, Y > B indicating that these alloys are super hard materials. The ductile or brittle nature of materials can be calculated by Cauchy's pressure (C_P = C₁₂ − C₄₄), which relates the nature of atomic bonding. Materials of brittle nature with directional bonding shows a negative value of C_p and is positive for metallic bonding with ductile nature. Both these materials have negative C_P, indicating the brittle nature of these compounds. Pugh's ratio (B/G) also determines the brittle or ductile nature of materials. The critical value that separates brittle and ductile materials is 1.75; the high value is associated with ductility, and the low value is associated with brittle nature. Both these compounds have (B/G) of less than the critical value verifying their brittle nature. Another criterion to confirm the ductile or brittle nature of an alloy is Poisson's ratio. The critical value of Poisson's ratio to differentiate brittle and ductile materials is 0.26. Materials with 0.26 < ν < 0.5 are regarded as ductile, while for 0.12 < ν < 0.26, they are regarded as being brittle. Since both compounds have ν = 0.19, it also confirmed their brittle nature. The measure of the degree of elastic anisotropy is given by Zener anisotropy factor, 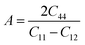. For a completely isotropic material ‘A’ = 1; otherwise, the material is anisotropic. Both materials having an ‘A’ of less than 1 implies the anisotropic nature of these compounds.

The Debye temperature of a material can be estimated by the classical method using average sound velocity v_m:⁴³

here, h is Planck's constant, k is Boltzmann's constant, N_A is Avogadro's number, ρ is the mass per unit volume and v_m is the average sound velocity.

The average velocity v_m can be approximated using longitudinal velocity (v_l) and transverse velocity (v_t):

v_l and v_t can be determined using the below equations:⁴⁴

Using these values, we obtained the value of θ_D, which is equal to 925.83 K for Ba₂ErTaO₆ and 950 K for Ba₂TmTaO₆.

The melting temperature T_m can be evaluated from elastic constants using relation:⁴⁵

T_m (K) = [553 + (5.911)C₁₁] ± 300 K

The calculated melting temperature of Ba₂ErTaO₆ came out to be 2106.35 ± 300 K and for Ba₂TmTaO₆ was found to be 2423 ± 300 K, respectively.

3.7 Optical properties

The optical properties are important for possible application in optoelectronics and solar cell applications. The optical properties were calculated from the frequency-dependent dielectric function ε(ω) as:

ε(ω) = ε₁(ω) + iε₂(ω)

where ε₁(ω) represents the real part, representing the dispersion of the electromagnetic waves in the system and ε₂(ω) gives the imaginary part of the dielectric function. ε₂(ω) was calculated from the momentum matrix element between occupied and unoccupied wave functions and shows dissipation or absorption of energy by the material. The real part of the dielectric function can be calculated from ε₂(ω) using Kramer's Kronig relation:
where P implies the principal value of the integral, and ω′ represents the complex angular frequency. From dielectric function, various other properties could be calculated such as refractive index (n(ω)) and coefficient of extinction (K(ω)) as:

(ε(ω)) = (n(ω) + iK(ω))²

These equations led to ε₁(ω) = n²(ω) − k²(ω) and ε₂(ω) = 2n(ω)k(ω)

These equations can be used to obtain the values of n(ω) and k(ω). From ε₁(ω) and ε₂(ω), the values of the absorption coefficient α(ω), reflectivity R(ω) and optical conductivity σ(ω) are derived as:

From the total dielectric function, the energy loss function L(ω) can be calculated using

The optical absorption coefficient determines how deep light of a particular wavelength can penetrate before it is absorbed. The variation of the optical absorption coefficient α(ω) with respect to photon energy is shown in Fig. 8(a). For Ba₂ErTaO₆, the absorption starts from 4 eV up to 14 eV with the highest peak being at 160 × 10⁴ cm⁻¹ at the energy value of 11 eV. In the case of Ba₂TmTaO₆, the absorption starts from zero photon energy and occupies the highest peak of 170 × 10⁴ cm⁻¹ at 13.8 eV. Therefore, the optically active region for both these perovskites is UV, and the IR spectrum and can absorb all the frequencies in this region. The optical conductivity spectrum of Ba₂MTaO₆ compounds is displayed in Fig. 8(b). The optical conductivity spectrum starts from the origin and displays a highest peak at 7 eV for Ba₂ErTaO₆ and at 9.5 eV for Ba₂TmTaO₆, as seen in Fig. 8(b). These peaks are mainly due to M = Er, Tm states which play a dominant role in the overall electronic structure and optical response of the material.

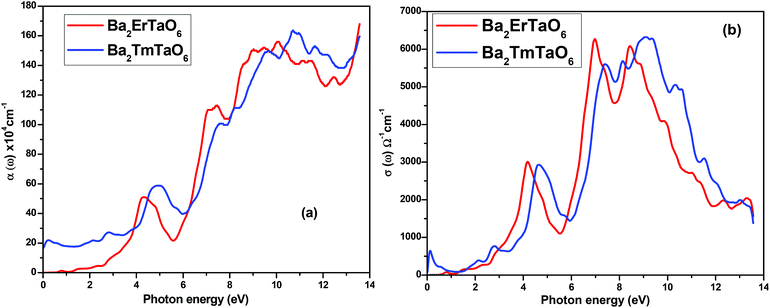Fig. 8 (a, b) The variation of the optical absorption coefficient and optical conductivity with photon energy for Ba₂MTaO₆ (M = Er, Tm).

In order to understand the interaction of light with matter, it is very essential to study the nature of the refractive index and the extinction coefficient. The refractive index is obtained from the real part of dielectric function and provides information about the phase velocity, while as an imaginary part, k(ω) termed as an extinction coefficient indicates the amount of loss in the absorption when electromagnetic wave propagates through the material. The refractive index and extinction coefficients plots are shown in Fig. 9(a) and (b). From these figures, we see that the highest peak for the refractive index has a magnitude of 8 at 4.3 eV and 7 at low energy values, as seen in Fig. 9(a). The extinction coefficient is highest at 9 eV, implying that absorption is also prominent at 9 eV. Also, the extinction coefficient has a highest peak magnitude of 4 at 9 eV for Ba₂ErTaO₆, while it is in the low-energy region for Ba₂TmTaO₆, as displayed in Fig. 9(b).

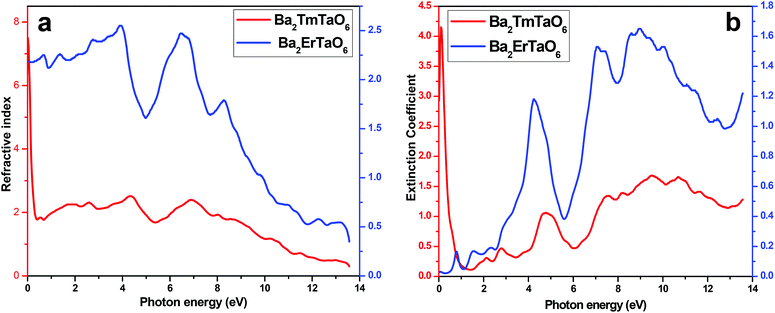Fig. 9 (a, b) The variation of the refractive index and extinction coefficient with photon energy for Ba₂MTaO₆ (M = Er, Tm).

The electron energy loss as a function of photon energy is shown in Fig. 10(a). It describes the optical spectra and excitations produced by fast-moving electrons. The electron energy loss is due to electron excitations occurring when a fast-moving electron traverses through a material. The most prominent peak for both compounds is seen at about 14 eV, as shown in Fig. 10(a). The prominent peaks in the loss function versus photon energy represent the characteristic plasma resonances occurring at the plasma frequency. The spectrum of reflectivity R(ω) as a function of photon energy is shown in Fig. 10(b), which starts from the origin. Reflectivity is the ratio of the energy of the reflected wave from the surface to the energy of the wave incident on the surface. From Fig. 10(b), we see that reflectivity has a highest peak at 0.65 for Ba₂TmTaO₆ and at 0.6 for Ba₂ErTaO₆.

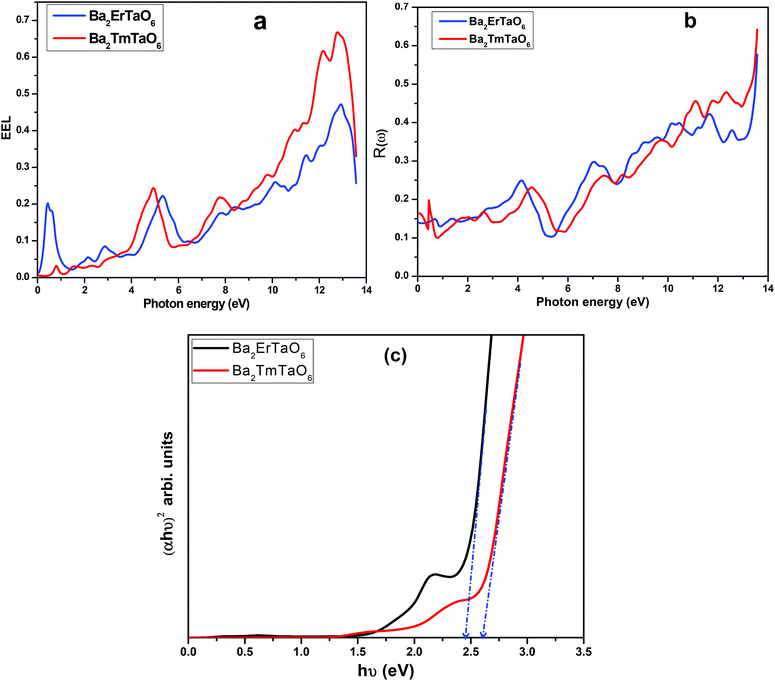Fig. 10 (a, b) The variation of reflectivity and electron energy loss function with photon energy for Ba₂MTaO₆ (M = Er, Tm). (c): (αhν)² versus hν plots for Ba₂MTaO₆ (M = Er, Tm).

The optical energy gaps were determined using the Tauc plots⁴⁶ along with the transmission spectra data and are shown in Fig. 10(c). Bandgaps for Ba₂MTaO₆ (M = Er, Tm) were observed to be 2.45 eV and 2.60 eV, respectively, which are close to the optimum value obtained by the band structure calculations.

3.8 Thermodynamic properties

In this section, we present the variation of thermodynamic properties with temperature and pressure. To calculate the thermodynamic properties of layered Ba₂MTaO₆ (M = Er, Tm), we used the quasi-harmonic Debye model via Gibbs2.³³ We studied properties such as (i) specific heat (C_v), (ii) the thermal expansion coefficient (α), and (iii) the Grüneisen parameter (γ) in the temperature range of 0–800 K and the pressure range of 0–30 GPa.

(i) Specific heat (C_v): the specific heat not only provides information about vibrational properties but is also useful in many applications. Since in solids, the volume doesn't change appreciably with temperature, we have, hence, computed the specific heat at constant volume C_v in the temperature range of 0–800 K and the pressure range of 0–30 GPa, as displayed in Fig. 11. For both compounds, we observed that C_v increases with increasing temperature. This is because of the fact that with increasing temperature, the atomic vibrations become more vigorous and then reaches a constant value at high temperatures, following Dulong–Petit law. However, at low temperatures, C_v changes abruptly with temperature, obeying Debye T³ law. It can also be seen that as the pressure increases, C_v decreases, but this decrease in C_v with pressure is insignificant.

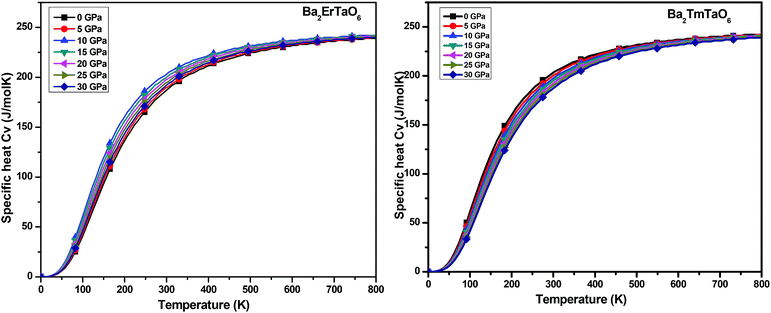Fig. 11 The variation of specific heat (C_v) of Ba₂MTaO₆ (M = Er, Tm) with temperature at different pressures.

(ii) Thermal expansion coefficient (α): the thermal expansion coefficient quantity describes how the dimensions of an object change upon application of the thermal gradient. It consists of three contributions, namely phonons, conduction electrons and f electron contributions, i.e., ΔL = ΔL_phonon+ ΔL_e+ΔL_f. It is temperature derivate of normalized length change ΔL/L. The variation of α with temperature for both compounds at various pressures is displayed in Fig. 12. We understand from this figure that α initially increases rapidly with temperature up to 550 K and then reaches an almost constant value, while the pressure dependence shows a reverse effect, i.e., the value of α decreases with increasing pressure although the change is very small. Both perovskites possess cubic symmetry, but the perovskite-type structure confers an anisometric structure. It is known that perovskite-type structures are sensitive to structural distortions; hence, both pressure and temperature can give rise to inclinations and/or the rotation of octahedral M–O₆ (M = Er, Tm) and Ta–O₆, elongation of the structure in certain crystallographic directions and eventual contractions in other directions. This type of response in α(T) is associated with the type of distortion or transition that occurs because of the application of temperature and pressure. Thus, in general, the thermal expansion coefficient gives a similar effect, as shown by the specific heat. Therefore, at low temperatures, α will be expressed as a summation of T-linear and T³ power law, which arises from conduction electrons and phonons, respectively.

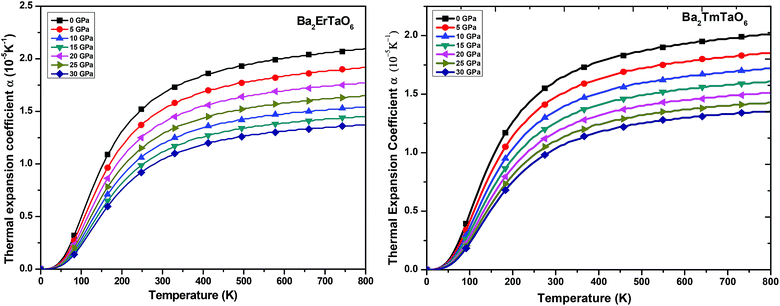Fig. 12 The variation of the thermal expansion coefficient of Ba₂MTaO₆ (M = Er, Tm) with temperature at different pressures.

(iii) Grüneisen parameter (γ): the Grüneisen parameter (γ) is used to describe the anharmonic effects of the lattice. It is used to characterize the thermodynamic behavior at high temperatures and high pressures. It also shows us the macroscopic behavior of solids. The variation of γ with temperature is displayed in Fig. 13. From Fig. 13, it can be concluded that γ remains almost constant and doesn't change with temperature. The obtained values of γ at zero temperature and zero pressure for Ba₂ErTaO₆ is 2.13 and changes to 1.96 at 30 GPa, and for Ba₂TmTaO₆ it is 2.07 and decreases to 1.92 at 30 GPa.

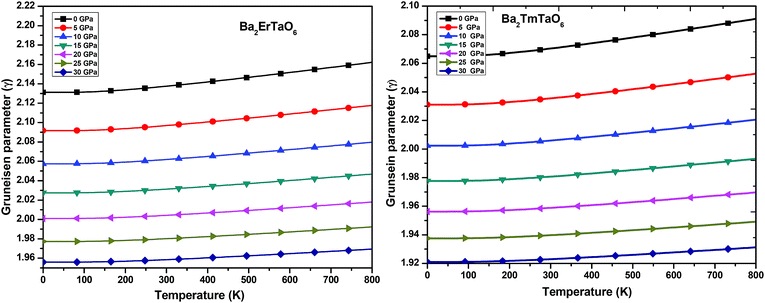Fig. 13 The variation of the Grüneisen parameter of Ba₂MTaO₆ (M = Er, Tm) with temperature at different pressures.

3.9 Thermoelectric properties

For the conversion of ravage heat into useful energy worldwide, there is a search for smart thermoelectric materials that fulfill our energy demands. The effectiveness of thermoelectricity is given by the dimensionless quantity called the figure of merit (ZT). Generally, the ZT is given by ZT = S²σT/κ,^47,48 where S is the Seebeck coefficient (also known as thermo-power), σ is electrical conductivity, T is the absolute temperature and κ is the total thermal conductivity. The attendance of large flat bands at the valence band corresponding to a larger effective mass and more dispersive nature at the valence band maxima dictates that these compounds shall prove to be promising materials for generating thermoelectricity. This motivated us to estimate the thermoelectric properties of these materials. From the PDOS, we see the contribution of electrons from different atomic orbitals to the Seebeck coefficient (S). The Er/Tm-f states contribute more towards the electrical conductivity and Ta-d states with a little contribution from the O-p states populating the DOS near the Fermi level. Therefore, thermally excited electrons from these orbitals will contribute to the value of S. Transport properties like electrical conductivity (σ/τ), electronic thermal conductivity (κ_e/τ), where τ is the relaxation time, and the Seebeck coefficient (S) are figured for both these materials. The overall ‘S’ as a function of temperature (T) for the materials is calculated via the two current model given as:⁴⁹

The electrical conductivity (σ) over relaxation time (τ) with temperature is reported in Fig. 14. From this figure, one can see that σ for both compounds decreases in the spin-down state, which confirms the metallic behavior. In the up-spin state, the electrical conductivity increases with temperature, confirming the semiconducting behavior and thus supports the band structure. In the case of the spin-down state of Ba₂ErTaO₆, the value of σ/τ decreases from 1.24 × 10²⁰ (Ω⁻¹ m⁻¹ s⁻¹) at 50 K to 1.19 × 10²⁰ (Ω⁻¹ m⁻¹ s⁻¹) at 800 K, while in the spin-up state, the value increases from 0.00 × 10²⁰ (Ω⁻¹ m⁻¹ s⁻¹) at 50 K to 0.017 × 10²⁰ (Ω⁻¹ m⁻¹ s⁻¹) at 800 K. In the case of the spin-down state of Ba₂TmTaO₆, the value of σ/τ decreases from 0.99 × 10²⁰ (Ω⁻¹ m⁻¹ s⁻¹) at 50 K to 0.96 × 10²⁰ (Ω⁻¹ m⁻¹ s⁻¹) at 800 K, while in the spin-up state, the value increases from 0.00 × 10²⁰ (Ω⁻¹ m⁻¹ s⁻¹) at 50 K to 0.022 × 10²⁰ (Ω⁻¹ m⁻¹ s⁻¹) at 800 K.

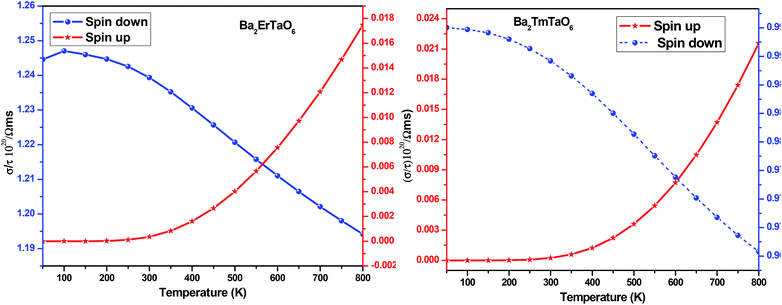Fig. 14 The variation of electrical conductivity (σ/τ) with temperature for Ba₂ErTaO₆ and Ba₂TmTaO₆.

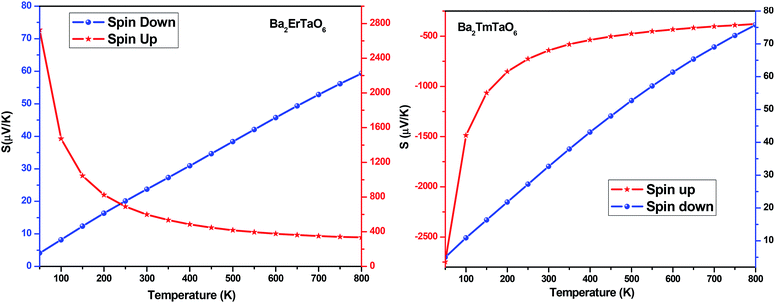
The Seebeck coefficient (S) for both compounds in both spin configurations was computed as a function of temperature and presented in Fig. 15. It was observed that in the case of Ba₂ErTaO₆, the Seebeck coefficient S is positive in the entire temperature range for both spin states, signifying the existence of p-type (holes) charge carriers. While in the case of Ba₂TmTaO₆ in the spin-up state, S as a function of temperature is negative, suggesting the existence of n-type charge carriers, in the spin-down state, S is positive, suggesting the existence of p-type charge carriers. The absolute value of S of Ba₂ErTaO₆ in the spin-down state increases from 5 μV K⁻¹ at 50 K to 60 μV K⁻¹ at 800 K, while in the spin-up state, it decreases from 2700 μV K⁻¹ at 50 K to 300 μV K⁻¹ at 800 K. In the case of the spin-up state of Ba₂TmTaO₆, the value increases from −2800 μV K⁻¹ at 50 K to −600 μV K⁻¹ at 800 K, while in the spin-down state, it increases from 5 μV K⁻¹ at 50 K to 75 μV K⁻¹ at 800 K.

Fig. 15 The variation of Seebeck coefficient (S) with temperature for Ba₂ErTaO₆ and Ba₂TmTaO₆.

The temperature variation of the total thermal conductivity (κ_tot) comprised of the lattice thermal conductivity (κ_L) and electronic thermal conductivity (κ_e) is shown in Fig. 16. We obtained the lattice part of thermal conductivity by the semi-classical Debye theory with the help of Slack's equation,⁴⁹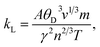where A is the physical constant (A ∼ 3.1 × 10⁻⁸), θ_D is the Debye temperature, γ is the Grüneisen parameter, n is the number of atoms in a primitive unit cell and ‘m’ is the average mass of all atoms in the crystal. It is clear from this figure that for Ba₂ErTaO₆, the electronic thermal conductivity shows an increasing trend from a small value at 100 K to 2.1 W m⁻¹ K⁻¹ at 800 K, while the lattice thermal conductivity decreases from 2 W m⁻¹ K⁻¹ at 100 K to 0.1 W m⁻¹ K⁻¹ at 800 K. The total thermal conductivity shows a decreasing trend from 2 W m⁻¹ K⁻¹ at 100 K to 2.5 W m⁻¹ K⁻¹ at 800 K. In the case of Ba₂TmTaO₆, the electronic thermal conductivity increases from a small value at 50 K to 4.2 W m⁻¹ K⁻¹ at 800 K, and the lattice thermal conductivity decreases from 2.6 W m⁻¹ K⁻¹ at 100 K to 0.1 W m⁻¹ K⁻¹ at 800 K. The total thermal conductivity shows a decreasing trend from 2.6 W m⁻¹ K⁻¹ at 50 K to 2.5 W m⁻¹ K⁻¹ at 800 K.

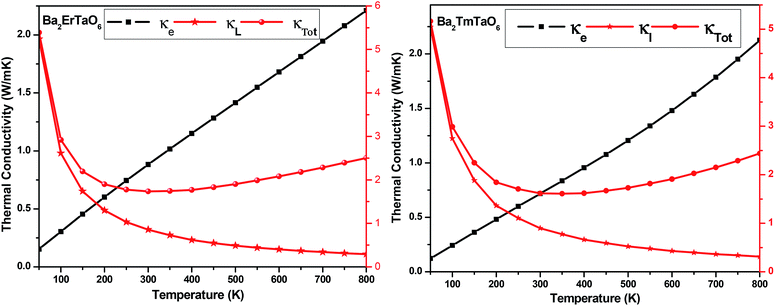Fig. 16 The variation of the lattice thermal conductivity (κ_L), electronic thermal conductivity (κ_e) and total thermal conductivity (κ_Total) with temperature in Ba₂MTaO₆ (M = Er, Tm).

The variation of the total Seebeck coefficient for both compounds with temperature is shown in Fig. 17(a). It can be seen from this figure that the total Seebeck coefficient increases almost linearly with temperature in both compounds and achieves a value of 60 μV K⁻¹ for Ba₂ErTaO₆ and 65 μV K⁻¹ for Ba₂TmTaO₆.

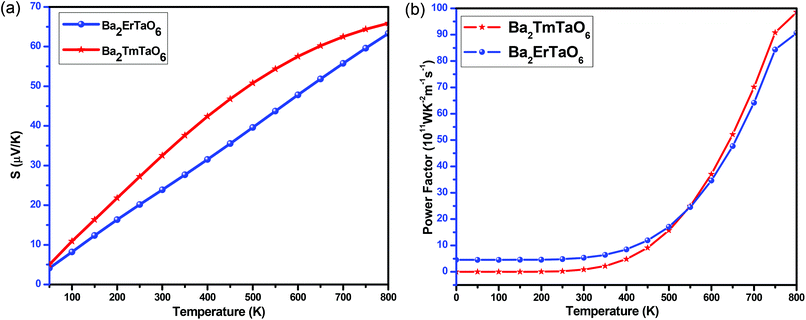Fig. 17 (a, b) The variation of the total Seebeck coefficient (S) and the power factor with temperature for Ba₂ErTaO₆ and Ba₂TmTaO₆.

To determine the performance of both compounds, we computed the power factor (PF). Fig. 17(b) shows the dependence of the power factor on temperature and shows that the power factor increases from a small value in the case of Ba₂TmTaO₆ at 0 K to 90 × 10¹¹ W m⁻¹ K⁻² s⁻¹ at 800 K, while in Ba₂ErTaO₆, it increases from 5 × 10¹¹ W m⁻¹ K⁻² s⁻¹ at 0 K to 85 × 10¹¹ W m⁻¹ K⁻² s⁻¹ at 800 K. Both materials hold a considerable power factor, which makes them desired for thermoelectric applications.

4 Conclusion

The overall DFT calculated structural, magneto-electronic, mechanical, optical, thermodynamic, and transport properties were calculated by the GGA + U method. Ba₂ErTaO₆ and Ba₂TmTaO₆ are stable in cubic structure with paramagnetic phases. The magnetic susceptibility curve confirms that the compounds are stable in the paramagnetic phase. The mechanical stability of the compounds was also confirmed from the elastic constants. Cauchy pressure, Pugh's and Poisson's ratio altogether confirm that both Ba₂ErTaO₆ and Ba₂TmTaO₆ are brittle in nature. The cohesive energy calculated for both materials was 6.03 eV per atom. The thermodynamic properties were calculated by the quasi-harmonic Debye model. Both materials possess high Seebeck coefficients and power factors at high temperatures. The reflectivity, electron energy loss, absorption coefficient and conductivity were also calculated. The reflectivity shows that these compounds might be useful for devices operating in the ultraviolet range of the electromagnetic spectrum. The overall properties envisioned confirm that both these alloys can find applications in thermoelectric, spintronic and optoelectronic applications.

Conflicts of interest

The authors have no conflict of interest.

References

1. B. Fisher, K. B. Chashka, L. Patlagan and G. M. Reisner, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 205109.
2. H. Kato, T. Okuda, Y. O. Kimoto and Y. Tomioka, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 184412.
3. A. Dias, L. A. Khalam, M. T. Sebastian and R. L. Moreira, J. Solid State Chem., 2007, 180, 2143.
4. T. Shizhe, Z. Junchai, Q. Congde, J. Xiangling and J. Bingzheng, J. Rare Earths, 2006, 24, 679.
5. M. Kobayashi, R. Katsuraya, T. Nara, Y. Tomita, H. Nakano and N. Kamegashira, J. Rare Earths, 2006, 24, 668.
6. A. Knyazev, A. Ershova and N. Chernorukov, J. Rare Earths, 2009, 27, 4.
7. S. Halder, Md. S. Sheikh, B. Ghosh and T. P. Sinha, Ceram. Int., 2014, 43, 11097.
8. S. Vasala and M. Karppinen, Prog. Solid State Chem., 2015, 43, 1.
9. S. M. Rao, J. K. Srivastava, M. K. Wu, B. H. Mok, C. L. Chen, M. C. Ling, H. L. Liu, Y. Y. Chen and J. C. Ho, J. Supercond. Novel Magn., 2011, 24, 1249.
10. K. I. Kobayashi, T. Kimura, Y. Tomioka, H. Sawada and K. Terakura, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 59, 11159.
11. S. A. Khandy and D. C. Gupta, J. Magn. Magn. Mater., 2017, 441, 166.
12. M. Li, M. J. Pietrowski, R. A. De Souza, H. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, Nat. Mater., 2014, 13, 31.
13. H. Tanaka and M. Misono, Curr. Opin. Solid State Mater. Sci., 2001, 5, 381.
14. N. A. Noor, S. M. Alay-e-Abbas, M. U. Sohaib, S. M. Ghulam Abbas and A. Shaukat, J. Magn. Magn. Mater., 2015, 374, 164.
15. N. A. Noor, S. Ali and A. Shaukat, J. Phys. Chem. Solids, 2011, 72, 836.
16. N. A. Noor, S. M. Alay-e-Abbas, Y. Saeed, S. M. Ghulam Abbas and A. Shaukat, J. Magn. Magn. Mater., 2013, 339, 11.
17. W. T. Fu and D. J. W. Ijdo, J. Solid State Chem., 2006, 179, 1022.
18. Y. Doi and Y. Hinatsu, J. Phys.: Condens. Matter, 2001, 13, 4194.
19. B. J. Kennedy, P. J. Saines, Y. Kubota, C. Minakata, H. Hano, K. Kato and M. Takata, Mater. Res. Bull., 2007, 40, 1875.
20. S. Calder, T. Fennell, W. Kockelmann, G. C. Lau, R. J. Cava and S. T. Bramwell, J. Phys.: Condens. Matter, 2010, 22, 116007.
21. Y. Kanaiwa, M. Wakeshima and Y. Hinatsu, Mater. Res. Bull., 2002, 37, 1825.
22. L. Brixner, J. Inorg. Nucl. Chem., 1960, 15, 352.
23. P. J. Saines, B. J. Kennedy and M. M. Elcombe, J. Solid State Chem., 2007, 180, 401.
24. J. A. Aguiar, C. C. D. Silva, Y. P. Yadava, D. A. L. Tellez, J. M. Ferreira and E. Montarroyos, J. Low Temp. Phys., 1998, 117, 969.
25. J. A. Alonso, C. Cascales, P. G. Casado and I. Rasines, J. Solid State Chem., 1997, 128, 247.
26. R. Mukherjee, S. Saha, A. Dutta and T. P. Sinha, J. Alloys Compd., 2015, 651, 222.
27. V. M. Nair, R. Jose, G. M. A. Kumar, M. M. Yusoff and P. R. S. Wariar, J. Alloys Compd., 2012, 512, 207.
28. R. Mukherjee, A. Dutta and T. P. Sinha, Mater. Sci. Semicond. Process., 2015, 39, 67.
29. A. Dias, R. G. Sa and R. L. Moreira, J. Raman Spectrosc., 2008, 39, 180.
30. M. N. Iliev, P. Padhan and A. Gupta, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 172303.
31. R. Mukherjee, A. Dutta and T. P. Sinha, J. Electron. Mater., 2016, 45, 846.
32. K. Schwarz, P. Blaha and G. K. H. Madsen, Comput. Phys. Commun., 2002, 147, 21.
33. P. Blaha, K. Schwarz, G. K. H. Madsen, D. Kvasnicka and J. Luitz, WIEN2k, An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties, Vienna University of Technology, Vienna, 2001.
34. M. A. Blanco, E. Francisco and V. Luania, Comput. Phys. Commun., 2004, 158, 57.
35. G. K. H. Madsen and D. J. Singh, Comput. Phys. Commun., 2006, 175, 67.
36. S. Yousuf and D. C. Gupta, Mater. Sci. Eng., B, 2017, 221, 73.
37. S. Dimitrovska, S. Aleksovska and I. Kuzmanovski, Cent. Eur. J. Chem., 2005, 3, 198.
38. S. Vasala and M. Karppinen, Prog. Solid State Chem., 2015, 43, 1.
39. A. Yakoubi, O. Baraka and B. Bouhafs, Results Phys., 2012, 2, 58.
40. M. J. Mehl, J. E. Osburn, D. A. Papaconstantopoulos and B. M. Klein, Phys. Rev. B: Condens. Matter Mater. Phys., 1990, 41, 10311.
41. A. Reuss, Z. Angew. Math. Mech., 1929, 9, 49.
42. R. Hill, J. Mech. Phys. Solids, 1963, 11, 375.
43. O. L. Anderson, J. Phys. Chem. Solids, 1963, 24, 909.
44. P. Ravindran, L. Fast, P. A. Korzhavyi, B. Johansson, J. Wills and O. Eriksson, J. Appl. Phys., 1998, 84, 4891.
45. S. A. Khandy, I. Islam, D. C. Gupta and A. Laref, J. Solid State Chem., 2019, 270, 173.
46. M. Burhanuz Zaman, T. Chandel and R. Poolla, J. Electron. Mater., 2019, 48, 3194.
47. T. M. Bhat and D. C. Gupta, RSC Adv., 2016, 6, 80302.
48. T. M. Bhat and D. C. Gupta, J. Electron. Mater., 2016, 45, 6012.
49. T. M. Bhat and D. C. Gupta, J. Phys. Chem. Solids, 2018, 112, 190.

---