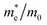Open Access Article
Open Access ArticleStrain sensitivity of band structure and electron mobility in perovskite BaSnO3: first-principles calculation
Yaqin Wang *ab,
Runqing Suia,
Mei Bia,
Wu Tangb and
Sude Maa
*ab,
Runqing Suia,
Mei Bia,
Wu Tangb and
Sude Maa
aKey Laboratory of Fluid and Power Machinery, School of Material Science and Engineering, Xihua University, Chengdu, 610039, China
bState Key Laboratory of Electronic Thin Films and Integrated Devices, University of Electronic Science and Technology of China, Chengdu, 610054, China. E-mail: wangyqyyxf@sina.com
First published on 7th May 2019
Abstract
A first-principles electronic structure calculation is utilized to contrastively investigate the crystal structure, band structure, electron effective mass and mobility of perovskite BaSnO3 under hydrostatic and biaxial strain. Strain-induced changes in relative properties are remarkable and more sensitive to hydrostatic strain than biaxial strain. The structure of BaSnO3 remains cubic under hydrostatic strain, while it becomes tetragonal under biaxial strain. Originating from the strain sensitivity of the Sn 5s orbitals in the conduction band minimum, the band gaps of BaSnO3 decrease for both types of strain from −3% to 3%. BaSnO3 under tensile hydrostatic strain exhibits higher electron mobility than it does under tensile biaxial strain because of the smaller electron effective mass in the corresponding strain. In contrast, the opposite phenomenon exists in compressive strain. Our results demonstrate that strain could be an alternative way to modify the band gap and electron mobility of BaSnO3.
1 Introduction
Recently perovskite-type oxide BaSnO3 has become a research hotspot, due to its high electron mobility and visible light transmittance at room temperature, as well as thermal stability.1 The cubic BaSnO3 with a band gap of 3.1 eV is stable at temperatures up to 1000 °C.2 Its high visible optical transparency makes it is commonly used as a transparent electrode material or as electronic components for power devices, and it is regarded as a good substitute material for the traditional transparent conductive oxides. On the other hand, due to the Sn 5s orbitals on the bottom of the conduction band, BaSnO3 has a high electron mobility at room temperature, with values of 320 cm2 V−1 s−1 (ref. 3) and 150 cm2 V−1 s−1 (ref. 4) for single crystal and film structures, respectively. These properties suggest that BaSnO3 is an ideal channel material in perovskite heterostructures, compared with the traditional SrTiO3 thin films. In the past 50 years, the best electron mobility and conductivity of SrTiO3 thin film has been 10 cm2 V−1 s−1 and 500 S cm−1 at room temperature,1 resulting in the related interesting properties of the LaAlO3/SrTiO3 heterostructure being limited to low temperatures.5 The appearance of BaSnO3 is expected to make the quantum effect appear in the perovskite heterostructure at room temperature, expanding the application ranges of perovskite electronic devices.To date, previous studies have used many methods to modify the band gap and electron mobility of BaSnO3 thin films. The typical method is “Doping engineering” with La into the Ba site and Sb into the Sn site. The band gap can be effectively adjusted from 3.48 eV to 4.23 eV.2,6–8 However, the electron mobility can only reach 70−150 cm2 V−1 s−1 at room temperature. In the earliest work, the electron mobility of (Ba, La)SnO3 thin films on SrTiO3 (001) substrate obtained by Kim et al.3 was 70 cm2 V−1 s−1 at a doping level of 4 × 1020 cm−3. Kookrin Char et al.9 and Shiogai et al.10 improved the electron mobility of La–BaSnO3 thin films to 80 cm2 V−1 s−1 and 78 cm2 V−1 s−1 by depositing the BaSnO3 and (Ba, Sr)SnO3 buffer layers on SrTiO3 (001) substrate, respectively. K. H. Kim et al.11 has reported that using single crystal BaSnO3 (001) as substrate can reduce the appearance of dislocation in BaSnO3 thin films, increasing the electron mobility up to 102 cm2 V−1 s−1. Bharat Jalan et al.,1 Lebens Higgins et al.,12 and Susanne Stemmer et al.4 have deposited La–BaSnO3 thin films with ultra-high crystallinity by molecular beam epitaxy, improving the electron mobility to 120 cm2 V−1 s−1, 81 cm2 V−1 s−1, and 150 cm2 V−1 s−1, respectively. All these studies indicate that due to the ionized impurities scattering caused by the La(Sb) atom doping in the La(Sb)–BaSnO3 thin films, the electron mobilities of La(Sb)–BaSnO3 are limited. So far, the highest electron mobility of BaSnO3 film obtained at room temperature is 150 cm2 V−1 s−1. Thus, other methods to tune the band gap and electron mobility of BaSnO3 are needed.
The method of “Strain engineering” is a widely used method to obtain desired properties of materials. Many studies have indicated that external stresses such as hydrostatic pressure and internal strains from lattice and thermal mismatch can alter the structure and electronic properties of semiconductors. The band type of ultrathin [0001] ZnO nanowire changes from direct to indirect under uniaxial compressive strain, along with the structural transition from wurtzite to hexagonal.13 The band gaps of Sn oxides with SnO6 octahedra decrease (increase) by 0.8–1.0 eV with a hydrostatic strain of 2% (−2%), showing that they are highly sensitive to hydrostatic strain.14 The tensile biaxial strain from the substrate destroys the two-dimensional electron gas (2DEG) at the LaAlO3/SrTiO3 (001) interface, while the compressive biaxial strain induces the 2DEG and increases the critical thickness of LaAlO3 thin films for the insulator-to-metal transition.15,16 Also, the tensile biaxial strain is experimentally demonstrated to be effective at reducing the mobility of the 2DEG at the LaAlO3/SrTiO3 (001) interface.16 The epitaxial strain dependence of the spontaneous polarizations and Curie temperatures varies considerably for different ferroelectric thin film systems, such as BaTiO3, PbTiO3, LiNbO3, and BiFeO3.17–20
To tune the electronic properties of BaSnO3 through epitaxial in-plane misfit strains and external hydrostatic pressure, we have used first-principles calculations to demonstrate a detailed study of strain engineering of BaSnO3. The changes in crystal structure, electronic structure, electron effective mass and mobility due to the imposed strain have been investigated. Some commercially available substrate materials have also been concluded in our work.
2 Methods and models
In this work, all the density functional theory (DFT) simulations were performed using the Vienna Ab initio Simulation Package (VASP).21 The electron-ion interactions were described by the projector augmented-wave (PAW)22 pseudopotentials method. A cutoff energy of 440 eV for the plane-wave basis set, and a Monkhorst–Pack k-point mesh of 6 × 6 × 6 for the unit cell of BaSnO3 was employed to get well-converged results. The force tolerance on every atom was smaller than 0.01 eV Å−1. For the electronic exchange–correlation interactions, the Heyd–Scuseria–Ernzerhof (HSE06)23 hybrid functional theory was used, and 43% contribution of Hartree–Fock (HF) exchange in HSE06 functional theory was set to obtain the accurate band gap of BaSnO3.A cubic perovskite BaSnO3 unit cell was used to model the variations of properties under hydrostatic strain (εxx = εyy = εzz) and biaxial strain (εxx = εyy ≠ εzz) from −3% to 3%, at intervals of 1%. The relaxed lattice constant of 4.129 Å from HSE06 theory was used to calculate the properties of unstrained BaSnO3. The lattice parameters along the x, y, and z-axes were adjusted to simulate various applied hydrostatic strains from −3% to 3%, and allowing the atoms to fully relax. For the case of biaxial strain, the lattice parameters along the x and y-axes were changed equally, and the structure was allowed to relax in the z-axial direction. The electron effective mass was determined by analyzing the calculated band structures at the energy band extremum using the standard equation24
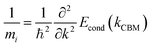 | (1) |
3 Discussion and results
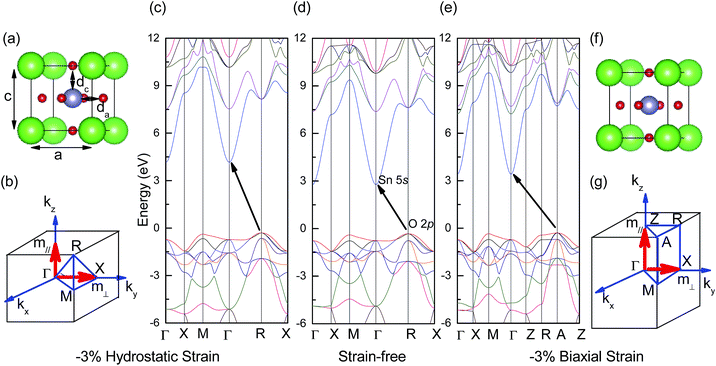
Strain-free BaSnO3 has a cubic perovskite structure and belongs to the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group. It is composed of a corner-sharing SnO6 octahedron, with a Ba2+ filling in the structure. For the case of hydrostatic strain (εxx = εyy = εzz), BaSnO3 remains cubic [Fig. 1(a)] and is the same as strain-free BaSnO3. However, when biaxial strain (εxx = εyy ≠ εzz) is imposed, the symmetry is changed and the crystal structure becomes tetragonal [Fig. 1(f)]. Along with the different structure changes between biaxial and hydrostatic strain, BaSnO3 also presents discrepant electronic properties. Fig. 1(c), (d) and (e) show typical band structures of BaSnO3 under −3% hydrostatic strain, 0 strain and −3% biaxial strain, respectively. The results show that BaSnO3 displays indirect band gaps in both strain and strain-free structures. The conduction band minimum (CBM) under biaxial and hydrostatic strain both occurs at the Γ point. However, originating from the different structural symmetry of BaSnO3 under biaxial and hydrostatic strain, the valence band maximum (VBM) appears at the R point under biaxial strain and at the A point under hydrostatic strain. The electron effective mass is determined by analyzing the calculated band structure near Γ along the z-axial direction in reciprocal space (m‖) and along the x-axial or y-axial directions (m⊥, perpendicular to the z-axial direction), as indicated in Fig. 1(b) and (g). According to the symmetry, it can be obtained that the electron effective masses in the x, y, and z-axials are equal under hydrostatic strain (m‖ = m⊥), while they are shown to be different under biaxial strain (m‖ ≠ m⊥). The accurate values are presented in the following content.
m space group. It is composed of a corner-sharing SnO6 octahedron, with a Ba2+ filling in the structure. For the case of hydrostatic strain (εxx = εyy = εzz), BaSnO3 remains cubic [Fig. 1(a)] and is the same as strain-free BaSnO3. However, when biaxial strain (εxx = εyy ≠ εzz) is imposed, the symmetry is changed and the crystal structure becomes tetragonal [Fig. 1(f)]. Along with the different structure changes between biaxial and hydrostatic strain, BaSnO3 also presents discrepant electronic properties. Fig. 1(c), (d) and (e) show typical band structures of BaSnO3 under −3% hydrostatic strain, 0 strain and −3% biaxial strain, respectively. The results show that BaSnO3 displays indirect band gaps in both strain and strain-free structures. The conduction band minimum (CBM) under biaxial and hydrostatic strain both occurs at the Γ point. However, originating from the different structural symmetry of BaSnO3 under biaxial and hydrostatic strain, the valence band maximum (VBM) appears at the R point under biaxial strain and at the A point under hydrostatic strain. The electron effective mass is determined by analyzing the calculated band structure near Γ along the z-axial direction in reciprocal space (m‖) and along the x-axial or y-axial directions (m⊥, perpendicular to the z-axial direction), as indicated in Fig. 1(b) and (g). According to the symmetry, it can be obtained that the electron effective masses in the x, y, and z-axials are equal under hydrostatic strain (m‖ = m⊥), while they are shown to be different under biaxial strain (m‖ ≠ m⊥). The accurate values are presented in the following content.
In order to clearly present structural changes of BaSnO3 under different strains, the lattice constants, bond lengths and volumes of BaSnO3 under different biaxial and hydrostatic strain are shown in Fig. 2. The lattice parameter of strain-free cubic BaSnO3 is 4.129 Å from HSE calculation, in agreement with the experimental value of 4.115 Å.25 The in-plane lattice constant a and bond length da (=a/2) increase with increasing biaxial strain from compressive strain to tensile strain. The out-of-plane lattice constant c and bond length dc (=c/2) decrease with the biaxial strain, resulting from the Poisson effect. For the case of hydrostatic strain, BaSnO3 remains cubic, and the change of lattice constants (a = c) and bond lengths (da = dc) is the same as the shift of a and da under biaxial strain, that is, an increase with hydrostatic strain from compressive strain to tensile strain. As a result, the volumes of BaSnO3 under hydrostatic strain shift significantly toward higher values than that under biaxial strain. The volume of BaSnO3 is 80.13 Å3 under 3% hydrostatic strain, which is about 4 Å3 larger than that of BaSnO3 with the same biaxial strain.
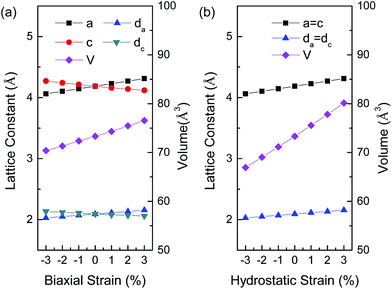 | ||
| Fig. 2 Lattice constants, bond lengths and volumes of the BaSnO3 unit cell as a function of (a) biaxial strain, and (b) hydrostatic strain. The corresponding lattices and bonds are marked in Fig. 1(a). | ||
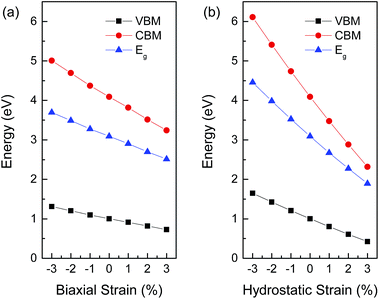
Next, we carried out comparison studies for the electronic properties of BaSnO3 under different strain. Table 1 lists the lattice and electronic parameters of strain-free BaSnO3. The band gap is obviously underestimated to be around 0.325 eV from the GGA calculation. The value from HSE calculation is 3.091 eV, consistent with the experimental values of 3.1 eV.28 Fig. 3 shows the relationships between the calculated band gap from HSE calculation and biaxial strain or hydrostatic strain. The band gap of BaSnO3 decreases with increasing strain from compressive strain to tensile strain for both biaxial and hydrostatic strain. With an increase in biaxial and hydrostatic strain from −3% to 3%, the values drop from 3.70 eV to 2.51 eV, and 4.46 eV to 1.89 eV, respectively. The linear relationships under biaxial strain and hydrostatic strain, respectively, can be expressed as follows:
| Eg,bi = 3.096 − 19.69εxx | (2) |
| Eg,hyd = 3.129 − 42.72εxx | (3) |
 for strain-free BaSnO3 calculated by GGA and HSE06 methods, compared to the available data
for strain-free BaSnO3 calculated by GGA and HSE06 methods, compared to the available data
To evaluate the change of band gap with strain, we further calculated the deformation potentials, which can determine the quality of device modeling33 and are difficult to obtain from experiment.34 The sum deformation potential under in-plane strain can be calculated by the following equation:33
| ΔEgX = D⊥X(εxx + εyy) | (4) |
| X | D⊥X (eV) | |
|---|---|---|
| Biaxial strain | Γ − R | −9.99 |
| Biaxial strain | Γ − Γ | −9.81 |
| Hydrostatic strain | Γ − A | −21.36 |
| Hydrostatic strain | Γ − Γ | −21.45 |
To further explain the change of band gap versus strain, we plotted the energy of the CBM and VBM as a function of strain in Fig. 3. The variation tendency of the CBM is more remarkable than that of the VBM under both biaxial and hydrostatic strain. The CBM of BaSnO3 is mainly comprised of Sn 5s orbitals, while the VBM consists of O 2p orbitals. The results thus indicate that the Sn 5s orbitals play a major role in the strain sensitivity of the band gap in BaSnO3.
In addition to the band structure, we also calculated the electron effective mass for the conduction band minimum at the Γ point along the x, y and z-axial directions in reciprocal space. The calculated longitudinal and transverse effective masses at the Γ point in strained BaSnO3 are shown in Fig. 4. The electron effective mass of BaSnO3 changes remarkably with the strain from −3% to 3%. For the case of biaxial strain, the transverse and longitudinal electron effective masses both decrease monotonically with increasing biaxial strain. The difference between transverse and longitudinal electron effective mass is very small under tensile strain and can be ignored under compressive strain. Since BaSnO3 is always cubic under hydrostatic strain, the transverse and longitudinal electron effective masses are equal and decrease linearly from compressive hydrostatic strain to tensile hydrostatic strain. The variations of effective mass with volume for BaSnO3, defined as dInm/dV, is −2.39 for both m‖ and m⊥, which is larger than that for GaN and AlN reported by Dreyer et al.35
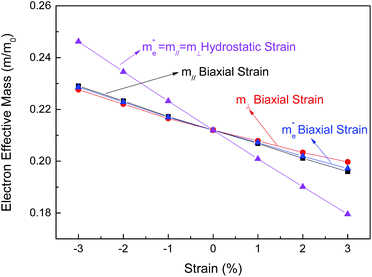 | ||
Fig. 4 The dependence of electron effective mass for BaSnO3 under different biaxial and hydrostatic strain. The average electron effective mass for conductivity 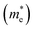 , longitudinal electron effective mass (m‖) and transverse electron effective mass (m⊥) shown in Fig. 1 are presented. m0 is the effective mass for a free electron. , longitudinal electron effective mass (m‖) and transverse electron effective mass (m⊥) shown in Fig. 1 are presented. m0 is the effective mass for a free electron. | ||
To estimate the electron mobility of BaSnO3, we calculated the average electron effective mass for conductivity using the following equation:36
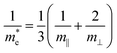 | (5) |
The change of electron effective mass with strain can be utilized to estimate the influence of strain on the electron mobility by the equation:37 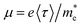 , with the assumption that <τ> is a constant. e,
, with the assumption that <τ> is a constant. e, 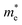 , and <τ> are the charge, electron effective mass, and average scattering time, respectively. The normalized electron mobility (μ/μ0) for BaSnO3 under different biaxial and hydrostatic strain with respect to the strain-free BaSnO3 are presented in Fig. 5. μ0 refers to the electron mobility of strain-free BaSnO3. Our results show that the electron mobility is more sensitive to hydrostatic strain than biaxial strain. With the strain change from −3% to 3%, the normalized electron mobility monotonously increases from 0.86 to 1.16 under biaxial strain, while increasing from 0.74 to 1.39 under hydrostatic strain. Both tensile hydrostatic and biaxial strain can enhance the electron mobility, while the compressive strain reduces the electron mobility.
, and <τ> are the charge, electron effective mass, and average scattering time, respectively. The normalized electron mobility (μ/μ0) for BaSnO3 under different biaxial and hydrostatic strain with respect to the strain-free BaSnO3 are presented in Fig. 5. μ0 refers to the electron mobility of strain-free BaSnO3. Our results show that the electron mobility is more sensitive to hydrostatic strain than biaxial strain. With the strain change from −3% to 3%, the normalized electron mobility monotonously increases from 0.86 to 1.16 under biaxial strain, while increasing from 0.74 to 1.39 under hydrostatic strain. Both tensile hydrostatic and biaxial strain can enhance the electron mobility, while the compressive strain reduces the electron mobility.
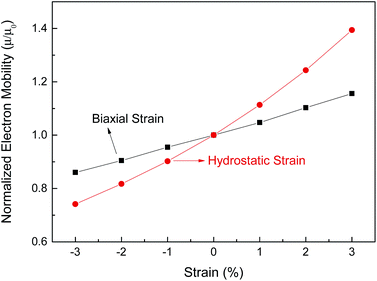 | ||
| Fig. 5 The normalized electron mobility (μ/μ0) for BaSnO3 under different biaxial and hydrostatic strain with respect to the strain-free BaSnO3. | ||
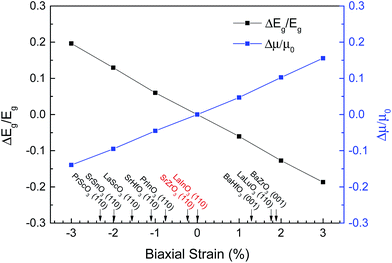
The variations of band gap and electron mobility compared with the strain-free BaSnO3 as a function of biaxial strain are shown in Fig. 6. The results show that the biaxial strain has opposite effects on the band gap and electron mobility. Compressive strain enhances the band gap and decreases the electron mobility, while tensile strain decreases the band gap and improves the electron mobility. For a change in compressive strain from 0 to 3%, the band gap increases by 19.6%, and the electron mobility drops 13.9%. On the other hand, for tensile strain, ΔEg/Eg is negative, and drops linearly with the strain from 0 to 3%. The tensile strain results in a significant improvement of electron mobility, for example, Δμ/μ0 is equal to 15.6% under 3% tensile strain.
Further, we expect that the biaxial strains in ultrathin epitaxial BaSnO3 films on suitable substrates can modify the electron mobility and band gap. A number of materials are investigated and some commercially available substrate materials are marked on Fig. 6. It should be pointed out that the substrates marked on the figure only rely on the lattice parameters. However, the strain is not only from the lattice mismatch, but also from the thermal expansion parameters between the film and substrate. In fact, it also depends on the preparation conditions, film thickness, misfit dislocations at the film-substrate interface, and external conditions. The lattice constants of SrZrO3 and LaInO3 are similar to that of BaSnO3, which seems suitable for epitaxial growth to avoid possible misfit dislocations at the film-substrate interface.
4 Conclusions
In summary, we have studied the structure, electronic properties, electron effective mass and mobility of perovskite BaSnO3 over a wide range of hydrostatic and biaxial strain using first-principles density functional theory calculations. Compared to the biaxial strain, the properties of perovskite BaSnO3 are more sensitive to hydrostatic strain. The structure of BaSnO3 remains cubic for the case of hydrostatic strain, while it changes to tetragonal under biaxial strain. With the change in biaxial and hydrostatic strain from −3% to 3%, the band gaps linearly drop from 3.70 eV to 2.51 eV, and 4.46 eV to 1.89 eV, respectively. The Sn 5s orbitals of the conduction band minimum play a major role in this strain sensitivity of the band gap. Due to the change of electron effective mass of BaSnO3 under strain, BaSnO3 under tensile strain exhibits higher normalized electron mobility than strain-free BaSnO3, with a value of 1.16 under biaxial strain and 1.39 under hydrostatic strain. On the other hand the compressive strain reduces the normalized electron mobility of BaSnO3 to 0.86 and 0.74 under biaxial and hydrostatic strain, respectively. Hence, the results are a guidance to experimental study, and are also useful to design electronic devices using strained perovskite BaSnO3.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Natural Science Foundation of China (Grant No: 51802268), the Key Laboratory of Fluid and Power Machinery and Young Scholars Support Program of Xihua University, Sichuan Science and Technology Program (Grant No: 2019JDTD0024), and the Yibin Science and Technology Program (Grant No: 2018YG05).References
- A. Prakash, P. Xu, A. Faghaninia, S. Shukla, J. W. Ager III, C. S. Lo and B. Jalan, Nat. Commun., 2017, 8, 15167 CrossRef CAS PubMed
.
- Q. Liu, J. Liu, L. Bing, L. Hong, G. Zhu, D. Kai, Z. Liu, Z. Peng and J. Dai, Appl. Phys. Lett., 2012, 101, 241901 CrossRef
.
- H. J. Kim, U. Kim, H. M. Kim, H. K. Tai, H. S. Mun, B. G. Jeon, K. T. Hong, W. J. Lee, C. Ju, K. H. Kim and K. Char, Appl. Phys. Express, 2012, 5, 061102 CrossRef
.
- S. Raghavan, T. Schumann, H. Kim, J. Y. Zhang, T. A. Cain and S. Stemmer, APL Mater., 2016, 4, 016106 CrossRef
.
- A. Ohtomo and H. Y. Hwang, Nature, 2004, 427, 423–426 CrossRef CAS PubMed
.
- H. F. Wang, Q. Z. Liu, F. Chen, G. Y. Gao, W. Wu and X. H. Chen, J. Appl. Phys., 2007, 101, 106105 CrossRef
.
- Q. Liu, J. Feng, G. Gao, L. Bing, Y. Zhang and Q. Liu, J. Alloys Compd., 2016, 684, 125–131 CrossRef CAS
.
- Q. Liu, J. Dai, Z. Liu, X. Zhang, G. Zhu and G. Ding, J. Phys. D: Appl. Phys., 2010, 43, 455401 CrossRef
.
- C. Park, U. Kim, J. J. Chan, S. P. Ji, Y. M. Kim and K. Char, Appl. Phys. Lett., 2014, 105, 203503 CrossRef
.
- J. Shiogai, K. Nishihara, K. Sato and A. Tsukazaki, AIP Adv., 2016, 6, 065305 CrossRef
.
- W. J. Lee, H. J. Kim, E. Sohn, H. K. Tai, J. Y. Park, W. Park, H. Jeong, T. Lee, H. K. Jin, K. Y. Choi and K. H. Kim, Appl. Phys. Lett., 2016, 108, 082105 CrossRef
.
- Z. Lebens-Higgins, D. O. Scanlon, H. Paik, S. Sallis, Y. Nie, M. Uchida, N. F. Quackenbush, M. J. Wahila, G. E. Sterbinsky and D. A. Arena, Phys. Rev. Lett., 2016, 116, 027602 CrossRef CAS PubMed
.
- Y. Zhang, Y. H. Wen, J. C. Zheng and Z. Z. Zhu, Appl. Phys. Lett., 2009, 94, 263116 CrossRef
.
- L. Hong, I. E. Castelli, K. S. Thygesen and K. W. Jacobsen, Phys. Rev. B, 2015, 91, 045204 CrossRef
.
- C. W. Bark, D. A. Felker, Y. Wang, Y. Zhang, H. W. Jang, C. M. Folkman, J. W. Park, S. H. Baek, H. Zhou and D. D. Fong, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 4720–4724 CrossRef CAS
.
- Z. Huang, Z. Q. Liu, M. Yang, S. W. Zeng, A. Annadi, W. M. Lü, X. L. Tan, P. F. Chen, L. Sun, X. Renshaw Wang, Y. L. Zhao, C. J. Li, J. Zhou, K. Han, W. B. Wu, Y. P. Feng, J. M. D. Coey, T. Venkatesan and Ariando, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 125156 CrossRef
.
- K. J. Choi, M. Biegalski, Y. L. Li, A. Sharan, J. Schubert, R. Uecker, P. Reiche, Y. B. Chen, X. Q. Pan and V. Gopalan, Science, 2004, 306, 1005–1009 CrossRef CAS PubMed
.
- E. Claude and N. A. Spaldin, Phys. Rev. Lett., 2005, 95, 257601 CrossRef PubMed
.
- Y. Umeno, T. Shimada, T. Kitamura and C. Elsasser, Phys. Rev. B, 2006, 74, 174111 CrossRef
.
- H. W. Jang, S. H. Baek, D. Ortiz, C. M. Folkman, R. R. Das, Y. H. Chu, P. Shafer, J. X. Zhang, S. Choudhury and V. Vaithyanathan, Phys. Rev. Lett., 2008, 101, 107602 CrossRef CAS PubMed
.
- G. Kresse and J. Furthmuller, Phys. Rev. B, 1996, 54, 11169–11186 CrossRef CAS
.
- G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758–1775 CrossRef CAS
.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS
.
- G. Hautier, A. Miglio, D. Waroquiers, G. M. Rignanese and X. Gonze, Chem. Mater., 2014, 26, 5447–5458 CrossRef CAS
.
- P. V. Wadekar, J. Alaria, M. O. Sullivan, N. L. O. Flack, T. D. Manning, L. J. Phillips, K. Durose, O. Lozano, S. Lucas, J. B. Claridge and M. J. Rosseinsky, Appl. Phys. Lett., 2014, 105, 052104 CrossRef
.
- E. Moreira, J. M. Henriques, D. L. Azevedo, E. W. S. Caetano, V. N. Freire and E. L. Albuquerque, J. Solid State Chem., 2012, 187, 186–194 CrossRef CAS
.
- D. O. Scanlon, Phys. Rev. B, 2013, 87, 161201 CrossRef
.
- H. Mizoguchi, P. Chen, P. Boolchand, V. Ksenofontov, P. M. Woodward, C. Felser and P. W. Barnes, Chem. Mater., 2013, 25, 3858–3866 CrossRef CAS
.
- S. Sallis, D. O. Scanlon, S. C. Chae, N. F. Quackenbush, D. A. Fischer, J. C. Woicik, J. H. Guo, S. W. Cheong and L. F. J. Piper, Appl. Phys. Lett., 2013, 103, 042105 CrossRef
.
- S. Chao, T. Huang, J. Zhang, M. Han, Y. Li, Z. Hu and J. Chu, J. Phys. Chem. C, 2014, 118, 6994–7001 CrossRef
.
- H. R. Liu, J. H. Yang, H. J. Xiang, X. G. Gong and S.-H. Wei, Appl. Phys. Lett., 2013, 102, 112109 CrossRef
.
- S. Dabaghmanesh, R. Saniz, M. N. Amini, D. Lamoen and B. Partoens, J. Phys.: Condens. Matter, 2013, 25, 415503 CrossRef CAS PubMed
.
- H. Peelaers and C. G. Van de Walle, Phys. Rev. B, 2012, 86, 241401 CrossRef
.
- Q. Yan, P. Rinke, M. Scheffler and C. G. V. D. Walle, Appl. Phys. Lett., 2009, 95, 121111 CrossRef
.
- C. E. Dreyer, A. Janotti and C. G. V. D. Walle, Appl. Phys. Lett., 2013, 102, 142105 CrossRef
.
- F. M. Steel, B. R. Tuttle, X. Shen and S. T. Pantelides, J. Appl. Phys., 2013, 114, 013702 CrossRef
.
- Y. U. Peter and M. Cardona, Fundamentals of Semiconductors: Physics and Materials Properties, Springer Science & Business Media, 2010 Search PubMed
.
| This journal is © The Royal Society of Chemistry 2019 |