DOI:
10.1039/C9RA02202C
(Paper)
RSC Adv., 2019,
9, 20989-20999
Nonlocal effects on the structural transition of gold clusters from planar to three-dimensional geometries†
Received
21st March 2019
, Accepted 22nd June 2019
First published on 5th July 2019
Abstract
Conventional density functional theory calculations heavily bias planar structures in gold clusters, failing to predict the structural transition from planar to three-dimensional geometries in experimentally detected gold species. Inspired by recent progress in calculating the defect energies of coinage metals with nonlocal effect-enhanced hybrid functionals, we have studied nonlocal effects in gold clusters. Although the hybrid functional was accurate for bulk gold, it heavily biased the planar structure for gold clusters. By including dispersive interactions into semilocal density functional calculations, we obtained an accurate vacancy formation energy of 0.72 eV for bulk gold along with the correct structural transition for gold clusters. The transition was found to occur at Au12− for gold anions and at Au8+ for gold cations, agreeing very well with the experimental results. For neutral gold clusters, we found the transition to occur at Au10, indicating the need for experimental verification. The results show the importance of nonlocal effects in the study of gold clusters, calling for further comprehensive theoretical and experimental studies to evaluate nonlocal effects in Au and other precious metals.
1. Introduction
Gold is inert in bulk but exhibits surprising activity as a heterogeneous catalyst when present as a nanostructured material. Since Haruta's discovery of the unexpected catalytic properties of gold particles,1 gold clusters have attracted unprecedented attention in both fundamental and applied research.2–29 Gold clusters prefer two-dimensional (2D) planar structures rather than three-dimensional (3D) geometries, even for large cluster sizes. This is attributed to the strong relativistic effects, which reduce the s–d energy separation resulting in the hybridization of the half-filled 6s orbital with the fully occupied 5dz2 orbital. Theoretical studies have shown that the low dimensionality of gold species plays an important role in their catalytic performance.17,18 The superior reactivities of small gold clusters containing one or two atomic layers have been experimentally confirmed using high-resolution electron microscopy.9 Therefore, studies on the size-dependent properties and the 2D–3D structural transitions of gold clusters show promise to provide insights into the mechanism of the unexpected catalytic properties.
Since experimental techniques cannot directly probe the atomic arrangement of a cluster, computational studies are required for assigning the cluster structure. Theory heavily biases the 2D geometries of gold clusters, making the assignment of the 2D–3D crossover cluster difficult solely based on density functional theory (DFT) calculations. For example, for Au16−, Au12−, and Au8+, DFT calculations using the generalized gradient approximation with Perdew, Burke, and Ernzerhof (GGA-PBE) functional30 favor the 2D geometries, whereas experimental studies indicate that the 3D configurations are preferred. Currently, one usually calculates the properties of several low-lying isomers and compares them with experimental observations to assign the ground-state geometry. However, the standard semilocal functionals heavily bias the 2D configurations for gold clusters, a problem that still puzzles theoretical researchers. The PBEsol revised to enhance surface energy31 along with the meta-GGA functional of the Tao–Perdew–Staroverov–Scuseria (TPSS) formalism32 and its revised functional revTPSS33 can improve the overall accuracy; however, the experimental results of gold clusters are still not well accounted for. As evidenced by the joint experiment/theory studies on clusters of gold anions conducted by Lechtken et al.34 and Johansson et al.,35 the TPSS and PBEsol functionals still tend to overestimate the stabilities of the 2D geometries. In addition, PBEsol, TPSS, and revTPSS cannot consistently calculate the vacancy formation energies of coinage metals. Recently, accurate vacancy formation energies of 1.06, 0.94, and 0.72 eV for Cu, Ag, and Au metals, respectively, were reported;36,37 however, the respective energies were calculated to be 1.27, 1.01, and 0.57 eV with PBEsol38 and 1.50, 1.25, and 0.92 eV with revTPSS.39 As discussed later in this paper, we calculated them to be 1.39, 1.12, and 0.76 eV, respectively, using the TPSS functional.
Recently, Chen and co-workers37 obtained accurate vacancy formation energies for bulk Cu, Ag, and Au by including nonlocal exchange interactions with the Heyd, Scuseria, and Ernzerhof (HSE) hybrid functional.40 The effects of the nonlocal exchange interaction were also found in Zhang et al.'s41 HSE calculations for Cu–Au intermetallic alloys. By including the nonlocal correlation energies in DFT calculations, Aguado et al.42 and Fernández et al.43 obtained improved results for Na, Au, and Hg clusters. However, for the typical Au12− cluster, the calculations carried out by Aguado et al. still biased the 2D structure in comparison to the experimental conclusions. By using the HSE functional with α = 0.4, following Chen's choice for bulk gold,37 our calculations show that the method of enhancing nonlocal exchange effects cannot properly treat gold clusters. With the goal of identifying a computational method that is appropriate for both bulk gold and gold clusters, we carried out DFT calculations while compensating the nonlocal effects by considering the dispersive interactions through the Tkatchenko–Scheffler dispersive (TSD) approach,44 which is based on the mean-field ground-state electronic density from DFT calculations and has only one empirical parameter for tuning the onset of the dispersive correction in the DFT energy. Using the vacancy formation energy of bulk gold as a reference, we first tuned this parameter and then studied the anionic, neutral, and cationic gold clusters. Interestingly, the obtained results agree very well with the experimental data, indicating the validity of the TSD-DFT method for studying both bulk and nanostructured gold materials.
2. Computational details
Our calculations were carried out using spin-polarized DFT implemented in the Vienna ab initio simulation package (VASP).45 The projector augmented-wave (PAW) method with the wavefunction expressed using a planewave basis set was employed. Relativistic effects were included using the scalar relativistic approach. A cutoff energy of 500 eV was used to account for the properties of bulk gold and gold clusters. The convergence tolerance of the electronic properties and atomic relaxation were set to 0.001 meV and 5 meV Å−1, respectively. To eliminate the interaction between neighboring vacancies in bulk gold, a fcc-type supercell containing 64 metal atoms was used. The lattices were first optimized using different exchange–correlation energy functionals with a 7 × 7 × 7 Monkhorst–Pack k-point mesh.46 For comparison with Chen's HSE studies,37 Cu, Ag, and Au metals were first calculated as reference to examine the validity of the TSD-PBE method. The calculation results obtained using PBE, PBEsol, TPSS, revTPSS, and TSD-PBE are provided in Table 1. For the optimized fcc-type supercell, we calculated the total energy E64 using a 13 × 13 × 13 Monkhorst–Pack k-point mesh. Subsequently, one of the atoms was removed, and the other atoms were fully relaxed. The obtained total energy E63 for the vacancy-defected bulk was used to calculate the vacancy formation energy Ev using the following formula:where μ is the chemical potential corresponding to the mean energy of a metal atom in the corresponding metal crystal. We also calculated the Au2−, Au2, and Au2+ dimers as references to validate the TSD-PBE method. In our calculations, a cubic supercell with an edge length of 20 Å was used to study the gold dimers and other gold clusters. This supercell is sufficiently large to ignore the interactions with their periodic images. The bond lengths and binding energies of the gold dimers are presented in Table 2. Based on the data shown in Tables 1 and 2, the TSD-PBE method can be used to treat both bulk gold and gold clusters.
Table 1 Lattice constants a (Å) and vacancy formation energies Ev (eV) of Cu, Ag, and Au fcc crystals calculated with the PBE, PBEsol, TPSS, revTPSS, and TSD-PBE methods. The experimental and HSE data are cited from ref. 36 and 37, respectively. EP stands for the empirical parameter α for the hybridization ratio in HSE or sR as the scaling factor in the Fermi-type damping function of the TSD-vdW method
| Method |
Cu |
Ag |
Au |
| a |
Ev |
EP |
a |
Ev |
EP |
a |
Ev |
EP |
| Exp. |
3.615 |
1.06 |
— |
4.069 |
0.94 |
|
4.077 |
— |
|
| PBE |
3.635 |
1.059 |
— |
4.148 |
0.790 |
|
4.157 |
0.390 |
|
| PBEsol |
3.569 |
1.230 |
— |
4.052 |
0.999 |
|
4.082 |
0.568 |
|
| TPSS |
3.587 |
1.391 |
— |
4.089 |
1.124 |
|
4.113 |
0.756 |
|
| revTPSS |
3.561 |
1.487 |
— |
4.052 |
1.228 |
|
4.077 |
0.870 |
|
| HSE |
3.623 |
1.06 |
0.10 |
4.142 |
0.94 |
0.25 |
4.124 |
0.72 |
0.40 |
| TSD-PBE |
3.634 |
1.064 |
3.989 |
4.129 |
0.944 |
1.287 |
4.143 |
0.724 |
0.796 |
Table 2 Bond length (Å) and binding energy (eV) data from the studied gold dimer. The empirical parameter in HSE was chosen as α = 0.4 following Chen.37 For the TSD-PBE calculation, the Fermi-type damping parameter sR = 0.796 obtained in the calculation of the vacancy formation energy of bulk gold was adopted. The experimental data are taken from ref. 47 and 48
| Method |
Au2− |
Au2 |
Au2+ |
| R |
E |
R |
E |
R |
E |
| PBE |
2.624 |
1.903 |
2.509 |
2.337 |
2.601 |
2.544 |
| PBEsol |
2.574 |
2.140 |
2.473 |
2.596 |
2.560 |
2.758 |
| HSE |
2.624 |
1.682 |
2.507 |
1.935 |
2.623 |
2.093 |
| TPSS |
2.609 |
1.896 |
2.498 |
2.315 |
2.594 |
2.479 |
| revTPSS |
2.591 |
1.994 |
2.488 |
2.429 |
2.579 |
2.562 |
| TSD-PBE |
2.626 |
1.907 |
2.512 |
2.345 |
2.612 |
2.566 |
| Expt. |
2.582 |
1.92 |
2.472 |
2.29 |
|
|
In addition to considering the structures of gold clusters published in the literature, we searched the geometric structures and selected low-energy structural configurations via global minimum structural searching with an efficient evolutionary algorithm implemented in the Universal Structure Predictor: Evolutionary Xtallography (USPEX)49–52 interfaced with VASP code. This method can efficiently predict geometric structures for crystalline material, nanostructure, polymer, surface, and interface systems containing as many as ∼200 atoms per cell. A certain number of structures were randomly produced to ensure the unbiased sampling of the energy landscape, and the generated structures were then subjected to first-principles structural optimization. The calculated total energies were used to select the low-lying isomers. In the evolutionary process of the structural search, the population of 30% of the candidate structures with low total energies were evolved over successive generations of random variation and selection.
3. Results and discussion
3.1 Calculations of Aun− clusters with semilocal functionals
We began our calculations using Aun− (n ≤ 16) clusters by combining the global minimum structural search with first-principles calculations using different semilocal functionals. The semilocal density functional PBE,30 the PBEsol functional revised for densely packed solids and their surfaces,31 the advanced semilocal functional meta-GGA TPSS,32 and the revTPSS functional constructed by restoring the second-order gradient expansion for exchange over a wide range of densities33 were used. First, we studied the 2D and 3D structures for each cluster. Among the studied 2D geometries, the one with the lowest energy was selected, as schematically illustrated in the ESI.† Similarly, the corresponding lowest-energy 3D geometry among all the calculated non-planar structures was selected for each cluster and is shown in the ESI.† Fig. S1–S4† show the structures obtained using the PBE, PBEsol, TPSS, and revTPSS functionals, respectively. We then calculated their relative energies (Er) aswhere E2D and E3D are the total energies of the corresponding 2D and 3D structures, respectively. The conventional PBE functional cannot accurately describe small gold clusters. As shown in Fig. 1, the PBE results did not show the 2D–3D structural transition with the 2D structures as the ground state for each cluster, conflicting with the experimental results. For example, the experimental studies indicated a hollow cage structure (see ESI Fig. S5†) as the ground state for the Au16− cluster.19 However, the PBE functional biased the planar structure as the ground state; its energy was ∼0.2 eV lower than that of the first 3D low-energy isomer. TPSS, the advanced semilocal functional, predicted 3D structures as the ground states for the Au13−, Au15−, and Au16− clusters. However, the prediction of a 2D ground state structure for the Au14− cluster does not agree with the experimental results.20 The PBEsol and revTPSS functionals, which accurately describe the surface energy and are expected to perform better when studying gold clusters, suggested that the 2D–3D structural transition occurred at n = 13, disagreeing with the experimental results. Although a 3D structure was experimentally determined as the ground state for Au12−,20 the total energies of the 2D structures were calculated to be 0.27 and 0.15 eV lower than those of the 3D structures using the PBEsol and revTPSS functionals, respectively.
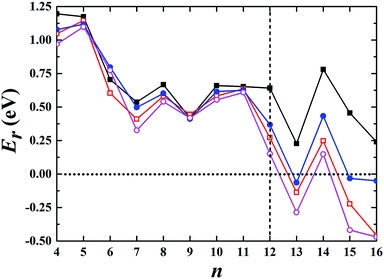 |
| | Fig. 1 Relative energy of the selected 3D structure with respect to the corresponding 2D structure. The black solid squares, red empty squares, blue solid circles, and purple empty circles correspond to the data calculated using the PBE, PBEsol, TPSS, and revTPSS functionals, respectively. A positive value indicates a planar geometry as the ground-state structure. | |
We also studied the first low-energy 3D structures calculated with the PBE functional for Au12− to facilitate discussion (see ESI Fig. S5†). The PBE calculations predict the 2D structure as the ground state with an energy 0.64 eV lower than that of the 3D geometry. Previously, Gong, Wang, and coworkers demonstrated that the temperature may affect the theoretical understanding of the experimental results.21 To evaluate the temperature effects by considering the contribution of entropy, we also calculated the free energy of the Au12− cluster via PBE calculations. These calculations were carried out using the calculated total binding energy (E0) at the PBE level at the zero temperature and the harmonic vibrational entropy as follows:21,53–55
| |
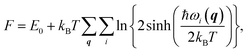 | (3) |
where
ℏ,
kB,
T, and
ωi(
q) are Plank's constant, Boltzmann's constant, temperature, and vibration frequency for the
ith phonon mode at wave vector
q in the Brillouin zone. The calculated free energies (see ESI Fig. S6
†) show that the 2D structure remains lower in energy, ruling out the possibility that temperature effects can bridge the difference between the theoretical and experimental results for Au
12−. Instead, the discrepancy is likely attributed to the failure to accurately describe the nonlocal energy of the semilocal density functional.
3.2 Nonlocal effects on Aun− clusters
The vacancy formation enthalpy is a fundamental parameter of metal crystals. Typical semilocal approximations such as PBE fail to yield accurate enthalpies of Ag and Au, although they give accurate values for Cu. Chen and co-workers37 carried out a comprehensive study by mixing 0.1, 0.25, and 0.4 nonlocal exchange interactions to extend the conventional DFT method for the study of the vacancy formation enthalpies of Cu, Ag, and Au. The obtained values agree very well with the experimental data, indicting the importance of nonlocality when studying Ag and Au materials. The nonlocal contributions were also found to be critical for studying Cu–Au intermetallic alloys, especially those with Au-rich compositions.56 Inspired by these findings, we hypothesized that including nonlocal effects in first-principles calculations could improve the accuracy of the DFT method for dealing with gold clusters.
Taking the best 2D and 3D structures for Au12−, Au16−, and Au20− (see ESI Fig. S5†) as prototypes, we calculated the corresponding relative energies Er using the HSE functional. Along with an increase in the hybridization ratio α for the nonlocal exchange interactions, Er continuously decreased (see ESI Fig. S7†). The 3D structure was always lower in energy for the Au20− cluster, while the 2D one remained the ground-state energy configuration for the Au12− cluster. The 3D structure became the lowest-energy configuration when α = 0.4 for Au16−. Based on the experimental confirmation of the 3D ground-state structure of the Au12− cluster, the HSE functional could not properly deal with the gold clusters, although it yielded an accurate vacancy formation enthalpy for bulk gold.
Compared to the HSE functional that incorporates nonlocal exchange energy, the van der Waals density functional (vdW-DF), which accounts for the dispersion interaction, can enhance the description of nonlocal effects in a different way. Previous studies on Na, Au, and Hg clusters using vdW-DFT carried out by Aguado et al.42 and Fernández et al.43 suggest that vdW-DFT improves the accuracy of DFT calculations of metal clusters. In these studies, the method proposed by Dion et al.57 was adopted to account for nonlocal energy by dividing the exchange–correlation energy into three parts:
| |
|
Exc[n(r)] = EGGAx[n(r)] + ELDAc[n(r)] + Enlc[n(r)],
| (4) |
where
EGGAx[
n(
r)] is the exchange energy of the semilocal GGA exchange functional,
ELDAc[
n(
r)] accounts for the correlation energy of the local density approximation (LDA), and
Enlc[
n(
r)] is the dispersion interaction energy as the nonlocal correlation energy. Although the vdW-DFT in Dion's functionalism improved the DFT results for gold clusters, it still failed to predict the 2D–3D structural transition of Au
12−.
43
Currently, vdW interactions are most commonly accounted for by adding a pairwise interatomic C6R−6 term to the DFT energy:
| |
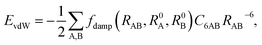 | (5) |
where
RAB is the distance between atoms A and B,
C6AB is the corresponding
C6 coefficient, and
R0A and
R0B are the vdW radii of atoms A and B, respectively. The
RAB−6 singularity at small distances is eliminated by the short-range damping factor
fdamp(
RAB,
R0A,
R0B). Most schemes used to include the vdW interaction in DFT calculation have a serious shortcoming arising from their empirical nature. In these approaches,
C6R−6 is determined by fitting to experimental
C6 coefficients and/or post-Hartree–Fock binding energy data rather than being obtained directly from the electronic structure. Recently, Tkatchenko and Scheffler
44 proposed an accurate method to determine the
C6 coefficients and vdW radii from the mean-field ground-state electronic density of DFT calculations. In their scheme, the Fermi-type damping function was adopted:
| |
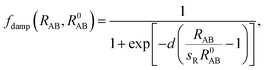 | (6) |
where
R0AB is the sum of the vdW radii of free atoms A and B, which are obtained from the corresponding electron density contours, and
d and
sR are free parameters. The parameter
d adjusts the damping function steepness and shows almost negligible effects for 12 <
d < 45. The choice of
d = 20 was carefully tested and was found to accurately describe the binding energy curves of rare gases and vdW-bonded organic molecule dimers. The parameter
sR remains as the single tunable empirical parameter to control the onset of the vdW correction to the DFT energy. The lager the value of
sR, the weaker the contribution of the vdW dispersion interaction to the DFT result. Previously, Tao
et al.58 and Klimes
et al.59 showed that vdW forces are indispensable in correctly describing metal solids. Thus, we used bulk metal as a reference to tune the onset contribution of the vdW interactions to PBE calculations. By tuning
sR, we first calculated the vacancy formation energies of Cu, Ag, and Au crystals using the PBE functional with the Tkatchenko–Scheffler dispersion vdW correction. The experimental and HSE results from Chen
et al.37 along with the values obtained from conventional semilocal exchange–correlation functionals such as PBE, PBEsol, TPSS, and revTPSS are also presented for comparison. The calculated data are tabulated in
Table 1. Compared to the experimental and HSE results, neither the conventional GGA functionals (PBE and PBEsol) nor the
meta-GGA functionals (TPSS and revTPSS) give consistently accurate results for Cu, Ag, and Au. The PBE gives accurate values of
a and
Ev for Cu but not for Ag and Au. The surface energy-enhanced PBEsol improves the description for Ag and Au but worsens it for Cu. TPSS and revTPSS perform well for the lattice constants of Cu, Ag, and Au; however, it overestimated the vacancy formation energies
Ev. As shown in
Table 1, including the dispersive interaction in the PBE calculation trough the TSD approach provided accurate vacancy formation energies for Cu, Ag, and Au solids. The calculated data show the same trend as Chen's HSE results obtained by turning the hybridization ratio
α of the HSE functionals to be 0.10, 0.25, and 0.40 for Cu, Ag, and Au, respectively.
37 The effects of nonlocal contributions on the calculation accuracy decreased in the following order: Au > Ag > Cu.
Interestingly, the TSD-vdW-corrected PBE functional with the scaling parameter sR = 0.796 accurately calculated the vacancy formation energy for Au solid and could be applied to the study of Au clusters, suggesting the crucial role of nonlocal contributions in gold clusters. Unlike our results obtained using PBE, PBEsol, TPSS, revTPSS, and HSE (α = 0.4), TSD-PBE confirmed the 2D–3D structural transition in the Au12− cluster, in agreement with experimental results. Starting from n = 12, the Aun− clusters prefer the 3D structures. We carefully studied the 2D geometric structures for Aun− (4 ≤ n ≤ 16) clusters using the TSD-PBE method, and the lowest-energy structure for each anionic cluster is shown in Fig. 2. Similarly, the best 3D structure for each cluster is also provided in Fig. 2. In addition, the first five low-lying isomers for the clusters with n ≥ 12 are provided in ESI Fig. S8.† The vertical detachment energy (VDE) accounting for the minimum energy cost to detach an electron from the cluster anion is often used to assign geometric structure of an anionic cluster through comparison with the theoretical and experimental values. Based on the optimized ground state structures, we evaluated the VDEs of the structures shown in Fig. 2 for Aun− (4 ≤ n ≤ 16) anions. VDE was estimated by Evs(Aun) − EGS(Aun−), where EGS(Aun−) and Evs(Aun) are the energies of the optimized Aun− anion and the anion geometry at the neutral state, respectively. The VDEs calculated with the TSD-PBE method are presented in Table 3. Within the calculation uncertainty,19,22 the VDEs of the 2D structures agree with the experimental data19,20,25,60 for smaller clusters, whereas the data for the 3D structures agree with the experimental values for lager clusters, suggesting that the 2D–3D structural transition occurs at n = 12. Wang and coworkers experimentally confirmed the coexistence of the 2D and 3D structures of the Au12− cluster.20 The 3D motif accounts for the larger contribution, suggesting that it has a slightly lower total energy than the 2D motif. Interestingly, the TSD-PBE calculations predict the 3D configuration (see Fig. 2) to be 30 meV lower in energy than the 2D structure. Johansson et al.35 previously estimated the intensity ratio to be 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 for 3D vs. 2D structures in anionic gold clusters generated at 100 K, which can be applied to the Boltzmann distribution function to estimate the relative energy of 2D geometry with respect to the 3D one. This ratio corresponds to a zero-Kelvin energy difference of ∼24 meV, in good agreement with the TSD-PBE value of 30 meV, indicating the validity of TSD-PBE for treating gold clusters. In addition to the Au12− cluster, another significant gold cluster is the Au16− anion, which was previously proposed as the first discovered fullerene-like metal cage cluster based on experimental investigations.19 In our previous studies carried out at the PBE level, the 2D structure of the Au16− anion, which had a similar structural configuration to that shown in Fig. 2, was found to be more than 0.2 eV lower in total energy than the cage geometry,22 contrary to the experimental observation. The nonlocal contributions-enhanced TSD-PBE method remedies this deficiency; the cage is now found to be 0.74 eV lower in energy than the 2D structure, ruling out the planar geometry.
15 for 3D vs. 2D structures in anionic gold clusters generated at 100 K, which can be applied to the Boltzmann distribution function to estimate the relative energy of 2D geometry with respect to the 3D one. This ratio corresponds to a zero-Kelvin energy difference of ∼24 meV, in good agreement with the TSD-PBE value of 30 meV, indicating the validity of TSD-PBE for treating gold clusters. In addition to the Au12− cluster, another significant gold cluster is the Au16− anion, which was previously proposed as the first discovered fullerene-like metal cage cluster based on experimental investigations.19 In our previous studies carried out at the PBE level, the 2D structure of the Au16− anion, which had a similar structural configuration to that shown in Fig. 2, was found to be more than 0.2 eV lower in total energy than the cage geometry,22 contrary to the experimental observation. The nonlocal contributions-enhanced TSD-PBE method remedies this deficiency; the cage is now found to be 0.74 eV lower in energy than the 2D structure, ruling out the planar geometry.
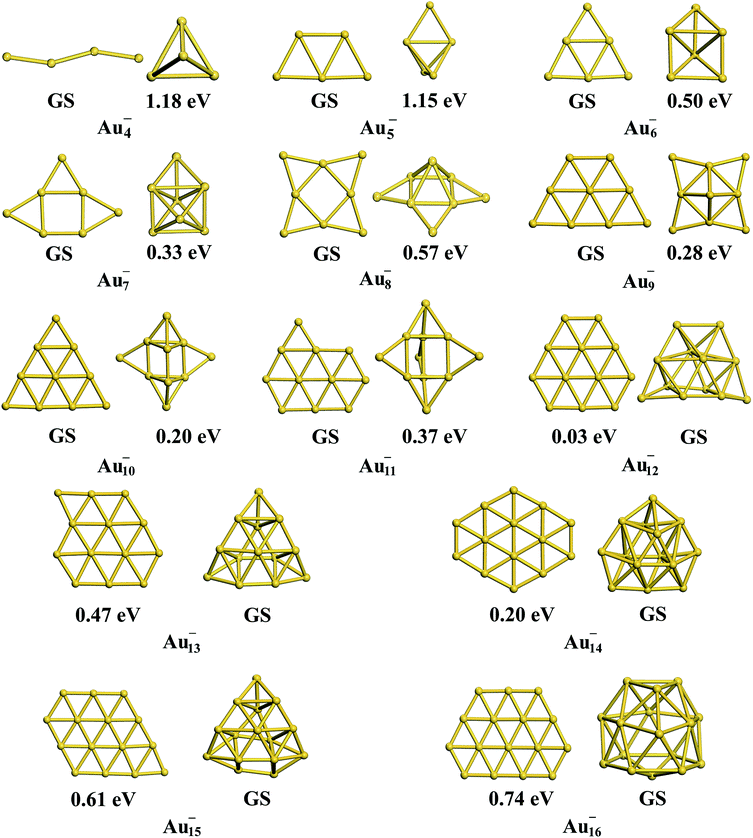 |
| | Fig. 2 The lowest-energy 2D and 3D structures among the corresponding planar and non-planar structures obtained using the TSD-PBE method for Aun− anionic clusters. GS stands for the ground-state structure. The relative energy is provided below the corresponding isomer. A dashed line is added at the experimentally determined 2D–3D structural transition size n = 12. | |
Table 3 VDEs in units of eV calculated using the TSD-PBE method for the structures of gold anions shown in Fig. 2
| Anion |
2D |
3D |
Expt. |
Anion |
2D |
3D |
Expt. |
| Au4− |
2.73 |
2.65 |
2.75 |
Au11− |
3.66 |
3.10 |
3.80 |
| Au5− |
3.08 |
2.81 |
3.09 |
Au12− |
3.17 |
3.09 |
3.06 |
| Au6− |
2.20 |
2.96 |
2.13 |
Au13− |
3.74 |
3.88 |
3.94 |
| Au7− |
3.44 |
3.60 |
3.46 |
Au14− |
3.77 |
3.03 |
3.00 |
| Au8− |
2.88 |
2.98 |
2.79 |
Au15− |
3.79 |
3.64 |
3.65 |
| Au9− |
3.70 |
3.55 |
3.83 |
Au16− |
3.72 |
3.89 |
4.03 |
| Au10− |
3.87 |
2.87 |
3.91 |
— |
— |
— |
— |
3.3 Cationic gold clusters
Using global minimum structure searching, we carefully optimized the geometric structures of cationic gold clusters. The ground-state structures obtained with TSD-PBE are schematically presented in Fig. 3. The corresponding optimal 2D and 3D structures calculated with the PBE, PBEsol, TPSS, revTPSS, and TSD-PBE functionals are provided in ESI Fig. S9–S13,† respectively. The energies used to illustrate whether the 3D structures are preferable, as defined by formula (2), are presented in Fig. 4. For Aun+, the 2D–3D structural transition is predicted with TSD-PBE to happen at Au8+, in agreement with the experimental results. Through experimental evaluations of ion mobility, Gilb et al.28 ruled out the planar geometry of the Au8+ cluster. As shown in Fig. 4, the TSD-PBE calculations favor the 3D structure by 61 meV. Referring to the Boltzmann distribution, this energy difference accounts for a 3D![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2D intensity ratio of ∼1560
2D intensity ratio of ∼1560![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 in cluster resource, significantly reducing the possibility of detecting the 2D structure through ion mobility measurement. The first five low-lying isomers calculated using the TSD-PBE method for Aun+ (n ≥ 8) cations are also shown in ESI Fig. S14.† In comparison, the PBE calculations seriously bias the 2D geometry. For Aun+ (n ≤ 16) clusters, the PBE functional only predicts the 3D structures as ground states for Aun+ with n = 9, 10, 11, and 15. For the Au8+ cluster, PBE indicates that the 2D structure is 0.16 eV lower in total energy than the 3D geometry. For the PBEsol calculations, the 3D structure of the Au8+ cluster is only 10 meV higher in energy than the 2D structure, which suggests their coexistence, contradicting the experimental results. Beginning at n = 8, the 3D geometries begin to dominate except at n = 12, for which the 3D structure is only 0.12 eV higher in energy than the 2D geometry. Beginning at n = 9, the TPSS functional starts to favor the 3D configurations for the studied Aun+ (n ≤ 16) clusters, with the exception of n = 12. The revTPSS performs better than the above functionals as it supports the 3D ground structures for Aun+ (9 ≤ n ≤ 16) clusters. However, it still biases the 2D geometry for Au8+, which is 43 meV lower in total energy than the 3D structure. In addition, the calculated energies of the 2D and 3D structures of Au12+ are almost identical, with the 2D structure being only 2 meV lower in total energy than the 3D structure. The revTPSS results support the 3D geometries as the dominant species in the corresponding clusters, contrary to the experimental findings. In comparison, only the TSD-PBE calculations support the 3D configurations as the ground-state structures for all the studied Aun+ (8 ≤ n ≤ 16) clusters, again suggesting the importance of nonlocal effects when describing gold clusters.
10 in cluster resource, significantly reducing the possibility of detecting the 2D structure through ion mobility measurement. The first five low-lying isomers calculated using the TSD-PBE method for Aun+ (n ≥ 8) cations are also shown in ESI Fig. S14.† In comparison, the PBE calculations seriously bias the 2D geometry. For Aun+ (n ≤ 16) clusters, the PBE functional only predicts the 3D structures as ground states for Aun+ with n = 9, 10, 11, and 15. For the Au8+ cluster, PBE indicates that the 2D structure is 0.16 eV lower in total energy than the 3D geometry. For the PBEsol calculations, the 3D structure of the Au8+ cluster is only 10 meV higher in energy than the 2D structure, which suggests their coexistence, contradicting the experimental results. Beginning at n = 8, the 3D geometries begin to dominate except at n = 12, for which the 3D structure is only 0.12 eV higher in energy than the 2D geometry. Beginning at n = 9, the TPSS functional starts to favor the 3D configurations for the studied Aun+ (n ≤ 16) clusters, with the exception of n = 12. The revTPSS performs better than the above functionals as it supports the 3D ground structures for Aun+ (9 ≤ n ≤ 16) clusters. However, it still biases the 2D geometry for Au8+, which is 43 meV lower in total energy than the 3D structure. In addition, the calculated energies of the 2D and 3D structures of Au12+ are almost identical, with the 2D structure being only 2 meV lower in total energy than the 3D structure. The revTPSS results support the 3D geometries as the dominant species in the corresponding clusters, contrary to the experimental findings. In comparison, only the TSD-PBE calculations support the 3D configurations as the ground-state structures for all the studied Aun+ (8 ≤ n ≤ 16) clusters, again suggesting the importance of nonlocal effects when describing gold clusters.
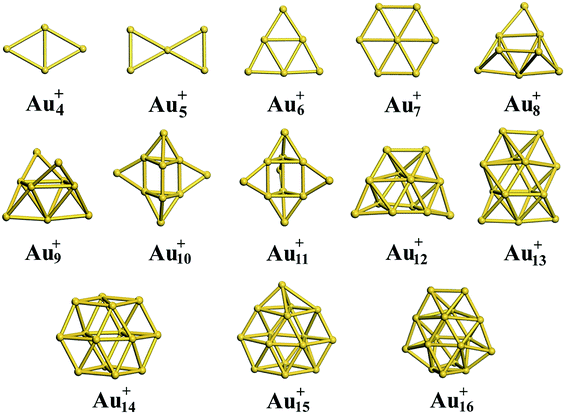 |
| | Fig. 3 Ground-state structures determined using the TSD-PBE method for Aun+ cationic clusters. | |
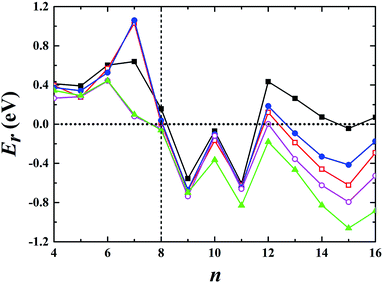 |
| | Fig. 4 Relative energy Er used to determine whether the preferred ground-state structures of Aun+ cationic clusters are 3D or 2D geometries. The black solid squares, red empty squares, blue solid circles, purple empty circles, and green solid triangles correspond to the data calculated using the PBE, PBEsol, TPSS, revTPSS, and TSD-PBE methods, respectively. A positive value indicates a planar geometry as the ground-state structure. | |
3.4 Neutral gold clusters
For the neutral Aun clusters, the ground-state structures obtained with the TSD-PBE method are schematically presented in Fig. 5. The 2D–3D structural transition happens at the Au10 cluster. In addition, the low-lying 2D isomers for each cluster were fully optimized. Accordingly, the optimized 2D and 3D geometries obtained with the PBE, PBEsol, TPSS, revTPSS, and TSD-PBE methods are provided in ESI Fig. S15–S19,† respectively. The relative energies, as defined by formula (2), are presented in Fig. 6. The first optimal ground-state 3D structure occurs at Au14 in the PBE and TPSS calculations and at Au13 in the PBEsol and revTPSS calculations. For the Au15 cluster, the PBE calculations still bias the 2D geometry as the ground-state structure. To the best of our knowledge, there are few experimental studies on the 2D–3D structural transition in neutral gold clusters. However, experimental evidence suggests that the transition occurs at n = 12 for Aun− clusters and n = 8 for Aun+ clusters. It seems that more valence electrons would make the 2D geometry more preferable. Thus, we expect the 2D–3D transition to occur at 8 < n < 12. If this is true, calculations using the PBE, PBEsol, TPSS, and revTPSS functionals cannot accurately predict the 2D–3D structural transition for neutral gold clusters. Interestingly, the TSD-PBE method predicts the transition to occur at n = 10 which seems reasonable (see Fig. 5 and 6). According to the electron counting rule,61 small-sized gold clusters can be treated with the Jellium shell closure rule, which describes metal clusters as two subsystems: valence electrons and the positively charged ionic core. The Jellium model of metal clusters applies the spherical potential, which may favor the 3D distribution of metal atoms (e.g., the spherically arranged Au atoms in the cage structure of Au16− anion). Here, we discuss the typical Jellium model cluster, the Nan cluster. The atomic radii of Na and Au are 1.80 and 1.35 Å, respectively. For a given 3D structural configuration, the structure would likely be more compact for Aun as compared to Nan, which may not be favorable for the Aun cluster due to its valence electron distribution in a more confined volume. The planar structure is confirmed by both experiment and theory to be preferable for small-sized gold clusters. As the cluster size increases, the number of low-coordination Au atoms on the corner or edge of the planar configuration also increase, thereby reducing the average coordination number in the planar structure. In contrast, the average coordination number in the 3D structure likely increase with increasing cluster size, contributing to the increase in total energy compared to the 2D geometry. This would in turn lead to the 2D–3D structural transition. Compared to the PBE results, the enhanced nonlocal effects help reduce the critical size for the appearance of the 3D ground-state structure from n = 14 to n = 10. Furthermore, the Au15 cluster, for which the 2D geometry was the lowest-energy configuration in the PBE calculations, is now found to have a 3D ground-state structure in the TSD-PBE calculations. Based on our careful studies, we can conclude that nonlocal effects are important when studying the 2D–3D structural transition for neutral gold clusters, although experimental validation is required. To facilitate the experimental studies, we have provided the first five low-lying isomers for Aun (n ≥ 10) obtained using the TSD-PBE method in ESI Fig. S20.†
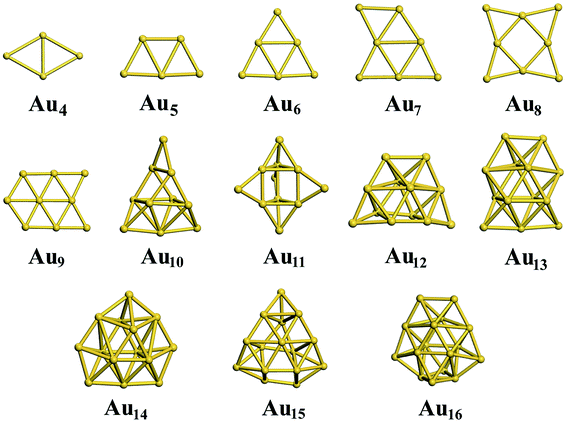 |
| | Fig. 5 The ground-state structures determined using the TSD-PBE method for Aun neutral clusters. | |
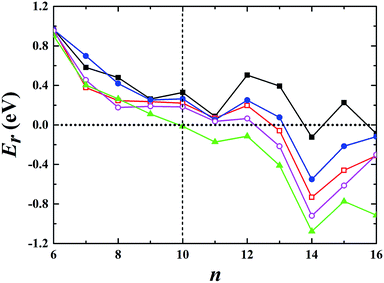 |
| | Fig. 6 Relative energy Er, as defined by formula (2), indicating whether the preferred ground-state structures of Aun neutral clusters are 3D or 2D geometries. The black solid squares, red empty squares, blue solid circles, purple empty circles, and green solid triangles correspond to the data calculated using the PBE, PBEsol, TPSS, revTPSS, and TSD-PBE methods, respectively. A positive value indicates a planar geometry as the ground-state structure. | |
3.5 Relative stabilities
To estimate the relative stabilities of the studied clusters, we calculated the second-order finite difference of binding energy Δ2 and dissociation energy Edissn as a function of the cluster size n, which are respectively defined as:| |
|
Δ2(n) = En+1 − 2En + En−1,
| (7) |
and| |
|
Edissn = En−1 + E1 − En.
| (8) |
The second-order finite difference of total energy is a general measure of relative stability. Dissociation energy is the energy required to evaporate an atom from the cluster, which is also useful to examine the stability. As shown in Fig. 7, the gold clusters exhibit odd–even oscillations in stability, which could be attributed to the electronic stability. Odd–even oscillations were previously observed experimentally.62 In addition, a discontinuous variation in cluster ion intensity at peculiar numbers was also observed in experimental mass spectra, in agreement with the magic numbers predicted by a spherically symmetric potential well model.63 In Fig. 7, no discontinuous variation is obviously seen in the limited size range of our studied clusters. According to the electron shell structure, when the gold cluster has an even number of valence electrons, it is relatively more stable compared to the cluster with an odd number of valence electrons due to the full filling of molecular orbitals. Fig. 8 presents the calculated density of states (DOS) of the studied anionic, neutral, and cationic gold clusters. The clusters with even numbers of valence electrons have obviously larger band gaps between the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), supporting their electronic stabilities. In addition, the oscillation agrees with the odd–even reactivity of gold clusters. In experiments, Salisbury et al.29 found that the gold cluster with an odd number of electrons could adsorb one molecule of O2 per cluster, whereas the cluster with an even number of electrons showed extremely low or zero reactivity. In the gold cluster with an odd number of electrons, the reactivity was enhanced by the unpaired electron according to the electron shell structure model.
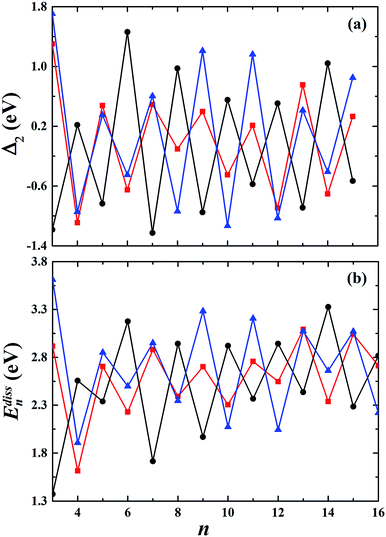 |
| | Fig. 7 The calculated second-order finite difference of binding energy Δ2 and the dissociation energy Edissn of the studied gold clusters. | |
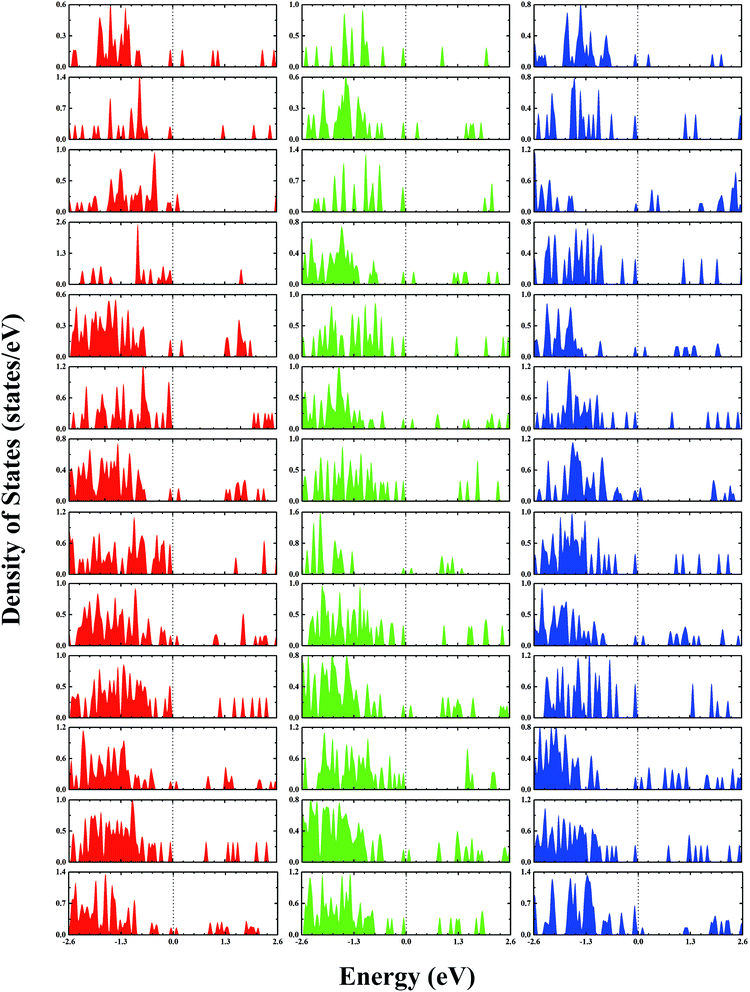 |
| | Fig. 8 The calculated densities of states of gold clusters with sizes of n = 4–16 from the upper row to the lower row, respectively. The red, green, and blue colors correspond to the densities of anion, neutral, and cation clusters, respectively. The Fermi levels are shifted to 0 eV. | |
4. Conclusions
Our careful studies suggest the importance of nonlocal effects when studying gold materials, in agreement with HSE studies of the vacancy formation energy of bulk gold. In the HSE studies, the nonlocal exchange energy is enhanced, while the PBE correlation energy remains unchanged during the transition; thus, HSE fails to correctly describe the gold clusters. Our calculations with the PBE, PBEsol, TPSS, and revTPSS functionals show that these semilocal functionals also cannot consistently give accurate results for bulk gold and gold clusters. The nonlocal contributions may play a key role. Based on the PBE exchange and correlation energy, the accuracy for calculating both bulk gold and gold clusters could be improved by including the dispersive interaction to enhance the nonlocal contributions. Besides calculating accurately the vacancy formation energy of bulk gold, this method can also remedy the well-known deficiency in which conventional semilocal density functional calculations heavily bias the 2D structures of gold clusters. The 2D–3D structural transitions are found to occur at Au12− for gold anions and Au8+ for gold cations, agreeing with the experimental results. Furthermore, the predicted transition at Au10 for neutral clusters seems reasonable, although it requires experimental verification. These findings suggest the importance of nonlocal effects when studying gold and other precious metal materials. This research area remains an important issue for both theoretical and experimental studies. Comprehensive studies on how to accurately account for nonlocal effects as corrections to the widely used semilocal DFT functionals and how much the nonlocal contributions need to be considered in studies of gold and other precious metals are highly needed. By using the vacancy formation energy of bulk gold and the structural transitions of small-sized gold clusters as examples, our study is expected to help stimulate subsequent studies on nonlocal effects.
Conflicts of interest
There are no conflicts of interest to declare.
Acknowledgements
The authors acknowledge financial support from the National Natural Science Foundation of China (NSFC) (Grant No. 11674129 and 11374128).
References
- M. Haruta, T. Kobayashi, H. Sano and N. Yamada, Chem. Lett., 1987, 16, 405 CrossRef.
- M. Haruta, Chem. Rec., 2003, 3, 75 CrossRef CAS PubMed.
- T. Ishida and M. Haruta, Angew. Chem., Int. Ed., 2007, 46, 7154 CrossRef CAS PubMed.
- B. Hammer and J. K. Nørskov, Nature, 1995, 376, 238 CrossRef CAS.
- M. Haruta, Angew. Chem., Int. Ed., 2014, 53, 52 CrossRef CAS PubMed.
- C. Louis and O. Pluchery, Gold Nanoparticles for Physics, Chemistry and Biology, Imperial College Press, Singapore, 2016 Search PubMed.
- M. Haruta, Nature, 2005, 437, 1098 CrossRef CAS PubMed.
- D. W. Goodman, Nature, 2008, 454, 948 CrossRef CAS PubMed.
- A. A. Herzing, C. J. Kiely, A. F. Carley, P. Landon and G. J. Hutchings, Science, 2008, 321, 1331 CrossRef CAS PubMed.
- M. Turner, V. B. Golovko, O. P. H. Vaughan, P. Abdulkin, A. Berenguer-Murcia, M. S. Tikhov, B. F. G. Johnson and R. M. Lambert, Nature, 2008, 454, 981 CrossRef CAS PubMed.
- B. Yoon, H. Häkkinen, U. Landman, A. S. Wörz, J.-M. Antonietti, S. Abbet, K. Judai and U. Heiz, Science, 2005, 307, 403 CrossRef CAS PubMed.
- P. Gruene, D. M. Rayner, B. Redlich, A. F. G. van der Meer, J. T. Lyon, G. Meijer and A. Fielicke, Science, 2008, 321, 674 CrossRef CAS PubMed.
- P. Pyykkö, Angew. Chem., Int. Ed., 2004, 43, 4412 CrossRef PubMed.
- H. Häkkinen, Chem. Soc. Rev., 2008, 37, 1847 RSC.
- U. Heiz and U. Landman, Nanocatalysis, Springer, New York, 2007 Search PubMed.
- J. Li, X. Li, H.-J. Zhai and L.-S. Wang, Science, 2003, 299, 864 CrossRef CAS PubMed.
- M. Chen and D. W. Goodman, Acc. Chem. Res., 2006, 39, 739 CrossRef CAS PubMed.
- C. Zhang, B. Yoon and U. Landman, J. Am. Chem. Soc., 2007, 129, 2228 CrossRef CAS PubMed.
- S. Bulusu, X. Li, L. S. Wang and X. C. Zeng, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 8326 CrossRef CAS PubMed.
- W. Huang and L.-S. Wang, Phys. Rev. Lett., 2009, 102, 153401 CrossRef PubMed.
- M. Ji, X. Gu, X. Li, X. G. Gong and L.-S. Wang, Angew. Chem., Int. Ed., 2005, 44, 7119 CrossRef CAS PubMed.
- G. Chen, Q. Wang, Q. Sun, Y. Kawazoe and P. Jena, J. Chem. Phys., 2010, 132, 194306 CrossRef PubMed.
- Q. Sun, Q. Wang, G. Chen and P. Jena, J. Chem. Phys., 2007, 127, 214706 CrossRef PubMed.
- G. Chen, S. J. Li, Y. Su, V. Wang, H. Mizuseki and Y. Kawazoe, J. Phys. Chem. C, 2011, 115, 20168 CrossRef CAS.
- F. Furche, R. Ahlrichs, P. Weis, C. Jacob, S. Gilb, T. Bierweiler and M. M. Kappes, J. Chem. Phys., 2002, 117, 6982 CrossRef CAS.
- X. Xing, B. Yoon, U. Landman and J. H. Parks, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 165423 CrossRef.
- M. P. Johansson, I. Warnke, A. Le and F. Furche, J. Phys. Chem. C, 2014, 118, 29370 CrossRef CAS.
- S. Gilb, P. Weis, F. Furche, R. Ahlrichs and M. M. Kappes, J. Chem. Phys., 2002, 116, 4094 CrossRef CAS.
- B. E. Salisbury, W. T. Wallace and R. L. Whetten, Chem. Phys., 2000, 262, 131 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- J. Tao, J. P. Perdew, V. N. Staroverov and G. E. Scuseria, Phys. Rev. Lett., 2003, 91, 146401 CrossRef PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, L. A. Constantin and J. Sun, Phys. Rev. Lett., 2009, 103, 026403 CrossRef PubMed.
- A. Lechtken, C. Neiss, M. M. Kappes and D. Schooss, Phys. Chem. Chem. Phys., 2009, 11, 4344 RSC.
- M. P. Johansson, A. Lechtken, D. Schooss, M. M. Kappes and F. Furche, Phys. Rev. A, 2008, 77, 053202 CrossRef.
- A. Glensk, B. Grabowski, T. Hickel and J. Neugebauer, Phys. Rev. X, 2014, 4, 011018 Search PubMed.
- W. Xing, P. Liu, X. Cheng, H. Niu, H. Ma, D. Li, Y. Li and X.-Q. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 144105 CrossRef.
- S.-L. Shang, B.-C. Zhou, W. Y. Wang, A. J. Ross, X. L. Liu, Y.-J. Hu, H.-Z. Fang, Y. Wang and Z.-K. Liu, Acta Mater., 2016, 109, 128 CrossRef CAS.
- B. Medasani, M. Haranczyk, A. Canning and M. Asta, Comput. Mater. Sci., 2015, 101, 96 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207 CrossRef CAS.
- Y. Zhang, G. Kresse and C. Wolverton, Phys. Rev. Lett., 2014, 112, 075502 CrossRef PubMed.
- A. Aguado, A. Largo, A. Vega and L. C. Balbás, Chem. Phys., 2012, 399, 252 CrossRef CAS.
- E. M. Fernández and L. C. Balbás, Phys. Chem. Chem. Phys., 2011, 13, 20863 RSC.
- A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005 CrossRef PubMed.
- G. Kress and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188 CrossRef.
- J. Ho, K. M. Ervin and W. C. Lineberger, J. Chem. Phys., 1990, 93, 6987 CrossRef CAS.
- E. M. Fernández, J. M. Soler, I. L. Garzón and L. C. Balbás, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 165403 CrossRef.
- A. R. Oganov and C. W. Glass, J. Chem. Phys., 2006, 124, 244704 CrossRef PubMed.
- A. R. Oganov, A. O. Lyakhov and M. Valle, Acc. Chem. Res., 2011, 44, 227 CrossRef CAS PubMed.
- A. O. Lyakhov, A. R. Oganov, H. T. Stokes and Q. Zhu, Comput. Phys. Commun., 2013, 184, 1172 CrossRef CAS.
- X.-F. Zhou, X. Dong, A. R. Oganov, Q. Zhu, Y. Tian and H.-T. Wang, Phys. Rev. Lett., 2014, 112, 085502 CrossRef.
- K. Huang, Statistical Mechanics, Wiley, New York, 2nd edn, 1987 Search PubMed.
- R. E. Allen and F. W. de Wetter, Phys. Rev., 1969, 179, 873 CrossRef CAS.
- J. Xie, S. P. Chen and J. S. Tse, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 9444 CrossRef CAS.
- Y. Zhang, G. Kresse and C. Wolverton, Phys. Rev. Lett., 2014, 112, 075502 CrossRef PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- J. Tao, P. Perdew and A. Ruzsinszky, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 233102 CrossRef.
- J. Klimes, D. R. Bowler and A. Michaelides, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 195131 CrossRef.
- H. Häkkinen, B. Yoon, U. Landman, X. Li, H.-J. Zhai and L.-S. Wang, J. Phys. Chem. A, 2003, 107, 6168 CrossRef.
- P. Jena and Q. Sun, Chem. Rev., 2018, 118, 5755–5870 CrossRef CAS PubMed.
- I. Katakuse, T. Ichihara, Y. Fujita, T. Matsuo, T. Sakurai and H. Matsuda, Int. J. Mass Spectrom. Ion Processes, 1985, 67, 229 CrossRef CAS.
- W. D. Knight, K. Clemenger, W. A. de Heer, W. A. Saunders, M. Y. Chou and M. L. Cohen, Phys. Rev. Lett., 1984, 52, 2141 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra02202c |
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *
*
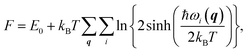
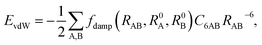
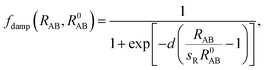
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 for 3D vs. 2D structures in anionic gold clusters generated at 100 K, which can be applied to the Boltzmann distribution function to estimate the relative energy of 2D geometry with respect to the 3D one. This ratio corresponds to a zero-Kelvin energy difference of ∼24 meV, in good agreement with the TSD-PBE value of 30 meV, indicating the validity of TSD-PBE for treating gold clusters. In addition to the Au12− cluster, another significant gold cluster is the Au16− anion, which was previously proposed as the first discovered fullerene-like metal cage cluster based on experimental investigations.19 In our previous studies carried out at the PBE level, the 2D structure of the Au16− anion, which had a similar structural configuration to that shown in Fig. 2, was found to be more than 0.2 eV lower in total energy than the cage geometry,22 contrary to the experimental observation. The nonlocal contributions-enhanced TSD-PBE method remedies this deficiency; the cage is now found to be 0.74 eV lower in energy than the 2D structure, ruling out the planar geometry.
15 for 3D vs. 2D structures in anionic gold clusters generated at 100 K, which can be applied to the Boltzmann distribution function to estimate the relative energy of 2D geometry with respect to the 3D one. This ratio corresponds to a zero-Kelvin energy difference of ∼24 meV, in good agreement with the TSD-PBE value of 30 meV, indicating the validity of TSD-PBE for treating gold clusters. In addition to the Au12− cluster, another significant gold cluster is the Au16− anion, which was previously proposed as the first discovered fullerene-like metal cage cluster based on experimental investigations.19 In our previous studies carried out at the PBE level, the 2D structure of the Au16− anion, which had a similar structural configuration to that shown in Fig. 2, was found to be more than 0.2 eV lower in total energy than the cage geometry,22 contrary to the experimental observation. The nonlocal contributions-enhanced TSD-PBE method remedies this deficiency; the cage is now found to be 0.74 eV lower in energy than the 2D structure, ruling out the planar geometry.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2D intensity ratio of ∼1560
2D intensity ratio of ∼1560![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 in cluster resource, significantly reducing the possibility of detecting the 2D structure through ion mobility measurement. The first five low-lying isomers calculated using the TSD-PBE method for Aun+ (n ≥ 8) cations are also shown in ESI Fig. S14.† In comparison, the PBE calculations seriously bias the 2D geometry. For Aun+ (n ≤ 16) clusters, the PBE functional only predicts the 3D structures as ground states for Aun+ with n = 9, 10, 11, and 15. For the Au8+ cluster, PBE indicates that the 2D structure is 0.16 eV lower in total energy than the 3D geometry. For the PBEsol calculations, the 3D structure of the Au8+ cluster is only 10 meV higher in energy than the 2D structure, which suggests their coexistence, contradicting the experimental results. Beginning at n = 8, the 3D geometries begin to dominate except at n = 12, for which the 3D structure is only 0.12 eV higher in energy than the 2D geometry. Beginning at n = 9, the TPSS functional starts to favor the 3D configurations for the studied Aun+ (n ≤ 16) clusters, with the exception of n = 12. The revTPSS performs better than the above functionals as it supports the 3D ground structures for Aun+ (9 ≤ n ≤ 16) clusters. However, it still biases the 2D geometry for Au8+, which is 43 meV lower in total energy than the 3D structure. In addition, the calculated energies of the 2D and 3D structures of Au12+ are almost identical, with the 2D structure being only 2 meV lower in total energy than the 3D structure. The revTPSS results support the 3D geometries as the dominant species in the corresponding clusters, contrary to the experimental findings. In comparison, only the TSD-PBE calculations support the 3D configurations as the ground-state structures for all the studied Aun+ (8 ≤ n ≤ 16) clusters, again suggesting the importance of nonlocal effects when describing gold clusters.
10 in cluster resource, significantly reducing the possibility of detecting the 2D structure through ion mobility measurement. The first five low-lying isomers calculated using the TSD-PBE method for Aun+ (n ≥ 8) cations are also shown in ESI Fig. S14.† In comparison, the PBE calculations seriously bias the 2D geometry. For Aun+ (n ≤ 16) clusters, the PBE functional only predicts the 3D structures as ground states for Aun+ with n = 9, 10, 11, and 15. For the Au8+ cluster, PBE indicates that the 2D structure is 0.16 eV lower in total energy than the 3D geometry. For the PBEsol calculations, the 3D structure of the Au8+ cluster is only 10 meV higher in energy than the 2D structure, which suggests their coexistence, contradicting the experimental results. Beginning at n = 8, the 3D geometries begin to dominate except at n = 12, for which the 3D structure is only 0.12 eV higher in energy than the 2D geometry. Beginning at n = 9, the TPSS functional starts to favor the 3D configurations for the studied Aun+ (n ≤ 16) clusters, with the exception of n = 12. The revTPSS performs better than the above functionals as it supports the 3D ground structures for Aun+ (9 ≤ n ≤ 16) clusters. However, it still biases the 2D geometry for Au8+, which is 43 meV lower in total energy than the 3D structure. In addition, the calculated energies of the 2D and 3D structures of Au12+ are almost identical, with the 2D structure being only 2 meV lower in total energy than the 3D structure. The revTPSS results support the 3D geometries as the dominant species in the corresponding clusters, contrary to the experimental findings. In comparison, only the TSD-PBE calculations support the 3D configurations as the ground-state structures for all the studied Aun+ (8 ≤ n ≤ 16) clusters, again suggesting the importance of nonlocal effects when describing gold clusters.








