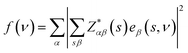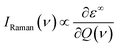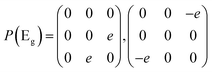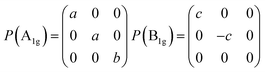Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Infrared and Raman spectra of Bi2O2X and Bi2OX2 (X = S, Se, and Te) studied from first principles calculations†
Yao-Di Xua,
Cong Wanga,
Yang-Yang Lva,
Y. B. Chenb,
Shu-Hua Yaoacd and
Jian Zhou *acd
*acd
aNational Laboratory of Solid State Microstructures and Department of Materials Science and Engineering, Nanjing University, Nanjing 210093, China. E-mail: zhoujian@nju.edu.cn
bNational Laboratory of Solid State Microstructures and Department of Physics, Nanjing University, Nanjing 210093, China
cCollaborative Innovation Center of Advanced Microstructures, Nanjing University, Nanjing, 210093, China
dJiangsu Key Laboratory of Artificial Functional Materials, Nanjing University, Nanjing 210093, China
First published on 10th June 2019
Abstract
The bismuth oxychalcogenide compounds contain many different kinds of materials, such as Bi2O2X and Bi2OX2 (X = S, Se, and Te). These materials have different but similar layered crystal structures and exhibit various interesting physical properties. Here, we have theoretically investigated their Raman and infrared spectra by first principles calculations based on density functional theory. It is found that in Bi2O2Se the calculated frequency of the A1g Raman active mode is in good agreement with the experimental measurements while the other three modes are ambiguous or not observed yet. The Raman and infrared spectra of other materials are also presented and need further confirmation. Our work provides the structural fingerprints of these materials, which could be helpful in identifying the crystal structures in future experiments.
1 Introduction
In recent years, bismuth oxychalcogenide materials Bi–O–X (X = S, Se, and Te) have attracted more and more attention. Among these materials, Bi2O2Se, synthesized more than forty years ago,1 is one of the most studied materials and has now become a very hot topic due to its various and interesting physical properties. First, Bi2O2Se was suggested to be a good thermoelectric material.2–7 In 2010, Ruleova et al. reported the thermoelectric properties of Bi2O2Se and they found that Bi2O2Se is an n-type semiconductor with a very low thermal conductivity and a relatively high figure of merit ZT about 0.2 at 800 K.2 Several theoretical works were also conducted to explore its thermoelectric properties.8–11 Second, Bi2O2Se has an ultrahigh electron mobility.12–17 An earlier work in 2012 found that the room temperature Hall mobility of Bi2O2Se single crystal was on the order of 300 cm2 s−1 V−1.12 Recently, it was found that the low temperature (about 2 K) Hall mobility can reach more than 2.0 × 104 cm2 s−1 V−1 in Bi2O2Se thin film13–15 and 4.0 × 104 cm2 s−1 V−1 in Bi2O2Se single crystal.16 Very recently, we have observed a superior Hall mobility of 2.2 × 105 cm2 s−1 V−1 at 2 K in a high quality Bi2O2Se single crystal.17 The high mobility in Bi2O2Se is possibly due to the self-modulation doping, i.e. the electron donor states lie above the lowest conduction band, not in the middle of the band gap.18 Furthermore, high mobility usually induces a large magnetoresistance (MR),19 which was also observed in Bi2O2Se. A longitudinal MR of about 600% (at 15 Tesla and 2 K) and 9000% (at 9 Tesla and 2 K) in Bi2O2Se single crystals was observed in two recent experiments.16,17 Third, due to its high mobility and suitable band gap (about 0.8 eV), Bi2O2Se was used in optoelectronic devices and infrared (IR) photo-detectors.20–22Bi2O2Te has the same crystal structure as that of Bi2O2Se, but it is much less studied. Luu and Vaqueiro found that Bi2O2Te ceramics is an n-type semiconductor with a smaller band gap (0.23 eV), electron mobility (47 cm2 s−1 V−1 at room temperatures), and ZT (0.13 at 573 K), compared with those of Bi2O2Se.23 The similar compound Bi2O2S is also less studied. Bi2O2S was first synthesized in 1984 and it has a different crystal structure to that of Bi2O2Se.24 There are only a few studies on its optical properties.25–27 For example, it was found that Bi2O2S has an indirect band gap of 1.12 eV and it is an excellent photoelectric material.27
On the other hand, there is another kind of bismuth oxychalcogenides Bi2OX2 (X = S, Se, and Te), which all share the same tetragonal lattice system. Among them, Bi2OS2 has been experimentally synthesized recently and it was a candidate as an optoelectronic material in the near-IR region.28 First principles calculations indicated that the two-dimensional Bi2OS2 nanosheet possesses a direct band gap and an ultrahigh electron mobility (up to 2.6 × 104 cm2 s−1 V−1).29 To the best of our knowledge, Bi2OSe2 and Bi2OTe2 have not been synthesized experimentally. However, first principles calculations showed that they have the same crystal structure as that of Bi2OS2.30 In particular, the calculated electron and hole effective mass of Bi2OX2 is very small. For example, the effective mass of Bi2OTe2 is only 0.02 and 0.012 for electron and hole.30 Another theoretical study indicated that Bi2OX2 materials show promising characteristics in applications for solar cells and thermoelectric devices.31
Besides Bi2O2X and Bi2OX2, the first BiS2 family superconductor Bi4O4S3 was studied over the past few years.32,33 Later, it was found that Bi4O4S3 is a mixture of the two phases, Bi2OS2 and Bi3O2S3.34 The former is non-superconducting, while the latter is superconducting.34–36
Therefore, we can see that the Bi–O–X system contains many kinds of materials with various interesting physical properties. From the experimental point of view, it is of course very important to identify the structure of the grown crystal from the many similar Bi–O–X materials. In this regard, Raman and IR spectra are convenient and powerful methods to provide the structural fingerprints of materials. However, we find that the Raman and IR studies of these materials are quite lacking. Only a few works about the Raman spectra of Bi2O2Se and Bi2O2Te have been reported until now.14,16,37,38 For this reason, we have systematically calculated the phonon, irreducible representations, Raman and IR spectra, vibrational eigenvectors of optical phonons, and polarized Raman configurations of six materials: Bi2O2X and Bi2OX2. We mainly present the results of Bi2O2Se and Bi2O2Te since they can be compared with other works. The Raman and IR spectra of the other four materials are also given briefly and could be referenced by future experiments.
2 Computational details
The vibrational properties of Bi2O2X and Bi2OX2 (X = S, Se, and Te) are calculated by density functional theory (DFT) implemented in the Vienna ab initio simulation package (VASP).39,40 The projected augmented wave method41,42 and the generalized gradient approximation with the Perdew–Burke–Ernzerhof exchange–correlation functional43 are used. The DFT-D3 method44,45 is used to correct the van der Waals interactions in these layered materials. The plane-wave cutoff energy is 520 eV for all materials. Both the internal atomic positions and the lattice constants are allowed to relax until the maximal residual Hellmann–Feynman forces on atoms are smaller than 0.002 eV Å−1. The k-mesh is 8 × 8 × 2 for Bi2O2S and Bi2OX2 and 8 × 8 × 8 for Bi2O2Se and Bi2O2Te. The Phonopy package46 is used to calculate the phonon frequencies, eigenvectors and irreducible representations of the materials. The crystal structures and eigenvectors are plotted by the VESTA program.47The IR and Raman activity of phonon modes can be analyzed by their irreducible representations. However their intensities need additional calculations. The IR intensity of a phonon mode is given by the corresponding oscillator strength:48
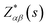 is the Born effective charge tensor of the sth atom. The Born effective charge tensor and the phonon eigenvectors are calculated by the density functional perturbation theory (DFPT) implemented in the VASP code. This method has been applied to different material systems.48–51
is the Born effective charge tensor of the sth atom. The Born effective charge tensor and the phonon eigenvectors are calculated by the density functional perturbation theory (DFPT) implemented in the VASP code. This method has been applied to different material systems.48–51
The off-resonance Raman intensity of a phonon mode can be estimated by calculating the derivative of the macroscopic dielectric tensor with respect to the normal mode coordinate:52
3 Results and discussions
3.1 Crystal structures of Bi2O2X and Bi2OX2
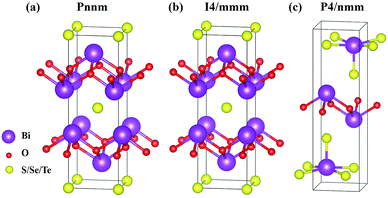
The six materials Bi2O2X and Bi2OX2 (X = S, Se, and Te) have three different crystal structures. Bi2O2S belongs to a primitive orthorhombic lattice with a space group Pnnm (no. 58),24 while Bi2O2Se and Bi2O2Te possess a body centered tetragonal lattice with a space group I4/mmm (no. 139).1,13,23 On the other hand, Bi2OX2 have a primitive tetragonal lattice with a space group P4/nmm (no. 129).28,55 All the materials show layered structures as shown in Fig. 1. Bi2O2X consists of two Bi2O2 and two X layers, while Bi2OX2 is composed of one Bi2O2 and two BiX2 layers in a unit cell. Although the symmetries of Bi2O2S and Bi2O2Se are totally different, the structure of Bi2O2S is a slightly distorted form of Bi2O2Se.24 Therefore, the difference between the two structures shown in Fig. 1(a) and (b) is hardly visible to the naked eye. All the structures shown in Fig. 1 contain ten atoms in the unit cell. However, Bi2O2Se and Bi2O2Te shown in Fig. 1(b) is a conventional cell, which in fact contains two primitive cells.It is noted that among the six materials, to the best of our knowledge, Bi2OSe2 and Bi2OTe2 have not been synthesized experimentally. Their crystal structures are predicted to be the same as that of Bi2OS2 by first principles calculations.30
The calculated lattice constants in this work with the DFT-D3 correction are listed in Table 1. It is obvious that our calculated results are well consistent with the experimental measurements with the largest difference less than 1%. Our results are also in good agreement with other theoretical work.30
| Symmetry | Material | Reference | a | b | c |
|---|---|---|---|---|---|
| Orthorhombic Pnnm | Bi2O2S | This work | 3.837 | 3.848 | 11.94 |
| Experiment24 | 3.840 | 3.874 | 11.92 | ||
| Theory30 | 3.87 | 3.89 | 11.99 | ||
| Tetragonal I4/mmm | Bi2O2Se | This work | 3.891 | 3.891 | 12.20 |
| Experiment1 | 3.891 | 3.891 | 12.21 | ||
| Experiment13 | 3.88 | 3.88 | 12.16 | ||
| Theory30 | 3.91 | 3.91 | 12.38 | ||
| Bi2O2Te | This work | 3.984 | 3.984 | 12.65 | |
| Experiment23 | 3.980 | 3.980 | 12.70 | ||
| Theory30 | 4.01 | 4.01 | 12.63 | ||
| Tetragonal P4/nmm | Bi2OS2 | This work | 3.950 | 3.950 | 13.84 |
| Experiment28 | 3.961 | 3.961 | 13.80 | ||
| Experiment55 | 3.964 | 3.964 | 13.83 | ||
| Theory30 | 3.96 | 3.96 | 13.69 | ||
| Bi2OSe2 | This work | 4.044 | 4.044 | 14.56 | |
| Theory30 | 4.05 | 4.05 | 14.46 | ||
| Bi2OTe2 | This work | 4.193 | 4.193 | 15.81 | |
| Theory30 | 4.17 | 4.17 | 15.99 |
With the optimized structures, the zone-centered phonon modes, irreducible representations, IR and Raman spectra of the six materials are calculated. In the following subsections, we first present the detailed results of Bi2O2Se and Bi2O2Te since both materials have the same crystal structure and the Raman spectrum of Bi2O2Se is better studied than other materials. Then the brief results of Bi2O2S and Bi2OX2 are also given.
3.2 I4/mmm tetragonal Bi2O2Se and Bi2O2Te
The calculated zone-centered optical phonon frequencies of Bi2O2Se and Bi2O2Te are listed in Table 2. The highest phonon frequency of Bi2O2Se is about 433.3 cm−1, while it is only 396.1 cm−1 in Bi2O2Te due to the heavier atom mass. Bi2O2Se and Bi2O2Te have the same space group of I4/mmm (point group D4h), and their irreducible representations at the Γ point in the Brillouin zone are:| Γacoustic = Eu + A2u |
| Γoptic = 2Eu + 2A2u + 2Eg + A1g + B1g |
| Symmetry | Bi2O2Se | Bi2O2Te | Activity | |||
|---|---|---|---|---|---|---|
| This work | Pereira37 | Cheng38 | This work | Cheng38 | ||
| Eu | 54.8 | 59.2 | 56.4 | IR | ||
| A2u | 65.0 | 64.5 | 63.3 | IR | ||
| Eg | 67.3 | 72.0 | 67.99 | 69.1 | 67.01 | Raman |
| A1g | 162.9 | 165.7 | 159.89 | 150.4 | 147.48 | Raman |
| Eu | 268.0 | 293.9 | 243.6 | IR | ||
| B1g | 354.3 | 369.4 | 364.02 | 336.0 | 340.33 | Raman |
| A2u | 377.8 | 402.8 | 347.3 | IR | ||
| Eg | 433.3 | 444.0 | 428.68 | 396.1 | 386.15 | Raman |
Recently, there have been two joint experimental and theoretical works by Pereira et al.37 and Cheng et al.,38 in which the phonon frequencies of Bi2O2Se and Bi2O2Te are also calculated. We listed their data in Table 2 for comparison. It is found that most of the calculated frequencies are in good agreement with ours, except for the two high-frequency IR active modes (Eu and A2u) in Bi2O2Se, which have a maximal discrepancy of about 25 cm−1. Phonon frequencies depend on the second derivative of the total energy, therefore the accuracy of the phonon calculation is usually not as good as the ones of the total energy calculations. Many parameters, such as the exchange–correlation functional, will affect the theoretical phonon frequencies. Therefore, we think such differences between these works are acceptable in phonon calculations.
We also illustrate the vibrational eigenvectors of Bi2O2Se in Fig. 2. It is found that the two low-frequency Raman active modes (Eg and A1g) are related to the in-plane and out-of-plane vibrations of Bi atoms, respectively. While the two high-frequency Raman active modes (B1g and Eg) represent the out-of-plane and in-plane vibrations of O atoms, respectively. Vibrations of Se atoms are not involved in any Raman active modes. The two low-frequency IR active modes (Eu and A2u) are related to the in-plane and out-of-plane vibrations of Bi and Se atoms, respectively. While the two high-frequency IR active modes (Eu and A2u) mainly represent the in-plane and out-of-plane vibrations of O atoms, respectively. The vibrational eigenvectors of Bi2O2Te are similar to those of Bi2O2Se, which are not shown here.
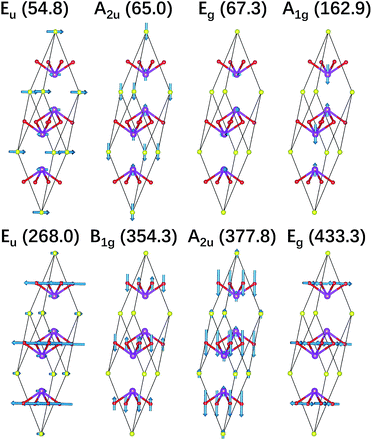 | ||
| Fig. 2 Vibrational eigenvectors of the zone-centered optical phonon modes shown in the primitive cell of Bi2O2Se. The purple, red, and yellow balls represent Bi, O, and Se atoms respectively. | ||
Then we present a detailed analysis about the polarized configurations for the Raman active modes of Bi2O2Se and Bi2O2Te. The Raman tensors of the D4h point group can be written as:
Qualitatively, the Raman intensity I of a phonon mode can be calculated by the formula I ∞ |ei·P·es|2, where ei and es are polarization directions of the incident and scattered light and P is the Raman tensor given above. In Table 3, we present the non-equivalent polarized configurations for the Raman active modes of Bi2O2Se and Bi2O2Te. In the configuration notation A(BC)D, A and D represent the propagation directions of the incident and scattered light respectively, while B and C represent the polarization directions of the incident and scattered light respectively. In the right angle scattering geometry, the propagation directions of the incident and scattered light are orthogonal (first five configurations in Table 3). In the back scattering geometry, the propagation directions of the incident and scattered light are anti-parallel (last four configurations in Table 3).
| Configurations | A1g | B1g | Eg |
|---|---|---|---|
| X(YY)Z | ✓ | ✓ | |
| Z(XX)Y | ✓ | ✓ | |
| X(ZZ)Y | ✓ | ||
| X(YZ)Y | ✓ | ||
| Z(XZ)X | ✓ | ||
| −Z(XX)Z | ✓ | ✓ | |
| −Y(XX)Y | ✓ | ✓ | |
| −X(ZZ)X | ✓ | ||
| −X(YZ)X | ✓ |
From Table 3, it is interesting to find that the Eg mode cannot be observed with the A1g and B1g ones simultaneously under the same polarized configuration. Also, only one A1g mode can be observed in the polarized configurations: X(ZZ)Y or −X(ZZ)X. Therefore, all of the Raman active modes can be well identified under different polarized configurations. Of course, in this case, the frequencies of the four Raman active modes in Bi2O2Se and Bi2O2Te are well separated and therefore it is quite easy to identify these modes in experiments according to their frequencies without considering their polarized configurations.
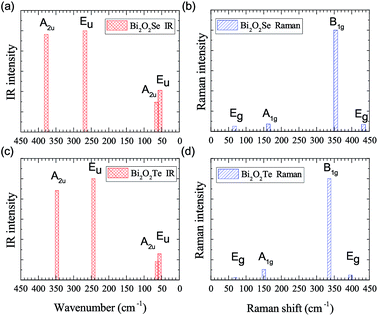
IR and Raman intensities of Bi2O2Se and Bi2O2Te are also calculated directly by first principles calculations based on the equations in Section II, which are shown in Fig. 3. From Fig. 3(a) and (c), we can see that the two high-frequency IR active modes (Eu and A2u) have relatively higher intensities than those of the low-frequency modes (Eu and A2u). On the other hand, in Fig. 3(b) and (d), the Raman active mode B1g has the highest intensity for both materials, while the other three modes have much lower intensities.
Recently, there have been four experimental works,14,16,37,38 in which the Raman spectrum of Bi2O2Se was given. Wu et al. have synthesized the atomically thin two-dimensional and the bulk Bi2O2Se crystals and they observed two Raman peaks located at about 100 and 159 cm−1.14 Tong et al. have grown high-quality Bi2O2Se single crystals and found two main Raman peaks located at around 90 and 159 cm−1, which are associated with the symmetries of E2g and A21g respectively.16 However, it seems that the E2g mode in their Figure is made up of two adjacent peaks located at 84 and 90 cm−1.16 Pereira et al. studied the physical properties of Bi2O2Se at high pressure, in which they only observed one most intense Raman peak at around 159.2 cm−1 at room pressure.37 The theoretical low-frequency Eg mode (near 70 cm−1) can only be observed at high pressure.37 Cheng et al. have measured the Raman spectra of Bi2O2Se and Bi2O2Te.38 These results are summarized in Table 4, from which we can see that the Raman active mode A1g at about 160 cm−1 can be well confirmed, while the Eg mode below 100 cm−1 is ambiguous. The discrepancy of the low-frequency Eg modes in the two experiments14,16 is more than 10 cm−1, and meanwhile both observed frequencies of the Eg modes are about 20–30 cm−1 higher than the theoretical result. Furthermore, the two high-frequency Raman active modes (B1g and Eg) have not been observed in all the experiments14,16,37,38 in spite of the high intensity of the B1g mode in our calculations. The possible reason is due to the phonon damping caused by the large carrier concentration in Bi2O2Se, as indicated in Pereira’s work.37
The Raman spectrum of Bi2O2Te was also measured in Cheng’s work,38 which is listed in Table 5. The two observed Raman modes (A1g and B1g) are well consistent with our calculations. However, the two Eg modes are not observed in their work. It is interesting to point out that the missing B1g mode in Bi2O2Se was observed in Bi2O2Te, although in a relatively low intensity compared to that of the A1g mode. Therefore, the Raman spectra of Bi2O2Se and Bi2O2Te need further investigations. For example, one could try to measure the Raman spectrum of Bi2O2Se with a lower carrier concentration by doping or at low temperatures in a proper Raman polarized configuration.
| Raman frequency (cm−1) | |
|---|---|
| This work | 69.1 (Eg), 147.48 (A1g), 336.0 (B1g), 396.1 (Eg) |
| Experiment38 | 147 (A1g), 340 (B1g) |
3.3 Pnnm orthorhombic Bi2O2S
Although Bi2O2S has a very similar crystal structure to the one of Bi2O2Se shown in Fig. 1(a) and (b), they have a different symmetry. In fact, Bi2O2S has an orthorhombic crystal structure with a space group of Pnnm (point group D2h). There are ten atoms in the unit cell of Bi2O2S resulting in thirty phonon modes. Its irreducible representations at the Γ point are presented as follows:| Γacoustic = B1u + B2u + B3u |
| Γoptic = 3Au + 2B1u + 5B2u + 5B3u + 4Ag + 4B1g + 2B2g + 2B3g |
| Symmetry | Bi2O2S | Activity | Symmetry | Bi2O2S | Activity |
|---|---|---|---|---|---|
| B2g | 9.5 | Raman | B3u | 218.8 | IR |
| Ag | 13.9 | Raman | Ag | 285.2 | Raman |
| Au | 53.7 | B3u | 286.3 | IR | |
| B2u | 54.9 | IR | B2g | 287.7 | Raman |
| B3u | 60.7 | IR | B1u | 288.5 | IR |
| B1u | 64.9 | IR | B3u | 364.4 | IR |
| B3g | 65.2 | Raman | Ag | 367.8 | Raman |
| B1g | 67.9 | Raman | B2u | 404.2 | IR |
| B2u | 75.7 | IR | Au | 448.9 | |
| B1g | 83.0 | Raman | B1g | 450.6 | Raman |
| Au | 113.1 | B3g | 452.4 | Raman | |
| B2u | 113.4 | IR | B2u | 457.5 | IR |
| B3u | 144.7 | IR | B1g | 519.1 | Raman |
| Ag | 170.6 | Raman |
The vibrational eigenvectors of all the zone-centered optical modes and the polarized configurations of the Raman active modes are shown in Fig. S1 and Tables S1 and S2 in the ESI.†
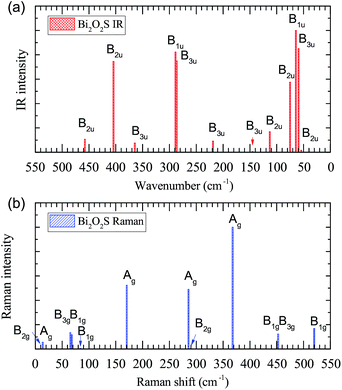
IR and Raman intensities of Bi2O2S are also calculated directly by first principles calculations, which are shown in Fig. 4. It is found that the IR modes near 60, 290 and 400 cm−1 have the highest intensities. In the Raman spectrum, the three Ag modes near 170, 285, and 370 cm−1 have the highest intensities.
It is noted that Bi2O2S has been synthesized in experiments,24–26 however no Raman spectrum was measured yet. Recently, Cheng et al. have also calculated the Raman spectrum of Bi2O2S by the density functional perturbation theory in the local density approximation and norm-conserving pseudopotentials implemented in Quantum Espresso (QE) software.38 We listed their data in Table 7 as well as ours for comparison. From the frequency perspective, we can see that the two calculations are in general consistent with each other. For example, in both works, there are five Raman modes below 100 cm−1, one mode between 100–200 cm−1, two modes between 200–300 cm−1, and etc. Although the largest difference in a B1g mode reaches 43 cm−1 (about 10%), we still think it is acceptable since the two works use totally different methods in their calculations.
| This work | B2g | Ag | B3g | B1g | B1g | Ag | Ag | B2g | Ag | B1g | B3g | B1g |
| 9.5 | 13.9 | 65.2 | 67.9 | 83.0 | 170.6 | 285.2 | 287.7 | 367.8 | 450.6 | 452.4 | 519.1 | |
| Cheng38 | B2g | Ag | B2g | Ag | Ag | Ag | B1g | B3g | B1g | B1g | B3g | B1g |
| 20.52 | 29.23 | 64.34 | 68.23 | 82.86 | 154.20 | 263.85 | 273.27 | 386.85 | 407.76 | 417.30 | 520.28 |
However, we noted that the Mulliken symbols in the two works are quite different. In particular, the four Ag modes in Cheng’s work are all below 200 cm−1, while we have two Ag modes below 200 cm−1 and two other ones above 200 cm−1. The highest Ag mode in our work is more than 210 cm−1 higher than theirs. This cannot be explained by the inaccuracy of the phonon frequency induced by the different parameters. It is possibly due to the different classification of the Mulliken symbols. In the D2h point group, the assignment of B1g, B2g, and B3g depends on the three mutually perpendicular 2-fold axes along the z, y, and x directions.56 We have tested that QE software will give different Mulliken symbols (B1g, B2g, and B3g) depending on the orientations of the orthorhombic unit cell of Bi2O2S. However, the assignment of the Ag mode should be unambiguous, which is independent of the directions of the unit cell. Therefore, we think the discrepancy of the Ag Raman modes in our work and Cheng’s work needs further investigations.
3.4 P4/nmm tetragonal Bi2OS2, Bi2OSe2, and Bi2OTe2
In experiment, Bi2OS2 has a space group of P4/mmm (point group D4h).28,55 However, to the best of our knowledge, Bi2OSe2 and Bi2OTe2 have not been synthesized in experiment. First principles calculations indicate that they share the same crystal structure as Bi2OS2.30 There are ten atoms in the unit cell of Bi2OX2 (X = S, Se, and Te) as shown in Fig. 1(c), resulting in thirty phonon modes. The irreducible representations of Bi2OX2 at the Γ point are:| Γacoustic = Eu + A2u |
| Γoptic = 4Eu + 4A2u + 5Eg + 4A1g + B1g |
| Symmetry | Bi2OS2 | Bi2OSe2 | Bi2OTe2 | Activity |
|---|---|---|---|---|
| Eu | 26.0 | 18.8 | 6.5 | IR |
| Eg | 30.7 | 25.9 | 20.0 | Raman |
| Eg | 63.2 | 55.8 | 41.1 | Raman |
| A2u | 63.9 | 54.6 | 50.6 | IR |
| A1g | 73.2 | 64.1 | 53.5 | Raman |
| Eu | 97.7 | 73.2 | 49.2 | IR |
| Eg | 111.4 | 80.5 | 54.8 | Raman |
| Eu | 126.6 | 89.4 | 83.5 | IR |
| A2u | 129.4 | 97.2 | 84.5 | IR |
| A1g | 132.2 | 88.6 | 75.1 | Raman |
| Eg | 138.4 | 100.2 | 101.1 | Raman |
| A1g | 149.7 | 138.6 | 123.9 | Raman |
| Eu | 262.1 | 228.1 | 183.7 | IR |
| A2u | 286.0 | 182.3 | 140.9 | IR |
| A1g | 346.5 | 217.9 | 163.2 | Raman |
| B1g | 363.5 | 342.2 | 311.2 | Raman |
| Eg | 415.0 | 376.0 | 321.9 | Raman |
| A2u | 466.0 | 420.0 | 372.1 | IR |
According to the character table for the D4h point group, the Eu and A2u modes are IR active, while the Eg, A1g, and B1g modes are Raman active. Therefore, there are ten Raman active (five double degenerated Eg modes, five non-degenerated A1g and B1g modes) and eight IR active modes (four double degenerated Eu modes and four non-degenerated A2u ones) in Bi2OX2.
The IR and Raman intensities of Bi2OX2 are also calculated directly by first principles calculations, which are shown in Fig. 5. It is found that in the IR spectrum of Bi2OS2, there are six modes (Eu modes around 98, 127, 262 cm−1 and A2u modes around 129, 286, 466 cm−1) which have relatively high intensities. For the Bi2OSe2 and Bi2OTe2, only four modes have high intensities. For the Raman spectra of Bi2OS2 and Bi2OSe2, there are two promising A1g peaks around 132 and 346 cm−1 for Bi2OS2, and 89 and 218 cm−1 for Bi2OSe2. For Bi2OTe2, the A1g Raman mode around 163 cm−1 has the highest intensity.
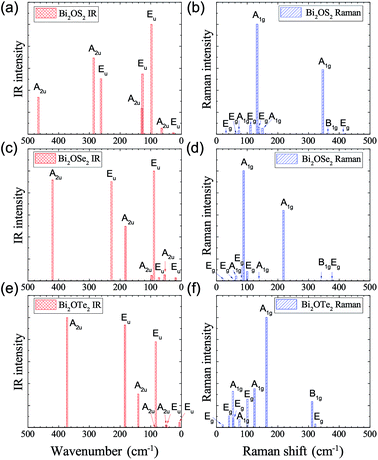 | ||
| Fig. 5 Calculated IR and Raman intensities (arbitrary unit) of tetragonal Bi2OX2 (X = S, Se, and Te). | ||
Since the tetragonal Bi2OSe2 and Bi2OTe2 have not been synthesized in experiments, we also calculated their phonon dispersion and densities of state, which are not shown here. No imaginary frequencies are found in both materials. Therefore we think the tetragonal phases of Bi2OSe2 and Bi2OTe2 are stable and they could possibly be synthesized in future experiments.
4 Conclusions
We have systematically calculated the Raman and infrared spectra of six Bi–O–X materials: Bi2O2X and Bi2OX2 (X = S, Se, and Te). For each material, we present their optical phonon frequencies, Raman and infrared activities and intensities, Raman polarization configurations, and vibrational eigenvectors. In particular, the Raman spectra of Bi2O2Se and Bi2O2Te are compared with the existing experimental results. In Bi2O2Se, only one A1g Raman mode is confirmed in experiments, while the other three are ambiguous or not observed yet. In Bi2O2Te, both A1g and B1g modes are well consistent with the experiments, while two Eg modes are not observed yet. Due to the various and important physical properties in these materials, our work could be helpful in identifying the crystal structure in future experiments.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the National Key R&D Program of China (Grant No. 2016YFA0201104), National Basic Research Program of China (Grant No. 2015CB659400), National Natural Science Foundation of China (Grant No. 51872134, No. 51890860, No. 11890702, and No. 51721001), and the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20171343). Y. Y. Lv acknowledges the financial support from the Innovation Program for the Talents of China Postdoctoral Science Foundation (BX20180137). The use of the computational resources in the High Performance Computing Center of Nanjing University for this work is also acknowledged.References
- H. Boller, Monatsh. Chem., 1973, 104, 916 CrossRef CAS.
- P. Ruleova, C. Drasar, P. Lostak, C. P. Li, S. Ballikaya and C. Uher, Mater. Chem. Phys., 2010, 119, 299 CrossRef CAS.
- K. Y. Zhang, C. G. Hu, Z. L. Kang, S. X. Wang, Y. Xi and H. Liu, Mater. Res. Bull., 2013, 48, 3968 CrossRef CAS.
- B. Zhan, Y. C. Liu, J. L. Lan, C. C. Zeng, Y. H. Lin and C. W. Nan, Materials, 2015, 8, 1568 CrossRef CAS.
- X. Tan, J. L. Lan, Y. C. Liu, G. K. Ren, C. C. Zeng, Y. H. Lin and C. W. Nan, J. Electroceram., 2016, 37, 66 CrossRef CAS.
- R. Liu, J. L. Lan, X. Tan, Y. C. Liu, G. K. Ren, C. Liu, Z. F. Zhou, C. W. Nan and Y. H. Lin, J. Eur. Ceram. Soc., 2018, 38, 2742 CrossRef CAS.
- X. Tan, J. L. Lan, K. R. Hu, B. Xu, Y. C. Liu, P. Zhang, X. Z. Cao, Y. C. Zhu, W. Xu, Y. H. Lin and C. W. Nan, J. Am. Ceram. Soc., 2018, 101, 4634 CrossRef CAS.
- D. L. Guo, C. G. Hu, Y. Xi and K. Zhang, J. Phys. Chem. C, 2013, 117, 21597 CrossRef CAS.
- T. V. Quang and M. Kim, J. Appl. Phys., 2016, 120, 195105 CrossRef.
- M. Liangruksa, Mater. Res. Express, 2017, 4, 035703 CrossRef.
- C. Wang, G. Q. Ding, X. M. Wu, S. S. Wei and G. Y. Gao, New J. Phys., 2018, 20, 123014 CrossRef.
- C. Drasar, P. Ruleova, L. Benes and P. Lostak, J. Electron. Mater., 2012, 41, 2317 CrossRef CAS.
- J. X. Wu, H. T. Yuan, M. M. Meng, C. Chen, Y. Sun, Z. Y. Chen, W. H. Dang, C. W. Tan, Y. J. Liu, J. B. Yin, Y. B. Zhou, S. Y. Huang, H. Q. Xu, Y. Cui, H. Y. Hwang, Z. F. Liu, Y. L. Chen, B. H. Yan and H. L. Peng, Nat. Nanotechnol., 2017, 12, 530 CrossRef CAS PubMed.
- J. X. Wu, C. W. Tan, Z. J. Tan, Y. J. Liu, J. B. Yin, W. H. Dang, M. Z. Wang and H. L. Peng, Nano Lett., 2017, 17, 3021 CrossRef CAS PubMed.
- C. Chen, M. X. Wang, J. X. Wu, H. X. Fu, H. F. Yang, Z. Tian, T. Tu, H. Peng, Y. Sun, X. Xu, J. Jiang, N. B. M. Schröter, Y. W. Li, D. Pei, S. Liu, S. A. Ekahana, H. T. Yuan, J. M. Xue, G. Li, J. F. Jia, Z. K. Liu, B. H. Yan, H. L. Peng and Y. L. Chen, Sci. Adv., 2018, 4, eaat8355 CrossRef PubMed.
- T. Tong, M. Zhang, Y. Chen, Y. Li, L. Chen, J. Zhang, F. Song, X. Wang, W. Zou, Y. Xu and R. Zhang, Appl. Phys.Lett., 2018, 113, 072106 CrossRef.
- Y. Y. Lv, L. Xu, S. T. Dong, Y. C. Luo, Y. Y. Zhang, Y. B. Chen, S. H. Yao, J. Zhou, Y. S. Cui, S. T. Zhang, M. H. Lu and Y. F. Chen, Phys. Rev. B, 2019, 99, 195143 CrossRef.
- H. X. Fu, J. X. Wu, H. L. Peng and B. H. Yan, Phys. Rev. B, 2018, 97, 241203 CrossRef CAS.
- Y. Y. Lv, X. Li, J. L. Zhang, B. Pang, S. S. Chen, L. Cao, B. B. Zhang, D. J. Lin, Y. B. Chen, S. H. Yao, J. Zhou, S. T. Zhang, M. H. Lu, M. L. Tian and Y. F. Chen, Phys. Rev. B, 2018, 97, 245151 CrossRef CAS.
- J. Li, Z. X. Wang, Y. Wen, J. W. Chu, L. Yin, R. Q. Cheng, L. Lei, P. He, C. Jiang, L. P. Feng and J. He, Adv. Funct. Mater., 2018, 28, 1706437 CrossRef.
- J. X. Wu, Y. J. Liu, Z. J. Tan, C. W. Tan, J. B. Yin, T. R. Li, T. Tu and H. L. Peng, Adv. Mater., 2017, 29, 1704060 CrossRef PubMed.
- J. Yin, Z. Tan, H. Hong, J. Wu, H. Yuan, Y. Liu, C. Chen, C. Tan, F. Yao, T. Li, Y. Chen, Z. Liu, K. Liu and H. Peng, Nat. Commun., 2018, 9, 3311 CrossRef PubMed.
- S. D. N. Luu and P. Vaqueiro, J. Solid State Chem., 2015, 226, 219 CrossRef CAS.
- E. Koyama, I. Nakai and K. Nagashima, Acta Crystallogr., Sect. B: Struct. Sci., 1984, 40, 105 CrossRef.
- A. L. Pacquette, H. Hagiwara, T. Ishihara and A. A. Gewirth, J. Photochem. Photobiol., A, 2014, 277, 27 CrossRef CAS.
- İ. A. Kariper, Spectrochim. Acta, Part A, 2016, 163, 102 CrossRef PubMed.
- X. Zhang, Y. Liu, G. Zhang, Y. Wang, H. Zhang and F. Huang, ACS Appl. Mater. Interfaces, 2015, 7, 4442 CrossRef CAS PubMed.
- A. Miura, Y. Mizuguchi, T. Takei, N. Kumada, E. Magome, C. Moriyoshi, Y. Kuroiwa and K. Tadanaga, Solid State Commun., 2016, 227, 19 CrossRef CAS.
- X. W. Zhang, B. Wang, X. H. Niu, Y. H. Li, Y. F. Chen and J. L. Wang, Mater. Horiz., 2018, 5, 1058 RSC.
- X. Ma, D. Chang, C. Zhao, R. Li, X. Huang, Z. Zeng, X. Huang and Y. Jia, J. Mater. Chem. C, 2018, 6, 13241 RSC.
- S. Azam, S. A. Khan and S. Goumri-Said, J. Electron. Mater., 2018, 47, 2513 CrossRef CAS.
- S. K. Singh, A. Kumar, B. Gahtori, S. G. Sharma, S. Patnaik and V. P. S. Awana, J. Am. Chem. Soc., 2012, 134, 16504 CrossRef CAS PubMed.
- Y. Mizuguchi, H. Fujihisa, Y. Gotoh, K. Suzuki, H. Usui, K. Kuroki, S. Demura, Y. Takano, H. Izawa and O. Miura, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 220510(R) CrossRef.
- W. A. Phelan, D. C. Wallace, K. E. Arpino, J. R. Neilson, K. J. Livi, C. R. Seabourne, A. J. Scott and T. M. McQueen, J. Am. Chem. Soc., 2013, 135, 5372 CrossRef CAS PubMed.
- L. Li, D. Parker, P. Babkevich, L. Yang, H. M. Ronnow and A. S. Sefat, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 104511 CrossRef.
- J. F. Shao, Z. H. Liu, X. Yao, L. Pi, S. Tan, C. J. Zhang and Y. H. Zhang, Phys. Status Solidi RRL, 2014, 8, 845 CrossRef CAS.
- A. L. J. Pereira, D. Santamaría-Pérez, J. Ruiz-Fuertes, F. J. Manjón, V. P. Cuenca-Gotor, R. Vilaplana, O. Gomis, C. Popescu, A. Muñoz, P. Rodríguez-Hernández, A. Segura, L. Gracia, A. Beltraán, P. Ruleova, C. Drasar and J. A. Sans, J. Phys. Chem. C, 2018, 122, 8853 CrossRef CAS.
- T. Cheng, C. W. Tan, S. Q. Zhang, T. Tu, H. L. Peng and Z. R. Liu, J. Phys. Chem. C, 2018, 122, 19970 CrossRef CAS.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272 CrossRef CAS.
- P. Giannozzi and S. Baroni, J. Chem. Phys., 1994, 100, 8537 CrossRef CAS.
- J. Zhou and J. Dong, J. Appl. Phys., 2010, 107, 024306 CrossRef.
- D. Karhánek, T. Bučko and J. Hafner, J. Phys.: Condens. Matter, 2010, 22, 265006 CrossRef PubMed.
- K. Esfarjani, Y. Hashi, J. Onoe, K. Takeuchi and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 223 CrossRef CAS.
- A. Fonari and S. Stauffer, vasp_raman.py, https://github.com/raman-sc/VASP/.
- J. M. Skelton, L. A. Burton, A. J. Jackson, F. Oba, S. C. Parker and A. Walsh, Phys. Chem. Chem. Phys., 2017, 19, 12452 RSC.
- D. T. Larson and E. Kaxiras, Phys. Rev. B, 2018, 98, 085406 CrossRef CAS.
- N. Takahashi, M. Nagao, A. Miura, S. Watauchi, K. Tadanaga, Y. Takano and I. Tanaka, J. Ceram. Soc. Jpn., 2018, 126, 591 CrossRef CAS.
- R. S. Mulliken, J. Chem. Phys., 1955, 23, 1997 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra02584g |
| This journal is © The Royal Society of Chemistry 2019 |