Open Access Article
Open Access ArticleSystematic exploration of N, C configurational effects on the ORR performance of Fe–N doped graphene catalysts based on DFT calculations†
Fan Liu‡
 a,
Guangqi Zhu
a,
Guangqi Zhu a,
Dongzi Yanga,
Dong Jiaa,
Fengmin Jin*a and
Wei Wang‡
a,
Dongzi Yanga,
Dong Jiaa,
Fengmin Jin*a and
Wei Wang‡ *ab
*ab
aSchool of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China. E-mail: wangweipaper@163.com; Fax: +86-22-27403389; Tel: +86-13512958953
bKey Laboratory of Metal Fuel Cell of Sichuan Province, China
First published on 23rd July 2019
Abstract
Metal single-atom catalysts (MSATs), such as Fe–N coordination doped sp2-carbon matrices, have emerged as a promising oxygen reduction reaction (ORR) catalyst to replace their costly platinum (Pt) based counterparts in fuel cells. In this work, we employ density functional theory (DFT) to systematically discuss the electronic-structure and surface-stress effects of N, C configurations on Fe–N doped graphene in single and double vacancy. The formation energy (Ef) of Fe–N-gra dropped off with the increase of N atoms incorporated for both single and double vacancy groups. The theoretical overpotentials on Fe–N–C sites were calculated and revealed that moderate N-doping levels and doping configuration could enhance the ORR activity of Fe–N coordination structures in the double vacancy and that doping N atoms is not effective for ORR activity in single vacancy. By exploring the d-band centers, we found that ligand effects and surface tension effects contribute to the modification of the d-band centers of metal Fe atoms. An optimum Fe–N–C ORR catalyst should exhibit moderate surface stress properties and an ideal N, C ligand configuration. This study provides new insight into the effects of N atom doping in Fe–N-gra catalysts and could help guide the rational design of high-performance carbon-based ORR electrocatalysts.
1. Introduction
Energy, as the driving force of human society, plays a crucial role in social development. The two major problems of rapid depletion of energy and environmental pollution have received the utmost attention in recent years. Many countries are committed to exploring and developing new energy sources that are clean, efficient, and renewable. Fuel cells1–3 have the advantages of high-energy density, low cost, earth-abundancy, non-pollution, safety, and environmental benignity. Nonetheless, the kinetics of the cathodic oxygen reduction reaction (ORR) is much slower than anodization, seriously restricting the overall efficiency.4–9 Platinum (Pt) and platinum-based catalysts have been suggested to be the most effective ORR catalysts with high current densities and low overpotentials.10–12 The high cost of Pt, declining activity, and poor CO tolerance are its core problems. Therefore, the development of cost-effective, high-activity, high-stability, non-precious metal ORR catalysts is of great significance for advancing large-scale commercial applications of fuel cells.Metal single-atom catalysts (MSACs) such as metal-nitrogen coordination structure doped carbon-based catalysts, in particular the non-noble metal Fe, have emerged as a promising alternative to Pt for catalyzing ORR in fuel cells. Zhang Chao13 has designed novel Fe–N doped carbon catalysts supported by reductive graphene oxides via simple pyrolysis of polypyrrole composites. Excellent ORR performance can be attributed to the combined catalysis of Fe–Nx sites and Fe based nanoparticles (Fe3O4, Fe4C), as well as the rapid mass transfer and available active sites benefiting from high specific surface area and mesoporous structure. Liu Zaojin et al.14 developed an effective method to prepare the Fe–N–C catalyst for the core–shell structure and by calcining at 800 °C in the atmosphere of NH3, Fe2N encapsulated by the N doped carbon layers showed high activity, which was attributed to the cooperative effect of the mesoporous structure and Fe2N with the N-doped graphitic carbon layers promoting the mass transfer. A highly active and stable isolated monatomic Fe/N-doped porous carbon catalyst with Fe loading up to 2.16 wt% was prepared by Chen YuanJun.15 The catalyst exhibits superior ORR performance and it has been proved experimentally that maintaining the Fe as isolated atoms and incorporating N were essential for providing high performance. Liu Jingyan16 provided Fe–N-doped porous carbon originated from cheap petroleum asphalt (NPCA) by using a facile template synthesis method with urea as N source and α-Fe2O3 nano-particles as template and Fe source. The as-prepared NPCA calcined at 900 °C exhibits remarkable ORR performance, which could be ascribed to the doping of Fe–N (especially pyridine-type N), large specific surface area, and abundant porosity.
In addition to these experimental studies, a series of advances have also been extensively studied about the electrocatalytic activity of these Fe–N doped carbon materials based on density functional theory (DFT). Bai Xiaowan17 suggested that Fe–N3-gra is thermodynamically stable and the active site of the reaction is the Fe–N3 matrix and the surrounding six C atoms. The ORR reaction path is a direct four-electron process and forming the second water molecules is the rate determining step. Shyam et al.18 demonstrated that the smaller formation energy of the graphitic in-plane Fe–N4 sites in comparison with Fe–N2 sites means that the formation of Fe–N4 sites is more preferential. The calculated Gibbs free energy change of the elementary reactions showed that in the Fe–Nx (x = 2, 4) sites are spontaneous and the ORR on Fe–Nx (x = 2, 4) proceed along a single site four-electron process. Fe–N4 sites are identified as the prime candidate due to their higher stability and operating voltage. As a result of DFT calculations, Shen et al.19 found that the FeN2 centers on the surface/edge of N doped mesoporous carbon are superior to those of FeN4 centers. Because of enhanced electron transport and the lower interaction between FeN2 centers and *O2 and *OH intermediates. Wei et al.20 studied 2 kinds of Fe–N doped graphene and the electrocatalytic activity of Fe–N4-gra and Fe–N3-gra for the ORR is determined by the reaction step of the reduction of adsorbed *OH in acid conditions by calculating the Gibbs free energy. Nevertheless, Shyam21 showed that the largest barrier is given by the step of *OOH dissociation reaction which is 0.56 eV in alkaline conditions, indicating the rate determining step of Fe–N4-gra is *O–OH cleavage producing *O and OH−. Jing et al.22 investigated the FeN4 and Fe(CN)N4 sites embedded in the graphene layers and found that the four-electron reaction pathway was preferred in both FeN4 and Fe(CN)N4 sites at 0.8 V, while the two-electron reaction pathway was kinetically also likely on the Fe(CN)N4 site. The free energy barrier of the *O–OH bond cleavage on Fe(CN)N4 site is 0.41 eV, which is the rate determining step, while the release of the *OH intermediate is the rate determining step on FeN4 site. Chen et al.23 proposed that the high ORR activity of the FeN4 graphene nanosheets is derived from the highly dispersed and high-density coordinatively unsaturated Fe centers and the excellent stability is due to the unique limitation of the graphene matrix through four N atoms.
Although Fe–N doped carbon-based catalysts have achieved some experimental and theoretical results, it is difficult to control the doping amount and doping structure in a highly graphitized carbon host structure, and the active center of the catalyst is still very controversial. In this paper, we provide a better understanding of the effects of N atoms on Fe–N doped graphene catalysts in single and double vacancy based on DFT calculations. In particularly, we have systematically investigated the stability of the materials and adsorption properties, to get a deeper insight into the effects of the doping number and the doping configuration of N atoms. Moreover, density of state (DOS) of adsorbed O on the Fe–N–C sites and d-band centers calculations provide valuable information regarding N doping. Besides, the d band filling and the surface stress properties were further calculated and found well connected with binding ability of the ORR intermediates. Our computations show that the regularity of N atoms tuning and provide a theoretical guide for the preparation of ORR catalysts.
2. Computational methodologies
2.1 Methods
All calculations in this paper were carried out within the spin-polarized DFT framework as implemented in DMol3 code.24,25 The PBE parameterization of the generalized gradient approximation (GGA)26 was adopted to describe the electronic exchange and correlation effects.27 The convergence tolerance for energy change, max force, and max displacement were 1 × 10−5 hartree, 2 × 10−3 hartree per Å, and 5 × 10−3 Å for geometry optimization. Double numerical plus polarization (DNP) function basis sets and semi-core pseudopotentials28 were employed in the calculations. The orbital occupation was applied with a smearing of 0.005 Ha to achieve an accurate electronic convergence. The Monkhorst–Pack scheme K-points grid sampling was set as 5 × 5 × 1. To ensure high quality results, the realspace global orbital cutoff radius was chosen as high as 4.4 Å. A conductor-like screening model (COSMO) was used to simulate water H2O environment29 and the dielectric constant was set as 78.54 for the H2O solvent. The calculated C–C bond length of graphene was 1.420 Å, consistent with the results obtained by previous calculations.30 Frequency analyses were further conducted for each models established to further confirm that all atoms involved were relaxed during geometry optimization.2.2 Computational content
(1) The adsorption energies (Eads) of the ORR intermediates is defined as| Eads = E*m − E* − Em | (1) |
(2) The variation of Gibbs free energy for each step of ORR is given by31–33
| ΔG = ΔEDFT + ΔZPE − TΔS + ΔGU + ΔGpH | (2) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 × pH × kBT, where kB is the Boltzmann constant and pH = 0 in acid conditions.
10 × pH × kBT, where kB is the Boltzmann constant and pH = 0 in acid conditions.
Especially, we considered the four-electron associative pathway for ORR in acid conditions, which is the dominant mechanism for Fe–N doped graphene catalysts.35
| * + O2(g) + H+ + e− → *OOH | (3) |
| *OOH + H+ + e− → *O + H2O(l) | (4) |
| *O + H+ + e− → *OH | (5) |
| *OH + H+ + e− → H2O(l) + * | (6) |
The ORR overpotential is then determined by
| ηORR = 1.23 − ΔGmin/e | (7) |
(3) The formation energies (Ef) of Fe–N–C defects were calculated by using the expression,
| Ef = EFe–N–C + yμC − (Egraphene + xμN + μFe) | (8) |
2.3 Model
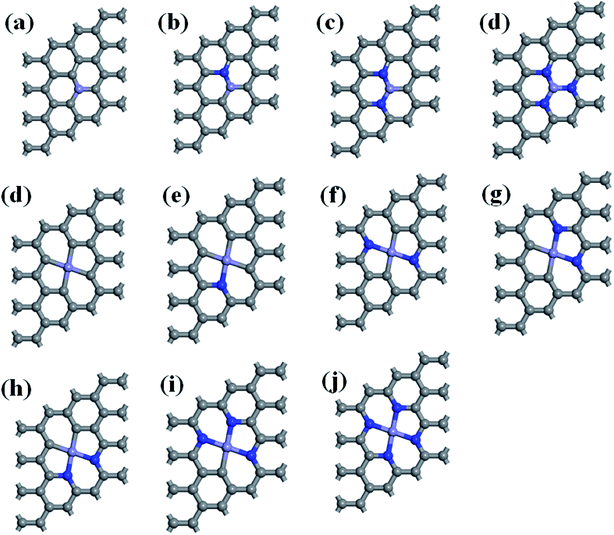
This study used a periodic (4 × 4) supercell of graphene with Fe–N–C coordinated structure. Graphitic Fe–N–C defects were created by decorating graphene single vacancy (SV) and double vacancy (DV) with N atoms, respectively, and then incorporating Fe atom at the center of SV and DV in a single step. The modulus unit cell vector in the z direction was set to 15 Å, which should be sufficiently large to avoid the interlayer interaction. We investigated several kinds of Fe–N–C structures, which are named as Fe–3C, Fe–1N, Fe–2N, Fe–3N defect in single vacancy and Fe–4C, Fe–1N–3C, Fe–2N–2C, Fe–3N–1C, Fe–4N defect in double vacancy, respectively. Fe–2N–2C defects correspond to three different configurations, which are Fe–2N–2C-oppo defect, two N atoms at the opposite sites of Fe atom. Fe–2N–2C-pen defect, two adjacent carbon atoms located in the five-membered ring. Fe–2N–2C-hex defect, two adjacent carbon atoms located in the six-membered ring as shown in Fig. 1.3. Results and discussions
3.1 Stability of Fe–N–C-gra
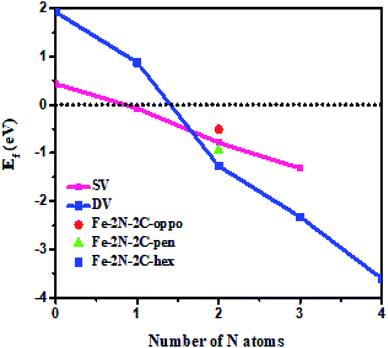
In the first step, we have calculated defect Ef and investigated the effects of the doping number and the doping configuration of N atoms on the Ef in single-double vacancy. The Ef of Fe–N–C defects are the function of the doping number and the doping configuration of N atoms as shown in Fig. 2. With the number of the N atoms increasing, the Ef dropped for the double vacancy group, resulting in the higher probability to observe the most stable Fe–4N defect in Fe–N–C-gra electrocatalysts41 and it is consistent with previous computations for the Co and Ni analogue defect motifs.42,43 The speed of Ef decreasing of the double vacancy structures is faster than that of single vacancy, indicating that the effect of adding N atoms in double vacancy is superior to that of single vacancy. Unfortunately, the Ef of Fe–3C, Fe–4C, and Fe–1N–3C defect are positive, indicating it cannot become a stable catalyst for ORR. The Ef of the other configurations are negative, corresponding to an exothermic process. The more negative Ef of the Fe–2N–2C-hex defect in comparison with other Fe–2N–2C systems demonstrates that the formation of Fe–2N–2C-hex defect is energetically favorable. Summing up, the reasons for the change in the Ef of N atoms doping can be explained: the defective graphene located on the surface contain a large number of dangling bonds and the additional electrons of the N atoms can stabilize the unpaired electrons of the uncoordinated C atoms, resulting in the reduction of system energy. The differences in the Ef of Fe–2N–2C systems are mainly caused by the relative positions of two N atoms. In comparison with Fe–2N–2C-hex defect, the lower doping density for Fe–2N–2C-oppo defect and the much stronger repulsive interaction for Fe–2N–2C-pen defect are the main drawbacks accounting for the inferior defect Ef. Hence, the formation of Fe–2N–2C-hex defect is more preferential. In term of the doping concentration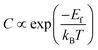 , where Ef, kB, T are the formation energy, Boltzmann constant and temperature, respectively. More negative Ef means that doping produces a higher doping concentration in the graphene plane. These results indicate that, when the doping number of N atoms is more than one (except Fe–2N–2C-oppo defect), the double vacancy structures have outstanding doping efficiency than the single vacancy.
, where Ef, kB, T are the formation energy, Boltzmann constant and temperature, respectively. More negative Ef means that doping produces a higher doping concentration in the graphene plane. These results indicate that, when the doping number of N atoms is more than one (except Fe–2N–2C-oppo defect), the double vacancy structures have outstanding doping efficiency than the single vacancy.
3.2 Adsorption properties of oxygenated species and ORR performance
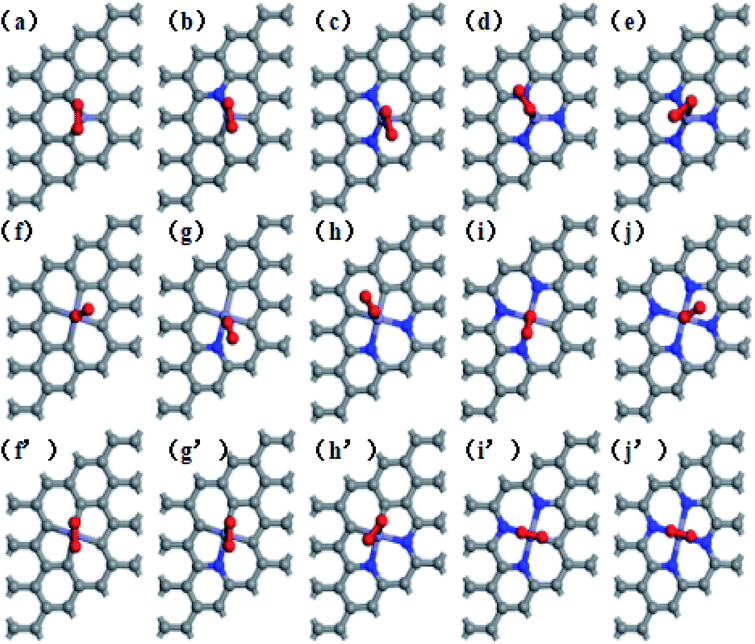
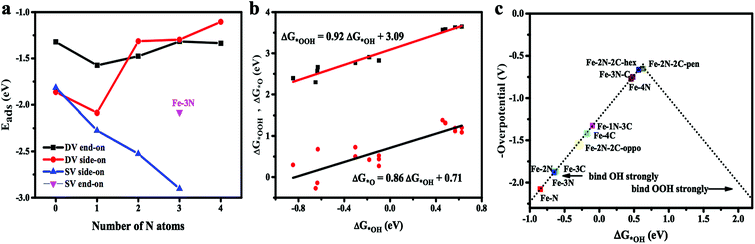
Adsorption of oxygen molecule is a prerequisite of the reactions proceeded on the active site of the catalyst. Oxygen adsorption process has two equilibrium configurations.44 One situation is that an oxygen atom is adsorbed on the metal, while the other O atom is pointing away from the catalyst surface, namely, end-on configuration. The other situation is that two oxygen atoms simultaneously form two Fe–O bonds with O2 molecular in parallel on the surface of the catalyst, namely, side-on configuration. The optimized adsorption configurations are shown in Fig. 3. As is clearly shown in Fig. 3a–c, that Fe–3C, Fe–1N, and Fe–2N site have only one adsorption configuration for O2 molecule in the single vacancy. The two obtained stable configurations of Fe–3N site (end-on and side-on) are presented in Fig. 3d and e, which shows that the O2 molecule is stably anchored on the Fe center with the Eads of −2.08 and −2.90 eV, respectively. It should be noticed that side-on mode is found to be energetically favorable. In double vacancy, both side-on configuration and end-on configuration exist simultaneously. Indeed, it clearly appears from Fig. 4a, which shows that with the increase of the number of N atoms in single vacancy, the Eads of O2 molecule on the side-on configuration gradually increases. The Eads of O2 molecule on side-on configuration in Fe–1N–3C site suffers a sharp increase, and then the Eads of O2 molecule decreases as the doping number ranging from 1 to 4 in double vacancy, consistent with the results obtained by the end-on configuration. With the increase of N doped atoms in single and double vacancy, the difference in the tendency of the Eads of O2 molecule might be due to the different hybridization modes of the central Fe atom. In double vacancy, the calculated Eads of O2 molecule is in the range of −2.17 to −1.10 eV in the side-on configuration (see ESI, Table S1†), which is greater than the end-on configuration, indicating that the doping of N atoms has a significant influence on the side-on configuration. Meanwhile, when two adjacent carbon atoms located in the five-membered ring, the most stable adsorption manner is changed from side-on to end-on configuration, which properly results from the repulsive effect between the two nitrogen atoms. This suggests that the repulsive interaction between long pair electrons of O2 molecule and graphene π electrons becomes weaker in end-on configuration. The reasons may be that as the number of N atoms increases, the increase in the repulsive interaction between O2 molecules and Fe–N doped graphene sheets results from a donation of electrons from the Fe–N doped graphene sheets to O2 molecules. Compared with the repulsive effect, the side-on configuration is somewhat stronger than end-on configuration (the doping number > 1 except Fe–2N–2C-oppo site), hence, the end-on configuration is more stable than side-on configuration. Not only different central transition metal atoms45 but also N atoms doping could result in different adsorption manner of O2 molecules. The details for the calculated Fe–O and O–O bond lengths are given in ESI (see Table S1†).Adsorption free energy for key oxygenated intermediates, *OOH, *O and *OH (* is defined as the surface of the Fe–N doped graphene) are calculated and the results are given in Table 1. For the ΔG*O, it can be seen from Table 1 that in the single vacancy, ΔG*O gradually decreases from 0.68 to −0.27 eV as the number of N atoms increases. The inverse direction in the change of the ΔG*O occurs in the double vacancy and ΔG*O gradually rises from 0.42 to 1.38 eV along with the number of N atoms growth. The calculation of the ΔG*OOH and ΔG*O is a function of the ΔG*OH in Fe–N doping structures in Fig. 4b. The data points of ΔG*OH vs. ΔG*OOH almost fall on the fitted linear line. The ΔG*OOH and ΔG*OH show a scaling relation of ΔG*OOH = 0.92 ΔG*OH + 3.09 with the coefficient of determination (R2) of 0.95 very similar to that observed with N-doped graphenes and metal-N coordination structures.46,47 However, it has been believed that the slope less than 1 is probably deriving from the weaker adsorption of *OOH. Comparatively, ΔG*O vs. ΔG*OH is a relatively poor correlation, ΔG*O = 0.81 ΔG*OH + 0.77, and the coefficient of determination (R2) is 0.73. In addition, the ΔG*OH vs. ΔG*O dependence on Fe–N doped graphene considered here exhibits a different slope from that N-doped graphenes and metal-N coordination structures.46,47 This is due to the chemisorption of *O is more complicated than that of *OH and *OOH, which could either form single bond with Fe atom or form epoxy bonds with Fe and C atom. It has been, indeed, found that data points which significantly deviate from the fitted linear line of ΔG*O vs. ΔG*OH are mainly the bridge adsorbed *O.
| Defect | ΔG*OOH | ΔG*OH | ΔG*O |
|---|---|---|---|
| Fe–3C | 2.66 | −0.63 | 0.68 |
| Fe–1N | 2.39 | −0.85 | 0.30 |
| Fe–2N | 2.57 | −0.64 | −0.14 |
| Fe–3N | 2.29 | −0.65 | −0.27 |
| Fe–4C | 2.91 | −0.18 | 0.42 |
| Fe–1N–3C | 2.82 | −0.10 | 0.44 |
| Fe–2N–2C-hex | 3.63 | 0.57 | 1.19 |
| Fe–3N–1C | 3.58 | 0.48 | 1.32 |
| Fe–4N | 3.57 | 0.46 | 1.38 |
However, results demonstrated that the difference between ΔG*OH and ΔG*OOH is 3.09 eV for Fe–N–C-gra catalysts instead of 2.46 eV,48 which is for an ideal catalyst, resulting in the overpotential deviating from the equilibrium potential, indicating it is impossible to avoid theoretical overpotential. A plot of ΔG*OH vs. the negative of the overpotentials (−η) of Fe–N doped graphene shows a volcano-shaped plot. From Fig. 4c, it can be seen that the Fe–2N–2C-pen defect is near the summit of the volcano and it is identified to have a minimum ORR overpotential, which is estimated to be 0.652 V. The Fe–2N–2C-pen-gra electrocatalyst exhibits remarkable electrocatalytic performance for ORR. The calculated overpotentials gradually grow in the following order: Fe–2N–2C-pen (0.652 V) < Fe–2N–2C-hex (0.663 V) < Fe–3N–C (0.748 V) < Fe–4N (0.772 V) < Fe–1N–3C (1.328 V) < Fe–4C (1.412 V) < Fe–2N–2C-oppo (1.534 V) < Fe–3C (1.861 V) ≈ Fe–2N (1.865 V) < Fe–3N (1.880 V) < Fe–1N (2.077 V), indicating that the overpotentials of the single vacancy structures prefer to increase while the overpotentials of the double vacancy structures fall after the addition of N atoms (except Fe–2N–2C-oppo site). A conclusion could be made that moderate N-doping levels and doping configuration could enhance the ORR activity of Fe–N coordination structures in double vacancy and doping N atoms is not effective for ORR activity in single vacancy. The Fe–N–C defects prefer to located at the left branch of the volcano plot, indicating that no matter the single vacancy or double vacancy, Fe–N–C active sites bind *OH strongly. According to the computed free energy diagram (Fig. 5), the ORR steps except the *OH reduction (eqn (6)) are all downhill at zero potential. The reaction step (eqn (6)) is uphill in single vacancy and part of the double vacancy structures (Fe–4C defect, Fe–1N–3C defect, Fe–2N–2C-oppo defect), which is the thermodynamic rate determining step (RDS). These calculated free energies suggest that formation of the second H2O (eqn (6)) moleculars might be rate determining step of ORR on Fe–N–C active sites except Fe–2N–2C-pen site, whose rate determining step is the transformation of *O to *OH (eqn (5)), which shows that *O is more stable on Fe–2N–2C-pen site. In addition, the rate-determined step for the ORR process of both single vacancy and double vacancy is the last step that the *OH reduced to H2O, indicating that the activity decrease in the Fe–N–C structures due to the intermediate *OH being difficult to remove from the surface sites.
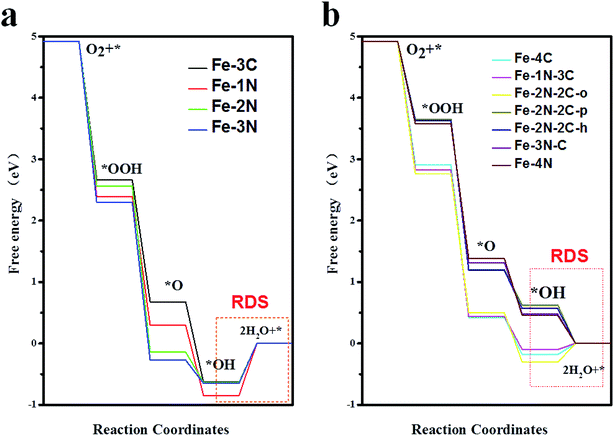 | ||
| Fig. 5 Free energy profiles of Fe–N doped in single vacancy (a) and double vacancy (b) graphene structures at zero potential. The red frame shows the rate-determined step (RDS) for each ORR process. | ||
3.3 DOS analyses of Fe–N–C sites with adsorbed O atoms
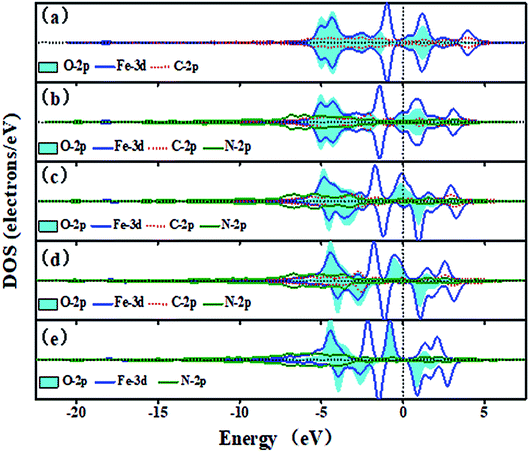
It is clear that the ORR activity of Fe–N doped graphene catalysts depends on the binding strength of oxygen-containing species based on the aforementioned analyses. The electronic structure of Fe–N–C sites with adsorbed O atoms has been investigated in order to understand the bonding characteristics. To facilitate comparison, projected density of states (PDOSs) are plotted for the same energy window from −20 to 5 eV and −22.5 to 7.5 eV in single-double vacancy, respectively.Fig. 6 shows the trend of PDOSs of adsorbed O atoms on the Fe–N–C-gra catalysts as the number of N atoms increases from 0 to 3 in single vacancy. As can be seen from Fig. 6, the PDOS analyses reveal that the overlap of O-2p and Fe-3d states is mainly localized at −6 to 5 eV and the nearest shark peak at the Fermi level mainly originates from O-2p and Fe-3d states. With the increase in the number of N atoms, p–d hybridizations between Fe, C, and N atoms cause O-2p and Fe-3d states to shift to lower energy, indicating that more electrons are transferred to the adsorbed O atoms. There are strong hybridizations between O-2p and Fe-3d states from −5 eV to Fermi level, indicating a strong interaction of adsorbed O atoms with the surface (Fig. 6a–d). From Fig. 6b–d, it is evident that introduction of N atoms induces a new phase α, which could provide additional electrons in the process of electrons transferring from Fe to O atom. In addition, the new phase α induced by N atoms matches well with the Fe-3d states, thereby suggesting the excellent adsorption interaction between the Fe and O atom in the subsequent proton-transfer process. The appearance of N atoms results in non-spin polarization, indicating that the adsorbed O atoms on the Fe–3C-gra contains unpaired electrons and the introduction of N atoms makes all the electrons be paired. When the N atoms appeared in the cell, a contribution at the Fermi level belonged to the bonding states formed by the Fe-3d and O-2p states. Bonding orbital filling of electrons enlarges the bond strength between Fe–N–C sites and O atoms (Fig. S2 in the ESI†). Meanwhile, the Eads of the O atoms gradually increases in the single vacancy, which is consistent with the results obtained by the DOS. The Fe–O bond length decreased first and then increased from Fig. S2.† When two N atoms are introduced into the single vacancy, the minimum bond length for Fe–O is calculated to be 1.617 Å. The anomalous Fe–O bond length in the Fe–3N site is due to the increase in the repulsive interaction between O atoms and N atoms.
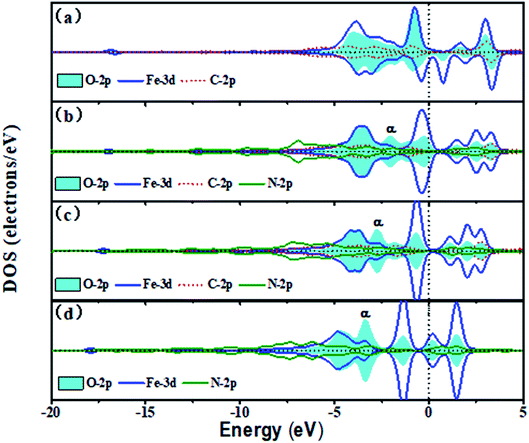 | ||
| Fig. 6 The DOS of the adsorbed O atom on the Fe–N–C-gra in single vacancy (a) O on Fe–3C site, (b) O on Fe–1N site, (c) O on Fe–2N site, (d) O on Fe–3N site. Spin up and down states are shown. | ||
Fig. 7 shows the trend of PDOSs of adsorbed O atoms on the Fe–N–C-gra catalysts as the number of N atoms increases from 0 to 4 in double vacancy. As can be seen from Fig. 7, the PDOS analyses reveal that the overlap of O-2p and Fe-3d states is mainly localized at −6 to 5 eV and the nearest shark peak at the Fermi level mainly originates from O-2p and Fe-3d states. When the number of N atoms is beyond one, the DOS for the absorbed O atoms on Fe–N–C sites changes from non-spin polarization to spin polarization, indicating that there exist unpaired electrons in the systems with more than one nitrogen atom. There are strong hybridizations between O-2p and Fe-3d states from −6 eV to Fermi level, indicating a strong interaction of adsorbed O atoms with the surface (Fig. 7a–e). Furthermore, for α electron, with the growth of the number of N atoms, p–d hybridizations between Fe, C, and N atoms cause the energy range of Fe-3d states to be narrower. The energy splitting for the Fe-3d states observed around −4 eV is gradually degraded from Fig. 7a–c. For β electron, the degree of energy splitting for the Fe-3d states observed around −5 eV progressively increases and moves toward the higher energy as the number of N atoms increases. The incorporation of N atoms results in the anti-bonding orbital formed by the Fe-3d and O-2p states moving toward the lower energy. The filling of electrons in the anti-bonding orbital weakens the bond strength between Fe–N–C sites and O atoms. From Fig. S2,† it also can be seen that in the double vacancy, the Fe–O bond length increases successively with the increasing numbers of the N atoms and when it is four N-coordinate, the bond length reaches the longest, which is 1.667 Å. The Eads of the O atoms decreases with the increase in N doping number, which proves that the interaction between metal Fe atoms and O atoms decreases and agrees well with the results obtained by the DOS. Plots in Fig. S1 in ESI,† exhibiting the DOS plots for the three Fe–2N–2C–O configurations, shows that Fe–2N–2C-hex site with adsorbed O atoms exhibits DOS very similar to that of the DOS of Fe–2N–2C-pen site. The rather small differences of them are the peak height and peak width at the Fermi level and the reason is that the repulsive effect caused by the relative positions of two N atoms.
It can be concluded from the above results that for both the single and vacancy structures, their ORR activity will be promoted by weakening the strong binding strength between the oxygenate species and their surface sites. The incorporation of N atoms results in the anti-bonding orbital formed by the Fe-3d and O-2p states moving toward the lower energy. It will make more electrons to fill in these anti-bonding orbital and thus weaken the strong interaction with the ORR species, which will push the Fe–N–C structures to the apex of the ORR activity volcano plot.
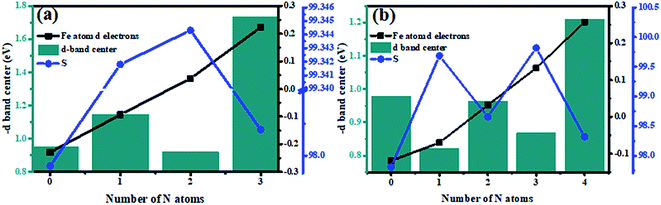
3.4 Calculations on d-band centers and surface area of each Fe–N–C-gra
The d-band center of the metal directly can exert great influences on the adsorption strength of the species and further determine its catalytic performance.49,50 The d-band centers of Fe–N–C-gra catalysts have been calculated and shown in Fig. S3 (see ESI†), it can be seen that the Fe–3N and Fe–4N sites with the highest N doping content exhibit the lowest energy level of d-band centers compared with the other sites among the single and double vacancy group, respectively. In addition, the geometric structure deformation among Fe–N–C-gra catalysts were further studied. For the single-double vacancy, the observed lattice constants (a, b and the included angle γ) them could be changed by the addition of N atoms, leading to surface stress effect. The magnitude of surface stress is usually reflected in the change of average bond lengths: surface tension corresponds to the elongation of the average bond lengths and the surface compress corresponds to the shortening of the average bond lengths. However, the average bond length cannot be used due to the following reasons: (1) three different atoms involved Fe, C, and N atoms in Fe–N–C-gra catalysts, the average bond lengths are therefore meaningless. (2) The changes of lattice constants are not synchronous. Therefore, the magnitude of the shift in the surface stress is represented by calculating area S (S = a × b × sin(γ)). When the surface of the lattice was tensed (S > S0, S0 represents the Fe–3C-gra (SV) or Fe–4C-gra (DV)), the d orbital overlaps are decreased, resulting in a sharpening of the d band and an upshift in its the d-band center. On the other hand, the surface of the lattice was pressed (S < S0), the d orbital overlaps will be increased, resulting in a broadening of the d band and a lowering of its d-band center.51,52 It can be seen from Fig. 8 that after addition of the N atoms, for either single vacancy or double vacancy structure, the surface atoms were stretched away from each other (larger surface area S), resulting in an upshift in its the d-band center. Moreover, except for the surface stress effect which will modify the energy levels of the d-band centers of catalysts. The ligand species and configurations will affect the d-band centers of Fe atoms as well. In order to study the ligand effect of N atom dopants on the d-band centers of Fe atoms, the Mulliken charge populations were conducted in Fe–N–C-gra catalysts and the d electrons of surface Fe atoms (d band filling) were shown in Fig. 8. It is obvious that d band filling decrease with increasing doping number of the N atoms. The decrease in d band filling of the surface Fe atoms result in the d-band center moving towards Fermi energy level, which will further ascend the energy of the anti-bonding orbital between Fe and O, thus leads to a stronger interaction between Fe and oxygenated species. From Fig. 8a, Fe–1N-gra and Fe–2N-gra monolayer are under more substantial tensile strain compared to other structures in single vacancy. Meanwhile, the S difference between Fe–1N-gra and Fe–2N-gra is only 0.003, but the γ of Fe–2N-gra is 120.452° larger than that of Fe–1N-gra (120.199°), indicating the tensile strain of Fe–2N-gra is larger than that of Fe–1N-gra, which will lead to d-band center of Fe–2N-gra closer to the Fermi energy level. At this point, the ligand effect and surface stress effect on the d-band center will result in the d-band center of Fe–2N-gra more inclined to Fermi level than Fe–1N-gra, which will lead to a higher binding ability and low activity corresponds with Fig. S2 in the ESI.† Besides, the case of double vacancy is similar to single vacancy. The surface atoms of Fe–1N–3C-gra and Fe–3N–1C-gra are subjected to tensile strain and the interactions between ligand effect and surface tension effect bring about the d-band centers of these two defects to move to Fermi level. Synthesis of the above situation, it is not difficult to find that the two critical factors that contribute to the modification of the d-band centers of metal Fe atoms. The incorporation of N atoms essentially regulates surface strain stress and the electron structure around the Fe–N–C moieties. The more nitrogen involved and the larger surface strain effect will lead a larger interaction between the Fe center and the ORR oxygenated species, which will further affect the ORR performance on the Fe atoms. Thus, a Fe–N–C catalyst that possesses the optimum ORR activity should exhibit a moderate surface stress property and an ideal N, C ligand configurations.4. Conclusions
The electrocatalytic activity of Fe–N doped graphene for promoting ORR has been systematically investigated based on DFT computations. The main results and conclusions of the calculations are as follows: (1) in the single-double vacancy, the Ef dropped off with the increasing number of the N atoms. When the doping number of N atoms is more than one (except Fe–2N–2C-oppo defect), the double vacancy structures have a more outstanding doping efficiency than the single vacancy. (2) N atom doping could result in a different adsorption manner of O2 molecules. (3) The calculated adsorption free energies of pivotal oxygenated species (*O, *OH, and *OOH) have an approximately scaling relationship with each other at surface sites in Fe–N doping structures. (4) The theoretical overpotential value of Fe–2N–2C-pen site is a minimum of 0.652 V, and correspondingly possesses the higher ORR catalytic activity. Moderate N-doping levels and doping configuration could enhance the ORR activity of Fe–N coordination structures in double vacancy and doping N atoms is not effective for ORR activity in single vacancy. (5) The rate determining step of the ORR on the Fe–N–C-gra surface is the desorption of *OH except Fe–2N–2C-pen site, whose rate determining step is the transformation of *O to *OH. (6) Both ligand effect and surface tension effect contribute to the modification of the d-band centers of metal Fe atoms after the addition of N atoms and the incorporation of N atoms essentially regulates surface stress and the electron structure around the Fe–N–C moieties. The more nitrogen involved and the larger surface strain effect will lead a larger interaction between the Fe center and the oxygenated species, which will further affect the ORR performance on the Fe atoms. A Fe–N–C catalyst that possesses the optimum ORR activity should exhibit a moderate surface stress property and an ideal N, C ligand configuration. This study provides new insight into the effects of N atom doping in Fe–N–C-gra catalysts and could help guide the rational design of high-performance carbon-based ORR electrocatalysts.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The simulation was carried out on the resources provided by the Tianjin University high performance computing center and we are thankful for the supports. The authors acknowledge the financial support of Key Laboratory of Metal Fuel Cell of Sichuan Province.References
- M. Armand and J. M. Tarascon, Building better batteries, Nature, 2008, 451(7179), 652–657 CrossRef CAS PubMed.
- M. W. And and R. J. Brodd, What are Batteries, Fuel Cells, and Supercapacitors, (Chem. Rev. 2003, 104, 4245−4269. Published on the Web 09/28/2004.), Chemical Reviews, 2005, 105(3), 1021 CrossRef.
- M. K. Debe, Electrocatalyst Approaches and Challenges for Automotive Fuel Cells, Nature, 2012, 486(7401), 43–51 CrossRef CAS PubMed.
- B. C. H. Steele and A. Heinzel, Review article materials for fuel-cell technologies, Nature, 2001,(6861), 345–352 CrossRef CAS PubMed.
- S. Guo, S. Zhang and S. Sun, Tuning Nanoparticle Catalysis for the Oxygen Reduction Reaction, Angew. Chem., Int. Ed., 2013, 52(33), 8526–8544 CrossRef CAS PubMed.
- B. Wang, Recent development of non-platinum catalysts for oxygen reduction reaction, J. Power Sources, 2005, 152(1), 1–15 CAS.
- G. Wu and P. Zelenay, Nanostructured nonprecious metal catalysts for oxygen reduction reaction, Acc. Chem. Res., 2013, 46(8), 1878–1889 CrossRef CAS PubMed.
- N. M. Marković, T. J. Schmidt, V. Stamenković and P. N. Ross, Oxygen Reduction Reaction on Pt and Pt Bimetallic Surfaces: A Selective Review, Fuel Cells, 2001, 1(2), 105–116 CrossRef.
- Y. Bing, H. Liu, L. Zhang, D. Ghosh and J. Zhang, ChemInform Abstract: Nanostructured Pt-Alloy Electrocatalysts for PEM Fuel Cell Oxygen Reduction Reaction, Chem. Soc. Rev., 2010, 39(6), 2184–2202 RSC.
- M. Shao, Q. Chang, J. P. Dodelet and R. Chenitz, Recent Advances in Electrocatalysts for Oxygen Reduction Reaction, Chem. Rev., 2016, 116(6), 3594–3657 CrossRef CAS.
- Y. Nie, L. Li and Z. Wei, Recent advancements in Pt and Pt-free catalysts for oxygen reduction reaction, Chem. Soc. Rev., 2015, 44(8), 2168–2201 RSC.
- Y. Jiao, Y. Zheng, M. Jaroniec and S. Z. Qiao, ChemInform Abstract: Design of Electrocatalysts for Oxygen- and Hydrogen-Involving Energy Conversion Reactions, ChemInform, 2015, 46(25), 2060–2086 CrossRef.
- C. Zhang, J. Liu, Y. Ye, Z. Aslam, R. Brydson and C. Liang, Fe-N-Doped Mesoporous Carbon with Dual Active Sites Loaded on Reduced Graphene Oxides for Efficient Oxygen Reduction Catalysts, ACS Appl. Mater. Interfaces, 2018, 10(3), 2423–2429 CrossRef CAS.
- Z. Liu, J. Yu, X. Li, L. Zhang, D. Luo and X. Liu, et al., Facile synthesis of N-doped carbon layer encapsulated Fe2N as an efficient catalyst for oxygen reduction reaction, Carbon, 2017, 127, 636–642 CrossRef.
- Y. Chen, S. Ji, Y. Wang, J. Dong, W. Chen and Z. Li, et al., Isolated Single Iron Atoms Anchored on N-Doped Porous Carbon as an Efficient Electrocatalyst for the Oxygen Reduction Reaction, Angew. Chem., 2017, 56(24), 6937–6942 CrossRef CAS PubMed.
- J. Liu, Y. Liu, P. Li, L. Wang, H. Zhang and H. Liu, et al., Fe-N-doped porous carbon from petroleum asphalt for highly efficient oxygen reduction reaction, Carbon, 2018, 126, 1–8 CrossRef CAS.
- X. Bai, E. Zhao, W. Wang, Y. Wang, K. Li and L. Lin, et al., A direct four-electron process on Fe-N3 doped graphene for the oxygen reduction reaction: a theoretical perspective, RSC Adv., 2017, 7(38), 23812–23819 RSC.
- S. Kattel, P. Atanassov and B. Kiefer, A density functional theory study of oxygen reduction reaction on non-PGM Fe-Nx-C electrocatalysts, Phys. Chem. Chem. Phys., 2014, 16(27), 13800–13806 RSC.
- H. Shen, E. Gracia-Espino, J. Ma, H. Tang, M. Xamxikamar and W. Thomas, et al., Atomically FeN2 moieties dispersed on mesoporous carbon: a new atomic catalyst for efficient oxygen reduction catalysis, Nano Energy, 2017, 35(5), 9–16 CrossRef CAS.
- W. Liang, J. Chen, Y. Liu and S. Chen, et al., Density-Functional-Theory Calculation Analysis of Active Sites for Four-Electron Reduction of O2 on Fe/N-Doped Graphene, ACS Catal., 2015, 4(11), 4170–4177 CrossRef.
- S. Kattel and G. Wang, Reaction Pathway for Oxygen Reduction on FeN4 Embedded Graphene, J. Phys. Chem. Lett., 2015, 5(3), 452–456 CrossRef.
- J. Sun, Y. Fang and Z. Liu, Electrocatalytic oxygen reduction kinetics on Fe-center of nitrogen-doped graphene, Phys. Chem. Chem. Phys., 2014, 16(27), 13733–13740 RSC.
- X. Chen, L. Yu, S. Wang, D. Deng and X. Bao, Highly active and stable single iron site confined in graphene nanosheets for oxygen reduction reaction, Nano Energy, 2016, 32, 353–358 CrossRef.
- B. Delley, From molecules to solids with the DMol3 approach, J. Chem. Phys., 2000, 113(18), 7756–7764 CrossRef CAS.
- B. Delley, J. Chem. Phys., 1990, 92, 508–518 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson and D. J. Singh, et al., Atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46(11), 6671–6687 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77(18), 3865–3868 CrossRef CAS PubMed.
- B. Delley, Hardness conserving semilocal pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66(15), 155125–155133 CrossRef.
- A. Klamt and G. Schuurmann, J. Chem. Soc., Perkin Trans. 2, 1993, 799–805 RSC.
- S. Kattel, P. Atanassov and B. Kiefer, Catalytic activity of Co-Nx/C electrocatalysts for oxygen reduction reaction: a density functional theory study, Phys. Chem. Chem. Phys., 2012, 15(1), 148–153 RSC.
- E. Skúlason, T. Bligaard, S. Gudmundsdóttir, F. Studt, J. Rossmeisl and F. Abild-Pedersen, et al., A theoretical evaluation of possible transition metal electro-catalysts for N2 reduction, Phys. Chem. Chem. Phys., 2011, 14(3), 1235–1245 RSC.
- J. G. Howalt and T. Vegge, Electrochemical ammonia production on molybdenum nitride nanoclusters, Phys. Chem. Chem. Phys., 2013, 15(48), 20957–20965 RSC.
- J. G. Howalt, T. Bligaard, J. Rossmeisl and T. Vegge, DFT based study of transition metal nano-clusters for electrochemical NH3 production, Phys. Chem. Chem. Phys., 2013, 15(20), 7785–7795 RSC.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin and T. Bligaard, et al., Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108(46), 17886–17892 CrossRef.
- C. M. Del, P. Ocón and J. Poyato, Comparative Study of Oxygen Reduction Reaction Mechanism on Nitrogen-, Phosphorus-, and Boron-Doped Graphene Surfaces for Fuel Cell Applications, J. Phys. Chem. C, 2015, 119(4), 2004–2009 CrossRef.
- R. Faccio, L. Fernandez-Werner, H. Pardo, C. Goyenola, O. N. Ventura and A. W. Mombru, Electronic and Structural Distortions in Graphene Induced by Carbon Vacancies and Boron Doping, J. Phys. Chem. C, 2010, 114, 18961–18971 CrossRef CAS.
- A. L. Garcia, S. E. Baltazar, A. H. Romero, J. F. Perez Robles and A. Rubio, Influence of S and P Doping in a Graphene Sheet, J. Comput. Theor. Nanosci., 2008, 5(5), 2221–2229 CrossRef CAS.
- Y. Shang, J. X. Zhao, H. Wu, Q. H. Cai, X. G. Wang and X. Z. Wang, Chemical functionalization of pyridine-like and porphyrin-like nitrogen-doped carbon (CNx) nanotubes with transition metal (TM) atoms: a theoretical study, Theor. Chem. Acc., 2010, 127(5–6), 727–733 Search PubMed.
- E. Finazzi, C. D. Valentin, A. Selloni and G. Pacchioni, First Principles Study of Nitrogen Doping at the Anatase TiO2 (101) Surface, J. Phys. Chem. C, 2007, 111(26), 9275–9282 CrossRef CAS.
- K. Yang, Y. Dai, B. Huang and S. Han, Theoretical study of N-doped TiO2 rutile crystals, J. Phys. Chem. B, 2006, 110(47), 24011–24014 CrossRef CAS PubMed.
- M. Ferrandon, A. J. Kropf, D. J. Myers, K. Artyushkova, U. Kramm and P. Bogdanoff, Multitechnique Characterization of a Polyaniline-Iron-Carbon Oxygen Reduction Catalyst, J. Phys. Chem. C, 2012, 116(30), 16001–16013 CrossRef CAS.
- S. Kattel, P. Atanassov and B. Kiefer, Stability, Electronic and Magnetic Properties of In-Plane Defects in Graphene: A First-Principles Study, J. Phys. Chem. C, 2012, 116(14), 8161–8166 CrossRef CAS.
- S. Kattel, P. Atanassov and B. Kiefer, Density Functional Theory Study of Ni-Nx/C Electrocatalyst for Oxygen Reduction in Alkaline and Acidic Media, J. Phys. Chem. C, 2012, 116(33), 17378–17383 CrossRef CAS.
- Z. Shi, H. Liu, K. Lee, E. Dy, J. Chlistunoff and M. Blair, et al., Theoretical Study of Possible Active Site Structures in Cobalt- Polypyrrole Catalysts for Oxygen Reduction Reaction, J. Phys. Chem. C, 2011, 115(33), 16672–16680 CrossRef CAS.
- Z. Wang, J. X. Zhao, Q. Cai and F. Li, Computational Screening for High-Activity MoS2 Monolayers-Based Catalysts for the Oxygen Reduction Reaction via Substitutional Doping with Transition Metal, J. Mater. Chem. A, 2017, 5(20), 9842–9851 RSC.
- J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Density functional theory in surface chemistry and catalysis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108(3), 937–943 CrossRef PubMed.
- M. Li, L. Zhang, Q. Xu, J. Niu and Z. Xia, N-doped graphene as catalysts for oxygen reduction and oxygen evolution reactions: theoretical considerations, J. Catal., 2014, 314, 66–72 CrossRef CAS.
- I. C. Man, H. Su, F. Calle-Vallejo, H. Hansen, J. Martinez and N. Inoglu, et al., Cover Picture: Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces (ChemCatChem 7/2011), ChemCatChem, 2011, 3(7), 1085 CrossRef.
- B. Hammer and J. K. Nørskov, Electronic factors determining the reactivity of metal surfaces, Surf. Sci., 1995, 343, 211–220 CrossRef CAS.
- A. Ruban, B. Hammer, P. Stoltze, H. L. Skriver and J. K. Nørskov, Surface electronic structure and reactivity of transition and noble metals 1, J. Mol. Catal. A: Chem., 1997, 115(3), 421–429 CrossRef CAS.
- J. Kitchin, J. K. Nørskov, M. A. Barteau and J. G. Chen, Role of strain and ligand effects in the modification of the electronic and chemical properties of bimetallic surfaces, Phys. Rev. Lett., 2004, 93, 156801–156804 CrossRef CAS PubMed.
- J. Kitchin, J. K. Nørskov, M. A. Barteau and J. G. Chen, Modification of the surface electronic and chemical properties of Pt (111) by subsurface 3d transition metals, J. Chem. Phys., 2004, 120, 10240–10246 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra02822f |
| ‡ Fan Liu and Guangqi Zhu are the co-first authors. |
| This journal is © The Royal Society of Chemistry 2019 |