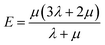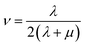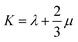Molecular dynamics simulations of a cyclotetramethylene tetra-nitramine/hydrazine 5,5′-bitetrazole-1,1′-diolate cocrystal

Abstract

An energetic ionic salt (EIS)-based cocrystal formation, cyclotetramethylene tetra-nitramine (HMX)/hydrazine 5,5′-bitetrazole-1,1′-diolate (HA·BTO), is predicted based on molecular dynamics simulations. HA·BTO is a newly-synthesized environmentally friendly energetic ionic salt with good detonation performance and low sensitivity. Calculated powder X-ray diffraction patterns and intermolecular interactions deduce the formation of the new cocrystal structure. Radial distribution function analysis suggests that hydrogen bonds and van der Waals (vdW) forces exist between the H⋯O pairs of HMX and HA·BTO, while the hydrogen bonds between the H of HA·BTO and the O of HMX play a prominent role. The cohesive energy density and mechanical properties are also analyzed. The cohesive energy density of the HMX/HA·BTO cocrystal is larger than that of the composite of HMX and HA·BTO, indicating an improvement in crystal stability by cocrystalization. Compared to both HMX and HA·BTO, HMX/HA·BTO has smaller Young modulus, bulk modulus and shear modulus values, but larger K/G values and a positive Cauchy pressure, suggesting decreased stiffness and improved ductibility. Moreover, the calculated formation energy is −405.79 kJ mol⁻¹ at 298 K, which implies that the proposed cocrystal structure is likely to be synthesized at ambient temperature. In summary, we have predicted an EIS-based cocrystal formation in which the safety and mechanical properties of HMX have been improved via cocrystalization with HA·BTO, and this provides deep insight into the formation mechanism of the EIS-based cocrystal.

---

1. Introduction

Energetic cocrystals have received great attention and have made considerable developments since their introduction inspired by pharmaceutical cocrystals.¹ Based on intermolecular interactions (hydrogen-bonding interactions, van der Waals (vdW) interactions, π–π stacking interactions, electrostatic interactions, etc.), the cocrystallization of sensitive high-energy-density materials and insensitive low-energy-density materials has achieved a better balance between the detonation performance and mechanical sensitivity.^2–6 Novel cocrystals have endlessly emerged, such as 2,4,6,8,10,12-hexanitro-2,4,6,8,10,12-hexaazatetracyclododecane (CL-20)/1-methyl-3,5-dinitropyrazole (MTNP),⁷ CL-20/2,4-dinitro-2,4-diazapentane (DNDAP),⁸ CL-20/1-amino-3-methyl-1,2,3-triazolium nitrate (1-AMTN),⁹ CL-20/1-methyl-2,4-dinitroimidazole (2,4-MDNI)¹⁰ or 1-methyl-4,5-dinitroimidazole (4,5-MDNI).¹⁰

High energy density is no longer the only goal in the modern development of energetic materials. Energetic ionic salts (EISs),^11–15 such as dihydroxylammonium 5,5′-bistetrazole-1,1′-diolate (TKX-50),¹⁴ with excellent comprehensive properties of high energy density, low impact sensitivity and low toxicity, have proved to be promising candidates in many applicational aspects. However, cocrystals with EISs as only one partner are rarely reported. To the best of our knowledge, only one EIS-based cocrystal formation of CL-20/1-AMTN has been synthesized, which has a structure similar to ternary perovskite energetic crystals.⁹ Due to the great differences in the structures, it is difficult to form cocrystals or gain high quality crystals. Consequently some simulation work on TKX-50/CL-20,¹⁶ TKX-50/cyclotetramethylene tetra-nitramine (HMX)¹⁷ and TKX-50/cyclotrimethylene trinitramine (RDX)¹⁸ cocrystals has been performed based on molecular dynamics (MD) simulations.

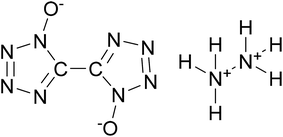
Considering the advantages of cocrystals with EISs as components, we constructed a cocrystal model of HMX/hydrazine 5,5′-bitetrazole-1,1′-diolate (HA·BTO). HA·BTO (Scheme 1) is an energetic ionic salt developed by the reaction of 1H,1′H-5,5′-bitetrazole-1,1′-diolate (BTO) and hydrazine hydrochloride (HA·HCl) with properties equal to or better than TKX-50.^12,19 Based on molecular dynamics simulations, the formation mechanism, energy and mechanical properties of the HMX/HA·BTO cocrystal have been analysed, contributing to a better understanding of the formation mechanism of EIS-based cocrystals.

Scheme 1 Molecular structure of HA·BTO.

2. Computational details

2.1 Construction of models

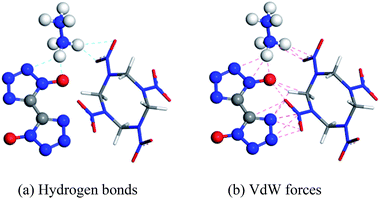
Molecular interactions, especially hydrogen bonds and vdW forces, play an important role in the formation of cocrystals. In Fig. 1, there are hydrogen bonds and vdW forces between the O⋯H pairs and N⋯H pairs of HMX and HA·BTO. Based on the formation mechanism, the cocrystal model of HMX/HA·BTO is constructed by randomly substituting the HA·BTO molecules with HMX molecules at a molar ratio of 1 : 2 (HMX : HA·BTO). In detail, the crystal facet parallel to the A- and B-axis is chosen as the substituting location of HA·BTO (see Fig. 2). We also chose the five dominant crystal facets (see Fig. S2†) of HA·BTO as the substituting locations. However, the structures and properties of those five cocrystal models are so poor that we believe there is no cocrystallization occurring among them. Therefore, we did not include those five cocrystal models in this paper. The crystal models of HMX and HA·BTO were constructed by the crystal parameters from X-ray diffraction.^12,20 The primary cell of HMX consists of two neutral molecules while that of HA·BTO consists of one divalent BTO anion and one divalent hydrazine cation. The initial model of HMX/HA·BTO consists of two HMX molecules and four HA·BTO molecules. Then, all initial models were built into (2 × 2 × 2) supercells and optimized with a 1000-step “smart algorithm”. The “smart algorithm”, which is a cascade of the steepest descent, involving ABNR and quasi-Newton methods, is a geometry optimization algorithm in the Forcite module of the Materials Studio 8.0 software.²¹ It should be noted that all the construction of the models and the following molecular dynamics simulations were conducted in this module. The quality was set to “fine” for all simulations. To eliminate unreasonable conformations, a five temperature cycle (150–500–150 K) anneal dynamic under an NVT ensemble with Anderson temperature control method²² was executed for all supercells, and the conformations with minimum energy were chosen for further molecular dynamic simulations.

Fig. 1 Probable interactions between HMX and HA·BTO (HA·BTO is represented with balls and sticks, while HMX is represented with sticks. C, H, O, and N are represented by gray, white, red, and blue balls or sticks, respectively).

Fig. 2 Equilibrium structure of the HMX/HA·BTO cocrystal model (HA·BTO is represented with balls and sticks, while HMX is represented with sticks. C, H, O, and N are represented by gray, white, red, and blue balls or sticks, respectively).

2.2 Choice of force field

A suitable force field is the key to obtaining reliable molecular dynamics simulation results. The popular COMPASS (condensed-phase optimized molecular potentials for atomistic molecular dynamics studies)²³ force field has proved to be suitable for molecular dynamic simulations with nitro (–NO₂) containing compounds such as RDX, HMX and CL-20. However, there were no reasonable parameters for the N-oxides on the azole ring of 5,5′-bitetrazole-1,1′-diolate when assigning force field types using COMPASS in our simulation tests. In the works of Xiong^16–18,24 and Yu,²⁵ the TKX-50, TKX-50-based PBXs and TKX-50-based cocrystals are parameterized by PCFF (the polymer consistent force field),^26–28 which predicts the lattice parameters, energy and mechanical properties precisely. Based on the parameter settings of these early works, the HMX/HA·BTO cocrystal model was simulated using the PCFF force field. The lattice parameters of the optimized HMX and HA·BTO primitive cells using the PCFF force field, as well as the experimental values, are listed in Table 1. From Table 1, we can see that both of the values agree well with each other.

Table 1 Lattice parameters of HMX and HA·BTO

Lattice parameters	HMX			HA·BTO
	Exp.^a	Comp.	Relative error/%	Exp.^b	Comp.	Relative error/%
a Cited from ref. 16.b Cited from ref. 10.
a/Å	6.54	6.64	1.52	4.75	4.52	−4.84
b/Å	11.05	11.81	6.88	5.91	5.62	−4.91
c/Å	8.70	8.79	1.03	6.70	6.81	1.64
α/(°)	90.00	90.00	0	98.68	87.64	−11.19
β/(°)	124.30	124.07	−0.19	90.70	89.17	−1.69
γ/(°)	90.00	90.00	0	109.08	106.20	−2.64
ρ/(g cm^−3)	1.89	1.72	−8.99	1.91	2.02	5.76

---

Further validation of the PCFF force field was conducted by predicting the crystal morphology of HA·BTO. There is no crystal morphology of HA·BTO reported, apart from a SEM image of morphology in the original work. We calculated the crystal morphology of HA·BTO using the Growth Morphology (GM) method^21,29 with PCFF in the Morphology module in Materials Studio 8.0. The results are shown in Fig. S2.† From Fig. S2,† we can see that the predicted crystal morphology of HA·BTO possesses five dominant facets and exhibits a prism-type morphology with regular shape, uniform size, and smooth and integrated surfaces. This is consistent with the original SEM image.¹² The aspect ratio is 2.98. More details are shown in Table S1.† Furthermore, it needs to be emphasized that both COMPASS and PCFF are not sufficiently sophisticated enough to model the chemical reaction that causes the material to explode. Therefore, the simulations are not able to provide much information regarding the stability of the solid to gas phase change.

2.3 Molecular dynamics simulations

Five molecular dynamics simulation tasks were conducted under the NPT (constant pressure and constant temperature) ensemble from an initial temperature of 198 K with a 50 K-step width to a final temperature of 398 K. The temperature was controlled with the Anderson method²² at a collision ratio of 1.0, while the pressure was controlled with the Parrinello–Rahman method^30,31 at a cell time constant of 1.0 ps. The Ewald and atom-based summation methods were chosen for the electrostatic and van der Waals forces calculations, at a buffer width of 0.5 Å and a cut-off distance of 15.5 Å, respectively. A fixed timestep of 1 fs was adopted throughout all simulations. We equilibrated the system for 200 ps. In Fig. S1,† we can see that the system proceeded at the equilibrium state in the last 100 ps. Then, we sampled the last 100 ps trajectory every 50 fs to get a total of 2000 frames for further statistical analysis.

3. Results and discussion

3.1 Powder X-ray diffraction (PXRD) simulations

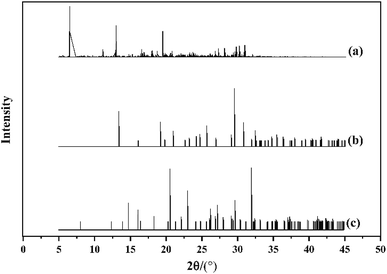
PXRD is universally used to detect polymorphism, and is also used to determine the phase transformation of single crystals. We conducted a PXRD simulating experiment on the cocrystal model of HMX/HA·BTO with the reflex module in Materials Studio 8.0. Cu was selected as the target and the scanning range was 5–45° with a step-width of 0.02°. The results of the PXRD are shown in Fig. 3. Compared to the diffraction patterns of HMX and HA·BTO, the characteristic peaks of the HMX/HA·BTO cocrystal model were evidently shifted to the left with new peaks occurring at θ = 6°, 13°, and 19°. The characteristic peaks of HMX and HA·BTO disappeared in the diffraction patterns of the HMX/HA·BTO cocrystal model. Consequently, the diffraction pattern of the HMX/HA·BTO cocrystal model is apparently not the simple superposition of the diffraction patterns of HMX and HA·BTO, and from this we can deduce the formation of a new cocrystal structure.

Fig. 3 The PXRD patterns of (a) HMX/HA·BTO, (b) HA·BTO and (c) HMX.

3.2 Radial distribution function (RDF) analysis

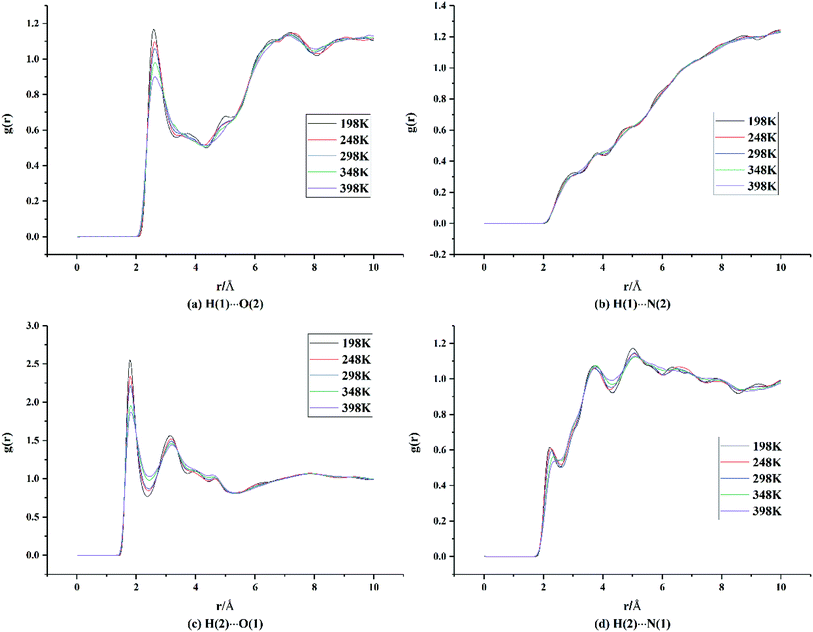
Hydrogen bonds and vdW forces are important driving forces in the formation of new cocrystals. To further explore the cocrystal structure of HMX/HA·BTO, we carried out RDF analysis between the H⋯O and H⋯N pairs in the cocrystal. RDF describes the probability of finding an atom at a distance from the other atom in an atomic pair. Usually the close contacts can be classified into hydrogen bonds, strong vdW forces and weak vdW forces by the interaction distance ranges of 1.1–3.1 Å, 3.1–5.0 Å and larger than 5.0 Å, respectively.^{16,17,32–36} We denote H, O, and N in HMX as H(1), O(1), and N(1), and those in HA·BTO as H(2), O(2), and N(2). For the two N atoms in the hydrazine cation surrounded by six H atoms, there are likely to be no apparent interactions between the N atom in the hydrazine cation and the H atom in HMX. Thus, only N atoms in the BTO anion are included in N(2). The results are shown in Fig. 4.

Fig. 4 RDF analysis data of the H⋯O and H⋯N pairs between HMX and HA·BTO in the cocrystal model (H, O, and N in HMX are denoted as H(1), O(1), and N(1), while those in HA·BTO are denoted as H(2), O(2), and N(2)).

From Fig. 4(a), it can be seen that there are two main peaks. One occurs at a distance of about 2.6 Å, which indicates that hydrogen bonds exist between the H atoms of HMX and the O atoms of BTO. The other occurs in the range of 6–8 Å, indicating weak vdW forces. There are no apparent peaks in Fig. 4(b), and this means that there are no evident interactions between the H atoms of HMX and the N atoms of BTO. In Fig. 4(c), there are two apparent peaks at distances of about 1.8 Å and 3.2 Å, respectively, which indicate that there are hydrogen bonds and strong vdW forces between the H atoms of HA·BTO and the O atoms of HMX. Moreover, the peak intensity for the hydrogen bonds in Fig. 4(c) is much higher than that in Fig. 4(a), and the distance at which the hydrogen bonds occurs in Fig. 4(c) is much shorter than the distance in Fig. 4(a), indicating that there are much stronger hydrogen bond interactions between the H atoms of HA·BTO and the O atoms of HMX than those between the H atoms of HMX and the O atoms of BTO. In Fig. 4(d), there are no apparent peaks, apart from some little convexities. It should be noted that the little convexities approximately match the peaks in Fig. 4(c) with a horizontal shift. We can assume that the little convexities result from the periodical arrangement of the cocrystal atoms, instead of close interactions. To conclude, there are hydrogen bonds and strong or weak vdW forces between the H⋯O pairs, and the hydrogen bonds between the H atoms of HA·BTO and the O atoms of HMX are much stronger than those between the H atoms of HMX and the O atoms of BTO.

On the other hand, in Fig. 4(a) and (c), it is apparent that the peak intensity for the hydrogen bonds decreases gradually as the temperature increases. And, at the same time, those peaks shift slightly to the right. We can ascribe this to the decreasing interactions between the H⋯O pairs due to the reinforcement of atomic thermal motion as the temperature increases, and this is in line with our expectations. As well as RDF, we can represent the interactions between HMX and HA·BTO by binding energy. Binding energy for molecules can be defined as non-bonding energy (electrostatic, vdW and long range corrections). The binding energy varies with temperature, as shown in Fig. S3.† It can be seen that the binding energy decreases as the temperature increases, which is in agreement with the variation trend of the RDF results described above.

3.3 Cohesive energy density

Cohesive energy for molecular crystals is defined as the average energy needed to separate all molecules to an infinite distance from each other. The cohesive energy density (CED) is the bulk density of cohesive energy, and this can be used to evaluate the stability of a molecular crystal. CED can be calculated as follows:

E_coh = −〈E_inter〉 = −(〈E_total〉 − 〈E_intra〉)

where E_inter is the interactions energy between all the molecules, which can be acquired from the total energy, E_total, minus the intramolecular energy, E_intra. V_m is the molar volume. The brackets 〈⋯〉 represent the ensemble average.

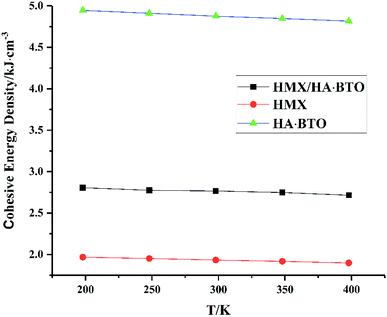
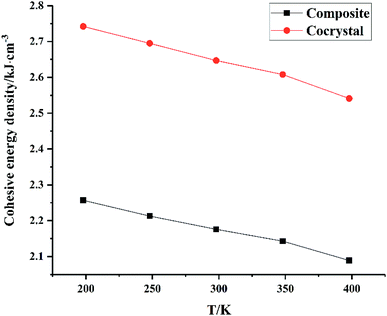
From Fig. 5, we can see that all CEDs of HMX, HA·BTO and HMX/HA·BTO decrease gradually as the temperature increases. We know that the stability of molecular systems decreases because of the reinforcement of the atomic thermal motion as the temperature increases. Thus, the value of CED can represent the degree of stability of a molecular crystal. We can see that the CED of HMX/HA·BTO is smaller than that of HA·BTO, but larger than that of HMX. However, we cannot arbitrarily say that the stability of the cocrystal model has been improved by cocrystalization. Due to the wildly different interaction mechanisms between HMX and HA·BTO, the increased CEDs of HMX/HA·BTO may be a mixed effect with a combination of both types of interaction. To determine whether cocrystalization is beneficial in improving the stability of molecular crystals, the composite model of HMX and HA·BTO was built. We mixed 16 HMX and 32 HA·BTO molecules randomly in a 50 Å × 50 Å cubic box, and then compressed it to the density close to the HMX/HA·BTO cocrystal. Consistent optimization, simulations and analysis processes were conducted. In Fig. 6, both CEDs of the cocrystal and the composite decrease gradually as the temperature increases, and the former is always larger than the latter, and this implies that an improvement in the stability of the cocrystal structure contributed to the cocrystalization.

Fig. 5 CED of HMX, HA·BTO and HMX/HA·BTO cocrystal.

Fig. 6 CED of the composite and the cocrystal.

We also calculated the formation energy of the HMX/HA·BTO cocrystal at a temperature of 298 K to see whether the proposed structure is easy to be synthesized. The formation energy is calculated as

E_form(HMX/HA·BTO) = E_crystal(HMX/HA·BTO) − E_crystal(HMX) − E_crystal(HA·BTO)

where E_form is the formation energy and E_crystal is the total crystal energy. The calculated formation energy is −405.79 kJ mol⁻¹ at 298 K, and this implies that the proposed cocrystal structure is likely to be synthesized under ambient temperature conditions.

3.4 Mechanical properties

Mechanical properties are important indices for the availability of energetic products in preparation, machining, transportation and application processes. The primary parameters for mechanical properties include the bulk modulus (K), the shear modulus (G), the Young modulus (E) and Poisson's ratio (ν). The Young modulus, also named tensile modulus, describes the resistance to the uniaxial deformation under uniaxial stress, while the bulk modulus describes the resistance to the uniform deformation under hydrostatic pressure. The shear modulus describes the resistance to shear. The ratio of the bulk modulus and the shear modulus (K/G), as well as the Cauchy pressure (C₁₂–C₄₄), can also be used to denote the ductibility of materials.³⁷ A larger value of K/G means more ductibility and less brittleness, and a positive value of C₁₂–C₄₄ means a ductile material, whilst a negative value means a brittle material. For a plastic, the value of Poisson's ratio ranges from 0.2 to 0.4. With the assumption of isotropic materials, we can calculate the moduli as follows:^32,38,39

G = μ

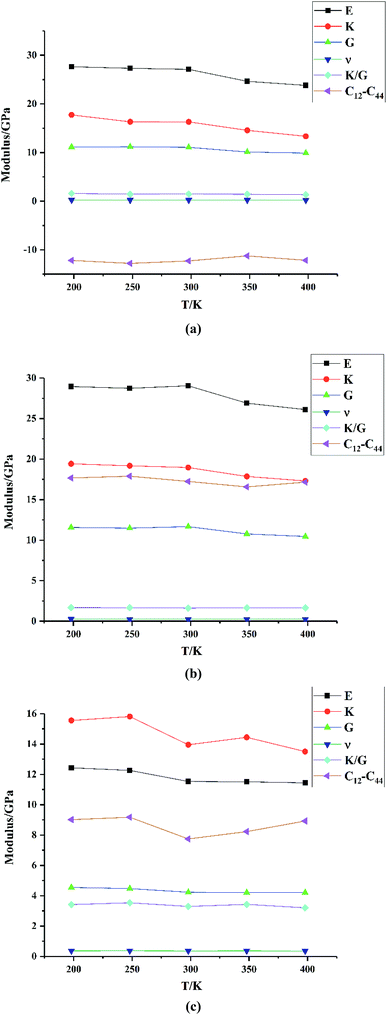
where λ and μ are the Lamé coefficients obtained from the static method. The results are shown in Fig. 7 and Table S2.†

Fig. 7 Mechanical properties of (a) HMX, (b) HA·BTO and (c) the HMX/HA·BTO cocrystal.

From Fig. 7, we can see that the Young modulus, bulk modulus and shear modulus of HMX, HA·BTO and HMX/HA·BTO all exhibit a downward trend with an increase in temperature, indicating that the stiffness of those crystals decreases as the temperature increases, and this corresponds to our expectations of the experiment. However, the Poisson's ratio, values of K/G, and the Cauchy pressure hardly change with temperature. HMX is similar to that of HA·BTO in the values of the Young modulus, bulk modulus and shear modulus, but it has smaller K/G values and a negative Cauchy pressure, which means that the ductibility of HMX is worse than that of HA·BTO. Compared to both HMX and HA·BTO, HMX/HA·BTO has a smaller Young modulus, bulk modulus and shear modulus, larger K/G values and a positive Cauchy pressure, which suggests decreased stiffness and improved ductibility. The Poisson's ratio of HMX/HA·BTO is also larger than those of HMX and HA·BTO, but it varies in the range of 0.2–0.4, indicating a plasticity with a more lateral strain capacity.

We also compared the mechanical properties of the HMX/HA·BTO cocrystal with those of another EIS-based cocrystal, HMX/TKX-50,¹⁷ as well as the traditional neutral cocrystal, HMX/CL-20.³³ Here we only list the mechanical moduli values of the cocrystals in Table 2. More computing details and data can be found in the original papers. The Young modulus, bulk modulus and shear modulus of the three cocrystal models all decrease with the increase in temperature. Compared to their parent components, all of the three cocrystal models exhibit decreased stiffness and improved ductibility, which can be attributed to cocrystalization. On the other hand, the K/G values are in the order of HMX/HA·BTO > HMX/TKX-50 > HMX/CL-20, and this means that both EIS-based cocrystal models have a better ductibility than the traditional neutral cocrystal. However, the Cauchy pressure of HMX/HA·BTO is smaller than that of HMX/TKX-50. There are no available Cauchy pressure values for HMX/CL-20. Therefore, our HMX/HA·BTO cocrystal model may have a better “K/G” ductibility, while the HMX/TKX-50 cocrystal model has a better “Cauchy pressure” ductibility.

Table 2 Mechanical moduli of CL-20/HMX, TKX-50/HMX and HA·BTO/HMX

Materials	T/K	Mechanical moduli
		E/GPa	K/GPa	G/GPa	ν	K/G	C12–C44
a Cited from ref. 35.b Cited from ref. 17.
CL-20/HMX^a	245	9.0	8.6	3.4	0.3	2.5	—
	295	8.6	8.3	3.3	0.3	2.5	—
	345	8.0	7.7	3.0	0.3	2.5	—
	395	7.4	7.1	2.8	0.3	2.6	—
	445	6.3	5.8	2.4	0.3	2.4	—
TKX-50/HMX^b	248	8.0	9.2	3.0	0.3	3.0	13.2
	298	7.6	8.9	2.8	0.3	3.1	12.3
	348	7.0	8.4	2.6	0.3	3.2	11.0
	398	6.6	8.0	2.4	0.3	3.3	10.0
	448	6.1	7.6	2.2	0.3	3.4	9.2
HA·BTO/HMX	198	12.44	15.56	4.55	0.37	3.42	9.02
	248	12.26	15.81	4.47	0.37	3.54	9.18
	298	11.54	13.95	4.23	0.36	3.29	7.74
	348	11.52	14.45	4.21	0.37	3.43	8.23
	398	11.45	13.50	4.21	0.36	3.21	8.93

---

4. Conclusions

In this study, we constructed a cocrystal model of HMX/HA·BTO, based on the probable interactions between HMX and HA·BTO. The calculated PXRD deduced the formation of a new cocrystal structure. Using RDF analysis, we found that there are hydrogen bonds and vdW forces between HMX and HA·BTO, and the prominent interactions are the hydrogen bonds between the H of HA·BTO and the O of HMX. Then, the CED and mechanical properties of the HMX/HA·BTO cocrystal were analysed. Compared to the composite of HMX and HA·BTO, and the parent HMX and HA·BTO models, the stability and ductibility of the HMX/HA·BTO cocrystal have been improved via cocrystalization. In addition, the calculated formation energy implies that the proposed structure can probably be synthesized at ambient temperature. Consequently, an EIS-based cocrystal formation with better safety and ductibility has been predicted by MD simulations, providing deep insight into the formation mechanism of EIS-based cocrystals.

Conflicts of interest

There are no conflicts of interest to declare.

Notes and references

1. O. Bolton and A. J. Matzger, Angew. Chem. Int. Ed., 2011, 50, 8960–8963.
2. C. Zhang, Z. Yang, X. Zhou, C. Zhang, Y. Ma, J. Xu, Q. Zhang, F. Nie and H. Li, Cryst. Growth Des., 2014, 14, 3923–3928.
3. C. Zhang, X. Xue, Y. Cao, J. Zhou, A. Zhang, H. Li, Y. Zhou, R. Xu and T. Gao, CrystEngComm, 2014, 16, 5905–5916.
4. J. Zhang and J. M. Shreeve, CrystEngComm, 2016, 18, 6124–6133.
5. X. Wei, A. Zhang, Y. Ma, X. Xue, J. Zhou, Y. Zhu and C. Zhang, CrystEngComm, 2015, 17, 9037–9047.
6. B. Moses Abraham, J. Prathap Kumar and G. Vaitheeswaran, ACS Omega, 2018, 3, 9388–9399.
7. Q. Ma, T. Jiang, Y. Chi, Y. Chen, J. Wang, J. Huang and F. Nie, New J. Chem., 2017, 41, 4165–4172.
8. N. Liu, B. Duan, X. Lu, H. Mo, M. Xu, Q. Zhang and B. Wang, CrystEngComm, 2018, 20, 2060–2067.
9. X. Zhang, S. Chen, Y. Wu, S. Jin, X. Wang, Y. Wang, F. Shang, K. Chen, J. Du and Q. Shu, Chem. Commun., 2018, 54, 13268–13270.
10. Z. Yang, H. Wang, Y. Ma, Q. Huang, J. Zhang, F. Nie, J. Zhang and H. Li, Cryst. Growth Des., 2018, 18, 6399–6403.
11. F. Li, Y. Bi, W. Zhao, T. Zhang, Z. Zhou and L. Yang, Inorg. Chem., 2015, 54, 2050–2057.
12. Z. Bin Zhang, C. X. Xu, X. Yin and J. G. Zhang, Dalton Trans., 2016, 45, 19045–19052.
13. N. Fischer, T. M. Klapötke, M. Reymann and J. Stierstorfer, Eur. J. Inorg. Chem., 2013, 2167–2180.
14. N. Fischer, D. Fischer, T. M. Klapötke, D. G. Piercey and J. Stierstorfer, J. Mater. Chem., 2012, 22, 20418.
15. A. A. Dippold and T. M. Klapötke, J. Am. Chem. Soc., 2013, 135, 9931–9938.
16. S. Xiong, S. Chen, S. Jin and C. Zhang, RSC Adv., 2016, 6, 4221–4226.
17. S. Xiong, S. Chen, S. Jin, Z. Zhang, Y. Zhang and L. Li, RSC Adv., 2017, 7, 6795–6799.
18. S. Xiong, S. Chen and S. Jin, J. Mol. Graph. Model., 2017, 74, 171–176.
19. B. M. Abraham, V. D. Ghule and G. Vaitheeswaran, Phys. Chem. Chem. Phys., 2018, 20, 29693–29707.
20. C. S. Choi and H. P. Boutin, Acta Crystallogr. Sect. B Struct. Crystallogr. Cryst. Chem., 1970, 26, 1235–1240.
21. Material Studio 8.0, Acceryls, Inc., San Diego, CA, 2014.
22. H. C. Andersen, J. Chem. Phys., 1980, 72, 2384–2393.
23. S. W. Bunte and H. Sun, J. Phys. Chem. B, 2002, 104, 2477–2489.
24. S. L. Xiong, S. Sen Chen, S. H. Jin and L. J. Li, J. Energ. Mater., 2016, 34, 384–394.
25. Y. Yu, S. Chen, X. Li, J. Zhu, H. Liang, X. Zhang and Q. Shu, RSC Adv., 2016, 6, 20034–20041.
26. H. Sun, Macromolecules, 1995, 28, 701–712.
27. H. Sun, S. J. Mumby, J. R. Maple and A. T. Hagler, J. Am. Chem. Soc., 1994, 116, 2978–2987.
28. H. Sun, J. Comput. Chem., 1994, 15, 752–768.
29. R. Docherty, G. Clydesdale, K. J. Roberts and P. Bennema, J. Phys. D Appl. Phys., 1991, 24, 89–99.
30. M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190.
31. M. Parrinello and A. rahman, Phys. Rev. Lett., 1980, 45, 1196–1199.
32. B. Wang, J. Zhang, X. Lu, N. Liu, Y. Lu, Y. Shu and B. Duan, RSC Adv., 2018, 8, 34690–34698.
33. T. Sun, J. Xiao, Q. Liu and H. Ming, J. Mater. Chem. A, 2014, 2, 13898–13904.
34. S. Xiong, S. Chen and S. Jin, J. Mol. Graph. Model., 2017, 74, 171–176.
35. X. J. Xu, J. J. Xiao, H. Huang, J. S. Li and H. M. Xiao, Sci. China, Ser. B: Chem., 2007, 50, 737–745.
36. J. P. Tidey, V. V. Zhurov, C. G. Gianopoulos, E. A. Zhurova and A. A. Pinkerton, J. Phys. Chem. A, 2017, 121, 8962–8972.
37. J. J. Xiao, W. R. Wang, J. Chen, G. F. Ji, W. Zhu and H. M. Xiao, Comput. Theor. Chem., 2012, 999, 21–27.
38. L. Qiu, W.-H. Zhu, J.-J. Xiao, W. Zhu, H.-M. Xiao, H. Huang and J.-S. Li, J. Phys. Chem. B, 2007, 111, 1559–1566.
39. B. Li, C. Dong, J. Yu, Q. Zhang, H. Zhou and R. Liu, RSC Adv., 2018, 8, 22127–22135.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra02966d

---