pH-induced conformational changes in histamine in the solid state

Abstract

Histamine is one of the most basic biogenic amino-compounds, which is composed of imidazole and a flexible ethylamine side chain moiety. Histamine is known to take the form of various types of cations, free base, monocation and dication form, where its conformational change is highly sensitively to the pH conditions. The details of these changes are still controversial due to a lack of detailed information on its crystal structures. Thus, in this study, the molecular packing structures of histidine at various pH were analyzed via X-ray diffraction in combination with vibrational spectroscopy and energy calculations. A variety of molecular conformations including the tautomeric phenomenon was found to be intimately related with intra- and intermolecular hydrogen bonds. The role of the hydrogen bonds was studied also to check the possibility of high proton conductivity of histamine, as predicted by computer simulation. Consequently, the thus-predicted proton conductivity was confirmed for the first time experimentally. During the heating process, the conductivity showed the relatively high maximum value of 10⁻⁴ S cm⁻¹ at around 60 °C, which is related to the effective proton transfer between the amino NH group of one histamine unit and the imidazole ring of another.

---

1. Introduction

Histamine is one of the most important biogenic amines, which is present in mammalian organisms.¹ The biological effects of histamine are involved in several defense mechanisms, with four different types of specific histamine receptors. Histamine causes an increase in vasodilation, drop in blood pressure, mediation of smooth contraction of muscle, regulation of allergic conditions (Histamine-H₁ receptor, HRH1), control of gastric acid secretion (Histamine-H₂ receptor, HRH2), modulation of neurotransmitter release (Histamine-H₃ receptor, HRH3),^2,3 increased expression of adhesion molecules and modulation of inflammatory conditions (Histamine-H₄ receptor, HRH4).⁴ The sensitivity of histamine to receptors was explored to determine their biological roles in the structure-dependent activity of histamine agonists.^5,6 These investigations suggested that the binding of histamine with receptors occurs in the trans conformation. For example, the X-ray structure analysis of the histamine-binding protein complex (found in tick saliva, HBP2) showed that monocation histamine molecules take the trans conformation and interact strongly with the negatively-charged amino acid residues in the binding pocket.⁵

Thus, it is important to know the variable molecular shapes of histamine, which sensitively change depending on the environmental conditions.^7–28

(i) Base and acid species: Depending on the pH value, histamine can take the form of three types of ions, free base (H1, pH > 10), monocation (H2, pH 6.5 ∼ 7.5) and dication (H3, pH < 5).

(ii) Tautomerism: A proton is attached to the N atom of the imidazole ring. When the imidazole–NH group is closer to the amine (NH₂ or NH₃⁺) unit of the ethyl amine group, this NH group is named the N^π unit. If the imidazole–NH group is far from the position of the amine unit, it is named the N^τ unit.

(iii) Torsional isomers: 3 types of internal rotations can be defined around the N(im)–C(im)–CH₂–CH₂ (τ₁), C(im)–CH₂–CH₂–N (τ₂), and CH₂–CH₂–N–H (τ₃) bonds, where “im” indicates the imidazole ring. The trans (T, 180°) and gauche (G, 60°) forms are possible for these three torsional angles.

By combining these three different types of local structures (i–iii), histamine molecules can take a variety of molecular forms. Scheme 1 summarizes the various molecular forms proposed for the gas, solution and solid phases of histamine species. For example, the histamine free base molecule in the gas phase is reported to take the N^π/GG and N^π/GT forms,¹⁵ where factors (ii) and (iii) are combined to express the molecular forms. The concrete forms are illustrated in Scheme 1. In solution, the N^π/GG, N^π/GT and N^τ/GG forms are reported to be possible.^7,15 In the solid phase, only the N^π/GT form was reported.⁸ On the other hand, monocation histamine can take the N^τ/GG and N^τ/GT forms in the gas phase, only the N^τ/GG form in solution and the N^π/GG and N^τ/GT forms in the solid state.^{9,15,16,21,22} The dication species cannot be detected in the gas phase, but it exists as TG and GT forms in solution,^25,26 and TG and TT forms in the solid state.^10–13

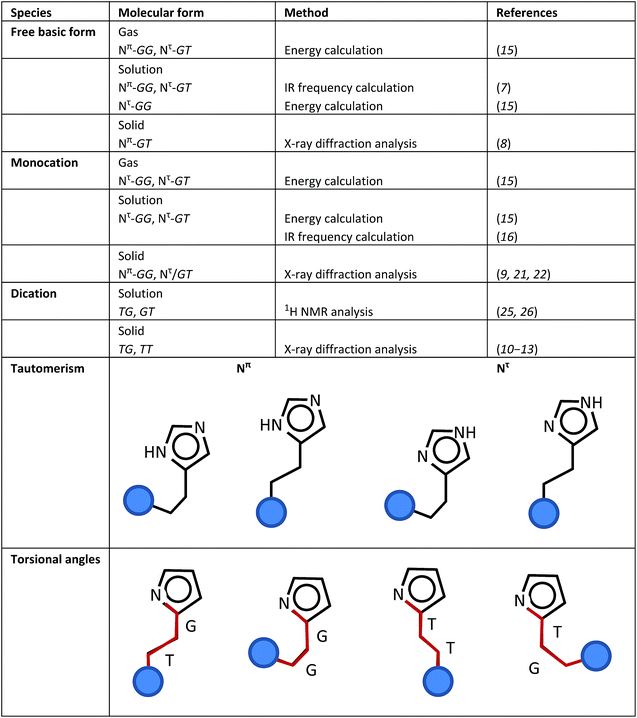Scheme 1 Definitions of the various structure factors of the histamine molecule and its proposed molecular forms in the gas, solution and solid states.

Accordingly, the combination of factors (i)–(iii) makes the structural description of histamine molecule quite complicated. Thus, the behavior of histamine under various conditions is still controversial.

To solve this problem, the structure study of the various histamine forms was investigated using numerous theoretical and experimental methods, but no clear answers have been obtained from a thorough search of the literature.^7–28

It is indispensable to know the systematic relation between the molecular conformations (including the tautomeric and internal rotation states) and the molecular packing mode in the solid state for the various cationic species of histamine. However, despite the long history of histamine and its significant role in physiological phenomena, structural studies of histamine are limited in the literature.^7–28

Of course, the above-mentioned structural information should be related to the characteristic properties of histamine. For example, as easily predicted from its chemical structure, histamine has an amino group and imidazole ring, which should cause high proton conductivity as a possibility.^29–32 However, the experimental evidence on its proton conductivity is quite limited in the literature. If histamine can show high proton conductivity, it may act as a proton-conducting composite for fuel cell applications. For example, Umeyama et al. constructed a composite of an aluminum-based micropore and histamine, and achieved conductivity of over 10⁻³ S cm⁻¹ at 150 °C under anhydrous conditions. However, no investigation was conducted on the proton conductivity of histamine itself.³³

As will be described in the first half part herein, histamine species prepared under various pH conditions were systematically characterized via the combination of various techniques such as X-ray crystal structure analysis, vibrational spectroscopy and quantum chemical calculations in addition to thermal data to the study the possibility of phase transition. The thus-established structural information was applied to determine the possibility of proton conductivity for the first time from both theoretical and experimental points of view, as will be reported in the second half herein.

As mentioned above, histamine is one of the most important basic compounds related to many physiological phenomena,^7–28 but its behavior must be understood concretely from a structural point of view. Although many papers have been published thus far about the molecular shape and packing state of histamine, herein, we reveal various new and basic information about the aggregation state of histamine subjected to different environments from various points of view.

2. Experimental

2.1 Samples

Histamine was purchased from Sigma Aldrich Chemical Co. (99% purity, pH ∼ 11). Histamine was dissolved in benzene and recrystallized to obtain long and colorless needle crystals,⁸ which were denoted as the histamine free base (H1). To prepare histamine monocation (H2), histamine free base was dissolved in an HCl solution of pH ∼ 7.⁹ Then, the solution was evaporated to obtain a white solid powder at room temperature. The powder was dissolved in methanol and recrystallized to obtain long needle-like crystals of histamine monohydrochloride. For the histamine dication (H3), the histamine free base was dissolved in HCl solution of pH ∼ 4.¹¹ The aqueous solution was filtrated and evaporated at room temperature. Recrystallization from aqueous solution afforded radially grown colorless needle-like crystals of histamine dihydrochloride. Histamine is hygroscopic and quickly deteriorates upon exposure to air. Therefore, the single crystal used for X-ray diffraction measurement was placed inside a glass capillary and filled with liquid paraffin.

2.2 Measurements

Raman spectra. Raman spectra were measured using a Japan Spectroscopic Company NRS-2100 laser Raman spectrometer in the back-scattering geometry with an excitation laser beam of 532 nm wavelength. The resolution power was 2 cm⁻¹. Raman spectra were recorded in the region of 3400–50 cm⁻¹.

Infrared spectra. FTIR spectral measurements were performed at a resolution of 2 cm⁻¹ in the frequency range of 4000–400 cm⁻¹ using a PerkinElmer Frontier™ Fourier transform infrared spectrometer in attenuated total reflection (ATR) mode.

Thermograms. Thermal analysis was performed using a TA Instrument Q2000 differential scanning calorimeter (DSC) at a heating and cooling rate of 5 °C min⁻¹ under a nitrogen atmosphere. The sample was packed into an aluminum pan. The thermogram was measured in the temperature region of −50 °C to 120 °C for H1, −50 °C to 150 °C for H2, and −50 °C to 250 °C for H3.

Single crystal X-ray diffraction measurement. The X-ray single crystal structure analysis was performed using a Rigaku R-axis VariMax X-ray diffractometer equipped with an imaging plate detector. The diffraction data was collected at room temperature using Mo-Kα (λ = 0.711 Å) radiation. The X-ray beam was focused using a confocal mirror. The X-ray diffraction data was analyzed using the Rigaku software AutoRun. The crystal structure was solved by a direct method (SIR92)³⁴ and refined by the full-matrix least-squares procedures for |F|² (F: structure factor). The positions and anisotropic thermal parameters of all the non-hydrogen atoms were refined. The structure analyses were carried out using the Crystal Structure software package.³⁵

Temperature-dependent X-ray diffraction measurement. X-ray powder diffraction measurement was performed using a Rigaku RINT TTR-III X-ray powder diffractometer combined with a Thermo plus DSC analyzer in the temperature range of 30 °C to 250 °C at a scan speed of 1 °C min⁻¹ under a nitrogen atmosphere. Graphite-monochromatized Cu-Kα (λ = 1.542 Å) radiation was used. The diffraction data was collected in the range of 2θ = 2–40° at a step of 0.01° and scan rate of 20° min⁻¹.

Temperature-dependent FTIR spectroscopic measurement. Temperature-dependent FTIR spectroscopic measurement was carried out using an in-house temperature-controlled sample holder with a Bruker ALPHA Fourier transform infrared spectrometer from 30 °C to 100 °C. The sample was prepared in KBr pellet form and the spectra were recorded in the range of 4000–400 cm⁻¹ at a resolution of 2 cm⁻¹.

2.3 Measurements

The proton conductivities of the histamine samples were measured via an impedance method with a μ-AUTOLAB Type-III connected to a PC running electrochemical impedance software in the frequency range of 100 kHz to 1 Hz with an AC signal of 50 mV at 30–190 °C. At each temperature, T, the impedance data was plotted based on the Nyquist equation, from which the conductivity σ(T) (S cm⁻¹) was calculated from impedance data based on eqn (1).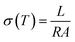where, L is the membrane thickness (cm), A is the cross-sectional area of the electrode (0.4418 cm²), and R is the membrane resistance (ohm) derived from the intersection of the Nyquist plot at the high frequencies (Z(ω_∞)) on the real axis according to the imaginary part equal to zero. Then, σ(T) was plotted against the temperature, T.

The sample was dissolved in methanol and dropped on glass filter paper (50 μL) and dried at room temperature. This process was repeated three times before drying under vacuum at room temperature for 4 h, and the thus-prepared samples were kept in desiccators until measurement. Dried glass filter paper was assembled in a sealed Teflon cell using gold-film-coated copper plates as the electrode.

2.4 Conformational analysis

The conformation of an isolated histamine molecule was studied by using the X-ray-analyzed structure as an initial model, which was energetically optimized using the DMol³ software by Materials Studio (Biovia).^36–38 DFT (density functional theory) calculation was carried out with the BLYP functional for the generalized gradient approximation (GGA) with a double numerical basis set plus polarization p-function on the hydrogen atoms and d-function of all the non-hydrogen atoms.³⁹

The thus-optimized models were used to search the energetically most stable structure by conformational analysis (the Conformers module with COMPASS⁴⁰ force field in Materials Studio). The most stable geometry of histamine molecule was sought by varying the two torsional angles: τ₁, between the plane of the aminoethyl side chain and imidazole ring (N(im)–C(im)–CH₂–CH₂) and τ₂, the plane of the C–C bond of the ethyl side chain (C(im)–CH₂–CH₂–N). A systematic approach was applied to search the molecular geometry for these two torsional angles with a 3-degree increment of the dihedral angle in the dihedral angle range from −180° to 180°.

2.5 Packing structure prediction

The Polymorph Predictor of Materials Studio (Biovia) was used to predict the possible crystal structures using the COMPASS force field.^36–38,40 By referring to the space group symmetries encountered frequently in the X-ray structure analysis, several representative space groups were employed (P1, P1̄, P2₁, P2₁/c, P2/c and Pbca). The initial positions of the molecules in the unit cell and the cell parameters were randomly given. The Metropolis Monte Carlo method was applied for the annealing procedure in the temperature range of 6 × 10⁴ to 300 K to obtain the most stable packing structure. The 250 crystal structure models produced for each selected space group were classified by a clustering process to obtain several representative structure models.^41,42 The energies were optimized, and the top ten structures with the lowest energies were picked up and compared with the X-ray-analyzed structure.

3. Results and discussion

3.1 Crystal structure analysis

The crystal structures of the three types of histamine species, H1, H2, and H3, were determined by X-ray single crystal analyses, as shown in Fig. 1. The crystallographic data and data collection parameters are listed in Table 1 for these compounds.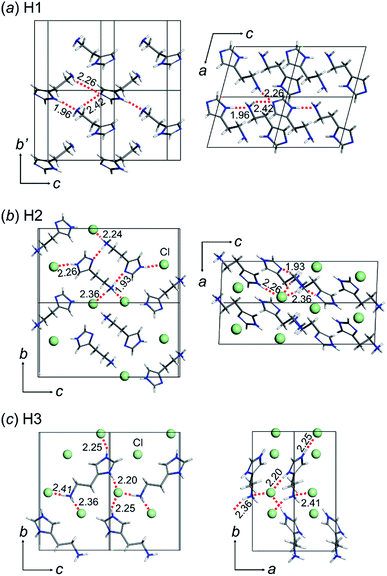

Fig. 1 Crystal structures of histamine ionic species: (a) free base (H1: CCDC 1912431), (b) monocation (H2: CCDC 1912450), and (c) dication (H3: CCDC 1912432). The green balls in the monocation and dication forms indicate the chloride anion (Cl⁻). The hydrogen bonds are shown as a red dotted line and the hydrogen bond distances are shown in Angstroms (Å).

Table 1 Crystal data of the three forms of histamine

Model compound	H1	H2	H3
Empirical formula	C5H9N3	C5H10N3·Cl	C5H11N3·2Cl
Formula weight	111.14	147.61	184.07
Crystal system	Monoclinic	Monoclinic	Monoclinic
Lattice type	Primitive	Primitive	Primitive
Space group	P21	P21/n	P21
a (Å)	5.698(3)	4.623(3)	4.449(6)
b (Å)	7.632(4)	9.204(9)	12.694(16)
c (Å)	7.250(4)	17.413(13)	7.577(9)
α (°)	90	90	90
β (°)	104.92(7)	92.31(18)	91.45(3)
γ (°)	90	90	90
V (Å^3)	304.6(3)	740.3(10)	427.7(9)
Z	2	2	2
Density (g cm^−3)	1.255	1.093	1.693
μ Mo Kα (cm^−1)	0.817	2.679	7.216
Radiation	Mo Kα	Mo Kα	Mo Kα
Temperature (K)	296	296	296
Max and min transmission	0.992 and 0.429	1.000 and 0.377	0.930 and 0.315
Reflections measured	2997	6937	4129
Independent reflections	1277 (Rint = 0.0596)	1675 (Rint = 0.0673)	1948 (Rint = 0.0628)
Observed reflections used for the refinements	555	1170	1325
Goodness-of-fit on F^2	1.178	1.194	1.142
Final R indices	R1 = 0.0412 [I > 4σ(I)]	R1 = 0.0579 [I > 4σ(I)]	R1 = 0.0850 [I > 4σ(I)]
	ωR2 = 0.0591	ωR2 = 0.0751	ωR2 = 0.1397
Δρmax and Δρmin (e Å^−3)	0.23 and −0.39	0.71 and −0.44	3.29 and −1.32

---

〈H1〉. The crystal structure of H1 belongs to the monoclinic system with the space group P2₁ (Fig. 1a). A herringbone-type packing structure of histamine molecules is formed in the unit cell. N–H⋯N hydrogen bonds were detected between the N–H bond of the imidazole ring and the amine side chain of the adjacent molecule at a distance of 1.96 Å. Another hydrogen bond is formed between the amine N–H group and the nitrogen atom of the neighboring imidazole ring with a length of 2.42 Å. The molecules of H1 take the N^π/GT form listed in Scheme 1: the GT conformation with the dihedral angle τ₁ 64.3° and τ₂ 170.1°,⁸ and an imidazole ring with an almost perfectly planar shape exists in the N^π–H tautomeric form.

〈H2〉. The crystal structure of histamine monohydro-chloride (H2) was revealed for the first time in the present work. The crystal structure belongs to the monoclinic system of the space group P2₁/n (Fig. 1b). The ammonium group of a histamine cation is linked to the imidazole ring of the adjacent molecules by hydrogen bonds to form a dimer. The distance between the nitrogen atom of the imidazole ring and the hydrogen atom of the ammonium group is 1.93 Å. Hydrogen bonds are also formed also between the Cl anion and the imidazole ring and between the Cl anion and the ammonium group at distances of 2.26 Å and 2.24 Å, respectively. The crystal structure of H2 is similar to that of the histamine monohydro-bromide reported in ref. 9. For its molecular conformation, the dihedral angle τ₁ is 84.3° and τ₂ is −176.0°, corresponding to the GT conformation. This is contrast to the situation in aqueous solution, where both the GG and GT forms are reported to exist together (Scheme 1).^15,16 The imidazole ring is found to take the N^τ–H tautomeric form. The same tautomerism was found for 6-histaminopurine dihydrate⁴³ and N-methyl-N′-{2-(5-methylimidazole-4-yl) methyl thioethyl}-thiourea.⁴⁴

〈H3〉. The crystal structure is of the monoclinic system with the space group P2₁ (Fig. 1c), which is essentially the same as that reported by Louhibi et al.¹¹ The histamine molecules are separated from each other by Cl anions. Three nitrogen atoms of the histamine molecule are protonated to form the dication, which takes the TT conformation with the dihedral angle τ₁ 159.6° and τ₂ 172.8°.^10–13 Different from the H1 and H2 cases, N–H⋯N hydrogen bonds between the histamine molecules were not detected due to the diprotonated nitrogen atoms of imidazolium and ammonium groups. The Cl anions are surrounded by the hydrogen atoms of the imidazolium and ammonium groups. The N–H bonds of the imidazolium ring form weak intermolecular interaction with the Cl anion, N–H⋯Cl. In this way, the layers of organic cations and Cl anions form a hydrogen bond network.

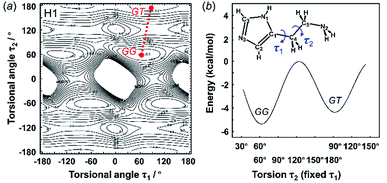
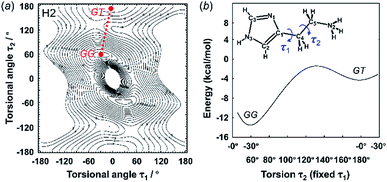
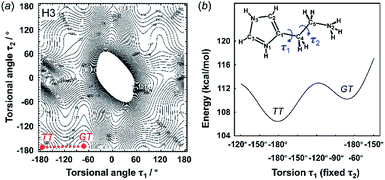
3.2 Energy stability of the molecular conformations

The X-ray crystal structure analysis clarified the molecular shapes of histidine in the solid state, as mentioned above. All the histamine species show the trans conformation with the dihedral angle of τ₂ ∼ 180° (Fig. 1). To clarify the reason for the histamine molecules taking the trans conformation, the conformational analysis was performed for an isolated molecule without additional perturbation and the most energetically stable structures were extracted. The dihedral angles τ₁ and τ₂ were varied at constant intervals and the conformational energy was calculated using the Conformers software of Materials Studio. Table 2 summarizes the energy terms obtained for the most preferable conformations of the histamines (see Fig. S1, ESI†).

Table 2 The most stable structures of the isolated molecules of histamine predicted by the conformational analysis

Model	Energy (kcal mol^−1)			Relative stability	Observed form
	GG	GT	TT
Free base (H1)	−5.36	−4.44	—	GG ≈ GT	GT
Monocation (H2)	−13.54	−4.77	—	GG ≫ GT	GT
Dication (H3)	—	110.21	106.45	TT > GT	TT

---

〈H1〉. Fig. 2a shows the 2D contour map of the potential energy of H1 plotted against the torsional angle τ₁ and τ₂. At the minimal positions, the two types of molecular conformation were detected as the most stable structures, which correspond to the GG and GT types listed in Scheme 1 and have the conformational energy of −5.36 and −4.44 kcal mol⁻¹, respectively. Fig. 2b shows the potential energy curve traced along the route connecting these two minimal points (see Fig. 2a). It can be noted that the GG form is the most preferable structure for the isolated H1 molecule, while the X-ray-analyzed conformation is the GT form, which originated from the effect of intermolecular hydrogen bonds formed between the GT-type molecules in the crystal lattice. However, the small energy difference of 1 kcal mol⁻¹ between the GG and GT forms suggests the easy transformation between these two molecular forms.

Fig. 2 2D contour map of potential energy (a) calculated for H1 as a function between the plane of the aminoethyl side chain and imidazole ring (τ₁) and the plane of the C–C bond of the ethyl side chain (τ₂). The solid circles show the minimal points of conformation as the stable molecular geometry: GG and GT forms, in which G and T represent the gauche and trans conformers, respectively. (b) Potential energy curves obtained along the conformational change pathway (straight red dotted line in the 2D contour map).

〈H2〉. Two kinds of molecular conformations were detected, the GG and GT forms. As seen in Fig. 3a, the GG form is the most stable with an energy value of −13.54 kcal mol⁻¹ due to the intramolecular hydrogen bond formation between the NH⁺ of the ammonium group and the unprotonated N^π atom of the imidazole ring. The GT form (energy value of −4.77 kcal mol⁻¹) is less stable than the GG form. The energy difference between these conformations is around 8 kcal mol⁻¹, while the energy barrier of the conformational change from the GG to GT form is 12.1 kcal mol⁻¹ (Fig. 3b).

Fig. 3 2D contour map of potential energy (a) calculated for H2 as a function between the plane of the ethylammonium side chain and imidazole ring (τ₁) and the plane of the C–C bond of the ethyl side chain (τ₂). The solid circles show the minimal points of conformation as the stable molecular geometry: GG and GT forms, in which G and T represent the gauche and trans conformers, respectively. (b) Potential energy curves obtained along the conformational change pathway (straight red dotted line in the 2D contour map).

〈H3〉. The TT form is the most stable conformation for the H3 species, corresponding well to the observed structure, as shown in Fig. 4. However, the energy values of all the possible structures of H3 (TT and GT form) were found to higher than that of the H1 and H2 models due to the repulsive force between the imidazolium ring and the ammonium group.

Fig. 4 2D contour map of potential energy (a) calculated for H3 as a function between the plane of the ethylammonium side chain and imidazolium ring (τ₁) and the plane of the C–C bond of the ethyl side chain (τ₂). The solid circles show the minimal points of conformation as the stable molecular geometry: GT and TT forms, in which G and T represent the gauche and trans conformers, respectively. (b) Potential energy curves obtained along the conformational change pathway (straight red dot line in the 2D contour map).

3.3 Prediction of crystal packing structure of histamine molecules

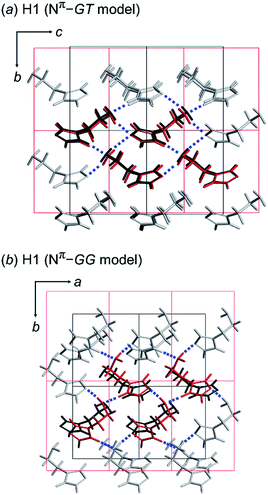
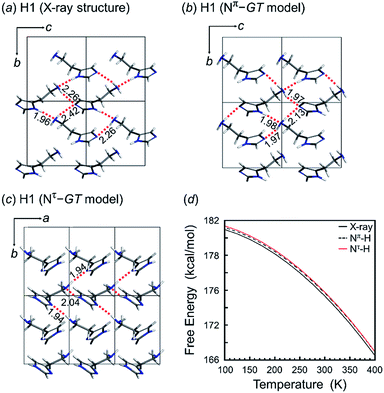
As discussed above, we found that the histamine molecule can take many types of conformations. Among them, the trans conformation (τ₂ angle) was found to be the most stable. However, the X-ray structure analysis revealed individually unique conformations in the solid state for the H1, H2 and H3 species. In the previous section, the conformationally-stable forms were predicted by taking only the intramolecular conformational energy into account. However, an energy calculation by considering both the intramolecular and intermolecular interactions must be performed for the prediction of the actually-realized molecular packing structure and the molecular conformation in the lattice. The actual calculation was performed using the annealing Monte Carlo simulation method with the Polymorph Predictor software of Materials Studio. Herein, the case of H1 is analyzed as an example.

As described in the previous section, the X-ray analysis revealed that H1 molecules take the GT-type conformation with the imidazole ring in the N^π–H tautomeric form. The packing structure prediction was carried out using this N^π/GT conformation as the packing unit. Among the various possible space groups listed in Table 3, the energetically lowest structure has the P2₁/c space group, but this crystal structure did not match the X-ray analyzed structures. Rather, the N^π/GT structure of the P2₁ space group was found to give good agreement with the X-ray result, as judged from the viewpoint of the unit cell parameters and the molecular conformation (GT), although this structure does not necessarily have the lowest energy. In addition, the thus-predicted packing structure has intermolecular hydrogen bonds, consistent with the observed structure (Fig. 5a).

Table 3 Cell parameters and molecular conformation predicted for the histamine free base (H1) with the N^π–H and N^τ–H tautomeric GT forms

Space group	Cell parameters						Density, g cm^−3	Total energy, kcal mol^−1	vdW energy, kcal mol^−1	Electrostatic energy, kcal mol^−1	Final shape	Torsion angle/°
	a/Å	b/Å	c/Å	α/°	β/°	γ/°						τ1	τ2	τ3
Observed
P21	5.69	7.63	7.25	90	104.9	90	1.255	—	—	—	GT	64.3	170.1	62.9
Calculated N^π–H
P21	5.71	7.49	7.93	90	59.7	90	1.259	−31.52	−11.20	−18.30	GT	62.4	167.8	57.6
P1	5.61	5.13	12.57	48.6	32.7	51.1	1.275	−31.40	−11.59	−17.20	GT	71.5	172.0	179.2
P1̄	7.19	9.45	5.07	87.2	93.1	122.9	1.279	−31.98	−11.04	−18.27	GT	103.7	−175.1	−52.1
P2/c	8.11	4.41	18.32	90	114.1	90	1.234	−30.59	−11.03	−16.93	GT	73.0	178.5	−61.3
P21/c	17.80	4.86	14.70	90	153.6	90	1.304	−32.18	−12.03	−17.49	GT	−80.8	179.3	77.8
Pbca	13.84	15.02	5.48	90	90.0	90	1.296	−31.55	−11.43	−17.34	GT	−136.1	179.7	68.8
N^τ–H
P21	5.16	7.67	7.56	90	98.6	90	1.249	−34.53	−11.07	−25.54	GT	−55.7	−176.5	56.2
P1	4.67	5.97	7.30	60.9	88.0	57.7	1.289	−33.57	−12.39	−22.98	GT	−78.8	−171.7	70.2
P1̄	7.93	5.29	9.09	123.5	104.7	98.4	1.286	−33.26	−12.31	−23.46	GT	−63.1	173.7	−57.4
P2/c	17.09	8.63	9.70	90	155.5	90	1.246	−33.63	−11.72	−24.94	GT	−81.2	175.8	−57.6
P21/c	6.81	11.80	12.10	90	142.4	90	1.245	−35.40	−11.31	−25.76	GT	−97.0	177.5	175.2
Pbca	13.80	11.20	7.51	90	90	90	1.273	−35.45	−11.31	−26.04	GT	64.0	175.4	178.3

---

Fig. 5 Comparison between the X-ray single crystal structure (black color) and the energetically lowest packing structure (red color) predicted for H1 using the (a) GT and (b) GG model with the space group P2₁. The hydrogen bonds are indicated as blue dotted lines.

Alternatively, the most preferable N^π–GG model predicted by the conformational analysis was used as an input in crystal structure prediction under the assumption of the same space group P2₁. The energetically lowest packing structure of the GG-type molecules is shown in Fig. 5b. The hydrogen bonding mode is different from that found in the X-ray crystal structure (Table 4).

Table 4 Cell parameters and molecular conformation predicted for the histamine free base form (H1) with the space group of P2₁

Model		Cell parameters						Density, g cm^−3	Total energy, kcal mol^−1	vdW energy, kcal mol^−1	Electrostatic energy, kcal mol^−1	Torsion angle/°
		a/Å	b/Å	c/Å	α/°	β/°	γ/°					τ1	τ2	τ3
Observed
GT		5.69	7.63	7.25	90	104.9	90	1.255	—	—	—	64.3	170.1	62.9
Calculated
Initial	Final
GT	GT	7.92	7.49	7.05	90	135.6	90	1.259	−31.52	−11.20	−18.30	62.4	167.8	57.6
GG	GG	6.92	9.45	4.64	90	107.6	90	1.276	−31.13	−12.09	−16.39	68.1	62.7	53.3

---

In this way, the packing structure predicted for the N^π/GT model was found to reproduce the actually observed crystal structure well. However, the energy difference was small among the many possible structures of the different conformations, suggesting the possibility of the detection of another crystal modification by changing the preparation conditions.

The tautomeric state was checked between the N^π–H and N^τ–H forms of the imidazole ring in the free base structure (H1). The GT-type conformation was predicted for the isolated molecule with the N^τ–H tautomeric form. For this N^τ–H tautomeric form, the packing structures predicted for the P2₁/c and Pbca space groups were found to show the lowest energy, although the energy difference among the various space groups was only 1–2 kcal mol⁻¹ (Table 3). Good agreement with the X-ray-analyzed structure was found for the models of the space group P2₁. However, the dihedral angles τ₁ −55.7° and τ₂ −176.5° of the N^τ/GT form are different from the X-ray values (τ₁ 64.3° and τ₂ 170.1°). The hydrogen bonding mode of the N^τ/GT model (Fig. 6c) is slightly different from the X-ray structure. The intermolecular hydrogen bonds formed between the amino group and the imidazole N^τ–H ring of the two adjacent molecules along the b axis are lost. Accordingly, the intermolecular N–H⋯N hydrogen bonds are important for the stability of the packing structure of tautomeric conformation.

Fig. 6 Packing structure of H1: (a) X-ray-analyzed crystal structure and the predicted packing structures for the (b) N^π–GT model and (c) N^τ–GT model. (d) Temperature dependence of the free energy calculated for the X-ray N^π–GT crystal structure (black line), N^π–GT model (black dash line) and N^τ–GT model (red line).

On the other hand, as seen in Fig. 6, the crystal structure of H1 predicted for the N^π/GT model shows the intermolecular hydrogen bonds along the b axis, corresponding to the X-ray crystal structure. The Gibbs free energy calculation indicated that the crystal structure with the N^π–H tautomeric form has a lower free energy than that of the N^τ–H tautomeric form by an energy difference 0.3 kcal mol⁻¹ at room temperature (Fig. 6d). Conclusively, the most preferable conformation is the N^π–H tautomeric GT structure for the free base compound (H1).

3.4 Tautomeric state of imidazole ring as checked by vibrational spectra data

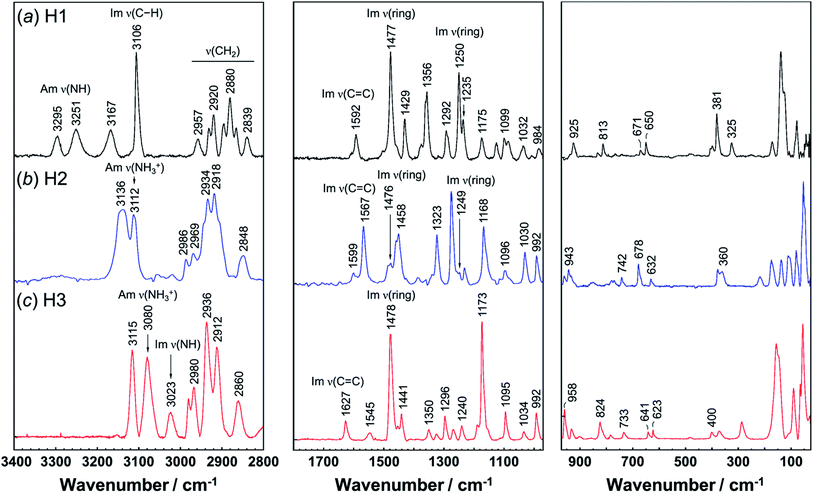
Vibrational spectral patterns are sensitive to the molecular conformation and packing structure of molecules. Thus, the reasonableness of the above-predicted structure models may be checked by comparing the calculated vibrational frequencies with the actually-observed data. The observed Raman and IR spectra of H1 are shown in Fig. 7 and 8, respectively. The band assignments were made by referring to the spectral data of related compounds such as imidazole, histidine, and histamine derivatives and the vibrational frequencies calculated by the DFT method.^{7,15–17,23,24,45} The vibrational frequencies and the peak assignments are listed in Table 5.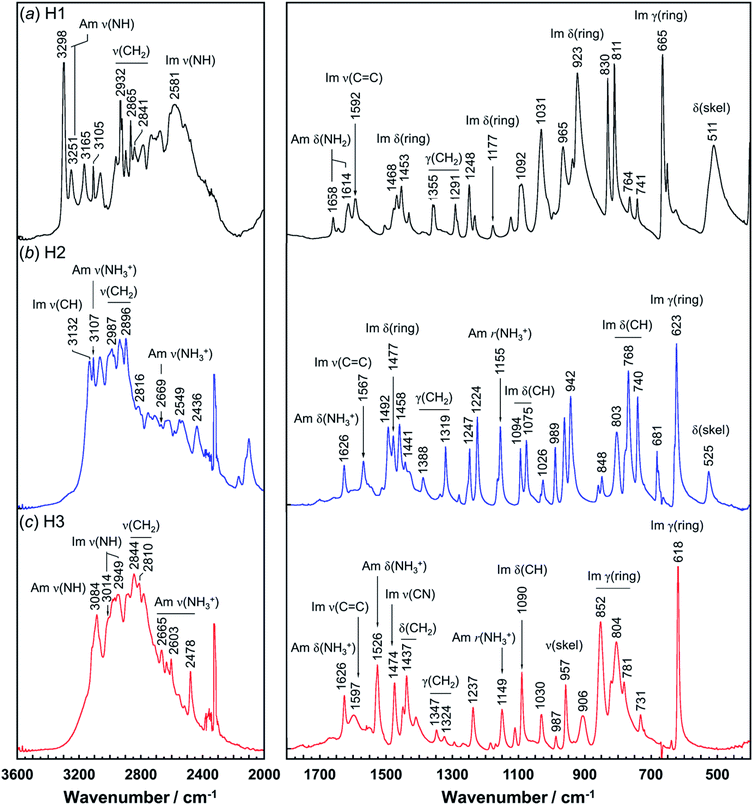

Fig. 7 Raman spectra of histamine species: (a) free base; H1, (b) monocation; H2, and (c) dication; H3. The spectra are shown in the 3400–2800 cm⁻¹, 1800–975 cm⁻¹, and 975–25 cm⁻¹ region, respectively.

Fig. 8 Infrared spectra of histamine species: (a) free base; H1, (b) monocation; H2, and (c) dication; H3. The spectra are shown in the 3600–2000 cm⁻¹ and 1800–400 cm⁻¹ region.

Table 5 The observed Raman and infrared spectral data (in cm⁻¹) for the various histamine species^a

Free base (H1)		Monocation (H2)		Dication (H3)		Assignments
Raman	Infrared	Raman	IR	Raman	IR
a Assignments: Am; amine, Im; imidazole ring, ν; stretching, δ; in-plane bending, γ; out-of-plane bending, r; rocking, ω; wagging, and skel; skeletal side-chain.
3295	3298					Am ν(NH)
3251	3251					Am ν(NH)
			3174			Am ν(NH3^+)
3167	3165	3136	3132	3115		Im ν(CH)
3106	3105					Im ν(CH)
		3112	3105	3080	3084	Am ν(NH3^+)
				3023	3014	Im ν(NH)
	2967	2986	2987	2980		ν(CH2)
2957	2955	2969		2968		ν(CH2)
2957	2955					ν(CH2)
2931	2932					ν(CH2)
2920	2894	2918	2896			ν(CH2)
2880	2865			2861	2844	ν(CH2)
2839	2841	2848	2816		2810	ν(CH2)
			2669	2792	2665	Am ν(NH3^+)
	2581					Im ν(NH)
	1614		1626	1627	1626	Im ν(C=C), Am δ(NH)
1592	1592	1567	1567		1597	Im ν(C=C)
				1545	1526	Am δ(NH3^+)
1477	1468	1476	1477	1478	1474	Im ν(ring), Im δ(NH)
1456	1453	1458	1458	1453	1454	Im ν(CN), Im δ(NH)
1429	1429			1441	1437	δ(CH2)
1356	1355	1385	1388	1350	1347	ω(CH2)
1292	1291	1248	1247			ω(CH2)
1250	1248		1224	1240	1237	δ(CH2)
1175	1177			1173	1178	Im δ(ring)
		1168	1155		1149	Am r(NH3^+)
1099	1092	1096	1094	1095	1090	Im δ(CH)
1032	1031	1030	1026	1034	1030	ν(skel)
984	965	992	989	992	987	Im δ(ring)
925	923	943	942	901	906	Im δ(ring)
834	830	851	848	824	852	Im γ(ring)
671	665	678	681	641		Im γ(ring)
650	628	632	623	623	618	Im γ(ring)
740	741	742	740		731	Im γ(CH), r(CH2)
	511		525			δ(skel)

---

In the Raman spectra, the histamine of H1 shows two bands in the frequency region higher than 3200 cm⁻¹, which are assigned to the N–H stretching mode (Am ν(NH)) of the hydrogen-bonded amine groups.^7,23,24 These bands correspond to the infrared bands at 3295 and 3251 cm⁻¹ (Fig. 8). These bands were reproduced well by the calculation with the small difference of 5−20 cm⁻¹ (see Table S1, ESI†). However, for the H2 species, the infrared band of the ammonium N–H stretching vibration (Am ν(NH₃⁺)) was detected at 2669 cm⁻¹, at about 600 cm⁻¹ lower than H1. In contrast, the Am ν(NH) bands of the H1 species are located at remarkably higher frequency positions (3295 and 3251 cm⁻¹ in Raman spectra), indicating the weaker NH(Am)⋯N(Im) hydrogen bonds in the crystal lattice of the H1 species compared with the H2 species. However, it may be better to say that the intermolecular hydrogen bonds of the H2 molecules are quite strong. The Raman bands of Am ν(NH) were observed at 3112 and 2934 cm⁻¹ for H2, and at 3080 cm⁻¹ for H3 species. In the infrared spectra, the corresponding bands were detected at 3105 and 3084 cm⁻¹ for the H2 and H3 compounds, respectively.^7,24 The imidazole N–H stretching vibration (Im ν(NH)) of the H1 species is observed at 2581 cm⁻¹ in the infrared spectra, which corresponds to the NH(Im)⋯N(Am) hydrogen bond interaction. The calculated vibrational frequency 2567 cm⁻¹ is in good agreement with the observed value (see Table S1 and Fig. S2, ESI†). The bands at around 3100 cm⁻¹ are assigned to the C–H stretching mode of the imidazole ring (Im ν(CH)). The bands in the region of 3000 to 2800 cm⁻¹ are due to the CH₂ stretching (ν(CH₂)) modes of each histamine form.

The tautomeric equilibrium form of the imidazole ring can be checked using the bands of the imidazole C=C stretching (Im ν(C=C)), where the band position should be shifted depending on the N^π–H and N^τ–H tautomeric forms.^7,16,17,45 The vibrational frequency calculated for the N^π–tautomer is 1587 cm⁻¹, which is in good agreement with the observed value of 1592 cm⁻¹, indicating H1 takes the N^π tautomer form. This is consistent with the X-ray structure analysis. H2 shows the Raman band at 1567 cm⁻¹, in good agreement with the value of 1550 cm⁻¹ calculated for the N^τ–tautomer (see Table S1 and Fig. S3, ESI†). This is also in good accordance with the X-ray structure analysis. For the H3 species at low pH (Fig. 7c), the dominant peak of the Im ν(C=C) band was found at 1627 and 1626 cm⁻¹ in the Raman and infrared spectra, respectively.⁴⁶ The Raman peak at 1545 cm⁻¹ and the IR peak at 1526 cm⁻¹ are assigned to the ammonium in-plane bending mode, consistent with the calculated values of about 1530 cm⁻¹ in both the Raman and infrared spectra (see Table S1 and Fig. S4, ESI†).

3.5 Hydrogen bonding and temperature-dependent experiments

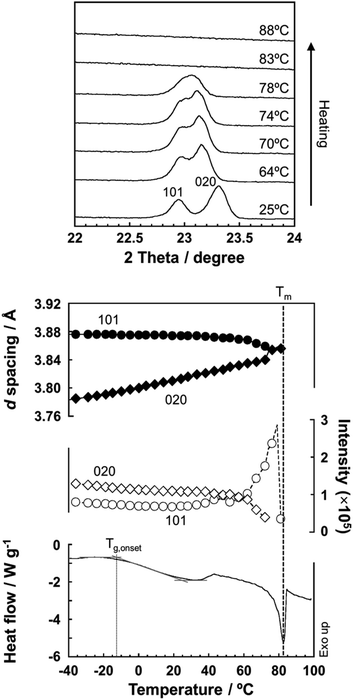
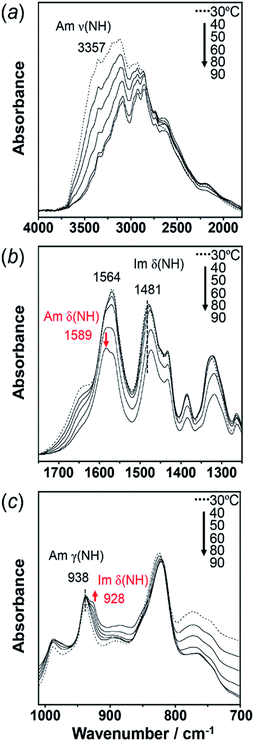
As predicted by the computer simulations, there are many possibilities for the crystal modification of the histamine species under the various conditions. This situation suggests that the crystal form may be changed by changing the temperature or the possibility of phase transition in the heating process. Then, by focusing on the histamine free base (H1), X-ray diffraction (XRD) measurements were performed in the high-temperature region. The thus-measured XRD patterns are shown in Fig. 9 (see Fig. S5, ESI†). No clear phase transition was detected at a temperature below the melting point (83 °C). This suggests that the crystal structure of the H1 species remained stable up to the high temperature region.

Fig. 9 (Top) Temperature dependence of the X-ray powder diffraction profile measured for the free base (H1) during the heating process. (Middle) Temperature dependence of the lattice spacing (black) and diffraction intensity (white) estimated for the peaks at 2θ = 22.9° (101 plane) and 23.3° (020 plane). The DSC thermogram is also shown for comparison. The glass transition T_g,onset = −12.7 °C and the melting point T_m = 83 °C.

To check the occurrence of conformational changes in the H1 molecules in the heating process, the temperature-dependent FTIR spectra were measured, as shown in Fig. 10. As the temperature increased, the peak at 3357 cm⁻¹ [hydrogen-bonded Am ν(NH)] shifted to the lower frequency side and became constant above 60 °C (Fig. 11a). Similar behavior was also detected for the peak at 938 cm⁻¹ [Am γ(NH)]. The lower frequency shift of the NH(Am) band in the 3350 cm⁻¹ region indicates the strengthening of the NH(Am)⋯N(Im) intramolecular hydrogen bond in H1 in the temperature region higher than 40 °C (see the DSC thermogram in Fig. 9). The relative intensity ratio of the Am γ(NH) 938 cm⁻¹ band increased in the heating process up to 60 °C. This observation also suggests an increase in the population of these hydrogen bonds.

Fig. 10 Temperature-dependent IR spectra of H1 in the frequency region of (a) 4000–1750 cm⁻¹, (b) 750–1250 cm⁻¹, and (c) 1010–700 cm⁻¹. The red arrow shows the new peaks appearing at high temperature.

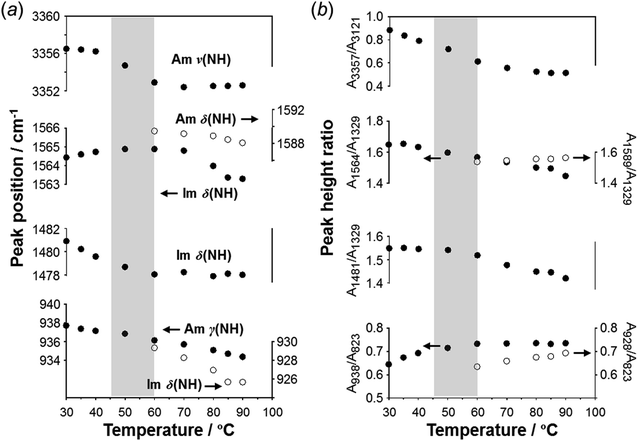Fig. 11 Temperature dependence of (a) peak position (cm⁻¹) and (b) intensity ratio of the various IR peaks measured for the H1 species.

Above 60 °C, new peaks appeared at 1589 and 928 cm⁻¹, which are assigned to the Am δ(NH) and Im δ(NH) modes as indicated by the normal mode calculation, respectively. These observations may correspond to the increase in hydrogen-bonding-free N atoms in the high temperature region.

3.6 Proton conductivity of H1

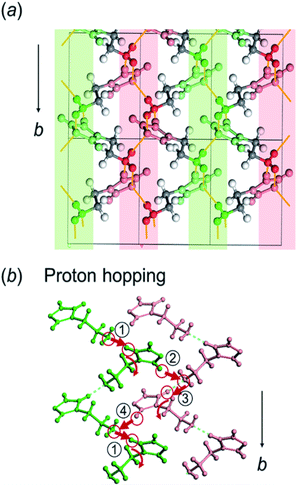
Here, the crystal structure of the H1 species is reviewed again in detail. As shown in Fig. 12, intermolecular hydrogen bonds are formed between the imidazole rings and the end NH₂ units. These hydrogen bonds form networks in the ab planes. These networks are alternately arrayed along the c axis, as indicated by the green and pink colors in Fig. 12a. The protons may transfer effectively between the imidazole rings and the NH₂ units along the b axis. The route for proton transfer through the hopping motion is illustrated in Fig. 12b. A proton of the NH₂ group of a histamine molecule jumps to the N atom of the imidazole ring of a neighboring molecule. This proton on the imidazole ring will be transferred to another NH₂ group through the 180° rotational motion of the ring. Then, similar proton hopping may occur continuously (1–2–3–4) between the neighboring molecules. In this way, effective and cooperative proton conduction is predicted to occur in the crystal lattice of the H1 species.

Fig. 12 (a) Illustration of the hydrogen bond network of the histamine free base (H1), which is separated in two layers (green and pink colors) along the ac plane. The hydrogen bonds between the neighboring histamine molecules are linked along the b axis. (b) Illustration of the proton hopping between the adjacent layers of histamine molecules in continuous steps (1–2–3–4). The proton on the imidazole ring will be transferred to the adjacent amino group via the rotation of the ring.

This prediction was checked by actually performing in situ impedance measurements during the heating process of the H1 sample (see Fig. S6, ESI†). As shown in Fig. 13, the proton conductivity in the solid state increased steeply with an increase in temperature (30 °C to 60 °C) and then decreased in the temperature region higher than the small endothermic peak in the DSC profile. This behavior of the proton conductivity corresponds well to the IR spectral changes observed in Fig. 11. The highest conductivity observed was 2.81 × 10⁻⁴ S cm⁻¹ at 60 °C. In Table 6, the proton conductivity of the H1 species is compared with that reported for various compounds with the hydrogen bonds. The present value is 1 order higher than that reported in ref. 33.

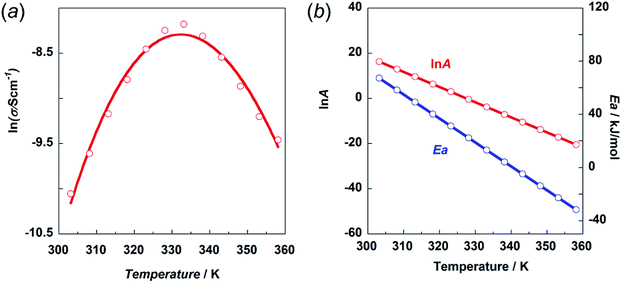Fig. 13 (a) Temperature dependence of proton conductivity (s) in the natural logarithmic form. (b) Frequency factor (ln A) and activation energy E_a vs. temperature.

Table 6 The proton conductivity and activation energy of histamine (H1) in comparison with that of other compounds

Sample	σ (S cm^−1)	Ea (kJ mol^−1)
Imidazole^49	1.65 × 10^−3	23 (at 348 K)
Ethylene oxide tethered imidazole^50
Imi-1EO	∼10^−5	48
Imi-5EO	∼10^−5	60
Imidazolium carboxylates^51
Im-Suc (parallel to HB)	4.94 × 10^−7	320
Im-Suc (perpendicular to HB)	3.55 × 10^−9	378
Im-Glu (parallel to HB)	2.40 × 10^−6	87
Im-Glu (perpendicular to HB)	5.92 × 10^−8	157
Histamine^33	9.40 × 10^−6
H1 (this work)	2.70 × 10^−4	18.9 (at 330 K)

---

Then, the activation energy was estimated and compared with that of other compounds, as listed in Table 6. The H1 species melted at around 83 °C. Accordingly, the proton conductivity measurement was performed in the temperature region below the melting point, and thus the proton transfer is speculated to occur under the proton hopping mechanism in the solid state. As shown in Fig. 13, the proton conductivity showed the maximal peak at around 330 K. This cannot be explained by introducing a simple Arrhenius type equation:

σ = A e^{−E_a/[R(T−T_o)]} (2)

where, R is a gas constant. T_o is generally assumed to be a temperature below the glass transition temperature (T_g), above which the proton conduction is speculated to start due to the activated thermal motion. Since the probability of proton hopping may be disordered by the thermal motion, the frequency factor A is assumed to be expressed as:

A = A₀ e^a_o+a₁T (3)

Simultaneously, the activation energy is also dependent on temperature, which may decrease with an increment in temperature. The activation energy, E_a, is now assumed to have the following shape: E_a = E_o + E′T, where E_o and E′ are adjustable parameters. Then, the conductivity due to a Grotthuss-type mechanism^47,48 may be expressed as:

σ = A₀ e^a_o+a₁T e^{−(E_o+E′T)/[R(T−T_o)]} (4)

In the present case, T_o was ignored for simplicity. The natural logarithm of σ is expressed as a function of temperature as follows:

ln(σ) = ln A_o + [a_o + a₁T − (E_o + E′T)/(RT)] (5)

The experimental data were fitted using eqn (5), as shown in Fig. 13a. The temperature dependence of the ln A and E_a values is shown in Fig. 13b. The physical meaning of these temperature-dependent values is now clear as mentioned above. The E_a value becomes almost zero or rather minus in the temperature region above the maximum peak. However, the frequency factor also becomes lower in this region, resulting in relatively low conductivity.

As seen in Table 6, the proton conductivity of imidazolium compounds is quite low, which can be attributed to their high activation energy. Imidazole itself has one order higher proton conductivity than H1 species. The E_a is much lower for the H1 species in the same temperature region. The thermal activity of the smaller imidazole molecule may be higher than that of H1 with relatively complicated thermal motion, including the trans–gauche conformational exchange. Also, the frequency factor of imidazole may be larger than that of H1.

4. Conclusions

Herein, we described the molecular conformation and molecular packing structure for the various types of histamine species created under various pH conditions. In addition to the conformational variation of the CH₂–CH₂–NH₂ segment, the imidazole ring shows tautomerism of the N atom, making the description of the molecular structure of the histamine species quite complicated. Initially, a conformational analysis was performed, allowing us to successfully predict the GG, GT and TT conformers for the isolated molecules. Depending on the ionic state, the conformational stability changes. Next, we calculated the packing structure of these variable molecules. When the histamine molecules are packed in the crystal lattice, the lattice energy was found to change sensitively depending on the ionic states. In particular, intra- and intermolecular hydrogen bonds were found to play an important role in the relative stability of the crystal lattice. The thus-predicted structures were found to correspond well to the actual X-ray-analyzed crystal structures. Since the conformational state of histamine is complicated, the assignment of the IR and Raman bands is useful for the characterization of these histamine species. Theoretical calculation was performed to determine the vibrational modes of these histamine species. The vibrational spectroscopic data will be a useful guide for the identification of histamine species in various states.

As expected from the hydrogen-bonded network of the crystal lattice, this compound is expected to exhibit high proton conductivity at high temperature. The proton conductivity was actually measured for histamine (free base form) for the first time, which showed the maximum peak at around 60 °C during the heating process in the solid state. The temperature-dependent IR spectral data showed the deflection point in this temperature region, suggesting the good correlation between the proton conductivity and the hydrogen bond network structure.

As mentioned above, histamine is very important in the field of biological and medical science. Thus far, the structural study of histamine has been widely reported in the literature; however, the systematic investigations were not thorough. We believe the present results may contribute to the further development of histamine science.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to acknowledge the scholarships from the Thailand Research Fund (TRF) through the Royal Golden Jubilee PhD Program (Grant No. PHD/0072/2556, 3.C.CM/56/P.1.N.XX to K. K., K. T. and P. N.). The authors also would like to extend their appreciation to Professor Suwabun Chirachanchai, Chulalongkorn University, Thailand, for his kind permission to perform the proton conductivity measurement in his laboratory. K. T. acknowledges the financial support by the MEXT in “the Strategic Project to Support the Formation of Research Bases at Private Universities” (2015-2019). P. N. acknowledges the partially financial support by the TRF Distinguished Research Professor Award (DPG6080002).

References

1. O. B. Reite, Physiol. Rev., 1972, 52, 778–819.
2. S. Micallef, H. Stark and A. Sasse, Life Sci., 2013, 93, 487–494.
3. P. J. Barnes, Pulm. Pharmacol. Therapeut., 2001, 14, 329–339.
4. E. Zampeli and E. Tiligada, Br. J. Pharmacol., 2009, 157, 24–33.
5. G. C. Paesen, P. L. Adams, K. Harlos, P. A. Nuttall and D. I. Stuart, Mol. Cell, 1999, 3, 661–671.
6. A. M. ter Laak, H. Timmerman, R. Leurs, P. H. J. Nederkoorn, M. J. Smit and G. M. Donné-Op den Kelder, J. Comput.-Aided Mol. Des., 1995, 9, 319–330.
7. F. J. Ramírez, I. Tuñón, J. A. Collado and E. Silla, J. Am. Chem. Soc., 2003, 125, 2328–2340.
8. J. J. Bonnet and J. A. Ibers, J. Am. Chem. Soc., 1973, 95, 4829–4833.
9. K. Prout, S. R. Critchley and C. R. Ganellin, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1974, 30, 2884–2886.
10. T. Yamane, T. Ashida and M. Kakudo, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1973, 29, 2884–2891.
11. S. Louhibi, I. Belfilali, L. Boukli-Hacene and T. Roisnel, Acta Crystallogr., Sect. E: Crystallogr. Commun., 2015, 71, o844–o845.
12. M. V. Veidis, G. J. Palenik, R. Schaffrin and J. Trotter, J. Chem. Soc. A, 1969, 1, 2659–2666.
13. L. B. Cole and E. M. Holt, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1990, 46, 1737–1739.
14. C. R. Ganellin, J. Pharm. Pharmacol., 1973, 25, 787–792.
15. E. D. Raczyńska, M. Darowska, M. K. Cyrański, M. Makowski, T. Rudka, J.-F. Gal and P.-C. Maria, J. Phys. Org. Chem., 2003, 16, 783–796.
16. J. A. Collado, I. Tuñón, E. Silla and F. J. Ramírez, J. Phys. Chem. A, 2000, 104, 2120–2131.
17. A. Torreggiani, M. Tamba, S. Bonora and G. Fini, Biopolymers, 2003, 72, 290–298.
18. A. Hernández-Laguna, Z. Cruz-Rodriguez, Y. G. Smeyers, G. A. Arteca, J. L. M. Abboud and O. Tapia, J. Mol. Struct.: THEOCHEM, 1995, 335, 77–87.
19. P. I. Nagy, G. J. Durant, W. P. Hoss and D. A. Smith, J. Am. Chem. Soc., 1994, 116, 4898–4909.
20. L. B. Kier, J. Med. Chem., 1968, 11, 441–445.
21. A. Wojtczak, M. Jaskolski and Z. Kosturkiewicz, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1983, 39, 545–547.
22. L. B. Cole and E. M. Holt, J. Chem. Soc., Perkin Trans. 1, 1986, 1, 151–154.
23. J. A. Collado and F. J. Ramírez, J. Raman Spectrosc., 1999, 30, 391–397.
24. J. A. Collado and F. J. Ramírez, J. Raman Spectrosc., 2000, 31, 925–931.
25. C. R. Ganellin, E. S. Pepper, G. N. J. Port and W. G. Richards, J. Med. Chem., 1973, 16, 610–616.
26. N. S. Ham, A. F. Casy and R. R. Ison, J. Med. Chem., 1973, 16, 470–475.
27. M. Kraszni, J. Kökösi and B. Noszál, J. Chem. Soc., Perkin Trans. 2, 2002, 914–917.
28. A. Wojtczak, M. Jaskolski and Z. Kosturkiewicz, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1988, 44, 1779–1781.
29. C. Jarumaneeroj, K. Tashiro and S. Chirachanchai, J. Power Sources, 2014, 249, 185–192.
30. A. Pangon, P. Totsatitpaisan, P. Eiamlamai, K. Hasegawa, M. Yamasaki, K. Tashiro and S. Chirachanchai, J. Power Sources, 2011, 196, 6144–6152.
31. P. Totsatitpaisan, K. Tashiro and S. Chirachanchai, J. Phys. Chem. A, 2008, 112, 10348–10358.
32. K. D. Kreuer, A. Fuchs, M. Ise, M. Spaeth and J. Maier, Electrochim. Acta, 1998, 43, 1281–1288.
33. D. Umeyama, S. Horike, M. Inukai, Y. Hijikata and S. Kitagawa, Angew. Chem., Int. Ed., 2011, 50, 11706–11709.
34. A. Altomare, G. Cascarano, C. Giacovazzo and A. Guagliardi, J. Appl. Crystallogr., 1993, 26, 343–350.
35. CrystalStructure 4.2, Crystal Structure Analysis Package, Rigaku Corporation, Tokyo 196-8666, Japan, 2000–2015.
36. P. Nimmanpipug, J. Yana, V. S. Lee, S. Vannarat, S. Chirachanchai and K. Tashiro, J. Power Sources, 2013, 229, 141–148.
37. P. Nimmanpipug, T. Laosombat, V. Sanghiran Lee, S. Vannarat, S. Chirachanchai, J. Yana and K. Tashiro, Chem. Eng. Sci., 2015, 137, 404–411.
38. Materials Studio, Accelrys Software Inc, 2011.
39. K. Kodchakorn, V. S. Lee, J. Yana and P. Nimmanpipug, Surf. Coat. Technol., 2016, 306, 35–40.
40. H. Sun, P. Ren and J. R. Fried, Comput. Theor. Polym. Sci., 1998, 8, 229–246.
41. K. Tashiro, P. Nimmanpipug and O. Rangsiman, J. Phys. Chem. B, 2002, 106, 12884–12895.
42. P. Nimmanpipug, K. Tashiro and O. Rangsiman, J. Phys. Chem. B, 2003, 107, 8343–8350.
43. U. Thewalt and C. E. Bugg, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1972, 28, 1767–1773.
44. G. J. Durant, C. R. Ganellin, D. W. Hills, P. D. Miles, M. E. Parsons, E. S. Pepper and G. R. White, J. Med. Chem., 1985, 28, 1414–1422.
45. J. G. Mesu, T. Visser, F. Soulimani and B. M. Weckhuysen, Vib. Spectrosc., 2005, 39, 114–125.
46. W. F. Reynolds, I. R. Peat, M. H. Freedman and J. R. Lyerla, J. Am. Chem. Soc., 1973, 95, 328–331.
47. P. Leiderman, R. Gepshtein, A. Uritski, L. Genosar and D. Huppert, J. Phys. Chem. A, 2006, 110, 9039–9050.
48. C. J. de Grotthuss, Biochim. Biophys. Acta, 2006, 1757, 871–875.
49. A. Kawada, A. R. McGhie and M. M. Labes, J. Chem. Phys., 1970, 52, 3121–3125.
50. G. R. Goward, M. F. H. Schuster, D. Sebastiani, I. Schnell and H. W. Spiess, J. Phys. Chem. B, 2002, 106, 9322–9334.
51. Y. Sunairi, A. Ueda, J. Yoshida, K. Suzuki and H. Mori, J. Phys. Chem. C, 2018, 122, 11623–11632.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 1912431, 1912432 and 1912450. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ra03418h

---