Open Access Article
Open Access ArticleShape-dependent structural and magnetic properties of Fe nanoparticles studied through simulation methods
Rida Essajai *a,
Younes Benhouriab,
Abdeljalil Rachadic,
Mbarek Qjanid,
Ahmed Mzerda and
Najem Hassanaina
*a,
Younes Benhouriab,
Abdeljalil Rachadic,
Mbarek Qjanid,
Ahmed Mzerda and
Najem Hassanaina
aGroup of STCE-Energy Research Center (ERC), Faculty of Science, Mohammed V University, B. P. 1014, Rabat, Morocco. E-mail: rida.essajai@gmail.com
bLaboratory of Physics of Materials and Modeling of Systems, (LP2MS), Unit Associated with CNRST-URAC 08, Faculty of Science, University Moulay Ismail, Physics Department, B. P. 11201, Meknes, Morocco
cLaboratory of Condensed Matter and Interdisciplinary Sciences (LaMScI), Faculty of Science, Mohammed V University, B. P. 1014 Rabat, Morocco
dLCMP, Faculty of Sciences, Chouaïb Doukkali University, El Jadida, Morocco
First published on 16th July 2019
Abstract
Studying the shape-dependent structural and magnetic properties of nanoparticles is one of the most necessary scientific challenges in order to match these nano-objects for adequate applications. In this research paper, the shape effect of iron nanoparticles (FeNPs) on structural and magnetic properties was investigated on the basis of a combination of Molecular Statics (MS) and Monte Carlo (MC) simulations. To this end, three kinds of FeNP shapes (such as spherical, planar and rod) in an equal volume have been considered. The coordination number distribution of FeNPs obtained from the data extracted by MS simulations was exploited for performing MC simulations on the familiar Ising model. The numerical findings obtained showed that the structural stability, the Curie temperature as well as the shape of the hysteresis loop are correlated with the FeNP shape.
Considerable research efforts have been devoted to iron nanoparticles (FeNPs) due to their remarkable performance for technological applications in many industrial areas. Owing to the fact that they exhibit very low toxicity and display high biocompatibility, FeNPs are very promising candidates for biomedical applications, such as hyperthermia treatment,1 magnetic resonance imaging (MRI) contrast enhancement,2 labelling and separation of biological materials,3 as well as direct drug delivery systems.4 In addition to biomedical exploitation, they have been applied in the fields of catalysis,5,6 environmental remediation,7 data storage,8 energy storage,9 etc. Furthermore, one of the most important properties behind the increased attention on FeNPs is their magnetism,10 making them very well suited for use as dispersants for the production of magnetic nanofluids (so-called ferrofluids).11,12 This type of colloidal suspension exhibits particular magnetic behaviors that make them useful for magnetic resonance imaging,13,14 audio speakers,15 magnetic recording media,16–18 seals,19,20 magnetic targeted drug delivery,21,22 lubrication,23 removal of water pollutants,24 targeted drug delivery,25,26 and so on. It is worth underlining that any application based on nanoscale magnetic particles requires specific properties27 that can be controlled through changing either the size or morphology of these nanoparticles.28 Hence, it is necessary to know the magnetic properties of FeNPs in different shapes in order to match them for adequate applications.
In the last decade, a significant amount of analytical models have been proposed to study magnetic solids with a size in the range of 1 to 100 nm, at least in one of the three dimensions of space. Fisher et al.29 established a model based on the spin–spin correlation length mechanism for magnetic thin films. Sun et al.30 proposed a model based on the bond order–length–strength correlation mechanism combined with the Ising proposition for ferromagnetic nanosolids. Yang et al.31 and Cao et al.32 utilized the cohesive energy of particles to study the effect of size and shape of nanosolids on their Curie temperature. All these proposed models are suitable to investigate some magnetic property of ferromagnetic nanosolids by taking into consideration the various parameters related to nanomaterials such as energy cohesive size and shape. However, another important geometrical parameter of particles, the coordination number distribution of nanoparticles, has not been paid enough attention before despite being influenced by the shape and size of the nanomaterials.33 Hence, it is expected that atomistic simulation techniques such as Molecular Statics (MS) combined with Monte Carlo (MC) simulations on the familiar Ising model can play an important role in this regard since the experimental studies of the nanomaterial encounter many technical difficulties.
The aim of the present work is to reflect the possible effect of the coordination number distribution to predict the magnetic properties depending on the shape of the FeNPs in a specific volume, including spherical, planar and rod. To this end, Molecular Statics (MS) simulations combined with Embedded-Atom-Method (EAM) and Monte Carlo (MC) simulations based on the Metropolis algorithm for the simulation of the familiar Ising model were employed. This paper is ordered as follows: Section 1 presents a description of computational methods and the calculation procedure. Our results are exposed in Section 2, where structural and magnetic properties are discussed. Finally, the conclusions arising from this work are summarized in Section 3.
1 Computational details and theoretical model
All MS simulations were realized by using the LAMMPS package34 and the atomistic visualization was carried out through the OVITO software.35 To accomplish the atomistic simulations, the Embedded-Atom Method (EAM) potential was adopted to describe the interatomic interaction that has been developed from the density functional theory (DFT) by Daw and Baskes.36 Moreover, this potential has been successfully employed by our group.37,38 The EAM potential parameterized by G. Mendelev et al.39 to describe the iron–iron interaction is used throughout this study.In the frame of the EAM approach, the energy of each atom is measured from the energy required to embed an atom into the local-electron density as provided by the other atoms of the system. The total energy of the EAM, ET, is written as follows:
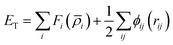 | (1) |
Here, 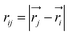 is the scalar distance, ϕij(rij) is the pair-potential between atoms i and j, Fi(
is the scalar distance, ϕij(rij) is the pair-potential between atoms i and j, Fi(![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) i) is the embedding energy function and
i) is the embedding energy function and ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) i is the host electron density induced by all encirclement atoms j at the position of atom i. The host electron density is given by:
i is the host electron density induced by all encirclement atoms j at the position of atom i. The host electron density is given by:
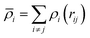 | (2) |
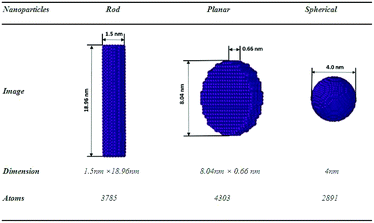
We start numerical experiments in this paper by generating three different shapes of FeNPs with equal volumes (V ≈ 33.5 nm3) such as spherical, planar and rod (see Fig. 1). Periodic Boundary Conditions (PBCs) were neglected in the three dimensions. The force/energy of each system is minimized at T = 0 K by employing the conjugate gradient (CG) algorithm (Polak–Ribiere version). The main aim of this minimization is to reduce the forces/energies over several iterations to set the new structures of each system (the coordinates of each atom are iteratively adjusted). The iterations are stopped only if one of the ending criteria is satisfied (the energy tolerance chosen is of the order 10−6 (unitless)). After this pretreatment step, we consider the relaxed configurations as the actual systems (i.e., reference configurations) for further investigation.
In order to characterize all actual systems in detail, two different techniques have been employed: Coordination Number (CN) analysis and the Common Neighbor Analysis (CNA) method, which are frequently applied in the study of the microscopic structure (at atomic level) of crystalline and liquid states in nanometals.38,40 The CN characterizing the number of nearest neighbors surrounding each atom is calculated by means of the area of first maximum peak of radial distribution function (g(r)). It is defined by the following form,41
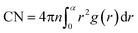 | (3) |
To investigate the magnetic properties of FeNPs, the MC method44 was performed using the Metropolis algorithm45 for the simulation of the familiar Ising model described by the following Hamiltonian:
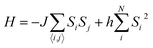 | (4) |
It is worth noting that the surface of monatomic metallic nanoparticles is bounded by low-index facets and characterized by different geometrical arrangements of low-coordinated atoms,37,38,46–49 reflecting the irregular nature of their structures. This makes the process of determining the number of nearest neighbor atoms for the nanoparticle surface very complicated, therefore the data extracted by MS simulations is a practical way of diverting this difficulty; particularly, CN analysis at T = 0 K for each actual system is considered as an input for the MC simulations. The spin configurations are achieved by selecting the sites sequentially through the system and making single-spin flip attempts, which are rejected/accepted by applying the Boltzmann statistics-based probability. In each sample, multiple iterations (104 MC steps per atom) were performed at each temperature to reach thermal equilibrium; then followed by 9 × 104 MC steps per atom to study the dependence of the average magnetization and average susceptibility on a dimensionless temperature (t), i.e. t = TKB/|J|, where KB is the Boltzmann constant. The hysteresis loops were computed by starting from a demagnetized state at zero of a reduced external magnetic field (h/|J| = 0), then increasing and decreasing quasi-continuously with a step of h/|J| taken as 0.25.
2 Results and discussion
2.1 Structural properties
All of the initial structures of the FeNPs are metastable, so it is important to get the real calculation models which correspond to the minimum energies before addressing the object of this work. During the energy minimization by means of the MD simulations, each structure of FeNPs passes through several states until it reaches a stable state corresponding to the minimum energy, but still remains metastable, resulting from its surface atoms always wanting to aggregate to reduce the surface energy as was indicated in ref. 50. After this step, the structural characterization of the actual structure of FeNPs with different shapes was studied by means of the CNA technique. Fig. 2 displays the variation of the structure fractions versus the FeNP shape using the CNA method. The result shows that each nanoparticle is characterized by two categories of atoms: those that are unidentified and those that have a local crystal environment, especially bcc structures. It was also noticed that for each equilibrium shape of FeNPs, the fraction of Fe atoms having bcc structures (67% for spherical, 61.6% for rod, and 55.9% for planar) is higher than that of those possessing unidentified structures (33% for spherical, 38.4% for rod, and 44.1% for planar).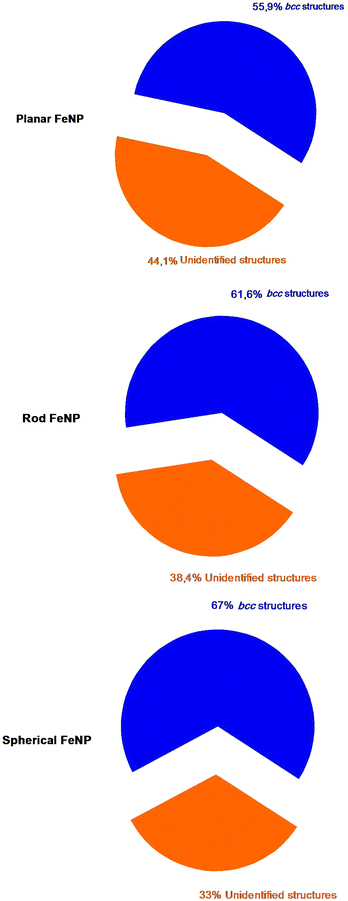 | ||
| Fig. 2 The percentage of each category of atoms in FeNPs counted by using the CNA method; navy for bcc structures and orange for unidentified structures. | ||
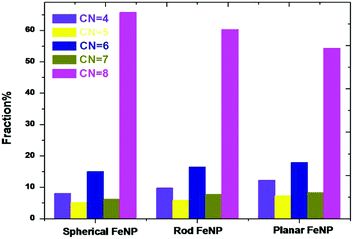
It is well known that the most significant inconvenience of the CNA technique is that it provides only a single result related to the atoms with a local crystal environment such as fcc, hcp and bcc structures. In this respect, another technique is needed to report a complete study of the required results in terms of structural characterization of single metal nanoparticles. For this, the CN method was used to characterize in more detail the local atomic structure in FeNPs. Fig. 3 exhibits the coordination number distribution of the systems studied. It was found that all FeNP shapes have a high fraction of bcc structure which corresponds to the coordination number of 8 (also called “fully-coordinated atoms”). As to the low-coordinated atoms, the dominant structures are as follows: CN = 6, 4, 7 and 5, meaning that the low-coordinated atoms possess a structure intermediate between the bulk liquid structure and the bulk solid one.
As a result, each of the three FeNP shapes possesses a core–shell structure, where the shell part has a complex structure characterised by an inhomogeneous arrangement of its undercoordinated atoms (4 ≤ CN < 8), while the core part is characterised by behavior analogous to the one characteristic of atomic species in pure crystalline bulk (fully-coordinated atoms, CN = 8). It is worth mentioning that the classification of FeNPs in core–shell constructions obtained here supports the previous works37,38,51–53 and it is operative for all FeNP forms, which is the main assumption of the bond-energy model (BEM).54 Furthermore, it was shown that a low-coordinated atoms-to-fully-coordinated atoms ratio of planar FeNP is the highest (0.84). This was followed by the rod FeNP (0.66) and the spherical FeNP (0.52). This result can suggest that the surface energy is prominent for the planar FeNP but lower for the spherical FeNP.
Whenever one discusses the structural properties of a bulk system or any materials at the nanoscale, the cohesive energy is one of the key parameters through which the strength of metallic bonds can be described and also the structural stability can be investigated; a larger cohesive energy suggests greater stability. In this regard, a comparative study on the shape-dependent cohesive energy of FeNPs was realized, and the results are given in Table 1. As expected, it was found that all actual structures of FeNP have smaller cohesive energies compared to the bulk Fe, which has been obtained in an experimental work (4.28 eV per atom).55 This finding is in agreement with other studies that suggest the cohesive energy of bulk metal is higher than those of nanoscale metal particles.37,38,56–59 Furthermore, it was established that the cohesive energy is very sensitive to the FeNP shape. Its value is as follows: ESpherical > ERod > EPlanar, reflecting that the structural stability is not similar for the three FeNP shapes and, also, the spherical shape exhibits better structural stability, while the planar shape has the lesser one.
| Nanoparticle shapes | Cohesive energy (eV per atom) |
|---|---|
| Spherical | 4.07 |
| Rod | 3.75 |
| Planar | 3.42 |
Thermodynamically, since the most stable morphology is characterized by the lowest ratio between dangling bonds and total bonds, i.e., lower surface energy, the shape-dependent structural stability of the FeNPs obtained here can be explained by the fact that the highest influence of the surface effect was found for the planar FeNP due to its higher ratio of low-coordinated atoms to fully-coordinated ones, whereas the spherical FeNP displays a lower ratio of low-coordinated atoms to fully-coordinated ones.
2.2 Magnetic properties
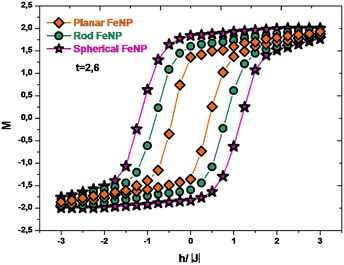
In order to give a coherent picture of the shape-dependent Curie temperature of FeNPs, the magnetization and thermal susceptibility as a function of reduced temperature were determined at zero h/|J| and plotted in Fig. 4. It was found that in the low-temperature range, the magnetization of each shape of FeNPs remains in the high-spin state and then drops to near zero, which clearly marks the occurrence of the phase transition from the ferromagnetic state to the paramagnetic one. Besides, the point corresponding to the drops to near zero in the magnetization curves occurs near the sharp peaks appearing in the susceptibility curves. These predictions appear to be virtually indistinguishable from each other and they indicate in a coherent way that the reduced Curie temperatures (tcp) of the planar FeNP, rod FeNP and spherical FeNP are equal to 2.8, 3.3 and 3.7, respectively. Moreover, 1043 K is the Curie point of bulk Fe according to an experimental prediction.60 The exchange interactions value between two nearest neighbor Fe atoms corresponding to the experimental lattice parameter of bulk Fe (0.2461 nm)61 was obtained from ref. 62, which is equal to 1.6 mRy. According to these latter values, the reduced Curie point for simulated bulk Fe can be found at about 4.17, indicating that the reduced Curie temperatures of all FeNP shapes are lower than that of bulk Fe. This difference has been observed in previous works which were carried out by different methods.63–67 Due to the inhomogeneous nature of the FeNP structures, where shell atoms of FeNPs have lower CNs and weaker bonding forces than core atoms, the reduced Curie temperature of bulk Fe being higher than those of FeNPs can be described by the coupling between two phases during the heating: the first is the paramagnetic particle shell phase which occurs at temperatures lower than the ferromagnetic–paramagnetic transition of the whole particles, while the second is the ferromagnetic particle core phase which remains in high-spin-states.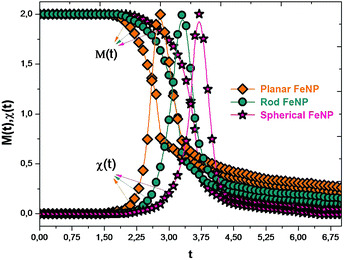 | ||
| Fig. 4 Magnetizations and the magnetic susceptibilities versus the reduced temperature for FeNPs with different shapes in zero field. | ||
Furthermore, it was found that tcp for FeNPs differs from one shape to another; its value is as follows: tcp for planar < tcp for rod < tcp for spherical. This finding is backing previous publications which have suggested that by changing not only the size but also the shape of nanostructures, it is possible to control the magnetic properties of these nano-objects.68–71 Besides, since spin canting in nanoparticles cannot be ignored because the shell atoms’ spins may be inclined at some angle to their normal directions originating from the low number of their magnetic nearest neighbors,65,72 it seems that the shape-dependent Curie point of NPs obtained in this work can be caused by modifications in the influence of the spin canting effect when the nanoparticle shape is changed, i.e., as the NP shape exhibits a larger ratio of low-coordinated atoms-to-fully-coordinated atoms, the incomplete alignment at the shell part has a significant contribution in enhancing the spin canting effect and, hence, the transformation of the NP magnetic state from ferromagnetic to paramagnetic may be required at a low temperature.
Now, we will turn to Fig. 5, which presents the hysteresis loops of FeNPs by increasing and decreasing the external magnetic field at t < tcp for planar FeNP (t = 2.6). It was found that the planar FeNP shows the smallest area of the hysteresis loop while the spherical FeNP has the largest one; it was moreover observed that the qualitative behavior for the coercive field value is planar < rod < spherical. These results suggest that the planar FeNP displays fast demagnetization at low magnetic fields with the lowest coercivity, whereas the spherical FeNP exhibits slow demagnetization at large magnetic fields with the highest coercivity. According to what was mentioned before, it was concluded that the modification of the FeNP shape leads to a change in its hysteresis loop characteristics. This is in total conformity with the previous experimental study.27 Besides, by taking into account the soft magnetic properties of bulk iron,73 the FeNP shape with a larger ratio of low-coordinated atoms to fully-coordinated ones (planar FeNP) tends to have more soft ferromagnetic behavior than that with a smaller one (spherical FeNP). Since all of the NPs used here possess the same volume, this suggests that it is the low-coordinated atoms to fully-coordinated atoms ratio which affects the hysteresis loop characteristics.74,75 This can be understood to be the cause of two competing factors; the first factor is the magnetic interaction at the core–shell interface which is expected to increase when the low-coordinated atoms to fully-coordinated atoms ratio increases, whereas the second factor is the magnetostatic anisotropy (also called magnetostatic effect) which competes with interface exchange coupling. As the ratio of low-coordinated atoms to fully-coordinated ones in nanoparticles is smaller, the effective core–shell interface is larger and the exchange coupling is high, resulting in an increased area of the hysteresis loop with the highest coercivity value and vice versa.
3 Conclusions
Herein, the structural stability, local structure characterization and magnetic properties of FeNPs of different shapes of a specific volume, including spherical, planar and rod, were studied. Investigations of the local structure characterization after the energy minimization process by means of MS simulation confirmed that all FeNPs revealed core–shell structures: they are constituted by crystalline iron cores that are surrounded by amorphous iron shells. Then, it was shown that the FeNP shape with larger cohesive energy tends to be energetically more stable. Besides, the magnetization and susceptibility curves of FeNPs were investigated by applying MC simulations in order to provide an insight into the shape-dependent Curie point. It was found that all FeNPs exhibit smaller calculated values of Curie temperatures than that of bulk Fe, and also the spherical FeNP possesses the highest Curie temperature, followed by the rod FeNP and the planar FeNP. Finally, by analyzing the magnetic hysteresis loops for the different shapes of FeNPs, it was found that the planar FeNP exhibits fast demagnetization at low magnetic fields with the lowest coercivity, whereas the spherical shape of the FeNP displays slow demagnetization at large magnetic fields with the highest coercivity.Conflicts of interest
The authors declare no conflict of interest.References
- W.-S. Lin, H.-M. Lin, H.-H. Chen, Y.-K. Hwu and Y.-J. Chiou, J. Nanomater., 2013, 2013, 9 Search PubMed.
- B. Chertok, B. A. Moffat, A. E. David, F. Yu, C. Bergemann, B. D. Ross and V. C. Yang, Biomaterials, 2008, 29, 487–496 CrossRef CAS.
- R. S. Molday and D. Mackenzie, J. Immunol. Methods, 1982, 52, 353–367 CrossRef CAS.
- M. A. Zeeshan, S. Pané, S. K. Youn, E. Pellicer, S. Schuerle, J. Sort, S. Fusco, A. M. Lindo, H. G. Park and B. J. Nelson, Adv. Funct. Mater., 2013, 23, 823–831 CrossRef CAS.
- M. C. Bahome, L. L. Jewell, D. Hildebrandt, D. Glasser and N. J. Coville, Appl. Catal., A, 2005, 287, 60–67 CrossRef CAS.
- S. Shylesh, V. Schünemann and W. Thiel, Angew. Chem., Int. Ed., 2010, 49, 3428–3459 CrossRef CAS.
- W.-x. Zhang, J. Nanopart. Res., 2003, 5, 323–332 CrossRef CAS.
- X. Zhang, G. Wen, S. Huang, L. Dai, R. Gao and Z. L. Wang, J. Magn. Magn. Mater., 2001, 231, 9–12 CrossRef.
- M. Reddy, T. Yu, C. Sow, Z. Shen, C. Lim, G. V. Subba Rao and B. Chowdari, Adv. Funct. Mater., 2007, 17, 2792–2799 CrossRef CAS.
- S. Singamaneni, V. N. Bliznyuk, C. Binek and E. Y. Tsymbal, J. Mater. Chem., 2011, 21, 16819–16845 RSC.
- B. Jeyadevan, C. N. Chinnasamy, K. Shinoda, K. Tohji and H. Oka, J. Appl. Phys., 2003, 93, 8450–8452 CrossRef CAS.
- K. Raj, B. Moskowitz and R. Casciari, J. Magn. Magn. Mater., 1995, 149, 174–180 CrossRef CAS.
- R. W. Briggs, Z. Wu, C. R. Mladinich, C. Stoupis, J. Gauger, T. Liebig, P. R. Ros, J. Ballinger and P. Kubilis, Magn. Reson. Imaging, 1997, 15, 559–566 CrossRef CAS.
- K. A. Hinds, J. M. Hill, E. M. Shapiro, M. O. Laukkanen, A. C. Silva, C. A. Combs, T. R. Varney, R. S. Balaban, A. P. Koretsky and C. E. Dunbar, Blood, 2003, 102, 867–872 CrossRef CAS.
- M. M. Miller, G. A. Prinz, S.-F. Cheng and S. Bounnak, Appl. Phys. Lett., 2002, 81, 2211–2213 CrossRef CAS.
- M. P. Sharrock, IEEE Trans. Magn., 1989, 25, 4374–4389 CrossRef CAS.
- R. Alkire, H. Gerischer, D. Kolb and C. Tobias, Advances in Electrochemical Science and Engineering, Wiley, 2008 Search PubMed.
- N. Zech, E. J. Podlaha and D. Landolt, J. Appl. Electrochem., 1998, 28, 1251–1260 CrossRef CAS.
- Y. Mitamura, S. Arioka, D. Sakota, K. Sekine and M. Azegami, J. Phys.: Condens. Matter, 2008, 20, 204145 CrossRef CAS.
- Y. S. Kim and Y. H. Kim, J. Magn. Magn. Mater., 2003, 267, 105–110 CrossRef CAS.
- S. Rudge, T. Kurtz, C. Vessely, L. Catterall and D. Williamson, Biomaterials, 2000, 21, 1411–1420 CrossRef CAS.
- F. Scherer, M. Anton, U. Schillinger, J. Henke, C. Bergemann, A. Krüger, B. Gänsbacher and C. Plank, Gene Ther., 2002, 9, 102–109 CrossRef CAS.
- M. Goldowsky, IEEE Trans. Magn., 1980, 16, 382–386 CrossRef.
- N. Ferroudj, J. Nzimoto, A. Davidson, D. Talbot, E. Briot, V. Dupuis, A. Bée, M. S. Medjram and S. Abramson, Appl. Catal., B, 2013, 136–137, 9–18 CrossRef CAS.
- M. Arruebo, R. Fernández-Pacheco, M. R. Ibarra and J. Santamaría, Nano Today, 2007, 2, 22–32 CrossRef.
- J. K. Oh and J. M. Park, Prog. Polym. Sci., 2011, 36, 168–189 CrossRef CAS.
- M. Krajewski, W. S. Lin, H. M. Lin, K. Brzozka, S. Lewinska, N. Nedelko, A. Slawska-Waniewska, J. Borysiuk and D. Wasik, Beilstein J. Nanotechnol., 2015, 6, 1652–1660 CrossRef CAS.
- D. Huber, Small, 2005, 1, 482–501 CrossRef CAS.
- M. E. Fisher and M. N. Barber, Phys. Rev. Lett., 1972, 28, 1516–1519 CrossRef.
- C. Q. Sun, W. H. Zhong, S. Li, B. K. Tay, H. L. Bai and E. Y. Jiang, J. Phys. Chem. B, 2004, 108, 1080–1084 CrossRef CAS.
- C. Yang and Q. Jiang, Acta Mater., 2005, 53, 3305–3311 CrossRef CAS.
- L. Fei Cao, D. Xie, M. Xing Guo, H. Park and T. Fujita, Trans. Nonferrous Met. Soc. China, 2007, 17, 1451–1455 CrossRef.
- J. Montejano-Carrizales, F. Aguilera-Granja and J. Morán-López, Nanostruct. Mater., 1997, 8, 269–287 CrossRef CAS.
- LAMMPS Manual 30, Sandia National Laboratories, Oct 2014, 2 Search PubMed.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2009, 18, 015012 CrossRef.
- M. S. Daw and M. I. Baskes, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 6443–6453 CrossRef CAS.
- R. Essajai and N. Hassanain, J. Mol. Liq., 2018, 261, 402–410 CrossRef CAS.
- R. Essajai, A. Rachadi, E. Feddi and N. Hassanain, Mater. Chem. Phys., 2018, 218, 116–121 CrossRef CAS.
- M. I. Mendelev, S. Han, D. J. Srolovitz, G. J. Ackland, D. Y. Sun and M. Asta, Philos. Mag., 2003, 83, 3977–3994 CrossRef CAS.
- H. Kart, H. Yildirim, S. O. Kart and T. Cagin, Mater. Chem. Phys., 2014, 147, 204–212 CrossRef CAS.
- D. Alfè, G. Kresse and M. J. Gillan, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61, 132–142 CrossRef.
- J. D. Honeycutt and H. C. Andersen, J. Phys. Chem., 1987, 91, 4950–4963 CrossRef CAS.
- A. Stukowski, Structure identification methods for atomistic simulations of crystalline materials, 2012, arXiv:1202.5005 Search PubMed.
- W. Janke, in Monte Carlo Methods in Classical Statistical Physics, ed. H. Fehske, R. Schneider and A. Weiße, Springer Berlin Heidelberg, Berlin, Heidelberg, 2008, pp. 79–140 Search PubMed.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- S. Wang, N. Omidvar, E. Marx and H. Xin, Phys. Chem. Chem. Phys., 2018, 20, 6055–6059 RSC.
- J. Pal and T. Pal, Nanoscale, 2015, 7, 14159–14190 RSC.
- Z.-Y. Zhou, N. Tian, J.-T. Li, I. Broadwell and S.-G. Sun, Chem. Soc. Rev., 2011, 40, 4167–4185 RSC.
- J. Hernández, J. Solla-Gullón, E. Herrero, A. Aldaz and J. M. Feliu, J. Phys. Chem. B, 2005, 109, 12651–12654 CrossRef.
- D. M. Wells, G. Rossi, R. Ferrando and R. E. Palmer, Nanoscale, 2015, 7, 6498–6503 RSC.
- W. J Huang, R. Sun, J. Tao, L. Menard, R. G. Nuzzo and J.-M. Zuo, Nat. Mater., 2008, 7, 308–313 CrossRef.
- W. Qi, Acc. Chem. Res., 2016, 49, 1587–1595 CrossRef CAS.
- W. Qi, B. Huang and M. Wang, Nanoscale Res. Lett., 2009, 4, 269 CrossRef CAS.
- W. Qi, B. Huang, M. Wang, Z. Li and Z. Yu, Phys. Lett. A, 2007, 370, 494–498 CrossRef CAS.
- P. Haas, F. Tran and P. Blaha, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 209902 CrossRef.
- W. H. Qi and M. P. Wang, J. Mater. Sci. Lett., 2002, 21, 1743–1745 CrossRef CAS.
- W. Qi, Solid State Commun., 2006, 137, 536–539 CrossRef CAS.
- W. Qi, M. Wang and W. Hu, Mater. Lett., 2004, 58, 1745–1749 CrossRef CAS.
- C. Q. Sun, Y. Wang, B. K. Tay, S. Li, H. Huang and Y. B. Zhang, J. Phys. Chem. B, 2002, 106, 10701–10705 CrossRef CAS.
- I. M. L. Billas, J. A. Becker, A. Châtelain and W. A. de Heer, Phys. Rev. Lett., 1993, 71, 4067–4070 CrossRef CAS.
- C. S. Barrett, Acta Crystallogr., 1956, 9, 671–677 CrossRef CAS.
- H. Wang, P.-W. Ma and C. H. Woo, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 144304 CrossRef.
- A. Jabar and R. Masrour, Phase Transitions, 2018, 91, 284–292 CrossRef CAS.
- W. Qi, Y. Li, S. Xiong and S.-T. Lee, Small, 2010, 6, 1996–1999 CrossRef CAS.
- H. Delavari H., H. M. Hosseini and A. Simchi, Chem. Phys., 2011, 383, 1–5 CrossRef CAS.
- H. yu Wang, Y. song Zhou and D. L. Lin, Chin. Phys. Lett., 2000, 17, 55–57 CrossRef.
- K. Kadau, M. Gruner, P. Entel and M. Kreth, Phase Transitions, 2003, 76, 355–365 CrossRef CAS.
- A. Aharoni, J. Appl. Phys., 1997, 81, 830–833 CrossRef CAS.
- C. Kittel, Phys. Rev., 1948, 73, 155–161 CrossRef CAS.
- F. Ma, J. Ma, J. Huang and J. Li, J. Magn. Magn. Mater., 2012, 324, 205–209 CrossRef CAS.
- A. Aharoni, J. Appl. Phys., 1991, 69, 7762–7764 CrossRef.
- G. Ferk, J. Stergar, D. Makovec, A. Hamler, Z. Jagličić, M. Drofenik and I. Ban, J. Alloys Compd., 2015, 648, 53–58 CrossRef CAS.
- M. Houshiar, F. Zebhi, Z. J. Razi, A. Alidoust and Z. Askari, J. Magn. Magn. Mater., 2014, 371, 43–48 CrossRef CAS.
- B. Issa, I. Obaidat, B. Albiss and Y. Haik, Int. J. Mol. Sci., 2013, 14, 21266–21305 CrossRef CAS.
- X. Sun, N. Frey Huls, A. Sigdel and S. Sun, Nano Lett., 2012, 12, 246–251 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2019 |