Open Access Article
Open Access ArticleMn promotes the rate of nucleation and growth of precipitates by increasing Frenkel pairs in Fe–Cu based alloys
Tong Lia,
Yaoping Xie *a,
Xiaojiao Wangb,
Qin Shenc,
Jiabao Lia,
Haibo Guod,
Jingxiang Xu
*a,
Xiaojiao Wangb,
Qin Shenc,
Jiabao Lia,
Haibo Guod,
Jingxiang Xu e and
Wenqing Liu*a
e and
Wenqing Liu*a
aInstitute of Materials, School of Materials Science and Engineering, Shanghai University, Shanghai 200444, China. E-mail: ypxie@shu.edu.cn; wqliu@shu.edu.cn
bShanghai Institute of Ceramics Academy of Science, Shanghai 201899, China
cSchool of Mechanical and Automotive Engineering, Shanghai University of Engineering Science, Shanghai 201620, China
dDepartment of Electronic Information Materials, School of Materials Science and Engineering, Shanghai University, Shanghai 200072, China
eCollege of Engineering Science and Technology, Shanghai Ocean University, Shanghai 201306, China
First published on 24th June 2019
Abstract
Fe–1.0Cu (at%) and Fe–1.2Cu–2.2Mn alloys aged at 450 °C for 0.25 h, 1 h, 2 h, and 16 h after solution treatment at 900 °C for 2 h are investigated to reveal the role of the addition of Mn on the Cu precipitates in Fe–Cu based alloys. Density functional theory (DFT) total energy calculations on point defects and their influence on Cu precipitates are also performed to understand the nucleation and growth of Cu precipitates. Experiments show that addition of Mn can slightly increase the aging peak hardness by 10 HV; by using atom probe tomography (APT) and optical microscopy, we identify that the increase in hardness derives from both grain refinement and the increase of number density of precipitates. DFT calculations show that Mn increases the formation possibility of Frenkel pairs, i.e., atomic vacancy and self-interstitial atoms, and these two types of defects both serve as nucleation sites of Cu precipitates, resulting in the increase of the nucleation centers number density, which is consistent with our APT experiments on the very initial stage of aging. Moreover, calculated results show that Mn increases the density of atomic vacancies and promotes the evolution rate of Cu precipitates, which accounts for our APT experiments where precipitates in Fe–Cu–Mn grow more quickly than in Fe–Cu. Finally, we also discuss the relationship between Mn content in reactor pressure vessel steels and its irradiation damage effects.
1. Introduction
Copper is very common in steels. Intentional addition of Cu into steels results in high-strength low-alloy steels (HSLA) with excellent properties;1–15 after aging, Cu can provide considerable precipitation strengthening effects. The effects of the unintentional presence of a trace amount of Cu in steels also attracts much attention, because it may induce serious problems in service. In reactor pressure vessel (RPV) steels which have a very low Cu content, the Cu precipitates also appear under long-term irradiation, and these Cu precipitates are considered to be the origin of embrittlement of RPV steels which limits the service time of nuclear power plants.16–25 Cu precipitate is typical in steels, and therefore investigating the evolution of Cu precipitates is a hot topic.Many alloying elements were confirmed to be able to influence the formation of Cu precipitates. The interaction between alloying elements and Cu precipitates is very complicated. On the one hand, the alloying elements can promote the formation of Cu precipitate and lead to multicomponent Cu-rich precipitates.1–3,7,9 On the other hand, the many other alloying elements can be clustered in the Cu precipitates or at the interface between Cu precipitates and matrix, such as NiAl phase,7–9,26–28 G phase, etc.29,30 Usually, HSLA steels are composed of many alloying elements, and the microstructure and mechanical properties have been well studied. For example, the evolution of precipitates in Northwestern University copper alloyed serveries steels (NUCu) has been well characterized, and the mechanical properties, such as hardness were also examined under different treatments.1–3,9 For RPV steels, it is very fortunate that many data on Cu-rich clusters in steels under neutron irradiation have been reported,16,17,19,21,31 though the data generally are rare for many other materials under neutron irradiation.
To understand the role of different elements on the Cu precipitates, many works were dedicated to reveal the interaction between alloying elements and Cu precipitates. It has been confirmed that Mn has obviously interaction with Cu precipitates. It segregates at the Cu precipitates,1 and also induces the formation of Mn clusters in steels alloyed with the composition of Cu, Ni, Si, and Mn.25 Furthermore, there is a combinative effect of Mn and Cu contents on embrittlement of RPV steels induced by neutron irradiation.
Since Mn and Cu have combined effect on the neutron irradiation induced embrittlement, Glade et al.20 investigated the influence of Mn on Cu precipitate in model RPV steel by using positron annihilation spectroscopy and small-angle neutron scattering. They found that the effect of Mn is to reduce the size and increase the number density of precipitates in the Fe–Cu–Mn alloy relative to the Fe–Cu alloy. Later, Miller et al.21 using atom probe tomography and small-angle neutron scattering (SANS) experiments, also confirmed that Mn can increase number density of precipitates, and it was approximately an order of magnitude higher in the Fe–Cu–Mn alloy compared to Fe–Cu alloy.
As a common element in steels, it was found very early that Mn increases Cu precipitation hardening effects. However, most of the investigations about the effect of Mn were performed in alloys containing C, Si and Al at non-negligible levels, and therefore the hardening effect cannot be confirmed to be only from Mn. Shabadi et al.32 performed a careful preparation of model alloys to elucidate the true effect of Mn, and they confirmed this effect. It was found clearly that the addition of Mn significantly increases the kinetics of aging, while its effect on the magnitude of precipitation strengthening is only marginal. In addition, the effect of Mn on the over-aging stage was also identified: Mn reduces increment of aging hardening in the region of over aging.
In the theoretical side, extensive investigations by using density functional theory (DFT) are performed to understand Cu precipitates in steels; many aspects related to magnetism, thermal dynamics, kinetics of this system have been revealed. It has been found that the dependence of phase separation tendency between Fe and Cu on temperature is more related to the magnetic phase transition compared to vibrational contribution.33–36 The calculations of elastic properties of bulk FeCu phase revealed that only FeCu with Cu content below 50% is mechanically stable;37 the segregation of alloying elements, such as Ni, Al, Mn, etc., was confirmed to derive from thermodynamic factors,27,38 and the segregation behaviors can change strain and chemical interactions at interfaces, resulting in the reduction of interface energy.39
Since point defects are tightly related to the microstructure evolution of steels, many studies were performed to reveal the interaction between point defects in body-centered cubic (bcc) Fe toward understanding the formation of precipitates. For example, the interactions between point solute atoms and intrinsic point defects in bcc Fe for extensive transition-metal alloying elements were investigated,40 and the stability of self-interstitial atoms (SIA) and small SIA clusters in the vicinity of solute atoms in Fe matrix were also investigated.41 The results of these researches revealed the basic rules of alloying element interaction and provided important information for larger scale simulations. In addition, there are also some attempts to use DFT calculations to directly understand and predict the formation of precipitates influenced by alloying elements. For example, it was revealed that, the reason that Ca, Ag can increase the number density of precipitates in Mg–Zn system is that these two elements can enhance the stability of G. P. zones in the very initial stage of formation of precipitates.42
For all above, it is confirmed that Mn can change the evolution of Cu precipitates and the mechanical properties of Fe–Cu based steels. However, the investigation on Fe–Cu based HSLA steels only reveals the response of hardness of alloys to Mn addition. Since the response of evolution of Cu precipitates to Mn addition is still not confirmed, how much the precipitates are responsible for the increase of hardness is not still identified. In another side, the DFT has become a powerful tool to understand the underlying mechanism in the evolution of precipitates. Therefore, we use both experiment and DFT calculations, to perform a systematic investigation on the influence of Mn on the evolution of Cu precipitates and its hardness, and try to reveal its mechanism at the atomic scale.
2. Methods
2.1 Experiments
The chemical compositions of Fe–1.0Cu (at%) and Fe–1.2Cu–2.2Mn alloys are shown in Table 1. To obtain the Cu precipitates with relative short experimental time, we choose to use alloys with relatively high contents of Cu and Mn. The alloys were fabricated as described in ref. 7. After solution treatment at 900 °C for 2 h, we quench alloys to room temperature, and then perform heat treatments at 450 °C for 0.25 h, 1 h, 2 h, and 16 h, respectively.| Alloy | Cu | Mn | C | Si | P | S | Ni | Cr | Fe |
|---|---|---|---|---|---|---|---|---|---|
| Fe–Cu | 1.2 | — | 0.0009 | 0.01 | 0.008 | 0.005 | 0.01 | 0.005 | Bal |
| Fe–Cu–Mn | 1.0 | 2.2 | — | — | 0.01 | 0.004 | 0.05 | — | Bal |
The hardness measurements are conducted on the polished surface of the samples by using Vickers hardness tester (HVS-1000) with a load of 100 g for 10 s, and at least seven indents are measured to obtain an average value for each sample. In order to prepare tip samples for APT, small rods with a cross-section of 0.5 × 0.5 mm2 are cut out from the aged bulk steels. Subsequently, the tip samples are polished by the two-stage electro-polishing method.43 The APT experiments and analyses are performed on a local electrode atom probe (LEAP 4000X HR) at specimen temperature of 50 K with a target evaporation rate of 0.5%, and the pulse fraction is 20% in an ultra-high vacuum of ∼10−11 Pa. The voltage pulse repetition rate is set to be 200 kHz. Data reconstructions and analyses are conducted using the Integrated Visualization and Analysis Software (IVAS 3.6.8). The maximum separation method44 is employed to identify Cu precipitates, and we select the minimum solute atom number (Nmin) of 20, and the maximum separation distance (dmax) of 0.5 nm.
2.2 Calculations
A. Point defect. The point defect is tightly related to the initial nucleation and growth of Cu precipitates. The typical point defects in steels are mono-vacancy and self-interstitial atom (SIA). The stability of these point defects is critical to reveal the evolution mechanism of Cu precipitates. Here, we use formation energy to reflect the stability of the point defect. The formation energy of a mono-vacancy or SIA (EPd) can be computed by the following eqn (1):
| EPd = EP − nEFe | (1) |
The formation energy of SIA with a M solute atom, (M@SIA, M = Cu or Mn), EPd(Fe,M), can be computed by the following eqn (2):
| EPd(Fe,M) = EPs + nEFe − (EFe(M) + (n + 1)EFe)) | (2) |
B. Frenkel pair. The formation energy of a Frenkel pair with mono-vacancy and pure Fe SIA (EFd) can be computed by the following eqn (3):
| EFd = EM + Es − 2nEFe | (3) |
The formation energy of a Frenkel pair with mono-vacancy and M@SIA (EFd(M@SIA)) can be computed by the following eqn (4):
| EFd(M@SIA) = EM + EMs − (nEFe + (EFe(M)) | (4) |
C. The interaction of defect with solute Cu. The binding energy between a point defect and a Cu atom (ΔE(D,Cu)) can be computed by the following eqn (5):
| ΔE(D,Cu) = ED,Cu + nEFe − (ED + ECu) | (5) |
D. Solute Cu cluster. The formation energy of Cu cluster (EClu) can be computed by the following eqn (6):
| EClu = (ECtot + (nCu −1)nEFe) − nCuECu) | (6) |
The formation energy of Cu cluster with defects (EClu,D), such as mono-vacancy, SIA and Mn@SIA, can be computed by the following eqn (7):
| EClu,D = ECtot,D + nCunEFe − (nCuECu + ED) | (7) |
By considering the balance between the precision and computation efficiency, here, we use supercells with 64 atoms to compute the formation energy of point defects, and use supercells with 128 atoms to compute the formation energy of Cu clusters. Tests have been done to verify that these sizes of supercells are sufficient for calculating formation energies of point defects and small Cu clusters. We only use 3-atom clusters to explore the trend of the influence on the stability of Cu clusters in bcc Fe.
3. The relationship between hardness and Cu precipitates
3.1 Age-hardening response
The Vickers hardness values of the Fe–Cu and Fe–Cu–Mn alloys as a function of aging time at 450 °C are shown in Fig. 1. The values of hardness of the Fe–Cu and Fe–Cu–Mn alloys at the as-quenched (AQ) state are 145 HV and 195 HV respectively, indicating that Mn can improve the hardness of Fe–Cu alloy. The values of peak hardness of Fe–Cu and Fe–Cu–Mn alloys are 225 and 235 HV, reflecting that the latter is slightly higher than the former. However, the hardness of Fe–Cu–Mn decreases obviously after the peak value (i.e. after 1 h); while the hardness of Fe–Cu almost does not decrease after the peak value. These findings agree well with previous results.33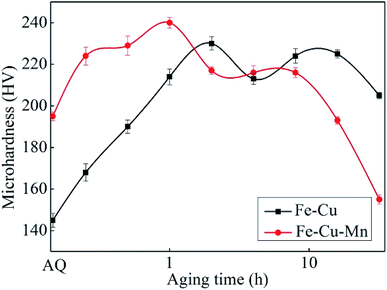 | ||
| Fig. 1 The Vickers hardness for Fe–Cu and Fe–Cu–Mn alloys aged at 450 °C after solid solution treatment at 900 °C for 2 h. | ||
Fig. 2 shows the optical micrographs of two alloys at AQ and age-peak states. It is found that the addition of Mn does not transform ferrite into other phases in both alloys, and therefore Fe–Cu–Mn showing higher hardness than Fe–Cu is not caused by phase transformation. However, the sizes of grains in Fe–Cu–Mn are obviously smaller than those of Fe–Cu, and the hardening effect on Fe–Cu–Mn can be attributed to grain refinement induced by Mn addition.
 | ||
| Fig. 2 Microstructures of the alloys: (a) as-quenched state of Fe–Cu; (b) the age-peak state of Fe–Cu; (c) as-quenched state of Fe–Cu–Mn; and (d) the age-peak state of Fe–Cu–Mn. | ||
To further understand the mechanism of Mn on the mechanical properties in Fe–Cu alloy, we use APT to investigate the evolution of Cu precipitates. Fig. 3 displays the positions of individual Cu and Mn atoms for Fe–Cu and Fe–Cu–Mn alloys aged at 450 °C for 0.25 h, 1 h, 2 h and 16 h, respectively. The number density (Nv) and average radius (Rp) based on the above APT results are calculated and shown in Table 2. As seen in Fig. 3 and Table 2, it is found that the average radius of Cu precipitates in two alloys increases, and the number density first increases and then decreases.
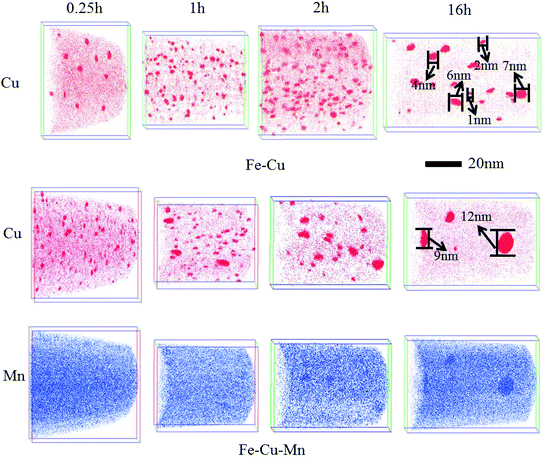 | ||
| Fig. 3 Three-dimensional atom maps of Cu and Mn of Fe–Cu and Fe–Cu–Mn alloys aged at 450 °C for 0.25 h, 1 h, 2 h, 16 h. | ||
| Rp (nm) | Nv (×1023 m−3) | |||
|---|---|---|---|---|
| Fe–Cu | Fe–Cu–Mn | Fe–Cu | Fe–Cu–Mn | |
| 0.25 h | 1.0 ± 0.3 | 1.0 ± 0.3 | 1.2 | 4.9 |
| 1 h | 1.0 ± 0.4 | 1.0 ± 0.5 | 8.1 | 8.8 |
| 2 h | 1.1 ± 0.3 | 1.3 ± 0.6 | 17.4 | 5.7 |
| 16 h | 2.1 ± 0.8 | 3.7 ± 0.9 | 2.2 | 0.6 |
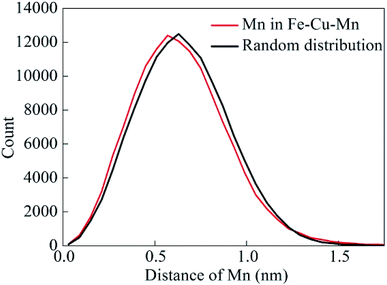
After aging for 0.25 h, we identify clearly that many Cu clusters have been formed from Fig. 3. However, it is difficult to identify Mn clusters in the atom maps. Therefore, as shown in Fig. 4, we present nearest neighbor distribution (NND) curve of Mn atoms for Fe–Cu–Mn alloys along with random distribution curve, and it shows that the NND curve of Mn slightly deviates from random distribution curve. It suggests that there is a slight trend of the clustering of Mn atoms in Fe–Cu–Mn after aging for 0.25 h. A more careful survey on atom maps from 0.25 to 16 h, we can confirm that Mn clusters overlap spatially with Cu clusters.
3.2 Temporal evolution of Cu precipitates
As shown in Table 2, after aging for 0.25 h, the average radius Rp of Cu clusters are both 1.0 nm, while the number density of Cu clusters in Fe–Cu–Mn alloy is 4 times than that in the Fe–Cu alloy. It indicates that the addition of Mn increases the nucleation rate of Cu precipitates at the initial aging stage, which is responsible for the higher increment of hardness for Fe–Cu–Mn compared to Fe–Cu as shown in Fig. 1.Table 2 shows, during the aging time from 0.25 to 1 h, the increase of number density of clusters for Fe–Cu is more rapid than that for Fe–Cu–Mn, which accounts for the increment of hardness for Fe–Cu–Mn is smaller than that for Fe–Cu. During the aging time from 1 h to 2 h, the number density of clusters for Fe–Cu still increases, while the number density of clusters for Fe–Cu–Mn begins to decrease and the size of clusters begins to increase, which accounts for that the hardness of the former still increases and the latter begins to decrease.
At the aging time of 16 h, the number density of clusters for Fe–Cu decreases to 2.2 × 1023 m−3, and that for Fe–Cu–Mn decreases to 0.6 × 1023 m−3. As shown in Fig. 5, there are still many smaller clusters observed in Fe–Cu while almost large clusters with radius larger than 4.0 nm in Fe–Cu–Mn. These findings account for that the hardness of Fe–Cu decreases slightly, but the hardness of Fe–Cu–Mn decreases abruptly.
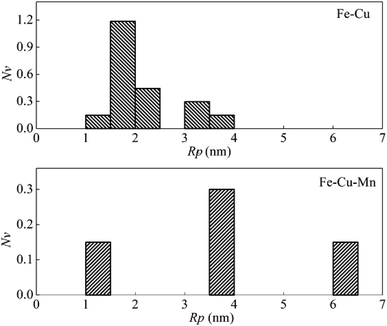 | ||
| Fig. 5 The dependence of number density on the radius of Cu precipitates in Fe–Cu and Fe–Cu–Mn aged for 16 h. | ||
4. The driving force for the formation of defects and Cu precipitates
The nucleation and growth of precipitates are tightly related to the point defects in alloys, but it is difficult to be observed by experiments. Therefore, we use DFT total energy calculations to obtain the formation energies in Fe–Cu and Fe–Cu–Mn systems, to reveal the thermal dynamical driving force for the formation of defects and Cu precipitates.4.1 Formation energy of point defects and Cu clusters
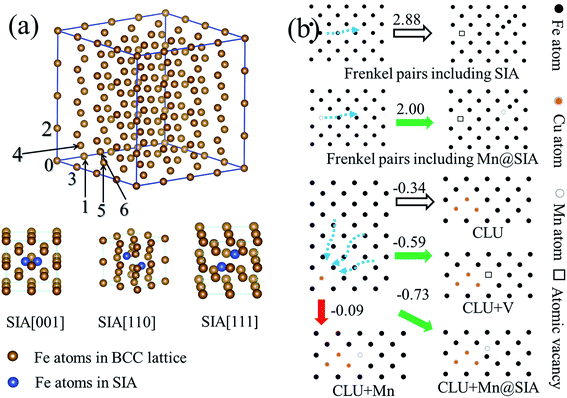
Fig. 6(a) shows the atomic configuration of SIA. The formation energies of Schottky mono-vacancy and SIA in the α-Fe are 2.19 and 1.78 eV respectively. As shown in Table 3, we can find that the SIA along the direction [110] is most favorable. Furthermore, we examine the formation energies of Cu@SIA and Mn@SIA. It is found that, for these structures, the SIA along [110] is still the most favorable. We find the formation energy of [110] Cu@SIA is higher than that of [110] SIA, indicating that the formation of self-interstitial atom for Cu is more difficult than that for Fe. In contrast, the formation energy of [110] Mn@SIA is lower than that of [110] SIA, indicating that the formation of self-interstitial atom for Mn is easier than that for Fe.| SIA | Cu@SIA | Mn@SIA | |
|---|---|---|---|
| [001] | 2.40 | 2.53 | 2.20 |
| [110] | 1.78 | 2.02 | 1.58 |
| [111] | 2.15 | 2.09 | 2.59 |
Table 4 shows that formation energies of Frenkel pair defects. The formation energy of [110] Mn@SIA + V is lower than that of [110] SIA + V, which reflects that the presence of Mn atoms is much easier to induce the formation of Frenkel pairs. Therefore, in the Fe–Cu–Mn system, the formation of atomic vacancy is much easier via a way of Frenkel pairs compared to that in the Fe–Cu system. The increase in the possibility of formation of vacancy in Fe–Cu–Mn system can promote the dynamics of precipitates, which accounts for that the growth of Cu precipitates in Fe–Cu–Mn is faster than that in Fe–Cu as shown in Fig. 3 and Table 2. Hereafter, for the interaction of SIA with other defects and Cu clusters, we only consider the most favorable structure of SIA, i.e., [110] SIA and [110] Mn@SIA.
| SIA | Cu@SIA | Mn@SIA | |
|---|---|---|---|
| EF−d | EF−d | EF−d | |
| [001] SIA + V | 3.50 | 3.67 | 2.99 |
| [110] SIA + V | 2.88 | 3.16 | 2.01 |
| [111] SIA + V | 3.25 | 3.22 | 3.37 |
4.2 Interaction between Cu atoms and point defects
The nucleation of Cu clusters at the very early stage is tightly related to the interaction between Cu atoms and point defects. Here, we compute the binding energy of dimer structures containing Cu atom and point defect in α-Fe. The binding configuration between a Cu atom and other defect is embodied in a 128-atoms supercell that is shown in Fig. 6(a), and the positions of Cu atoms and defect are listed in Table 5. The lowest binding energy of Cu–V dimer is −0.27 eV, indicating that Cu atoms are preferred to bind with mono-vacancy. The lowest binding energy of Mn–Cu dimer is −0.004 eV, indicating that Cu atoms and Mn atoms almost have no attractive effect. Moreover, the lowest binding energy of Cu-SIA and Cu–Mn@SIA are −0.19 eV and −0.18 eV respectively, indicating that the Cu atoms are preferred to bind with the SIA or Mn@SIA. Based on these findings, we can infer the trend that mono-vacancy, SIA and Mn@SIA can promote the gathering of Cu atoms to form clusters, but substitutional Mn solute atom cannot promote the gathering of Cu atoms.| Position | Cu atom + V | Cu atom + Mn |
|---|---|---|
| 3 | −0.02 | 0.01 |
| 4 | −0.27 | −0.004 |
| Position | Cu atom + [110] SIA | ||
|---|---|---|---|
| (110) SIA | (101) SIA | (011) SIA | |
| 3 | −0.19 | −0.12 | −0.12 |
| 4 | −0.12 | −0.12 | −0.12 |
| Position | Cu atom + [110] Mn@SIA | ||
|---|---|---|---|
| (110) SIA | (101) SIA | (011) SIA | |
| 3 | −0.18 | −0.08 | −0.08 |
| 4 | −0.003 | −0.003 | −0.003 |
4.3 The interaction of point defect and Cu cluster
To confirm the effect of point defects on the Cu gathering, we compute the formation energy of 3-Cu-atom cluster without and with point defects. The clusters are embodied in a 128-atoms supercell that is shown in Fig. 6(a), and the positions of Cu atoms and defect are listed in Table 6. The formation energies of 3-Cu-atom clusters along (001), (110), and (111) are −0.11, −0.34 and 0.002 eV, respectively. It indicates that the formation of Cu cluster in α-Fe is thermodynamically favorable. The results also suggest that the (110) cluster is the most stable one, which is consistent with previous calculations.54 We also perform calculations on 4-Cu-atom clusters and also obtain the same trend on thermodynamics about Cu precipitates without and with defects. We here only use the result of a 3-Cu-atom cluster with defects under typical geometric structures to illustrate the interaction between Cu clusters and defects.| Position | CLU + V | CLU + Mn | CLU + SIA | CLU + Mn@SIA | ||||
|---|---|---|---|---|---|---|---|---|
| [110] SIA | [101] SIA | [011] SIA | [110] SIA | [101] SIA | [011] SIA | |||
| Atom number for Cu cluster OR: (001): 0,1,3 | ||||||||
| 5 | 0.11 | −0.08 | −0.45 | −0.50 | −0.50 | −0.38 | −0.46 | −0.46 |
| 4 | 0.13 | −0.06 | −0.73 | −0.44 | −0.44 | −0.59 | −0.22 | −0.22 |
| 2 | −0.47 | 0.14 | −0.50 | −0.41 | −0.41 | −0.19 | −0.08 | −0.08 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Atom number for Cu cluster OR: (110): 0,3,4 | ||||||||
| 6 | −0.38 | −0.07 | −0.31 | −0.31 | −0.36 | −0.16 | −0.16 | −0.24 |
| 2 | −0.38 | −0.09 | −0.49 | −0.39 | −0.49 | −0.46 | −0.40 | −0.45 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||||
| Atom number for Cu cluster OR: (111): 1,2,3 | ||||||||
| 0 | 0.21 | 0.30 | −0.16 | −0.16 | −0.16 | −0.15 | −0.15 | −0.15 |
| 4 | −0.59 | 0.32 | −0.30 | −0.30 | −0.30 | −0.17 | −0.17 | −0.17 |
There are many configurations for the combination of a 3-Cu-atom cluster with atomic vacancy or substitutional Mn atom. We present some structures that the mono-vacancy or Mn is located at the first and second nearest position to the cluster plane. It is found the formation energy of the most stable cluster with mono-vacancy is −0.59 eV, which is 0.25 eV lower than that of the cluster without mono-vacancy. It indicates that the mono-vacancy can stabilize the Cu cluster, which results in the increase in formation probability of nucleation sites for Cu clusters. In contrast, the formation energy of the most stable cluster with substitutional Mn is −0.09 eV, which is 0.25 eV higher than that of the cluster without Mn, which indicates that substitutional Mn has no effect on stabilizing Cu clusters.
In Table 6, we also present the formation energies of complexes comprised of 3-Cu-atom cluster and SIA. We consider placing the SIA at three nearest sites from the cluster plane, and vary the orientation of cluster and the direction of SIA, and finally, we can obtain 42 configurations, whose formation energies are listed in Table 6. It is found that the most stable cluster with SIA has the formation energy of −0.73 eV, which is 0.39 eV lower than that of a pure Cu cluster. We also find that, among these structures, almost half of them with the formation energies are lower than that of pure Cu cluster. These findings show that both SIA and Mn@SIA increase the driving force of formation of Cu clusters.
5. Discussions
From the APT experiments, we find that the evolution of precipitate in Fe–Cu–Mn is much faster than that in Fe–Cu. At very initial stage from 0 to 0.25 h, the number density of Cu clusters in Fe–Cu–Mn is much larger than that in Fe–Cu, which is the reason why the hardness increment of Fe–Cu–Mn is larger than that of Fe–Cu during this period. At the aging peak, the hardness of Fe–Cu–Mn is slightly higher than that of Fe–Cu, but the number density of precipitates of the former is only half of the latter. It reflects that the hardening effect of Mn on alloys is mainly induced by the grain refinement and the increased number density of precipitates.The number density of precipitates increases very fast in Fe–Cu–Mn during aging. It takes two hours to reach the peak value for Fe–Cu, but only takes one hour for Fe–Cu–Mn. Also, the increase in the size of precipitates for Fe–Cu–Mn is also much faster than that for Fe–Cu. At the aging time of 16 h, the average diameter of precipitates in Fe–Cu–Mn is 7 nm, which is obviously larger than that in Fe–Cu, 4 nm. Since the Cu precipitates larger than 5 nm will transform from bcc coherent precipitates into face center cubic precipitates structures and lose the hardening effect,55,56 the hardness of Fe–Cu–Mn at aging time of 16 h decreases very fast.
Based on computational results, we summary some important formation energies in Fig. 6(b), and we find that the presence of Mn causes that the formation of vacancy and SIA to become easier. First, the vacancy and SIA both can enhance the driving force of the formation of nucleation sites for Cu precipitates. Therefore, the presence of Mn will increase the formation possibility of vacancy and SIA and the nucleation rate of Cu precipitates. It accounts for the APT experiments, at the very initial aging stage, the number density of precipitates in Fe–Cu–Mn is much larger than that in Fe–Cu. Second, since Mn can reduce the formation energy of Frenkel pairs, the formation of mono-vacancy becomes easier; therefore Mn can increase the density of mono-vacancy in Fe matrix, which increases the diffusion of atoms and evolution of precipitates. Since Frenkel pairs can provide both SIA and mono-vacancy, it can influence both processes of nucleation and growth of Cu precipitates; therefore Frenkel pairs have a very large influence on the evolution of Cu precipitates.
For self-interstitial atoms (SIA), it is generally recognized that SIA extensively occurs in steels under irradiation. However, we emphasis that the possibility of Mn self-interstitial atoms (Mn@SIA) also could exist at a considerable concentration in steels under the condition of heat-treatment, even its concentration is definitely lower than that in steels under irradiation. There are two reasons that support this assumption: (I) the formation energy of Mn@SIA is much lower than any other M@SIA (M = Fe, Co, Ni, Cu, Ti…, more than 20 types of element57). (II) The Mn can segregate at Cu precipitate in steels under both irradiation and heat treatment condition,1,16 DFT calculation38 shows that the segregation only occurs when Mn exists as self-interstitial atom. Therefore, a considerable content of Mn should exist in the form of self-interstitial atom in steels under heat treatment condition. Therefore, the formation of Frenkel pairs in steels under heat-treatment is reasonable.
In addition, based on our results from experiments and theoretical calculations, we also give some understanding of the formation of Cu precipitates in RPV steels with very low copper content under irradiation. The formation energy of Mn@SIA is lower than SIA, indicating that the displacement damage in Fe–Cu–Mn is more serious than that in Fe–Cu. Moreover, since the copper content is very low and the RPV steels are far away from the over-aging state, the increase of Mn in RPV steels will increase the number density of precipitates, which is consistent with the experiment of RPV steels under irradiation.58,59
6. Conclusion
The evolution of Cu precipitates in Fe–1.2Cu (at%) and Fe–1.0Cu–2.2Mn after aging at 450 °C are investigated experimentally. Moreover, the point defects and its influence on nucleation and growth of Cu precipitates are investigated by DFT calculations. The conclusions can be summarized as follows:(1) By addition 2.2% Mn into Fe–Cu alloy, the peak hardness for the alloy only increases from 225 to 235 HV; and the slight increase in hardness derives from the grain refinement instead of the increase of the number density of precipitates.
(2) Besides grain refinement and solid solution strengthening, the addition of Mn also can increase the evolution rate of Cu precipitates. The effect of Mn on increasing the evolution rate of Cu precipitates is very obvious, and it can induce that the hardness of alloys decrease dramatically in the stage of over aging.
(3) DFT calculations reveal that the reason why Mn increases the nucleation rate is that Mn can increase the formation possibility of atomic vacancy and SIA. Both atomic vacancy and SIA can serve as nucleation sites for Cu precipitates, and therefore the nucleation centers of Cu precipitates in Fe–Cu–Mn at the very initial stage of aging should be much more than that in Fe–Cu. This point has also been confirmed by our APT experiments.
(4) The formation energy of a Frenkel pair in Fe–Cu–Mn is much lower than that in Fe–Cu, indicating that the formation of Frenkel pairs in the former is much easier than that in the latter. It results that a large number of atomic vacancies can be produced by the way of formation of Frenkel pairs in Fe–Cu–Mn. The increase of vacancies will promote the evolution rate of Cu precipitates. Therefore, the formation possibility of Frenkel pairs is responsible for the increase of the evolution rate of Cu precipitates in Fe–Cu–Mn at the stage of over aging.
(5) We also discuss the role of Mn in RPV that serves under irradiation condition, and point out that, based on calculated results, Mn will enhance the displacement damage in RPV steels.
To recap, we have revealed the role of the Mn on the Cu precipitates and their effects on hardness. It is confirmed that Mn can increase the evolution rate of Cu precipitates. Based on this point, one can use the effect of Mn on Cu precipitates reasonably when designs new alloys or estimates the service behavior of Fe–Cu based alloys.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by National Key Research and Development Program of China (No. 2017YFB0703002, 2016YFB0700401), the State Key Lab of Rolling and Automation of Northeastern University Development Fund (No. 2016002), China Academy of Engineering Physics Joint Funds of National Natural Science Foundation of China (U1530115), Science and Technology Commission of Shanghai Municipality (15ZR1416000), Special Funding for the Development of Science and Technology of Shanghai Ocean University (No. A2-0203-00-100231) and Shanghai Pujiang Program (No. 18PJ1404200). High performance computing resources are provided by the Ziqiang Supercomputer Centre at Shanghai University.References
- D. Isheim, M. S. Gagliano, M. E. Fine and D. N. Seidman, Acta Mater., 2006, 54, 841–849 CrossRef CAS.
- D. Isheim, R. P. Kolli, M. E. Fine and D. N. Seidman, Scr. Mater., 2006, 55, 35–40 CrossRef CAS.
- R. P. Kolli, Z. G. Mao and D. N. Seidman, Microsc. Microanal., 2007, 13, 272–284 CrossRef CAS PubMed.
- R. P. Kolli and D. N. Seidman, Acta Mater., 2008, 56, 2073–2088 CrossRef CAS.
- Z. B. Jiao, J. H. Luan, W. Guo, J. D. Poplawsky and C. T. Liu, Mater. Res. Lett., 2017, 5, 562–568 CrossRef CAS.
- Z. B. Jiao, J. H. Luan, W. Guo, J. D. Poplawsky and C. T. Liu, Acta Mater., 2016, 120, 216–227 CrossRef CAS.
- Q. Shen, X. Y. Xiong, T. Li, H. Chen, Y. M. Cheng and W. Q. Liu, Mater. Sci. Eng., A, 2018, 723, 279–286 CrossRef CAS.
- Z. B. Jiao, J. H. Luan, M. K. Miller, Y. W. Chung and C. T. Liu, Mater. Today, 2016, 20, 142–154 CrossRef.
- R. P. Kolli, Z. G. Mao and D. N. Seidman, Appl. Phys. Lett., 2007, 91, 241903 CrossRef.
- J. C. Yan, H. W. Xu, X. W. Zuo, T. Jia and E. G. Wang, Mater. Sci. Eng., A, 2019, 739, 225–234 CrossRef CAS.
- S. P. Shu, P. B. Wells, N. Almirall, G. R. Odette and D. D. Morgan, Acta Mater., 2018, 157, 298–306 CrossRef CAS.
- D. Isheim, M. S. Gagliano, M. E. Fine and D. N. Seidman, Metall. Mater. Trans. A, 2016, 47, 3860–3872 CrossRef.
- Y. R. Wen, A. Hirata, Z. W. Zhang, T. Fujita, C. T. Liu, J. H. Jiang and M. W. Chen, Acta Mater., 2013, 61, 2133–2147 CrossRef CAS.
- Z. M. Wang, H. Li, Q. Shen, W. Q. Liu and Z. Y. Wang, Acta Mater., 2018, 156, 158–171 CrossRef CAS.
- Z. M. Wang, X. L. Fang, H. Li and W. Q. Liu, Microsc. Microanal., 2017, 23, 340–349 CrossRef CAS.
- M. K. Miller and K. F. Russell, J. Nucl. Mater., 2007, 371, 145–160 CrossRef CAS.
- Q. Xu, T. Yokotani, T. Onitsuka and K. Sato, J. Nucl. Mater., 2018, 512, 314–319 CrossRef CAS.
- L. T. Belkacemi, E. Meslin, B. Decamps, B. Radiguet and J. Henry, Acta Mater., 2018, 161, 61–72 CrossRef CAS.
- S. P. Shu, N. Almirall, P. B. Wells, T. Yamamoto, G. R. Odette and D. D. Morgan, Acta Mater., 2018, 157, 72–82 CrossRef CAS.
- S. C. Glade, B. D. Wirht, G. R. Odettes, P. A. Kumar, P. A. Sterne and R. H. Howell, Philos. Mag., 2005, 85, 629–639 CrossRef CAS.
- M. K. Miller, B. D. Wirth and G. R. Odette, Mater. Sci. Eng., A, 2003, 353, 133–139 CrossRef.
- S. Kobayashi, H. Kikuchi, S. Takahashi, Y. Kamada, K. Ara, T. Yamamoto, D. Klingensmith and G. R. Odette, J. Nucl. Mater., 2009, 384, 109–114 CrossRef CAS.
- S. Kobayashi, H. Kikuchi, S. Takahashi, Y. Kamada, K. Ara, T. Yamamoto, D. Klingensmith and G. R. Odette, Philos. Mag., 2007, 87, 4047–4058 CrossRef CAS.
- M. Lambrecht, L. Malerba and A. Almazouzi, J. Nucl. Mater., 2008, 378, 282–290 CrossRef CAS.
- E. Meslin, M. Lambrecht, M. Hernández-Mayoral, F. Bergner, L. Malerba, P. Pareige, B. Radiguet, A. Barbu, D. Gómez-Briceño, A. Ulbricht and A. Almazouzi, J. Nucl. Mater., 2010, 406, 73–83 CrossRef CAS.
- R. Schnitzer, M. Schober, S. Zinner and H. Leitner, Acta Mater., 2010, 58, 3733–3741 CrossRef CAS.
- Y. P. Xie and S. J. Zhao, Comput. Mater. Sci., 2012, 63, 329–335 CrossRef CAS.
- Z. B. Jiao, J. H. Luan, M. K. Miller and C. T. Liu, Acta Mater., 2015, 97, 58–67 CrossRef CAS.
- Z. Jiao, S. Taller, K. Field, G. M. Yeli, M. P. Moody and G. S. Was, J. Nucl. Mater., 2018, 504, 122–134 CrossRef CAS.
- G. M. Yeli, M. A. Auger, K. Wilford, G. D. W. Smith, P. A. J. Bagot and M. P. Moody, Acta Mater., 2017, 125, 38–49 CrossRef CAS.
- A. Barashev, S. Golubov, D. Bacon, P. E. J. Flewitt and T. A. Lewis, Acta Mater., 2004, 52, 877–886 CrossRef CAS.
- R. Shabadi, R. Taillard, B. Radiguet, J. D. Baerdemaeker and E. Leunis, Solid State Phenom., 2011, 172–174, 297–302 CAS.
- I. Gorbatov, I. K. Razumov, Y. N. Gornostyrev, V. I. Razumovskiy, P. A. Korzhavyi and A. V. Ruban, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 174113 CrossRef.
- W. X. Song and S. j. Zhao, Phys. Chem. Chem. Phys., 2014, 16, 7222–7230 RSC.
- Y. F. Wen and J. Sun, J. Appl. Phys., 2012, 111, 053517 CrossRef.
- I. Gorbatov, S. V. Okatov, Y. N. Gornostyrev, P. A. Korzhavyi and A. V. Ruban, Phys. Met. Metallogr., 2013, 114, 642–653 CrossRef.
- J. Z. Liu, A. van de Walle, G. Ghosh and M. Asta, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 144109 CrossRef.
- Y. P. Xie and S. J. Zhao, J. Nucl. Mater., 2014, 445, 43–49 CrossRef CAS.
- Y. P. Xie and S. J. Zhao, Comput. Mater. Sci., 2011, 50, 2586–2591 CrossRef CAS.
- P. Olsson, T. P. C. Klaver and C. Domain, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 054102 CrossRef.
- C. S. Becquart, H. R. Ngayam, P. Olsson and C. Domain, J. Nucl. Mater., 2018, 500, 92–109 CrossRef CAS.
- H. T. Ma, R. Yuan, Y. P. Xie, H. Gao, L. J. Hu, X. D. Li, Y. C. Qian and Z. H. Dai, Acta Mater., 2018, 147, 42–50 CrossRef CAS.
- M. K. Miller, K. Michael and R. G. Forbes, Atom probe tomography, Springer, US, 2000 Search PubMed.
- M. K. Miller and R. G. Forbes, Introduction to atom probe tomography, Springer, US, 2014 Search PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, 864–871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 137, 1697–1705 CrossRef CAS.
- R. O. Jones and O. Gunnarsson, Rev. Mod. Phys., 1989, 61, 689–746 CrossRef CAS.
- W. Dong, G. Kresse, J. Furthmyüller and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 2157–2166 CrossRef CAS PubMed.
- Y. Wang and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 13298–13307 CrossRef.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 46, 6671–6687 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- H. Choi, K. Chiho and Y. C. Chung, J. Appl. Phys., 2009, 106, 083910 CrossRef.
- J. H. Shim, Y. W. Cho, S. C. Kwon, W. W. Kim and B. D. Wirth, Appl. Phys. Lett., 2007, 90, 021906 CrossRef.
- Z. Z. Chen, N. Kioussis and N. Ghoniem, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 184104 CrossRef.
- P. Olsson, T. P. C. Klaver and C. Domain, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 054102 CrossRef.
- S. Kobayashi, H. Kikuchi, S. Takahashi, K. Chiba, Y. Kamada and K. Ara, Philos. Mag., 2007, 87, 4047–4058 CrossRef CAS.
- M. K. Miller, K. F. Russell, M. A. Sokolov and R. K. Nanstad, J. Nucl. Mater., 2007, 361, 248–261 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2019 |