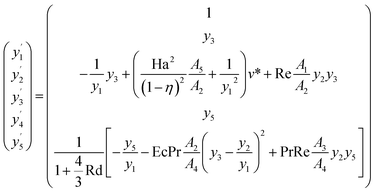DOI:
10.1039/C9RA03286J
(Paper)
RSC Adv., 2019,
9, 22185-22197
A numerical simulation for magnetohydrodynamic nanofluid flow and heat transfer in rotating horizontal annulus with thermal radiation
Received
2nd May 2019
, Accepted 22nd June 2019
First published on 17th July 2019
Abstract
The impact of an axial magnetic field on the heat transfer and nanofluid flow among two horizontal coaxial tubes in the presence of thermal radiation was considered in this study. The impact of viscous dissipation was also considered. The well-known KKL (Koo–Kleinsteuer–Li) model was applied to approximate the viscosity of the nanofluid and the effective thermal conductivity. Furthermore, proper transformations for the velocity and temperature were applied in this study to obtain a set of ODEs (ordinary differential equations) for basic equations governing the flow, heat and mass transfer. In addition, the 4th order Runge–Kutta (RK) numerical scheme was applied to solve the differential equations along with the associated boundary conditions. The impacts of different parameters, including Hartmann number, Reynolds number, radiation parameter and aspect ratio, on the heat transfer and flow features were studied. According to the results, the value of the Nusselt number increases with an increase in the radiation parameter, Hartmann number and aspect ratio and a decrease in the Reynolds number and Eckert number.
1. Introduction
Effective heat transfer in liquids has become a challenging issue in industries and academia because of its importance in the improvement of the efficiency of different devices. Accordingly, different approaches have been proposed by researchers to improve the ability of heat transfer in fluids; one of the best methods to advance the heat transfer rate in liquids is the use of nanofluids, which are materials suspended with nanoparticles (size ≤ 50 nm). These nanoparticles significantly improve the convective heat transfer in liquids by altering the basic features of the base fluid. Carbides or carbon nanotubes (CNTs), metals and oxides are usually used as particles. Because of the superior features of nanofluids, extensive studies have been performed to evaluate the effectiveness of this heat transfer approach. The results obtained from different studies indicate that the effect of addition of nanoparticles to the base fluid becomes more significant under the influence of a magnetic field. To achieve the full potential of nanofluids, it is important to investigate the impact of different impressive parameters that affect the behavior of nanofluids.
Computational approaches have been broadly applied for the simulation of engineering-related issues;1–15 in the field of nanofluids, researchers have applied these approaches to investigate the behavior of these kinds of liquids to achieve the full potential of nanofluids. The influences of the 2nd order temperature jump and velocity slip B.Cs for 3rd-grade nanofluids over a coaxial tube have been investigated by Zhu et al.16 Their findings show that thermophoresis movement and Brownian motion cause the temperature to increase. For power-law nanofluids, Lin et al. have examined the Marangoni convection flow and heat transfer driven by the temperature gradient.17 Furthermore, using a model that contains the influences of thermophoresis and Brownian motion, the boundary layer flow of a nanofluid over an extending plate was studied by Khan and Pop.18 They have considered the Prandtl number, Brownian motion, Lewis number and thermophoresis in their study and demonstrated that the reduced Nusselt number is a declining function of each nondimensional number. Khan et al.19 have also scrutinized the laminar 3D nanofluid flow by a bi-directional stretching sheet. According to this study, the convective heat transfer in different fluids improves because of the presence of nanoparticles in the host liquid.
When the value of the convection heat transfer factor is insignificant, thermal radiation significantly affects the total surface heat transfer. Bakier20 investigated the influence of thermal radiation on mixed convection from a vertical surface in a porous material. The corresponding equations were solved by a 4th-order RK scheme in the abovementioned study. The influence of magnetic field and radiation on the mixed convection stagnation point flow over a vertical stretching plate in a porous structure was investigated by Hayat et al.21 According to their findings, for both types of flows, i.e. assisting and opposing, the values of the local Nusselt number and coefficient of skin friction were tabulated. Hayat et al.22 studied the impact of thermal radiation and Joule heating on the MHD flow of a Maxwell fluid in the presence of thermophoresis. The impact of thermal radiation on heat transfer and magnetohydrodynamics nanofluid flow was scrutinized by Sheikholeslami et al.23 Their findings show that an increase in the radiation parameter causes a decrease in the thickness of the concentration boundary layer.
The investigation of the electrically conductive fluid flow, called magnetohydrodynamic (MHD), is a topic of numerous studies reported in the literature because of its various applications. The study of solar plasma, terrestrial cores and stellar structures are examples of its applications in astrophysics and geophysics. Moreover, MHD has numerous industrial applications such as in the extraction of geothermal energy, nuclear reactors, heat and mass transfer and the stability of convective flows. Sheikholeslami et al.24 have studied the heat transfer and nanofluid flow characteristics among two horizontal parallel sheets in a rotary system and proved that an increase in the Reynolds number and volume fraction of the nanoparticle leads to an increase in the Nusselt number. However, the Nusselt number reduces as the Eckert number, rotation and magnetic parameters increase. Sheikholeslami and Ganji25 have investigated the magnetohydrodynamic and ferrohydrodynamic influences on convective heat transfer and ferrofluid flow and found that depending on the value of the Rayleigh number, magnetic number has a different influence on the Nusselt number. The influence of magnetic field on the CuO–water heat transfer and nanofluid flow in a chamber that is heated from beneath was scrutinized by Sheikholeslami et al.26 According to their findings, at high Rayleigh numbers, the influence of heat source length and Hartmann number is more obvious. Reddy et al.27 scrutinized the MHD flow, heat and mass transfer features of water combined with Cu and Ag nanoparticles above a rotary disk via a porous media by chemical reactions, thermal radiation and partial slip. They studied the impact of significant parameters, including chemical reactions, temperature slip, thermal radiation, velocity slip, nanoparticle volume fraction and magnetic and porous parameters, on concentration, temperature, azimuthal velocity and radial velocity evaluations in the boundary layer zone. The influence of the abovementioned parameters on local Sherwood number, local skin friction coefficient and local Nusselt number was further examined. According to their findings, an increase in the volume fraction parameter of the nanoparticles results in the elevation of the temperature.
Reddy and Chamkha28 have further scrutinized the MHD flow and heat and mass transfer of a viscous incompressible nanofluid over a uniform sheet through a porous medium considering the chemical reaction, thermal radiation, heat generation/absorption, thermo-diffusion and diffusion-thermo effect. They examined the impact of important parameters, such as Dufour parameter, Soret parameter, magnetic parameter, Prandtl number, the volume fraction of nanoparticles, space-dependent and temperature-dependent heat source/sink parameters, on the Sherwood number, Nusselt number, skin-friction coefficient, nanoparticle concentration fields, velocity and temperature. Al-Mudhaf and Chamkha29 used a numerical approach to scrutinize the Marangoni convection flow over a smooth surface because of the existence of a temperature and concentration gradient. They studied the impact of the thermo-solutal surface tension ratio, heat generation or absorption coefficient, Hartmann number, the chemical reaction coefficient and the suction or injection parameter on the quantities belonging to the Sherwood and Nusselt numbers, boundary-layer mass flow rate, wall velocity, concentration profiles, temperature and velocity. Based on their results, it can be concluded that Sherwood and Nusselt numbers and the wall velocity increase by a first-order chemical reaction. However, it has a regressive effect on the mass flow rate in the boundary layer. Furthermore, it is predicted that the Sherwood and Nusselt numbers, the wall velocity and the boundary-layer mass flow rate are augmented with an increase in the thermo-solutal surface tension ratio. The KKL correlation was used by Sheikholeslami Kandelousi for the simulation of heat transfer and nanofluid flow in a permeable channel.30 According to the findings, the augmentation of heat transfer is directly related to the Reynolds number when the power law index vanishes. However, for other amounts of power law index, a reverse trend was observed. Recently, different researchers have scrutinized heat transfer improvement in nanofluids.31–41
In this study, the influence of an exterior axial magnetic field used for the obliging convection nanofluid flow among two horizontal concentric tubes was numerically investigated considering the impacts of thermal radiation and viscous heat dissipation. A rotary internal tube with a low constant angular velocity value induced the forced flow, and the external tube was fixed. The impacts of numerous parameters, namely, aspect ratio, radiation parameter, Hartmann number and Reynolds number, on the characteristics of heat transfer and flow were studied.
2. Problem definition
To resolve engineering-related problems, the main governing equation should be initially derived, and effective terms must be determined. Then, the applied boundary conditions are defined according to the physics of the problem.42–51 Since most of the engineering-related problems contain nonlinear terms in the main governing equations, various techniques52–73 have been developed to solve these equations.
A steady, laminar and unidirectional flow is considered. Thus, the components of the velocity in axial and radial directions as well as the derivatives of the velocity with respect to θ and z vanish. In this situation, the equations governing the flow of the nanofluid and heat transfer in cylindrical coordinates become
| |
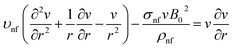 | (1) |
| |
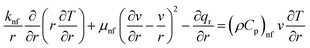 | (2) |
| |
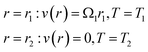 | (3) |
where
qr represents the radiation heat flux that can be specified according to the Rosseland estimation as
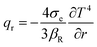
. Furthermore,
βR and
σe represent the mean absorption factor and Stefan–Boltzmann coefficient, respectively. With adequately small alterations in the fluid temperature inside the flow, a linear function of
T can be used to express
T4.
72 We can use the well-known Taylor's series expansion to expand
T4 around
T2. By ignoring higher order terms,
T4 ≅ 4
T23T − 3
T24 was obtained. Hence, the effective density, electrical conductivity and heat capacity of the nanofluid can be stated as follows:
| |
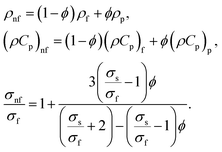 | (4) |
Brownian motion significantly affects the effective thermal conductivity. According to Koo and Kleinstreuer,30 two different components, i.e. a Brownian motion part and the particle's conventional static part, compose the effective thermal conductivity. The influences of base fluid combinations, types of particle, temperature, particle volume fraction and particle size are considered in this double-component thermal conductivity model.
| |
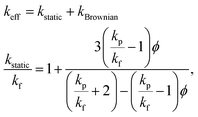 | (5) |
where
kstatic denotes the Maxwell-based static thermal conductivity. The improved thermal conductivity constituent created by the micro-sized convective heat transfer of a particle's Brownian motion and influenced by the surrounding fluid motion was acquired by analyzing the Stokes' flow around a spherical domain (
i.e. nanoparticles). Koo and Kleinstreuer
30 presented two experimental functions (
β and
f) and combined the interaction among nanoparticles in addition to the temperature influence in the model, which resulted into
| |
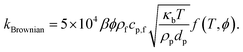 | (6) |
| |
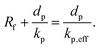 | (7) |
Various base fluids and nanoparticles have various functions. In this study, only nanofluids based on water were considered. The following format is valid for CuO–water nanofluids:
| |
g′(T,ϕ,dp) = (b1 + b2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(dp) + b3 ln(dp) + b3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ϕ) + b4 ln(ϕ) + b4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ϕ)ln(dp) + b5 ln(ϕ)ln(dp) + b5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(dp)2)ln(T) + (b6+b7 ln(dp)2)ln(T) + (b6+b7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(dp) + b8 ln(dp) + b8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ϕ) + b9 ln(ϕ) + b9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ϕ)ln(dp) + b10 ln(ϕ)ln(dp) + b10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(dp)2) ln(dp)2)
| (8) |
where the constants
bi (
i = 0 to 10) are based on the types of nanoparticles. Since the CuO nanoparticles are widely applied in different applications, such as in electronic and optoelectronic devices, field-effect transistors, gas actuators and solar cells, we used this type of nanoparticles in this study. Moreover, based on the values defined in
Tables 1 and
2 for the coefficients of the CuO–water nanofluids, the values of
R2 for the CuO–water nanofluids were found to be 96% and 98%, respectively.
30 Consequently, the KKL correlation is represented as follows:
| |
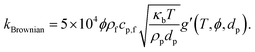 | (9) |
Table 1 Thermophysical properties of water and nanoparticles14
| |
ρ (kg m−3) |
Cp (J kg−1 K−1) |
k (W m−1 K−1) |
dp (nm) |
σ (Ω m)−1 |
| Pure water |
997.1 |
4179 |
0.613 |
— |
0.05 |
| CuO |
6500 |
540 |
18 |
29 |
10−10 |
Table 2 The coefficient values of CuO–water nanofluids14
| Coefficient values |
CuO–water |
| a1 |
−26.593310846 |
| a2 |
−0.403818333 |
| a3 |
−33.3516805 |
| a4 |
−1.915825591 |
| a5 |
6.42185846658 × 10−2 |
| a6 |
48.40336955 |
| a7 |
−9.787756683 |
| a8 |
190.245610009 |
| a9 |
10.9285386565 |
| a10 |
−0.72009983664 |
The laminar nanofluid flow in micro heat sinks was further studied by Koo and Kleinstreuer30 using the effective nanofluid thermal conductivity model introduced by them. The authors suggest the following relation for the effective viscosity because of micromixing in suspensions:
| |
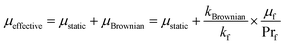 | (10) |
where
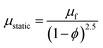
denotes the viscosity of the nanofluid. Hence, we can write the governing relation and the corresponding B.Cs,
i.e. from
eqn (1)–(3), in a dimensionless format as follows:
| |
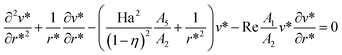 | (11) |
| |
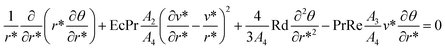 | (12) |
| |
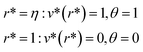 | (13) |
whereas
| |
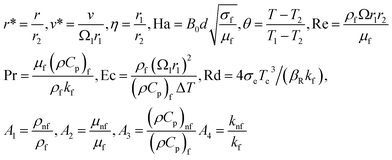 | (14) |
Note that for the readers' convenience, the star signs have been dropped from the equations. The Nusselt number Nu and the skin friction coefficient Cf along the internal wall can be expressed as follows:
| |
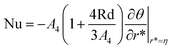 | (15) |
| |
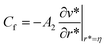 | (16) |
Various researchers have introduced different goal parameters.74–95
3. Numerical method
The corresponding equations in this study were solved by the 4th order RK scheme. To use this numerical method, initially, the governing differential relations must be reduce into a set of 1st order ODEs. Let 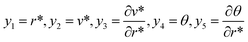 . Various numerical techniques can help researchers in modeling.96–130 The following system of equations can be achieved:
. Various numerical techniques can help researchers in modeling.96–130 The following system of equations can be achieved:| |
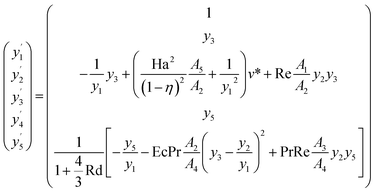 | (17) |
and the related initial conditions are as follows:| |
 | (18) |
Next, eqn (17) along with the initial conditions (18) can be solved using the 4th order RK integration scheme. Note that to approximate the proper values for the unknown initial conditions u1 and u2, Newton's scheme was used, and the process was repeated till the B.Cs at v*(1) = 0, θ(1) = 0 were satisfied. MAPLE was used to perform the computations. Furthermore, the supreme value of r* = 1 for each set of factors was recognized when the values of the anonymous B.Cs at r* = η did not alter to an effective loop with error less than 10−6. Optimized models can be used for better accuracy.131–149
4. Results and discussion
In the current study, the heat transfer and nanofluid flow among two horizontal coaxial tubes was studied. Note that the fluid flow influenced by an axial magnetic field and the impact of thermal radiation were also considered. The impacts of aspect ratio, Hartmann number, radiation parameter and Reynolds number on the heat transfer and flow features were studied (Fig. 1).
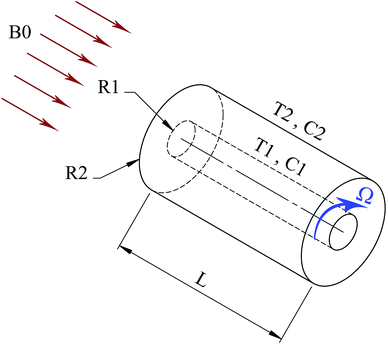 |
| | Fig. 1 Geometry of the problem. | |
The results of the current study for the velocity profile were compared with those of Aberkane et al.73 in Fig. 2. According to this figure, a good agreement can be observed between these findings, which shows the reliability of the method used in this study. The flow velocity and temperature changes at different Hartmann numbers are shown in Fig. 3. According to this figure, an increase in the value of the Hartmann number causes a decrease in both the temperature and the velocity. Furthermore, Fig. 4 demonstrates the impact of Reynolds number on the velocity of the fluid flow and temperature. The results show that as the Reynolds number increases, the thermal boundary layer thicknesses and velocity increases. The changes in the Nusselt number and skin friction coefficient at different Hartmann and Reynolds numbers are demonstrated in Fig. 5. According to this plot, an increase in the Hartmann number and a decrease in the Reynolds number result in the augmentation of the Nusselt number. Moreover, in the case of skin friction constant, similar trend can be detected in this figure.
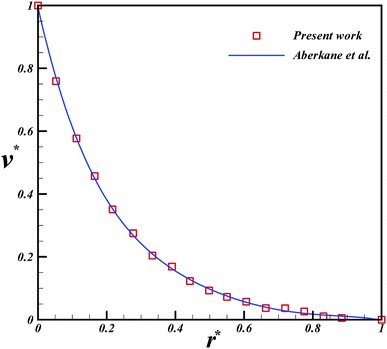 |
| | Fig. 2 Comparison of the results obtained by Aberkane et al.73 and present results of the velocity profile for η = 0.5 and Ha = 4. | |
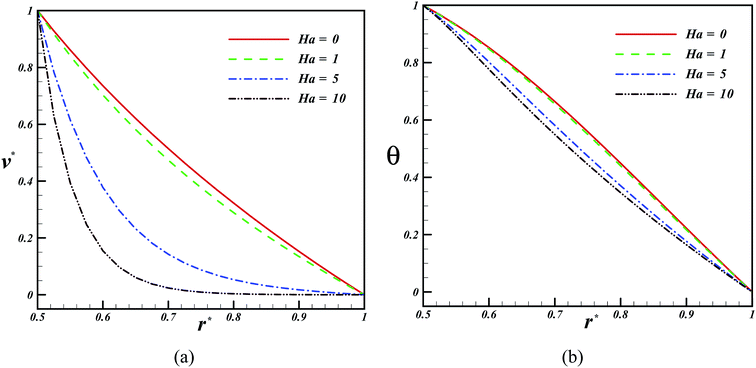 |
| | Fig. 3 Effect of Hartmann number on the velocity and temperature profiles when Pr = 6.8, η = 0.5, Ec = 0.01, Rd = 0.1, Re = 1, ϕ = 0.04. | |
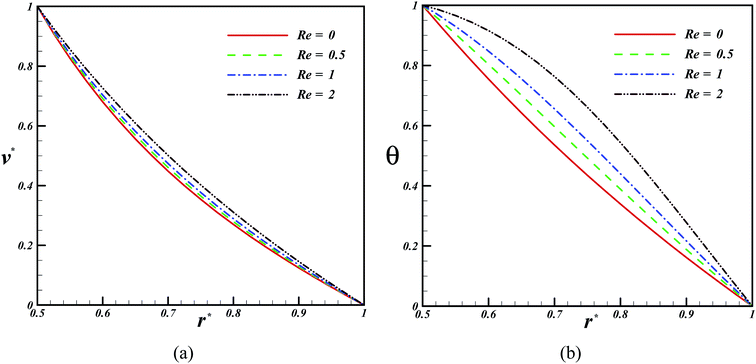 |
| | Fig. 4 Effect of Reynolds number on the velocity and temperature profiles when Pr = 6.8, η = 0.5, Ha = 1, Ec = 0.01, Rd = 0.1, ϕ = 0.04. | |
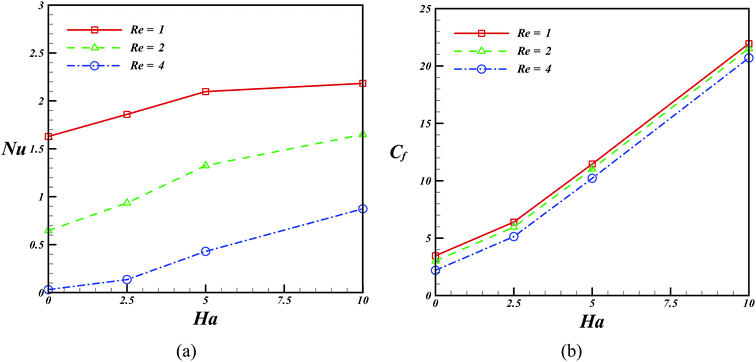 |
| | Fig. 5 Effect of Reynolds number and Hartmann number on the Nusselt number and skin friction coefficient when Pr = 6.8, η = 0.5, Ec = 0.01, Rd = 0.1, ϕ = 0.04. | |
The impact of the Eckert number on the Nusselt number and temperature profile is presented in Fig. 6. This graph shows that the augmentation of the Eckert number causes the thickness of the thermal boundary layer to reduce. Hence, the Nusselt number is affected by the Eckert number and reduced upon its augmentation. The change in temperature and Nusselt number at different radiation parameters is revealed in Fig. 7. According to this figure, the value of temperature reduces when the radiation parameter is taken into account, and an increase in the radiation parameter results in the augmentation of the Nusselt number. The influences of the aspect ratio on the skin friction constant and Nusselt number are presented in Fig. 8. This plot displays that an increase in the amount of the aspect ratio leads to a reduction in the space between the hot and the cold walls. Hence, the value of the Nusselt number increases with an increase in the aspect ratio.
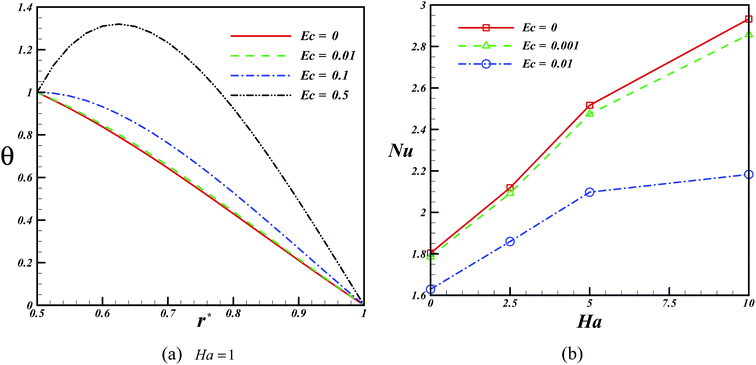 |
| | Fig. 6 Effect of the Eckert number on the temperature profile and Nusselt number when Pr = 6.8, η = 0.5, Rd = 0.1, Re = 1, ϕ = 0.04. | |
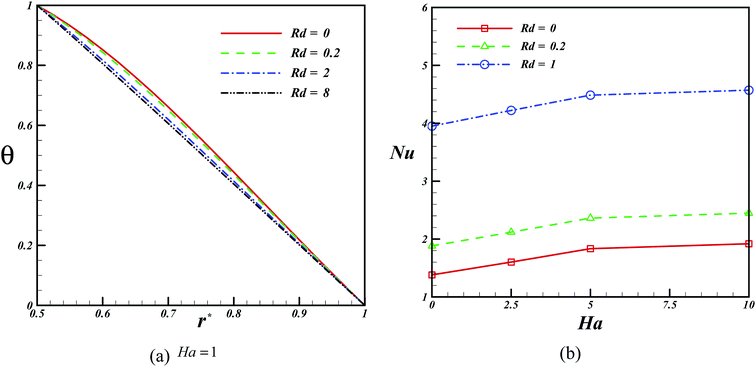 |
| | Fig. 7 Effect of the radiation parameter on the temperature profile and Nusselt number when Pr = 6.8, η = 0.5, Ec = 0.01, Re = 1, ϕ = 0.04. | |
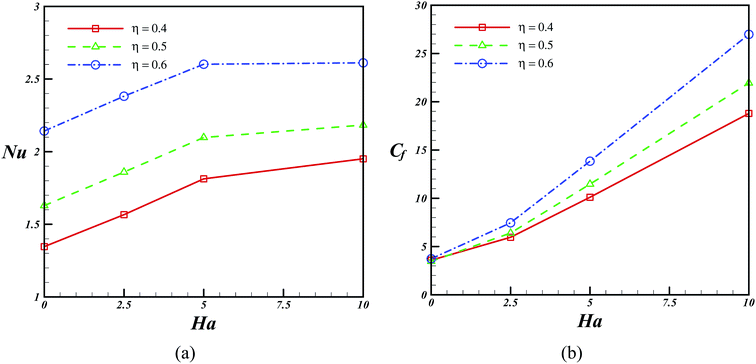 |
| | Fig. 8 Effect of aspect ratio on the Nusselt number and skin friction coefficient when Pr = 6.8, η = 0.5, Ec = 0.01, Rd = 0.1, Re = 1, ϕ = 0.04. | |
5. Conclusions
In the current study, the impact of axial magnetic field on the heat transfer and nanofluid flow among two horizontal coaxial tubes was examined. It was supposed that the magnetic field considered in this study was uniform and constant. Moreover, the influence of thermal radiation and viscous dissipation was considered. The corresponding PDEs were initially converted to a set of ODEs and then solved by the 4th-order RK scheme. The impact of active parameters on the heat transfer and flow was considered. The results indicate that an increase in the radiation parameters and Hartmann number causes the velocity and the temperature boundary layer thicknesses to decrease. However, an enhancement in the Eckert number and Reynolds number may lead to an increase in the velocity and temperature boundary layer thicknesses.
Conflicts of interest
There is no conflict of interest related to this paper.
Acknowledgements
The first author acknowledges the support provided by the Natural Science Foundation of Guangdong Province, China, Grant No. 2018A030310522; Shenzhen Science and Technology Planning Project, China, Grant No. JCYJ20170818100522101; and Natural Science Foundation of Shenzhen University, China, Grant No. 2017032.
References
- H. S. Takhar, A. J. Chamkha and G. Nath, Unsteady mixed convection flow from a rotating vertical cone with a magnetic field, Heat Mass Transfer, 2003, 39(4), 297–304 CrossRef.
- A. J. Chamkha and A. Al-Mudhaf, Unsteady heat and mass transfer from a rotating vertical cone with a magnetic field and heat generation or absorption effects, Int. J. Therm. Sci., 2005, 44(3), 267–276 CrossRef.
- A. J. Chamkha and A.-R. A. Khaled, Hydromagnetic combined heat and mass transfer by natural convection from a permeable surface embedded in a fluid-saturated porous medium, Int. J. Numer. Methods Heat Fluid Flow, 2000, 10(5), 455–477 CrossRef CAS.
- Z. Li, M. Sheikholeslami, M. Jafaryar, S. Ahmad and A. J. Chamkha, Investigation of nanofluid entropy generation in a heat exchanger with helical twisted tapes, J. Mol. Liq., 2018, 266, 797–805 CrossRef CAS.
- R. Kumar, R. Kumar, M. Sheikholeslami and A. J. Chamkha, Irreversibility analysis of the three dimensional flow of carbon nanotubes due to nonlinear thermal radiation and quartic chemical reactions, J. Mol. Liq., 2019, 274, 379–392 CrossRef CAS.
- S. M. Imani, A. M. Goudarzi, S. M. Rabiee and M. Dardel, The modified Mori-Tanaka scheme for the prediction of the effective elastic properties of highly porous ceramics, Ceram. Int., 2018, 44, 16489–16497 CrossRef CAS.
- Z. Li, M. Sheikholeslami, S. Ahmad, S. Saleem and A. J. Chamkha, Effect of dispersing nanoparticles on solidification process in existence of Lorenz forces in a permeable media, J. Mol. Liq., 2018, 266, 181–193 CrossRef CAS.
- M. Imani, M. H. Hojjati, N. Eshghi and A. M. Goudarzi, Finite element simulation of mechanical behaviors of coronary stent in a vessel with plaque, AIP Conf. Proc., 2011, 1400, 523–528 CrossRef.
- Z. Li, M. Sheikholeslami, A. J. Chamkha, Z. A. Raizah and S. Saleem, Control Volume Finite Element Method for nanofluid MHD natural convective flow inside a sinusoidal annulus under the impact of thermal radiation, Comput. Methods Appl. Mech. Eng., 2018, 338, 618–633 CrossRef.
- A. L. Aghili, A. M. Goudarzi, M. H. Hojjati, S. M. Rabiee, M. Imani and A. Paknahad, Biomechanical investigation of human femur by reverse engineering as a robust method and applied simplifications, World Appl. Sci. J., 2013, 28, 2152–2157 Search PubMed.
- M. Imani, A. M. Goudarzi and M. H. Hojjati, Finite element analysis of mechanical behaviors of multi-link stent in a coronary artery with plaque, World Appl. Sci. J., 2013, 21, 1597–1602 CAS.
- M. Imani, Simulation of mechanical behaviors of NIR stent in a stenotic artery using finite element method, World Appl. Sci. J., 2013, 22, 892–897 Search PubMed.
- A. L. Aghili, A. M. Goudarzi, A. Paknahad, M. Imani and A. A. Mehrizi, Finite Element Analysis of Human Femur by Reverse Engineering Modeling Method, Indian J. Sci. Technol., 2015, 8, 47884 Search PubMed.
- M. Sheikholeslami, T. Hayat and A. Alsaedi, MHD free convection of Al2O3–water nanofluid considering thermal radiation: A numerical study, Int. J. Heat Mass Transfer, 2016, 96, 513–524 CrossRef CAS.
- A. J. Chamkha, C. Issa and K. Khalil, Natural convection from an inclined plate embedded in a variable porosity porous medium due to solar radiation, Int. J. Therm. Sci., 2002, 41(1), 73–81 CrossRef.
- J. Zhu, D. Yang, L. Zheng and X. Zhang, Second-Order Slip Effects on Heat Transfer of Nanofluid with Reynolds Model of Viscosity in a Coaxial Cylinder, Int. J. Nonlinear Sci. Numer. Simul., 2015, 16(6), 285–292 CAS.
- Y.-H. Lin, L.-C. Zheng and J.-H. Zhang, Marangoni Convection Flow and Heat Transfer of Power Law Nanofluids Driven by Temperature Gradient with Modified Fourier's Law, Int. J. Nonlinear Sci. Numer. Simul, 2014, 15(6), 337–345 CAS.
- W. A. Khan and I. Pop, Boundary-layer flow of a nanofluid past a stretching sheet, Int. J. Heat Mass Transfer, 2010, 53, 2477–2483 CrossRef CAS.
- J. Ahmad Khan, M. Mustafa, T. Hayat, M. Asif Farooq, A. Alsaedi and S. J. Liao, On model for three-dimensional flow of nanofluid: An application to solar energy, J. Mol. Liq., 2014, 194, 41–47 CrossRef.
- A. Y. Bakier, Thermal radiation effect on mixed convection from vertical surface in saturated porous media, Int. Commun. Heat Mass Transfer, 2001, 28(1), 119–126 CrossRef CAS.
- T. Hayat, Z. Abbas, I. Pop and S. Asghar, Effects of radiation and magnetic field on the mixed convection stagnation-point flow over a vertical stretching sheet in a porous medium, Int. J. Heat Mass Transfer, 2010, 53, 466–474 CrossRef CAS.
- T. Hayat and M. Qasim, Influence of thermal radiation and Joule heating on MHD flow of a Maxwell fluid in the presence of thermophoresis, Int. J. Heat Mass Transfer, 2010, 53, 4780–4788 CrossRef.
- M. Sheikholeslami, D. Domiri Ganji, M. Younus Javed and R. Ellahi, Effect of thermal radiation on magnetohydrodynamics nanofluid flow and heat transfer by means of two phase model, J. Magn. Magn. Mater., 2015, 374, 36–43 CrossRef CAS.
- M. Sheikholeslami, S. Abelman and D. Domiri Ganji, Numerical simulation of MHD nanofluid flow and heat transfer considering viscous dissipation, Int. J. Heat Mass Transfer, 2014, 79, 212–222 CrossRef.
- M. Sheikholeslami and D. Domiri Ganji, Ferrohydrodynamic and Magnetohydrodynamic effects on ferrofluid flow and convective heat transfer, Energy, 2014, 75, 400–410 CrossRef CAS.
- M. Sheikholeslami, M. M. Rashidi, T. Hayat and D. D. Ganji, Free convection of magnetic nanofluid considering MFD viscosity effect, J. Mol. Liq., 2016, 218, 393–399 CrossRef CAS.
- P. S. Reddy, P. Sreedevi and A. J. Chamkha, MHD boundary layer flow, heat and mass transfer analysis over a rotating disk through porous medium saturated by Cu-water and Ag-water nanofluid with chemical reaction, Powder Technol., 2017, 307, 46–55 CrossRef CAS.
- P. S. Reddy and A. J. Chamkha, Soret and Dufour effects on MHD convective flow of Al2O3–water and TiO2–water nanofluids past a stretching sheet in porous media with heat generation/absorption, Adv. Powder Technol., 2016, 27(4), 1207–1218 CrossRef CAS.
- A. Al-Mudhaf and A. J. Chamkha, Similarity solutions for MHD thermosolutal Marangoni convection over a flat surface in the presence of heat generation or absorption effects, Heat Mass Transfer, 2005, 42(2), 112–121 CrossRef CAS.
- M. S. Kandelousi, KKL correlation for simulation of nanofluid flow and heat transfer in a permeable channel, Phys. Lett. A, 2014, 378(45), 3331–3339 CrossRef.
- R. S. Saif, T. Hayat, R. Ellahi, T. Muhammad and A. Ahmed, Stagnation-point flow of second grade nanofluid towards a nonlinear stretching surface with variable thickness, Results Phys., 2017, 7, 2821–2830 CrossRef.
- S. Hariri, M. Mokhtari, M. B. Gerdroodbary and K. Fallah, Numerical investigation of the heat transfer of a ferrofluid inside a tube in the presence of a non-uniform magnetic field, Eur. Phys. J. Plus, 2017, 132(2), 65 CrossRef.
- M. Sheikholeslami, M. B. Gerdroodbary, R. Moradi, A. Shafee and Z. Li, Numerical mesoscopic method for transportation of H2O-based nanofluid through a porous channel considering Lorentz forces, Int. J. Mod. Phys. C, 2019, 30(02n03), 1–13 CrossRef.
- A. Hassanvand, M. B. Gerdroodbary, R. Moradi and Y. Amini, Application of Knudsen thermal force for detection of inert gases, Results Phys., 2018, 9, 351–358 CrossRef.
- M. Sheikholeslami and A. J. Chamkha, Flow and convective heat transfer of a ferro-nanofluid in a double-sided lid-driven cavity with a wavy wall in the presence of a variable magnetic field, Numer. Heat Transfer, Part A, 2016, 69(10), 1186–1200, DOI:10.1080/10407782.2015.1125709.
- J. Ahmad Khan, M. Mustafa, T. Hayat, M. Sheikholeslami and A. Alsaedi, Three-Dimensional Flow of Nanofluid Induced by an Exponentially Stretching Sheet: An Application to Solar Energy, PLoS One, 10(3), e0116603, DOI:10.1371/journal.pone.0116603.
- M. Sheikholeslami, K. Vajravelu and M. M. Rashidi, Forced convection heat transfer in a semi annulus under the influence of a variable magnetic field, Int. J. Heat Mass Transfer, 2016, 92, 339–348 CrossRef CAS.
- M. Sheikholeslami and R. Ellahi, Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid, Int. J. Heat Mass Transfer, 2015, 89, 799–808 CrossRef CAS.
- A. Edalatpour, A. Hassanvand, M. B. Gerdroodbary, R. Moradi and Y. Amini, Injection of multi hydrogen jets within cavity flameholder at supersonic flow, Int. J. Hydrogen Energy, 2019, 44(26), 13923–13931 CrossRef CAS.
- T. K. Nguyen, A. Saidizad, M. Jafaryar, M. Sheikholeslami and M. B. Gerdroodbary, Influence of various shapes of CuO nanomaterial on nanofluid forced convection within a sinusoidal channel with obstacles, Chem. Eng. Res. Des., 2019, 146, 478–485 CrossRef CAS.
- M. B. Gerdroodbary, A. Anazadehsayed, A. Hassanvand and R. Moradi, Calibration of low-pressure MEMS gas sensor for detection of hydrogen gas, Int. J. Hydrogen Energy, 2018, 43(11), 5770–5782 CrossRef.
- Y. Qin, J. Luo, Z. Chen, G. Mei and L.-E. Yan, Measuring the albedo of limited-extent targets without the aid of known-albedo masks, Sol. Energy, 2018, 171, 971–976 CrossRef.
- Y. Qin, A review on the development of cool pavements to mitigate urban heat island effect, Renewable Sustainable Energy Rev., 2015, 52, 445–459 CrossRef.
- Y. Qin, Y. He, J. E. Hiller and G. Mei, A new water-retaining paver block for reducing runoff and cooling pavement, J. Cleaner Prod., 2018, 199, 948–956 CrossRef.
- Y. Qin, Y. Zhao, X. Chen, L. Wang, F. Li and T. Bao, Moist curing increases the solar reflectance of concrete, Constr. Build. Mater., 2019, 215, 114–118 CrossRef.
- Y. Qin, M. Zhang and J. E. Hiller, Theoretical and experimental studies on the daily accumulative heat gain from cool roofs, Energy, 2017, 129, 138–147 CrossRef.
- Y. Qin and H. He, A new simplified method for measuring the albedo of limited extent targets, Sol. Energy, 2017, 157(suppl. C), 1047–1055 CrossRef.
- W. Gao and W. F. Wang, The eccentric connectivity polynomial of two classes of nanotubes, Chaos, Solitons Fractals, 2016, 89, 290–294 CrossRef.
- W. Gao and W. F. Wang, Analysis of k-partite ranking algorithm in area under the receiver operating characteristic curve criterion, Int. Comput. Cent., Bull., 2018, 95(8), 1527–1547 Search PubMed.
- W. Gao, J. L. G. Guirao and H. L. Wu, Two tight independent set conditions for fractional (g,f,m)-deleted graphs systems, Qualitative Theory of Dynamical Systems, 2018, 17(1), 231–243 CrossRef.
- W. Gao and W. F. Wang, Degree sum condition for fractional ID-k-factor-critical graphs, Miskolc Math. Notes, 2017, 18(2), 751–758 CrossRef.
- W. Gao, L. Liang and Y. H. Chen, An isolated toughness condition for graphs to be fractional (k, m)-deleted graphs, Utilitas Mathematica, 2017, 105, 303–316 Search PubMed.
- Y. Qin, Y. He, B. Wu, S. Ma and X. Zhang, Regulating top albedo and bottom emissivity of concrete roof tiles for reducing building heat gains, Energy Build., 2017, 156(suppl. C), 218–224 CrossRef.
- Y. Qin, Pavement surface maximum temperature increases linearly with solar absorption and reciprocal thermal inertial, Int. J. Heat Mass Transfer, 2016, 97, 391–399 CrossRef.
- Y. Qin, J. Liang, K. Tan and F. Li, A side by side comparison of the cooling effect of building blocks with retro-reflective and diffuse-reflective walls, Sol. Energy, 2016, 133, 172–179 CrossRef.
- Y. Qin, J. Liang, H. Yang and Z. Deng, Gas permeability of pervious concrete and its implications on the application of pervious pavements, Measurement, 2016, 78, 104–110 CrossRef.
- Y. Qin and J. E. Hiller, Understanding pavement-surface energy balance and its implications on cool pavement development, Energy Build., 2014, 85, 389–399 CrossRef.
- Y. Qin, M. Zhang and G. Mei, A new simplified method for measuring the permeability characteristics of highly porous media, J. Hydrol., 2018, 562, 725–732 CrossRef.
- Y. Qin, Urban canyon albedo and its implication on the use of reflective cool pavements, Energy Build., 2015, 96, 86–94 CrossRef.
- W. Gao and M. R. Farahani, Generalization bounds and uniform bounds for multi-dividing ontology algorithms with convex ontology loss function, Comput. J., 2017, 60(9), 1289–1299 Search PubMed.
- W. Gao, L. Liang, T. W. Xu and J. H. Gan, Topics on data transmission problem in software definition network, Open Phys., 2017, 15, 501–508 Search PubMed.
- M. Sheikholeslami, M. Barzegar Gerdroodbary, R. Moradi, S. Ahmad and L. Zhixiong, Application of Neural Network for estimation of heat transfer treatment of Al2O3-H2O nanofluid through a channel, Comput. Methods Appl. Mech. Eng., 2019, 344, 1–12 CrossRef.
- M. Mokhtari, M. B. Gerdroodbary, R. Yeganeh and K. Fallah, Numerical study of mixed convection heat transfer of various fin arrangements in a horizontal channel, Engineering Science and Technology, an International Journal, 2017, 20(3), 1106–1114 CrossRef.
- M. B. Gerdroodbary, M. Sheikholeslami, S. V. Mousavi, A. Anazadehsayed and R. Moradi., The influence of non-uniform magnetic field on heat transfer intensification of ferrofluid inside a T-junction, Chem. Eng. Process., 2018, 123, 58–66 CrossRef.
- W. Gao, Three algorithms for graph locally harmonious colouring, J. Differ. Equ. Appl., 2017, 23(1–2), 8–20 CrossRef.
- W. Gao, L. Yan and L. Shi, Generalized Zagreb index of polyomino chains and nanotubes, Optoelectron. Adv. Mater., Rapid Commun., 2017, 11(1–2), 119–124 Search PubMed.
- W. Gao, Y. Guo and K. Y. Wang, Ontology algorithm using singular value decomposition and applied in multidisciplinary, Clust. Comput., 2016, 19(4), 2201–2210 CrossRef.
- W. Gao, W. F. Wang, M. K. Jamil and M. R. Farahani, Electron energy studying of molecular structures via forgotten topological index computation, J. Chem., 2016, 1053183, DOI:10.1155/2016/1053183.
- W. Gao, L. L. Zhu and K. Y. Wang, Ranking based ontology scheming using eigenpair computation, J. Intell. Fuzzy. Syst., 2016, 31(4), 2411–2419 Search PubMed.
- P. Valipour, R. Moradi and F. Shakeri Aski, CNT-water nanofluid thermal radiation heat transfer over a stretching sheet considering heat generation, J. Mol. Liq., 2017, 237, 242–246 CrossRef CAS.
- M. Mokhtari, S. Hariri, M. B. Gerdroodbary and R. Yeganeh, Effect of non-uniform magnetic field on heat transfer of swirling ferrofluid flow inside tube with twisted tapes, Chem. Eng. Process., 2017, 117, 70–79 CrossRef CAS.
- A. Raptis, Radiation and free convection flow through a porous medium, Int. Commun. Heat Mass Transfer, 1998, 25, 289–295 CrossRef CAS.
- S. Aberkane, M. Mouderes, M. Ihdene and A. Ghezal, Effect of Magnetic Field on the Heat and Mass Transfer in a Rotating Horizontal Annulus, Proceedings of the International Conference on Heat Transfer and Fluid Flow, Prague, Czech Republic, August 11-12, 2014 Search PubMed.
- M. Sheikholeslami, A. J. Chamkha, P. Rana and R. Moradi, Combined thermophoresis and Brownian motion effects on nanofluid free convection heat transfer in an L-shaped enclosure, Chin. J. Phys., 2017, 55, 2356–2370 CrossRef CAS.
- M. Sheikholeslami and A. J. Chamkha, Influence of Lorentz forces on nanofluid forced convection considering Marangoni convection, J. Mol. Liq., 2017, 225, 750–757 CrossRef CAS.
- M. Sheikholeslami and A. J. Chamkha, Electrohydrodynamic free convection heat transfer of a nanofluid in a semi-annulus enclosure with a sinusoidal wall, Numer. Heat Transfer, Part A, 2016, 69(7), 781–793, DOI:10.1080/10407782.2015.1090819.
- M. Sheikholeslami and H. B. Rokni, Numerical simulation for impact of Coulomb force on nanofluid heat transfer in a porous enclosure in presence of thermal radiation, Int. J. Heat Mass Transfer, 2018, 118, 823–831 CrossRef CAS.
- M. Sheikholeslami, S. A. Shehzad, F. M. Abbasi and Z. Li, Nanofluid flow and forced convection heat transfer due to Lorentz forces in a porous lid driven cubic enclosure with hot obstacle, Comput. Methods Appl. Mech. Eng., 2018, 338, 491–505 CrossRef.
- M. Sheikholeslami, H. Keramati, S. Ahmad, Z. Li, O. A. Alawad and I. Tlili, Nanofluid MHD forced convection heat transfer around the elliptic obstacle inside a permeable lid drive 3D enclosure considering lattice Boltzmann method, Phys. A, 2019, 523, 87–104 CrossRef CAS.
- M. Sheikholeslami and H. B. Rokni, Simulation of nanofluid heat transfer in presence of magnetic field: A review, Int. J. Heat Mass Transfer, 2017, 115, 1203–1233 CrossRef CAS.
- M. Sheikholeslami, Influence of magnetic field on nanofluid free convection in an open porous cavity by means of Lattice Boltzmann Method, J. Mol. Liq., 2017, 234, 364–374 CrossRef CAS.
- M. Sheikholeslami and K. Vajravelu, Forced convection heat transfer in Fe3O4-ethylene glycol nanofluid under the influence of Coulomb force, J. Mol. Liq., 2017, 233, 203–210 CrossRef CAS.
- M. Sheikholeslami and H. B. Rokni, Influence of EFD viscosity on nanofluid forced convection in a cavity with sinusoidal wall, J. Mol. Liq., 2017, 232, 390–395 CrossRef CAS.
- M. Sheikholeslami, Magnetohydrodynamic nanofluid forced convection in a porous lid driven cubic cavity using Lattice Boltzmann Method, J. Mol. Liq., 2017, 231, 555–565 CrossRef CAS.
- M. Sheikholeslami, Influence of Lorentz forces on nanofluid flow in a porous cylinder considering Darcy model, J. Mol. Liq., 2017, 225, 903–912 CrossRef CAS.
- M. Sheikholeslami, M. Jafaryar, M. Hedayat, S. Ahmad, Z. Li, T. K. Nguyen and M. Bakouri, Heat transfer and turbulent simulation of nanomaterial due to compound turbulator including irreversibility analysis, Int. J. Heat Mass Transfer, 2019, 137, 1290–1300 CrossRef CAS.
- M. Sheikholeslami, M. A. Sheremet, S. Ahmad and Z. Li, CVFEM approach for EHD flow of nanofluid through porous medium within a wavy chamber under the impacts of radiation and moving walls, J. Therm. Anal. Calorim., 2019 DOI:10.1007/s10973-019-08235-3.
- M. Sheikholeslami, A. Zareei, M. Jafaryar, S. Ahmad, Z. Li, S. Amor and I. Tlili, Heat transfer simulation during charging of nanoparticle enhanced PCM within a channel, Phys. A, 2019, 525, 557–565 CrossRef CAS.
- M. Sheikholeslami, M. Jafaryar, S. Ahmad, Z. Li and H. Rizwan-ul, Heat transfer of nanoparticles employing innovative turbulator considering entropy generation, Int. J. Heat Mass Transfer, 2019, 136, 1233–1240 CrossRef CAS.
- M. Sheikholeslami, M. Jafaryar, S. Ahmad and Z. Li, Hydrothermal and second law behavior for charging of NEPCM in a two dimensional thermal storage unit, Chin. J. Phys., 2019, 58, 244–252 CrossRef CAS.
- M. Sheikholeslami and M. K. Sadoughi, Simulation of CuO-water nanofluid heat transfer enhancement in presence of melting surface, Int. J. Heat Mass Transfer, 2018, 116, 909–919 CrossRef CAS.
- M. Sheikholeslami, A. Ahmad, I. Khan, S. Ahmad and Z. Li, Impact of Lorentz forces on Fe3O4-water ferrofluid entropy and exergy treatment within a permeable semi annulus, J. Cleaner Prod., 2019, 221, 885–898 CrossRef CAS.
- M. Sheikholeslami, H. Rizwan-ul, S. Ahmad, Z. Li, Y. G. Elaraki and I. Tlili, Heat transfer simulation of heat storage unit with nanoparticles and fins through a heat exchanger, Int. J. Heat Mass Transfer, 2019, 135, 470–478 CrossRef CAS.
- M. Sheikholeslami, S. Ahmad, A. Zareei, H. Rizwan-ul and Z. Li, Heat transfer of magnetic nanoparticles through porous media including exergy analysis, J. Mol. Liq., 2019, 279, 719–732 CrossRef CAS.
- M. Sheikholeslami and O. Mahian, Enhancement of PCM solidification using inorganic nanoparticles and an external magnetic field with application in energy storage systems, J. Cleaner Prod., 2019, 215, 963–977 CrossRef CAS.
- M. Sheikholeslami, S. A. M. Mehryan, S. Ahmad and M. A. Sheremet, Variable magnetic forces impact on Magnetizable hybrid nanofluid heat transfer through a circular cavity, J. Mol. Liq., 2019, 277, 388–396 CrossRef CAS.
- M. Sheikholeslami, Z. Shah, S. Ahmad, I. Khan and I. Tlili, Uniform magnetic force impact on water based nanofluid thermal behavior in a porous enclosure with ellipse shaped obstacle, Sci. Rep., 2019 DOI:10.1038/s41598-018-37964-y.
- M. Sheikholeslami, H. Rizwan-ul, S. Ahmad and Z. Li, Heat transfer behavior of Nanoparticle enhanced PCM solidification through an enclosure with V shaped fins, Int. J. Heat Mass Transfer, 2019, 130, 1322–1342 CrossRef CAS.
- M. Sheikholeslami, M. Jafaryar, S. Ahmad and Z. Li, Nanofluid heat transfer and entropy generation through a heat exchanger considering a new turbulator and CuO nanoparticles, J. Therm. Anal. Calorim., 2019 DOI:10.1007/s10973-018-7866-7.
- M. Sheikholeslami, New computational approach for exergy and entropy analysis of nanofluid under the impact of Lorentz force through a porous media, Comput. Methods Appl. Mech. Eng., 2019, 344, 319–333 CrossRef.
- M. Sheikholeslami, Numerical approach for MHD Al2O3-water nanofluid transportation inside a permeable medium using innovative computer method, Comput. Methods Appl. Mech. Eng., 2019, 344, 306–318 CrossRef.
- M. Sheikholeslami, I. Khan and I. Tlili, Non-equilibrium model for nanofluid free convection inside a porous cavity considering Lorentz forces, Sci. Rep., 2018, 8, 16881, DOI:10.1038/s41598-018-33079-6.
- M. Sheikholeslami, Magnetic source impact on nanofluid heat transfer using CVFEM, Neural Comput. Appl., 2018, 30(4), 1055–1064 CrossRef.
- M. Sheikholeslami, Application of Darcy law for nanofluid flow in a porous cavity under the impact of Lorentz forces, J. Mol. Liq., 2018, 266, 495–503 CrossRef CAS.
- M. Sheikholeslami, Z. Li and S. Ahmad, Lorentz forces effect on NEPCM heat transfer during solidification in a porous energy storage system, Int. J. Heat Mass Transfer, 2018, 127, 665–674 CrossRef CAS.
- M. Sheikholeslami, M. Jafaryar, S. Saleem, Z. Li, S. Ahmad and Y. Jiang, Nanofluid heat transfer augmentation and exergy loss inside a pipe equipped with innovative turbulators, Int. J. Heat Mass Transfer, 2018, 126, 156–163 CrossRef CAS.
- M. Sheikholeslami, A. Ghasemi, Z. Li, S. Ahmad and S. Saleem, Influence of CuO nanoparticles on heat transfer behavior of PCM in solidification process considering radiative source term, Int. J. Heat Mass Transfer, 2018, 126, 1252–1264 CrossRef CAS.
- M. Sheikholeslami, M. Darzi and Z. Li, Experimental investigation for entropy generation and exergy loss of nano-refrigerant condensation process, Int. J. Heat Mass Transfer, 2018, 125, 1087–1095 CrossRef CAS.
- M. Sheikholeslami, S. A. Shehzad and Z. Li, Water based nanofluid free convection heat transfer in a three dimensional porous cavity with hot sphere obstacle in existence of Lorenz forces, Int. J. Heat Mass Transfer, 2018, 125, 375–386 CrossRef CAS.
- H. B. Rokni, J. D. Moore, A. Gupta, M. A. McHugh and M. Gavaises, Entropy scaling based viscosity predictions for hydrocarbon mixtures and diesel fuels up to extreme conditions, Fuel, 2019, 241, 1203–1213 CrossRef CAS.
- W. Gao, M. K. Siddiqui, M. K. Jamil and M. R. Farahani, Forgotten topological index of chemical structure in drugs, Saudi Pharm. J., 2016, 24(3), 258–264 CrossRef.
- H. B. Rokni, A. Gupta, J. D. Moore, M. A. McHugh, B. A. Bamgbaded and M. Gavaises, Purely predictive method for density, compressibility, and expansivity for hydrocarbon mixtures and diesel and jet fuels up to high temperatures and pressures, Fuel, 2019, 236, 1377–1390 CrossRef CAS.
- M. Sheikholeslami, M. Jafaryar and Z. Li, Nanofluid turbulent convective flow in a circular duct with helical turbulators considering CuO nanoparticles, Int. J. Heat Mass Transfer, 2018, 124, 980–989 CrossRef CAS.
- M. Sheikholeslami, Investigation of Coulomb forces effects on Ethylene glycol based nanofluid laminar flow in a porous enclosure, Appl. Math. Mech., 2018, 39(9), 1341–1352 CrossRef.
- M. Sheikholeslami and A. Ghasemi, Solidification
heat transfer of nanofluid in existence of thermal radiation by means of FEM, Int. J. Heat Mass Transfer, 2018, 123, 418–431 CrossRef CAS.
- M. Sheikholeslami and S. A. Shehzad, CVFEM simulation for nanofluid migration in a porous medium using Darcy model, Int. J. Heat Mass Transfer, 2018, 122, 1264–1271 CrossRef CAS.
- M. Sheikholeslami and R. Ellahi, Simulation of ferrofluid flow for magnetic drug targeting using Lattice Boltzmann method, Z. Naturforsch., A: Phys. Sci., 2015, 70(2), 115–124 Search PubMed.
- M. Sheikholeslami, R. Ellahi, M. Hassan and S. Soleimani, A study of natural convection heat transfer in a nanofluid filled enclosure with elliptic inner cylinder, Int. J. Numer. Methods Heat Fluid Flow, 2014, 24(8), 1906–1927 CrossRef.
- M. Sheikholeslami and H. B. Rokni, Magnetic nanofluid flow and convective heat transfer in a porous cavity considering Brownian motion effects, Phys. Fluids, 2018, 30(1) DOI:10.1063/1.5012517.
- M. Sheikholeslami and S. A. Shehzad, Simulation of water based nanofluid convective flow inside a porous enclosure via Non-equilibrium model, Int. J. Heat Mass Transfer, 2018, 120, 1200–1212 CrossRef CAS.
- M. Sheikholeslami, Numerical investigation of nanofluid free convection under the influence of electric field in a porous enclosure, J. Mol. Liq., 2018, 249, 1212–1221 CrossRef CAS.
- M. Sheikholeslami and A. Zeeshan, Analysis of flow and heat transfer in water based nanofluid due to magnetic field in a porous enclosure with constant heat flux using CVFEM, Comput. Methods Appl. Mech. Eng., 2017, 320, 68–81 CrossRef.
- M. Sheikholeslami and K. Vajravelu, Nanofluid flow and heat transfer in a cavity with variable magnetic field, Appl. Math. Comput., 2017, 298, 272–282 CrossRef.
- M. Sheikholeslami, M. Darzi and M. K. Sadoughi, Heat transfer improvement and Pressure Drop during condensation of refrigerant-based Nanofluid; An Experimental Procedure, Int. J. Heat Mass Transfer, 2018, 122, 643–650 CrossRef CAS.
- M. Sheikholeslami, Numerical modeling of Nano enhanced PCM solidification in an enclosure with metallic fin, J. Mol. Liq., 2018, 259, 424–438 CrossRef CAS.
- M. Sheikholeslami and M. Shamlooei, Fe3O4-H2O nanofluid natural convection in presence of thermal radiation, Int. J. Hydrogen Energy, 2017, 42(9), 5708–5718 CrossRef CAS.
- M. Sheikholeslami, Solidification of NEPCM under the effect of magnetic field in a porous thermal energy storage enclosure using CuO nanoparticles, J. Mol. Liq., 2018, 263, 303–315 CrossRef CAS.
- M. Sheikholeslami, Numerical simulation for solidification in a LHTESS by means of Nano-enhanced PCM, J. Taiwan Inst. Chem. Eng., 2018, 86, 25–41 CrossRef CAS.
- M. Sheikholeslami, Q. M. Zaigham Zia and R. Ellahi, Influence of Induced Magnetic Field on Free Convection of Nanofluid Considering Koo-Kleinstreuer-Li (KKL) Correlation, Appl. Sci., 2016, 6, 324, DOI:10.3390/app6110324.
- M. Sheikholeslami, S. A. Shehzad, Z. Li and S. Ahmad, Numerical modeling for Alumina nanofluid magnetohydrodynamic convective heat transfer in a permeable medium using Darcy law, Int. J. Heat Mass Transfer, 2018, 127, 614–622 CrossRef CAS.
- M. Sheikholeslami, Influence of magnetic field on Al2O3-H2O nanofluid forced convection heat transfer in a porous lid driven cavity with hot sphere obstacle by means of LBM, J. Mol. Liq., 2018, 263, 472–488 CrossRef CAS.
- M. Sheikholeslami and B. Houman, Rokni, Melting heat transfer influence on nanofluid flow inside a cavity in existence of magnetic field, Int. J. Heat Mass Transfer, 2017, 114, 517–526 CrossRef CAS.
- M. Sheikholeslami, Finite element method for PCM solidification in existence of CuO nanoparticles, J. Mol. Liq., 2018, 265, 347–355 CrossRef CAS.
- M. Sheikholeslami and S. A. Shehzad, CVFEM for influence of external magnetic source on Fe3O4–H2O nanofluid behavior in a permeable cavity considering shape effect, Int. J. Heat Mass Transfer, 2017, 115, 180–191 CrossRef CAS.
- M. Sheikholeslami, Magnetic field influence on CuO-H2O nanofluid convective flow in a permeable cavity considering various shapes for nanoparticles, Int. J. Hydrogen Energy, 2017, 42, 19611–19621 CrossRef CAS.
- M. Sheikholeslami, CuO-water nanofluid flow due to magnetic field inside a porous media considering Brownian motion, J. Mol. Liq., 2018, 249, 921–929 CrossRef CAS.
- M. Sheikholeslami and M. Seyednezhad, Simulation of nanofluid flow and natural convection in a porous media under the influence of electric field using CVFEM, Int. J. Heat Mass
Transfer, 2018, 120, 772–781 CrossRef CAS.
- A. Divsalar, N. Entesari, M. N. Dods, R. W. Prosser, F. N. Egolfopoulos and T. T. Tsotsis, A UV Photodecomposition Reactor for Siloxane Removal from Biogas: Modeling Aspects, Chem. Eng. Sci., 2018, 192, 359–370 CrossRef CAS.
- A. Divsalar, L. Sun, M. N. Dods, H. Divsalar, R. W. Prosser, F. N. Egolfopoulos and T. T. Tsotsis, Feasibility of Siloxane Removal from Biogas Using UV Photodecomposition Technique, Ind. Eng. Chem. Res., 2018, 57(22), 7383–7394 CrossRef CAS.
- A. Divsalar, Lab-scale and field-scale study of siloxane contaminants removal from landfill gas, PhD thesis, University of Southern California, Los Angeles, CA, Dec. 2017, 94 pages.
- H. Rafatijo and D. L. Thompson, General application of Tolman's concept of activation energy, J. Chem. Phys., 2017, 147, 224111, DOI:10.1063/1.5009751.
- H. Rafatijo, M. Monge-Palacios and D. L. Thompson, Identifying Collisions of Various Molecularities in Molecular Dynamics Simulations, J. Phys. Chem. A, 2019, 123(6), 1131–1139, DOI:10.1021/acs.jpca.8b11686.
- W. Gao, W. F. Wang and M. R. Farahani, Topological indices study of molecular structure in anticancer drugs, J. Chem., 2016, 3216327, DOI:10.1155/2016/3216327.
- W. Gao and W. F. Wang, The vertex version of weighted wiener number for bicyclic molecular structures, Comput. Math. Methods Med., 2015, 418106, DOI:10.1155/2015/418106.
- W. Gao and W. F. Wang, Second atom-bond connectivity index of special chemical molecular structures, J. Chem., 2014, 906254, DOI:10.1155/2014/906254.
- W. Gao and W. F. Wang, Degree sum condition for fractional ID-k-factor-critical graphs, Miskolc Math. Notes, 2017, 18(2), 751–758 CrossRef.
- W. Gao, L. Liang and Y. H. Chen, An isolated toughness condition for graphs to be fractional (k, m)-deleted graphs, Utilitas Mathematica, 2017, 105, 303–316 Search PubMed.
- W. Gao, Three algorithms for graph locally harmonious colouring, J. Differ. Equ. Appl., 2017, 23(1–2), 8–20 CrossRef.
- W. Gao, L. Liang, T. W. Xu and J. X. Zhou, Degree conditions for fractional (g,f,n',m)-critical deleted graphs and fractional ID-(g,f,m)-deleted graphs, Bulletin of the Malaysian Mathematical Sciences Society, 2016, 39, 315–330 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2019 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *e
*e
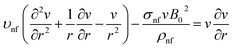
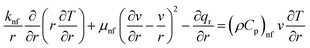
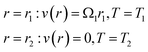
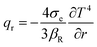 . Furthermore, βR and σe represent the mean absorption factor and Stefan–Boltzmann coefficient, respectively. With adequately small alterations in the fluid temperature inside the flow, a linear function of T can be used to express T4.72 We can use the well-known Taylor's series expansion to expand T4 around T2. By ignoring higher order terms, T4 ≅ 4T23T − 3T24 was obtained. Hence, the effective density, electrical conductivity and heat capacity of the nanofluid can be stated as follows:
. Furthermore, βR and σe represent the mean absorption factor and Stefan–Boltzmann coefficient, respectively. With adequately small alterations in the fluid temperature inside the flow, a linear function of T can be used to express T4.72 We can use the well-known Taylor's series expansion to expand T4 around T2. By ignoring higher order terms, T4 ≅ 4T23T − 3T24 was obtained. Hence, the effective density, electrical conductivity and heat capacity of the nanofluid can be stated as follows: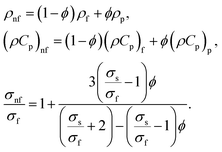

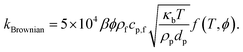
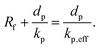
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(dp) + b3
ln(dp) + b3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ϕ) + b4
ln(ϕ) + b4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ϕ)ln(dp) + b5
ln(ϕ)ln(dp) + b5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(dp)2)ln(T) + (b6+b7
ln(dp)2)ln(T) + (b6+b7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(dp) + b8
ln(dp) + b8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ϕ) + b9
ln(ϕ) + b9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(ϕ)ln(dp) + b10
ln(ϕ)ln(dp) + b10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(dp)2)
ln(dp)2)
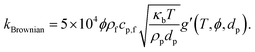
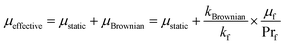
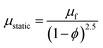 denotes the viscosity of the nanofluid. Hence, we can write the governing relation and the corresponding B.Cs, i.e. from eqn (1)–(3), in a dimensionless format as follows:
denotes the viscosity of the nanofluid. Hence, we can write the governing relation and the corresponding B.Cs, i.e. from eqn (1)–(3), in a dimensionless format as follows: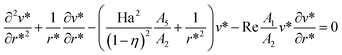
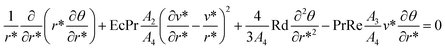
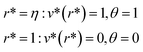
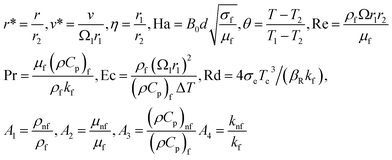
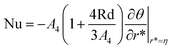
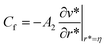
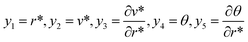 . Various numerical techniques can help researchers in modeling.96–130 The following system of equations can be achieved:
. Various numerical techniques can help researchers in modeling.96–130 The following system of equations can be achieved: