Open Access Article
Open Access ArticleStudies on the thermal behavior and safety of a novel thermostable explosive BPTAP†
Fang Yang *,
Ya Chen,
Chuande Zhao* and
Long Zhang
*,
Ya Chen,
Chuande Zhao* and
Long Zhang
Institute of Chemical Materials, China Academy of Engineering Physics, Mianyang Sichuan 621900, China. E-mail: yangfang@caep.cn; c.d.zhao@caep.cn
First published on 17th July 2019
Abstract
Thermal decomposition of a highly thermostable explosive dihydroxylammonium 2,4,8,10-tetranitro-benzopyrido-1,3a,6,6a-tetraazapentalene (BPTAP) was studied using conventional thermal analysis techniques (Thermal Gravimetric Analysis and Differential Scanning Calorimetry). To obtain more comprehensive insight into the kinetics mechanism of BPTAP decomposition, thermoanalytical experiments were performed under non-hermetic and hermetic conditions. Several widely used thermoanalytical data processing techniques based on model-free kinetics (Flynn–Wall–Ozawa, Kissinger, Freidman, numerical optimization) were studied and compared. Furthermore, to fully understand the thermal safety property of BPTAP, the kinetic model and the kinetic parameters were evaluated based on the non-isothermal DSC data by using a non-linear optimization method. The kinetic models of thermal decomposition of BPTAP under non-hermetic and hermetic conditions were different, which were identified as the generalized autocatalysis reaction and two parallel generalized autocatalysis reactions, respectively. On the basis of the aforementioned study, two important safety parameters including the time to maximum rate under adiabatic conditions and self-accelerating decomposition temperature for BPTAP in DEWAR were calculated and discussed.
1. Introduction
High energy materials (HEMs) are widely used in military and civil technology. When looking for new compounds, it is crucial that the HEMs should exhibit high detonation parameters and low sensitivity to mechanical stimuli and temperature. In many HEMs applications, high thermal stability is important in military, space, and civilian uses. A frequent civilian application, for example, is the use of such explosives in shaped charges that explosively perforate downhole well pipes and penetrate surrounding rock to improve oil recovery. The explosive in these downhole penetrators should have a high detonation velocity (vD, km s−1) and detonation pressure (PCJ, kbar) and must withstand high temperatures and still initiate and perform reliably. The same is true for military and space applications in which explosives are subjected to high temperatures. Therefore, thermostable materials constitute a very important group of HEMs. This group includes long-known compounds such as: 1,3,5-triamino-2,4,6-trinitrobenzene (TATB),1 1,3,7,9-tetranitrodibenzo-1,3a,4,6a-tetraazapentalene (z-TACOT),2 2,6-bis(picrylamino)-3,5-dinitropyridine (PYX).3 The research carried out in many laboratories led to the synthesis of new thermostable HEMs, such as: 2,4,8,10-tetranitro-benzopyrido-1,3a,6,6a-tetraazapentalene (BPTAP),4 5,5′,6,6′-tetranitro-2,2′-bibenzimidazole (TNBBI),5 5,5′-bis(2,4,6-trinitrophenyl)-2,2′-bi(1,3,4-oxadiazole) (TKX-55)6 and N,N′-bis(1,2,4-triazol-3-yl-)-4,4′-diamino-2,2′,3,3′,5,5′,6,6′-octanitroazobenzene (BTDAONAB).7 BPTAP is a highly thermostable compound which was described for the first time in 2006.4 Its structure is shown in Fig. 1. BPTAP is insensitive to initiation by spark and friction and has a drop height of 59 cm; it is easy and cheap to prepare in a three-step process without any purification and recrystallization, and has a fast vD (7.43 km s−1) and a high PCJ (294 kbar). Based on the reported excellent properties of BPTAP, we anticipated that it will be a very promising energetic material to be used for military and civil purposes.The main threat associated with the production, storage and use of high energy materials is thermal explosion, which occurs as a result of the accumulation of heat released in the decomposition reaction.8 This threat is particularly relevant in case of thermostable materials, designed to operate at increased temperatures. It is necessary to examine their decomposition process in order to estimate the hazards associated with the thermal explosion of these HEMs. During the decomposition, a series of parallel and subsequent (consecutive) chemical reactions and physical processes may take place. Therefore it is important to understand the impact of conditioning on the course of the decomposition process and determine the kinetic parameters of the decomposition reactions and their changes along with the increase in the level of conversion. Up to now, the studies about the thermal risk behaviors of BPTAP have rarely been reported.
The results presented in this manuscript constitute an intensive study on the properties of BPTAP in terms of safety of use. The aim of the work was to investigate the process of thermal decomposition of BPTAP under non-hermetic and hermetic conditions, determine kinetic model and kinetic parameters of decomposition reactions, as well as to estimate the safety of BPTAP use and storage.
2. Experimental section
2.1 Materials
All chemicals were analytical grade and commercially available (Aladdin, Sigma-Aldrich). BPTAP was synthesized as described in the publication by Huynh et al.9 IR (cm−1): νC–H = 3091, νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N = 1641, νNO2 = 1540 and 1337, νC
N = 1641, νNO2 = 1540 and 1337, νC![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C = 1452, νC–N = 1418, δC–H = 1245. 1H NMR (DMSO-d6) (85 °C) δ 9.27 (s, 1H), 9.30 (d, 1H) 9.38 (d, 1H). 13C NMR (DMSO-d6) (85 °C) d 103.1, 111.2, 118.9, 122.8, 130.9, 132.5, 135.2, 139.6, 140.9, 153.6, 157.8. The purity of the sample is higher than 99% (HPLC).
C = 1452, νC–N = 1418, δC–H = 1245. 1H NMR (DMSO-d6) (85 °C) δ 9.27 (s, 1H), 9.30 (d, 1H) 9.38 (d, 1H). 13C NMR (DMSO-d6) (85 °C) d 103.1, 111.2, 118.9, 122.8, 130.9, 132.5, 135.2, 139.6, 140.9, 153.6, 157.8. The purity of the sample is higher than 99% (HPLC).
2.2 Characterizations
The morphology of BPTAP was analyzed by ZEISS Scanning Electron Microscopy (SEM) instrument (Germany).Thermal Gravimetric Analysis-Differential Scanning Calorimetry (TG-DSC) experiments were measured in the Al2O3 crucible at the heating rate of 5 °C min−1 (NETZSCH STA 449C). The Differential Scanning Calorimetry (DSC) experiments were measured separately in a non-hermetic or a hermetic vessel, under the heating rates of 2, 4, 6, 8 and 10 °C min−1, respectively (PerkinElmer DSC 8500). For all the DSC experiments, the temperature range was from 250 to 450 °C, while the mass of sample was about 1–2 mg and nitrogen was chosen as the protect gas with a flow rate of 30 mL min−1.
2.3 Kinetics analysis approach
Chemical reaction rates are usually considered to be a function of temperature T and chemical conversion α. The relationship combined with Arrhenius equation can be described as eqn (1):
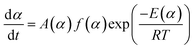 | (1) |
In order to know about the process rate and reaction progress at arbitrarily chosen values of temperature T or time t and predict some other parameters under any thermal mode (isothermal, non-isothermal, adiabatic, etc.), the model-free method, which does not require an explicit assumption of the form of f(α) and does not assume the constancy of A and E during the course of process, was employed in this work, firstly. The assumption for model-free analysis is the reaction rate at a constant value of conversion is only a function of temperature, which can be clearly described by the following eqn (2) that is obtained by taking the logarithmic derivative of eqn (1).
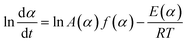 | (2) |
It should be noted that the pre-exponential factor A can be found by model-free analysis only assumption of known function f(α), which very often is used in the view of reaction of nth order in model-free analysis. The thermoanalytical signal is equal to the reaction rate, multiplied by the total effect of reaction, which is the total enthalpy for DSC. NETZSCH Kinetics Neo10-a popular thermokinetics software, was employed for model-free analysis.
And then the kinetics-based simulation which is an advanced and effective approach for solving complex challenge was employed for reliable estimation of the thermal safety of the HEMs. The first step is the evaluation of the kinetic model from the experimental data. As long as the precise reaction kinetics is obtained, safety parameters for the HEMs such as self-accelerating decomposition temperature (SADT) and time to maximum rate under adiabatic conditions (TMR) can be obtained. Being free of essential simplifications, this approach can be applied to a wide variety of practical problems.11,12 Of course, kinetics-based simulation approach is not for complete replacement of the model-free method. On the contrary, they mutually complement each other. In this paper, kinetics-based simulation was accomplished by the thermal safety software (TSS).13
The thermal safety software (TSS) series were employed to process experimental data for the estimation of the reaction kinetics and for the simulation of the reactions under various operation conditions and so on. For the key step of the creation for the kinetic model, a plausible reaction model was firstly created by taking into account the results of model-free analysis. Then the model's parameters were estimated by non-linear optimization method with the aim to provide the best possible fit for the experimental data. The detailed information about the kinetic model can be found in the ref. 14.
3. Results and discussion
3.1 Micrographs of BPTAP power
SEM characterization was applied to the BPTAP powder to show the microscopic structure of the BPTAP. As shown in the Fig. 2, the BPTAP powder exhibited a flower shaped crystal with an average size of 30 μm, which was assembled by BPTAP microsheets with lateral size of about 5 to 10 μm.3.2 Thermal behaviors of BPTAP
For the first stage study of the thermal behaviors of the BPTAP, typical TG-DSC curves for the decomposition process of the BPTAP in the non-hermetic vessel were obtained at the temperature rate of 5 °C min−1 (Fig. 3). It can be seen that there is only one mass loss in the temperature range from 333.9 to 410.5 °C during the decomposition of the BPTAP at heating rate of 5 °C min−1, which showed a mass loss of 55.5 wt% and a summit peak locating at 380.3 °C in DSC curve.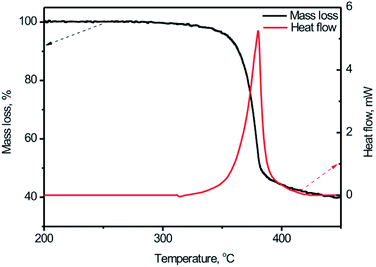 | ||
| Fig. 3 The TG-DSC curves for the BPTAP decomposition in the non-hermetic vessel at heating rate of 5 °C min−1. | ||
Afterwards the DSC study for the BPTAP sample was carried out in the closed and open vessels, respectively, to study and compare the decomposition process of the BPTAP under the non-hermetic and hermetic conditioning. As shown in Fig. 4, the decomposition of BPTAP sample in the hermetic vessel showed an exothermic process with onset temperature of the decomposition (Tonset) of 334.8 °C, peak temperature of the decomposition (Tpeak) of 379.7 °C and the enthalpy of conversion (ΔH) of 2255.9 kJ g−1, respectively. For comparison, the decomposition of the BPTAP sample in the non-hermetic vessel exhibited an exothermic process with Tonset of 345.7 °C, Tpeak of 384.8 °C and ΔH of 1792.3 kJ g−1, respectively. It can be seen that the Tonset of the BPTAP sample tested in the hermetic vessel was 10 °C lower than that of the BPTAP sample tested in the non-hermetic vessel. This is probably because volatile intermediates were formed during the thermal decomposition of BPTAP in the hermetic vessel, which can increase the pressure in the hermetic vessel and thus accelerate the decomposition of the BPTAP.
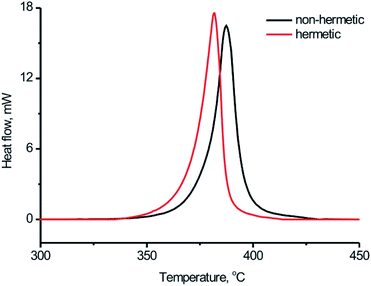 | ||
| Fig. 4 Typical DSC curves for the thermal decomposition process of BPTAP sample at the temperature rate of 8 °C min−1 in the hermetic and non-hermetic vessel. | ||
3.3 Thermal decomposition kinetics of BPTAP
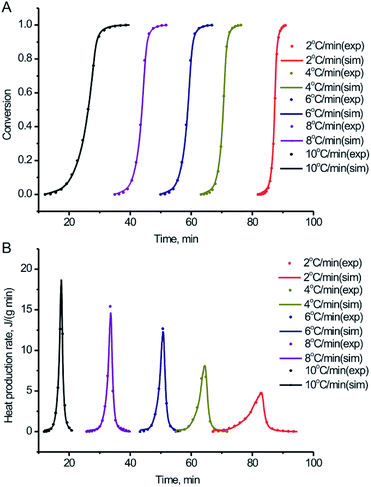
In order to further study the thermal decomposition kinetics of the BPTAP, DSC experiments were performed under different temperature rate in the non-hermetic and hermetic vessels, respectively. As shown in the Fig. 5, the Tonset, Tpeak and ΔH for the BPTAP decomposition in the non-hermetic or hermetic vessel were all increased with the higher heating rate. A one-stage decomposition process was observed for all the measurements. Using the obtained DSC results, the kinetic analysis of the thermal decomposition process was determined and further discussed in the following text, which involved two steps including the application of the model-free kinetics for preliminary analysis and then the creating of the reaction kinetic model by non-linear optimization method.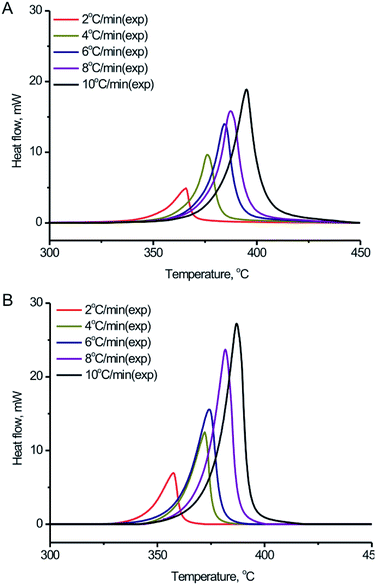 | ||
| Fig. 5 DSC curves of the BPTAP decomposition in (A) non-hermetic vessels and (B) hermetic vessels at temperature rates of 2, 4, 6, 8 and 10 °C min−1, respectively. | ||
Four model-free kinetics methods including Flynn–Wall–Ozawa, Kissinger, Freidman and numerical optimization15–18 were applied and compared the correlation coefficients by using NETZSCH Kinetics Neo software. The results based on the experimental DSC data in the non-hermetic vessel indicated that the obtained correlation coefficients when using Flynn–Wall–Ozawa, Kissinger, Freidman and numerical optimization methods were −0.788, −0.671, 0.940 and 0.996, respectively, which indicated that the numerical optimization method can provide the best results for the evaluation of the correlation coefficient. Therefore, the numerical optimization method was used and discussed in the following study.
Numerical optimization optimizes the activation energy and pre-exponential factor numerically to achieve the best agreement between simulated and experimental curves. There is no assumption about the reaction type. Based on the experimental DSC data under the different temperature rate in the non-hermetic vessel, the conversion and heat production rate were both calculated and fitted based on the numerical optimization method. From the Fig. 6 we can see that the experimental and simulated results exhibited a good fitting with the correlation coefficient of 0.996, which is very helpful for the following study of the activation energy, pre-exponential factor and the degree of the conversion. Similar work has been done for the experimental DSC data under the different temperature rate in the hermetic vessel, which showed a relatively lower correlation coefficient of 0.986 (Fig. S1†). This is probably because the sublimation of BPTAP in the hermetic vessel may lead to complex two-phase (solid and gas) decomposition reaction.
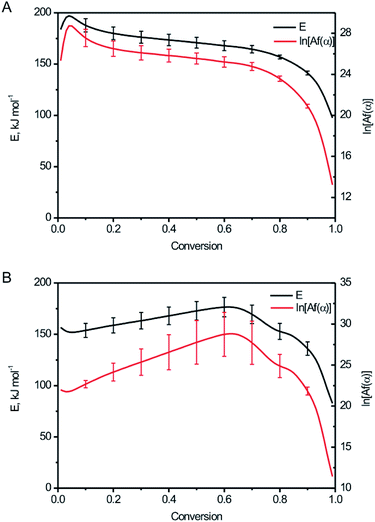
The relationship between the activation energy (E), ln[Af(α)] and degree of the conversion (α) for BPTAP were shown in Fig. 7. The conversions within the range 0.1–0.9 were used for calculation.19,20 It can be seen from Fig. 7A that the E value between α = 0.1 to α = 0.7 was not changed obviously based on DSC experiment tests in the non-hermetic vessel, which implies that the decomposition of BPTAP under the non-hermetic conditioning is a single-step process. Then a rapid decrease of E occurred from α = 0.7 to α = 0.9 and the lowest E is about 141.25 kJ mol−1, which is probably attributed to the generation of large amounts of product catalyst. However, there was a dramatically change of the E value based on DSC experiment tests in the hermetic vessel (Fig. 7B), which implies that the decomposition of BPTAP under the hermetic conditioning is a complex process.
As shown in Fig. 5A, Tonset increases with the increase of heating rates, this characteristic of dynamic DSC experimental results clearly reveals autocatalytic nature of the reaction,22 and the results of the model-free analysis also implied that the decomposition of BPTAP under the non-hermetic conditioning is a single-step process. Therefore the model of generalized autocatalysis is chosen for describing thermal decomposition of BPTAP. It is represented by eqn (3):
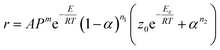 | (3) |
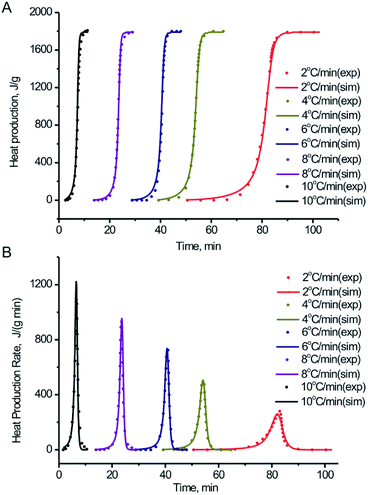 | ||
| Fig. 8 Comparison between experiment tests in the non-hermetic vessel and simulation of: (A) heat production vs. time for BPTAP; (B) heat production rate vs. time for BPTAP. | ||
According to Fig. 8, the TSS simulation results show a reasonable fitting of the DSC experimental data under various heating rate. It indicates that the reaction model is suitable for BPTAP. Therefore, the decomposition of BPTAP under the non-hermetic conditioning is considered as the generalized autocatalytic reaction. The kinetic parameters of the reaction model for BPTAP are shown in Table 1. The E and A values are in good accordance with the results using numerical optimization method (Fig. 7). The decomposition of BPTAP under the hermetic conditioning is determined as two parallel generalized autocatalytic reactions. Fig. S2 and Table S1† showed the TSS simulation results using the DSC experiments taken in hermetic condition and the corresponding kinetic parameters. The determined kinetic model and kinetic parameters of the reaction process were used to estimate the safety of material.
| Parameters | Units | Autocatalytic |
|---|---|---|
| ln(A) | ln(s−1) | 30.21 |
| Ea | kJ mol−1 | 182.25 |
| n1 | — | 1.17 |
| n2 | — | 1.54 |
| ln(z0) | — | −3.55 |
| Ez | kJ mol−1 | 0.74 |
| m | — | 0.05 |
| Q | kJ kg−1 | 1785.54 |
3.4 Safety analysis
It is known that the DSC experimental results can't be directly applied to industrial production due to heat accumulation in large amount of substance, while DSC experiments are carried out with mg-scale samples. However, the kinetic model can be employed for prediction and simulation to evaluate the thermal safety, because the kinetics of any reaction doesn't depend on the sample mass.23Based on the kinetic model and kinetic parameters of the decomposition process determined in the measurements taken in non-hermetic and hermetic vessels, applying kinetic simulation by means of TSS software, thermal safety of BPTAP was predicted, respectively.
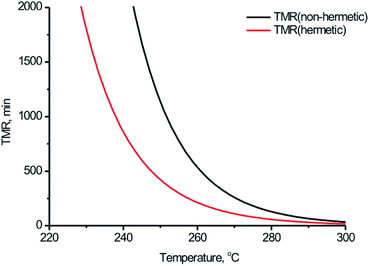
Thermal safety of BPTAP can be implemented by estimating adiabatic time to maximum rate (TMR). TMR is determined from the self-heating rate (dT/dt) for a reaction course as the time instant that corresponds to maximal value of (dT/dt). The dependency of TMR on the onset temperature estimated by simulation based on the kinetic model determined in the measurements taken in non-hermetic and hermetic vessels was shown in Fig. 9, from which we can conclude that the starting temperatures strongly influenced the time to the rate of the temperature evolution under adiabatic conditions and the temperatures when the occurrence of thermal decomposition after 24 hours (Td,24)24,25 of BPTAP based on the kinetic model determined in the measurements taken in non-hermetic and hermetic vessels were 246.91 °C and 238.47 °C, respectively. It can be seen that the Td,24 of the BPTAP based on the kinetic model determined in the measurements taken in the hermetic vessel was lower than that of the BPTAP based on the kinetic model determined in the measurements taken in the non-hermetic vessel. This is probably because the Tonset of the BPTAP sample tested in the hermetic vessel was 10 °C lower than that of the BPTAP sample tested in the non-hermetic vessel, which decreased the safety of BPTAP.
SADT, which is defined as the temperature of self-accelerating decomposition for different packages of chemical, is also an important parameter for safety assessment. More specifically, it is the lowest temperature at which an overheating in the middle of specific packaging exceeds 6 °C after a lapse of the period of 7 days or less, which is measured from the time when the packing center temperature reaches 2 °C below the surrounding temperature.26 SADT for BPTAP in DEWAR (simulation of the heat accumulation H4 test, UN Recommendations on the Transport of Dangerous Goods, Manual of Tests and Criteria27) has been simulated by Termex software (one module of TSS series). The detailed parameters of reactor description were listed in Table 2. Based on the kinetic model determined in the measurements taken in non-hermetic and hermetic vessels, the SADT values of BPTAP stored in such barrel were calculated, which amounted to 242 °C and 228 °C, respectively. The determined temperature values are very high, which confirms the high thermal stability of BPTAP.
| Geometry | Barrel | ||
| External dimensions | Radius (m) | 0.041 | |
| Height (m) | 0.1222 | ||
| Void fraction | 0 | ||
| Barrel lid description | Top lid | Type | Flat |
| Height (m) | 0 | ||
| Bottom lid | Type | Spherical | |
| Height (m) | 0.02 | ||
| Shell | Material | Steel | |
| Thickness (m) | 0.001 | ||
4. Conclusions
In conclusion, thermal decomposition, kinetic parameters and safety assessment of BPTAP under non-hermetic and hermetic conditions were reported in detail. The thermal decomposition of BPTAP exhibited one main mass loss process. By using and comparing several widely used thermoanalytical data processing techniques based on model-free kinetics, the relationship between the activation energy E, ln[Af(α)], and conversion α for BPTAP was obtained. Based on the non-linear optimization method, the non-isothermal kinetic models of the exothermic process under non-hermetic and hermetic conditions were evaluated. On the basis of the determined kinetic models, the simulation results showed that the Td,24 values of BPTAP were 246.91 °C and 238.47 °C, respectively. The calculated SADT values of BPTAP in DEWAR were 242 °C and 228 °C, respectively. The determined safety parameters based on the kinetic model determined in the measurements taken in non-hermetic and hermetic vessels have certain differences. This is probably because volatile intermediates were formed during the thermal decomposition of BPTAP in the hermetic vessel, which can increase the pressure in the hermetic vessel and thus accelerate the decomposition of the BPTAP, to further decrease the assessment safety of BPTAP.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is financially supported by the National Nature Science Foundation of China (No. 61701459).References
- T. Chang, B. Li, L. Chen, L. Ge and M. Lu, Cent. Eur. J. Energ. Mater., 2017, 14, 47 CrossRef CAS.
- U. R. Nair, G. M. Gore, R. Sivabalan, S. J. Pawar, S. N. Asthana and S. Venugopalan, J. Hazard. Mater., 2007, 143, 500 CrossRef CAS.
- T. Gołofit and M. Szala, J. Therm. Anal. Calorim., 2017, 130, 2047 CrossRef.
- Nuclear Weapons Journal, Issue 1, 2006.
- Ł. Gutowski, W. Trzciński and M. Szala, Chempluschem, 2018, 83, 87 CrossRef.
- J. Zhou, L. Ding, F. Bi, B. Wang and J. Zhang, J. Anal. Appl. Pyrolysis, 2018, 129, 189 CrossRef CAS.
- P. Pagoria, Propellants, Explos., Pyrotech., 2016, 41, 452 CrossRef CAS.
- N. N. Semsenov, Chemical kinetics and chain reactions, Oxford University Press, London, 1935 Search PubMed.
- M. H. V. Huynh and M. A. Hiskey, J. Energ. Mater., 2004, 22, 109 CrossRef CAS.
- NETZSCH site, https://kinetics.netzsch.com/en/.
- A. Kossoy, A. Benin and Y. Akhmetshin, J. Hazard. Mater., 2005, 118, 9 CrossRef CAS PubMed.
- M. H. Yuan, C. M. Shu and A. Kossoy, Thermochim. Acta, 2005, 430, 67 CrossRef CAS.
- CISP site. http://www.cisp.spb.ru/tss.
- A. Kossoy and Y. Akhmetshin, Process Saf. Prog., 2007, 263, 209 CrossRef.
- H. L. Friedman, J. Polym. Sci., Part C: Polym. Symp., 1964, 183 CAS.
- D. M. Badgujar, M. B. Talawar, S. N. Asthana and P. P. Mahulikar, J. Hazard. Mater., 2008, 151, 289 CrossRef CAS.
- J. H. Yi, F. Q. Zhao, S. Y. Xu, L. Y. Zhang, H. X. Gao and R. Z. Hu, J. Hazard. Mater., 2009, 165, 853 CrossRef CAS.
- H. X. Ma, J. R. Song, H. M. Xiao, R. Z. Hu, H. L. Wang, P. G. Jin and Y. Wang, J. Hazard. Mater., 2006, 128, 116 CrossRef CAS.
- G. B. Lu, T. Yang, L. P. Chen, Y. S. Zhou and W. H. Chen, J. Therm. Anal. Calorim., 2016, 124, 471 CrossRef CAS.
- J. Y. Lv, W. H. Chen and L. P. Chen, J. Ind. Eng. Chem., 2013, 11, 4054 Search PubMed . (in Chinese).
- J. D. Sewry and M. E. Brown, Thermochim. Acta, 2002, 390, 217 CrossRef CAS.
- L. Bou-Diab and H. Fierz, Proceedings of the 10th International Symposium (2001), Elsevier, Stockholm, Sweden, 2001 Search PubMed.
- B. Roduit, Ch. Borgeat and B. Berger, J. Therm. Anal. Calorim., 2005, 80, 91 CrossRef CAS.
- T. Grewer, H. Klusacek, U. Löffler, R. L. Rogers and J. Steinbach, J. Loss Prev. Process Ind., 1989, 2, 215 CrossRef.
- T. Lakshminarasimhan, Org. Process Res. Dev., 2014, 18, 315 CrossRef CAS.
- H. Niu, S. S. Chen, S. H. Jin, L. J. Li, B. C. Jing, Z. M. Jiang, J. W. Ji and Q. H. Shu, J. Therm. Anal. Calorim., 2016, 126, 473 CrossRef CAS.
- A. A. Kossoy and I. Y. Sheinman, J. Hazard. Mater., 2007, 142, 626 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c9ra03385h |
| This journal is © The Royal Society of Chemistry 2019 |