Open Access Article
Open Access ArticleCrystal structure of vyacheslavite, U(PO4)(OH), solved from natural nanocrystal: a precession electron diffraction tomography (PEDT) study and DFT calculations†
Gwladys Steciuka,
Seyedayat Ghazisaeedb,
Boris Kieferb and
Jakub Plášil *a
*a
aInstitute of Physics, Academy of Sciences of the Czech Republic, v.v.i, Na Slovance 2, Prague 18221, Czech Republic. E-mail: plasil@fzu.cz
bDepartment of Physics, New Mexico State University, Las Cruces, NM 88003, USA
First published on 24th June 2019
Abstract
The crystal structure of the U(IV)-phosphate mineral vyacheslavite has been solved from precession electron diffraction tomography (PEDT) data from the natural nano-crystal and further refined using density-functional theory (DFT) calculations. Vyacheslavite is orthorhombic, with the space group Cmca, with a ≈ 6.96 Å, b ≈ 9.07 Å and c ≈ 12.27 Å, V ≈ 775 Å3 (obtained from PEDT data at 100 K), Z = 8. Its structure is a complex heteropolyhedral framework consisting of sheets of UO7(OH) and PO4 polyhedra, running parallel to (001), interconnected by additional PO4 polyhedra. There is an (OH) group associated with the U(IV) polyhedron. The question of H2O presence within the small cavities of the framework has been addressed by the DFT calculations, which have proved that vyacheslavite does not contain any significant amount of H2O at room temperature.
Introduction
Uranium is tetravalent and is typical namely for primary minerals, such as uraninite, UO2+x (always containing some U as hexavalent) or coffinite, USiO4. It is due to the easy oxidation transformation of U(IV) to U(VI) when in contact with oxygen. Two U(IV) phosphates without additional metal cations are known from nature. They form as products of a back-reduction of U(VI) to U(IV) in the supergene enrichment areas of the oxidation zones of U deposits. Those are lermontovite, ideally UIV(PO4)(OH)(H2O), and vyacheslavite, UIV(PO4)(OH)(H2O)n.1–3 Despite the fact that under the circumstances both of them, together with, e.g. ningyoite, CaUIV(PO4)2(H2O)2, coffinite and uraninite, can form secondary deposits of economic importance,4 both of them still remain poorly defined. The fact that these alteration products are usually poorly crystalline or only form nano-crystalline structures prevents them from being characterized in detail since they do not provide reasonable single-crystal or powder diffraction patterns. Vyacheslavite was recognized as the new mineral species from the second-enrichment zone of U deposits in the Auminzatau Mountains, Kyzylkum Desert, Uzbekistan.2 The mineral forms green aggregates on quartz closely associated with pyrite, which suggests strongly reducing conditions that took place during its formation. The electron diffraction data provided by the original paper indicate vyacheslavite to be orthorhombic, with possible space groups Cmcm, Cmc21 or C2cm, with unit-cell parameters a = 6.96(1) Å, b = 9.10(1) Å, c = 12.38(1) Å.2 In that work, there is a description of two vyacheslavite varieties: a green and a dark-green one. The distinctive hydration state is reported for them (expressed as nH2O in the corresponding formulae): 2.19 and 2.70 for the green variety and 0.35 for the dark variety. It should be mentioned that these values were not obtained by direct determinations (e.g., by thermogravimetry) but via a difference in the chemical analyses only.Here we report the first structure determination of vyacheslavite from natural nano-crystals using precession electron diffraction tomography (PEDT) method. It provided a complete structure model including the position of the H atom. Moreover, we carried out Density-Functional-Theory (DFT) calculations documenting, unlike previous results that vyacheslavite should not contain any molecular H2O since the uptake, even small, is endothermic.
Materials and methods
Sample
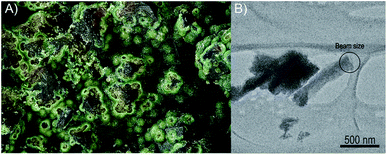
The sample investigated in this study was removed from the specimen containing vyacheslavite that originates from the Menzenschwand (Krunkelbach) uranium deposit, Black Forest Mountains, Germany. The matrix of the specimen consists of quartz, which crystallized into cavities. The pyramidal terminations of quartz are covered by limonite overgrown by dark-green to the green crust of vyacheslavite (Fig. 1A). The nanocrystal used in this study (Fig. 1B) was separated from the dark-green parts of the crust.Single-crystal electron diffraction
For transmission electron microscopy (TEM) investigations, small pieces of vyacheslavite crystals were mildly crushed and deposited on a Cu-grid with a thin film of holey amorphous carbon. The grid was plunged into liquid nitrogen and then transferred to a Philips CM120 electron transmission microscope (TEM) (acceleration voltage of 120 kV, LaB6) using a Gatan cryo-transfer holder. Precession electron diffraction tomography (PEDT) data sets of non-oriented patterns were recorded at 100 K on several crystals with the precession device Nanomegas Digistar and a side-mounted CCD camera Olympus Veleta with 14 bit dynamic range. The precession angle was set to 1° and a tilt step of 1° as well. A condenser aperture of 10 μm and low illumination setting (spot size 7) were used to reduce the electron dose. PEDT data were analyzed using computer programs PETS and Jana2006.5,6 For each data set, the result is a list of hkl-indices with associated intensities and estimated standard deviations based on counting statistics. The analysis of the PEDT data at 100 K gives an orthorhombic unit cell with a ≈ 6.96 Å, b ≈ 9.07 Å and c ≈ 12.27 Å that is consistent with the previous works on synthetic vyacheslavite at 298 K: a = 7.0100(2) Å, b = 9.1200(2) Å, c = 12.3665(3) Å.7–9 The space group Cmca was also confirmed from the sections of the reciprocal space built in the PETS program (Fig. S1†). The structure was solved ab initio with the program Superflip in Jana2006 using the kinematical approximation.10 The dynamical refinement against PEDT data was performed in order to reveal the missing hydrogen atom position. Despite its weak scattering power, the possibility to obtain hydrogen positions from the dynamical refinement using PEDT data has been demonstrated, already.11 Three data sets were combined and the parameters used to select the reflections involved in the dynamical refinement were chosen following the suggestions given in:12,13 RSg(max) = 0.6, Sg(max) (matrix) = 0.01 Å−1, g(max) = 1.8 Å−1. The refinement parameters as well as the refined structural parameters are given in ESI (Tables S1 and S2†). The dynamical refinement converged to R(obs) = 0.0888 and wR(obs) = 0.0841 for 4010 reflections. The position of the hydrogen atom is apparent from the difference potential map where one weak maximum is found ≈0.81 Å far from O4 (see Fig. 2). The possibility to see a residual potential related to hydrogen among heavy atoms like uranium is not as obvious as in previous works on materials containing lighter atoms.11,14 However, this maximum corresponds to an ideal O–H distance and the hydrogen position is also supported by the DFT computations. Because of the presence of uranium, a further refinement including hydrogen is not significant and does not provide any improvement of further information.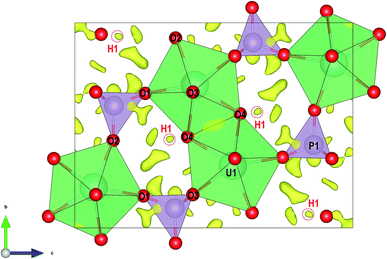 | ||
| Fig. 2 Structure of vyacheslavite viewed along the [001] direction. Superimposed is a difference-Fourier map of electron-density, with highlighted maxima corresponding to H1 atom. | ||
Density-functional theory (DFT) calculations
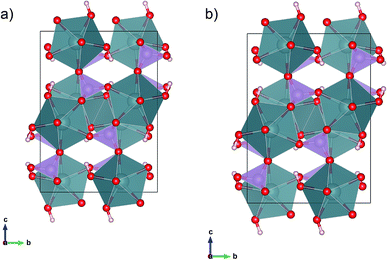
We augmented out experiments with density-functional-theory (DFT) computations to validate the structure refinements.15,16 All computations are performed within the context of 3D periodic DFT as implemented in the software package VASP.17 Electrons were treated within the all-electron like PAW framework.18,19 The plane-wave cutoff energy Ecut = 520 eV, was adopted following previous computations on UO2.20 The k-point grid was chosen as 4 × 4 × 2, taken into account the asymmetry of the lattice. DFT computations result in a metallic ground state, inconsistent with the green crystal colour. However, charge neutrality suggests that uranium is in an open shell +4 oxidation state. Therefore, we adopted a Hubbard+U approach to treat the open shells on uranium.21 We tested two sets of Hubbard+U parameters, U − J = 3 eV, and U − J = 6 eV, and applied to the uranium 5f-states. Both sets share, that crystals are predicted to be insulating and that the magnetic moment is largely confined to uranium. The computed magnetic moment per uranium ion is m = 2 μB, consistent with two unpaired electrons and an uranium +4 oxidation state. Moreover, our computations show that the finite atomic magnetic moment can be attributed to the uranium f-shell. Since the results for the two Hubbard+U parameter sets are indistinguishable, we report below only results for U − J = 3 eV. The void spaces in vyacheslavite may accommodate water molecules and the formation of an extended hydrogen bonding network is possible. In order to address water solubility in vyacheslavite we included van der Waals corrections as parameterized within the opt88-vdW functional.22 Unless noted otherwise, we fixed the simulation cell at the experimental geometry. In addressing the water solubility in vyacheslavite, an initial model of the water array is needed. For this purpose, we adopted a two-step process. In the first step we placed the oxygen in the water molecules and for fixed oxygen location we found the rotational equilibrium orientation of the water molecules based on electrostatic forces and derived torques (we assumed a TIP3P water model and formal charges of +4, +5, +1, and −2, for U, P, H, and O, respectively), using the TORQUE method.23 We determined the rotational equilibrium for 150 randomly chosen initial water configurations, in order to identify possible different water orientations. In a second step, we determined the H2O position using DFT+U+vdW. Since the structure models obtained at different levels of the DFT theory calculations are differing only insignificantly (Fig. 3a and b), we further report (atom coordinates) the DFT+U model, only. Results of the DFT calculations are given in the ESI (Tables S3a, b, S4a and b†).Results
General structural architecture as revealed from PEDT
The structure of vyacheslavite revealed from electron-diffraction data contains one U site, one P site, four O sites, and one H site. The structural model obtained at 100 K is similar to the model at the room temperature for the synthetic phase.9 At our case, the bond-valence calculations and stoichiometry considerations suggest that H-atom missing in the previous determination is associated with the O4 position and was successfully localized from the precession electron diffraction tomography data and subsequently confirmed by our DFT computations.The structure of vyacheslavite contains UIV cation coordinated in the form of a distorted square antiprism. One of the ligands is, in fact, a protonized O atom (O4); thus, the UO7(OH) polyhedra share edges with each other and adjacent PO4 tetrahedra to form chains extending parallel to [100]. The chains polymerize along the [010] by sharing edges between UO7(OH) polyhedra, and by UO7(OH) polyhedra sharing corners with the PO4 tetrahedra of the adjacent chains. The structure thus contains complex uranium phosphate sheets running parallel to (001). These are interlinked by PO4 tetrahedra that share corners with UO7(OH) polyhedra from the next layer. The result is a framework, which contains cavities (of ∼2 Å in diameter) that may host some H2O. Nevertheless, no assignable residual electron density could be reasonably associated with additional O atoms (Fig. 2). The structural formula obtained for the natural vyacheslavite is, therefore, UIV(OH)(PO4), Z = 8. Based on the structure study of natural nanocrystal it is not likely that vyacheslavite contains H2O.
Crystal structure based on DFT calculations
DFT computations were used to address the stability of the crystal structure. For simplicity, we did not include any interstitial water molecules (see below) and addressed the geometry of the O–H group only. Placing hydrogen in a general (8f) site allows for multiple solutions describing a cone with the oxygen at its apex. We constraint the initial O–H vector to be parallel to [001] and having a length of 1.0 Å. During the relaxation, the hydrogen rotated in the (y, z)-plane, to a final position ∼ 21.0° off the [001] axis. In order to test the uniqueness of our DFT solution, we performed a second calculation, where the initial H–O vector was constraint to the (y, z)-plane as well but on the opposite side of the intersection of the (y, z)-plane and the cone. Upon relaxation, the O–H vector rotated back to the first solution. This result can be rationalized by considering the bond geometry of the unstable site, that is characterized by a comparatively short and repulsive d(U⋯H) = 2.35 Å. If released from this (unstable) position, the hydrogen bond array evolves toward a lower energy state that is 17 meV per hydrogen lower in energy and d(U⋯H) = 2.95 Å. The final orientations of the O–H vectors differ by less than 0.003 Å with an average final 8f position of (0, 0.399, 0.668). The vdW corrected computations corroborate the presence of a single position-H orientation. Thus, the DFT computations support the existence of a single fully occupied hydrogen (8f) site for –OH formation, consistent with our electron diffraction observations (Fig. 3a and b).Uptake of H2O based on DFT calculations
The determination of water solubility depends on the balance of chemical potentials of water in the crystal and water in the surrounding chemical environment. Our X-ray and electron diffraction observations do not show any evidence for extensive intercrystalline H2O. We performed two sets of computations to shed light on the water solubility: DFT+U only, as well as DFT+U+vdW. In contrast to the –OH hydrogen placement, described above, with a strong affinity for single oxygen, H2O is a charge neutral molecular unit that is bonded to the surrounding crystal through hydrogen bonds. To place the H2O molecules in a rational fashion, we placed its oxygen at the (8e) site and explored the initial water orientation of eight water molecules through the TORQUE method.23,24 We tested 150 randomly chosen initial orientations to explore the possibility of multiple equilibrium orientations. The analysis shows the existence of two equilibrium orientations that are symmetrically related through an inversion operation about the oxygen in each water molecule. Each hydrogen bond array (8H2O molecules) consists of hydrogen atoms in (16g) sites, and the two hydrogen atoms per water molecule are connected to surrounding crystal by d(O–H⋯O) = 1.29 Å and 1.68 Å and O–H⋯O angles of 160° and 155°, respectively. Since the two equilibrium orientations are symmetrically equivalent, we picked one and generated the remaining hydrogen atoms by applying the space group operations to this set. The resulting eight H2O configurations were used as the initial configuration for our DFT computations: we retained subsets of these eight water molecules to explore the energetics of water solubility, similar to that given elsewhere.25 We performed computations for 0, 1, 2, 3, and 8 water molecules in the unit cell, at the DFT+U+vdW level, where only water molecules are relaxed for otherwise fixed experimental structure, we find that water solubility is an unfavourable endothermic process. Thus, the water solubility is predicted to be zero. If the structure is allowed to relax for fixed lattice, we observe a limited solubility of water with a maximum of stabilization energy of ∼0.28 eV/H2O for 2H2O molecules in the unit cell. The hydrogen bonding array is slightly asymmetric, d(O–H1) = 0.979 Å, d(H1⋯O) = 2.10 Å; and d(O–H2) = 1.019 Å, and d(H2⋯O) = 2.09 Å. Moreover, for the H2 atom, we find an additional short H2⋯O bond of length 1.52 Å, which links the water molecules to the hydroxyl group coordinating uranium, and explains the unequal intramolecular O–H bond length. If the water content is increased to 3H2O, we find that the average (H⋯O) distance increases to 1.64 Å. This 7.7% increase of d(H⋯O), attributed to increased repulsion between like ion pairs, leads to a less favourable energy for water solubility. Therefore, even without vibrational effects, the solubility is not expected to extend beyond 3/8 H2O molecules pfu, leading to the nominal chemical formula: U(PO4)(OH)·0.375H2O. Thus, the water solubility may be over-estimated by energy-only based calculation, since entropy is expected to facilitate H2O release with increasing temperature. Moreover, allowing for relaxation of atomic positions for fixed experimental lattice shows that the H2O molecule migrates to the nearest uranium atom and increases its coordination number from 8 to 9, an effect of the small size of the cavity. For computation with the n = 8 case, d(U–O) ranges from 2.198 Å to 2.782 Å, and the U–OH2 bond length is 2.595 Å. Furthermore, if we consider the oxygen coordination of the ninth coordinating oxygen (OH2), we can estimate local distortions. For the PEDT refined structure (Tables S1 and S2†) we identified the (four) oxygen ions of the uranium polyhedra that form the neighbours in the corresponding n = 8 computation of OH2. The four O–O distances are: 2.804 Å, 3.109 Å, 2.674 Å, and 2.980 Å. The corresponding distances for n = 8 are 3.010 Å, 3.587 Å, 2.718 Å, and 3.334 Å, with distortions that could be as high as ∼14% of the bond length. Such a large distortion is far beyond the PEDT resolution limit and would have been resolved during our structure refinement. Even in the case of n = 1, we find significant distortions, 2.848 Å, 3.548 Å, 2.718 Å, and 3.334 Å. To conclude, the energetics obtained from the DFT computations support low if any water solubility at room temperature, consistent with our PEDT observations. Similarly, the DFT calculations predict significant changes of some of the U–O bond distances, and a coordination change from 8 to 9. None of these predicted changes has been observed in our experiments providing further evidence of very limited if any H2O solubility in vyacheslavite.Implications
Current structure determination on vyacheslavite proved that the crystal data given originally were correct and that natural vyacheslavite has the same structure as the synthetic phase and contains small cavities that occasionally may host some molecular H2O. Nevertheless, based on DFT calculations the water uptake at room temperature is not thermodynamically favoured. Furthermore, our conclusions have not closed the controversy between the status of vyacheslavite and lermontovite as mineral species. Lermontovite is reported to have a formula UIV(PO4)(OH). H2O, thus only slightly differing from that of vyacheslavite, nevertheless its structure remains unknown.26 Although based on current results, it is clear that the structure of lermontovite is entirely different from that of vyacheslavite, the volume of the cavity that can potentially host some additional H2O in vyacheslavite-like structures is small. Therefore we conclude that lermontovite is most probably based upon sheet structure, similarly to, e.g., běhounekite,27 since the reported unit-cell volume of lermontovite, ∼1850 Å3,28 is much higher than that of vyacheslavite, ∼780 Å3. Furthermore, the type material for lermontovite is not defined; therefore the conclusions of the original analyses cannot be verified.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Stephan Wolfsried (Waiblingen, Germany) is thanked for providing us a microphotography of vyacheslavite specimen. We thank Lukáš Palatinus (Institute of Physics, ASCR, v.v.i, Prague, Czechia) for discussions on processing of electron diffraction tomography data. This research was financially supported by the project of the Czech Science Foundation (project GACR 17-09161S) to JP; BK and SG would like to acknowledge the Extreme Science and Engineering Discovery Environment (XSEDE) resource Stampede II at the University of Texas at Austin through allocation DMR TG-110093.References
- V. G. Melkov, L. N. Belova, A. I. Gorshkov, O. A. Ivanova, A. V. Sivtsov and V. A. Voronikhin, Mineral. Zh., 1983, 5, 82 CAS.
- L. N. Belova, A. I. Gorshkov, O. A. Ivanova, A. V. Sivtsov, L. I. Lizorkina and V. A. Voronikhin, Zap. Ross. Mineral. O-va., 1984, 113, 360 CAS.
- S. V. Krivovichev and J. Plášil, in Uranium: from Cradle to Grave, ed. P. C. Burns and G. E. Sigmon, MAC Short Course, 2013, vol. 43, pp. 15–119 Search PubMed.
- O. A. Doynikova, Geol. Ore Deposits, 2007, 49, 80 CrossRef.
- L. Palatinus, PETS: program for analysis of electron diffraction data, Institute of Physics of the ASCR, Prague, Czechia, 2011 Search PubMed.
- V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr., 2014, 229, 345 Search PubMed.
- J. H. Albering and W. Jeitschko, Z. Kristallogr., 1995, 210, 878 CAS.
- P. Benard, D. Louer, N. Dacheux, V. Brandel and M. Genet, An. Quim. Int. Ed., 1996, 92, 79 CAS.
- N. Dacheux, N. Clavier, G. Wallez and M. Quarton, Solid State Sci., 2007, 9, 619 CrossRef CAS.
- L. Palatinus and G. Chapuis, J. Appl. Crystallogr., 2007, 40, 786 CrossRef CAS.
- L. Palatinus, P. Brázda, P. Boullay, O. Perez, M. Klementová, S. Petit, V. Eigner, M. Zaarour and S. Mintová, Science, 2017, 355, 166 CrossRef CAS PubMed.
- L. Palatinus, V. Petříček and C. A. Corrêa, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 235 CrossRef CAS PubMed.
- L. Palatinus, C. A. Corrêa, G. Steciuk, D. Jacob, P. Roussel, P. Boullay, M. Klementová, M. Gemmi, J. Kopeček, M. C. Domeneghetti, F. Cámara and V. Petříček, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 740 CrossRef CAS PubMed.
- T. Gruene, J. T. C. Wennmacher, C. Zaubitzer, J. J. Holstein, J. Heidler, A. Fecteau-Lefebvre, S. De Carlo, E. Müller, K. N. Goldie, I. Regeni, T. Li, G. Santiso-Quinones, G. Steinfeld, S. Handschin, E. van Genderen, J. A. van Bokhoven, G. H. Clever and R. Pantelic, Angew. Chem., Int. Ed., 2018, 57, 16313 CrossRef CAS PubMed.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, 864 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 137, 1697 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. C. Crowhurst, J. R. Jeffries, D. Åberg, J. M. Zaug, Z. R. Dai, W. J. Siekhaus, N. E. Teslich, K. S. Holliday, K. B. Knight, A. J. Nelson and I. D. Hutcheon, J. Phys.: Condens. Matter, 2015, 27, 265401 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505 CrossRef CAS.
- J. Klimeš, D. R. Bowler and A. Michaelides, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef PubMed.
- S. Ghazisaeed, J. Majzlan, J. Plášil and B. Kiefer, J. Appl. Crystallogr., 2018, 51, 1116 CrossRef CAS.
- S. Ghazisaeed, B. Kiefer and J. Plášil, RSC Adv., 2019, 9, 10058 RSC.
- J. Plášil, J. Majzlan, M. Wierzbicka-Wieczorek and B. Kiefer, Mineral. Mag., 2015, 79, 1159 CrossRef.
- V. Brandel and N. Dacheux, J. Solid State Chem., 2004, 177, 4755 CrossRef CAS.
- J. Plášil, K. Fejfarová, M. Novák, M. Dušek, R. Škoda, J. Hloušek, J. Čejka, J. Majzlan, J. Sejkora, V. Machovič and D. Talla, Mineral. Mag., 2011, 75, 2739 CrossRef.
- V. G. Melkov, L. N. Belova, A. I. Gorshkov, O. A. Ivanova, A. V. Sivtsov and V. A. Boronikhin, Mineral. Zh., 1983, 5, 82 CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Atom positions, equivalent and anisotropic displacement parameters, and interatomic distances; crystallographic information file. CCDC 1916477. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c9ra03694f |
| This journal is © The Royal Society of Chemistry 2019 |